A Semi-Discretization Method Based on Finite Difference and Differential Transform Methods to Solve the Time-Fractional Telegraph Equation
Abstract
1. Introduction
2. Fractional Differential Transform Method
- (a)
- if , then ,
- (b)
- if , then , where
- (c)
- if , then ,
- (a)
- and α arbitrary or
- (b)
- , γ arbitrary, and for , where .
3. FD-FDTM for Solving the FTE
4. Convergence of FD-FDTM for FTE
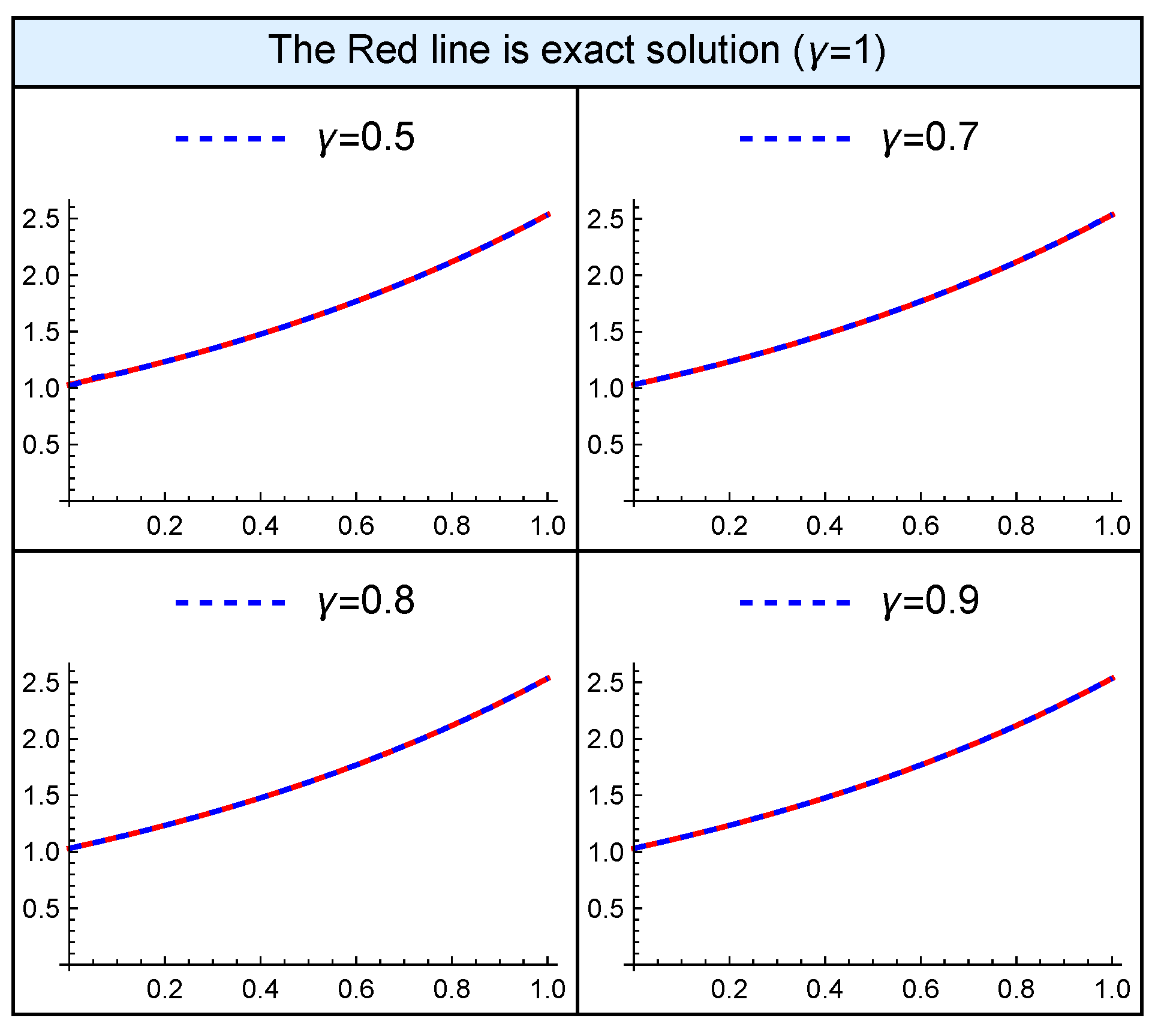
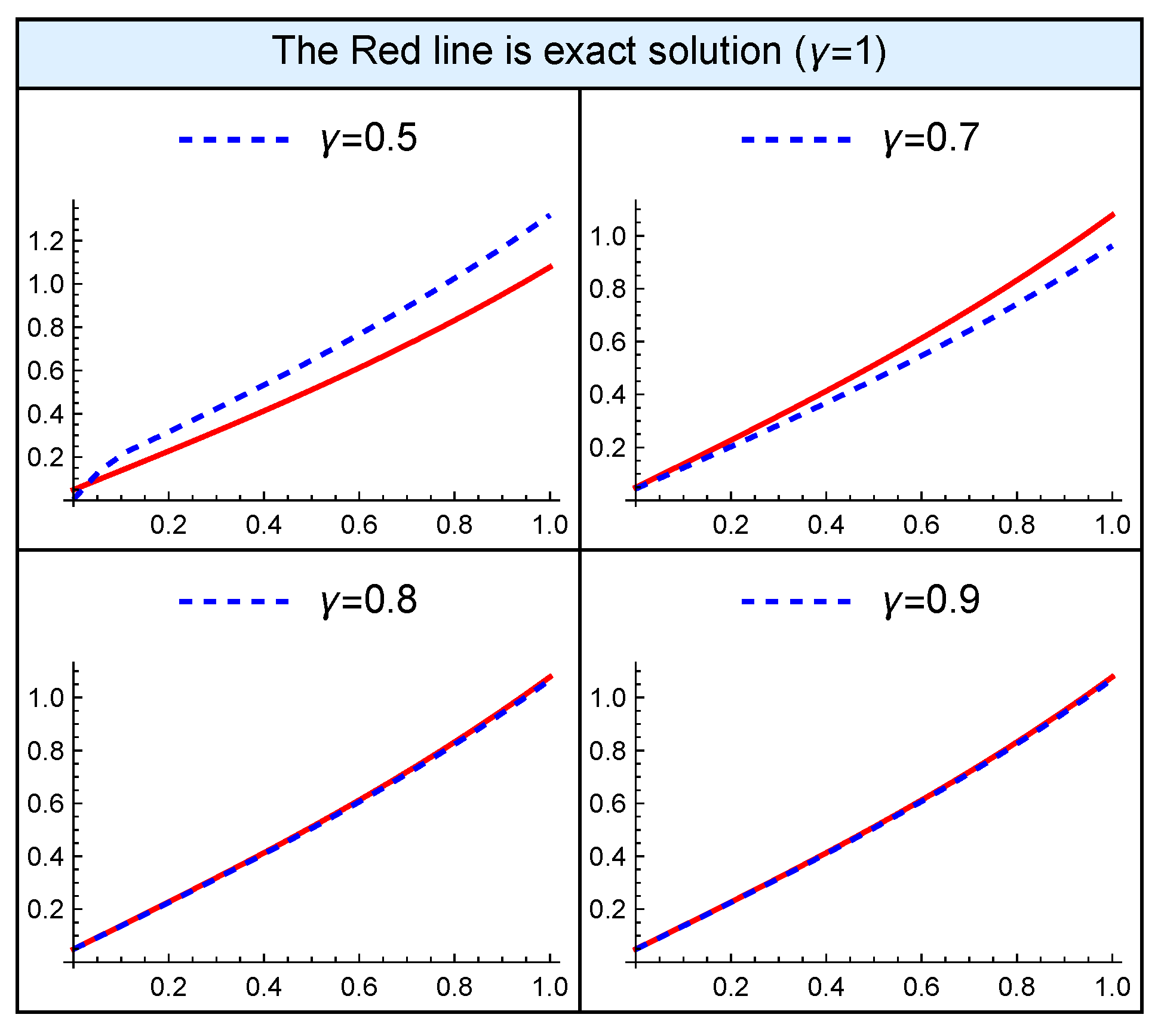
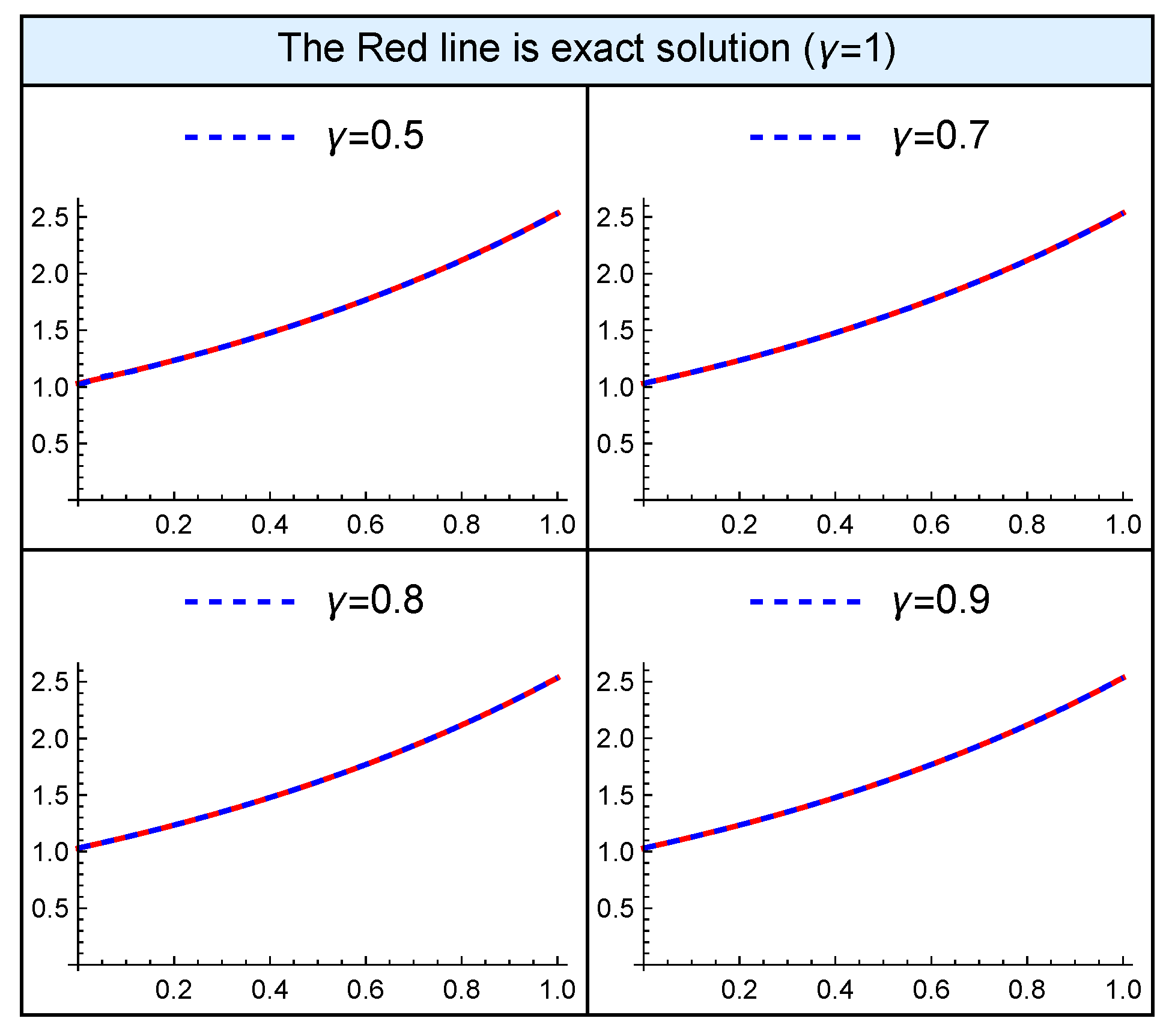
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, C.K.; Ho, S.H. Application of differential transformation to eigenvalue problems. Appl. Math. Comput. 1996, 79, 173–188. [Google Scholar] [CrossRef]
- Zhou, J.K. Differential Transformation and Its Applications for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986. [Google Scholar]
- Jang, M.J.; Chen, C.L.; Liy, Y.C. On solving the initial-value problems using the differential transformation method. Appl. Math. Comput. 2000, 115, 145–160. [Google Scholar] [CrossRef]
- Ayaz, F. Applications of differential transform method to differential-algebraic equations. Appl. Math. Comput. 2004, 152, 649–657. [Google Scholar] [CrossRef]
- Hassan, I.A.H. On solving some eigenvalue problems by using a differential transformation. Appl. Math. Comput. 2002, 127, 1–22. [Google Scholar]
- Alquran, M.T. Applying differential transform method to nonlinear partial differential equations: A modified approach. Appl. Appl. Math. Int. J. (AAM) 2012, 7, 10. [Google Scholar]
- Mirzaee, F.; Yari, M.K. A novel computing three-dimensional differential transform method for solving fuzzy partial differential equations. Ain Shams Eng. J. 2016, 7, 695–708. [Google Scholar] [CrossRef]
- Ertürk, V.S.; Momani, S. Solving systems of fractional differential equations using differential transform method. J. Comput. Appl. Math. 2008, 215, 142–151. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 2008, 21, 194–199. [Google Scholar] [CrossRef]
- Ibis, B.; Bayram, M.; Agargun, A.G. Applications of fractional differential transform method to fractional differential-algebraic equations. Eur. J. Pure Appl. Math. 2011, 4, 129–141. [Google Scholar]
- Ertürk, V.S. Computing eigenelements of Sturm–Liouville problems of fractional order via fractional differential transform method. Math. Comput. Appl. 2011, 16, 712–720. [Google Scholar] [CrossRef]
- Secer, A.; Akinlar, M.A.; Cevikel, A. Efficient solutions of systems of fractional PDEs by the differential transform method. Adv. Differ. Equ. 2012, 2012, 1–7. [Google Scholar] [CrossRef]
- Zain, F.A.S. Comparison study between differential transform method and Adomian decomposition method for some delay differential equations. Int. J. Phys. Sci. 2013, 8, 744–749. [Google Scholar]
- Rahimi, E.; Taghvafard, H.; Erjaee, G.H. Fractional differential transform method for solving a class of weakly singular Volterra integral equations. Iran. J. Sci. Technol. 2014, 38, 69. [Google Scholar]
- Hosseini, V.R.; Chen, W.; Avazzadeh, Z. Numerical solution of fractional telegraph equation by using radial basis functions. Eng. Anal. Bound. Elem. 2014, 38, 31–39. [Google Scholar] [CrossRef]
- Asghari, M.; Ezzati, R.; Allahviranloo, T. Numerical solutions of time-fractional order telegraph equation by Bernstein polynomials operational matrices. Math. Probl. Eng. 2016, 2016, 1683849. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ismail, A.I.; Ali, N.H.M.; Baleanu, D. Extended cubic B-splines in the numerical solution of time fractional telegraph equation. Adv. Differ. Equ. 2019, 2019, 365. [Google Scholar] [CrossRef]
- Orsingher, E.; Beghin, L. Time-fractional telegraph equations and telegraph processes with Brownian time. Probab. Theory Relat. Fields 2004, 128, 141–160. [Google Scholar] [CrossRef]
- Chen, J.; Liu, F.; Anh, V. Analytical solution for the time-fractional telegraph equation by the method of separating variables. J. Math. Anal. Appl. 2008, 338, 1364–1377. [Google Scholar] [CrossRef]
- Biazar, J.; Eslami, M. Analytic solution for telegraph equation by differential transform method. Phys. Lett. A 2010, 374, 2904–2906. [Google Scholar] [CrossRef]
- Garg, M.; Manohar, P.; Kalla, S.L. Generalized differential transform method to space-time fractional telegraph equation. Int. J. Differ. Equ. 2011, 2011, 548982. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, C. Fractional difference/finite element approximations for the time-space fractional telegraph equation. Appl. Math. Comput. 2012, 219, 2975–2988. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Awasthi, M.K.; Tamsir, M. RDTM solution of Caputo time fractional-order hyperbolic telegraph equation. AIP Adv. 2013, 3, 032142. [Google Scholar] [CrossRef]
- Kumar, S. A new analytical modelling for fractional telegraph equation via Laplace transform. Appl. Math. Model. 2014, 38, 3154–3163. [Google Scholar] [CrossRef]
- Joice Nirmala, R.; Balachandran, K. Analysis of solutions of time fractional telegraph equation. J. Korean Soc. Ind. Appl. Math. 2014, 18, 209–224. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Mohabbati, M. Numerical solution of fractional telegraph equation via the tau method. Math. Rep. 2015, 17, 155–166. [Google Scholar]
- Li, H. A new analytical modelling for fractional telegraph equation via Elzaki transform. J. Adv. Math. 2015, 11, 5617–5625. [Google Scholar] [CrossRef]
- Dhunde, R.R.; Waghmare, G.L. Double Laplace transform method for solving space and time fractional telegraph equations. Int. J. Math. Math. Sci. 2016, 2016, 1414595. [Google Scholar] [CrossRef]
- Eltayeb, H.; Abdalla, Y.T.; Bachar, I.; Khabir, M.H. Fractional telegraph equation and its solution by natural transform decomposition method. Symmetry 2019, 11, 334. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Baleanu, D.; Arif, M. An efficient analytical technique, for the solution of fractional-order telegraph equations. Mathematics 2019, 7, 426. [Google Scholar] [CrossRef]
- Abdel-Rehim, E.A.; El-Sayed, A.M.A.; Hashem, A.S. Simulation of the approximate solutions of the time-fractional multi-term wave equations. Comput. Math. Appl. 2017, 73, 1134–1154. [Google Scholar] [CrossRef]
- Abdel-Rehim, E.A.; Hashem, A.S. Simulation of the Space-Time-Fractional Ultrasound Waves with Attenuation in Fractal Media. In Fractional Calculus, Proceedings of the ICFDA 2018, Amman, Jordan, 16–18 July 2019; Springer: Singapore, 2019; pp. 173–197. [Google Scholar]
- Abdel-Rehim, E.A. The approximate and analytic solutions of the time-fractional intermediate diffusion wave equation associated with the fokker–planck operator and applications. Axioms 2021, 10, 230. [Google Scholar] [CrossRef]
- Chu, H.-P.; Chen, C.-L. Hybrid differential transform and finite difference method to solve the nonlinear heat conduction problem. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1605–1614. [Google Scholar] [CrossRef]
- Süngü, I.Ç.; Demir, H. Application of the hybrid differential transform method to the nonlinear equations. Sci. Res. 2012, 3, 246–250. [Google Scholar] [CrossRef][Green Version]
- Arsalan, D. The numerical study of a hybrid method for solving telegraph equation. Appl. Math. Nonlinear Sci. 2020, 5, 293–302. [Google Scholar] [CrossRef]
- Du, Y.; Qin, B.; Zhao, C.; Zhu, Y.; Cao, J.; Ji, Y. A novel spatio-temporal synchronization method of roadside asynchronous MMW radar-camera for sensor fusion. IEEE Trans. Intell. Transp. Syst. 2021, 23, 22278–22289. [Google Scholar] [CrossRef]
- Odibat, Z.; Shawagfeh, N. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Erturk, V.S.; Momani, S.; Odibat, Z. Application of generalized differential transform method to multi-order fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1642–1654. [Google Scholar] [CrossRef]
- Odibat, Z.; Kumar, S.; Shawagfeh, N.; Alsaedi, A.; Hayat, T. A study on the convergence conditions of generalized differential transform method. Math. Methods Appl. Sci. 2016, 40, 40–48. [Google Scholar] [CrossRef]
| N | - | ROC | - | ||
|---|---|---|---|---|---|
| 10 | — | ||||
| 20 | 1.89 | ||||
| 40 | 2.01 | ||||
| 80 | 2.16 | ||||
| 160 | 2.51 |
| FD-FDTM | 2D-FDTM | ||
|---|---|---|---|
| N | - | ROC | - | ||
|---|---|---|---|---|---|
| 10 | — | ||||
| 20 | 1.8 | ||||
| 40 | 1.97 | ||||
| 80 | 2.06 | ||||
| 160 | 2.61 |
| FD-FDTM | 2D-FDTM | ||
|---|---|---|---|
| N | - | - | ||
|---|---|---|---|---|
| 10 | ||||
| 20 | ||||
| 40 | ||||
| 80 | ||||
| 160 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahraee, Z.; Arabameri, M. A Semi-Discretization Method Based on Finite Difference and Differential Transform Methods to Solve the Time-Fractional Telegraph Equation. Symmetry 2023, 15, 1759. https://doi.org/10.3390/sym15091759
Sahraee Z, Arabameri M. A Semi-Discretization Method Based on Finite Difference and Differential Transform Methods to Solve the Time-Fractional Telegraph Equation. Symmetry. 2023; 15(9):1759. https://doi.org/10.3390/sym15091759
Chicago/Turabian StyleSahraee, Zahra, and Maryam Arabameri. 2023. "A Semi-Discretization Method Based on Finite Difference and Differential Transform Methods to Solve the Time-Fractional Telegraph Equation" Symmetry 15, no. 9: 1759. https://doi.org/10.3390/sym15091759
APA StyleSahraee, Z., & Arabameri, M. (2023). A Semi-Discretization Method Based on Finite Difference and Differential Transform Methods to Solve the Time-Fractional Telegraph Equation. Symmetry, 15(9), 1759. https://doi.org/10.3390/sym15091759







