On Asymptotic Properties of Stochastic Neutral-Type Inertial Neural Networks with Mixed Delays
Abstract
1. Introduction
- (1)
- (2)
- For constructing a suitable Lyapunov–Krasovskii functional, the mixed delays and the neutral terms are taken into consideration.
- (3)
- Unlike the previous papers, we introduce a new unified framework, to deal with mixed delays, inertia terms and D-operators. It is noted that our main results are also valid in cases of non-neutral systems.
2. Preliminaries and Problem Formulation
- (i)
- is injective on ;
- (ii)
- for , then is homeomorphic on .
- (H1)
- There exist constants , such that
- (H2)
- There exist constants , such that
- (H3)
- There exist constants , such that
3. Existence of Equilibrium Points
4. Stochastically Globally Asymptotic Stability
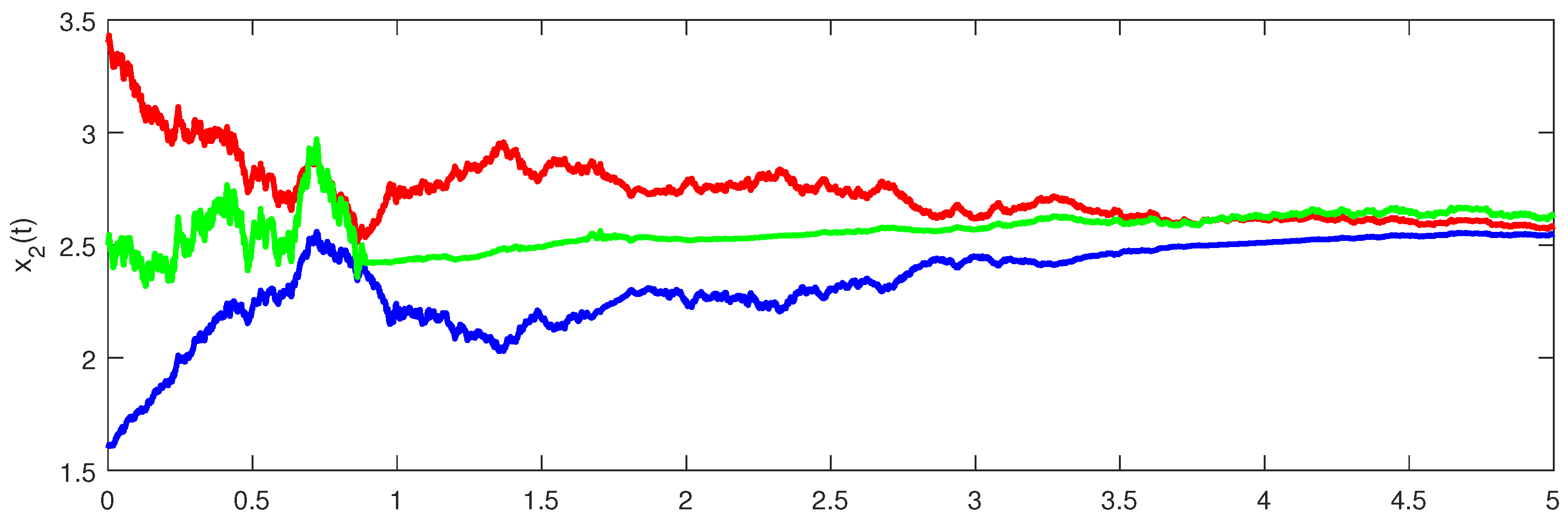
5. Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wheeler, D.; Schieve, W. Stability and chaos in an inertial two-neuron system. Phys. D Nonlinear Phenom. 1997, 105, 267–284. [Google Scholar] [CrossRef]
- Liu, Q.; Liao, X.; Yang, D.; Guo, S. The research for Hopf bifurcation in a single inertial neuron model with external forcing. IEEE Int. Conf. Granul. Comput. 2007, 85, 528–833. [Google Scholar]
- Liu, Q.; Liao, X.; Guo, S.; Wu, Y. Stability of bifurcating periodic solutions for a single delayed inertial neuron model under periodic excitation. Nonlinear Anal. Real World Appl. 2009, 10, 2384–2395. [Google Scholar] [CrossRef]
- Li, C.; Chen, G.; Liao, X.; Yu, J. Hopf bifurcation and chaos in a single inertial neuron model with time delay. Eur. Phys. J. B 2004, 41, 337–343. [Google Scholar] [CrossRef][Green Version]
- Liu, Q.; Liao, X.; Liu, Y.; Zhou, S.; Guo, S. Dynamics of an inertial two-neuron system with time delay. Nonlinear Dyn. 2009, 58, 574–609. [Google Scholar] [CrossRef]
- Arik, S. Global robust stability analysis of neural networks with discrete time delays. Chaos Solitons Fractals 2005, 26, 1407–1414. [Google Scholar] [CrossRef]
- Tu, Z.; Cao, J.; Hayat, T. Global exponential stability in Lagrange sense for inertial neural networks with time-varying delays. Neurocomputing 2016, 171, 524–531. [Google Scholar] [CrossRef]
- Wang, J.; Tian, L. Global Lagrange stability for inertial neural networks with mixed time-varying delays. Neurocomputing 2017, 235, 140–146. [Google Scholar] [CrossRef]
- Wan, P.; Jian, J. Global convergence analysis of impulsive inertial neural networks with time-varying delays. Neurocomputing 2017, 245, 68–76. [Google Scholar] [CrossRef]
- Tang, Q.; Jian, J. global exponential convergence for impulsive inertial complex-valued neural networks with time-varying delays. Math. Comput. Simul. 2019, 159, 39–56. [Google Scholar] [CrossRef]
- Ke, Y.; Miao, C. Anti-periodic solutions of inertial neural networks with time delays. Neural Process. Lett. 2017, 45, 523–538. [Google Scholar] [CrossRef]
- Ke, Y.; Miao, C. Stability analysis of inertial Cohen-Grossberg-type neural networks with time delays. Neurocomputing 2013, 117, 196–205. [Google Scholar] [CrossRef]
- Ke, Y.; Miao, C. Exponential stability of periodic solutions for inertial Cohen-Grossberg-type neural networks. Neural Netw. World 2014, 4, 377–394. [Google Scholar] [CrossRef]
- Huang, Q.; Cao, J. Stability analysis of inertial Cohen-Grossberg neural networks with Markovian jumping parameters. Neurocomputing 2018, 282, 89–97. [Google Scholar] [CrossRef]
- Ke, Y.; Miao, C. Stability analysis of BAM neural networks with inertial term and.time delay. WSEAS Trans. Syst. 2011, 10, 425–438. [Google Scholar]
- Ke, Y.; Miao, C. Stability and existence of periodic solutions in inertial BAM neural networks with time delay. Neural Comput. Appl. 2013, 23, 1089–1099. [Google Scholar]
- Zhang, Y.; Kong, L. Photovoltaic power prediction based on hybrid modeling of neural network and stochastic differential equation. ISA Trans. 2022, 128, 181–206. [Google Scholar] [CrossRef]
- Shu, J.; Wu, B.; Xiong, L.; Zhang, H. Stochastic stabilization of Markov jump quaternion-valued neural network using sampled-data control. Appl. Math. Comput. 2021, 400, 126041. [Google Scholar] [CrossRef]
- Guo, Y. Globally robust stability analysis for stochastic Cohen- Grossberg neural networks with impulse control and time-varying delays. Ukr. Math. J. 2018, 69, 1220–1233. [Google Scholar] [CrossRef]
- Hu, J.; Zhong, S.; Liang, L. Exponential stability analysis of stochastic delayed cellular neutral networks. Chaos Solitons Fractals 2006, 27, 1006–1010. [Google Scholar] [CrossRef]
- Xu, J.; Chen, L.; Li, P. On p-th moment exponential stability for stochastic cellular neural networks with distributed delays. Int. J. Control. Autom. Syst. 2018, 16, 1217–1225. [Google Scholar] [CrossRef]
- Liu, L.; Deng, F.; Zhu, Q. Mean square stability of two classes of theta methods for numerical computation and simulation of delayed stochastic Hopfield neural networks. J. Comput. Appl. Math. 2018, 343, 428–447. [Google Scholar] [CrossRef]
- Yang, L.; Fei, Y.; Wu, W. Periodic Solution for del-stochastic high-Order Hopfield neural networks with time delays on time scales. Neural Process. Lett. 2019, 49, 1681–1696. [Google Scholar] [CrossRef]
- Chen, G.; Li, D.; Shi, L.; van Gaans, O.; Lunel, S.V. Stability results for stochastic delayed recurrent neural networks with discrete and distributed delays. J. Differ. Equ. 2018, 264, 3864–3898. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, Q.; Lu, J.; Chu, Y.; Li, Y. Synchronization control of neutral-type neural networks with sampled-data via adaptive event-triggered communication scheme. J. Frankl. Inst. 2021, 358, 1999–2014. [Google Scholar] [CrossRef]
- Yang, X.; Cheng, Z.; Li, X.; Ma, T. xponential synchronization of coupled neutral-type neural networks with mixed delays via quantized output control. J. Frankl. Inst. 2019, 356, 8138–8153. [Google Scholar] [CrossRef]
- Si, W.; Xie, T. Further Results on Exponentially Robust Stability of Uncertain Connection Weights of Neutral-Type Recurrent Neural Networks. Complexity 2021, 2021, 6941701. [Google Scholar] [CrossRef]
- Du, B. Anti-periodic solutions problem for inertial competitive neutral-type neural networks via Wirtinger inequality. J. Inequalities Appl. 2019, 2019, 187. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, D. Existence and global exponential stability of a periodic solution for a discrete-time interval general BAM neural networks. J. Frankl. Inst. 2010, 347, 763–780. [Google Scholar] [CrossRef]
- Park, J.; Kwon, O.; Lee, S. LMI optimization approach on stability for delayed neural networks of neutral-type. Appl. Math. Comput. 2008, 196, 236–244. [Google Scholar] [CrossRef]
- Yu, K.; Lien, C. Stability criteria for uncertain neutral systems with interval time-varying delays. Chaos Solitons Fractals 2008, 38, 650–657. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, A.; Yang, G. Periodicity on Neutral-Type Inertial Neural Networks Incorporating Multiple Delays. Symmetry 2021, 13, 2231. [Google Scholar] [CrossRef]
- Wang, C.; Song, Y.; Zhang, F.; Zhao, Y. Exponential Stability of a Class of Neutral Inertial Neural Networks with Multi-Proportional Delays and Leakage Delays. Mathematics 2023, 11, 2596. [Google Scholar] [CrossRef]
- Hale, J. The Theory of Functional Differential Equations; Springer: New York, NY, USA, 1977. [Google Scholar]
- Wang, K.; Zhu, Y. Stability of almost periodic solution for a generalized neutral-type neural networks with delays. Neurocomputing 2010, 73, 3300–3307. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Horwood: Chichester, UK, 1997. [Google Scholar]
- Forti, M.; Tesi, A. New conditions for global stability of neural networks with application to linear and quadratic programming problems. IEEE Trans. Circuits Syst. 1995, 42, 354–366. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.; Jiang, W. Stability of stochastic and intertial neural networks with time delays. Appl. Math. J. Chin. Univ. 2020, 35, 83–98. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Yin, H.; Du, B. On Asymptotic Properties of Stochastic Neutral-Type Inertial Neural Networks with Mixed Delays. Symmetry 2023, 15, 1746. https://doi.org/10.3390/sym15091746
Wang B, Yin H, Du B. On Asymptotic Properties of Stochastic Neutral-Type Inertial Neural Networks with Mixed Delays. Symmetry. 2023; 15(9):1746. https://doi.org/10.3390/sym15091746
Chicago/Turabian StyleWang, Bingxian, Honghui Yin, and Bo Du. 2023. "On Asymptotic Properties of Stochastic Neutral-Type Inertial Neural Networks with Mixed Delays" Symmetry 15, no. 9: 1746. https://doi.org/10.3390/sym15091746
APA StyleWang, B., Yin, H., & Du, B. (2023). On Asymptotic Properties of Stochastic Neutral-Type Inertial Neural Networks with Mixed Delays. Symmetry, 15(9), 1746. https://doi.org/10.3390/sym15091746





