Dynamical Coupling between Particle and Antiparticle in Relativistic Quantum Mechanics: A Multistate Perspective on the Energy–Momentum Relation
Abstract
1. Introduction
2. Theoretical Models
2.1. Two-State System
2.2. Four-State System
3. Discussions
3.1. ESD and Energy Transformation
3.2. Free Particle and Generalized Relativistic Quantum Mechanics
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
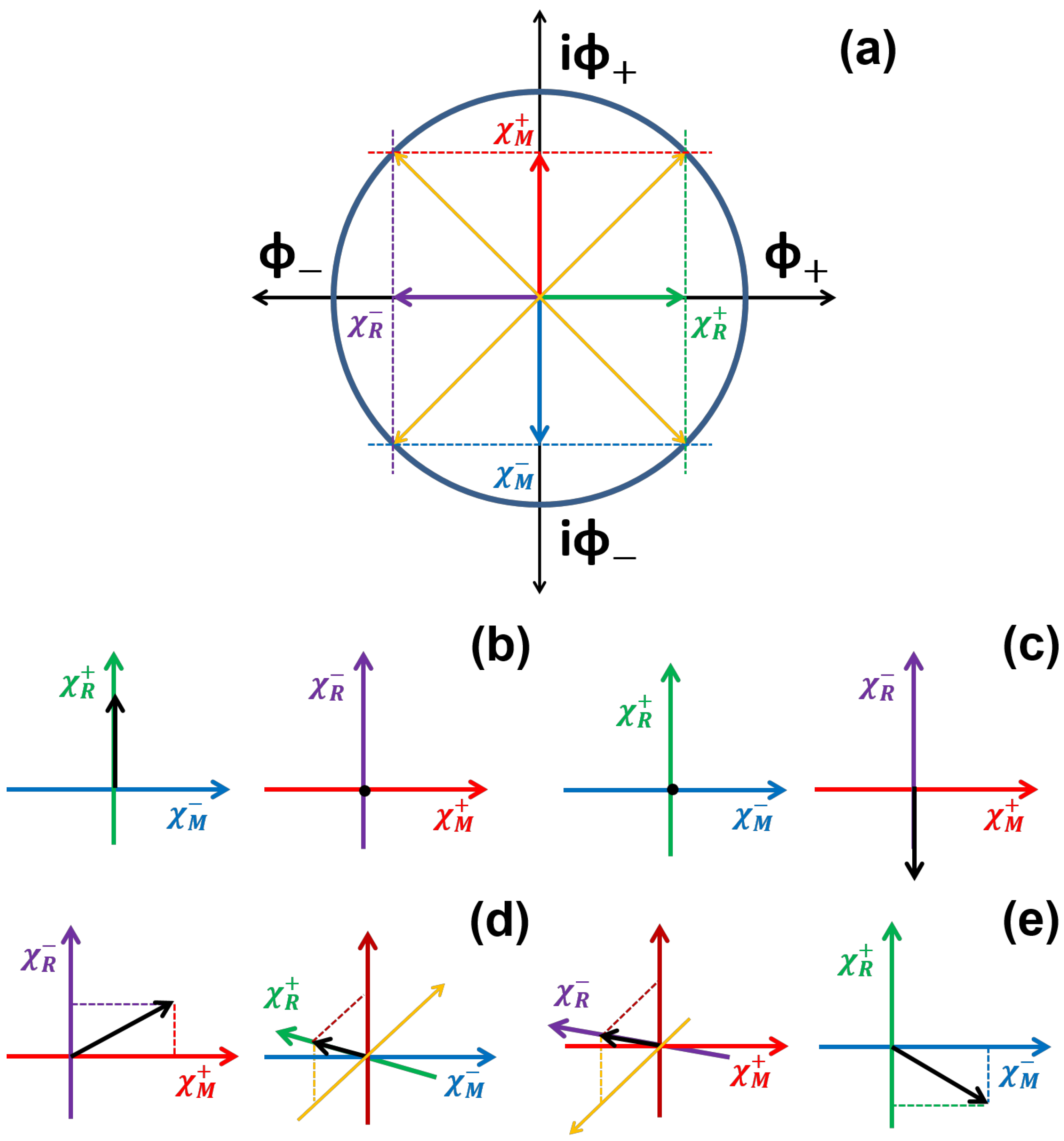
- Comparison with conventional treatments
- 2.
- The explicit solutions for the four-state system.
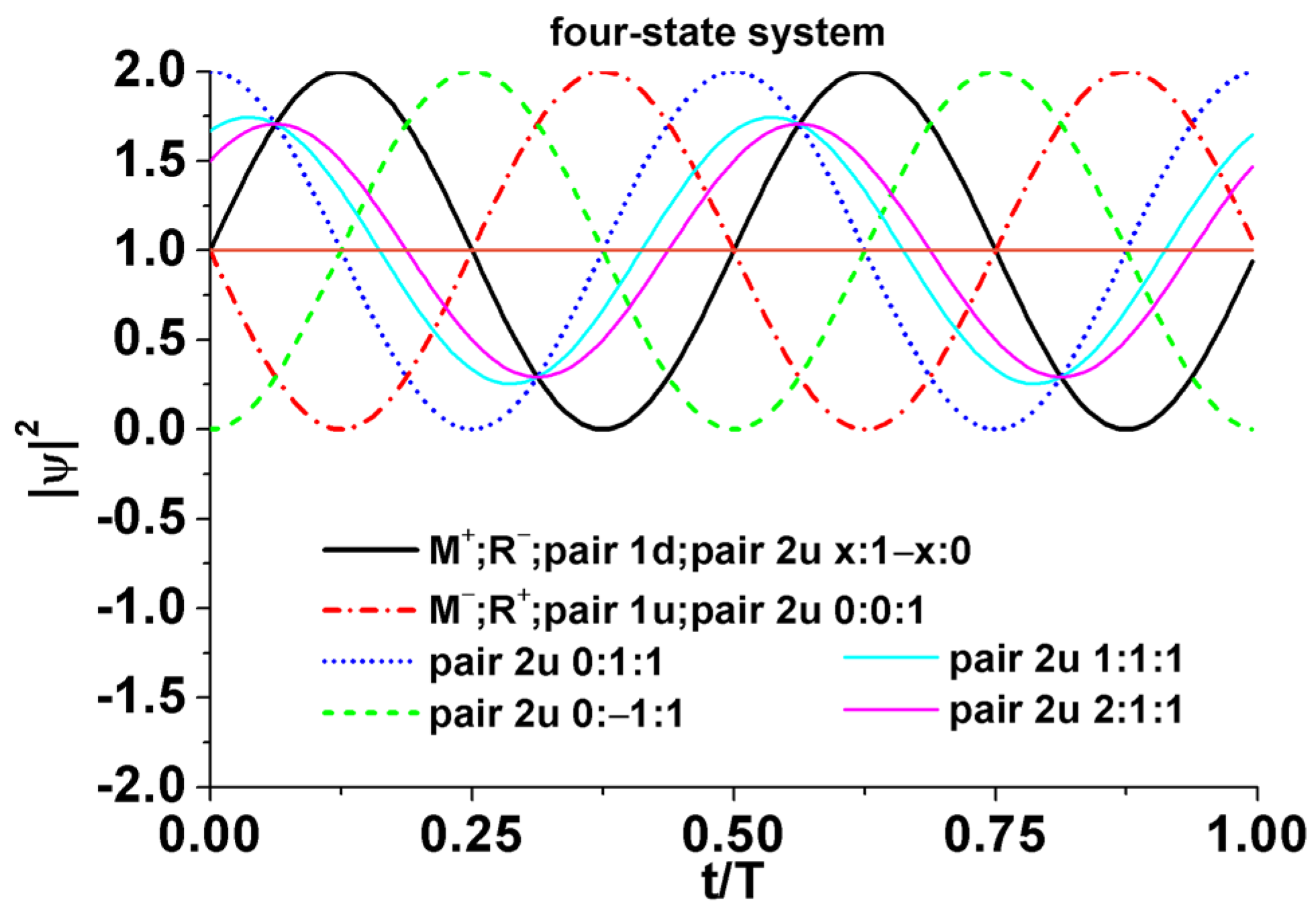
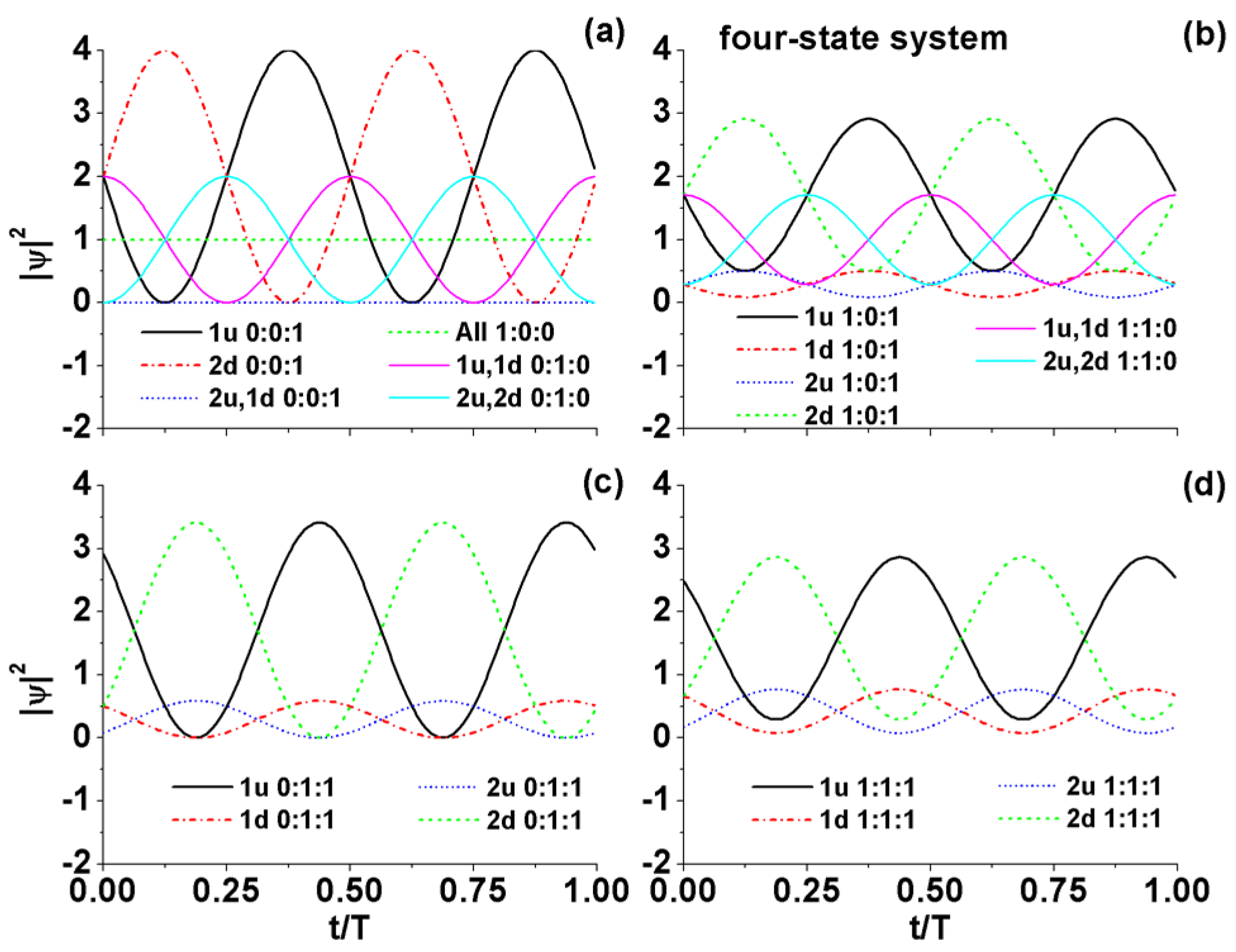
References
- Zeng, J. Quantum Mechanics I, II, 5th ed.; Science Press: Beijing, China, 2014. [Google Scholar]
- Nikolić, H. Quantum Mechanics: Myths and Facts. Found. Phys. 2007, 37, 1563–1611. [Google Scholar] [CrossRef]
- Holland, P.R. The Quantum Theory of Motion: An Account of the de Broglie-Bohm Causal Interpretation of Quantum Mechanics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Bassi, A.; Lochan, K.; Satin, S.; Singh, T.P.; Ulbricht, H. Models of wave-function collapse, underlying theories, and experimental tests. Rev. Mod. Phys. 2013, 85, 471–527. [Google Scholar] [CrossRef]
- Wachter, A. Relativistic Quantum Mechanics; Reprinted in China; Springer Science+Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields; Reprinted in China; Cambridge University Press: Cambridge, UK, 1995; Volume 1. [Google Scholar]
- Pauli, W.; Weisskopf, V. Quantisation of the scalar relativistic wave equation. Helv. Phys. Acta 1934, 7, 709–731. [Google Scholar]
- Gell-Mann, M.; Pais, A. Behavior of Neutral Particles under Charge Conjugation. Phys. Rev. 1955, 97, 1387–1389. [Google Scholar] [CrossRef]
- Alba, D.; Crater, H.W.; Lusanna, L. Relativistic quantum mechanics and relativistic entanglement in the rest-frame instant form of dynamics. J. Math. Phys. 2011, 52, 062301. [Google Scholar] [CrossRef]
- Céleri, L.C.; Kiosses, V.; Terno, D.R. Spin and localization of relativistic fermions and uncertainty relations. Phys. Rev. A 2016, 94, 062115. [Google Scholar] [CrossRef]
- Marolf, D.; Rovelli, C. Relativistic quantum measurement. Phys. Rev. D 2002, 66, 023510. [Google Scholar] [CrossRef]
- Anderson, C.D. The positive electron. Phys. Rev. 1933, 43, 491–494. [Google Scholar] [CrossRef]
- Chamberlain, O.; Segrè, E.; Wiegand, C.; Ypsilantis, T. Observation of antiprotons. Phys. Rev. 1955, 100, 947–950. [Google Scholar] [CrossRef]
- Cork, B.; Lambertson, G.R.; Piccioni, O.; Wenzel, W.A. Antineutrons produced from antiprotons in charge-exchange collisions. Phys. Rev. 1956, 104, 1193–1197. [Google Scholar] [CrossRef]
- Baur, G.; Boero, G.; Brauksiepe, A.; Buzzo, A.; Eyrich, W.; Geyer, R.; Grzonka, D.; Hauffe, J.; Kilian, K.; LoVetere, M.; et al. Production of antihydrogen. Phys. Lett. B 1996, 368, 251–258. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Alekseev, I.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barnby, L.S. Observation of an antimatter hypernucleus. Science 2010, 328, 58–62. [Google Scholar] [PubMed]
- The STAR Collaboration. Observation of the antimatter helium-4 nucleus. Nature 2011, 473, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Planck Collaboration. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% determination of the local value of the Hubble constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Aubourg, É.; Bailey, S.; Bautista, J.E.; Beutler, F.; Bhardwaj, V.; Bizyaev, D.; Blanton, M.; Blomqvist, M.; Bolton, A.S.; Bovy, J.; et al. Cosmological implications of baryon acoustic oscillation measurements. Phys. Rev. D 2015, 92, 123516. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Feshbach, H.; Villars, F. Ementary Relativistic Wave Mechanics of Spin 0 and Spin 1/2 Particles. Rev. Mod. Phys. 1958, 30, 24–45. [Google Scholar] [CrossRef]
- Foldy, L.L.; Wouthuysen, S.A. On the Dirac Theory of Spin 1/2 Particles and Its Non-relativistic Limit. Phys. Rev. 1950, 78, 29–36. [Google Scholar] [CrossRef]
- Foldy, L.L. Synthesis of covariant particle equations. Phys. Rev. 1956, 102, 568–581. [Google Scholar] [CrossRef]
- Silenko, A.J. Foldy-Wouthyusen transformation and semiclassical limit for relativistic particles in strong external fields. Phys. Rev. A 2008, 77, 012116. [Google Scholar] [CrossRef]
- Silenko, A.J. General properties of the Foldy-Wouthuysen transformation and applicability of the corrected original Foldy-Wouthuysen method. Phys. Rev. A 2016, 93, 022108. [Google Scholar] [CrossRef]
- Chen, T.-W.; Chiou, D.-W. Correspondence between classical and Dirac-Pauli spinors in view of the Foldy-Wouthuysen transformation. Phys. Rev. A 2014, 89, 032111. [Google Scholar] [CrossRef]
- Obukhov, Y.N. Spin, Gravity, and Inertia. Phys. Rev. Lett. 2001, 86, 192. [Google Scholar] [CrossRef] [PubMed]
- Heully, J.-L.; Lindgren, I.; Lindroth, E.; Mrtensson-Pendrill, A.-M. Comment on relativistic wave equations and negative-energy states. Phys. Rev. A 1985, 33, 4426–4429. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, F. Separation of Dirac’s Hamiltonian by Van Vleck transformation. Mol. Phys. 2017, 115, 190–213. [Google Scholar] [CrossRef]
- Reiher, M.; Wolf, A. Relativisitc Quantum Chemistry, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Lévai, G.; Del Sol Mesa, A. On some solutions of the Dirac equation. J. Phys. A Math. Gen. 1996, 29, 2827. [Google Scholar] [CrossRef]
- Gerritsma, R.; Kirchmair, G.; Za, F.; Solano, E.; Blatt, R.; Roos, C.F. Quantum simulation of the Dirac equation. Nature 2010, 463, 68–72. [Google Scholar] [CrossRef]
- Znojil, M. Non-Hermitian interaction representation and its use in relativistic quantum mechanics. Ann. Phys. 2017, 385, 162–179. [Google Scholar] [CrossRef]
- Jones-Smith, K.; Mathur, H. Relativistic non-Hermitian quantum mechanics. Phys. Rev. D 2014, 89, 125014. [Google Scholar] [CrossRef]
- Panahi, H.; Bakhshi, Z. Dirac equation with position-dependent effective mass and solvable potentials in the Schrödinger equation. J. Phys. A Math. Theor. 2011, 44, 175304. [Google Scholar] [CrossRef]
- Dattoli, G.; Sabia, E.; Górska; Horzela, A.; Penson, K.A. Relativistic wave equations: An operational approach. J. Phys. A Math. Theor. 2015, 48, 125203. [Google Scholar] [CrossRef]
- Mironov, V.L.; Mironov, S.V. Octonic second-order equations of relativistic quantum mechanics. J. Math. Phys. 2009, 50, 012302. [Google Scholar] [CrossRef]
- Chiou, D.-W.; Chen, T.-W. Exact Foldy-Wouthuysen transformation of the Dirac-Pauli Hamiltonian in the weak-field limit by the method of direct perturbation theory. Phys. Rev. A 2016, 94, 052116. [Google Scholar] [CrossRef]
- Aliyev, Z.S.; Rzayeva, H.S. Oscillation properties for the equation of the relativistic quantum theory. Appl. Math. Comput. 2015, 271, 308–316. [Google Scholar] [CrossRef]
- Heinzl, T.; Ilderton, A. Superintegrable relativistic systems in spacetime-dependent background fields. J. Phys. A Math. Theor. 2017, 50, 345204. [Google Scholar] [CrossRef]
- Donker, H.C.; Katsnelson, M.I.; De Raedt, H.; Michielsen, K. Logical inference approach to relativistic quantum mechanics: Derivation of the Klein–Gordon equation. Ann. Phys. 2016, 372, 74–82. [Google Scholar] [CrossRef]
- Simulik, V.M.; Krivsky, I.Y. Quantum-Mechanical Description of the Fermionic Doublet and its Link with the Dirac Equation. Ukr. J. Phys. 2018, 58, 1192. [Google Scholar] [CrossRef]
- Sakurai, J.J. Modern Quantum Mechanics, Revised ed.; Tuan, S.F., Ed.; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Tao, G. Multi-State Trajectory Approach to Non-Adiabatic Dynamics: General Formalism and the Active State Trajectory Approximation. J. Chem. Phys. 2017, 147, 044107. [Google Scholar] [CrossRef]
- Biernat, E.P.; Klink, W.H.; Schweiger, W.; Zelzer, S. Point-form quantum field theory. Ann. Phys. 2008, 323, 1361–1383. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, G. Dynamical Coupling between Particle and Antiparticle in Relativistic Quantum Mechanics: A Multistate Perspective on the Energy–Momentum Relation. Symmetry 2023, 15, 1649. https://doi.org/10.3390/sym15091649
Tao G. Dynamical Coupling between Particle and Antiparticle in Relativistic Quantum Mechanics: A Multistate Perspective on the Energy–Momentum Relation. Symmetry. 2023; 15(9):1649. https://doi.org/10.3390/sym15091649
Chicago/Turabian StyleTao, Guohua. 2023. "Dynamical Coupling between Particle and Antiparticle in Relativistic Quantum Mechanics: A Multistate Perspective on the Energy–Momentum Relation" Symmetry 15, no. 9: 1649. https://doi.org/10.3390/sym15091649
APA StyleTao, G. (2023). Dynamical Coupling between Particle and Antiparticle in Relativistic Quantum Mechanics: A Multistate Perspective on the Energy–Momentum Relation. Symmetry, 15(9), 1649. https://doi.org/10.3390/sym15091649





