Analysis of Heat Transfer Behavior of Porous Wavy Fin with Radiation and Convection by Using a Machine Learning Technique
Abstract
:1. Introduction
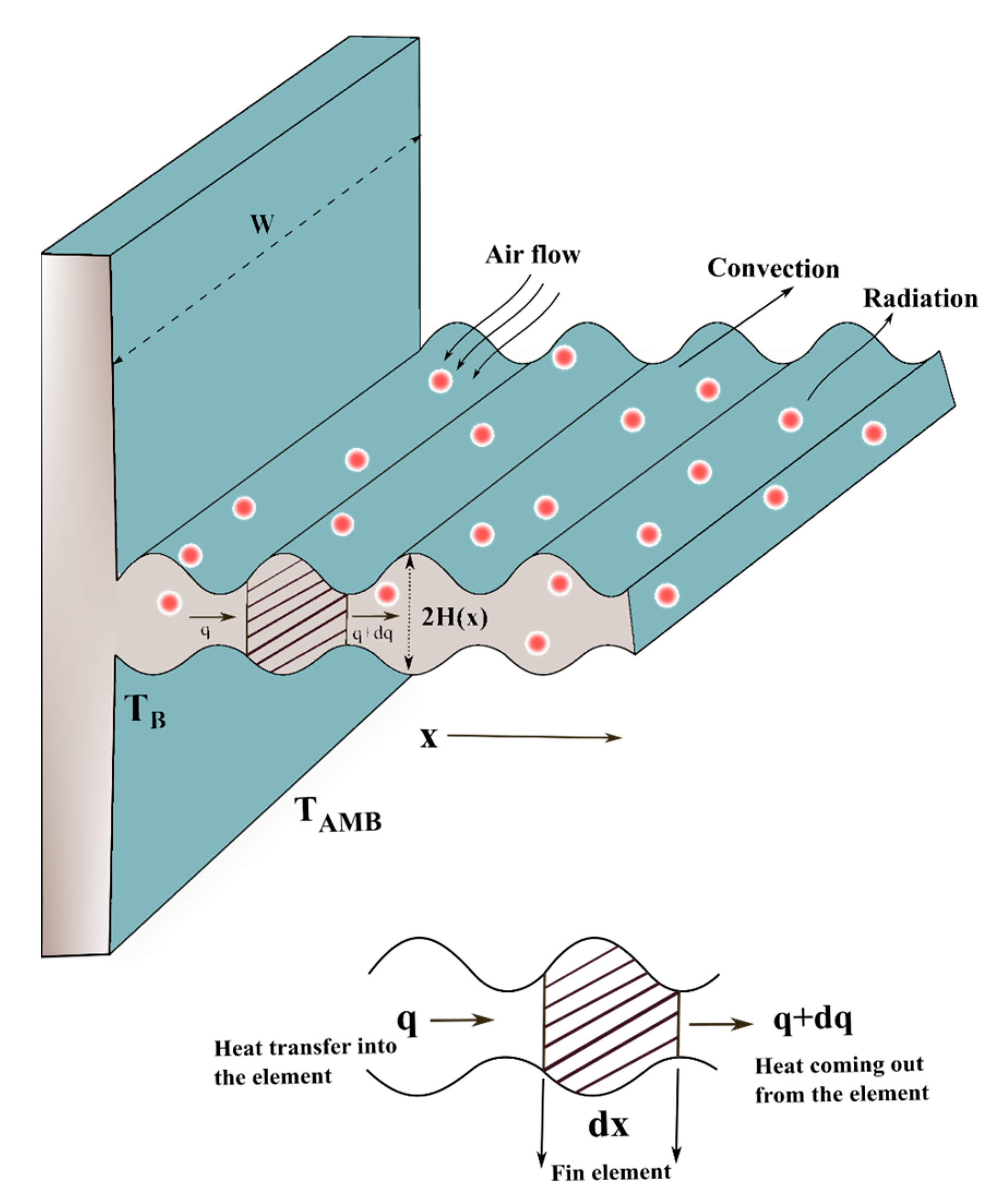
2. Formulation of the Problem
- The proposed fin geometry is symmetric around the length axis and wavy along the x-direction.
- It is presumed that the temperature varies only longitudinally and does not vary across the thickness.
- Convection and radiation heat transfer with constant ambient temperature are considered to be the heat-exchanging mechanism of PWF.
- The porous medium, which is homogeneous and isotropic, is saturated with a single-phase fluid.
- The fin tip is assumed to be adiabatic, comparable to ignoring the fin tip transferring heat due to its minimal area.
3. Stochastic Machine Learning Modeling
3.1. Artificial Neural Networks
3.2. Grid Search
3.3. Differential Evolution
4. Results and Discussion
5. Conclusions
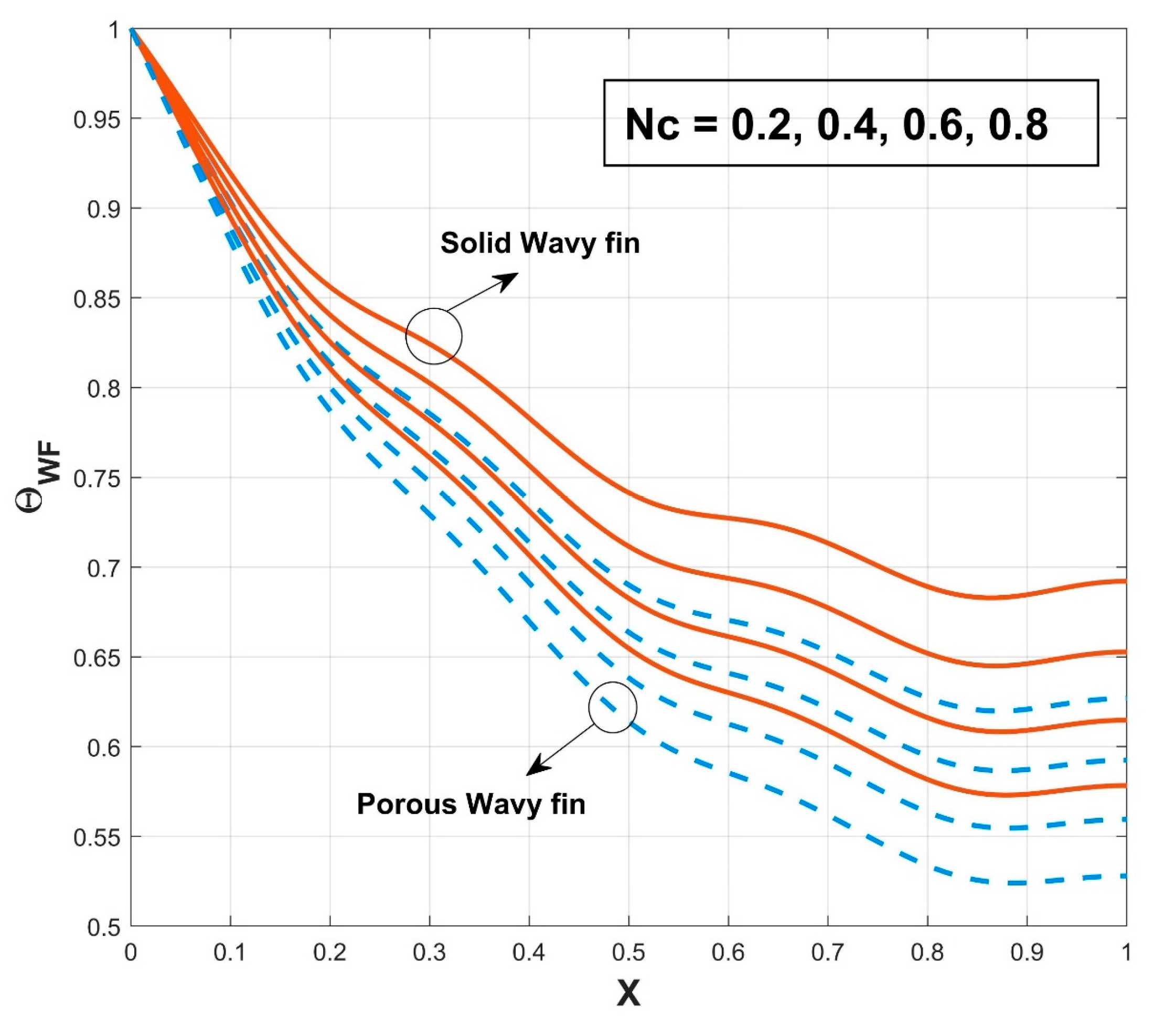
- The effect of convective heat exchange is prominent in the distribution of temperature through the fin inducing the decremental change of temperature dispersion in the PWF with variation of the convective–radiative parameter.
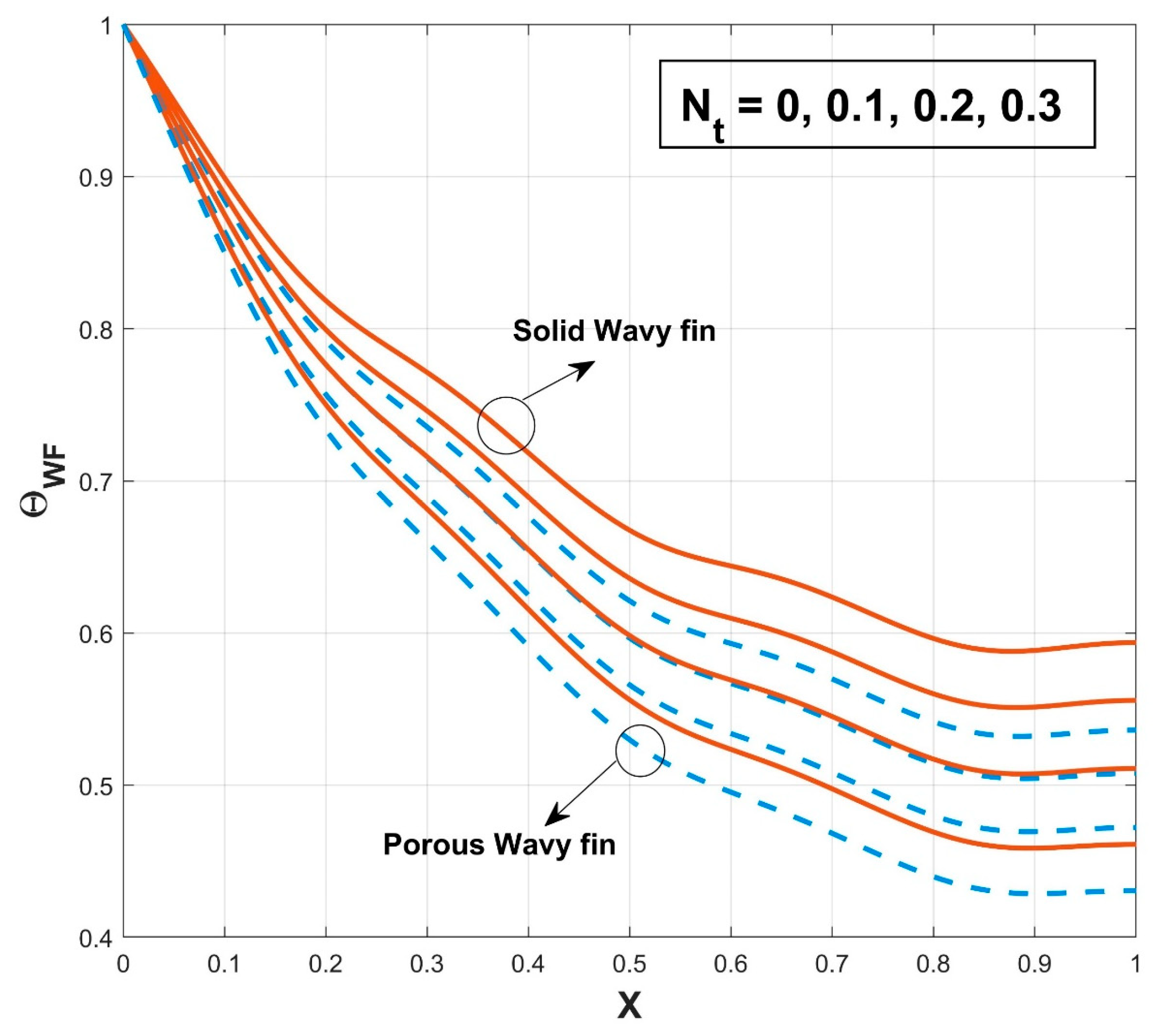
- Radiation heat transmission impacts the fin’s overall heat transfer rate, leading to a reduction in the thermal distribution through PWF.
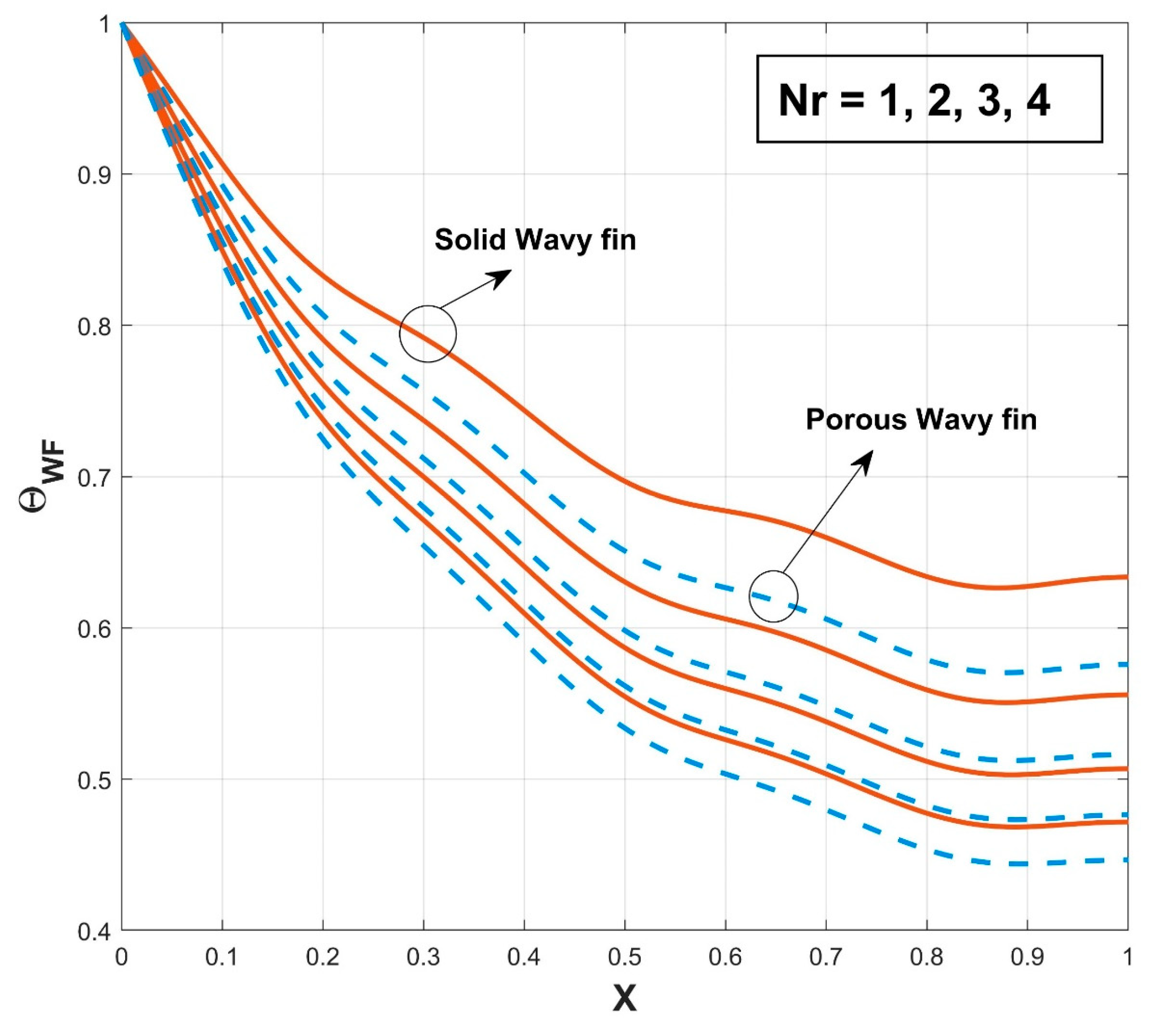
- The wavy structured porous fin provides more heat transfer than the solid wavy fin.
- The heat transfer rate estimated by the intelligent DE-ANN model outperforms the GS-ANN model, due to its high non-linear fitting ability.
- The DE-ANN forecasting model has consistent performance, whereas conventional ANN models (such as GS-ANN), that are not thoroughly designed, can easily overfit.
- The DE technique can select the appropriate ANN model parameters, potentially improving prediction accuracy, and capturing growing curve patterns more easily.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| fin’s area | |
| fin profile aspect ratio | |
| specific heat | |
| acceleration due to gravity | |
| generation count | |
| fin half height | |
| fin base half height | |
| convective heat transfer coefficient | |
| permeability | |
| thermal conductivity | |
| fin’s length | |
| exponent constant | |
| convection–conduction parameter | |
| radiation–conduction parameter | |
| temperature ratio parameter | |
| wave number | |
| heat transfer rate (non-dimensional) | |
| heat transfer rate | |
| temperature | |
| fin’s length (dimensionless) | |
| fin axial distance | |
| Greek symbols | |
| volumetric expansion index | |
| surface wave dimensionless amplitude | |
| emissivity | |
| non-dimensional temperature | |
| kinematic viscosity | |
| density | |
| Stefan–Boltzmann constant | |
| surface wave phase shift | |
| porosity | |
| Subscript | |
| AMB | ambient |
| B | base |
| CS | cross-sectional |
| eff | effective |
| f | fluid |
| PWF | porous wavy fin |
| r | relative quantity |
| Sd | solid |
| SF | surface area |
| WF | wavy fin |
References
- Jo, J.; Kim, J.; Kim, S.J. Experimental Investigations of Heat Transfer Mechanisms of a Pulsating Heat Pipe. Energy Convers. Manag. 2019, 181, 331–341. [Google Scholar] [CrossRef]
- Hu, C.; Sun, M.; Xie, Z.; Yang, L.; Song, Y.; Tang, D.; Zhao, J. Numerical Simulation on the Forced Convection Heat Transfer of Porous Medium for Turbine Engine Heat Exchanger Applications. Appl. Therm. Eng. 2020, 180, 115845. [Google Scholar] [CrossRef]
- Hassan, H.; Shafey, N.Y.A. 3D Study of Convection-Radiation Heat Transfer of Electronic Chip inside Enclosure Cooled by Heat Sink. Int. J. Therm. Sci. 2021, 159, 106585. [Google Scholar] [CrossRef]
- Prakash, O.; Singh, S.N. Experimental and Numerical Study of Mixed Convection with Surface Radiation Heat Transfer in an Air-Filled Ventilated Cavity. Int. J. Therm. Sci. 2022, 171, 107169. [Google Scholar] [CrossRef]
- Zhang, Z.; Lou, C. Thermodynamics Second-Law Analysis in an Unsteady Conduction and Radiation Heat Transfer System with Internal Heat Source. Int. J. Heat Mass Transf. 2023, 203, 123848. [Google Scholar] [CrossRef]
- Ndlovu, P.L. The Significance of Fin Profile and Convective-Radiative Fin Tip on Temperature Distribution in a Longitudinal Fin. Nano Hybrids Compos. 2019, 26, 93–105. [Google Scholar] [CrossRef]
- El Ghandouri, I.; El Maakoul, A.; Saadeddine, S.; Meziane, M. Design and Numerical Investigations of Natural Convection Heat Transfer of a New Rippling Fin Shape. Appl. Therm. Eng. 2020, 178, 115670. [Google Scholar] [CrossRef]
- Li, H.; Hu, C.; He, Y.; Tang, D.; Wang, K.; Huang, W. Effect of Perforated Fins on the Heat-Transfer Performance of Vertical Shell-and-Tube Latent Heat Energy Storage Unit. J. Energy Storage 2021, 39, 102647. [Google Scholar] [CrossRef]
- Luo, L.; Yan, H.; Du, W.; Su, W.; Wang, S.; Huang, D. Numerical Study of a Novel Curved Pin Fin for Heat Transfer Enhancement within Aeroengine Turbine Blade. Aerosp. Sci. Technol. 2022, 123, 107436. [Google Scholar] [CrossRef]
- Dogmaz, M.A.; Safak, I.; Gunes, S.; Reddy, J.N. An Investigation of the Thermal Performance of Functionally Graded Annular Fins on a Horizontal Cylinder Under Natural Convection. Appl. Therm. Eng. 2023. [Google Scholar]
- Kiwan, S.; Al-Nimr, M.A. Using Porous Fins for Heat Transfer Enhancement. J. Heat Transf. 2001, 123, 790–795. [Google Scholar] [CrossRef]
- Ndlovu, P.L.; Moitsheki, R.J. Steady State Heat Transfer Analysis in a Rectangular Moving Porous Fin. Propuls. Power Res. 2020, 9, 188–196. [Google Scholar] [CrossRef]
- Emamifar, A.; Moghadasi, H.; Noroozi, M.J.; Saffari, H. Transient Analysis of Convective-Radiative Heat Transfer through Porous Fins with Temperature-Dependent Thermal Conductivity and Internal Heat Generation. J. Therm. Eng. 2022, 8, 656–666. [Google Scholar] [CrossRef]
- Das, R.; Kundu, B. Simultaneous Estimation of Heat Generation and Magnetic Field in a Radial Porous Fin from Surface Temperature Information. Int. Commun. Heat Mass Transf. 2021, 127, 105497. [Google Scholar] [CrossRef]
- Xuan Hoang Khoa, L.; Pop, I.; Sheremet, M.A. Numerical Simulation of Solid and Porous Fins’ Impact on Heat Transfer Performance in a Differentially Heated Chamber. Mathematics 2022, 10, 263. [Google Scholar] [CrossRef]
- Abbas, M.M.; Torabi, M.; Jain, A. Transient Thermal Management Characteristics of a Porous Fin with Radially Outwards Fluid Flow. Int. J. Heat Mass Transf. 2023, 214, 124435. [Google Scholar] [CrossRef]
- Altun, A.H.; Ziylan, O. Experimental Investigation of the Effects of Horizontally Oriented Vertical Sinusoidal Wavy Fins on Heat Transfer Performance in Case of Natural Convection. Int. J. Heat Mass Transf. 2019, 139, 425–431. [Google Scholar] [CrossRef]
- Luo, C.; Wu, S.; Song, K.; Hua, L.; Wang, L. Thermo-Hydraulic Performance Optimization of Wavy Fin Heat Exchanger by Combining Delta Winglet Vortex Generators. Appl. Therm. Eng. 2019, 163, 114343. [Google Scholar] [CrossRef]
- Chimres, N.; Chittiphalungsri, T.; Asirvatham, L.G.; Dalkılıç, A.S.; Mahian, O.; Wongwises, S. Experimental and Numerical Studies on Heat Transfer Enhancement for Air Conditioner Condensers Using a Wavy Fin with a Rectangular Winglet. J. Mech. Sci. Technol. 2020, 34, 4307–4322. [Google Scholar] [CrossRef]
- Boland, S.; Majidi, S. Thermal Improvement in Double-Layered Microchannel Heat Sink with Incorporating Wavy Porous Fins. Heat Transf. Eng. 2022, 43, 485–502. [Google Scholar] [CrossRef]
- Okon, J.O.; Effiom, S.O. Numerical Simulation of the Thermal Performance of a Wavy Fin Configuration for a Straight Fin Array. Sci. Afr. 2022, 16, e01265. [Google Scholar] [CrossRef]
- Alizadeh, R.; Mohebbi Najm Abad, J.; Fattahi, A.; Alhajri, E.; Karimi, N. Application of Machine Learning to Investigation of Heat and Mass Transfer Over a Cylinder Surrounded by Porous Media—The Radial Basic Function Network. J. Energy Resour. Technol. 2020, 142, 112109. [Google Scholar] [CrossRef]
- Krishnayatra, G.; Tokas, S.; Kumar, R. Numerical Heat Transfer Analysis & Predicting Thermal Performance of Fins for a Novel Heat Exchanger Using Machine Learning. Case Stud. Therm. Eng. 2020, 21, 100706. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Q.; Rao, Y. Searching for Irregular Pin-Fin Shapes for High Temperature Applications Using Deep Learning Methods. Int. J. Therm. Sci. 2021, 161, 106746. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Alshammari, F.S. Heat Transfer Analysis of an Inclined Longitudinal Porous Fin of Trapezoidal, Rectangular and Dovetail Profiles Using Cascade Neural Networks. Struct Multidisc Optim 2022, 65, 251. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Maghsoudi, E.; Roberts, S.N.; Kwon, B. Shape Optimization of Pin Fin Array in a Cooling Channel Using Genetic Algorithm and Machine Learning. Int. J. Heat Mass Transf. 2023, 202, 123769. [Google Scholar] [CrossRef]
- Sowmya, G.; Lashin, M.M.A.; Khan, M.I.; Kumar, R.S.V.; Jagadeesha, K.C.; Prasannakumara, B.C.; Guedri, K.; Bafakeeh, O.T.; Mohamed Tag-ElDin, E.S.; Galal, A.M. Significance of Convection and Internal Heat Generation on the Thermal Distribution of a Porous Dovetail Fin with Radiative Heat Transfer by Spectral Collocation Method. Micromachines 2022, 13, 1336. [Google Scholar] [CrossRef]
- Kumar, R.S.V.; Alsulami, M.D.; Sarris, I.E.; Sowmya, G.; Gamaoun, F. Stochastic Levenberg–Marquardt Neural Network Implementation for Analyzing the Convective Heat Transfer in a Wavy Fin. Mathematics 2023, 11, 2401. [Google Scholar] [CrossRef]
- Abdulrahman, A.; Gamaoun, F.; Varun Kumar, R.S.; Khan, U.; Singh Gill, H.; Nagaraja, K.V.; Eldin, S.M.; Galal, A.M. Study of Thermal Variation in a Longitudinal Exponential Porous Fin Wetted with TiO2−SiO2/ Hexanol Hybrid Nanofluid Using Hybrid Residual Power Series Method. Case Stud. Therm. Eng. 2023, 43, 102777. [Google Scholar] [CrossRef]
- Cui, W.; Si, T.; Li, X.; Li, X.; Lu, L.; Ma, T.; Wang, Q. Heat Transfer Analysis of Phase Change Material Composited with Metal Foam-Fin Hybrid Structure in Inclination Container by Numerical Simulation and Artificial Neural Network. Energy Rep. 2022, 8, 10203–10218. [Google Scholar] [CrossRef]
- Suresh Goud, J.; Srilatha, P.; Varun Kumar, R.S.; Sowmya, G.; Gamaoun, F.; Nagaraja, K.V.; Singh Chohan, J.; Khan, U.; Eldin, S.M. Heat Transfer Analysis in a Longitudinal Porous Trapezoidal Fin by Non-Fourier Heat Conduction Model: An Application of Artificial Neural Network with Levenberg–Marquardt Approach. Case Stud. Therm. Eng. 2023, 49, 103265. [Google Scholar] [CrossRef]
- Motahar, S. Experimental Study and ANN-Based Prediction of Melting Heat Transfer in a Uniform Heat Flux PCM Enclosure. J. Energy Storage 2020, 30, 101535. [Google Scholar] [CrossRef]
- Varun Kumar, R.S.; Alsulami, M.D.; Sarris, I.E.; Prasannakumara, B.C.; Rana, S. Backpropagated Neural Network Modeling for the Non-Fourier Thermal Analysis of a Moving Plate. Mathematics 2023, 11, 438. [Google Scholar] [CrossRef]
- Tikadar, A.; Kumar, S. Investigation of Thermal-Hydraulic Performance of Metal-Foam Heat Sink Using Machine Learning Approach. Int. J. Heat Mass Transf. 2022, 199, 123438. [Google Scholar] [CrossRef]
- Storn, R. Differrential Evolution-a Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces. Tech. Rep. Int. Comput. Sci. Inst. 1995, 11, 20000924911. [Google Scholar]
- Centeno-Telleria, M.; Zulueta, E.; Fernandez-Gamiz, U.; Teso-Fz-Betoño, D.; Teso-Fz-Betoño, A. Differential Evolution Optimal Parameters Tuning with Artificial Neural Network. Mathematics 2021, 9, 427. [Google Scholar] [CrossRef]
- Atangana Njock, P.G.; Shen, S.-L.; Zhou, A.; Modoni, G. Artificial Neural Network Optimized by Differential Evolution for Predicting Diameters of Jet Grouted Columns. J. Rock Mech. Geotech. Eng. 2021, 13, 1500–1512. [Google Scholar] [CrossRef]


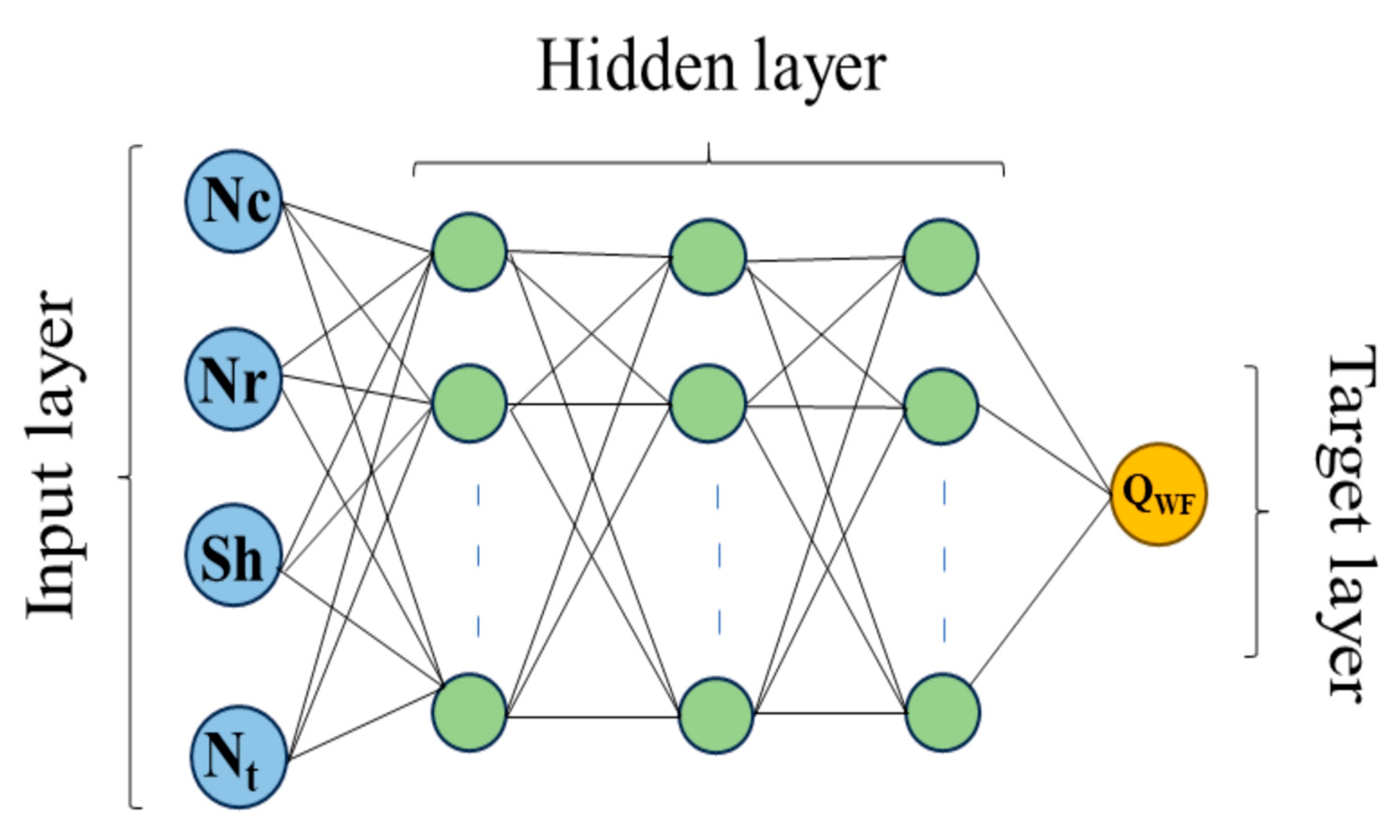
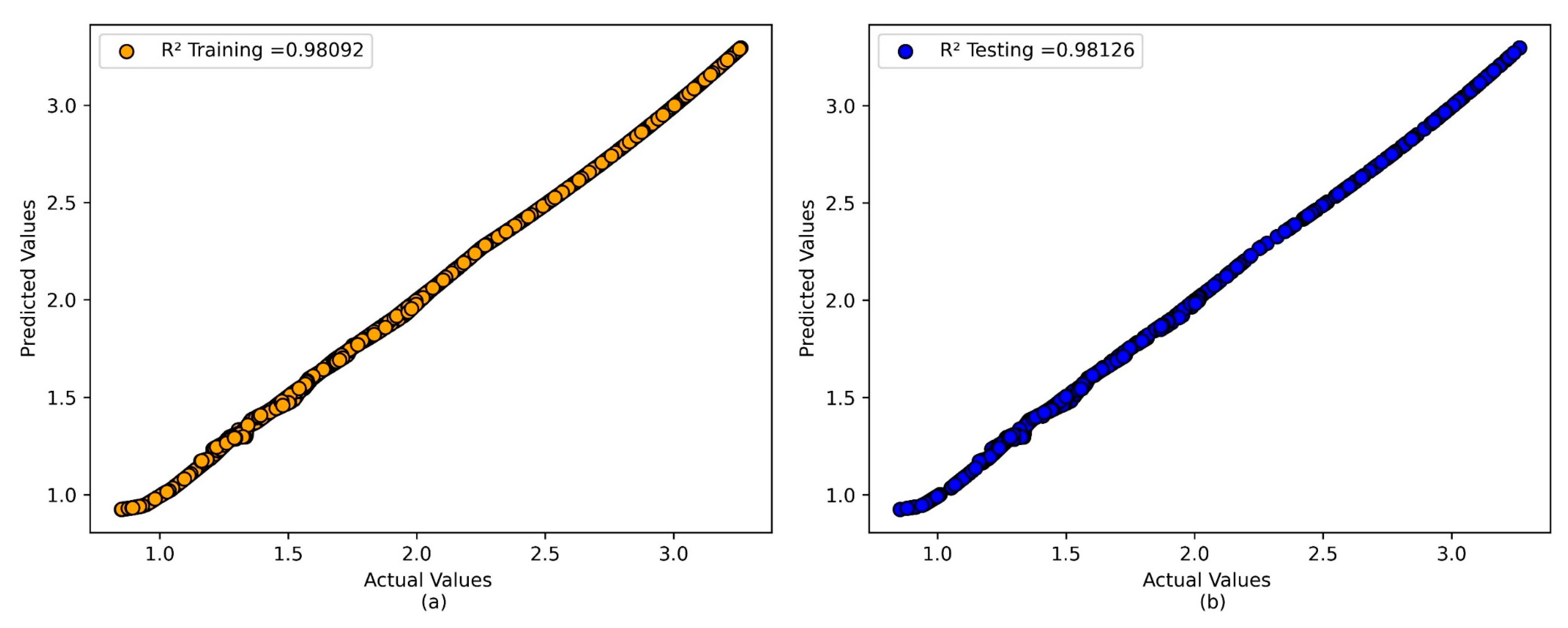
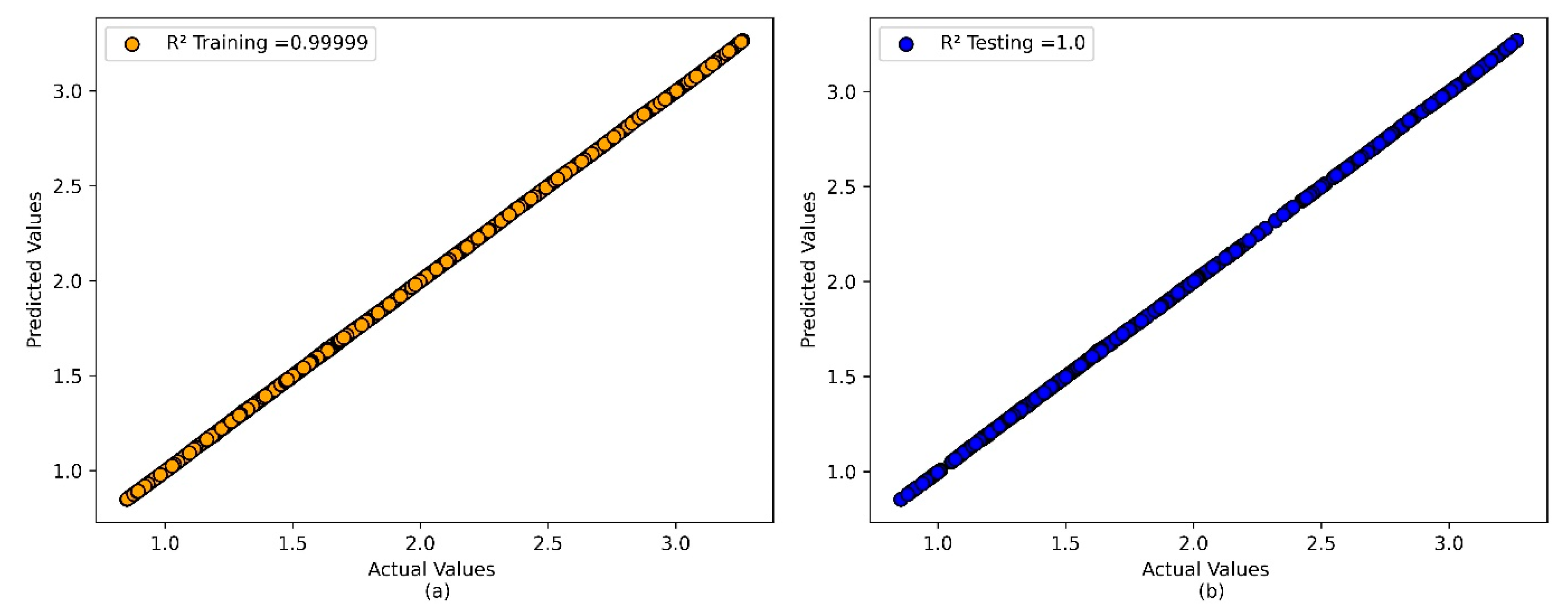
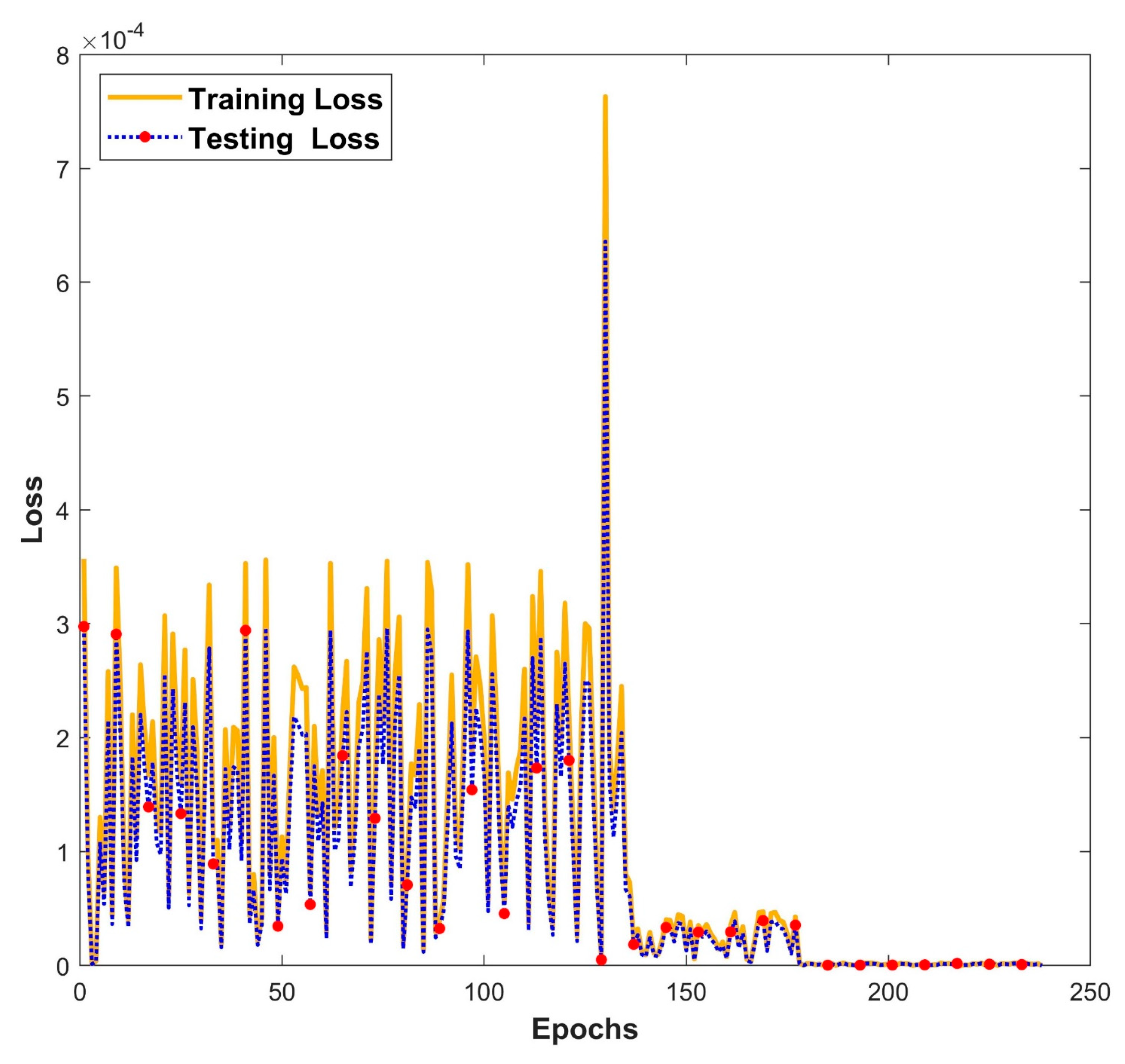
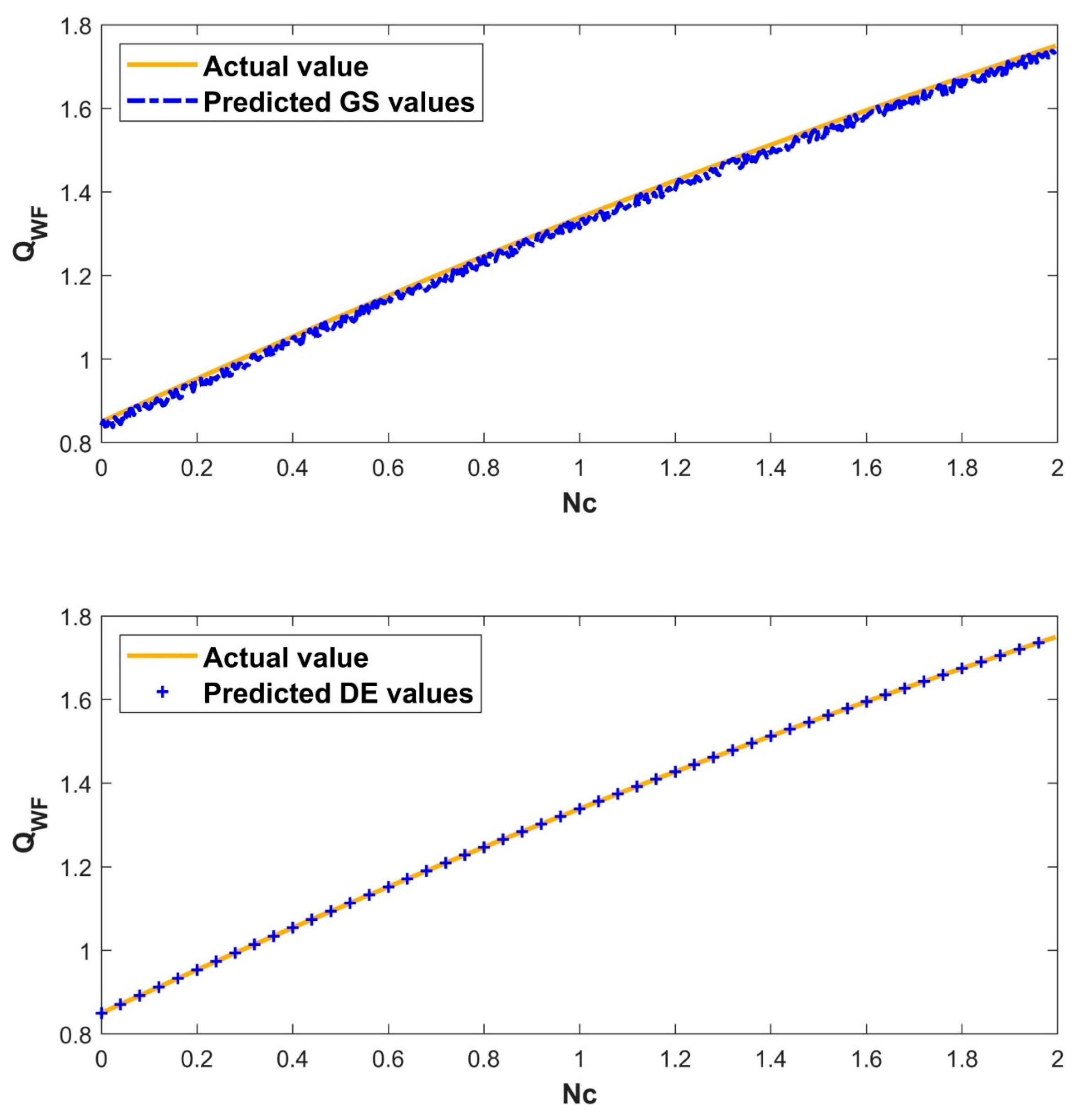

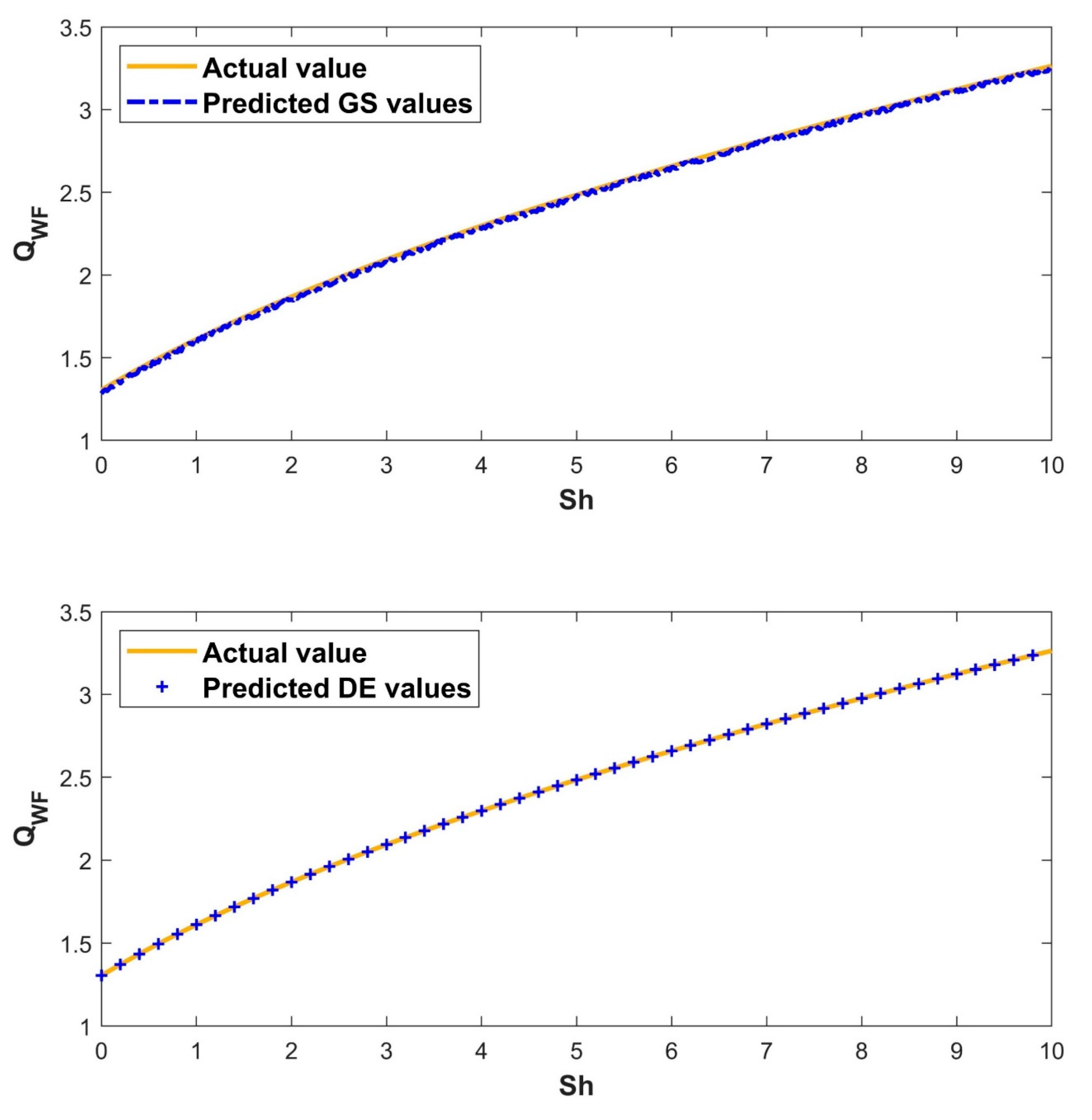
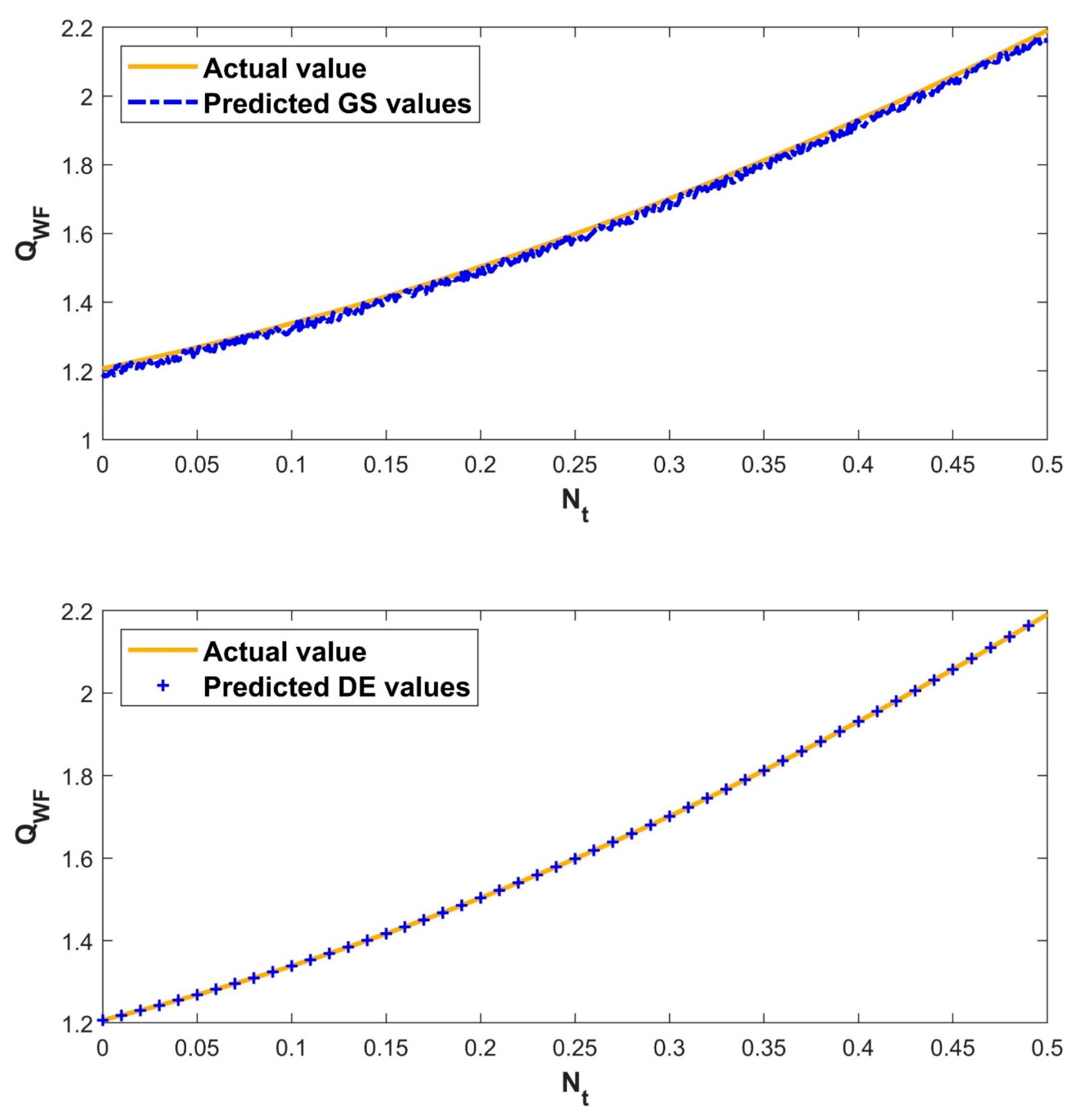
| Model | Training | Testing | ||
|---|---|---|---|---|
| MSE | ME | MSE | ME | |
| GS-ANN | 2.94 × 10−5 | 3.82 × 10−2 | 2.36 × 10−5 | 2.87 × 10−2 |
| DE-ANN | 3.34 × 10−7 | 8.43 × 10−5 | 2.84 × 10−7 | 8.01 × 10−5 |
| (RKF-45) | (GS-ANN) | Error | ||||
|---|---|---|---|---|---|---|
| 0 | 0.85011405 | 0.840990228 | 0.009123822 | |||
| 0.2 | 0.95328066 | 0.94328785 | 0.00999281 | |||
| 0.4 | 1.0539614 | 1.050534536 | 0.003426864 | |||
| 0.5 | 1.1600689 | 1.134471762 | 0.025597138 | |||
| 0.7 | 1.2348873 | 1.23078651 | 0.00410079 | |||
| 0.9 | 1.305011 | 1.295292965 | 0.009718035 | |||
| 0 | 1.3049402 | 1.28276164 | 0.02217856 | |||
| 2 | 1.8682498 | 1.850384554 | 0.017865246 | |||
| 4 | 2.2973224 | 2.280442338 | 0.016880062 | |||
| 0 | 1.2073227 | 1.180933459 | 0.026389241 | |||
| 0.3 | 1.7016177 | 1.673833355 | 0.027784345 | |||
| 0.5 | 2.1908957 | 2.163965102 | 0.026930598 |
| (RKF-45) | (DE-ANN) | Error | ||||
|---|---|---|---|---|---|---|
| 0.1 | 0.90198715 | 0.90195635 | 0.0000308156 | |||
| 0.5 | 1.1032758 | 1.1032435 | 0.0000323278 | |||
| 1.0 | 1.3385787 | 1.338533 | 0.000045695 | |||
| 1.5 | 1.5542698 | 1.5542114 | 0.0000583956 | |||
| 2.0 | 1.7511475 | 1.7510726 | 0.0000748647 | |||
| 0.60 | 1.1981278 | 1.19811899 | 0.00000880819 | |||
| 0.65 | 1.2166612 | 1.2166363 | 0.0000248735 | |||
| 0.70 | 1.2348873 | 1.2348065 | 0.0000808085 | |||
| 0.75 | 1.2528216 | 1.2527606 | 0.0000610428 | |||
| 0.80 | 1.2704784 | 1.270429 | 0.0000494225 | |||
| 1 | 1.6111099 | 1.6110987 | 0.0000111584 | |||
| 3 | 2.0938689 | 2.093848 | 0.0000208749 | |||
| 5 | 2.4841792 | 2.484161 | 0.0000181909 | |||
| 7 | 2.8213522 | 2.8213307 | 0.0000214986 | |||
| 9 | 3.1230257 | 3.1229542 | 0.0000714896 | |||
| 0.1 | 1.3385787 | 1.33856911 | 0.00000958838 | |||
| 0.2 | 1.5034813 | 1.5034201 | 0.0000611585 | |||
| 0.3 | 1.7016177 | 1.70161562 | 0.0000020828 | |||
| 0.4 | 1.9314589 | 1.9314027 | 0.0000562394 | |||
| 0.5 | 2.1908957 | 2.1908335 | 0.0000622346 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, C.; Nimmy, P.; Nagaraja, K.V.; Kumar, R.S.V.; Verma, A.; Alkarni, S.; Shah, N.A. Analysis of Heat Transfer Behavior of Porous Wavy Fin with Radiation and Convection by Using a Machine Learning Technique. Symmetry 2023, 15, 1601. https://doi.org/10.3390/sym15081601
Kumar C, Nimmy P, Nagaraja KV, Kumar RSV, Verma A, Alkarni S, Shah NA. Analysis of Heat Transfer Behavior of Porous Wavy Fin with Radiation and Convection by Using a Machine Learning Technique. Symmetry. 2023; 15(8):1601. https://doi.org/10.3390/sym15081601
Chicago/Turabian StyleKumar, Chandan, P. Nimmy, Kallur Venkat Nagaraja, R. S. Varun Kumar, Amit Verma, Shalan Alkarni, and Nehad Ali Shah. 2023. "Analysis of Heat Transfer Behavior of Porous Wavy Fin with Radiation and Convection by Using a Machine Learning Technique" Symmetry 15, no. 8: 1601. https://doi.org/10.3390/sym15081601
APA StyleKumar, C., Nimmy, P., Nagaraja, K. V., Kumar, R. S. V., Verma, A., Alkarni, S., & Shah, N. A. (2023). Analysis of Heat Transfer Behavior of Porous Wavy Fin with Radiation and Convection by Using a Machine Learning Technique. Symmetry, 15(8), 1601. https://doi.org/10.3390/sym15081601







