Feature Description Method for Contracted Graphs of Kinematic Chains and Automatic Synthesis by CAD
Abstract
:1. Introduction
2. CGs and Feature Descriptions
2.1. The Structure of CGs and Related Definitions
2.2. Characteristic String Description for CGs
3. Standardized Description of CGs
3.1. Component Sequence String and Component Number
3.2. Connection Method Substring of CGs
3.3. Standardized Description and Determination of CGs
- (1)
- The number of strings contained in each CS is the same as the number of basic links in the AL, both of which are n.
- (2)
- According to the basic links arrangement, in a CS, write out the string representing the connection method of each basic link from left to right.
- (3)
- Each string in the CS includes one or several digits, and the number of digits in any string is smaller than n, that is, the number of basic links in an AL.
- (4)
- Each digit of a string representing the number of curves connected by two basic links connected to each other. The sum of the digits is equal to the number of curves that the link needs to connect. The sum of digits representing the connection method of basic links H, P, Q, and T is 6, 5, 4 and 3, respectively.
- (5)
- In a CS, the last digit of the ith (i < n) string is the same as the first digit of the (i + 1)th string, and the first digit of the first string is the same as the last digit of the nth string.
- (6)
- The sum of all the digits in the n strings of a CS is equal to 2ne.
- (7)
- The sum of the same digits in each string of a CS must be an even number.
- (1)
- Number all strings in the CS sequentially to obtain a CSS;
- (2)
- Remove the first and last digits of each CS to form a new character string. Where the original bit of digits is two, it is indicated by “-”;
- (3)
- Connect the digits in the new string generated in step (2). In order to ensure that the generated CMS can draw a CG, and that the drawn CG is different but not isomorphic, the following criteria need to be satisfied:
- (a)
- The difference between the CNs of two interconnected links is greater than 1;
- (b)
- The head and tail links cannot be connected to each other, that is, the two links with CN 1 and n cannot be connected;
- (c)
- The number of curves connected to each other by two interconnected links is equal, that is, the corresponding digits in the new string generated in step (2) are the same, and different digits cannot be connected to each other;
- (d)
- In the generated CMSs, if the respective strings in the two CMSs correspond to the same without considering the sequence of the respective strings, only one is retained, and the others need to be deleted;
- (e)
- In the generated CMS, when the CNs of the two connected links repeatedly appear, the generated CMS needs to be deleted, as well as the corresponding CSs.
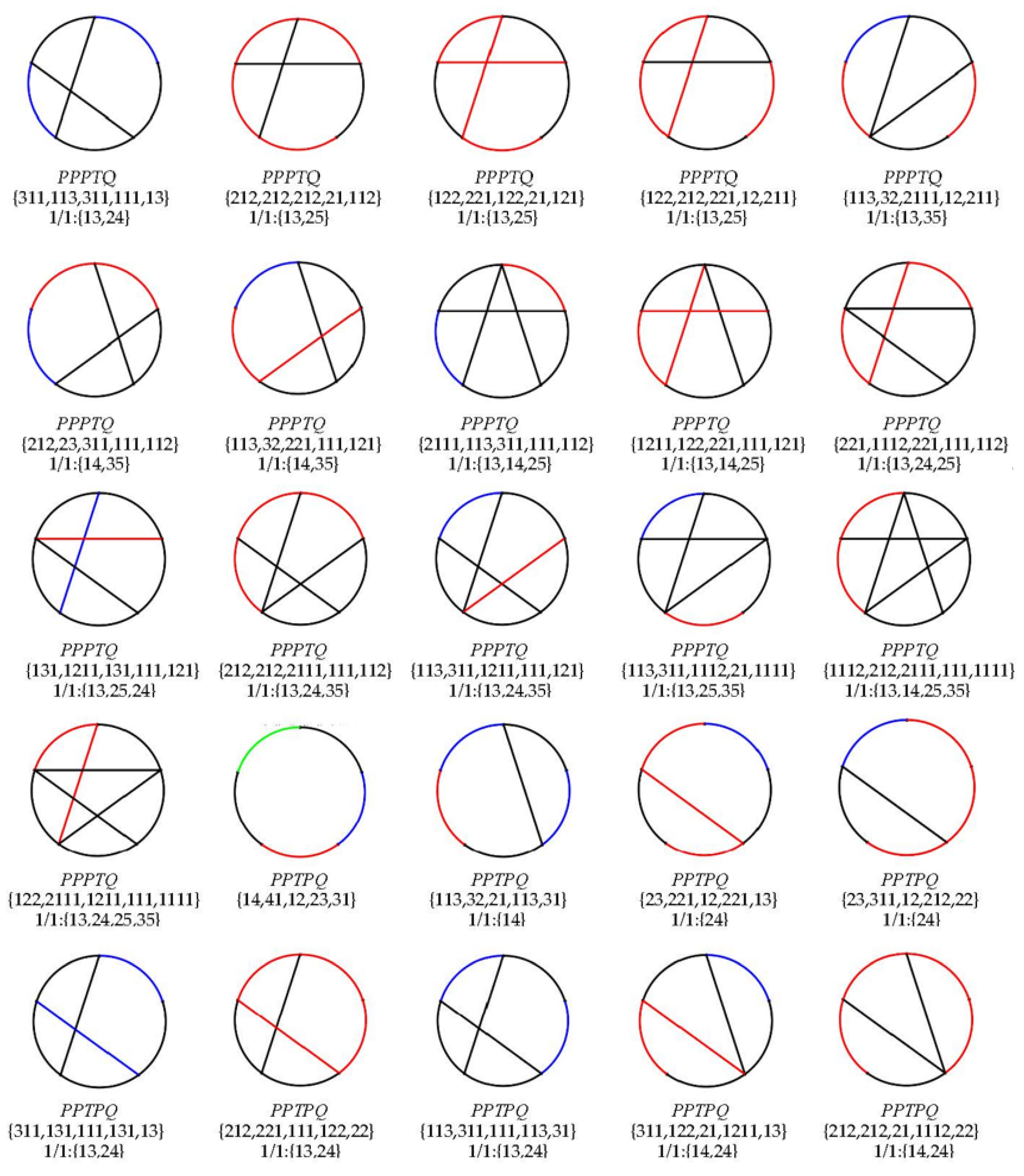
3.4. An Example for Synthesizing CGs
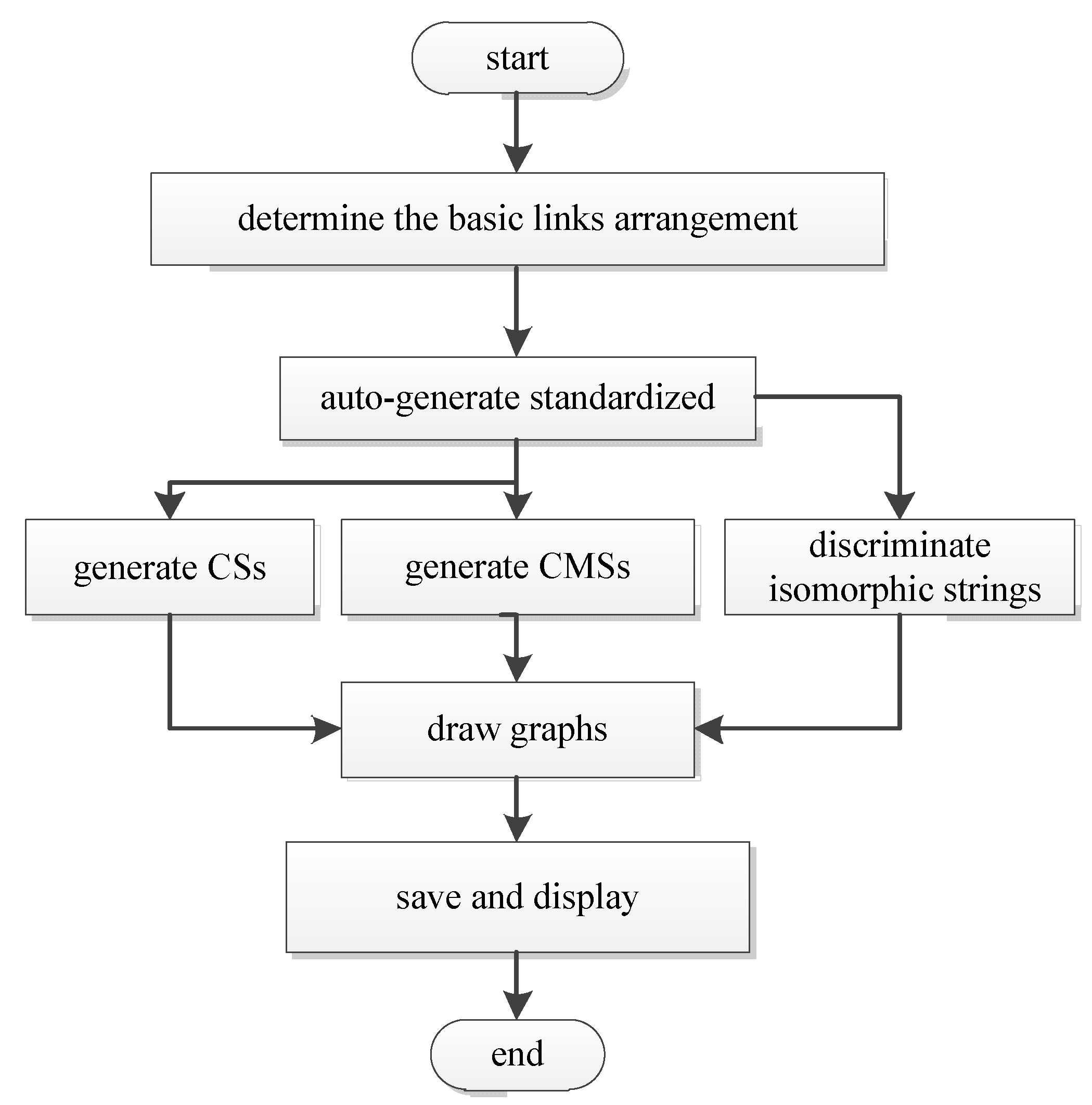
4. Automatic Synthesis of CGs by CAD
4.1. Establishment of Functional Modules and Interface
- (1)
- Generation of basic link arrangement.
- (2)
- Generation of standardized description of CGs.
- (3)
- Automatic Drawing of CGs.
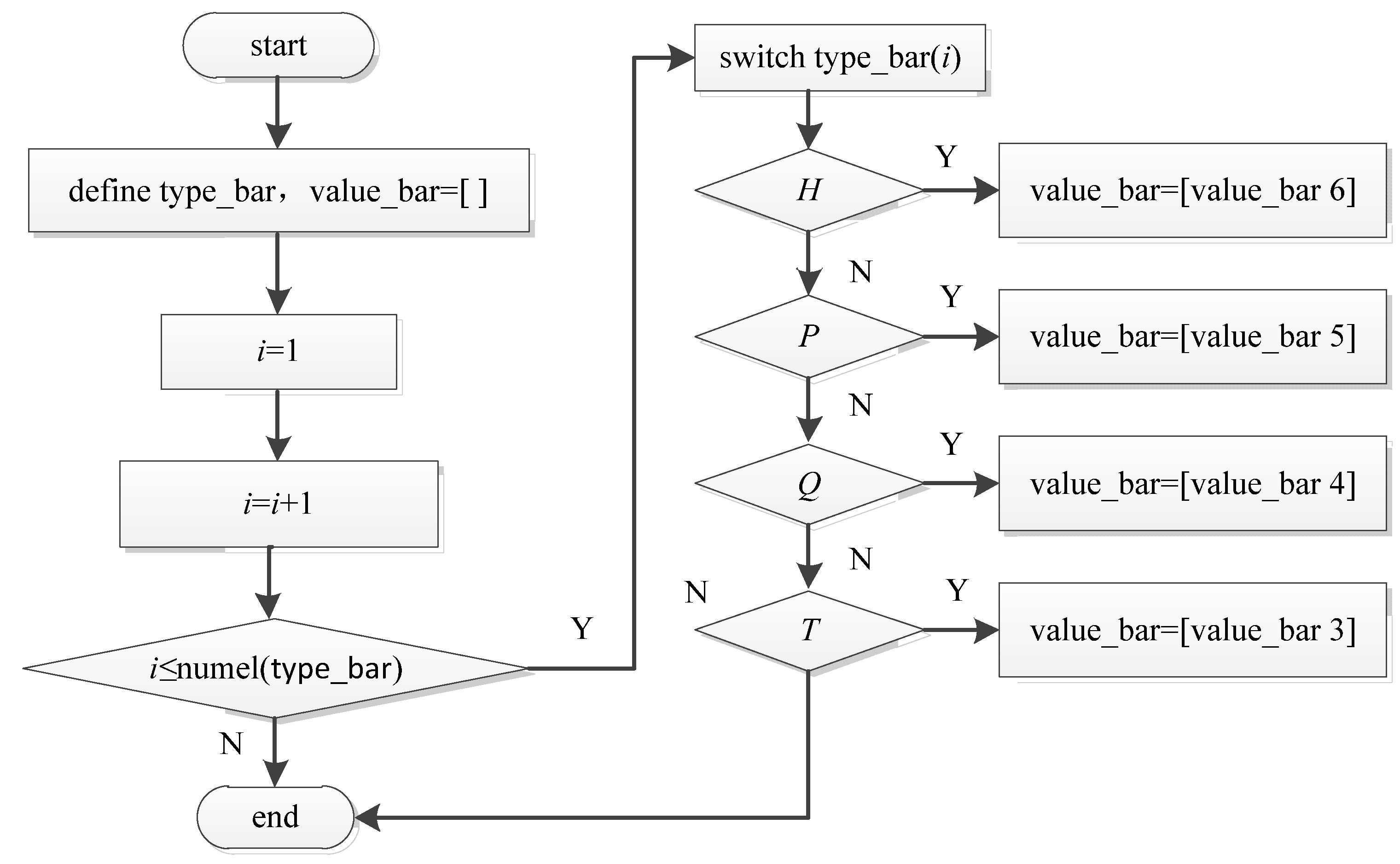
4.2. Algorithm of Programs in Software
4.2.1. Generating the Basic Links Arrangement
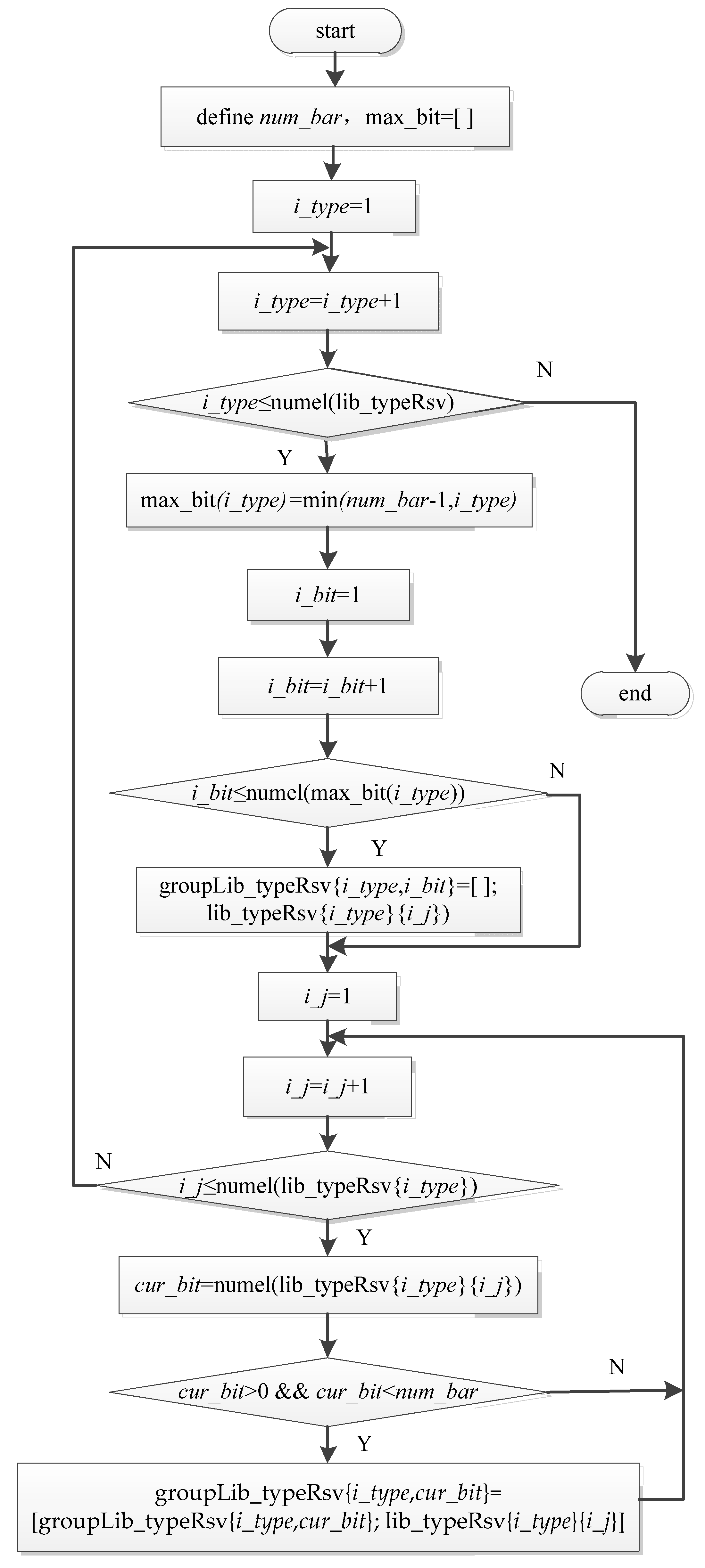
4.2.2. Generating the Valid CSs
- Numeric string representation for basic links arrangement
- 2.
- Connection strings of different basic links
- 3.
- Group connection strings of basic links
- 4.
- Determine the bit distribution mode of each basic link connection strings
- (1)
- The sum of the bits of n strings contained in each CS must be an even number, which is a multiple of 2.
- (2)
- When n is equal to 2, the number of bits in each connection string must be one.
- (3)
- When n is greater than 2, in order to ensure the closure of the drawn CG, the minimum number of bits in the connection string contained in it is two, and the maximum cannot exceed n.
- (1)
- Verify whether the connection string of each basic link in the generated CS can connect with each other, that is, the last digit of the previous basic link connection string is equal to the first digit of the current basic link connection string, and the last digit of the last basic link connection string is the same as the first digit of the first basic link connection string.
- (2)
- Verify whether the sum of the same digits in the basic link connection string in the generated CS is even.
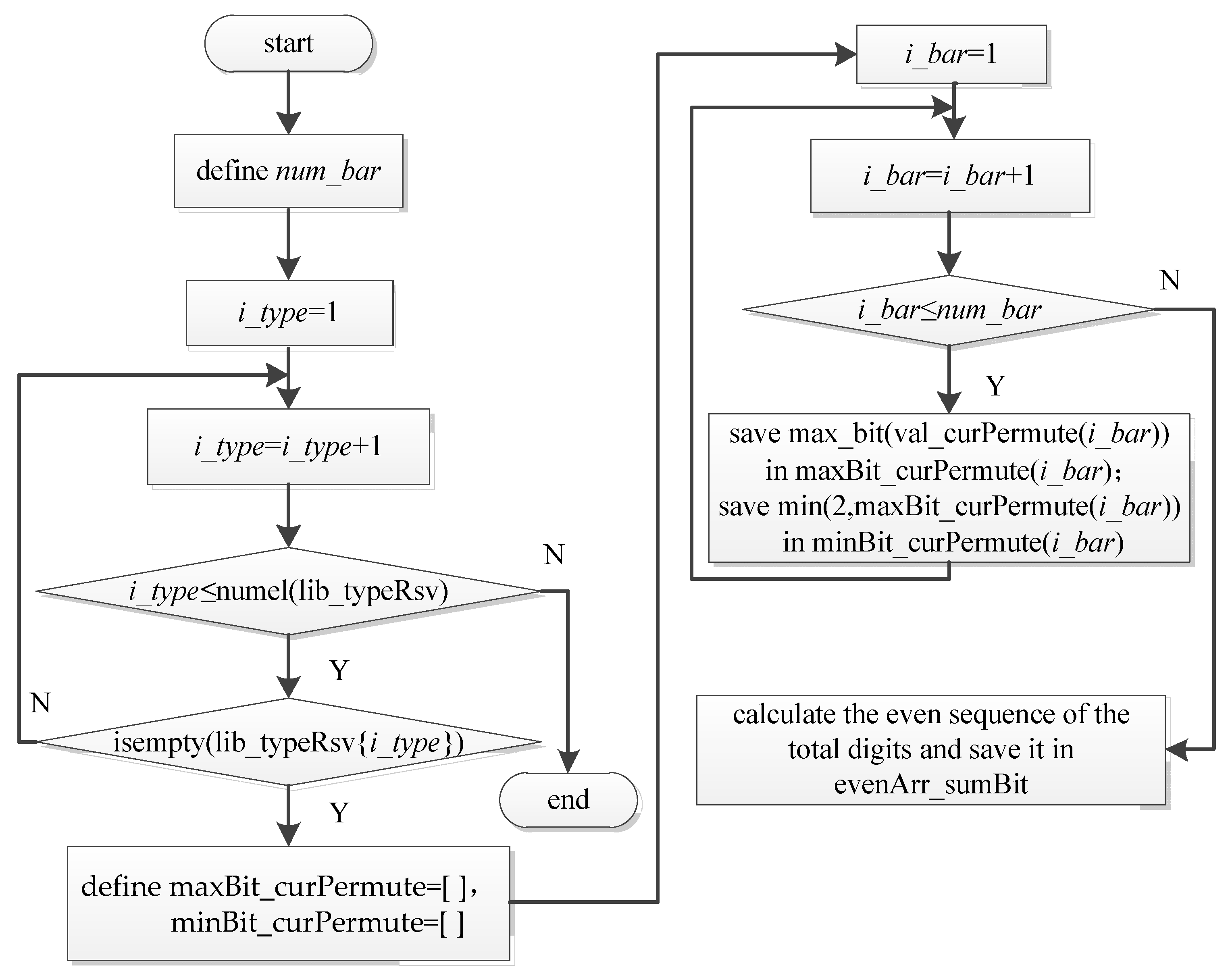
4.2.3. Generating the Valid CMSs
4.2.4. Drawing CGs
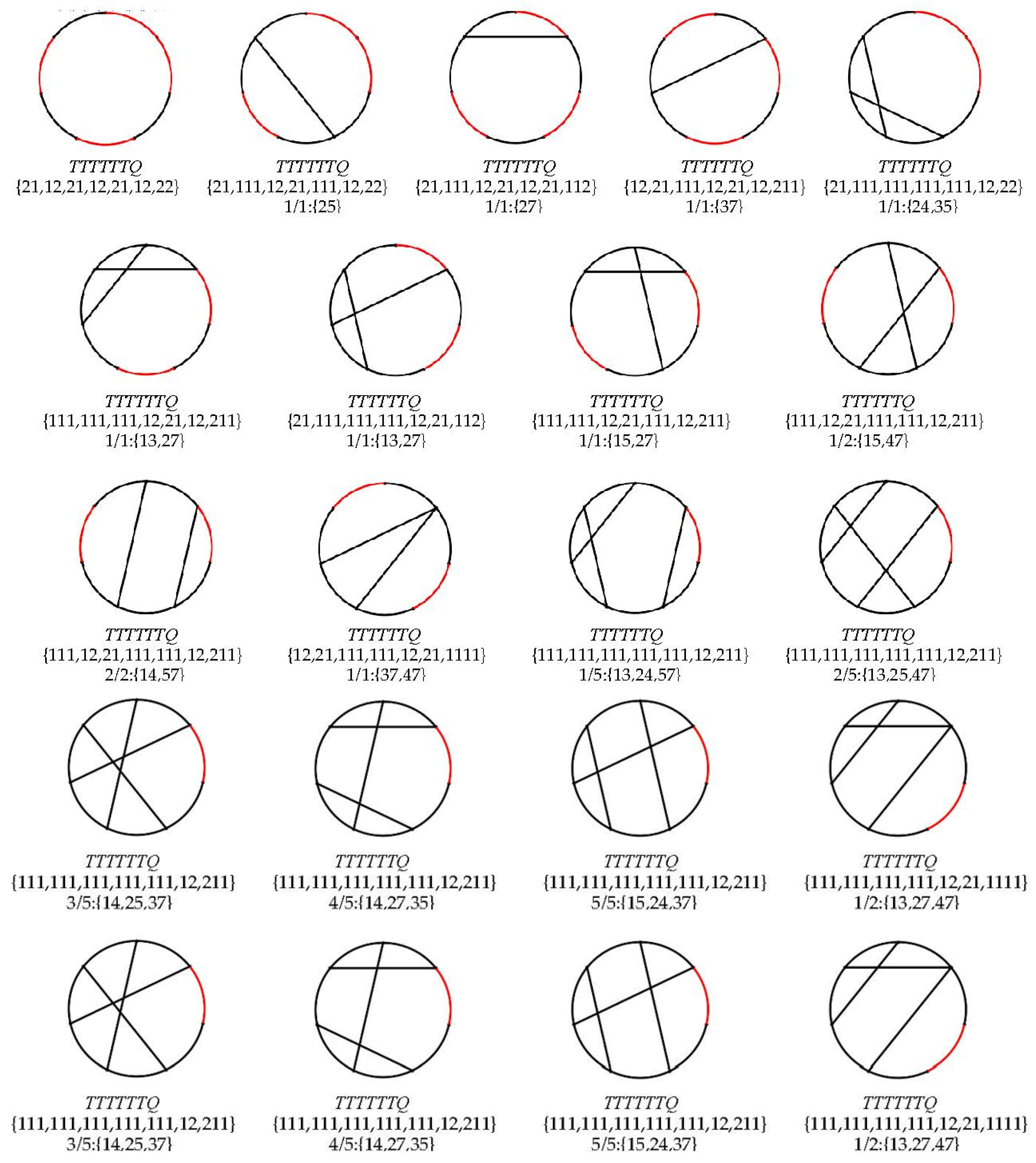
5. Application Examples of Automatic Synthesis of CGs
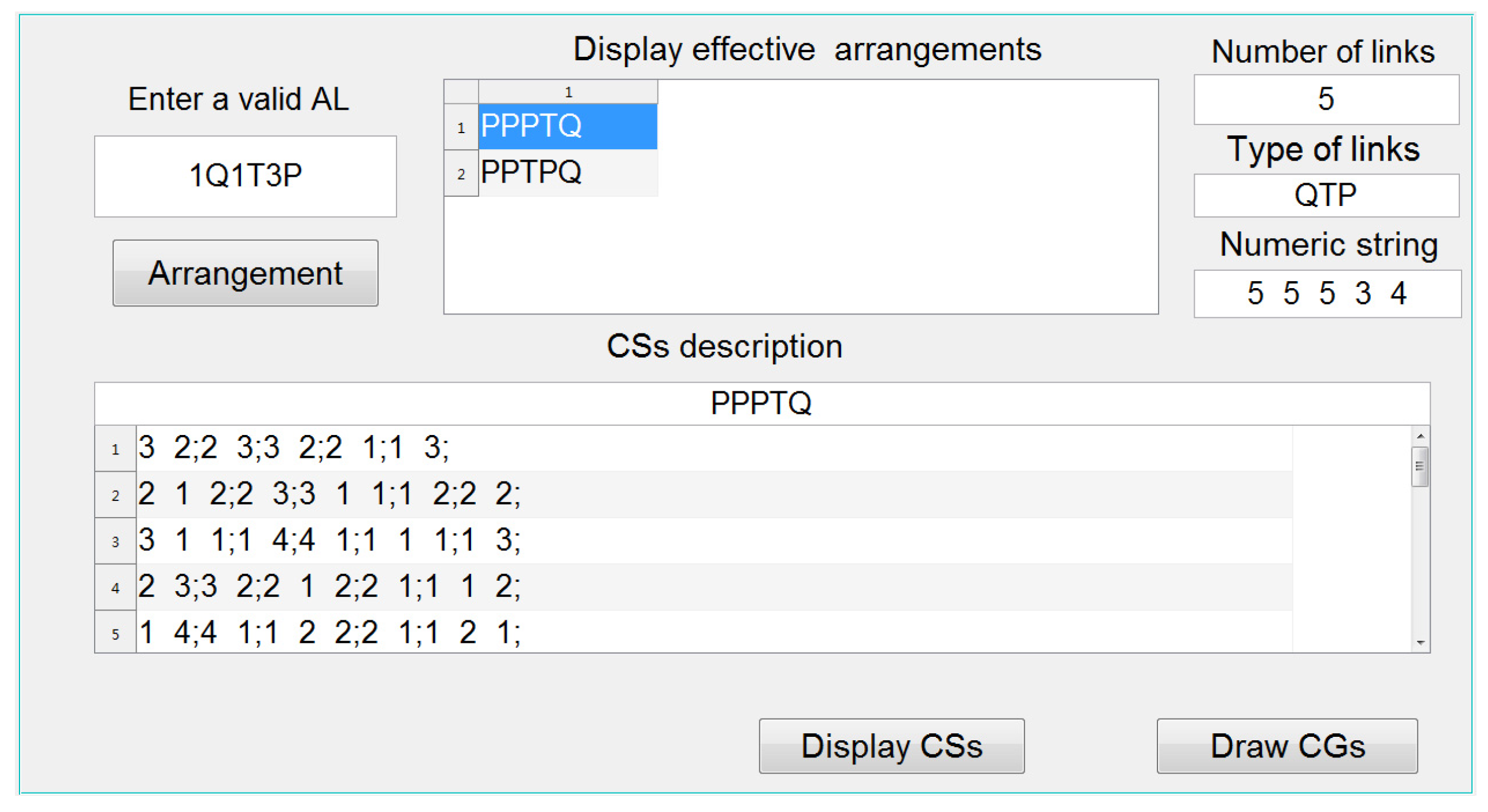
5.1. CGs of 1Q1T3P and Time Complexity Analysis
5.2. CGs of 1Q6T
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, L.; Wang, Y.; Pattabiraman, K.; Danesh, P.; Siddiqui, M.K.; Cancan, M. Topological indices and QSPR modeling of new antiviral drugs for cancer treatment. Polycycl. Aromat. Compd. 2022, 150, 1–22. [Google Scholar] [CrossRef]
- Wang, X.J.; Hanif, M.F.; Mahmood, H.; Manzoor, S.; Siddiqui, M.K.; Cancan, M. On computation of entropy measures and their statistical analysis for complex benzene systems. Polycycl. Aromat. Compd. 2022, 66, 1–15. [Google Scholar]
- Ullah, A.; Zeb, A.; Zaman, S. A new perspective on the modeling and topological characterization of H-Naphtalenic nanosheets with applications. J. Mol. Model. 2022, 28, 211. [Google Scholar] [CrossRef] [PubMed]
- Biggs, N.L.; Keyth, L.E.; Wilson, R.J. Graph Theory; Clarendon Press: Oxford, UK, 1976. [Google Scholar]
- Johnson, R.C. Mechanical Design Synthesis-Creative Design and Optimize, 2nd ed.; Huntington: New York, NY, USA, 1987. [Google Scholar]
- Vucina, D.; Freudenstein, F. Application of graph theory and non-linear programming to the kinematic synthesis of mechanisms. Mech. Mach. Theory 1991, 26, 553–563. [Google Scholar] [CrossRef]
- Dobrjanskyj, L.; Freudenstein, F. Some applications of graph theory to the structural analysis of mechanisms. J. Eng. Ind. 1967, 89, 153–158. [Google Scholar] [CrossRef]
- Yan, H.S.; Hsu, C.H. Contracted graphs of kinematic chains with multiple joints. Math. Comput. Model. 1988, 10, 681–695. [Google Scholar] [CrossRef]
- Jin, Q.; Yang, T.L. Theory for topology synthesis of parallel manipulators and its application to three-dimension-translation parallel manipulators. J. Mech. Des. 2004, 126, 625–639. [Google Scholar] [CrossRef]
- Lu, Y.; Leinonen, T. Type synthesis of unified planar-spatial mechanisms by systematic linkage and topology matrix-graph technique. Mech. Mach. Theory 2005, 40, 1145–1163. [Google Scholar] [CrossRef]
- Tsai, L.W. Mechanism Design: Enumeration of Kinematic Structures According to Function; CRC Press: Boca Raton, FL, USA, 2001; pp. 45–328. [Google Scholar]
- Yang, T.L.; Jin, Q.; Liu, A.X. Structural synthesis and classification of the 3DOF translational parallel robot mechanisms based on the units of single-opened-chain. Chin. J. Mech. Eng. 2002, 38, 31–36. [Google Scholar] [CrossRef]
- Gogu, G. Structural Synthesis of Parallel Robots; Part I: Methodology; Springer: New York, NY, USA, 2008; pp. 99–119. [Google Scholar]
- Moon, Y.M.; Kota, S. Automated synthesis of mechanisms using dual-vector algebra. Mech. Mach. Theory 2002, 37, 143–166. [Google Scholar] [CrossRef]
- Zhou, H.; Ting, K.L. Topological synthesis of compliant mechanisms using spanning tree theory. J. Mech. Des. 2005, 127, 753–759. [Google Scholar] [CrossRef]
- Yan, H.S.; Kang, C.H. Configuration synthesis of mechanisms with variable topologies. Mech. Mach. Theory 2009, 44, 896–911. [Google Scholar] [CrossRef]
- Yan, H.S.; Kuo, C.H. Topological representations and characteristics of variable kinematic joints. J. Mech. Des. 2006, 128, 384–391. [Google Scholar] [CrossRef]
- Martin, A.P.; Alberto, C. An automated method for type synthesis of planar linkages based on a constrained subgraph isomorphism detection. Multibody Syst. Dyn. 2007, 18, 233–258. [Google Scholar]
- Martin, A.P.; Alberto, C. Synthesis of planar multiloop linkages starting from existing parts or mechanisms: Enumeration and initial sizing. Mech. Based Des. Struct. Mach. 2008, 36, 364–391. [Google Scholar]
- Ding, H.F.; Yang, W.J.; Huang, P. Automatic structural synthesis of planar multiple joint kinematic chains. ASME J. Mech. Des. 2013, 135, 091007. [Google Scholar] [CrossRef]
- Ding, H.F.; Cao, W.A.; Cai, C.W.; Kecskemethy, A. Computer-aided structural synthesis of 5-DOF parallel mechanisms and the establishment of kinematic structure databases. Mech. Mach. Theory 2014, 83, 14–30. [Google Scholar] [CrossRef]
- Saura, M.; Celdran, A.; Dopico, D.; Cuadrado, J. Computational structural analysis of planar multibody systems with lower and higher kinematic pairs. Mech. Mach. Theory 2014, 71, 79–92. [Google Scholar] [CrossRef]
- Ding, H.F.; Cao, W.A.; Chen, Z.M.; Kecskemethy, A. Structural synthesis of two-layer and two-loop spatial mechanisms with coupling chains. Mech. Mach. Theory 2015, 92, 289–313. [Google Scholar] [CrossRef]
- Sun, L.; Cui, R.J.; Yang, W.J.; Ye, Z.Z.; Zhou, Y.Z.; Wu, C.Y. Automatic synthesis of the complete set of contracted graphs for planar kinematic chains with up to seven independent loops. Mech. Mach. Theory 2021, 156, 1–19. [Google Scholar] [CrossRef]
- Ding, L.; Cui, W. Isomorphism identification of kinematic chain topology graph based on embryonic graphs. J. Mach. Des. 2015, 11, 60–62. [Google Scholar]
- Lu, Y.; Wang, Y.; Lu, Y.; Ye, N.J. Derivation of contracted graphs with ternary/quaternary links for type synthesis of parallel mechanisms by characteristic strings. Robotica 2015, 33, 548–562. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Y. Determination of Permutation and Combination of Basic Links in Associated Linkage of Closed Mechanisms. J. Mech. Eng. 2016, 52, 130–136. [Google Scholar] [CrossRef]





| CGs | Basic Link Arrangement | CSs |
|---|---|---|
| 1 | HPQT | {213, 32, 211, 12} |
| 2 | HPQT | {114, 41, 112, 21} |
| 3 | HPQT | {123, 311, 121, 111} |
| 4 | HQPT | {123, 31, 122, 21} |
| 5 | HQPT | {222, 22, 221, 12} |
| 6 | HQPT | {132, 211, 131, 111} |
| 7 | HPTQ | {33, 32, 21, 13} |
| 8 | HPTQ | {24, 41, 12, 22} |
| 9 | HPTQ | {213, 311, 111, 112} |
| No. | H | T | T | T | T | T | T |
|---|---|---|---|---|---|---|---|
| 1 | 2112 | 21 | 12 | 21 | 111 | 111 | 12 |
| 2 | 2112 | 21 | 111 | 12 | 21 | 111 | 12 |
| 3 | 2112 | 21 | 111 | 111 | 111 | 111 | 12 |
| 4 | 21111 | 12 | 21 | 111 | 111 | 111 | 12 |
| 5 | 21111 | 111 | 111 | 111 | 111 | 111 | 12 |
| 6 | 111111 | 111 | 111 | 111 | 111 | 111 | 111 |
| CSs | Connection Method of Intermediate Bit |
|---|---|
| {2112, 21, 111, 111, 111, 111, 12} |  |
| {21111, 111, 111, 111, 111, 111, 12} | 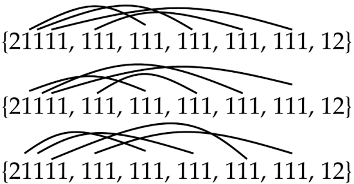 |
| No. | CMS |
|---|---|
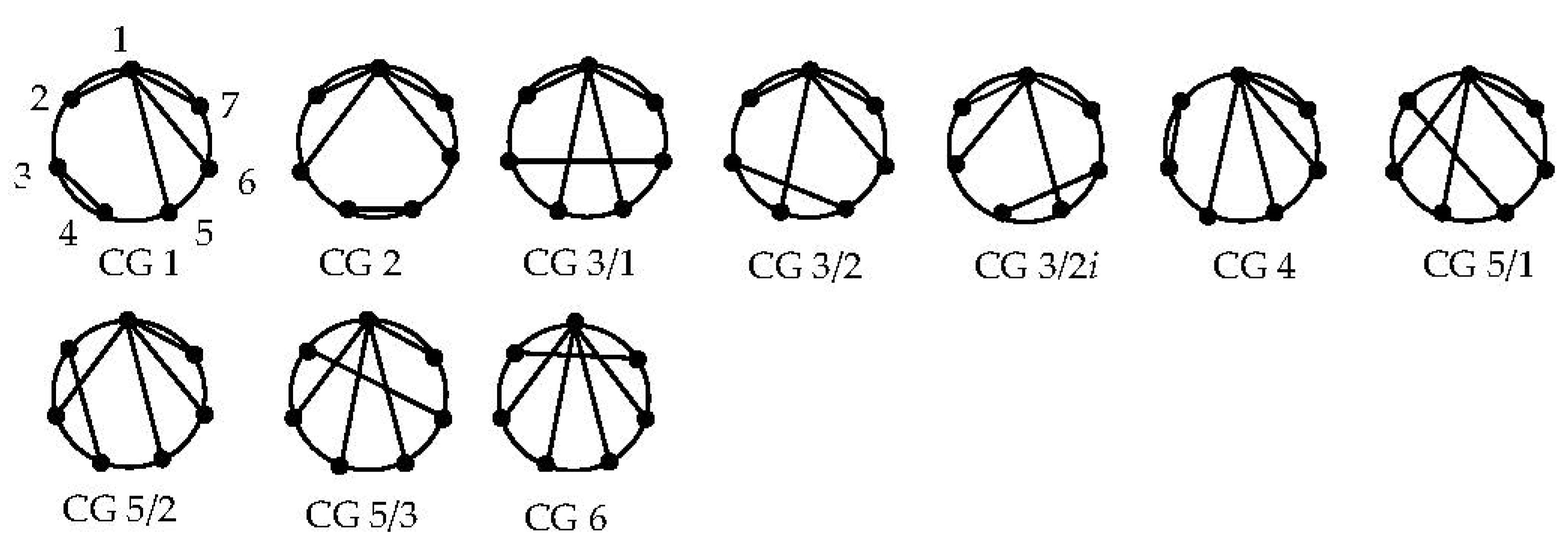
| CG 1 | {15, 16} |
| CG 2 | {13, 16} |
| CG 3/1 | {14, 15, 36} |
| CG 3/2 | {14, 16, 35} |
| CG 3/2i | {13, 15, 46} |
| CG 4 | {14, 15, 16} |
| CG 5/1 | {13, 14, 16, 25} |
| CG 5/2 | {13, 15, 16, 24} |
| CG 5/3 | {13, 14, 15, 26} |
| CG 6 | {13, 14, 15, 16, 27} |
| Basic Links Arrangement | No. | CSs | CMSs |
|---|---|---|---|
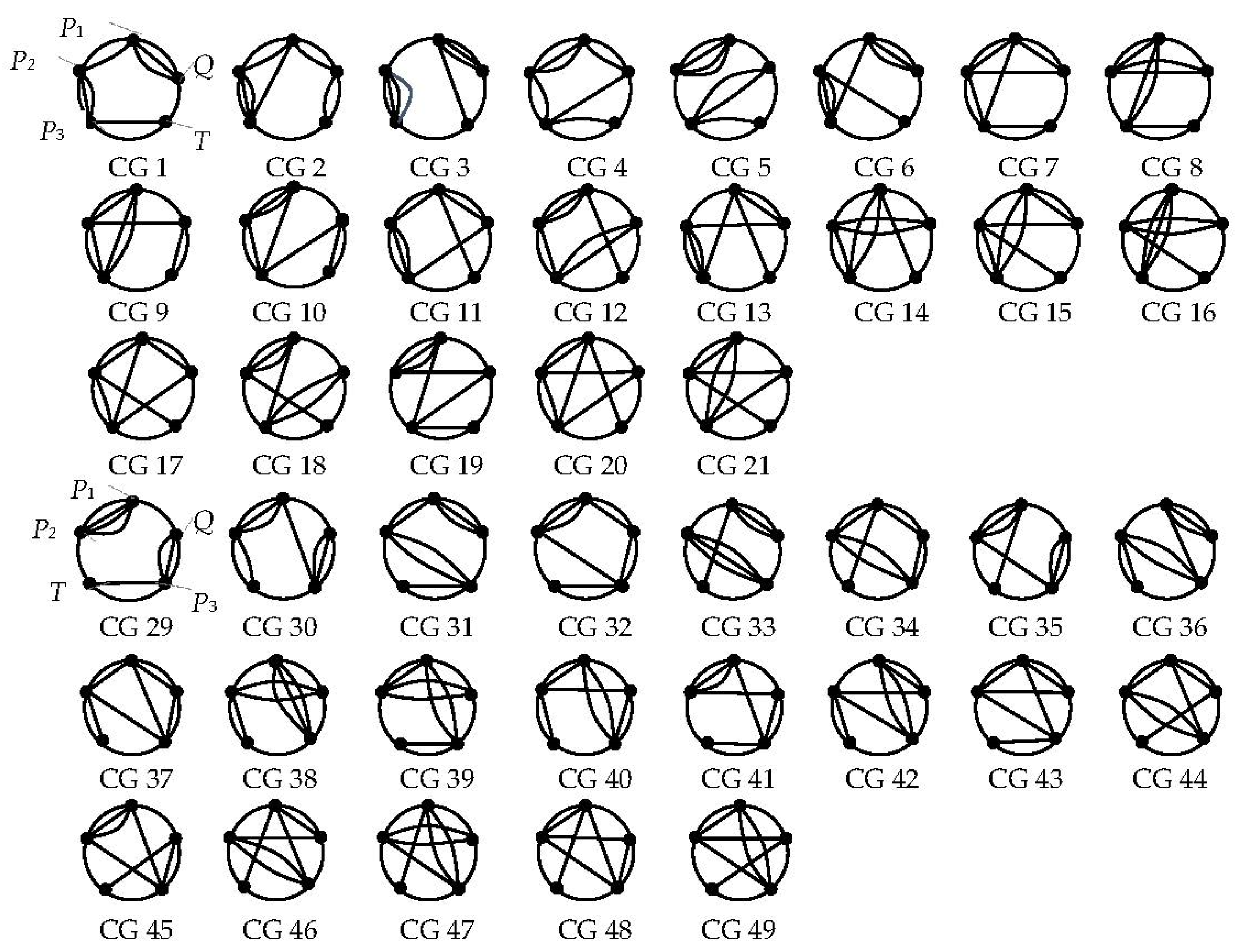
| PPPTQ | 1 | {32, 23, 32, 21, 13} | —— |
| 2 | {212, 23, 311, 12, 22} | {13} | |
| 3 | {311, 14, 41, 111, 13} | {14} | |
| 4 | {23, 32, 212, 21, 112} | {35} | |
| 5 | {14, 41, 122, 21, 121} | {35} | |
| 6 | {311, 113, 311, 111, 13} | {13, 24} | |
| 7 | {212, 212, 212, 21, 112} | {13, 25} | |
| 8 | {122, 221, 122, 21, 121} | {13, 25} | |
| 9 | {122, 212, 221, 12, 211} | {13, 25} | |
| 10 | {113, 32, 2111, 12, 211} | {13, 35} | |
| 11 | {212, 23, 311, 111, 112} | {14, 35} | |
| 12 | {113, 32, 221, 111, 121} | {14, 35} | |
| 13 | {2111, 113, 311, 111, 112} | {13, 14, 25} | |
| 14 | {1211, 122, 221, 111, 121} | {13, 14, 25} | |
| 15 | {221, 1112, 221, 111, 112} | {13, 24, 25} | |
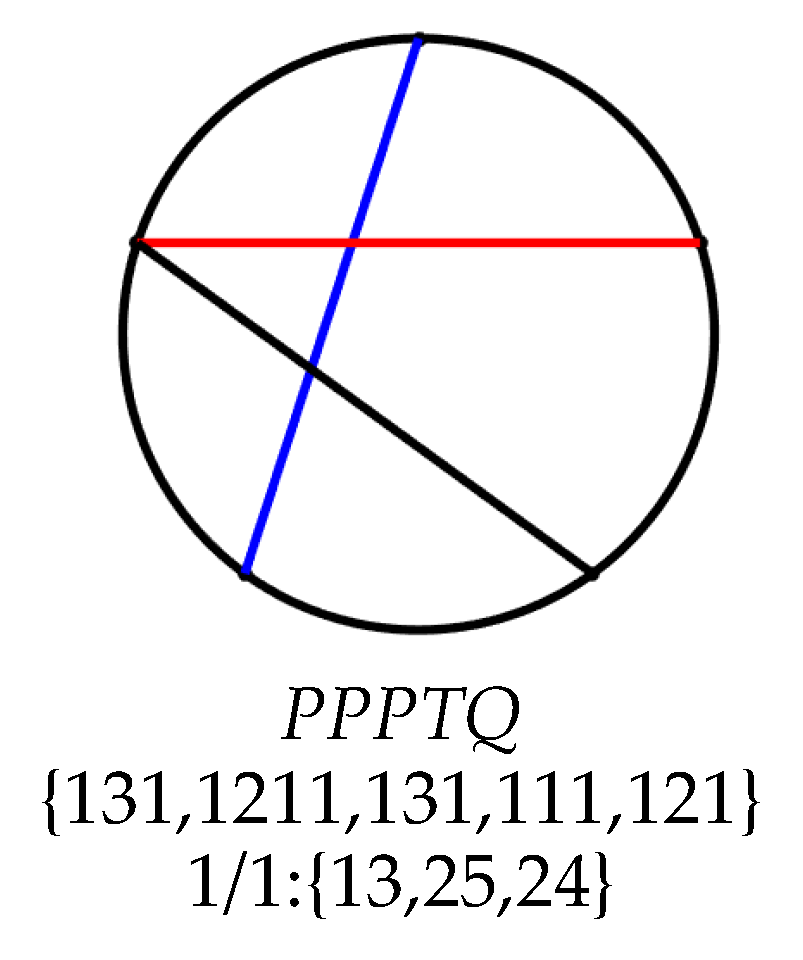
| 16 | {131, 1211, 131, 111, 121} | {13, 25, 24} | |
| 17 | {212, 212, 2111, 111, 112} | {13, 24, 35} | |
| 18 | {113, 311, 1211, 111, 121} | {13, 24, 35} | |
| 19 | {113, 311, 1112, 21, 1111} | {13, 25, 35} | |
| 20 | {1112, 212, 2111, 111, 1111} | {13, 14, 25, 35} | |
| 21 | {122, 2111, 1211, 111, 1111} | {13, 24, 25, 35} | |
| 22 | {14, 41, 1112, 21, 1111} | {35, 35} | |
| 23 | {1112, 221, 1112, 21, 121} | {13, 13, 25} | |
| 24 | {1112, 212, 2111, 12, 211} | {13, 13, 25} | |
| 25 | {113, 32, 2111, 111, 1111} | {14, 35, 35} | |
| 26 | {2111, 1112, 2111, 111, 112} | {13, 13, 24, 25} | |
| 27 | {1211, 1211, 1211, 111, 121} | {13, 13, 25, 24} | |
| 28 | {1211, 1112, 221, 111, 1111} | {13, 14, 25, 25} | |
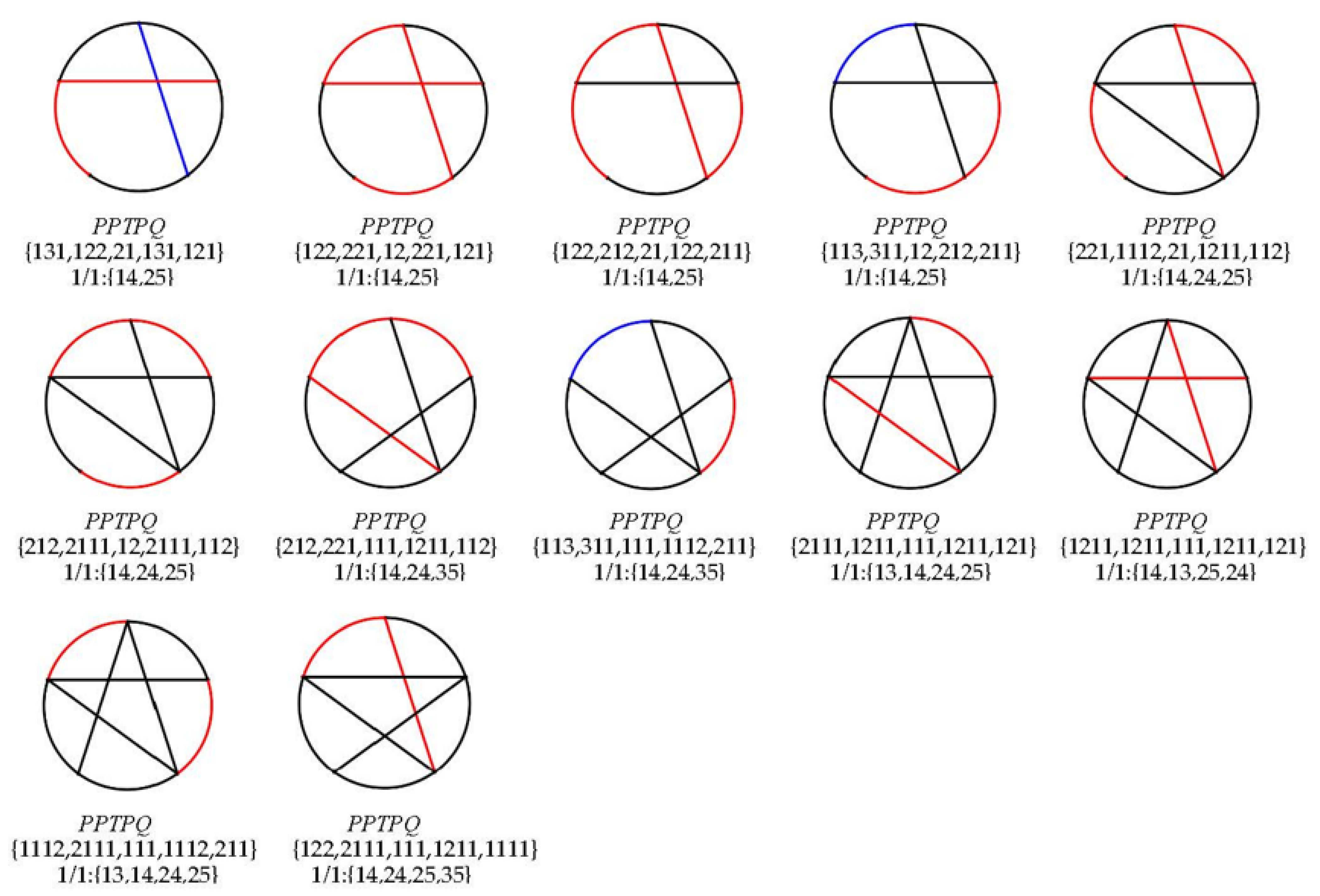
| PPTPQ | 29 | {14, 41, 12, 23, 31} | —— |
| 30 | {113, 32, 21, 113, 31} | {14} | |
| 31 | {32, 221, 12, 221, 13} | {24} | |
| 32 | {23, 311, 12, 212, 22} | {24} | |
| 33 | {311, 131, 111, 131, 13} | {13, 24} | |
| 34 | {212, 221, 111, 122, 22} | {13, 24} | |
| 35 | {113, 311, 111, 113, 31} | {13, 24} | |
| 36 | {311, 122, 21, 1211, 13} | {14, 24} | |
| 37 | {212, 212, 21, 1112, 22} | {14, 24} | |
| 38 | {131, 122, 21, 131, 121} | {14, 25} | |
| 39 | {122, 221, 12, 221, 121} | {14, 25} | |
| 40 | {122, 212, 21, 122, 211} | {14, 25} | |
| 41 | {113, 311, 12, 212, 211} | {14, 25} | |
| 42 | {221, 1112, 21, 1211, 112} | {14, 24, 25} | |
| 43 | {212, 2111, 12, 2111, 112} | {14, 24, 25} | |
| 44 | {212, 221, 111, 1211, 112} | {14, 24, 35} | |
| 45 | {113, 311, 111, 1112, 211} | {14, 24, 35} | |
| 46 | {2111, 1211, 111, 1211, 112} | {13, 14, 24, 25} | |
| 47 | {1211, 1211, 111, 1211, 121} | {14, 13, 25, 24} | |
| 48 | {1112, 2111, 111, 1112, 211} | {13, 14, 24, 25} | |
| 49 | {122, 2111, 111, 1211, 1111} | {14, 24, 25, 35} |
| Bits | T | Q | P |
|---|---|---|---|
| one-bit | {3} | {4} | {5} |
| two-bit | {12}, {21} | {13}, {31}, {22} | {14}, {41}, {23}, {32} |
| three-bit | {111} | {112}, {121}, {211} | {113}, {131}, {311}, {122}, {212}, {221} |
| four-bit | {1111} | {1112}, {1211}, {2111} |
| Total Digits | Bit Distribution for Connection Methods of Basic Links | No. |
|---|---|---|
| 10 | {2 2 2 2 2} | 1 |
| 12 | {4 2 2 2 2}, {3 3 2 2 2}, {2 4 2 2 2}, {3 2 3 2 2}, {2 3 3 2 2}, {2 2 4 2 2}, {3 2 2 3 2}, {2 3 2 3 2}, {2 2 3 3 2}, {3 2 2 2 3}, {2 3 2 2 3}, {2 2 3 2 3}, {2 2 2 3 3}, {2 2 2 2 4} | 14 |
| 14 | {4 4 2 2 2}, {4 3 3 2 2}, {3 4 3 2 2}, {4 2 4 2 2}, {3 3 4 2 2}, {2 4 4 2 2}, {4 3 2 3 2}, {3 4 2 3 2}, {4 2 3 3 2}, {3 3 3 3 2}, {2 4 3 3 2}, {3 2 4 3 2}, {2 3 4 3 2}, {4 3 2 2 3}, {3 4 2 2 3}, {4 2 3 2 3}, {3 3 3 2 3}, {2 4 3 2 3}, {3 2 4 2 3}, {2 3 4 2 3}, {4 2 2 3 3}, {3 3 2 3 3}, {2 4 2 3 3}, {3 2 3 3 3}, {2 3 3 3 3}, {2 2 4 3 3}, {4 2 2 2 4}, {3 3 2 2 4}, {2 4 2 2 4}, {3 2 3 2 4}, {2 3 3 2 4}, {2 2 4 2 4}, {3 2 2 3 4}, {2 3 2 3 4}, {2 2 3 3 4} | 35 |
| 16 | {4 4 4 2 2}, {4 4 3 3 2}, {4 3 4 3 2}, {3 4 4 3 2}, {4 4 3 2 3}, {4 3 4 2 3}, {3 4 3 2 3}, {4 4 2 3 3}, {4 3 3 3 3}, {3 4 3 3 3}, {4 2 4 3 3}, {3 3 4 3 3}, {2 4 4 3 3}, {4 4 2 2 4}, {4 3 3 2 4}, {3 4 3 2 4}, {4 2 4 2 4}, {3 3 4 2 4}, {2 4 4 2 4}, {4 3 2 3 4}, {3 4 2 3 4}, {4 2 3 3 4}, {3 3 3 3 4}, {2 4 3 3 4}, {3 2 4 3 4}, {2 3 4 3 4} | 26 |
| 18 | {4 4 4 3 3}, {4 4 4 2 4}, {4 4 3 3 4}, {4 3 4 3 4}, {3 4 4 3 4} | 5 |
| Bit Distribution | {2 2 2 2 2} |
|---|---|
| P | 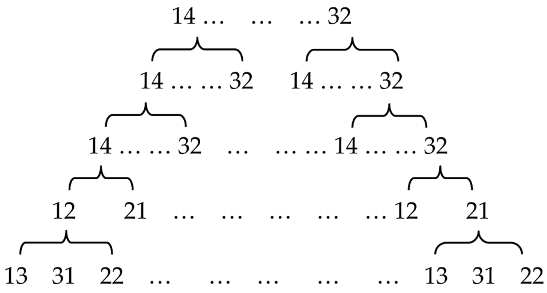 |
| P | |
| P | |
| T | |
| Q |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, S.; Chen, Z. Feature Description Method for Contracted Graphs of Kinematic Chains and Automatic Synthesis by CAD. Symmetry 2023, 15, 1559. https://doi.org/10.3390/sym15081559
Wang Y, Chen S, Chen Z. Feature Description Method for Contracted Graphs of Kinematic Chains and Automatic Synthesis by CAD. Symmetry. 2023; 15(8):1559. https://doi.org/10.3390/sym15081559
Chicago/Turabian StyleWang, Ying, Shuang Chen, and Zhipeng Chen. 2023. "Feature Description Method for Contracted Graphs of Kinematic Chains and Automatic Synthesis by CAD" Symmetry 15, no. 8: 1559. https://doi.org/10.3390/sym15081559
APA StyleWang, Y., Chen, S., & Chen, Z. (2023). Feature Description Method for Contracted Graphs of Kinematic Chains and Automatic Synthesis by CAD. Symmetry, 15(8), 1559. https://doi.org/10.3390/sym15081559





