Homotopy Double Copy of Noncommutative Gauge Theories
Abstract
1. Introduction
1.1. KLT Double Copy
1.2. BCJ Double Copy
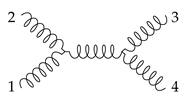
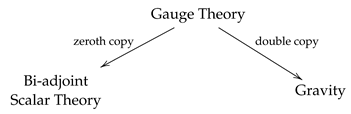
1.3. Homotopy Double Copy

1.4. Noncommutative Gauge Theories and Gravity
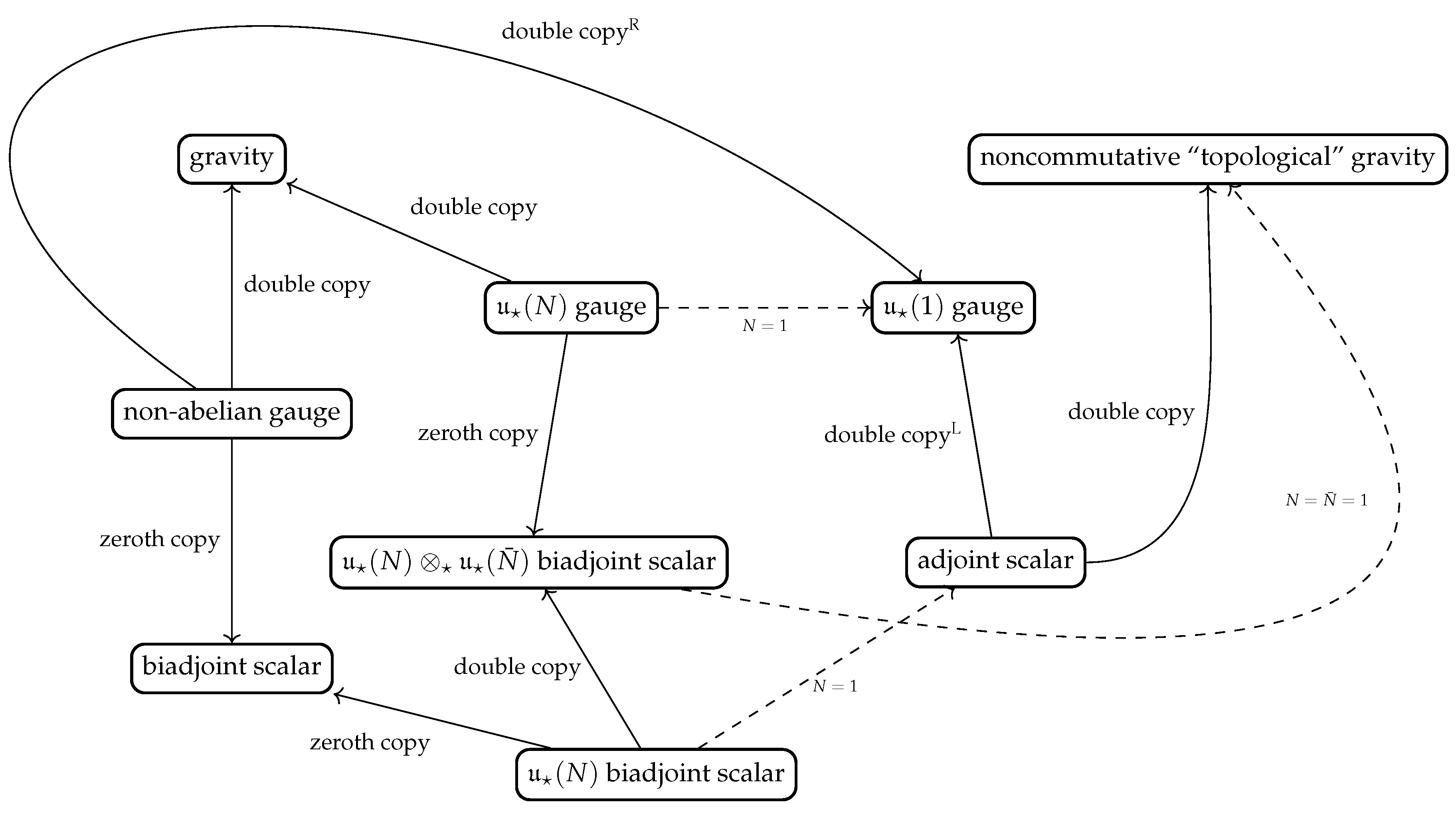
1.5. Outline
2. Building Blocks: Scalar Field Theories
2.1. Cubic Scalar Field Theory

2.2. Biadjoint Scalar Theory
2.2.1. Homotopy Factorisation
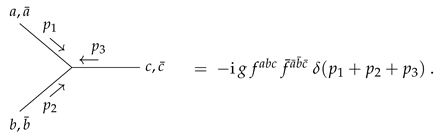
2.2.2. Amplitudes
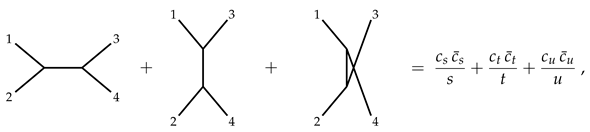
2.2.3. Colour Ordering and Decomposition
3. Noncommutative Scalar Theories with Rigid Colour Symmetries
3.1. Moyal–Weyl Deformation of Scalar Fields
3.1.1. The Kinematical Lie Algebra
3.1.2. The Colour Lie Algebra
3.2. Noncommutative Biadjoint Scalar Theory
3.2.1. Twisted Homotopy Factorisation
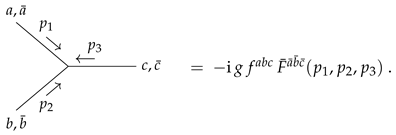
3.3. Adjoint Scalar Theory
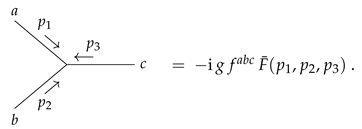
Twisted Factorisation
3.4. Colour–Kinematics Duality
3.4.1. Perturbative Calculations
3.4.2. Colour–Kinematics Duality
3.5. Homotopy Double Copy
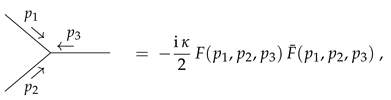
Perturbative Calculations
3.6. Binoncommutative Biadjoint Scalar Theory
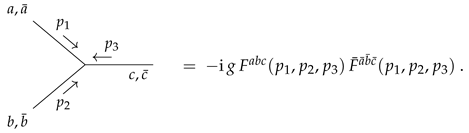
Colour Ordering and Decomposition
3.7. Applications: Special Galileons and Self–Dual Gravity
3.7.1. Zakharov–Mikhailov Theory and Special Galileons
3.7.2. Self–Dual Yang–Mills Theory and Gravity
4. Noncommutative Chern–Simons Theory
4.1. Moyal–Weyl Deformation of Differential Forms
4.2. The -Structure of Noncommutative Chern–Simons Theory
Batalin–Vilkovisky Formalism
4.3. Twisted Homotopy Factorisation
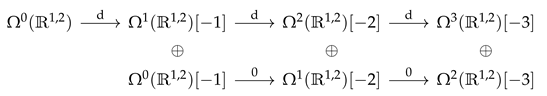
4.4. Twisted Colour–Kinematics Duality
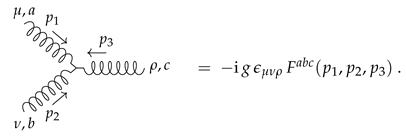
4.4.1. Perturbiner Solutions
4.4.2. Colour–Kinematics Duality
4.5. Homotopy Double Copy

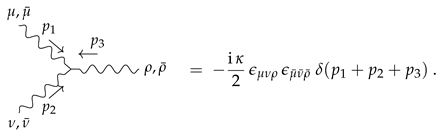
4.6. Chern–Simons Theory as a Double Copy
Diffeomorphism Invariance
5. Noncommutative Yang–Mills Theory
5.1. The -Structure of Noncommutative Yang–Mills Theory
5.1.1. Batalin–Vilkovisky Formalism
5.1.2. Colour Ordering and Decomposition
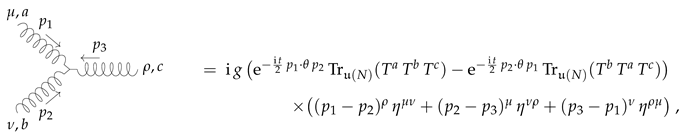
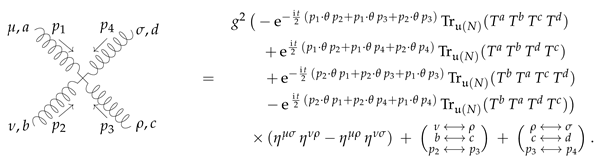
5.2. Strictification and Twisted Homotopy Factorisation
5.2.1. Strictification in the Second-Order Formalism

5.2.2. First-Order Formalism

5.2.3. Factorisation in the First-Order Formalism
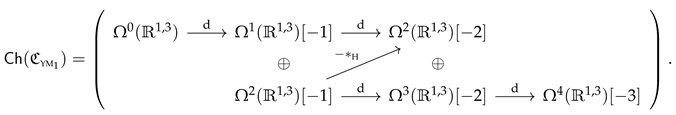
5.3. Noncommutative Gauge Theories on D-Branes
5.3.1. Open Strings in Kalb–Ramond Fields
5.3.2. Seiberg–Witten Limit
5.4. Bern–Carrasco–Johansson Relations
5.5. Kawai–Lewellen–Tye Relations
5.5.1. Kawai–Lewellen–Tye Relations with B-Fields
5.5.2. Double Copy Relations
5.6. Yang–Mills Theory as a Double Copy
5.7. Noncommutative Self–Dual Yang–Mills Theory
6. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Homotopical Techniques in Quantum Field Theory
Appendix A.1. Primer on Quantum Field Theory
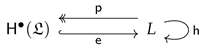
Appendix A.2. Homotopy Algebra Methods
Appendix A.2.1. L∞-Algebras
Appendix A.2.2. Cyclic Structures
Appendix A.2.3. Maurer–Cartan Theory
Appendix A.2.4. Batalin–Vilkovisky Theory
Appendix A.2.5. Morphisms of -Algebras
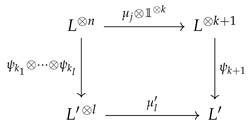
Appendix A.2.6. Minimal Models and Recursion Relations
Appendix A.2.7. Twisted Tensor Products and C∞-Algebras
Appendix A.3. Scattering in the L∞-Algebra Formalism
Appendix A.3.1. Tree-Level Amplitudes
Appendix A.3.2. Perturbiner Expansions
Appendix A.3.3. Word Combinatorics
Appendix A.3.4. Biadjoint Scalar Theory
References
- Bern, Z.; Carrasco, J.J.; Chiodaroli, M.; Johansson, H.; Roiban, R. The Duality between Color and Kinematics and its Applications. arXiv 2019, arXiv:1909.01358. [Google Scholar]
- Bern, Z.; Carrasco, J.J.; Chiodaroli, M.; Johansson, H.; Roiban, R. The SAGEX review on scattering amplitudes Chapter 2: An invitation to color-kinematics duality and the double copy. J. Phys. A 2022, 55, 443003. [Google Scholar] [CrossRef]
- Adamo, T.; Carrasco, J.J.M.; Carrillo-González, M.; Chiodaroli, M.; Elvang, H.; Johansson, H.; O’Connell, D.; Roiban, R.; Schlotterer, O. Snowmass White Paper: The Double Copy and its Applications. arXiv 2022, arXiv:2204.06547. [Google Scholar]
- Kawai, H.; Lewellen, D.C.; Tye, S.H.H. A Relation Between Tree Amplitudes of Closed and Open Strings. Nucl. Phys. B 1986, 269, 1–23. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.M.; Johansson, H. New Relations for Gauge-Theory Amplitudes. Phys. Rev. D 2008, 78, 085011. [Google Scholar] [CrossRef]
- Monteiro, R.; O’Connell, D. The Kinematic Algebra from the Self-Dual Sector. J. High Energy Phys. 2011, 2011, 7. [Google Scholar] [CrossRef]
- Bjerrum-Bohr, N.E.J.; Damgaard, P.H.; Monteiro, R.; O’Connell, D. Algebras for Amplitudes. J. High Energy Phys. 2012, 2012, 61. [Google Scholar] [CrossRef]
- Fu, C.-H.; Du, Y.-J.; Feng, B. An algebraic approach to BCJ numerators. J. High Energy Phys. 2013, 2013, 50. [Google Scholar] [CrossRef]
- Kleiss, R.; Kuijf, H. Multi-gluon Cross-sections and Five Jet Production at Hadron Colliders. Nucl. Phys. B 1989, 312, 616–644. [Google Scholar] [CrossRef]
- Cachazo, F.; He, S.; Yuan, E.Y. Scattering of Massless Particles: Scalars, Gluons and Gravitons. J. High Energy Phys. 2014, 2014, 33. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.M.; Johansson, H. Perturbative Quantum Gravity as a Double Copy of Gauge Theory. Phys. Rev. Lett. 2010, 105, 061602. [Google Scholar] [CrossRef]
- Borsten, L.; Jurčo, B.; Kim, H.; Macrelli, T.; Sämann, C.; Wolf, M. Double Copy from Homotopy Algebras. Fortsch. Phys. 2021, 69, 2100075. [Google Scholar] [CrossRef]
- Borsten, L.; Jurčo, B.; Kim, H.; Macrelli, T.; Sämann, C.; Wolf, M. Kinematic Lie Algebras From Twistor Spaces. arXiv 2022, arXiv:2211.13261. [Google Scholar] [CrossRef]
- Bonezzi, R.; Chiaffrino, C.; Diaz-Jaramillo, F.; Hohm, O. Gauge invariant double copy of Yang–Mills theory: The quartic theory. arXiv 2022, arXiv:2212.04513. [Google Scholar] [CrossRef]
- Bonezzi, R.; Diaz-Jaramillo, F.; Nagy, S. Gauge Independent Kinematic Algebra of Self-Dual Yang–Mills. arXiv 2023, arXiv:2306.08558. [Google Scholar]
- Douglas, M.R.; Nekrasov, N.A. Noncommutative field theory. Rev. Mod. Phys. 2001, 73, 977. [Google Scholar] [CrossRef]
- Szabo, R.J. Quantum field theory on noncommutative spaces. Phys. Rep. 2003, 378, 207–299. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Brunner, I.; Kupriyanov, V.; Lüst, D. Bootstrapping noncommutative gauge theories from L∞-algebras. J. High Energy Phys. 2018, 2018, 97. [Google Scholar] [CrossRef]
- Giotopoulos, G.; Szabo, R.J. Braided symmetries in noncommutative field theory. J. Phys. A 2022, 55, 353001. [Google Scholar] [CrossRef]
- Minwalla, S.; Van Raamsdonk, M.; Seiberg, N. Noncommutative perturbative dynamics. J. High Energy Phys. 2000, 2000, 020. [Google Scholar] [CrossRef]
- Pajer, E.; Stefanyszyn, D.; Supeł, J. The Boostless Bootstrap: Amplitudes without Lorentz boosts. J. High Energy Phys. 2020, 2020, 198, Erratum in J. High Energy Phys. 2022, 2022, 23. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Rodina, L.; Yin, Z.; Zekioglu, S. Simple encoding of higher derivative gauge and gravity counterterms. Phys. Rev. Lett. 2020, 125, 251602. [Google Scholar] [CrossRef]
- Low, I.; Yin, Z. New Flavor-Kinematics Dualities and Extensions of Nonlinear Sigma Models. Phys. Lett. B 2020, 807, 135544. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Rodina, L.; Zekioglu, S. Composing effective prediction at five points. J. High Energy Phys. 2021, 2021, 169. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Pavao, N.H. Virtues of a symmetric-structure double copy. Phys. Rev. D 2023, 107, 065005. [Google Scholar] [CrossRef]
- Mizera, S. Inverse of the String Theory KLT Kernel. J. High Energy Phys. 2017, 2017, 84. [Google Scholar] [CrossRef]
- Chi, H.-H.; Elvang, H.; Herderschee, A.; Jones, C.R.T.; Paranjape, S. Generalizations of the double copy: The KLT bootstrap. J. High Energy Phys. 2022, 2022, 77. [Google Scholar] [CrossRef]
- Cheung, C.; Mangan, J.; Parra-Martinez, J.; Shah, N. Non-perturbative Double Copy in Flatland. Phys. Rev. Lett. 2022, 129, 221602. [Google Scholar] [CrossRef]
- Armstrong-Williams, K.; White, C.D.; Wikeley, S. Non-perturbative aspects of the self-dual double copy. J. High Energy Phys. 2022, 2022, 160. [Google Scholar] [CrossRef]
- Ishibashi, N.; Iso, S.; Kawai, H.; Kitazawa, Y. String scale in noncommutative Yang–Mills. Nucl. Phys. B 2000, 583, 159–181. [Google Scholar] [CrossRef]
- Gross, D.J.; Hashimoto, A.; Itzhaki, N. Observables of noncommutative gauge theories. Adv. Theor. Math. Phys. 2000, 4, 893–928. [Google Scholar] [CrossRef]
- Lizzi, F.; Szabo, R.J.; Zampini, A. Geometry of the gauge algebra in noncommutative Yang–Mills theory. J. High Energy Phys. 2001, 2001, 032. [Google Scholar] [CrossRef][Green Version]
- Langmann, E.; Szabo, R.J. Teleparallel gravity and dimensional reductions of noncommutative gauge theory. Phys. Rev. D 2001, 64, 104019. [Google Scholar] [CrossRef]
- Rivelles, V.O. Noncommutative field theories and gravity. Phys. Lett. B 2003, 558, 191–196. [Google Scholar] [CrossRef]
- Yang, H.S. Exact Seiberg–Witten map and induced gravity from noncommutativity. Mod. Phys. Lett. A 2006, 21, 2637–2647. [Google Scholar] [CrossRef]
- Szabo, R.J. Symmetry, gravity and noncommutativity. Class. Quant. Grav. 2006, 23, R199. [Google Scholar] [CrossRef]
- Steinacker, H. Emergent Gravity from Noncommutative Gauge Theory. J. High Energy Phys. 2007, 2007, 049. [Google Scholar] [CrossRef]
- Steinacker, H. Emergent Geometry and Gravity from Matrix Models: An Introduction. Class. Quant. Grav. 2010, 27, 133001. [Google Scholar] [CrossRef]
- Ben-Shahar, M.; Johansson, H. Off-shell color-kinematics duality for Chern–Simons. J. High Energy Phys. 2022, 2022, 35. [Google Scholar] [CrossRef]
- Lopez-Arcos, C.; Vélez, A.Q. L∞-algebras and the perturbiner expansion. J. High Energy Phys. 2019, 2019, 10. [Google Scholar] [CrossRef]
- Mafra, C.R. Berends–Giele recursion for double-color-ordered amplitudes. J. High Energy Phys. 2016, 2016, 80. [Google Scholar] [CrossRef]
- Dolan, L.; Goddard, P. The Polynomial Form of the Scattering Equations. J. High Energy Phys. 2014, 2014, 29. [Google Scholar] [CrossRef][Green Version]
- Hoppe, J. Diffeomorphism Groups, Quantization and (∞). Int. J. Mod. Phys. A 1989, 4, 5235–5248. [Google Scholar] [CrossRef]
- Pope, C.N.; Romans, L.J.; Shen, X. W∞ and the Racah–Wigner Algebra. Nucl. Phys. B 1990, 339, 191–221. [Google Scholar] [CrossRef]
- Monteiro, R. From Moyal deformations to chiral higher-spin theories and to celestial algebras. J. High Energy Phys. 2023, 2023, 62. [Google Scholar] [CrossRef]
- Bridges, E.; Mafra, C.R. Algorithmic construction of SYM multiparticle superfields in the BCJ gauge. J. High Energy Phys. 2019, 2019, 22. [Google Scholar] [CrossRef]
- Filk, T. Divergencies in a field theory on quantum space. Phys. Lett. B 1996, 376, 53–58. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Mikhailov, A.V. Relativistically Invariant Two-Dimensional Models in Field Theory Integrable by the Inverse Problem Technique. Sov. Phys. J. Exp. Theor. Phys. 1978, 47, 1017–1027. [Google Scholar]
- Cheung, C.; Kampf, K.; Novotny, J.; Trnka, J. Effective Field Theories from Soft Limits of Scattering Amplitudes. Phys. Rev. Lett. 2015, 114, 221602. [Google Scholar] [CrossRef]
- Cheung, C.; Kampf, K.; Novotny, J.; Shen, C.-H.; Trnka, J. On-Shell Recursion Relations for Effective Field Theories. Phys. Rev. Lett. 2016, 116, 041601. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Joyce, A. Hidden symmetry of the Galileon. Phys. Rev. D 2015, 92, 023503. [Google Scholar] [CrossRef]
- Chacón, E.; García-Compeán, H.; Luna, A.; Monteiro, R.; White, C.D. New heavenly double copies. J. High Energy Phys. 2021, 2021, 247. [Google Scholar] [CrossRef]
- Leznov, A.N.; Mukhtarov, M.A. Deformation of Algebras and Solution of Self-duality Equation. J. Math. Phys. 1987, 28, 2574–2578. [Google Scholar] [CrossRef]
- Park, Q.-H. Self-dual Gravity as a Large N Limit of the Two-dimensional Nonlinear σ Model. Phys. Lett. B 1990, 238, 287–290. [Google Scholar] [CrossRef]
- Parkes, A. A cubic action for self-dual Yang–Mills. Phys. Lett. B 1992, 286, 265–270. [Google Scholar] [CrossRef]
- Plebański, J.F. Some solutions of complex Einstein equations. J. Math. Phys. 1975, 16, 2395–2402. [Google Scholar] [CrossRef]
- Ooguri, H.; Vafa, C. Geometry of = 2 strings. Nucl. Phys. B 1991, 361, 469–518. [Google Scholar] [CrossRef]
- Strachan, I.A.B. The Moyal algebra and integrable deformations of the self-dual Einstein equations. Phys. Lett. B 1992, 283, 63–66. [Google Scholar] [CrossRef]
- Takasaki, K. Dressing operator approach to Moyal algebraic deformation of self-dual gravity. J. Geom. Phys. 1994, 14, 111–120. [Google Scholar] [CrossRef][Green Version]
- Plebański, J.F.; Przanowski, M.; Rajca, B.; Tosiek, J. The Moyal deformation of the second heavenly equation. Acta Phys. Polon. B 1995, 26, 889–902. [Google Scholar]
- Monteiro, R. Celestial chiral algebras, colour-kinematics duality and integrability. J. High Energy Phys. 2023, 2023, 92. [Google Scholar] [CrossRef]
- Bu, W.; Heuveline, S.; Skinner, D. Moyal deformations, W1+∞ and celestial holography. J. High Energy Phys. 2022, 2022, 11. [Google Scholar] [CrossRef]
- Guevara, A. Towards Gravity From a Color Symmetry. arXiv 2022, arXiv:2209.00696. [Google Scholar]
- Bittleston, R.; Heuveline, S.; Skinner, D. The Celestial Chiral Algebra of Self-Dual Gravity on Eguchi–Hanson Space. arXiv 2023, arXiv:2305.09451. [Google Scholar]
- Shyam, V.; Yargic, Y. TT deformed scattering happens within matrices. J. High Energy Phys. 2023, 2023, 132. [Google Scholar] [CrossRef]
- Lechtenfeld, O.; Popov, A.D.; Spendig, B. Open = 2 strings in a B-field background and noncommutative self-dual Yang–Mills. Phys. Lett. B 2001, 507, 317–326. [Google Scholar] [CrossRef][Green Version]
- Takasaki, K. Anti-self-dual Yang–Mills equations on noncommutative space-time. J. Geom. Phys. 2001, 37, 291–306. [Google Scholar] [CrossRef][Green Version]
- Hamanaka, M. Noncommutative Ward’s conjecture and integrable systems. Nucl. Phys. B 2006, 741, 368–389. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. J. High Energy Phys. 1999, 1999, 032. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Brinkmann, M.; Kupriyanov, V.; Traube, M. On the Uniqueness of L∞-bootstrap: Quasi-isomorphisms are Seiberg–Witten Maps. J. Math. Phys. 2018, 59, 123505. [Google Scholar] [CrossRef]
- Kupriyanov, V.; Sharapov, A. What is the Seiberg–Witten map exactly? arXiv 2023, arXiv:2302.07175. [Google Scholar]
- Barnich, G.; Brandt, F.; Grigoriev, M. Seiberg–Witten maps in the context of the antifield formalism. Fortsch. Phys. 2002, 50, 825–830. [Google Scholar] [CrossRef]
- Barnich, G.; Brandt, F.; Grigoriev, M. Local BRST cohomology and Seiberg–Witten maps in noncommutative Yang–Mills theory. Nucl. Phys. B 2004, 677, 503–534. [Google Scholar] [CrossRef][Green Version]
- Axelrod, S.; Singer, I.M. Chern–Simons perturbation theory. In Differential Geometric Methods in Theoretical Physics; World Scientific: Singapore, 1991; pp. 3–45. [Google Scholar]
- Jurčo, B.; Raspollini, L.; Sämann, C.; Wolf, M. L∞-Algebras of Classical Field Theories and the Batalin–Vilkovisky Formalism. Fortsch. Phys. 2019, 67, 1900025. [Google Scholar] [CrossRef]
- Martin, C.P.; Trampetić, J.; You, J. UV/IR mixing in noncommutative (N) Yang–Mills theory. Eur. Phys. J. C 2021, 81, 878. [Google Scholar] [CrossRef]
- Mangano, M.L.; Parke, S.J. Multiparton amplitudes in gauge theories. Phys. Rep. 1991, 200, 301–367. [Google Scholar] [CrossRef]
- Raju, S. The Noncommutative S-Matrix. J. High Energy Phys. 2009, 2009, 005. [Google Scholar] [CrossRef][Green Version]
- Huang, J.-H.; Huang, R.; Jia, Y. Tree amplitudes of noncommutative (N) Yang–Mills Theory. J. Phys. A 2011, 44, 425401. [Google Scholar] [CrossRef][Green Version]
- Reiterer, M. A homotopy BV algebra for Yang–Mills and color-kinematics. arXiv 2019, arXiv:1912.03110. [Google Scholar]
- Benaoum, H.B. Perturbative BF Yang–Mills theory on noncommutative 4. Nucl. Phys. B 2000, 585, 554–566. [Google Scholar] [CrossRef]
- Abouelsaood, A.; Callan, C.; Nappi, C.; Yost, S. Open strings in background gauge fields. Nucl. Phys. B 1987, 280, 599–624. [Google Scholar] [CrossRef]
- Kontsevich, M. Deformation Quantization of Poisson Manifolds. Lett. Math. Phys. 2003, 66, 157–216. [Google Scholar] [CrossRef]
- Cattaneo, A.S.; Felder, G. A path integral approach to the Kontsevich quantization formula. Commun. Math. Phys. 2000, 212, 591–611. [Google Scholar] [CrossRef]
- Stieberger, S. Open & Closed vs. Pure Open String Disk Amplitudes. arXiv 2009, arXiv:0907.2211. [Google Scholar]
- Boels, R.H.; Marmiroli, D.; Obers, N.A. On-shell Recursion in String Theory. J. High Energy Phys. 2010, 2010, 34. [Google Scholar] [CrossRef][Green Version]
- Mizera, S. Combinatorics and Topology of Kawai–Lewellen–Tye Relations. J. High Energy Phys. 2017, 2017, 97. [Google Scholar] [CrossRef]
- Mafra, C.R.; Schlotterer, O. Non-abelian Z-theory: Berends–Giele recursion for the α′-expansion of disk integrals. J. High Energy Phys. 2017, 2017, 31. [Google Scholar] [CrossRef]
- Mizera, S. Aspects of Scattering Amplitudes and Moduli Space Localization. Ph.D. Thesis, Princeton, Inst. Advanced Study, Princeton, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Stieberger, S. A Relation between One-Loop Amplitudes of Closed and Open Strings (One-Loop KLT Relation). arXiv 2022, arXiv:2212.06816. [Google Scholar]
- Bjerrum-Bohr, N.E.J.; Damgaard, P.H.; Sondergaard, T.; Vanhove, P. The Momentum Kernel of Gauge and Gravity Theories. J. High Energy Phys. 2011, 2011, 1. [Google Scholar] [CrossRef]
- Frost, H. The Algebraic Structure of the KLT Relations for Gauge and Gravity Tree Amplitudes. Symmetry Integr. Geom. Methods Appl. 2021, 17, 101. [Google Scholar] [CrossRef]
- Zeitlin, A.M. Conformal Field Theory and Algebraic Structure of Gauge Theory. J. High Energy Phys. 2010, 2010, 56. [Google Scholar] [CrossRef]
- Bonezzi, R.; Diaz-Jaramillo, F.; Hohm, O. The gauge structure of double field theory follows from Yang–Mills theory. Phys. Rev. D 2022, 106, 026004. [Google Scholar] [CrossRef]
- Latas, D.; Trampetić, J.; You, J. Seiberg–Witten map invariant scatterings. Phys. Rev. D 2021, 104, 015021. [Google Scholar] [CrossRef]
- Trampetić, J.; You, J. Seiberg–Witten maps and scattering amplitudes of noncommutative QED. Phys. Rev. D 2022, 105, 075016. [Google Scholar] [CrossRef]
- Nekrasov, N.; Schwarz, A.S. Instantons on noncommutative 4 and (2, 0) superconformal six-dimensional theory. Commun. Math. Phys. 1998, 198, 689–703. [Google Scholar] [CrossRef]
- Szabo, R.J. The L∞-structure of noncommutative gravity. Proc. Sci. 2022, 406, 218. [Google Scholar] [CrossRef]
- Dimitrijević Ćirić, M.; Giotopoulos, G.; Radovanović, V.; Szabo, R.J. Braided L∞-algebras, braided field theory and noncommutative gravity. Lett. Math. Phys. 2021, 111, 148. [Google Scholar] [CrossRef]
- Arvanitakis, A.S. The L∞-algebra of the S-matrix. J. High Energy Phys. 2019, 2019, 115. [Google Scholar] [CrossRef]
- Macrelli, T.; Sämann, C.; Wolf, M. Scattering amplitude recursion relations in Batalin–Vilkovisky-quantizable theories. Phys. Rev. D 2019, 100, 045017. [Google Scholar] [CrossRef]
- Kajiura, H. Homotopy algebra morphism and geometry of classical string field theory. Nucl. Phys. B 2002, 630, 361–432. [Google Scholar] [CrossRef]
- Kajiura, H. Noncommutative homotopy algebras associated with open strings. Rev. Math. Phys. 2007, 19, 1–99. [Google Scholar] [CrossRef]
- Berends, F.; Giele, W. Recursive calculations for processes with n gluons. Nucl. Phys. B 1988, 306, 759–808. [Google Scholar] [CrossRef]
- Lee, K. Quantum off-shell recursion relation. J. High Energy Phys. 2022, 2022, 51. [Google Scholar] [CrossRef]
- Gomez, H.; Jusinskas, R.L.; Lopez-Arcos, C.; Quintero Vélez, A. One-Loop Off-Shell Amplitudes from Classical Equations of Motion. Phys. Rev. Lett. 2023, 130, 081601. [Google Scholar] [CrossRef]
- Jurčo, B.; Macrelli, T.; Sämann, C.; Wolf, M. Loop Amplitudes and Quantum Homotopy Algebras. J. High Energy Phys. 2020, 2020, 3. [Google Scholar] [CrossRef]
- Okawa, Y. Correlation functions of scalar field theories from homotopy algebras. arXiv 2022, arXiv:2203.05366. [Google Scholar]
- Frost, H.; Mafra, C.R.; Mason, L. A Lie bracket for the momentum kernel. arXiv 2020, arXiv:2012.00519. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szabo, R.J.; Trojani, G. Homotopy Double Copy of Noncommutative Gauge Theories. Symmetry 2023, 15, 1543. https://doi.org/10.3390/sym15081543
Szabo RJ, Trojani G. Homotopy Double Copy of Noncommutative Gauge Theories. Symmetry. 2023; 15(8):1543. https://doi.org/10.3390/sym15081543
Chicago/Turabian StyleSzabo, Richard J., and Guillaume Trojani. 2023. "Homotopy Double Copy of Noncommutative Gauge Theories" Symmetry 15, no. 8: 1543. https://doi.org/10.3390/sym15081543
APA StyleSzabo, R. J., & Trojani, G. (2023). Homotopy Double Copy of Noncommutative Gauge Theories. Symmetry, 15(8), 1543. https://doi.org/10.3390/sym15081543




