Symmetric Perfect and Symmetric Semiperfect Colorings of Groups

Abstract

Let G be a group. A k-coloring of G is a surjection $\lambda :G\to \{1,2,\dots ,k\}$. Equivalently, a k-coloring $\lambda$ of G is a partition $\mathcal{P}=\{P_1,P_2,\dots ,P_k\}$ of G into k subsets. If $g\mathcal{P}=\mathcal{P}$ for all g in G, we say that $\lambda$ is perfect. If $h\mathcal{P}=\mathcal{P}$ only for all $h\in H\le G$ such that $[G:H]=2$, then $\lambda$ is semiperfect. If there is an element $g\in G$ such that $\lambda \left(x\right)=\lambda \left(g{x}^{-1}g\right)$ for all $x\in G$, then $\lambda$ is said to be symmetric. In this research, we relate the notion of symmetric colorings with perfect and semiperfect colorings. Specifically, we identify which perfect and semiperfect colorings are symmetric in relation to the subgroups of G that contain the squares of elements in G, in H, and in $G\setminus H$. We also show examples of colored planar patterns that represent symmetric perfect and symmetric semiperfect colorings of some groups.

1. Introduction

The study of color symmetry, whose motivation comes primarily from the field of art, has generated interest in recent years due to its applications in branches of science like chemistry and biology. For instance, the crystal structure of different crystalline materials can be modeled using colored tilings [1]. In physics and materials engineering, nanotubes with several types of atoms such as carbon–boron nitride are characterized by constructing colorings of the associated single-wall carbon nanotube [2]. Apart from these applications, color symmetry in itself provides an enjoyable way of learning fundamental concepts in group theory and geometry by analyzing aesthetically pleasing designs and colored patterns like those of Escher.

Shubnikov’s work on antisymmetry laid the foundations for the study of color symmetry (see [3,4,5]). Since then, concepts orbiting around colored patterns in the Euclidean plane and in higher-dimensional spaces have been explored and a great level of enthusiasm has been achieved, leading to numerous studies in the area. One such study was carried out by Grunbaum and Shephard in [6], where the notion of a perfect coloring was formally defined. In [7], the relationship between group theory and color symmetry was extensively discussed. These eventually led to a coloring framework in [8] that resulted in a method to come up with perfect colorings of any symmetrical object. On the matter of semiperfect colorings, Felix and Loquias [9] gave results on how to obtain all semiperfect colorings of any symmetrical pattern.

In [10], Gryshko introduced the idea of symmetric colorings of groups and was initially motivated by colorings of the vertices of regular polygons. However, the origins of symmetric colorings can be traced back to [11] using the concept originally known as symmetries of groups. Subsequent studies on symmetric colorings dealt with various groups, as can be seen in [12,13,14,15,16]. In contribution to this stage wherein concepts on color symmetry are being generalized, this research aims to relate the concept of perfect and semiperfect colorings with symmetric colorings. As of this writing, no article has been published yet that connects these different types of colorings. In this present work, we derive conditions so that a perfect coloring and a semiperfect coloring of a group are also symmetric. We also present colored patterns to represent symmetric perfect colorings and symmetric semiperfect colorings of certain groups.

2. Preliminaries

Let $\mathcal{X}$ be (the set of objects in) a given pattern to be colored and let G be a group acting on $\mathcal{X}$. If $x\in \mathcal{X}$, the G-orbit of x is the set $Gx=\left\{gx:g\in G\right\}$, while the stabilizer of $x\in \mathcal{X}$ is given by ${Stab}_G\left(x\right)=\left\{g\in G:gx=x\right\}$. Throughout this paper, we observe the coloring setting considered in [9]: G acts transitively on $\mathcal{X}$, and for all $x\in \mathcal{X}$, ${Stab}_G\left(x\right)=\left\{e\right\}$. With this, we obtain a one-to-one correspondence between G and $\mathcal{X}$ given by $g\leftrightarrow gx$. As a consequence, we can associate a partition $\mathcal{P}=\left\{P_1,\dots ,P_k\right\}$ of G with the partition $\left\{P_{1}x,\dots ,P_{k}x\right\}$ of $\mathcal{X}$. If $\mathcal{C}=\left\{c_1,\dots ,c_k\right\}$ is a set of k colors, the bijection $P_{i}x\mapsto c_i$ is called a k-coloring of $\mathcal{X}$ that corresponds to the partition $\mathcal{P}$ of G. We can therefore regard a coloring of a pattern as a partition $\mathcal{P}$ of G with every element of $\mathcal{P}$ representing a unique color. This allows us to make the following natural definition. A k-coloring$\lambda$ of a group G is an onto function from G to a set $\mathcal{C}=\left\{c_1,\dots ,c_k\right\}$ of k colors where $\lambda \left(g\right)$ is the color assigned to an element $g\in G$. Simply speaking, a k-coloring of a group G is just a partition of G into k subsets where $P_i=\left\{g\in G:\lambda \left(g\right)=c_i\right\}$ is the set of elements of G assigned the color $c_i$.

Let $\mathcal{A}$ be the set of all partitions of G. Then the group G acts on $\mathcal{A}$ by left multiplication. If $\mathcal{P}\in \mathcal{A}$, let H be the stabilizer of $\mathcal{P}$. Then $h\in H\iff h\mathcal{P}=\mathcal{P}$. The partition $\mathcal{P}$ is referred to as an H-invariant partition of G. The coloring $\mathcal{P}$ of G is called perfect if $[G:H]=1$, that is, if $G=H$. Whenever $[G:H]=2$, the coloring is called semiperfect. As regards the pattern $\mathcal{X}$, an element $h\in H$ permutes the colors in the coloring of $\mathcal{X}$ that correspond to the partition $\mathcal{P}$ of G. A perfect coloring of $\mathcal{X}$ is one for which every element of G effects a permutation of $\mathcal{C}$. If the only elements of G that permute the colors in the coloring of $\mathcal{X}$ belong to an index-2 subgroup H of G, the coloring is semiperfect. We emphasize that the definitions of perfect and semiperfect colorings of patterns are old notions. What is new here are the concepts of perfect and semiperfect colorings of groups. These arise from the equivalence among the three sets considered in the previous paragraph given our coloring setting.

Perfect colorings of patterns have been characterized in [8] where sufficient and necessary conditions for a coloring to be perfect are determined. In particular, Theorem 5 of the said article shows that a coloring of a set $\mathcal{X}$ forming only one G-orbit is perfect if and only if it is given by the partition $\mathcal{P}=\left\{gJx:g\in G\right\}$, where $x\in \mathcal{X}$, and ${Stab}_G\left(x\right)\le J\le G$. Since we require that ${Stab}_G\left(x\right)=\left\{e\right\}$ for all $x\in \mathcal{X}$, then any subgroup of G can be used to come up with a perfect coloring of $\mathcal{X}$. This translates to the following result regarding perfect colorings of groups.

Theorem 1.

Let G be a group. A coloring of G is perfect if and only if it is given by the partition $\mathcal{P}=\left\{gJ:g\in G\right\}$ where J is any subgroup of G.

By the above theorem, every perfect group coloring is always a partition of G by left cosets of a subgroup J. In the case where $[G:J]=k$, the coloring given by $\mathcal{P}=\left\{gJ:g\in G\right\}$ is a perfect k-coloring of G. If $J=G$, we obtain a trivial coloring of G using only one color. If $J=\left\{e\right\}$, then all the elements of G obtain distinct colors.

Semiperfect colorings of patterns are studied in [9] where it was shown that every such coloring falls under one of two possible types of partition of a group G. The next two theorems are restatements of results of [9] on semiperfect colorings.

Theorem 2

(Type I Semiperfect Coloring). Let $H\le G$ with $[G:H]=2$, $J\le H$, and $y\in G\setminus H$. The partition of G given by ${\mathcal{P}}_1=\left\{h(J\cup Jy):h\in H\right\}$ is a semiperfect coloring of G if and only if $yJ\ne Jy$ or $y^2\notin J$.

Theorem 3

(Type II Semiperfect Coloring). Let $H\le G$ with $[G:H]=2$, $J_1,J_2\le H$, and $y\in G\setminus H$. The partition of G given by ${\mathcal{P}}_2=\left\{h{J}_1:h\in H\right\}\cup y\left\{h{J}_2:h\in H\right\}$ is a semiperfect coloring of G if and only if $J_1\ne J_2$.

Note that both ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ are H-invariant partitions of G, that is, $h{\mathcal{P}}_1={\mathcal{P}}_1$ and $h{\mathcal{P}}_2={\mathcal{P}}_2$$\forall h\in H$. ${\mathcal{P}}_1$ corresponds to a perfect coloring of G if and only if $yJ=Jy$ (or $y\in N_G\left(J\right)$, the normalizer of J in G) and $y^2\in J$. Moreover, if $J=H$, the partition will yield a coloring of G with only one color and thus be perfect. For the partition ${\mathcal{P}}_2$, a perfect coloring of G is obtained whenever $J_1=J_2$.

Next, we define what it means for a coloring of a group to be symmetric. Given a group G, the mappings $x\mapsto g{x}^{-1}g$ where $g\in G$ are called symmetries of G [11]. In [16] and other related articles by the same author, a k-coloring of a group G is defined as any map $\lambda :G\to \left\{1,\dots ,k\right\}$ without the condition of being surjective. We adhere to our previous definition so that a k-coloring remains as a partitioning of G into k subsets. Now, we say that a coloring of G is symmetric if there is a $g\in G$ such that $\lambda \left(x\right)=\lambda \left(g{x}^{-1}g\right)$ for all $x\in G$. In essence, $\lambda$ is symmetric if the elements x and $g{x}^{-1}g$ have the same color.

We say that $\mathcal{P}$ and $\mathcal{Q}$ are equivalent colorings of G if $\mathcal{P}=x\mathcal{Q}$ for some $x\in G$. The following result from [9] gives all equivalent H-partitions of a group G if $[G:H]=2$.

Theorem 4.

Let G be a group and $\mathcal{P}$ an H-invariant partition of G. If $[G:H]=2$ then there are only two partitions of G that are equivalent to $\mathcal{P}$, namely, $\mathcal{P}$ and $y\mathcal{P}$, for some $y\in G\setminus H$. Moreover, the stabilizer of $y\mathcal{P}$ in G is also H.

Note that in listing symmetric colorings of groups, we do not distinguish between partitions $\mathcal{P}$ and $\mathcal{Q}$ which are equivalent colorings.

In this paper, we are interested in determining which perfect colorings and semiperfect colorings of a group G are symmetric with respect to some element $g\in G$. We first consider perfect colorings of G and derive conditions for this coloring to be symmetric. Next, we consider the two types of semiperfect colorings of G described in Theorems 2 and 3. We give conditions for a Type II semiperfect coloring of G to be symmetric. We also show that no Type I semiperfect colorings of G are symmetric. Lastly, we give actual symmetric perfect colorings and symmetric semiperfect colorings of some groups that can be represented by planar patterns.

3. Results

We start this section by describing symmetric perfect colorings. Note that from Theorem 1, the coloring of a group G given by the partition $\mathcal{P}=\left\{aJ:a\in G\right\}$ where $J\le G$ gives a perfect coloring. The next theorem gives the condition for a perfect coloring to be symmetric.

Theorem 5.

Let G be a group and let J be a subgroup of G. The coloring of G given by the partition $\mathcal{P}=\left\{aJ:a\in G\right\}$ yields a symmetric perfect coloring with respect to some $g\in G$ if and only if J contains $\left\{x^2\right|x\in G\}$.

Proof. 

Suppose the coloring of G induced by the left cosets of J is symmetric with respect to some $g\in G$. Then $\forall x\in G$, $xJ=g{x}^{-1}gJ$, implying that ${\left(g^{-1}x\right)}^2\in J$. Thus $\left\{{\left(g^{-1}x\right)}^2\right|x\in G\}=\left\{x^2\right|x\in G\}\subseteq J$.

On the other hand, if $\left\{x^2\right|x\in G\}\subseteq J$ then ${\left(g^{-1}x\right)}^{2}J=J$ for all $g,x\in G$. Thus for all $g,x\in G$, $xJ=g{x}^{-1}gJ$. Hence, the coloring is symmetric with respect to any $g\in G$. □

Using Theorem 5, we may obtain symmetric perfect colorings of a group G by observing the following procedure:

• Form the group $G^2=⟨x^2:x\in G⟩$.
• Choose a subgroup J of G such that $G^2\le J$.
• Form the partition $\mathcal{P}=\left\{gJ:g\in G\right\}$.

We note that if the left coset coloring of G induced by J is symmetric with respect to some $g\in G$, then the coloring is symmetric with respect to every element of G. By Theorem 5, the number of proper subgroups of G that contain the set $\left\{x^2:x\in G\right\}$ is the number of inequivalent symmetric nontrivial perfect colorings of G. Let $J,J^{\prime }\le G$ and consider the partitions $\mathcal{P}=\left\{gJ:g\in G\right\}$ and ${\mathcal{P}}^{\prime }=\left\{g{J}^{\prime }:g\in G\right\}$. If $\mathcal{P}$ and ${\mathcal{P}}^{\prime }$ are equivalent, then there exists $x\in G$ such that $x\mathcal{P}={\mathcal{P}}^{\prime }$. This implies that $xgJ=J^{\prime }$ for some $g\in G$. As both J and $J^{\prime }$ are subgroups of G, we must have $J=J^{\prime }$. We have therefore shown that distinct subgroups of G containing $\left\{x^2:x\in G\right\}$ give rise to inequivalent symmetric perfect colorings of G.

Moreover, we note that $G^2=⟨x^2:x\in G⟩$ is a normal subgroup of G and that the quotient $G/G^2$ is an abelian group whose non-identity elements are of order 2. Thus, $G/G^2$ can be viewed as a vector space over ${\mathbb{F}}_2$ and each subgroup J containing $G^2$ is a lifting of a subspace of $G/G^2$. This implies that the number of such J (and thus the number of symmetric perfect colorings of G) is a sum of 2-binomial coefficients.

Theorem 5 has many other consequences. For instance, a group G of odd order has only the trivial coloring which is symmetric perfect since $⟨x^2|x\in G⟩=G$. For a cyclic group G of order n, either G has exactly one or no nontrivial symmetric perfect coloring depending on whether n is even or odd. Also, a finite non-abelian simple group has only the trivial coloring as a perfect symmetric coloring.

Next, we derive conditions such that a semiperfect group coloring is also symmetric. For now, we postpone our search for symmetric Type I semiperfect colorings and proceed to identifying Type II semiperfect group colorings that are symmetric. By Theorem 3, recall that the partition ${\mathcal{P}}_2=\left\{h{J}_1:h\in H\right\}\cup y\left\{h{J}_2:h\in H\right\}$ is a semiperfect coloring of G if and only if $J_1\ne J_2$ where $J_1,J_2$ are subgroups of an index-2 subgroup H of G and $y\in G\setminus H$.

Suppose ${\mathcal{P}}_2$ is a symmetric coloring with respect to $g\in G$ and let $x\in G.$

If $x\in H$, then $x\in h{J}_1$ for some $h\in H$. That is, $h^{-1}x\in J_1$. Since the coloring is symmetric with respect to g, we have $g{x}^{-1}g\in h{J}_1\Rightarrow h^{-1}g{x}^{-1}g=\left(h^{-1}x\right)\left(x^{-1}g{x}^{-1}g\right)=\left(h^{-1}x\right){\left(x^{-1}g\right)}^2\in J_1$. Since $h^{-1}x\in J_1$, we have ${\left(x^{-1}g\right)}^2\in J_1$ for all $x\in H$. Thus, ${\left(xg\right)}^2\in J_1$ for all $x\in H$.

If $x\in G\setminus H$, then $x\in yh{J}_2$ for some $h\in H$. That is, $h^{-1}{y}^{-1}x\in J_2$. Since the coloring is symmetric with respect to g, we have $g{x}^{-1}g\in yh{J}_2\Rightarrow h^{-1}{y}^{-1}g{x}^{-1}g=\left(h^{-1}{y}^{-1}x\right)\left(x^{-1}g{x}^{-1}g\right)\in J_2$. Since $h^{-1}{y}^{-1}x\in J_2$, we have ${\left(x^{-1}g\right)}^2\in J_2$ for all $x\in G\setminus H$. Thus, ${\left(xg\right)}^2\in J_2$ for all $x\in G\setminus H$.

We formalize these results below.

Theorem 6.

Let G be a group and let $H\le G$ such that $[G:H]=2$. Fix $y\in G\setminus H$ and choose subgroups $J_1,J_2$ of H. The partition given by ${\mathcal{P}}_2=\left\{h{J}_1:h\in H\right\}\cup y\left\{h{J}_2:h\in H\right\}$ corresponds to a symmetric semiperfect coloring of G with respect to $g\in G$ if and only if the following conditions are satisfied:

• $J_1\ne J_2$;
• ${\left(xg\right)}^2\in J_1$ for all $x\in H$;
• ${\left(xg\right)}^2\in J_2$ for all $x\in G\setminus H$.

If a semiperfect coloring of Type II is symmetric with respect to some $g\in G$, then conditions (2) and (3) of the theorem above give the following cases: (i) the coloring is symmetric with respect to all $g\in H$; (ii) the coloring is symmetric with respect to all $g\notin H$; and (iii) the coloring is symmetric with respect to all $g\in G$. The following result is immediate from Theorem 6.

Corollary 1.

Consider the partition ${\mathcal{P}}_2=\left\{h{J}_1:h\in H\right\}\cup y\left\{h{J}_2:h\in H\right\}$ of G where $[G:H]=2$, $J_1,J_2\le H$, and $y\in G\setminus H$. Then, the following hold:

• ${\mathcal{P}}_2$ is symmetric with respect to an element $g\in H$ if and only if $h^2\in J_1$ for all $h\in H$ and $w^2\in J_2$ for all $w\in G\setminus H$.
• ${\mathcal{P}}_2$ is symmetric with respect to an element $g\notin H$ if and only if $h^2\in J_2$ for all $h\in H$ and $w^2\in J_1$ for all $w\in G\setminus H$.

Certainly, if $J_1$ and $J_2$ both contain $\left\{x^2:x\in G\right\}$, then the coloring is symmetric with respect to every element $g\in G$.

Similar to what was done for symmetric perfect colorings of G, we give a method on how to obtain symmetric semiperfect colorings of a group G. The following steps need to be carried out to attain the required colorings:

• Choose a subgroup H of G such that $[G:H]=2$.
• Compute $H^2=⟨h^2:h\in H⟩$ and ${(G\setminus H)}^2=⟨w^2:w\in G\setminus H⟩$.
• Find $J_1\le H$ with $H^2\le J_1$ and $J_2\le H$ with ${(G\setminus H)}^2\le J_2$ where $J_1\ne J_2$.
• Form the partition ${\mathcal{P}}_2=\left\{h{J}_1:h\in H\right\}\cup y\left\{h{J}_2:h\in G\setminus H\right\}$ where $y\in G\setminus H$.

In [9], it was established that the number of inequivalent semiperfect colorings of Type II for a given index-2 subgroup H is equal to $\left(\begin{array}{c}n\\ 2\end{array}\right)$ where n is the number of subgroups of H. With the conditions imposed in Theorem 6 on the subgroups $J_1$ and $J_2$, it is reasonable to expect that for most groups, the number of symmetric Type II semiperfect colorings of a group is less than $\left(\begin{array}{c}n\\ 2\end{array}\right)$. An illustration will be given in the next section.

We now show that there exists no nontrivial symmetric Type I semiperfect coloring of any group.

Let G be a group and let $H\le G$ such that $[G:H]=2$. Fix $y\in G\setminus H$ and let J be a proper subgroup of H. Suppose that the partition given by ${\mathcal{P}}_1=\left\{h(J\cup Jy):h\in H\right\}$ corresponds to a symmetric coloring of G with respect to some $g\in G$.

Let $x\in G$. Then $x\in h(J\cup Jy)$ for some $h\in H$. This implies that either $x\in hJ$ or $x\in hJy$. Now, since the coloring is symmetric with respect to g, then $g{x}^{-1}g\in hJ$ or $g{x}^{-1}g\in hJy$. We consider two cases.

If $x\in H$, then $x\in hJ$ and either $g{x}^{-1}g\in hJ$ or $g{x}^{-1}g\in hJy$. If $x\in hJ$, it follows that $h^{-1}x$ and its inverse $x^{-1}h$ are in J. Meanwhile, $h^{-1}g{x}^{-1}g\in J$ or $h^{-1}g{x}^{-1}g{y}^{-1}\in J$. We thus obtain $\left(x^{-1}h\right)\left(h^{-1}x\right)\left(x^{-1}g{x}^{-1}g\right)={\left(x^{-1}g\right)}^2\in J$ or $\left(x^{-1}h\right)\left(h^{-1}x\right)\left(x^{-1}g{x}^{-1}g\right)y^{-1}={\left(x^{-1}g\right)}^2{y}^{-1}\in J\iff {\left(x^{-1}g\right)}^2\in Jy$. Hence, ${\left(xg\right)}^2\in J\cup Jy$ for all $x\in H$.

If $x\in G\setminus H$, then $x\in hJy$ and either $g{x}^{-1}g\in hJ$ or $g{x}^{-1}g\in hJy$. If $x\in hJy$, then $h^{-1}x{y}^{-1}\in J$ and its inverse $y{x}^{-1}h$ are in J. Similar computations yield ${\left(xg\right)}^2\in y^{-1}(J\cup Jy)=y^{-1}J\cup y^{-1}Jy$ for all x not in H.

By the computations above, the partition given by ${\mathcal{P}}_1=\left\{h(J\cup Jy):h\in H\right\}$ corresponds to a symmetric coloring of G with respect to $g\in G$ if and only if the following conditions are satisfied:

(1)

${\left(xg\right)}^2\in J\cup Jy$ for all $x\in H$;

(2)

${\left(xg\right)}^2\in y^{-1}J\cup y^{-1}Jy$ for all $x\in G\setminus H$.

Now, $[G:H]=2$ so $a^2\in H$ for all $a\in G$. Since $y\in G\setminus H$ and $J<H$, the cosets $Jy$ and $y^{-1}J$ are both outside H. Hence, (1) can be rewritten as ${\left(xg\right)}^2\in J$ for all $x\in H$ while (2) becomes ${\left(xg\right)}^2\in y^{-1}Jy$ for all $x\in G\setminus H$. Depending on whether g is found in H or not, conditions (1) and (2) give the following possibilities:

(a)

$h^2\in J$ for all $h\in H$ and $w^2\in y^{-1}Jy$ for all $w\in G\setminus H$;

(b)

$h^2\in y^{-1}Jy$ for all $h\in H$ and $w^2\in J$ for all $w\in G\setminus H$.

Suppose that (a) holds. Since y is outside H, then $y^{-1}h\notin H$. So we have ${\left(y^{-1}h\right)}^2\in y^{-1}Jy$ for all $h\in H$. It follows that $y^{-1}h{y}^{-1}h\in y^{-1}Jy\iff h{y}^{-1}h\in Jy\iff h{y}^{-1}h{y}^{-1}\in J\iff {\left(h{y}^{-1}\right)}^2\in J$. But $h{y}^{-1}$ are all the elements outside H as h runs through all the elements of H. This implies that the squares of all the elements of $G\setminus H$ are also in J. Thus, J contains the squares of all the elements of G. If (b) is assumed to be true, then similar arguments imply that J also contains the set $\left\{x^2:x\in G\right\}$. In particular, $y^2\in J$. Moreover, since $\left\{x^2:x\in G\right\}\subseteq J$, then J is normal in G, which implies that $G=N_G\left(J\right)$ and thus $y\in N_G\left(J\right)$. But Theorem 2 requires that $yJ\ne Jy$ or $y^2\notin J$ so that ${\mathcal{P}}_1$ corresponds to a semiperfect coloring of G. We have therefore proved the following theorem.

Theorem 7.

Let H be an index-2 subgroup of G, $J\le H$, and $y\in G\setminus H$. No partition of G of the form ${\mathcal{P}}_1=\left\{h(J\cup Jy):h\in H\right\}$ yields a symmetric semiperfect coloring, that is, there exists no symmetric Type I semiperfect group coloring for any group G.

4. Examples

To illustrate the results in the previous section, we consider the dihedral group $D_6$, the group $D_{\infty }\times {\mathbb{Z}}_2$, and the triangle group $\ast 642$. In all the examples, patterns using right triangles are used to represent every group G where each right triangle corresponds to an element of the group. In fact, the elements of the group are all the plane isometries that leave the pattern unchanged. In other words, G is the symmetry group of the pattern. For $D_{\infty }\times {\mathbb{Z}}_2$ and $\ast 642$, the program GAP [17] is used to obtain all the required subgroups. Note that all symmetric semiperfect colorings presented here are only those that are consistent with partitions given by ${\mathcal{P}}_2=\left\{h{J}_1:h\in H\right\}\cup y\left\{h{J}_2:h\in H\right\}$, as no Type I semiperfect colorings exist which are symmetric.

4.1. Colorings of $D_6$

We represent the elements of the diheral group $D_6=⟨a,b:a^6=b^2=e,aba=b⟩$ as ${30}^{\circ }$-${60}^{\circ }$-${90}^{\circ }$ triangles whose union is the hexagonal pattern shown in Figure 1a. Here, a represents a ${60}^{\circ }$ counterclockwise rotation about the center of the hexagon, while b is a mirror reflection about the horizontal line passing through the center of the hexagon. From Theorem 5, to find all the symmetric perfect colorings of $D_6$, we only need to determine all the subgroups of $D_6$ that contain the subgroup $⟨x^2|x\in D_6⟩$ generated by squares. This subgroup of $D_6$ is $S=⟨a^2⟩$. There exist four proper subgroups of $D_6$ which contain S, namely $J_1=⟨a^2,b⟩$, $J_2=⟨a^2,ab⟩$, $J_3=⟨a⟩$, and $J_4=⟨a^2⟩$. The corresponding colorings by left cosets of $J_i$, $i\in \left\{1,2,3,4\right\}$ are shown in Figure 1b–e. Therefore, $D_6$ has four inequivalent symmetric perfect colorings.

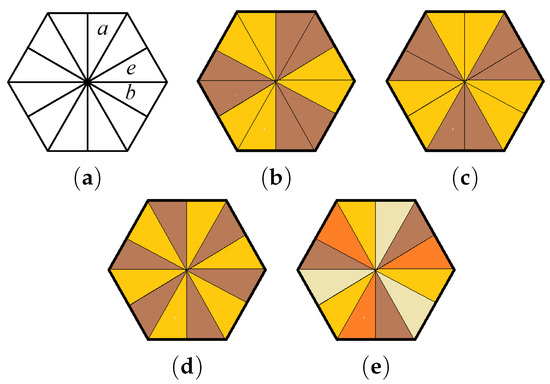
Figure 1. (a) A hexagonal pattern consisting of right triangles with some of the triangles labeled with the generators of the group $D_6$. (b–e) Symmetric perfect colorings of the dihedral group $D_6$.

For the symmetric semiperfect colorings of $D_6$, we look for all partitions ${\mathcal{P}}_2$ of the group based on Theorem 6. There are three index-2 subgroups of $D_6$, namely $H_1=⟨a⟩$, $H_2=⟨a^2,b⟩$, and $H_3=⟨a^2,ab⟩$. For each of these index-2 subgroups of G, we choose the subgroups $J_1$ and $J_2$ such that conditions (1)–(3) are fulfilled. Table 1 shows the possible combinations of $J_1$ and $J_2$ relative to every subgroup $H_i$ ($i=1,2,3$) of $D_6$ of index 2. The resulting seven inequivalent symmetric semiperfect colorings are shown in Figure 2. Observe that $\left\{h{J}_1:h\in H\right\}\cup y\left\{h{J}_2:h\in H\right\}$ and $\left\{h{J}_2:h\in H\right\}\cup y\left\{h{J}_1:h\in H\right\}$ are equivalent colorings according to Theorem 4.

Table 1. Subgroups $J_1$ and $J_2$ that can be used to construct the coloring ${\mathcal{P}}_2$ for each index-2 subgroup H of $D_6$.

${\mathit{H}}_1=⟨\mathit{a}⟩$		${\mathit{H}}_2=⟨{\mathit{a}}^2,\mathit{b}⟩$		${\mathit{H}}_3=⟨{\mathit{a}}^2,\mathit{a}\mathit{b}⟩$
${\mathit{J}}_{\mathbf{1}}$	${\mathit{J}}_{\mathbf{2}}$	${\mathit{J}}_{\mathbf{1}}$	${\mathit{J}}_{\mathbf{2}}$	${\mathit{J}}_{\mathbf{1}}$	${\mathit{J}}_{\mathbf{2}}$
$⟨a⟩$	$⟨a^2⟩$
$⟨a⟩$	$⟨a^3⟩$
$⟨a⟩$	$\left\{e\right\}$	$⟨a^2,b⟩$	$⟨a^2⟩$	$⟨a^2,ab⟩$	$⟨a^2⟩$
$⟨a^2⟩$	$⟨a^3⟩$
$⟨a^2⟩$	$\left\{e\right\}$

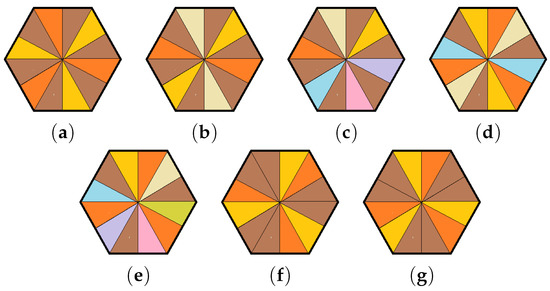
Figure 2. (a–e) Symmetric semiperfect colorings of $D_6$ induced by the subgroup $H_1=⟨a⟩$. (f) Symmetric semiperfect coloring of $D_6$ induced by the subgroup $H_2=⟨a^2,b⟩$. (g) Symmetric semiperfect coloring of $D_6$ induced by the subgroup $H_3=⟨a^2,ab⟩$.

For instance, the coloring in Figure 2a is described by the set $\mathcal{P}=\left\{h⟨a⟩:h\in H_1\right\}\cup b\left\{h⟨a^2⟩:h\in H_1\right\}=\left\{\left\{e,a,a^2,a^3,a^4,a^5\right\},\left\{b,a^{2}b,a^{4}b\right\},\left\{ab,a^{3}b,a^{5}b\right\}\right\}$ where $H_1=⟨a⟩$, $J_1=H_1$, and $J_2=⟨a^2⟩$. If the roles of $J_1$ and $J_2$ are interchanged, we obtain the coloring $\mathcal{Q}=\left\{h⟨a^2⟩:h\in H_1\right\}\cup b\left\{⟨a⟩\right\}=\left\{\left\{e,a^2,a^4\right\},\left\{a,a^3,a^5\right\},\left\{b,ab,a^{2}b,a^{3}b,a^{4}b,a^{5}b\right\}\right\}$ which is equivalent to $\mathcal{P}$ since $x\mathcal{Q}=\mathcal{P}$ for any $x\in G\setminus H_1$. Note that $\mathcal{P}$ is symmetric with respect to every $g\in D_6$ since both $J_1$ and $J_2$ contain the set of squares of elements of $D_6$. In contrast, the coloring ${\mathcal{P}}^{\prime }=\left\{\left\{e,a^2,a^4\right\},\left\{a,a^3,a^5\right\},\left\{b\right\},\left\{ab\right\},\left\{a^{2}b\right\},\left\{a^{3}b\right\},\left\{a^{4}b\right\},\left\{a^{5}b\right\}\right\}$ in Figure 2e is only symmetric with respect to each $g\in H_1$. However, an equivalent coloring given by $b{\mathcal{P}}^{\prime }=\left\{\left\{b,a^{2}b,a^{4}b\right\},\left\{ab,a^{3}b,a^{5}b\right\},\left\{e\right\},\left\{a\right\},\left\{a^2\right\},\left\{a^3\right\},\left\{a^4\right\},\left\{a^5\right\}\right\}$ is symmetric only with respect to all the elements outside $H_1$. These can be verified from Table 2.

Table 2. The elements x and $g{x}^{-1}g$ for all $x,g\in D_6$.

x	e	a	${\mathit{a}}^2$	${\mathit{a}}^3$	${\mathit{a}}^4$	${\mathit{a}}^5$	b	$\mathit{a}\mathit{b}$	${\mathit{a}}^2\mathit{b}$	${\mathit{a}}^3\mathit{b}$	${\mathit{a}}^4\mathit{b}$	${\mathit{a}}^5\mathit{b}$	g
$g{x}^{-1}g$	e	$a^5$	$a^4$	$a^3$	$a^2$	a	b	$ab$	$a^{2}b$	$a^{3}b$	$a^{4}b$	$a^{4}b$	e
	$a^2$	a	e	$a^5$	$a^4$	$a^3$	b	$ab$	$a^{2}b$	$a^{3}b$	$a^{4}b$	$a^{5}b$	a
	$a^4$	$a^3$	$a^2$	a	e	$a^5$	b	$ab$	$a^{2}b$	$a^{3}b$	$a^{4}b$	$a^{5}b$	$a^2$
	e	$a^5$	$a^4$	$a^3$	$a^2$	a	b	$ab$	$a^{2}b$	$a^{3}b$	$a^{4}b$	$a^{5}b$	$a^3$
	$a^2$	a	e	$a^5$	$a^4$	$a^3$	b	$ab$	$a^{2}b$	$a^{3}b$	$a^{4}b$	$a^{5}b$	$a^4$
	$a^4$	$a^3$	$a^2$	a	e	$a^5$	b	$ab$	$a^{2}b$	$a^{3}b$	$a^{4}b$	$a^{5}b$	$a^5$
	e	a	$a^2$	$a^3$	$a^4$	$a^5$	b	$a^{5}b$	$a^{4}b$	$a^{3}b$	$a^{2}b$	$ab$	b
	e	a	$a^2$	$a^3$	$a^4$	$a^5$	$a^{2}b$	$ab$	b	$a^{5}b$	$a^{4}b$	$a^{3}b$	$ab$
	e	a	$a^2$	$a^3$	$a^4$	$a^5$	$a^{4}b$	$a^{3}b$	$a^{2}b$	$ab$	b	$a^{5}b$	$a^{2}b$
	e	a	$a^2$	$a^3$	$a^4$	$a^5$	b	$a^{5}b$	$a^{4}b$	$a^{3}b$	$a^{2}b$	$ab$	$a^{3}b$
	e	a	$a^2$	$a^3$	$a^4$	$a^5$	$a^{2}b$	$ab$	b	$a^{5}b$	$a^{4}b$	$a^{3}b$	$a^{4}b$
	e	a	$a^2$	$a^3$	$a^4$	$a^5$	$a^{4}b$	$a^{3}b$	$a^{2}b$	$ab$	b	$a^{5}b$	$a^{5}b$

Notice that $H_1$ has four distinct subgroups and so we expect a total of $\left(\begin{array}{c}4\\ 2\end{array}\right)=6$ inequivalent Type II semiperfect colorings of $D_6$ that arise from $H_1$. Of these six possible colorings, five are symmetric (Figure 2a–e). The one left out is the partition with $J_1=⟨a^3⟩$ and $J_2=\left\{e\right\}$, as none of these subgroups contain $H_1^2=⟨a^2⟩$. It is also worth mentioning that each of $H_2=⟨a^2,b⟩$ and $H_3=⟨a^2,ab⟩$ has six subgroups. However, there is only one symmetric semiperfect coloring that results from each of these subgroups (Figure 2f,g).

4.2. Colorings of $D_{\infty }\times {\mathbb{Z}}_2$

We now look at symmetric perfect and symmetric semiperfect colorings of the group $G=D_{\infty }\times {\mathbb{Z}}_2=⟨h,v,t:h^2=v^2=e,tv=v{t}^{-1},ht=th,hv=vh⟩$, also denoted $pmm2$, which is the symmetry group of a frieze pattern of type $F_7$. In Figure 3, we see a portion of an infinite strip that is left invariant by G with some of the triangles labeled using the generators of $D_{\infty }\times {\mathbb{Z}}_2$. Here, h is a mirror reflection with a horizontal axis indicated by the green line, v is a mirror reflection with a vertical axis represented by the red line, and t is the translation given by the blue vector. Note that the aforementioned isometries leave the pattern unchanged. The subgroup generated by squares of the elements of $D_{\infty }\times {\mathbb{Z}}_2$ is $S=⟨t^2⟩$. Using GAP, we obtain 15 nontrivial subgroups of $D_{\infty }\times {\mathbb{Z}}_2$ that contain S. These subgroups are given in Table 3 with the corresponding colorings shown in Figure 4 in the order by which the subgroups appear in the table.

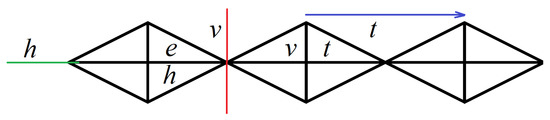
Figure 3. Generators of $D_{\infty }\times {\mathbb{Z}}_2$ as labels of some tiles of a frieze pattern of type $pmm2$.

Table 3. Subgroups of $G=D_{\infty }\times {\mathbb{Z}}_2$ that contain $⟨t^2⟩$.

Subgroup	Index	Subgroup	Index	Subgroup	Index
$⟨h,vt,v{t}^{-1}⟩$	2	$⟨v,ht⟩$	2	$⟨v,t^2⟩$	4
$⟨h,t⟩$	2	$⟨hv,t⟩$	2	$⟨hv,t^2⟩$	4
$⟨h,v,t^2⟩$	2	$⟨h,t^2⟩$	4	$⟨t⟩$	4
$⟨v,t⟩$	2	$⟨vt,v{t}^{-1}⟩$	4	$⟨th⟩$	4
$⟨hv,ht⟩$	2	$⟨tvh,t^2⟩$	4	$⟨t^2⟩$	8

Figure 4. (a–o) Symmetric perfect colorings of $D_{\infty }\times {\mathbb{Z}}_2$.

By Theorem 6, we can obtain symmetric semiperfect colorings of $G=D_{\infty }\times {\mathbb{Z}}_2$ given any index-2 subgroup H of G by choosing the appropriate subgroups $J_1$ and $J_2$ of H. We see in Table 3 seven index-2 subgroups of G, which are in fact all the index-2 subgroups of G. Let us take $H=⟨h,vt,v{t}^{-1}⟩$. Note that the set of squares of all the elements in H is $S=⟨t^2⟩$, which is also the set of squares of all the elements in $G\setminus H$. Therefore, we need $⟨t^2⟩\le J_i$ ($i=1,2$). From GAP, there are five subgroups of H that satisfy this inclusion: H, $⟨h,t^2⟩$, $⟨vt,v{t}^{-1}⟩$, $⟨t^2,tvh⟩$, and $⟨t^2⟩$. Since $\left(\begin{array}{c}5\\ 2\end{array}\right)=10$, there are exactly 10 inequivalent symmetric semiperfect colorings of $D_{\infty }\times {\mathbb{Z}}_2$ relative to the subgroup H. All the said colorings, presented in Figure 5, are symmetric with respect to any element $g\in G$. Note that these are not all the symmetric semiperfect colorings of $D_{\infty }\times {\mathbb{Z}}_2$ but only the symmetric colorings that are invariant under the subgroup $H=⟨h,vt,v{t}^{-1}⟩$. The rest of the index-2 subgroups of G will yield more symmetric semiperfect colorings of G.

Figure 5. (a–j) Symmetric semiperfect colorings of $D_{\infty }\times {\mathbb{Z}}_2$ induced by the subgroup $H=⟨h,vt,v{t}^{-1}⟩$.

4.3. Colorings of $\ast 642$

We finish this section by giving examples of colorings of the triangle group $\ast 642$. This particular group is defined by $\ast 642=⟨p,q,r:p^2=q^2=r^2={\left(qp\right)}^2={\left(rq\right)}^6={\left(pr\right)}^4=e⟩$. Geometrically, $p,q,$ and r can be taken as the mirror reflections along the lines containing the sides of a triangle e whose interior angles are of measure $\frac{\pi }{6}$, $\frac{\pi }{4}$, and $\frac{\pi }{2}$ (see Figure 6), with the axes of the reflections p, q, and r opposite to the angles $\frac{\pi }{6}$, $\frac{\pi }{4}$, and $\frac{\pi }{2}$, respectively.

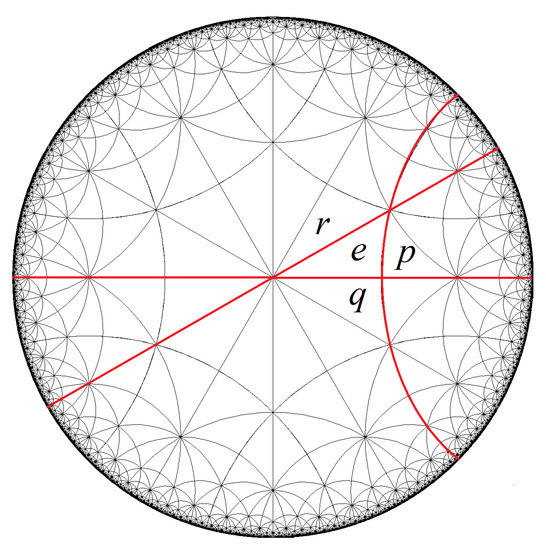
Figure 6. Generators of $\ast 642$ as labels of some tiles of a hyperbolic tiling by triangles with interior angles $\frac{\pi }{6}$, $\frac{\pi }{4}$, and $\frac{\pi }{2}$.

In Figure 7a, we see a symmetric perfect coloring of $G=\ast 642$ that corresponds to the partition $\mathcal{P}=\left\{gJ:g\in G\right\}$ where $J=⟨{\left(rq\right)}^2,p{\left(rq\right)}^{2}p,rp⟩$, an index-4 subgroup of $\ast 642$ which contains the subgroup $S=⟨{\left(rp\right)}^2,{\left(rq\right)}^2,p{\left(rq\right)}^{2}p⟩$ of squares of elements of G. Figure 7b is another symmetric perfect coloring of $\ast 642$ induced by the index-2 subgroup $H=⟨q,r,prp⟩$. Using this subgroup H, we obtain the symmetric semiperfect coloring of $\ast 642$ in Figure 7c, which is described by the partition ${\mathcal{P}}_2=\left\{h{J}_1:h\in H\right\}\cup y\left\{h{J}_2:h\in H\right\}$ where $J_1=⟨q,{\left(rp\right)}^2,rqr⟩,J_2=⟨rq,prqp⟩$, and $y\in G\setminus H$. As with the group $D_{\infty }\times {\mathbb{Z}}_2$, $\ast 642$ has other symmetric semiperfect colorings arising from each index-2 subgroup of $\ast 642$. All these subgroups, together with all the others that contain $S=⟨{\left(rp\right)}^2,{\left(rq\right)}^2,p{\left(rq\right)}^{2}p⟩$, which can be used to form symmetric perfect colorings of $\ast 642$, are found in Table 4.

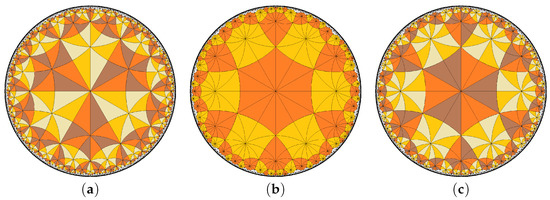
Figure 7. (a,b) Symmetric perfect colorings of $\ast 642$. (c) Symmetric semiperfect coloring of the group $\ast 642$ induced by the subgroup $H=⟨q,r,prp⟩$.

Table 4. Subgroups of $G=\ast 642$ that contain $S=⟨{\left(rp\right)}^2,{\left(rq\right)}^2,p{\left(rq\right)}^{2}p⟩$.

Subgroup	Index	Subgroup	Index	Subgroup	Index
$⟨p,q,rpr,rqr⟩$	2	$⟨qp,r,prp⟩$	2	$⟨r,prp,qrq,pqrqp⟩$	4
$⟨p,r,qrq⟩$	2	$⟨qp,rp⟩$	2	$⟨rp,qrqp⟩$	4
$⟨p,rq⟩$	2	$⟨p,rpr,{\left(rq\right)}^2⟩$	4	$⟨rq,prqp⟩$	4
$⟨q,r,prp⟩$	2	$⟨q,{\left(rp\right)}^2,rqr⟩$	4	$⟨pqr,prq⟩$	4
$⟨q,rp⟩$	2	$⟨qp,{\left(rp\right)}^2,rqrp⟩$	4	$⟨{\left(rp\right)}^2,{\left(rq\right)}^2,p{\left(rq\right)}^{2}p⟩$	8

5. Conclusions and Outlook

This paper focuses on the relationship between various concepts in group colorings. Specifically, we provide a characterization of symmetric perfect and semiperfect group colorings. Among the two possible partition types for semiperfect group colorings, we demonstrate the nonexistence of symmetric colorings for the first type. By investigating these different notions of group colorings, we aim to deepen our understanding of their properties and shed light on the interplay between symmetry and perfect/semiperfect colorings.

We present constructions of symmetric perfect colorings and symmetric semiperfect colorings using the dihedral group $D_6$, the frieze group $pmm2$, and the triangle group $\ast 642$. To facilitate practical implementation, we provide an algorithm that outlines the step-by-step process for obtaining all the symmetric perfect colorings and symmetric semiperfect colorings of any group G.

In this study, our primary focus was to investigate colorings of patterns, where each tile within a given pattern corresponds uniquely to an element in the symmetry group G associated with that pattern. It is worth noting that there are additional avenues in the realm of pattern colorings, such as considering cases where the tiles in a pattern are not necessarily in one-to-one correspondence with the elements of its symmetry group. By expanding the scope of investigation to encompass such scenarios, researchers may uncover and analyze various methods of coloring a given pattern that will yield other symmetric perfect and symmetric semiperfect colorings.

Furthermore, exploring symmetric colorings of group partitions $\mathcal{P}$ that are invariant under subgroup H, where the index $[G:H]$ is greater than or equal to three ($n\ge 3$), could also be an intriguing avenue of investigation.