1. Introduction
Inequalities are fundamental concepts in mathematics that play an important role in establishing relationships between various quantities. Inequalities play a critical role in applied mathematics, where they are used to model and analyze real-world phenomena. In many applications, the quantities of interest are subject to constraints, and inequalities are used to model and analyze these constraints. Inequalities are essential tools in mathematical analysis, providing a means to compare and analyze functions, establish bounds on integrals, and model real-world constraints. Integral inequalities are widely applied in modern mathematical analysis, making them an important component in this area of study. A broad spectrum of integral inequalities, each with multiple applications in both pure and applied sciences, is known to us. The Simpson’s integral inequality is one of the most renowned integral inequalities among them. Simpson’s integral inequality is a result of mathematical analysis that provides an upper bound on the error in approximating the integral of a function using Simpson’s rule. Simpson’s rule is a numerical integration technique that uses quadratic polynomials to approximate the value of an integral. Simpson’s integral inequality is an important result in numerical analysis, and it has applications in various fields of science and engineering, where numerical integration techniques are commonly used to solve problems that involve complex functions.
Let
be a four times continuous differentiable on
, where
is the interior of
I and
. Then, the following inequality is known as Simpson’s inequality:
For more details, see [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21]. The theory of convexity plays a significant role in mathematics, especially in optimization theory, functional analysis, and geometry. Convexity refers to the property of a set or a function that any line segment between two points in the set or on the graph of the function lies entirely within the set or above the graph. One of the most important applications of convexity is in the optimization theory, where it provides a powerful tool for solving optimization problems. The classical concept of convexity also has a knit connection with the concept of symmetry. In the literature, there exist numerous properties of symmetric convex sets. One fascinating aspect of this relationship is that we work on one and apply it to the other. The theory of convexity also played a significant role in the development of the theory of integral inequalities. In particular, the theory of convex functions is closely related to the theory of integral inequalities. Many important integral inequalities can be derived using convex functions. In 2020, Chu et al. [
22] introduced the notion of higher-order
n-ploynomial strongly convex functions involving Katugampola fractional operators. In [
23], Iqbal and colleagues derived new Simpson-type inequalities involving generalized fractional operators together with convexity characteristics. In [
24], the authors visualized some upper error estimations involving generalized strongly convexity named
F convex functions. For details, see [
25].
New versions of classical integral inequalities have been developed using a range of modern techniques in recent years. One of the key approaches involves the use of quantum calculus instead of classical calculus, which provides a significant tool for deriving quantum (
q-)analogues of classical integral inequalities. In quantum calculus, the traditional derivatives and integrals are replaced by
q-derivatives and
q-integrals, which depend on a parameter
q. The
q-derivatives and
q-integrals have different algebraic properties than their classical counterparts. For more details, see [
26].
The aim of this study is to derive new quantum versions of Simpson’s inequality by mainly exploiting the convexity property of functions. Furthermore, the study assesses the validity of the obtained outcomes by providing relevant numerical examples and also graphical analysis.
2. Preliminaries
Some fundamental concepts and definitions of
q-calculus are presented in this section. Throughout this paper, let
and
be an interval with
. The
q-number is expressed as follows:
The left
q-derivative and integral established in [
27] are presented as follows:
Definition 1 ([
27])
. For a continuous function , the left q-derivative on is defined as:The function Ξ is called a left q-differentiable function if exists.
In Definition 1, if
, then (
1) is recaptured as follows:
which is the
q-Jackson derivative; see [
28] for more details.
Definition 2 ([
27])
. For a continuous function , the left q-integral on is defined as:for The function Ξ is called a left q-integrable function if for all exists. In Definition 2, if
, then (
2) is recaptured as follows:
which is the
q-Jackson integral; see [
28] for more details. Moreover, Jackson [
28] gave the
q-Jackson integral on the interval
as follows:
The right
q-derivative and integral established in [
29] are presented as follows:
Definition 3 ([
29])
. For a continuous function , the right q-derivative on is defined as:The function Ξ is called a right q-differentiable function if exists.
Definition 4 ([
29])
. For a continuous function , the right q-integral on is defined as:The function Ξ is called a right q-integrable function if for all exists.
Now, we provide Lemmas which can help us to prove our main findings.
Lemma 1 ([
30])
. For continuous functions , the following expression holds: Lemma 2 ([
31])
. For continuous functions , the following expression holds: The following result will be useful in calculating q-integrals.
Lemma 3 ([
32])
. The following expression holds:where . 3. Main Results
Within this segment, we will create quantum inequalities connected to Simpson’s integral inequalities for smooth, convex functions. To demonstrate the primary outcomes, it is vital to first introduce the subsequent significant lemma.
Lemma 4. Suppose that is a q-differentiable function on such that and are continuous and integrable functions on ; then, Proof. Using Lemmas 1 and 2 and Definitions 2 and 4, we have
and
Thus, from inequalities (
10) and (
9), we have
which completes the proof. □
Remark 1. If we take the limit as in Lemma 4, then the equality (8) becomeswhich is found in [33]. Theorem 1. Suppose that is a q-differentiable function on such that and are continuous and integrable functions on . If and are convex and integrable functions on , thenwhere are defined by Proof. By taking the absolute value of both sides of inequality (
8), we observe that
Using Lemma 3, one can easily compute the integrals as follows:
which completes the proof. □
Remark 2. If we take the limit as in Theorem 1, then the inequality (11) becomeswhich is found in [33]. Theorem 2. Suppose that is a q-differentiable function on such that and are continuous and integrable functions on and . If and are convex and integrable functions on , thenwhere are defined in Theorem 1 and is defined by Proof. Taking the absolute value of both sides of inequality (
8), applying the power mean inequality, and using the convexity of
and
, we have
Using Lemma 3, one can easily compute the integral as follows:
which completes the proof. □
Remark 3. If we take the limit as in Theorem 2, then the inequality (12) becomeswhich is found in [33]. Theorem 3. Suppose that is a q-differentiable function on such that and are continuous and integrable functions on and , if and are convex and integrable functions on . Then, Proof. Taking the absolute value of both sides of inequality (
8), applying the Hölder’s inequality, and using the convexity of
and
, we have
Using Lemma 3, it is easy to see that
Thus, the proof is completed. □
Remark 4. If we take the limit as in Theorem 3, then the inequality (13) becomeswhich is found in [33]. 4. Numerical Examples
Within this section, we provide illustrations that bolster the recently established inequalities outlined in the previous section.
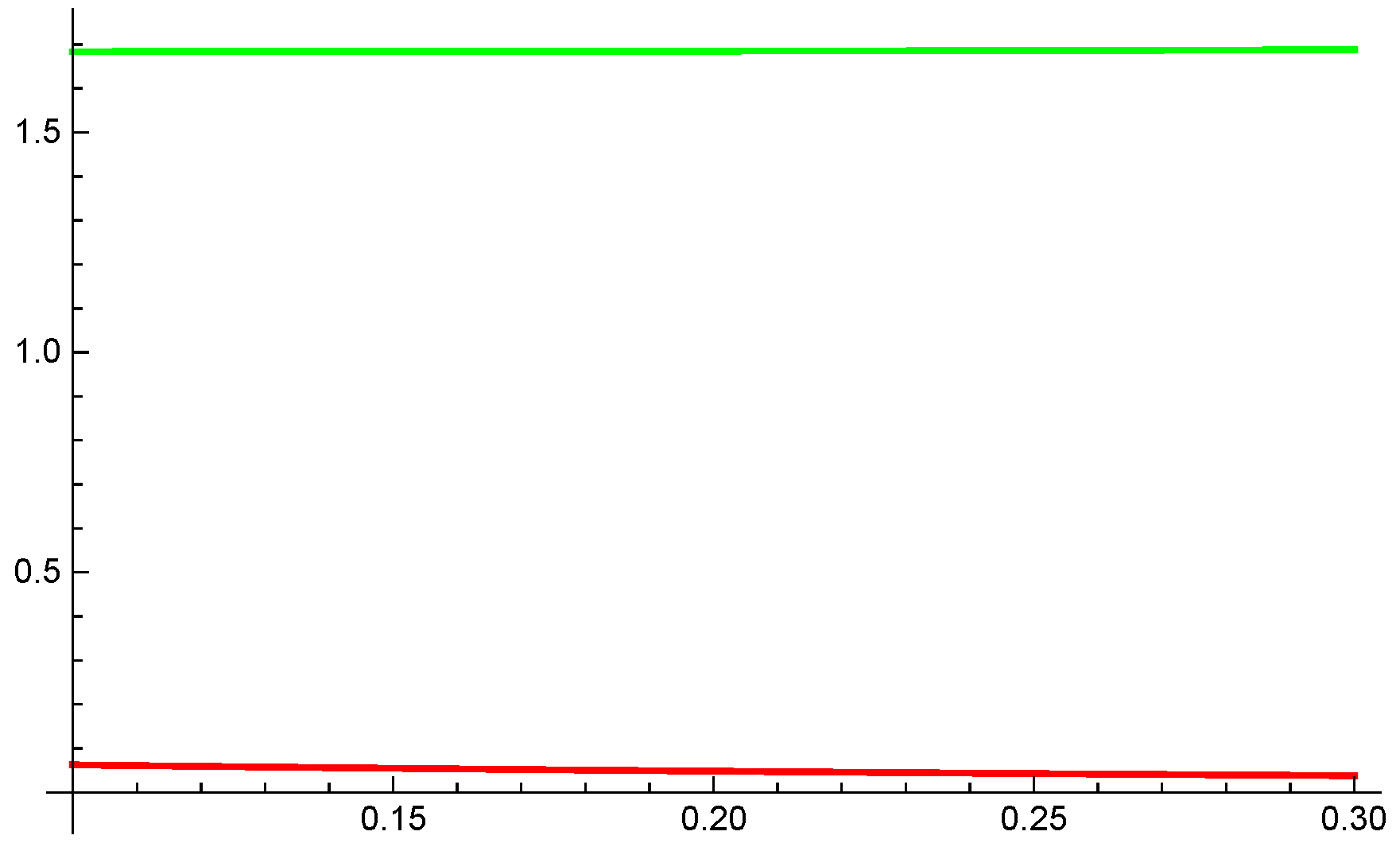
Example 1. Define function by . From Theorem 1 with , the left side of the inequality (11) becomesand the right side of the inequality (11) becomes It is clear thatwhich shows that the inequality (11) is valid. In
Figure 1 green and red lines indicate the right and left hand sides of Theorem 1 respectively.
Example 2. Define function by . From Theorem 2 with and , the left side of the inequality (12) becomesand the right side of the inequality (12) becomes It is clear thatwhich shows that the inequality (12) is valid. In
Figure 2 green and red lines indicate the right and left hand sides of Theorem 2 respectively.
Example 3. Define function by . From Theorem 3 with and , the left side of the inequality (13) becomesand the right side of the inequality (13) becomes It is clear thatwhich shows that the inequality (13) is valid. In
Figure 3 green and red lines indicate the right and left hand sides of Theorem 3 respectively.
5. Conclusions
This paper has introduced various fresh quantum versions of Simpson’s inequality, relying on the convexity of the functions. To verify our findings, we have provided numerical illustrations and graphical analysis. Our intention is that the concepts and methods presented in this research will inspire additional exploration in this area. In the future, we plan to extend these findings to additional classes of convexity and expand them to post-quantum calculus.
Author Contributions
Conceptualization, S.I., M.U.A. and H.B; methodology, S.I.; software, M.U.A.; validation, H.B.; formal analysis, S.I., M.U.A. and H.B.; investigation, S.I. and M.U.A.; resources, H.B.; data curation, S.I.; writing—original draft preparation, S.I. and M.U.A.; writing—review and editing, H.B.; visualization, M.U.A.; supervision, S.I., M.U.A. and H.B.; funding acquisition, S.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Xiamen University Malaysia under grant number: XMUMRF/2022-C10/IMAT/0022.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are thankful to the editor and the anonymous reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ali, M.A.; Budak, H.; Zhang, Z.; Yildirim, H. Some new Simpson’s type inequalities for coordinated convex functions in quantum calculus. Math. Methods Appl. Sci. 2021, 44, 4515–4540. [Google Scholar] [CrossRef]
- Budak, H.; Erden, S.; Aamir Ali, M. Simpson and Newton type inequalities for convex functions via newly defined quantum integrals. Math. Methods Appl. Sci. 2021, 44, 378–390. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Agarwal, R.P.; Cerone, P. On Simpson’s inequality and applications. J. Ineqal. Appl. 2000, 5, 533–579. [Google Scholar] [CrossRef]
- Alomari, M.; Darus, M.; Dragomir, S.S. New inequalities of Simpson’s type for s-convex functions with applications. RGMIA Res. Rep. Coll. 2009, 4, 12. [Google Scholar]
- Kashuri, A.; Mohammed, P.O.; Abdeljawad, T.; Hamasalh, F.; Chu, Y.M. New Simpson type integral inequalities for s-convex functions and their applications. Math. Probl. Eng. 2020, 2020, 8871988. [Google Scholar] [CrossRef]
- Li, Y.; Du, T. Some Simpson type integral inequalities for functions whose third derivatives are (α,m)-GA-convex functions. J. Egypt. Math. Soc. 2016, 24, 175–180. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Budak, H.; Erden, S. On new inequalities of Simpson’s type for generalized convex functions. Korean J. Math. 2019, 27, 279–295. [Google Scholar]
- Qaisar, S.; He, C.; Hussain, S. A generalizations of Simpson’s type inequality for differentiable functions using (α,m)-convex functions and applications. J. Inequal. Appl. 2013, 2013, 158. [Google Scholar] [CrossRef]
- Noor, M.A.; Noor, K.I.; Awan, M.U. Simpson-type inequalities for geometrically relative convex functions. Ukr. Math. J. 2018, 70, 1145–1154. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Rashid, S.; Hammouch, Z.; İşcan, İ.; Chu, Y.M. Some new Simpson-type inequalities for generalized p-convex function on fractal sets with applications. Adv. Differ. Equ. 2020, 2020, 496. [Google Scholar] [CrossRef]
- Du, T.S.; Li, Y.J.; Yang, Z.Q. A generalization of Simpson’s inequality via differentiable mapping using extended (s,m)-convex functions. Appl. Math. Comput. 2017, 293, 358–369. [Google Scholar] [CrossRef]
- Matloka, M. Weighted Simpson type inequalities for h-convex functions. J. Nonlinear Sci. Appl. 2017, 10, 5770–5780. [Google Scholar] [CrossRef]
- Xi, B.Y.; Qi, F. Integral inequalities of Simpson type for logarithmically convex functions. Adv. Stud. Contemp. Math. 2013, 23, 559–566. [Google Scholar]
- Ernst, T. A Comprehensive Treatment of q-Calculus; Springer: Basel, Switzerland, 2012. [Google Scholar]
- Kalsoom, H.; Wu, J.D.; Hussain, S.; Latif, M.A. Simpson’s type inequalities for co-ordinated convex functions on quantum calculus. Symmetry 2019, 11, 768. [Google Scholar] [CrossRef]
- Tunc, M.; Göv, E.; Balgecti, S. Simpson type quantum integral inequalities for convex functions. Miskolc Math. Notes 2018, 19, 649–664. [Google Scholar] [CrossRef]
- Deng, Y.; Awan, M.U.; Wu, S. Quantum integral inequalities of Simpson-type for strongly preinvex functions. Mathematics 2019, 7, 751. [Google Scholar] [CrossRef]
- Ali, M.A.; Abbas, M.; Budak, H.; Agarwal, P.; Murtaza, G.; Chu, Y.M. New quantum boundaries for quantum Simpson’s and quantum Newton’s type inequalities for preinvex functions. Adv. Differ. Equ. 2021, 2021, 64. [Google Scholar] [CrossRef]
- Siricharuanun, P.; Erden, S.; Ali, M.A.; Budak, H.; Chasreechai, S.; Sitthiwirattham, T. Some new Simpson’s and Newton’s formulas type inequalities for convex functions in quantum calculus. Mathematics 2021, 9, 1992. [Google Scholar] [CrossRef]
- You, X.X.; Ali, M.A.; Budak, H.; Vivas-Cortez, M.; Qaisar, S. Some parameterized quantum Simpson’s and quantum Newton’s integral inequalities via quantum differentiable convex mappings. Math. Probl. Eng. 2021, 17, 1–17. [Google Scholar] [CrossRef]
- Ali, M.A.; Budak, H.; Zhang, Z. A new extension of quantum Simpson’s and quantum Newton’s type inequalities for quantum differentiable convex functions. Math. Meth. Appl. Sci. 2022, 45, 1845–1863. [Google Scholar] [CrossRef]
- Chu, Y.M.; Awan, M.U.; Javad, M.Z.; Khan, A.G. Bounds for the remainder in Simpson’s inequality via n-polynomial convex functions of higher order using Katugampola fractional integrals. J. Math. 2020, 2020, 4189036. [Google Scholar] [CrossRef]
- Iqbal, M.; Qaisar, S.; Hussain, S. On Simpson’s type inequalities utilizing fractional integrals. J. Comput. Anal. Appl. 2017, 23, 1137–1145. [Google Scholar]
- Sarikaya, M.Z.; Tunc, T.; Budak, H. Simpson’s type inequality for F-convex function. Facta Univ. Ser. Math. Inform. 2018, 5, 747–753. [Google Scholar]
- Pecaric, J.E.; Proschan, F.; Tong, Y.L. Convex Functions, Partial Orderings and Statistical Applications; Academic Press: New York, NY, USA, 1992. [Google Scholar]
- Kac, V.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2002. [Google Scholar]
- Tariboon, J.; Ntouyas, S.K. Quantum calculus on finite intervals and applications to impulsive difference equations. Adv. Differ. Equ. 2013, 2013, 282. [Google Scholar] [CrossRef]
- Jackson, F.H. On a q-definite integrals. Q. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
- Bermudo, S.; Kórus, P.; Napoles Valdes, J.E. On q-Hermite-Hadamard inequalities for general convex functions. Acta Math. Hungar. 2020, 162, 364–374. [Google Scholar] [CrossRef]
- Soontharanon, J.; Ali, M.A.; Budak, H.; Nanlaopon, K.; Abdullah, Z. Simpson’s and Newton’s type inequalities for (α,m)-convex functions via quantum calculus. Symmetry 2022, 14, 736. [Google Scholar] [CrossRef]
- Sial, I.B.; Mei, S.; Ali, M.A.; Nonlaopon, K. On some generalized Simpson’s and Newton’s inequalities for (α,m)-convex functions in q-calculus. Mathematics 2021, 9, 3266. [Google Scholar] [CrossRef]
- Tariboon, J.; Ntouyas, S.K. Quantum integral inequalities on finite intervals. J. Inequal. Appl. 2014, 2014, 121. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Set, E.; Özdemir, M.E. On new inequalities of Simpson’s type for s-convex functions. Comput. Math. Appl. 2010, 160, 2191–2199. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).