Rényi Entropy for Past Lifetime Distributions with Application in Inactive Coherent Systems

Abstract

In parallel with the concept of Rényi entropy for residual lifetime distributions, the Rényi entropy of inactivity time of lifetime distributions belonging to asymmetric distributions is a useful measure of independent interest. For a system that turns out to be inactive in time t, the past entropy is considered as an uncertainty measure for the past lifetime distribution. In this study, we consider a coherent system that includes n components and has the property that all the components of the system have failed at time t. To assess the predictability of the coherent system’s lifetime, we use the system’s signature to determine the Rényi entropy of its past lifetime. We study several analytical results, including expressions, bounds, and order properties for this measure.

1. Introduction

An accurate quantification of the uncertainty in system lifetime is an important task for engineers engaged in survival analysis. The importance of reducing uncertainty and increasing system lifetime is widely recognized, with longer lifetimes and lower uncertainties being key indicators of higher system reliability (see, e.g., [1]). The problem of extending the life cycle of engineering systems is extremely important and has serious practical applications. To this end, we use the concept of Rényi entropy, denoted ${\overline{H}}_{\alpha }\left(X\right)$, which measures the uncertainty associated with a non-negative continuous random variable (rv) X with a probability density function (pdf) $f,$ defined as the Rényi entropy of order $\alpha$, which is as follows

$$\begin{array}{c}\hfill H_{\alpha }\left(X\right)=H_{\alpha }\left(f\right)=\frac{1}{1-\alpha }\log {\int }_0^{\infty }{f}^{\alpha }\left(x\right)dx,\alpha >0,\end{array}$$

(1)

where “log” stands for the natural logarithm. In general, the uncertainty in the lifetime of a device or organism can be described by a non-negative rv X with a pdf $f$. This is different from the uncertainty associated with a probability p, which is measured by the Shannon entropy $H\left(p\right)$. The notion of uncertainty associated with a distribution, which is well defined for a discrete distribution, should be used with caution when dealing with a continuous distribution, and even more so when choosing Rényi entropy. In the continuous case, it is important to note that, unlike the discrete case, the Rényi entropy does not have to be positive. A probability distribution is typically used to quantify uncertainty and depends on information about the probability that the uncertain quantity has a single, true value. The frequency of instances of the variable, obtained from observed data, is used to quantify the variation. In our case, the variable is the random lifetime of the device, and the uncertainty is a function of event probabilities. Events, in the context of rvs, are those where a random lifetime has certain numerical values.

Rényi entropy has many applications in measuring uncertainty in dynamical systems and has also proved to be a useful criterion for optimization problems (see, e.g., Erdogmus and Principe [2], Lake [3], Bashkirov [4] Henríquez et al. [5]), Guo et al. [6], Ampilova and Soloviev [7], Koltcov [8], and Wang et al. [9]. Shannon’s differential entropy (Shannon [10]), a fundamental concept in information theory, can be derived as follows:

$$\begin{array}{c}\hfill H\left(X\right)=\underset{\alpha \to 1}{lim}{H}_{\alpha }\left(X\right)=-{\int }_0^{\infty }f\left(x\right)logf\left(x\right)dx.\end{array}$$

(2)

By consideration of the lifetime a fresh system has, denoted by X, the Rényi entropy $H_{\alpha }\left(X\right)$ is a useful measure of uncertainty. However, in certain scenarios, actors may know the current age of the system. For example, they know that the system has been in operation for a certain period of time t and want to measure the uncertainty induced by the remaining lifetime of the system, denoted by $X^t=X-t|X>t$. In such cases, Rényi entropy is no longer an appropriate measure of uncertainty. To address this problem, we introduce the residual Rényi entropy, which is specifically designed to measure the uncertainty associated with the remaining lifetime of a system. The residual Rényi entropy is (see [11])

$$\begin{array}{ccc}\hfill H_{\alpha }\left(X^t\right)& =& \frac{1}{1-\alpha }log{\int }_0^{\infty }{f}_t^{\alpha }\left(x\right)dx=\frac{1}{1-\alpha }log{\int }_t^{\infty }{\left(\frac{f\left(x\right)}{S\left(t\right)}\right)}^{\alpha }dx,\hfill \end{array}$$

(3)

for all $\alpha >0,$ where $S\left(t\right)$ denotes the survival function of the rv $X$. The concept of $H_{\alpha }\left(X^t\right)$ provides a fascinating aspect of lifetime units in reliability engineering as the behavior of its fluctuations with respect to t (the current age of an item with original lifetime X) may be helpful to create models. This area of research has attracted the attention of researchers in various fields of science and engineering. This entropy measure is a generalization of the classical Shannon entropy, and it has been shown to have numerous valuable properties and applications in different contexts. In this area, Asadi et al. [12], Gupta and Nanda [13], Nanda and Paul [14], Mesfioui et al. [15], and many other researchers have studied the properties and applications of $H_{\alpha }\left(X^t\right)$.

Uncertainty is a pervasive feature of a given (specific) parameter in real systems, such as their random lifetime, and its effects are felt not only in the future but also in the past. Even if there are facts in the past that we are not aware of, uncertainty remains. There are many real situations in nature, in society, in history, in geology, in other branches of science, and even in medicine, where there is no information about the exact timing of some past events. For example, the exact time when a disease began in a person’s body. This gives rise to a complementary notion of entropy, which captures the uncertainty of past events and is distinct from residual entropy, which describes uncertainty about future events. For another example, consider a system that is observed only at certain inspection times. If the system is inspected for the first time at time t and is in a failed state, the uncertainty relates to the past, more specifically to the time of failure within the interval $[0,t]$. Moreover, when an aircraft is discovered in a non-functional state, it is critical to quantify the degree of uncertainty associated with this situation, which is in the past. The uncertainty is in determining the exact point in the aircraft’s operational history that led to its current condition. Therefore, it is appropriate to introduce a complementary notion of uncertainty that refers to past events rather than future events and is distinct from residual entropy. Let $(Z\mid Z\in A)$ denote an rv with the conditional distribution of Z under the assumption that Z lies in $A,$ where A is a subset of $\mathbb{R}$ such that $P(Z\in A)>0$. Suppose that X is the random lifetime of a fresh system that has a cumulative distribution function (cdf) F, and suppose that an inspection at time t finds that the system is inactive. Then, $X_{\left(t\right)}=(t-X\mid X<t)$ for all $t\ge 0:F\left(t\right)>0$, which is known as the inactivity time of the system and measures the time elapsed since the time when the failure of the system occurred (cf. Kayid and Ahmad [16]). The rv $X_t=(X\mid X<t)$ is also called the past lifetime. The uncertainty in the distribution of $X_t$ is equivalent to the uncertainty in the rv $X_{\left(t\right)}$. The study of past entropy, which deals with the entropy properties of the distribution of past lifetimes and its statistical applications, has received considerable attention in the literature, as evidenced by works such as Di Crescenzo and Longobardi [17], Nair and Sunoj [18], and Nair and Sunoj [19]. Li and Zhang [20] studied the monotonic properties of entropy in order statistics, record values, and weighted distributions in terms of Rényi entropy. Gupta et al. [21] have made significant contributions to the field by studying the properties and applications of past entropy in the context of order statistics. In particular, they have studied the residual and past entropies of order statistics and made stochastic comparisons between them. In general, the informational properties of the residual lifetime distribution are not related to the informational aspects of the past lifetime distribution, at least not for lifetime distributions, which is the case in this work. For further illustrative descriptions on this issue we refer the reader to Ahmad et al. [22]. Therefore, the study of uncertainty in the past life distribution was considered as a new problem compared to the uncertainty properties of the residual life distribution.

On the other hand, coherent systems are well-known in reliability engineering as a large class of such systems and as typical systems in practice (see, e.g., Barlow and Proschan [23] for the formal definition and initial properties of such systems). An example is the k-out-of-n system, which denotes a structure with n components, of which at least k components must be active for the whole system to work. This structure is one of the most important special cases of coherent systems, which has many applications. For example, an airplane with three engines, where at least two engines must be active for it to continue flying smoothly. The $(n-1)$-out-of-n structure, referred to in the literature as a fail-safe system, has many applications in the real world. A fail-safe system is a special design feature that, when a failure occurs, reacts in such a way that no damage is done to the system itself. The brake system on a train is an excellent example of a fail-safe system, where the brakes are held in the off position by air pressure. If a brake line ruptures or a car is cut off, the air pressure is lost; in this case, the brakes are applied by a local air reservoir. Consider a coherent system that turns out to be inactive at time t, when all components of the system are also inactive. The time t is the first time at which the coherent system is found to be inactive. The predictability of the exact time at which the system fails depends largely on the uncertainty properties of the past lifetime distributions. The goal of this work is to quantify the uncertainty about the exact time of failure of the coherent system that is inactive at time t, and furthermore, the uncertainty about the exact time of failure of a particular component of this inactive system. To this end, we will utilize the Rényi entropy of past life distribution.

In the context of lifetime distributions, the study of the Rényi entropy of the past lifetime and its associated information properties does not follow from the Rényi entropy properties of the residual lifetime distribution. To illustrate and explain this problem, we denote by X a random variable with a normal distribution with mean $\mu$ and variance ${\sigma }^2$. We know that X has a symmetric distribution around $\mu$, so $\mu -X{=}_{st}X-\mu$, where ${=}_{st}$ denotes equality in the distribution. This gives $X_{\left(t\right)}{=}_{st}{X}^{2\mu -t}$, and therefore the Rényi entropy property of $X_t=\left(X\right|X\le t)$ follows directly from the same Rényi entropy property of $\left(X\right|X>2\mu -t)$. However, in the context of lifetime distributions (with support $[0,+\infty )$), there is no symmetry. For example, the Gamma distribution and the Weibull distribution as two standard lifetime distributions are asymmetric distributions.

In this paper, we present a comprehensive study of Rényi entropy for the distribution of past lifetimes, providing a generalized version of Equation (3). By allowing different averaging of the conditional probabilities by the parameter $\alpha$, our proposed measure allows for a nuanced comparison of the shapes of different distributions of past lifetimes. The present results demonstrate the potential of this measure to uncover new insights into the mechanisms underlying these distributions. Furthermore, we assume a coherent system of n components, characterized by the property that all components of the system have failed at time $t.$ We use the system signature method to calculate the Rényi entropy of the past lifetime of a coherent system. Throughout the manuscript, we will not use the words “increasing” and “decreasing” in the strict sense.

2. Results on the Past Rényi Entropy

Let us consider an rv X representing the lifetime of a system with the pdf f and the cdf F. Recall that the pdf of $X_t=\left[X\right|X\le t]$ is given by $f_t\left(x\right)=f\left(x\right)/F\left(t\right),$ where $0<x<t$ and $f_t\left(x\right)=0,$ for $x\le 0$ and $x\ge t$. The rvs $X_t$ and $Y_t$ are called right-truncated rvs associated with X and $Y,$ respectively. In this context, the past Rényi entropy at time t of X is defined as (see, e.g., [13])

$$\begin{array}{ccc}\hfill {\overline{H}}_{\alpha }\left(X_t\right)& =& \frac{1}{1-\alpha }log{\int }_0^{+\infty }{f}_t^{\alpha }\left(x\right)dx\hfill \\ & =& \frac{1}{1-\alpha }log{\int }_0^t{\left(\frac{f\left(x\right)}{F\left(t\right)}\right)}^{\alpha }dx,\hfill \end{array}$$

(4)

for all $\alpha >0.$ Note that ${\overline{H}}_{\alpha }\left(X_t\right)\in [-\infty ,\infty ]$. Suppose that at time t it is determined that a lifetime unit has failed. Then, ${\overline{H}}_{\alpha }\left(X_t\right)$ measures the uncertainty about its past lifetime, i.e., about $X_t$. The role of past Rényi entropy in comparing random lifetimes is illustrated by the following example. This highlights the importance of our proposed measure in detecting subtle differences in the shapes of different distributions of past lifetimes and underscores its potential to shed light on the mechanisms underlying these phenomena.

Example 1.

Let us consider two components in a system having random lifetimes X and Y with pdfs

$$f\left(x\right)=2x,0<x<1,andg\left(x\right)=2(1-x),0<x<1,$$

respectively. The Rényi entropy of both X and Y are elegantly captured by the expression:

$${\overline{H}}_{\alpha }\left(X\right)={\overline{H}}_{\alpha }\left(Y\right)=\frac{1}{1-\alpha }\left(\alpha log2-log(\alpha +1)\right),$$

(5)

This result implies that the expected uncertainty regarding the predictability of the outcomes of X and Y in terms of Rényi entropy is identical for f and g. In the case where both components failed at time $t\in (0,1)$ during the inspection, the past Rényi entropy can be used to measure the uncertainty around the respective failure time points, in the spirit of Equation (4) as follows:

$$\begin{array}{ccc}\hfill {\overline{H}}_{\alpha }\left(X_t\right)& =& \frac{1}{1-\alpha }\left(\alpha log2-log(\alpha +1)-(\alpha -1)logt\right),\hfill \\ \hfill {\overline{H}}_{\alpha }\left(Y_t\right)& =& \frac{1}{1-\alpha }\left(\alpha log2-log(1-{(1-t)}^{\alpha +1})-\alpha log(2t-t^2)-log(\alpha +1)\right),\hfill \end{array}$$

It can be shown that ${\overline{H}}_{\alpha }\left(X_t\right)\le {\overline{H}}_{\alpha }\left(Y_t\right)$, for all $t\in (0,1),$ i.e., the expected uncertainty related to the predictability of the failure time of the first component with original lifetime X, as long as $X<t$, is greater than that of the second component with original lifetime Y provided that $Y<t$, even if ${\overline{H}}_{\alpha }\left(X\right)={\overline{H}}_{\alpha }\left(Y\right)$.

As mentioned before in Section 1, an interesting observation is that the statement in Equation (4) can be interpreted as the Rényi entropy of the inactivity time $X_{\left(t\right)}=[t-X|X\le t].$ This alternative identification sheds new light on the underlying dynamics. From (4), we also obtain the following expression for the past Rényi entropy:

$${\overline{H}}_{\alpha }\left(X_t\right)=\frac{log\alpha }{\alpha -1}-\frac{1}{\alpha -1}logE\left[{\tau }^{\alpha -1}\left(X_{\alpha ,t}\right)\right],$$

(6)

where $\tau \left(x\right)=f\left(x\right)/F\left(x\right)$ denotes the reversed hazard rate of X and $X_{\alpha ,t}$ has the pdf

$$f_{\alpha ,t}\left(x\right)=\alpha f_t\left(x\right)F_t^{\alpha -1}\left(x\right),$$

(7)

for all $\alpha >0$, so that $F_t\left(x\right)=F\left(x\right)/F\left(t\right)$ for all $t\ge 0$. The following definition, which can be found in Shaked and Shanthikumar [24], is used throughout the paper.

Definition 1.

Suppose that X and Y are two general rvs with arbitrary supports with density functions f and g and reversed hazard rate functions ${\tau }_X$ and ${\tau }_Y,$ respectively. Then,

(i) 

We say X is smaller than Y in the reversed hazard rate order (denoted by $X{\le }_{rhr}Y$) whenever ${\tau }_X\left(a\right)\le {\tau }_Y\left(a\right),$ for all a, or equivalently if $\frac{G\left(a\right)}{F\left(a\right)}$ is increasing in $a.$

(ii) 

X is said to have a decreasing [resp. increasing] reversed hazard rate property (denoted as DRHR [resp. IRHR]) whenever ${\tau }_X\left(a\right)$ is a decreasing [resp. increasing] function in a.

(iii) 

We say X is smaller than Y in the dispersion order (denoted by $X{\le }_{disp}Y$) whenever $g\left(G^{-1}\left(u\right)\right)\le f\left(F^{-1}\left(u\right)\right),$ for all $u\in (0,1)$

Our analysis sheds new light on the behavior of past Rényi entropy in the presence of a decreasing reversed hazard rate (DRHR) property, contributing to our understanding of this important class of stochastic processes.

Theorem 1.

If X is DRHR, then ${\overline{H}}_{\alpha }\left(X_t\right)$ is increasing in t.

Proof. 

Differentiating (4) with respect to t implies

$$\begin{array}{ccc}\hfill (1-\alpha ){\overline{H}}_{\alpha }^{\prime }\left(X_t\right)& =& \frac{f^{\alpha }\left(t\right)}{{\int }_0^t{f}^{\alpha }\left(x\right)dx}-\alpha \tau \left(t\right)\hfill \\ & =& \frac{\alpha \frac{f^{\alpha }\left(t\right)}{F^{\alpha }\left(t\right)}}{\alpha {\int }_0^t\frac{f^{\alpha }\left(x\right)}{F^{\alpha }\left(t\right)}dx}-\alpha \tau \left(t\right)\hfill \\ & =& \frac{\alpha {\tau }^{\alpha }\left(t\right)}{{\int }_0^t{\tau }^{\alpha -1}\left(x\right)f_{\alpha ,t}\left(x\right)dx}-\alpha \tau \left(t\right),\hfill \end{array}$$

(8)

where $f_{\alpha ,t}\left(x\right)$ is given in (7). Since X is DRHR, then $\tau \left(x\right)$ is decreasing in t and this results in for all $\alpha >1(\alpha <1)$ that ${\tau }^{\alpha -1}\left(x\right)\ge (\le ){\tau }^{\alpha -1}\left(t\right)$ when $x\le t.$ Thus, Equation (8) yields

$$\frac{\alpha {\tau }^{\alpha }\left(t\right)}{{\int }_0^t{\tau }^{\alpha -1}\left(x\right)f_{\alpha ,t}\left(x\right)dx}-\alpha \tau \left(t\right)\le (\ge )0,$$

or equivalently

$$(1-\alpha ){\overline{H}}_{\alpha }^{\prime }\left(X_t\right)\le (\ge )0,$$

and this gives the results.    □

The result of Theorem 1 shows that the DRHR property of a component lifetime translates to the increasing property of the past Rényi entropy for the component lifetime as a function of time. Thus, an interesting conclusion is that when we first find that a component with a random lifetime exhibiting the DRHR property has failed, the uncertainty about the exact time of failure (with respect to the past Rényi entropy) of the component increases accordingly. The following theorem refers to the ordering of the rvs according to the Rényi entropy of the right-truncated distributions and the ordering of the rvs based on the basis of the reversed hazard rates order.

Theorem 2.

Let X and Y be two continuous rvs having cdfs F and G with pdfs f and $g,$ and reversed hazard rate functions ${\tau }_X$ and ${\tau }_Y,$ respectively. If $X{\le }_{rhr}Y$ and either X or Y has IRHR property, then, for all $\alpha >0$, we have ${\overline{H}}_{\alpha }\left(X_t\right)\ge {\overline{H}}_{\alpha }\left(Y_t\right)$.

Proof. 

Notice that $X_t=\left[X\right|X\le t]$ and $Y_t=\left[Y\right|Y\le t]$, as two right-truncated rvs, have pdfs $f_t$ and $g_t,$ respectively. The condition that $X{\le }_{rhr}Y$ implies that for all $x\le t$

$$\frac{F\left(x\right)}{F\left(t\right)}\ge \frac{G\left(x\right)}{G\left(t\right)}.$$

For every $\alpha >0$, the inequality

$$\frac{F^{\alpha }\left(x\right)}{F^{\alpha }\left(t\right)}\ge \frac{G^{\alpha }\left(x\right)}{G^{\alpha }\left(t\right)},$$

then holds, which further implies that $X_{\alpha ,t}{\le }_{st}{Y}_{\alpha ,t}$, where $X_{\alpha }$ and $Y_{\alpha }$ have the cdfs $F^{\alpha }\left(x\right)$ and $G^{\alpha }\left(x\right)$, respectively. Now, let us assume that X has IRHR property. For $\alpha >1$ we obtain the following result

$$E\left[{\tau }_X^{\alpha -1}\left(X_{\alpha ,t}\right)\right]\le E\left[{\tau }_X^{\alpha -1}\left(Y_{\alpha ,t}\right)\right]\le E\left[{\tau }_Y^{\alpha -1}\left(Y_{\alpha ,t}\right)\right],$$

where the former inequality follows from the definition of the usual stochastic order and the fact that $E\left[\varphi \left(X_{\alpha ,t}\right)\right]\le E\left[\varphi \left(Y_{\alpha ,t}\right)\right]$ for all increasing functions $\varphi ,$ and in particular, for $\varphi \left(x\right)={\tau }_X^{\alpha -1}\left(x\right)$, which is an increasing function of x as X is IRHR and also since $\alpha >1$. The latter inequality above is also satisfied because $X{\le }_{rhr}Y$. For $\alpha <1$, we can easily check that

$$E\left[{\tau }_X^{\alpha -1}\left(X_{\alpha ,t}\right)\right]\ge E\left[{\tau }_X^{\alpha -1}\left(Y_{\alpha ,t}\right)\right]\ge E\left[{\tau }_Y^{\alpha -1}\left(Y_{\alpha ,t}\right)\right].$$

For all $\alpha >0,$ we finally obtain

$$-\frac{1}{\alpha -1}logE\left[{\tau }_X^{\alpha -1}\left(X_{\alpha ,t}\right)\right]\ge -\frac{1}{\alpha -1}logE\left[{\tau }_Y^{\alpha -1}\left(Y_{\alpha ,t}\right)\right],$$

and this gives ${\overline{H}}_{\alpha }\left(X_t\right)\ge {\overline{H}}_{\alpha }\left(Y_t\right)$ by recalling (6). A similar conclusion can be drawn if we assume instead that the rv Y possesses the IRHR property.    □

According to Theorem 2, between two rvs, at least one of which has the IRHR property, the one with a larger reversed hazard rate leads to a smaller uncertainty in the Rényi entropy of the right-truncated distribution. Therefore, the rv which is stochastically smaller is expected to be less predictable.

In the next theorem, we give a bound for ${\overline{H}}_{\alpha }\left(X_t\right)$ in terms of the reversed hazard rate function.

Theorem 3.

Assume that $\tau \left(x\right)<\infty .$ If X is DRHR, then for all $\alpha >0,$ it holds that

$${\overline{H}}_{\alpha }\left(X_t\right)\le \frac{log\alpha }{\alpha -1}-log\tau \left(t\right),t>0.$$

Proof. 

If X is DRHR, then $\tau \left(t\right)$ is decreasing in $t,$ and so recalling (6) for all $\alpha -1>0 (\alpha -1<0),$ we have

$$\begin{array}{ccc}\hfill {\overline{H}}_{\alpha }\left(X_t\right)& =& \frac{log\alpha }{\alpha -1}-\frac{1}{\alpha -1}log\left({\int }_0^t{\tau }^{\alpha -1}\left(x\right)f_{\alpha ,t}\left(x\right)dx\right)\hfill \\ & \le & \frac{log\alpha }{\alpha -1}-\frac{1}{\alpha -1}log\left({\tau }^{\alpha -1}\left(t\right){\int }_0^t{f}_{\alpha ,t}\left(x\right)dx\right)\hfill \\ & =& \frac{log\alpha }{\alpha -1}-log\tau \left(t\right),\hfill \end{array}$$

and this completes the proof.  □

3. Results on the Past Lifetimes of Coherent Systems

This section presents the application of the system signature approach to find a definition for the past life entropy of a coherent system with arbitrary structure. It is assumed that all components of the system have failed at a given time $t$. A coherent system is defined as one that satisfies two conditions: First, it contains no irrelevant components, and second, its structure function is monotonic. An n-dimensional vector $\mathbf{p}=(p_1, \dots , p_n)$, whose ith element is given by $p_i=P(T=X_{i:n}),i=1, 2, \dots , n;$ is the signature of such a system (see [25]). Consider a coherent system with independent and identically distributed (i.i.d.) component lifetimes $X_1, \dots , X_n$, and a known signature vector $\mathbf{p}=(p_1, \dots , p_n)$. If $T_t=[t-T|X_{n:n}\le t]$ stands for the past lifetime of the coherent system under the condition that, at time t all components of the system have failed, then from the results of Khaledi and Kochar [26], the survival function of $T_t$ can be expressed as

$$P(T_t>x)=\sum _{i=1}^n{p}_{i}P(t-X_{i:n}>x|X_{n:n}\le t),$$

(9)

where

$$P(t-X_{i:n}>x|X_{n:n}\le t)=\sum _{k=i}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){\left(\frac{F(t-x)}{F\left(t\right)}\right)}^k{\left(1-\frac{F(t-x)}{F\left(t\right)}\right)}^{n-k},0<x<t,$$

denotes the past life survival function of an i-out-of-n system under the condition that all components have failed at time t. From (9), it follows that

$$f_{T_t}\left(x\right)=\sum _{i=1}^n{p}_i{f}_{T_t^i}\left(x\right),$$

(10)

where

$$f_{T_t^i}\left(x\right)=\frac{\mathsf{\Gamma }(n+1)}{\mathsf{\Gamma }\left(i\right)\mathsf{\Gamma }(n-i+1)}{\left(\frac{F(t-x)}{F\left(t\right)}\right)}^{i-1}{\left(1-\frac{F(t-x)}{F\left(t\right)}\right)}^{n-i}\frac{f(t-x)}{F\left(t\right)},0<x<t,$$

(11)

such that $\mathsf{\Gamma }(·)$ is the complete gamma function and $T_t^i=[t-X_{i:n}|X_{n:n}\le t],i=1, 2, \dots , n,$ is the time that has passed from the failure of the component with lifetime $X_{i:n}$ in the system given that the system has failed at or before time $t$. It is worth mentioning, by (9), that $T_t^i$ denotes the ith order statistics consisting of n i.i.d. components with the cdf $\frac{F(t-x)}{F\left(t\right)},0<x<t$. Hereafter, we provide an expression for the entropy of $T_t.$ To this aim, let us keep in mind that $F_t\left(x\right)=\frac{F\left(x\right)}{F\left(t\right)},0<x<t$. The probability integral transformation $V=F_t\left(T_t\right)$, as a crucial reformulation, plays an important role in our aim. It is evidently seen that $U_{i:n}=F_t\left(T_t^i\right)$ has the beta distribution with parameters i and $n-i+1$ with the following pdf

$$g_i\left(u\right)=\frac{\mathsf{\Gamma }(n+1)}{\mathsf{\Gamma }\left(i\right)\mathsf{\Gamma }(n-i+1)}{u}^{i-1}{(1-u)}^{n-i},0<u<1,$$

(12)

for all $i=1, \dots , n$. In the forthcoming theorem, we provide an expression for the Rényi entropy of $T_t$ by using the earlier mentioned transforms.

Theorem 4.

Let $T_t$ stand for the past lifetime of the coherent system under the condition that, at time t all components of the system have failed. The Rényi entropy of $T_t$ can be expressed as follows:

$${\overline{H}}_{\alpha }\left(T_t\right)=\frac{1}{1-\alpha }log{\int }_0^1{g}_V^{\alpha }\left(u\right)f_t^{\alpha -1}\left(F_t^{-1}\left(u\right)\right)du,t>0,$$

(13)

where V is the lifetime of the coherent system, with the pdf $g_V\left(v\right)={\sum }_{i=1}^n{p}_i{g}_i\left(v\right)$, and $F_t^{-1}\left(u\right)=inf\{x;F_t\left(x\right)\ge u\}$ is the quantile function of $F_t\left(x\right)=F\left(x\right)/F\left(t\right),0<x\le t$ for all $\alpha >0.$

Proof. 

By (1) and (10), and by substituting $z=t-x$ and $\overline{\alpha }=1-\alpha$, we have

$$\begin{array}{ccc}\hfill {\overline{H}}_{\alpha }\left(T_t\right)& =& \frac{1}{1-\alpha }log{\int }_0^t{\left(f_{T_t}\left(x\right)\right)}^{\alpha }dx\hfill \\ & =& \frac{1}{\overline{\alpha }}log{\int }_0^t{\left(\sum _{i=1}^n{p}_i{f}_{T_t^i}\left(x\right)\right)}^{\alpha }dx\hfill \\ & =& \frac{1}{\overline{\alpha }}log{\int }_0^t{\left(\sum _{i=1}^n{p}_i\frac{\mathsf{\Gamma }(n+1)}{\mathsf{\Gamma }\left(i\right)\mathsf{\Gamma }(n-i+1)}{\left(\frac{F(t-x)}{F\left(t\right)}\right)}^{i-1}{\left(1-\frac{F(t-x)}{F\left(t\right)}\right)}^{n-i}\frac{f(t-x)}{F\left(t\right)}\right)}^{\alpha }dx\hfill \\ & =& \frac{1}{\overline{\alpha }}log{\int }_0^t{\left(\sum _{i=1}^n{p}_i\frac{\mathsf{\Gamma }(n+1)}{\mathsf{\Gamma }\left(i\right)\mathsf{\Gamma }(n-i+1)}{\left(F_t\left(z\right)\right)}^{i-1}{\left(1-F_t\left(z\right)\right)}^{n-i}{f}_t\left(z\right)\right)}^{\alpha }dx\hfill \\ & =& \frac{1}{\overline{\alpha }}log{\int }_0^1{g}_V^{\alpha }\left(u\right){\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}du.\hfill \end{array}$$

The identity at the last line above is acquired by substituting $u=F_t\left(z\right)$, which ends the proof.  □

If all components have failed at time t, then $\overline{H}\left(T_t\right)$ measures the expected uncertainty contained in the conditional density of $t-T$ given $X_{n:n}\le t,$ about the predictability of the past lifetime of the system. In the special case, if we consider an i-out-of-n system with the system signature $\mathbf{p}=(0, \dots , 0, 1_i, 0, \dots , 0),i=1, 2, \dots ,n$, then Equation (13) reduces to

$${\overline{H}}_{\alpha }\left(T_t^i\right)={\overline{H}}_{\alpha }\left(U_{i:n}\right)-\frac{1}{\alpha -1}log\mathbb{E}\left[f_t^{\alpha -1}\left(F_t^{-1}\left(Z_i\right)\right)\right],$$

(14)

where $Z_i$ has the beta distribution with parameters $\alpha (i-1)+1$ and $\alpha (n-i)+1$ and

$$H_{\alpha }\left(U_{i:n}\right)=\frac{\alpha }{\alpha -1}logB(i,n-i+1)-\frac{1}{\alpha -1}logB(\alpha (i-1)+1,\alpha (n-i)+1),$$

(15)

so that $B(a,b)=\mathsf{\Gamma }\left(a\right)\mathsf{\Gamma }\left(b\right)/\mathsf{\Gamma }(a+b)$ stands for the beta function. In the special case when t goes to infinity, (14) coincides with the results of Abbasnejad and Arghami [27].

The next theorem immediately follows from Theorem 4 in terms of the property that the reversed hazard rate of X, i.e., $\tau \left(x\right)$, is decreasing.

Theorem 5.

If X is DRHR, then ${\overline{H}}_{\alpha }\left(T_t\right)$ is increasing in t.

Proof. 

By noting that $f_t\left(F_t^{-1}\left(x\right)\right)=x{\tau }_t\left(F_t^{-1}\left(x\right)\right),$ Equation (13) can be rewritten as

$$\begin{array}{c}\hfill e^{(1-\alpha ){\overline{H}}_{\alpha }\left({T_t}^{1,n}\right)}={\int }_0^1{g}_V^{\alpha }\left(u\right)u^{\alpha -1}{\left({\tau }_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}du,\end{array}$$

(16)

for all $\alpha >0.$ It is easy to verify that $F_t^{-1}\left(u\right)=F^{-1}\left(uF\left(t\right)\right)$ for all $0<u<1,$ and hence we have

$$\begin{array}{ccc}\hfill {\tau }_t\left(F_t^{-1}\left(u\right)\right)& =& \tau \left(F^{-1}\left(uF\left(t\right)\right)\right),0<u<1.\hfill \end{array}$$

If $t_1\le t_2$, then $F^{-1}\left(uF\left(t_1\right)\right)\le F^{-1}\left(uF\left(t_2\right)\right)$. Consequently, when X is DRHR, then for all $\alpha >1 (0<\alpha \le 1)$ we have

$$\begin{array}{ccc}\hfill {\int }_0^1{g}_V^{\alpha }\left(u\right)u^{\alpha -1}{\left({\tau }_{t_1}\left(F_{t_1}^{-1}\left(u\right)\right)\right)}^{\alpha -1}du& =& {\int }_0^1{g}_V^{\alpha }\left(u\right)u^{\alpha -1}{\left(\tau \left(F^{-1}\left(uF\left(t_1\right)\right)\right)\right)}^{\alpha -1}du\hfill \\ & \ge (\le )& {\int }_0^1{g}_V^{\alpha }\left(u\right)u^{\alpha -1}{\left(\tau \left(F^{-1}\left(uF\left(t_2\right)\right)\right)\right)}^{\alpha -1}du\hfill \\ & =& {\int }_0^1{g}_V^{\alpha }\left(u\right)u^{\alpha -1}{\left({\tau }_{t_2}\left(F_{t_2}^{-1}\left(u\right)\right)\right)}^{\alpha -1}du,\hfill \end{array}$$

for all $t_1\le t_2.$ Using (16), we obtain

$$\begin{array}{c}\hfill e^{(1-\alpha ){\overline{H}}_{\alpha }\left(T_{t_1}\right)}\ge (\le )e^{(1-\alpha ){\overline{H}}_{\alpha }\left(T_{t_2}\right)},\end{array}$$

for all $\alpha >1 (0<\alpha \le 1).$ This requires that ${\overline{H}}_{\alpha }\left(T_{t_1}\right)\le {\overline{H}}_{\alpha }\left(T_{t_2}\right)$ for all $\alpha >0$. Hence, the proof is obtained.  □

Remark 1.

Another proof of Theorem 5 can be as follows, as one of the referees pointed out. Suppose that X has the DRHR property and, thus, F is log-concave. Then, from Theorem 3.B.19 in Shaked and Shanthikumar [24], $\left[X\right|X\le t_1]{\le }_{disp}\left[X\right|X\le t_1]$ for all $t_1\le t_2.$ Thus, from definition, $f_{t_1}\left(F_{t_1}^{-1}\left(u\right)\right)\ge f_{t_1}\left(F_{t_1}^{-1}\left(u\right)\right)$ for all $t_1\le t_2.$ It is plain to observe, in view of (13), that ${\overline{H}}_{\alpha }\left(T_{t_1}\right)\le {\overline{H}}_{\alpha }\left(T_{t_2}\right)$ for all $\alpha >0$.

The result of Theorem 5 in turn shows that when the component lifetimes in a coherent system satisfy the DRHR property, the past Rényi entropy increases when all components of the coherent system are inactive, thus decreasing predictability and making it very difficult to determine the exact time of failure in the past.

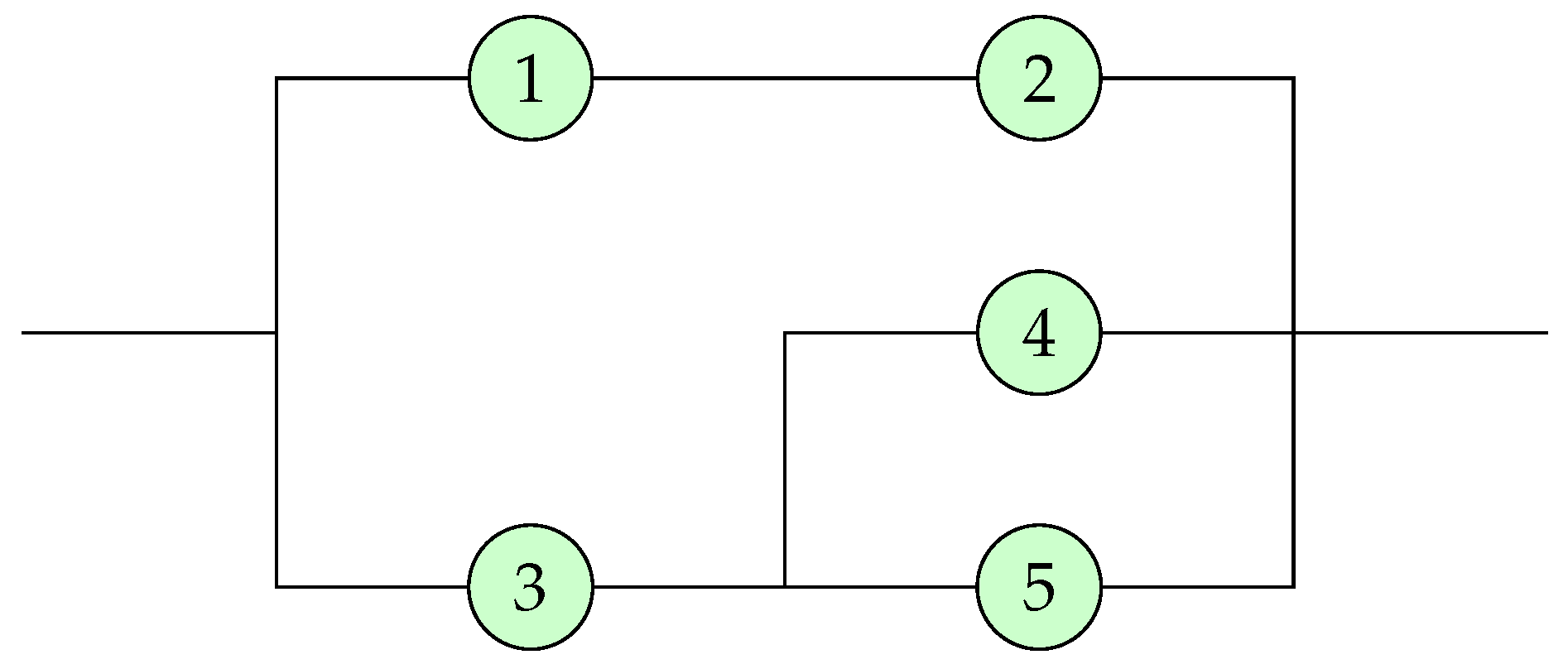
The next example is given to apply Theorems 4 and 5.

Example 2.

Let us consider a coherent system with the system signature $\mathit{p}=(0,\frac{3}{10},\frac{1}{2},\frac{1}{5},0)$ depicted in Figure 1. The exact value of ${\overline{H}}_{\alpha }\left(T_t\right)$ can be computed using relation (13) when the component lifetime distributions are given. To this aim, let us suppose the following lifetime distributions.

(i) 

Let X follow the uniform distribution in $[0,1].$ From (13), we immediately obtain

$${\overline{H}}_{\alpha }\left(T_t\right)=log\left(t\right)+\frac{1}{1-\alpha }log{\int }_0^1{g}_V^{\alpha }\left(u\right)du,t>0.$$

It reveals that the Rényi entropy ${\overline{H}}_{\alpha }\left(T_t\right)$ of the rv $T_t$ is a decreasing function of time t. This observation is consistent with previous results on the behavior of Rényi entropy for certain classes of rvs. In particular, the uniform distribution is known to possess the DRHR property, which implies that the Rényi entropy of $T_t$ should be an increasing function of time t, in line with Theorem 5.

(ii) 

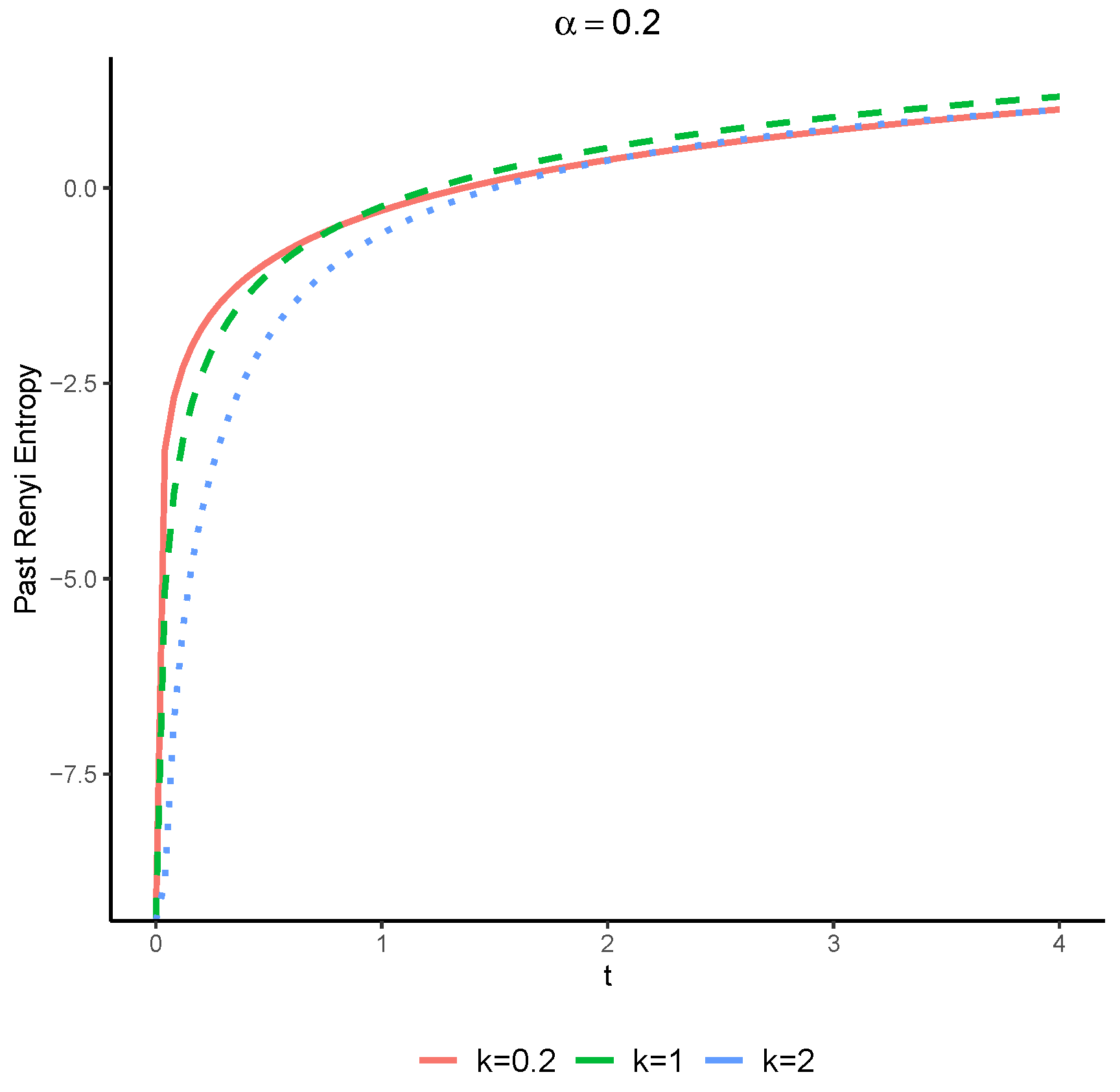
Consider an rv X with the cdf given by

$$F\left(x\right)=e^{-x^{-k}},x>0,k>0.$$

With some algebraic manipulation, we arrive at the following expression:

$${\overline{H}}_{\alpha }\left(T_t\right)=\frac{1}{1-\alpha }log{\int }_0^1{\left(t^{-k}-logu\right)}^{(\frac{1}{k}+1)(\alpha -1)}{u}^{\alpha -1}{g}_V^{\alpha }\left(u\right)du-logk,t>0.$$

The numerical results, which are presented in Figure 2, showcase the increasing nature of the Rényi entropy of $T_t$ as a function of time t for $\alpha =0.2$ and various values of k (in this case, the past Rényi entropy for $\alpha >1$ is not defined). This observation is in line with Theorem 5, which predicts the monotonicity properties of the Rényi entropy in the case of DRHR rvs.

The above example sheds light on the complicated relationship between the Rényi entropy of an rv and time t (the time of inspection) where the failure of the device is realized, and highlights the importance of considering the DRHR property when analyzing such systems. Thus, our results suggest that the DRHR property of X plays a crucial role in shaping the temporal behavior of the Rényi entropy of $T_t$, which could have far-reaching implications for various applications, including the analysis of complex systems and the development of efficient data compression techniques.

It is possible to lower the computing cost for determining the signatures of all coherent systems of a certain size by around half thanks to the widely used notion of a system’s dual in reliability and industry. A duality link between a system’s signature and that of its dual has been proposed by Kochar et al. [28]. If $\mathbf{p}=(p_1, \dots , p_n)$ signifies the signature of a coherent system with lifetime T, then the signature by which its dual system with lifetime $T^D$ is recognized is given by ${\mathbf{p}}^D=(p_n, \dots , p_1)$. In the following theorem, by the condition that $f_t\left(F_t^{-1}\left(u\right)\right)$ is a symmetric function of u around $u=\frac{1}{2}$, we apply the duality property to simplify the calculation of the past Rényi entropy for coherent systems.

Theorem 6.

Let $T_t$ be the lifetime of a coherent system with signature $\mathit{p}$ consisting of n i.i.d. components. If $f_t\left(F_t^{-1}\left(u\right)\right)=f_t\left(F_t^{-1}(1-u)\right)$ is satisfied for all $0<u<1$ and $t,$ then ${\overline{H}}_{\alpha }\left(T_t\right)={\overline{H}}_{\alpha }\left(T_t^D\right)$ for all $\mathit{p}$ and all $n.$

Proof. 

To prove sufficiency, let us assume that $f_t\left(F_t^{-1}\left(u\right)\right)=f_t\left(F_t^{-1}(1-u)\right)$ for all $0<u<1$. It is worth noting that $g_i(1-u)=g_{n-i+1}\left(u\right)$ for all $i=1, \dots , n$ and $0<u<1$. Consequently, utilizing (13), we obtain that:

$$\begin{array}{ccc}\hfill {\int }_0^1{g}_{V^D}^{\alpha }\left(u\right){\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}du& =& -{\int }_0^1{\left(\sum _{i=1}^n{p}_{n-i+1}{g}_i\left(u\right)\right)}^{\alpha }{\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}du\hfill \\ & =& {\int }_0^1{\left(\sum _{r=1}^n{p}_r{g}_{n-r+1}\left(u\right)\right)}^{\alpha }{\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}du\hfill \\ & =& {\int }_0^1{\left(\sum _{r=1}^n{p}_r{g}_r(1-u)\right)}^{\alpha }{\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}du\hfill \\ & =& {\int }_0^1{\left(\sum _{r=1}^n{p}_r{g}_r\left(u\right)\right)}^{\alpha }{\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}du\hfill \\ & =& {\int }_0^1{g}_V^{\alpha }\left(u\right){\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}du,\hfill \end{array}$$

and in the spirit of Equation (13) the proof is obtained.  □

In the following, a direct conclusion is drawn from Theorem 6 for the case that an i-out-of-n-system is the designated coherent system.

Corollary 1.

Let $T_t^i$ be the lifetime of an i-out-of-n system consisting of n i.i.d. components. If $f_t\left(F_t^{-1}\left(u\right)\right)=f_t\left(F_t^{-1}(1-u)\right)$ is satisfied for all $0<u<1$ and $t,$ then ${\overline{H}}_{\alpha }\left(T_t^i\right)={\overline{H}}_{\alpha }\left(T_t^{n-i+1}\right)$ for all n and $i=1, 2, \dots , n/2$ if n is even and $i=1, 2, \dots , (n-1)/2$ if n is odd.

4. Bounds for the Past Rényi Entropy of Coherent Systems

For complex systems or uncertain distributions of component lifetimes, accurately calculating the past Rényi entropy ${\overline{H}}_{\alpha }\left(T_t\right)$ of a coherent system can be a daunting task. This scenario is not uncommon in practice, and, thus, there is a growing need for effective approximations of the system behavior. One promising approach is to use previous Rényi entropy bounds, which have been shown to accurately approximate the lifetimes of coherent systems under such circumstances.

Toomaj and Doostparast [29,30] pioneered the development of such barriers for a new system, while more recently Toomaj et al. [31] have extended this work by deriving bounds on the entropy of a coherent system when all its components are working; see also Mesfioui et al. [15]. In the following theorem, we introduce new bounds on the past Rényi entropy of the coherent system’s lifetime, expressed in terms of the past Rényi entropy of the higher-order distribution ${\overline{H}}_{\alpha }\left(X_t\right)$. By incorporating these bounds into our analysis, we can achieve a more accurate and efficient characterization of complex systems, even in the face of limited information about component lifetimes.

Theorem 7.

Assume a coherent system with the past lifetime $T_t=[t-T|X_{n:n}\le t]$ consisting of n i.i.d. component lifetimes having the common cdf F with the signature $\mathit{p}=(p_1, \dots , p_n)$. Then, we have

$$\begin{array}{c}\hfill {\overline{H}}_{\alpha }\left(T_t\right)\ge (\le )\frac{\alpha }{1-\alpha }log{B}_n\left(\mathit{p}\right)+{\overline{H}}_{\alpha }\left(X_t\right),\end{array}$$

(17)

for $\alpha >1(0<\alpha <1)$ where $B_n\left(\mathit{p}\right)={\sum }_{i=1}^n{p}_i{g}_i\left(m_i\right),$ and $m_i=\frac{n-i}{n-1}.$

Proof. 

The beta distribution with parameters $n-i+1$ and i is a well-known distribution, where its mode, denoted by $m_i$, can be conveniently expressed as $m_i=\frac{n-i}{n-1}$. This result allows us to obtain the following expression:

$$g_V\left(v\right)\le \sum _{i=1}^n{p}_i{g}_i\left(m_i\right)=B_n\left(\mathit{p}\right),0<v<1.$$

(18)

Thus, for $\alpha >1(0<\alpha <1),$ we have

$$\begin{array}{ccc}\hfill {\overline{H}}_{\alpha }\left(T\right)& =& \frac{1}{1-\alpha }log{\int }_0^1{g}_V^{\alpha }\left(v\right){\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}dv\hfill \\ & & \ge (\le )\frac{1}{1-\alpha }log{\int }_0^1{\left(B_n\left(\mathit{p}\right)\right)}^{\alpha }{\left(f_t\left(F_t^{-1}\left(u\right)\right)\right)}^{\alpha -1}dv\hfill \\ & =& \frac{\alpha }{1-\alpha }log{B}_n\left(\mathit{p}\right)+{\overline{H}}_{\alpha }\left(X_t\right).\hfill \end{array}$$

The last equality is obtained from (4), from which the desired result follows. □

The lower and upper bounds shown in Equation (17) are a valuable tool for analyzing systems with a large number of components or complex configurations. However, in situations where these bounds are not applicable, we can resort to the Rényi information measure and mathematical concepts to derive a more general lower bound. This approach leverages the power of the Rényi information measure and mathematical ideas to provide new insights into the behavior of complex systems, which will be presented in the next theorem.

Theorem 8.

In the setting of Theorem 7,

$${\overline{H}}_{\alpha }\left(T_t\right)\ge {\overline{H}}_{\alpha }^L\left(T_t\right),$$

(19)

where ${\overline{H}}_{\alpha }^L\left(T_t\right)=\frac{1}{1-\alpha }log\left({\sum }_{i=1}^n{p}_i{\int }_0^t{f}_{T_t^i}^{\alpha }\left(x\right)dx\right)$ for all $\alpha >0.$

Proof. 

The Jensen’s inequality for the function $x^{\alpha }$ (it is concave (convex) for $0<\alpha <1 (\alpha >1)$) yields

$${\left(\sum _{i=1}^n{p}_i{f}_{T_t^i}\left(x\right)\right)}^{\alpha }\ge (\le )\sum _{i=1}^n{p}_i{f}_{T_t^i}^{\alpha }\left(x\right),x>0,$$

and hence we obtain

$$\left({\int }_0^t{f}_{T_t}^{\alpha }\left(x\right)dx\right)\ge (\le )\left(\sum _{i=1}^n{p}_i{\int }_0^t{f}_{T_t^i}^{\alpha }\left(x\right)dx\right).$$

(20)

The above inequality is obtained by the linearity property of integration. Since $1-\alpha >0 (1-\alpha <0)$, by multiplying both sides (20) in $1/(1-\alpha )$, we obtain the desired result. □

It is noteworthy that the equality condition in (19) holds true for i-out-of-n systems, where the failure probability $p_j$ is zero for $j\ne i$, and one for $j=i$. In this case, the conditional entropy of the system ${\overline{H}}_{\alpha }\left(T_t\right)$ is equal to the conditional entropy of the ith component ${\overline{H}}_{\alpha }\left(T_t^i\right)$. When the lower bounds for $0<\alpha <1$ in both parts of Theorems 7 and 8 can be computed, one may use the maximum of the two lower bounds.

Example 3.

Let $T_t=[t-T|X_{3:3}\le t]$ represent the past lifetime of a coherent system with the signature $\mathit{p}=(\frac{1}{3},\frac{2}{3},0)$ consisting of $n=3$ i.i.d. component lifetimes according to the standard exponential distribution, with cdf $F\left(t\right)=1-e^{-t},t>0.$ It is easily seen that

$${\overline{H}}_{\alpha }\left(X_t\right)=\frac{1}{1-\alpha }\left(log\frac{(1-e^{-\alpha t})}{{(1-e^{-t})}^{\alpha }}-log\alpha \right),t>0.$$

Moreover, we can obtain $B_3\left(\mathit{p}\right)=2.$ Thus, by Theorem 7, the Rényi entropy of $T_t$ is bounded for $\alpha >1(0<\alpha <1)$ as follows:

$${\overline{H}}_{\alpha }\left(T_t\right)\ge (\le )\frac{1}{1-\alpha }\left(log\frac{2^{\alpha }}{\alpha }+log\frac{(1-e^{-\alpha t})}{{(1-e^{-t})}^{\alpha }}\right),t>0.$$

(21)

It is easily seen that

$$f_t\left(F_t^{-1}\left(u\right)\right)=\frac{1-u(1-e^{-t})}{1-e^{-t}},t>0,$$

for all $0<u<1.$ So, the lower bound given in (19) can be obtained as follows:

$${\overline{H}}_{\alpha }\left(T_t\right)\ge \frac{1}{1-\alpha }log\left(\sum _{i=1}^n{p}_i{\int }_0^1{g}_i^{\alpha }\left(u\right){(1-u(1-e^{-t}))}^{\alpha -1}du\right)-log(1-e^{-t}),t>0,$$

(22)

for all $\alpha >0.$ Figure 3 depicts the time evolution of the Rényi entropy ${\overline{H}}_{\alpha }\left(T_t\right)$ for the standard exponential distribution. The solid line represents the exact value of ${\overline{H}}_{\alpha }\left(T_t\right)$, while the dashed and dotted lines correspond to the bounds derived from Equations (21) and (22), respectively. The figure provides a clear visualization of the behavior of the past Rényi entropy over time and highlights the remarkable agreement between the exact value and the bounds. Notably, for $\alpha >1$, the lower bound from (22) (dotted line) surpasses the lower bound from (21).

5. Concluding Remarks

In recent years, the assessment of predictability has become very important when considering the lifetimes of engineering systems. Quantification of uncertainty is a crucial criterion for measuring the degree of predictability in such systems. The Rényi entropy has proven to be an attractive measure for quantifying the uncertainty associated with the lifetimes of systems. In this work, we have presented an expression for the Rényi entropy of the lifetime of a system, under the condition that all system components have failed at time t. This situation may arise in practice because the time at which we normally observe a system and detect the failure of a system is quite late, so all components of the coherent system have also failed at that time. Moreover, we investigate the various properties of this proposed measure, including the determination of boundaries and partial orders between the random time points that have elapsed since the failure of two coherent systems, based on their Rényi entropy uncertainties using the concept of the system signature. Our approach provides an effective method for assessing the predictability of system lifetimes and is useful for engineering applications. We demonstrate the effectiveness of our proposed measure using several application examples. It is worth noting that the results of this paper can be used to study the predictability of engineering systems and its relevance to current research. The results presented provide compelling evidence for the value of Rényi entropy in engineering reliability analysis and highlight its potential for future research in this area.