A Family of 1D Chaotic Maps without Equilibria
Abstract
1. Introduction
2. Preliminaries
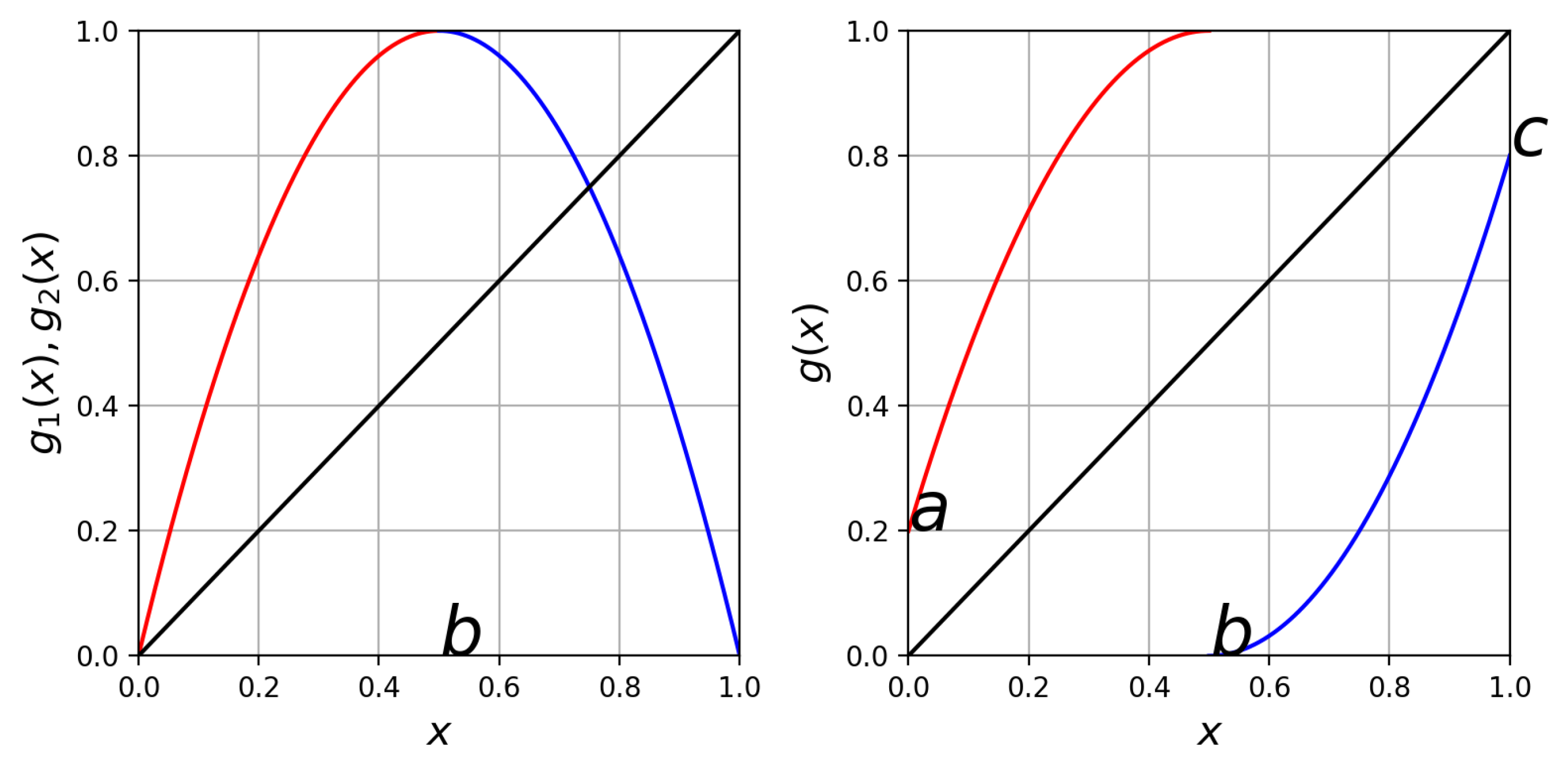
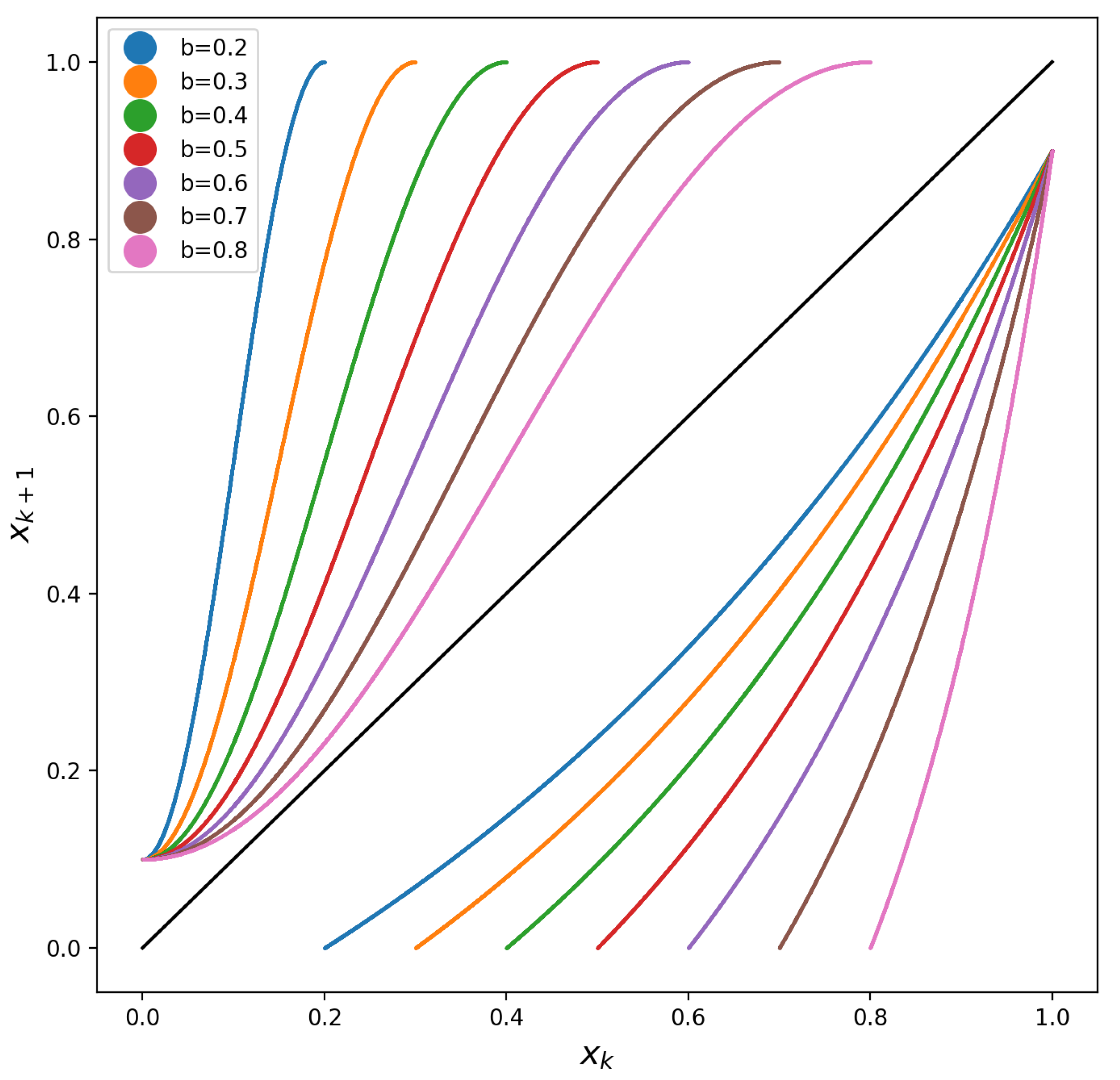
3. The Proposed Family of Maps
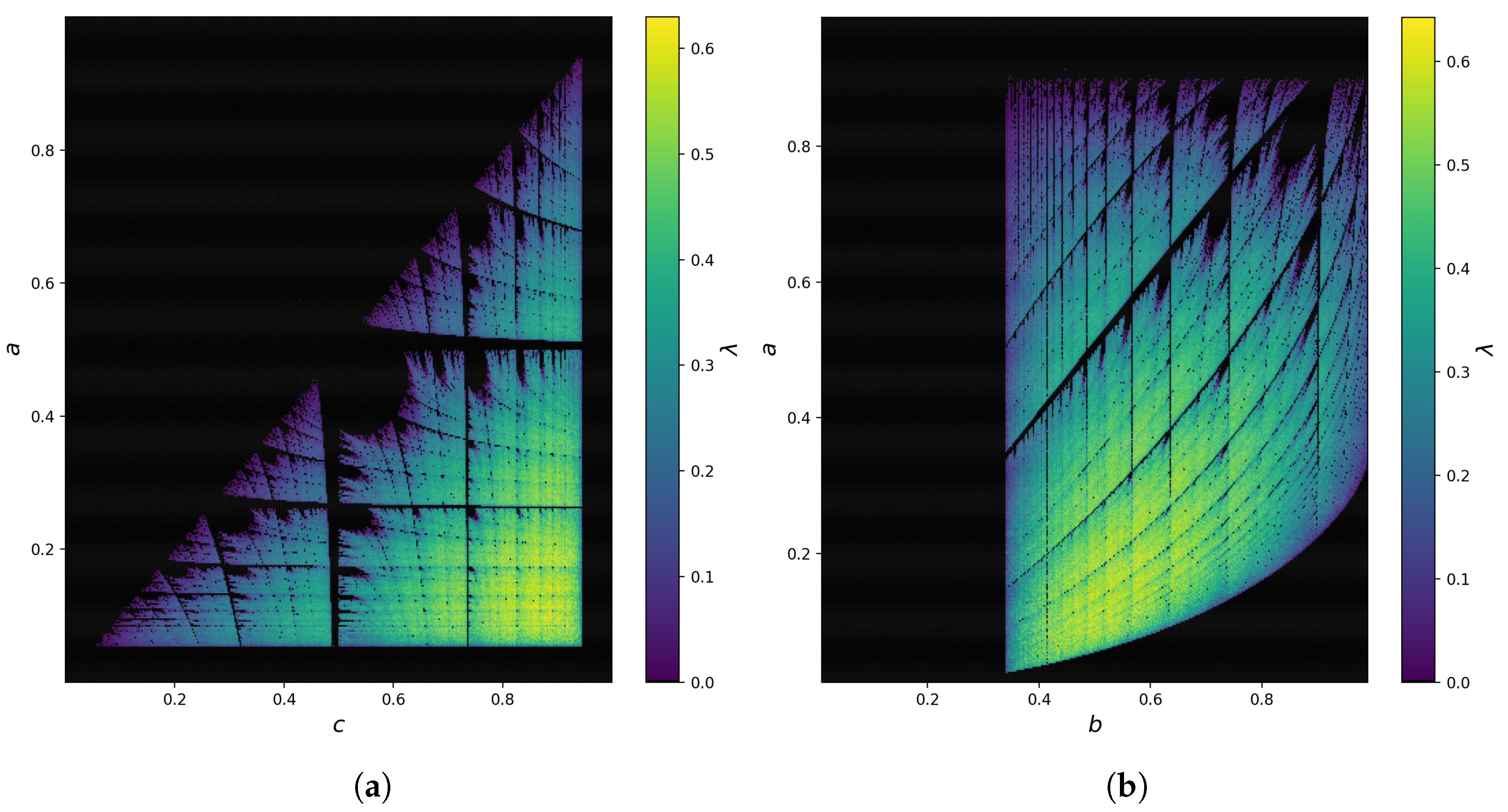
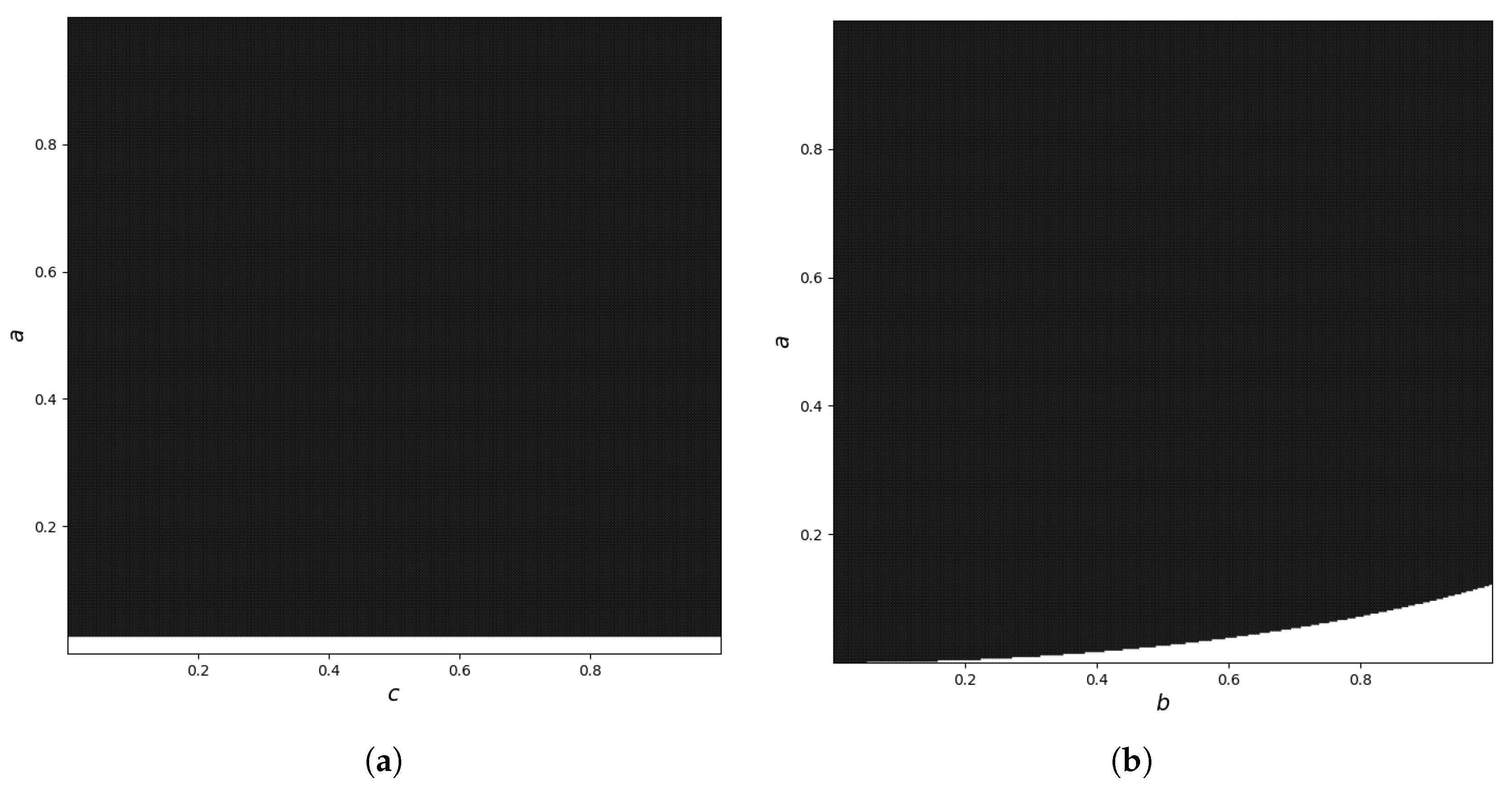
4. Chaotic Map Examples
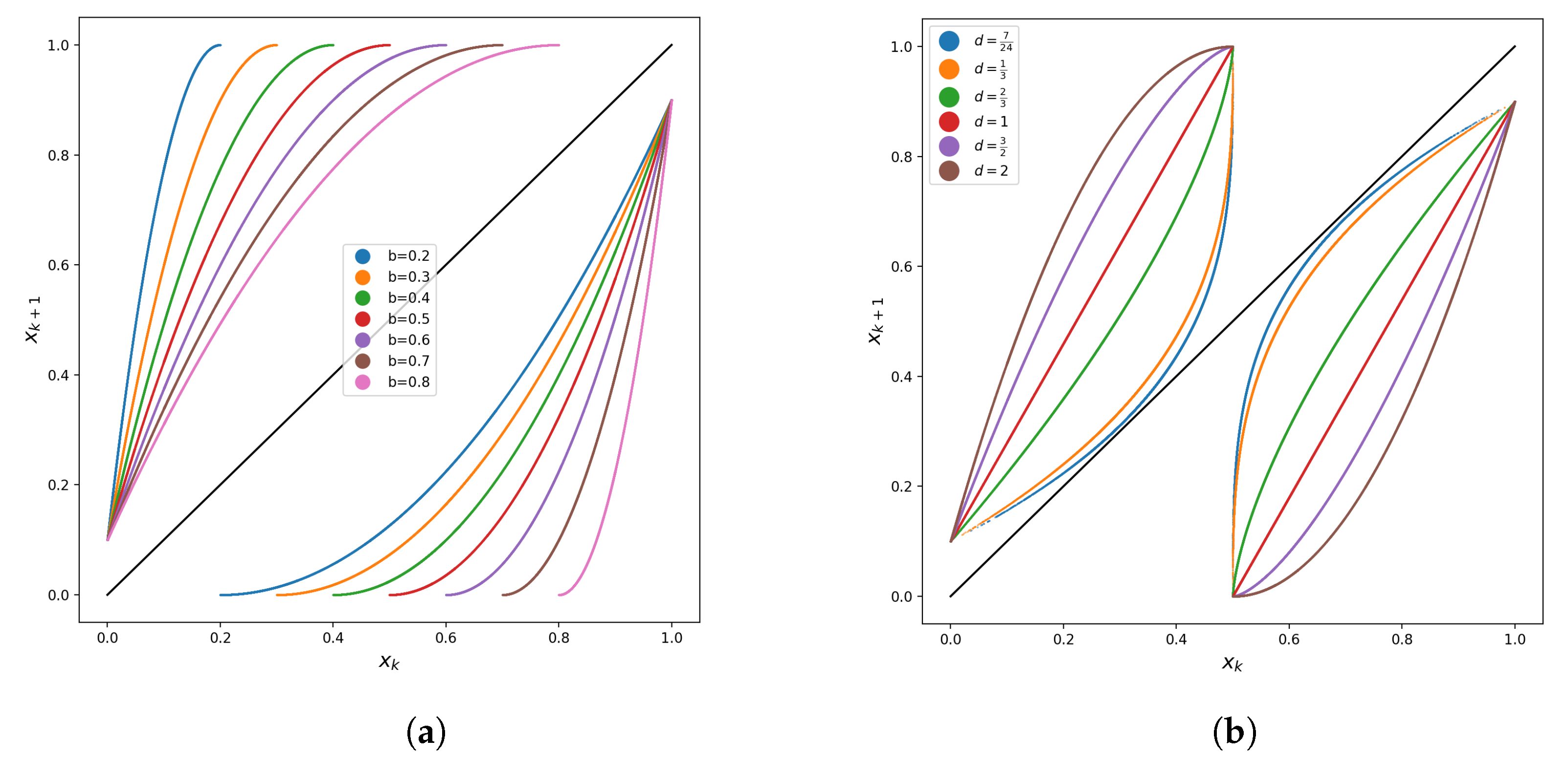
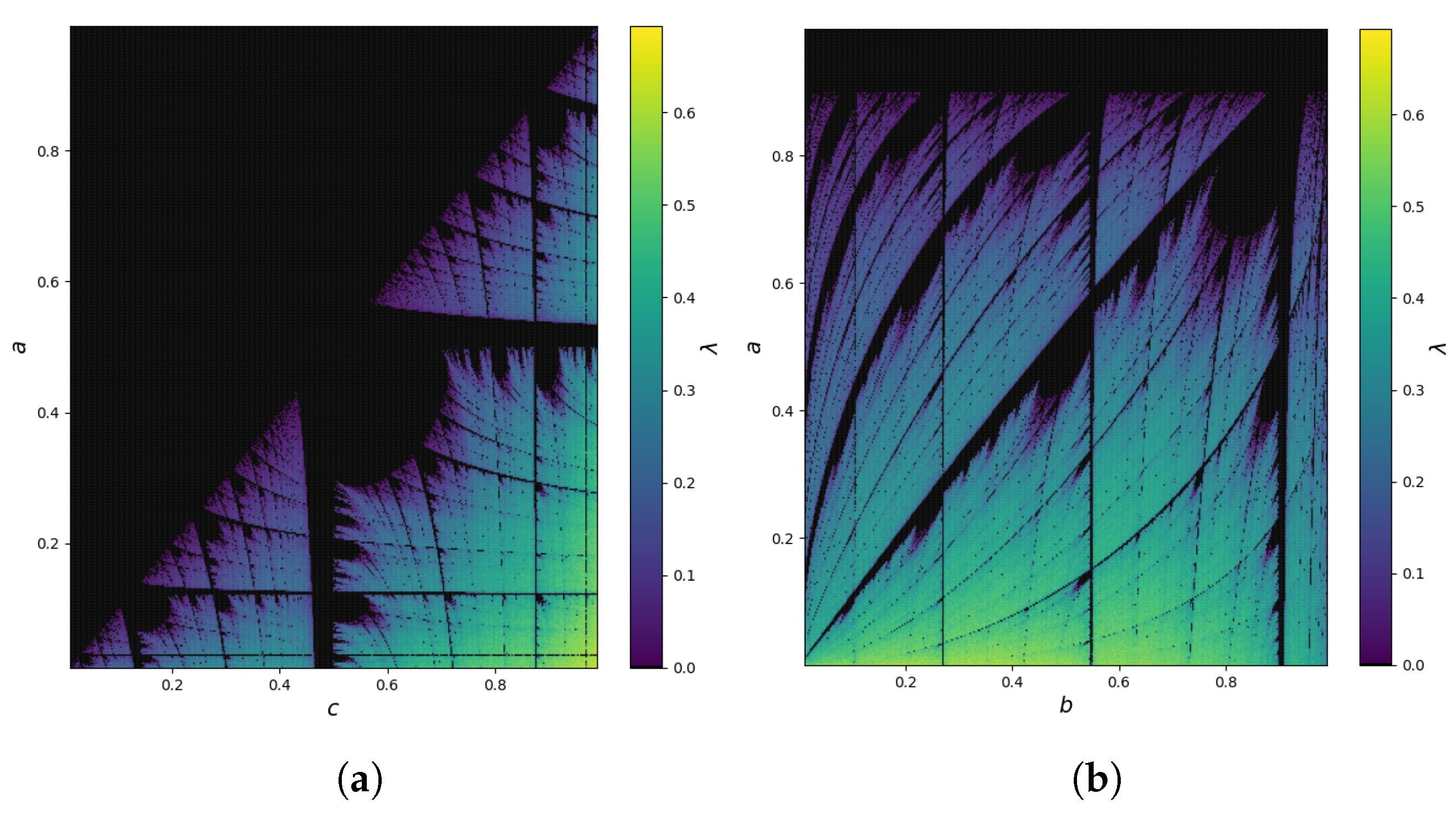
4.1. Example 1—Polynomial Piecewise Map
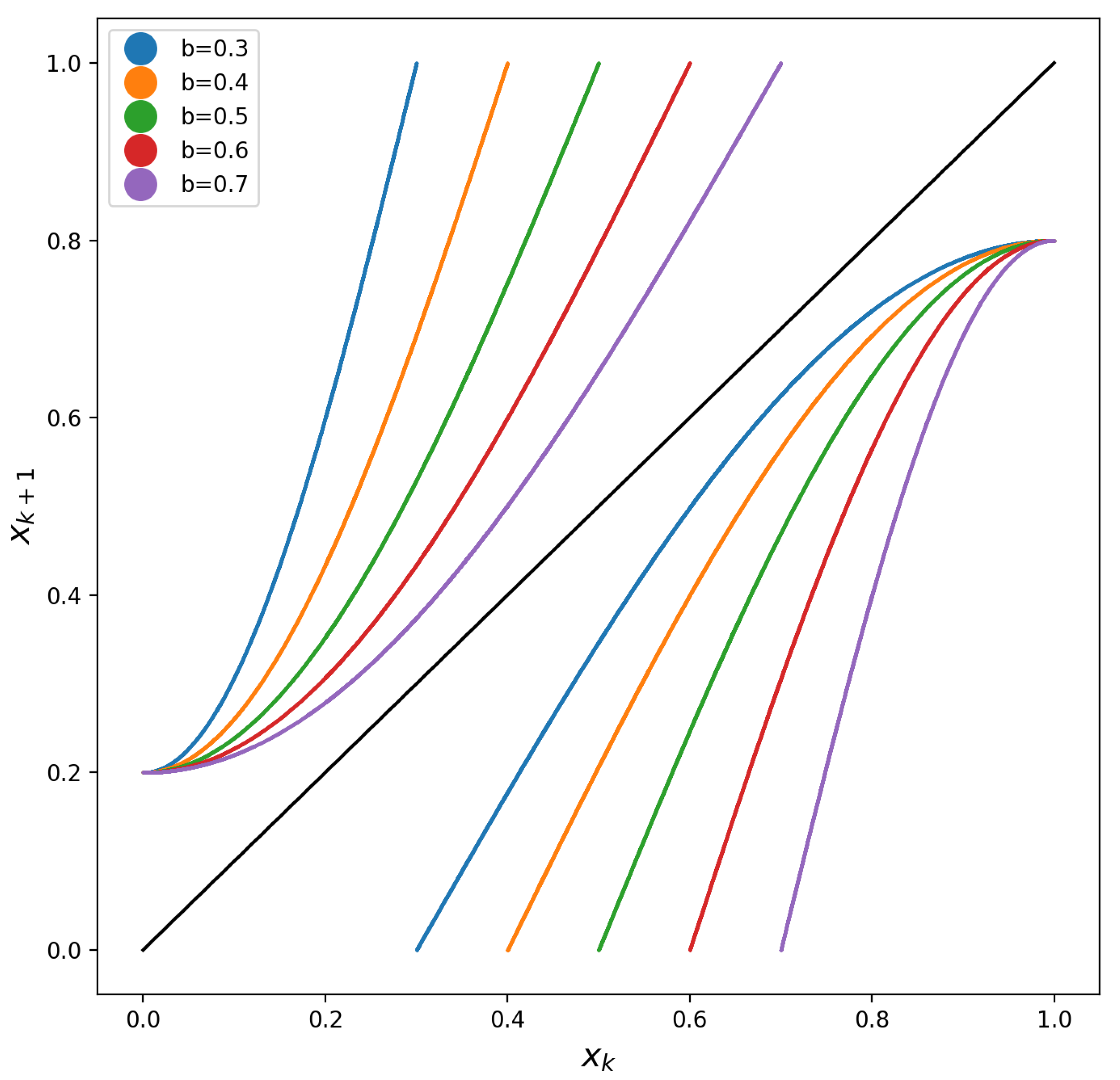
4.2. Example 2—Cosine Piecewise Map
4.3. Example 3—Sine-Exponential Piecewise Map
5. Applications of the Proposed Mappings
A Proposed PseudoRandom Bit Generator
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Oestreicher, C. A history of chaos theory. Dialogues Clin. Neurosci. 2007, 9, 279–289. [Google Scholar] [CrossRef] [PubMed]
- Grassi, G. Chaos in the real world: Recent applications to communications, computing, distributed sensing, robotic motion, bio-impedance modelling and encryption systems. Symmetry 2021, 13, 2151. [Google Scholar] [CrossRef]
- Akmeşe, Ö.F. Bibliometric Analysis of Publications on Chaos Theory and Applications during 1987–2021. Chaos Theory Appl. 2022, 4, 169–178. [Google Scholar] [CrossRef]
- Baptista, M.S. Chaos for communication. Nonlinear Dyn. 2021, 105, 1821–1841. [Google Scholar] [CrossRef]
- Teh, J.S.; Alawida, M.; Sii, Y.C. Implementation and practical problems of chaos-based cryptography revisited. J. Inf. Secur. Appl. 2020, 50, 102421. [Google Scholar] [CrossRef]
- Lawnik, M.; Moysis, L.; Volos, C. Chaos-Based Cryptography: Text Encryption Using Image Algorithms. Electronics 2022, 11, 3156. [Google Scholar] [CrossRef]
- Kumar, M.; Saxena, A.; Vuppala, S.S. A survey on chaos based image encryption techniques. In Multimedia Security Using Chaotic Maps: Principles and Methodologies; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–26. [Google Scholar]
- Tutueva, A.V.; Nepomuceno, E.G.; Karimov, A.I.; Andreev, V.S.; Butusov, D.N. Adaptive chaotic maps and their application to pseudo-random numbers generation. Chaos Solitons Fractals 2020, 133, 109615. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.; Cruz-Hernández, C.; Cardoza-Avendaño, L.; Méndez-Ramírez, R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. 2017, 87, 407–425. [Google Scholar] [CrossRef]
- Bin Faheem, Z.; Ali, A.; Khan, M.A.; Ul-Haq, M.E.; Ahmad, W. Highly dispersive substitution box (S-box) design using chaos. ETRI J. 2020, 42, 619–632. [Google Scholar] [CrossRef]
- Shakiba, A. A randomized CPA-secure asymmetric-key chaotic color image encryption scheme based on the Chebyshev mappings and one-time pad. J. King Saud Univ. Comput. Inf. Sci. 2021, 33, 562–571. [Google Scholar] [CrossRef]
- Rybin, V.; Karimov, T.; Bayazitov, O.; Kvitko, D.; Babkin, I.; Shirnin, K.; Kolev, G.; Butusov, D. Prototyping the Symmetry-Based Chaotic Communication System Using Microcontroller Unit. Appl. Sci. 2023, 13, 936. [Google Scholar] [CrossRef]
- Artemiou, P.; Moysis, L.; Kafetzis, I.; Bardis, N.G.; Lawnik, M.; Volos, C. Chaotic Agent Navigation: Achieving Uniform Exploration Through Area Segmentation. In Proceedings of the 2022 12th International Conference on Dependable Systems, Services and Technologies (DESSERT), Athens, Greece, 9–11 December 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Biogeography-based optimisation with chaos. Neural Comput. Appl. 2014, 25, 1077–1097. [Google Scholar] [CrossRef]
- Moysis, L.; Lawnik, M.; Antoniades, I.P.; Kafetzis, I.; Baptista, M.S.; Volos, C. Chaotification of 1D Maps by Multiple Remainder Operator Additions—Application to B-Spline Curve Encryption. Symmetry 2023, 15, 726. [Google Scholar] [CrossRef]
- Natiq, H.; Banerjee, S.; Said, M. Cosine chaotification technique to enhance chaos and complexity of discrete systems. Eur. Phys. J. Spec. Top. 2019, 228, 185–194. [Google Scholar] [CrossRef]
- Ablay, G. Lyapunov exponent enhancement in chaotic maps with uniform distribution modulo one transformation. Chaos Theory Appl. 2022, 4, 45–58. [Google Scholar] [CrossRef]
- Wang, Z.; Akgul, A.; Pham, V.T.; Jafari, S. Chaos-based application of a novel no-equilibrium chaotic system with coexisting attractors. Nonlinear Dyn. 2017, 89, 1877–1887. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X.; Zeng, Z. A simple no-equilibrium chaotic system with only one signum function for generating multidirectional variable hidden attractors and its hardware implementation. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 053129. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Chaos in a new fractional-order system without equilibrium points. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2919–2927. [Google Scholar] [CrossRef]
- Rahman, Z.A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A New No Equilibrium Fractional Order Chaotic System, Dynamical Investigation, Synchronization, and Its Digital Implementation. Inventions 2021, 6, 49. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Grassi, G.; Pham, V.T. Chaos and control of a three-dimensional fractional order discrete-time system with no equilibrium and its synchronization. AIP Adv. 2020, 10, 045310. [Google Scholar] [CrossRef]
- Tamba, V.K.; Pham, V.T.; Hoang, D.V.; Jafari, S.; Alsaadi, F.E.; Alsaadi, F.E. Dynamic system with no equilibrium and its chaos anti-synchronization. Automatika 2018, 59, 35–42. [Google Scholar] [CrossRef]
- Azar, A.T.; Volos, C.; Gerodimos, N.A.; Tombras, G.S.; Pham, V.T.; Radwan, A.G.; Vaidyanathan, S.; Ouannas, A.; Munoz-Pacheco, J.M. A Novel Chaotic System without Equilibrium: Dynamics, Synchronization, and Circuit Realization. Complexity 2017, 2017, 7871467. [Google Scholar] [CrossRef]
- García-Grimaldo, C.; Campos, E. Chaotic Features of a Class of Discrete Maps without Fixed Points. Int. J. Bifurc. Chaos 2021, 31, 2150200. [Google Scholar] [CrossRef]
- García-Grimaldo, C.; Campos-Cantón, E. Comparative Analysis of Chaotic Features of Maps Without Fixed Points. In Complex Systems and Their Applications; Huerta Cuéllar, G., Campos Cantón, E., Tlelo-Cuautle, E., Eds.; Springer: Cham, Switzerland, 2022; pp. 151–176. [Google Scholar]
- García-Grimaldo, C.; Bermudez-Marquez, C.F.; Tlelo-Cuautle, E.; Campos-Cantón, E. FPGA Implementation of a Chaotic Map with No Fixed Point. Electronics 2023, 12, 444. [Google Scholar] [CrossRef]
- Jafari, S.; Pham, V.T.; Golpayegani, S.M.R.H.; Moghtadaei, M.; Kingni, S.T. The relationship between chaotic maps and some chaotic systems with hidden attractors. Int. J. Bifurc. Chaos 2016, 26, 1650211. [Google Scholar] [CrossRef]
- Panahi, S.; Sprott, J.C.; Jafari, S. Two simplest quadratic chaotic maps without equilibrium. Int. J. Bifurc. Chaos 2018, 28, 1850144. [Google Scholar] [CrossRef]
- Wang, C.; Ding, Q. A New Two-Dimensional Map with Hidden Attractors. Entropy 2018, 20, 322. [Google Scholar] [CrossRef]
- Almatroud, O.A.; Pham, V.T. Building Fixed Point-Free Maps with Memristor. Mathematics 2023, 11, 1319. [Google Scholar] [CrossRef]
- Nestor, T.; De Dieu, N.J.; Jacques, K.; Yves, E.J.; Iliyasu, A.M.; Abd El-Latif, A.A. A multidimensional hyperjerk oscillator: Dynamics analysis, analogue and embedded systems implementation, and its application as a cryptosystem. Sensors 2019, 20, 83. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, Q.; Wei, X.; Liu, C. Image encryption based on improved Lorenz system. IEEE Access 2020, 8, 75728–75740. [Google Scholar] [CrossRef]
- Bassham, L.E.; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Sp 800-22 Rev. 1a; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Rand, D.; Ostlund, S.; Sethna, J.; Siggia, E.D. Universal transition from quasiperiodicity to chaos in dissipative systems. Phys. Rev. Lett. 1982, 49, 132. [Google Scholar] [CrossRef]




| Map Equation (15) | Map Equation (20) | Map Equation (21) | |||||
|---|---|---|---|---|---|---|---|
| No. | Test | Ratio | Result | Ratio | Result | Ratio | Result |
| 1 | Frequency | 990/1000 | Pass | 990/1000 | Pass | 987/1000 | Pass |
| 2 | BlockFrequency | 988/1000 | Pass | 993/1000 | Pass | 992/1000 | Pass |
| 3 | CumulativeSums | 990/1000 | Pass | 991/1000 | Pass | 984/1000 | Pass |
| 4 | Runs | 989/1000 | Pass | 992/1000 | Pass | 989/1000 | Pass |
| 5 | LongestRun | 991/1000 | Pass | 989/1000 | Pass | 993/1000 | Pass |
| 6 | Rank | 992/1000 | Pass | 991/1000 | Pass | 992/1000 | Pass |
| 7 | FFT | 995/1000 | Pass | 990/1000 | Pass | 986/1000 | Pass |
| 8 | NonOverlappingTemplate | 990/1000 | Pass | 988/1000 | Pass | 990/1000 | Pass |
| 9 | OverlappingTemplate | 990/1000 | Pass | 994/1000 | Pass | 990/1000 | Pass |
| 10 | Universal | 987/1000 | Pass | 986/1000 | Pass | 987/1000 | Pass |
| 11 | ApproximateEntropy | 985/1000 | Pass | 983/1000 | Pass | 995/1000 | Pass |
| 12 | RandomExcursions | 628/634 | Pass | 626/636 | Pass | 616/623 | Pass |
| 13 | RandomExcursionsVariant | 626/634 | Pass | 632/636 | Pass | 615/623 | Pass |
| 14 | Serial | 987/1000 | Pass | 988/1000 | Pass | 989/1000 | Pass |
| 15 | LinearComplexity | 993/1000 | Pass | 987/1000 | Pass | 987/1000 | Pass |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawnik, M.; Moysis, L.; Volos, C. A Family of 1D Chaotic Maps without Equilibria. Symmetry 2023, 15, 1311. https://doi.org/10.3390/sym15071311
Lawnik M, Moysis L, Volos C. A Family of 1D Chaotic Maps without Equilibria. Symmetry. 2023; 15(7):1311. https://doi.org/10.3390/sym15071311
Chicago/Turabian StyleLawnik, Marcin, Lazaros Moysis, and Christos Volos. 2023. "A Family of 1D Chaotic Maps without Equilibria" Symmetry 15, no. 7: 1311. https://doi.org/10.3390/sym15071311
APA StyleLawnik, M., Moysis, L., & Volos, C. (2023). A Family of 1D Chaotic Maps without Equilibria. Symmetry, 15(7), 1311. https://doi.org/10.3390/sym15071311








