Abstract
Legendre coefficients of an integrable function are proved to coincide with the Fourier coefficients with a nonnegative index of a suitable Abel-type transform of the function itself. The numerical computation of N Legendre coefficients can thus be carried out efficiently in operations by means of a single fast Fourier transform of the Abel-type transform of . Symmetries associated with the Abel-type transform are exploited to further reduce the computational complexity. The dual problem of calculating the sum of Legendre expansions at a prescribed set of points is also considered. We prove that a Legendre series can be written as the Abel transform of a suitable Fourier series. This fact allows us to state an efficient algorithm for the evaluation of Legendre expansions. Finally, some numerical tests are illustrated to exemplify and confirm the theoretical results.
MSC:
42C10; 44A05; 65R10; 65T50
1. Introduction
The computation of the coefficients of Legendre expansions is a very important problem in applied mathematics and numerical analysis, with a wide range of applications including, just to name a few, approximation theory [1], special function theory [2], spectral methods for differential equations [3], and the construction of quadrature formulae [3,4]. Its importance has also emerged in connection with the computation of spectra of highly oscillatory Fredholm integral operators, which play an important role in laser engineering [5]. Due to its relevance, this problem has attracted a significant amount of research attention since the 1970s [6,7].
The essential difficulty of the problem is that these coefficients are represented by integrals whose integrands oscillate rapidly for large values of the index of the polynomial. Standard quadrature procedures for the calculation of N Legendre coefficients lead only to slow algorithms (see [6,8]). The first contribution toward a more efficient computation of Legendre coefficients traces back to the work of Orszag [9], where the algorithm used a slowly converging first-order WKB expansion of the Legendre polynomials.
More efficiently, in [10], the Legendre coefficients are obtained by transforming the corresponding Chebyshev coefficients through a multipole-like expansion, which yields a fast algorithm, despite requiring a considerable and rather expensive initialization phase. In this context, various improvements have been proposed, e.g., in [11,12]. Remaining within this kind of approach, Hale and Townsend [13] described an Chebyshev–Legendre transform, which is based on Stieltjes’ asymptotic formula for Legendre polynomials of large degree. Mori et al. [14] employed the same asymptotic formula to produce a fast algorithm, but this algorithm was affected by the problem of numerical instability for large values of N. The connection between Legendre and Chebyshev coefficients is also analyzed in [15] in the case of piecewise smooth functions. In Ref. [16] (see also [17]), an algorithm is given for a value of N equal to a power of two, which requires a suitably preprocessed data structure.
Another way to tackle this problem was described by Iserles in [18], where an algorithm for the rapid computation of the Legendre coefficients is presented when the analytic expression of the input function is known on a Bernstein ellipse in the complex plane. The complexity of the algorithm is but requires knowledge of the region of analyticity of the function in .
In this paper, an alternative procedure is presented. The basic idea of our method consists of exploiting the Dirichlet–Murphy integral representation of the Legendre polynomials. We prove that the coefficients of the Legendre expansion of a function are connected with a subset of the Fourier coefficients (the ones with a nonnegative index) of an Abel-type transform of [19,20,21].
The numerical implementation of the algorithm follows straightforwardly and is very efficient. The aforementioned Fourier coefficients (which represent the sought-for Legendre coefficients) can be computed in operations by a single fast Fourier transform (FFT) after the evaluation of the Abel-type integral by means of standard quadrature techniques.
The dual problem of calculating the values of (finite) Legendre expansions at a set of prescribed points is analyzed in Section 3. In Section 3.1, we prove that the Legendre expansions can be computed by an (inverse) cosine transform of a sequence of coefficients, which is obtained by a suitable linear transformation of the given set of N Legendre coefficients. Further, a novel algorithm is presented in Section 3.2, where the Legendre expansions are proved to be the Abel-type transform of a Fourier series, whose coefficients coincide with the Legendre coefficients of the function . This leads to an efficient algorithm that requires the calculation of one FFT and one Abel-type integral.
2. Connection between Legendre Expansions and Fourier Series
The standard form of the Legendre expansion reads
where are the Legendre polynomials, which can be defined by the generating function [22]
and the coefficients are given by
The conditions to be satisfied by to guarantee the uniform convergence of the series in (1) will be discussed in the next section. However, for our current purpose of computing the Legendre coefficients , it is sufficient to assume that must be absolutely integrable on the interval . For later convenience, we define the normalized Legendre coefficients as
We can now state the following theorem.
Theorem 1.
The normalized Legendre coefficients coincide with the Fourier coefficients (with ) of an Abel-type transform of ; that is:
where the -periodic function is defined by
with being the sign function.
Proof.
We consider the Dirichlet–Murphy integral representation of the Legendre polynomials [23] (Ch. III, §5.4):
Interchanging the order of integration in (8), we obtain
Next, changing the variables and , the second integral on the right-hand side of (9) reads
It is immediate to see from (6) that satisfies the symmetry relation,
which, by (5), induces the following symmetry on :
Numerical Issues
Let us now consider the actual problem of computing the first N Legendre coefficients (or, equivalently, Nnormalized coefficients ) associated with the function (see (1) and (3)).
The numerical implementation of the algorithm suggested by Theorem 1 requires the computation of the Fourier coefficients (5) of the Abel-type integral function defined in (6). For what concerns the computation of , the integrand has a weak algebraic singularity at the lower boundary of the integration domain, which can be effectively treated by means of a proper nonlinear change of variable. This technique, along with the use of a standard quadrature formula (e.g., the Gauss–Legendre one), produces high accuracy with a small number of nodes [24]. Quadrature formulae suited to end-point singular integrands can also be used [25,26].
It is important to stress that the function does not depend on the order n of the Legendre polynomial. Therefore, the computational cost for evaluating is independent of the number N of Legendre coefficients to be computed. This means that the number of knots that are necessary to compute the integral in (with a prescribed fixed accuracy ) does not depend on N but depends only upon the oscillatory characteristics of the function (i.e., the number of samples needed to determine uniquely) and on the accuracy [27]. The oscillatory contributions due to the Legendre polynomials or, in other words, the dependence on the order n of the Legendre polynomial, are accounted for only in the Fourier formula (5) and are neatly separated from the oscillatory contributions ascribable to the input function . The consequence of this decoupling is the low computational complexity of the whole algorithm. In fact, Formula (5) makes it possible to take full benefit of the computational efficiency of the fast Fourier transform either in terms of speed of computation and accuracy [28,29,30]. The first N Fourier coefficients of (which coincide with the normalized Legendre coefficients of ) can thus be computed by a single FFT from the values (samples) of at N distinct points in time. As we have seen above, the number of operations for the calculation of each sample of is independent of N and, consequently, the (asymptotic) computational complexity of the entire algorithm for the computation of the Legendre coefficients coincides with that of the FFT, i.e., . Moreover, in view of the symmetry Relation (10), the number of calls to the procedure for the computation of the Abel integral is halved. Of course, if samples are needed to uniquely determine the function and we want the error to be as small as possible, then all the samples of must be used for the numerical computation of the Abel integral and, consequently, the total number of operations in the algorithm will be . Therefore, following logical lines similar to those adopted by Alpert and Rokhlin in [1] (and, more generally, in methods such as, e.g., the fast multipole methods [31]), the reduction of complexity from to is obtained by accepting a lower precision in the computation (in our case, a lower precision in the computation of the Abel integral).
We want to remark on two additional features of the algorithm just presented. First, the algorithm does not require the knowledge of the input function at a specific and prescribed set of knots (see, for instance, [10] where the input function is supposed to be known at Chebyshev knots). The function enters the algorithm only through its Abel-type integral. This gives a significant amount of flexibility in choosing the quadrature scheme, which is more suitable for the distribution of knots at which the input function is known (e.g., a uniform grid, Chebyshev grid, or a set of measurements of that are non-uniformly distributed).
The final remark concerns the robustness of the algorithm against the noise. In the case for which the values of are only approximately known, e.g., when the input samples of represent measurements affected by error, the effects of the noise in the calculation of the coefficients are damped by the algorithm. In fact, the noisy input samples of are smoothed by the Abel integral operator [32] before being analyzed (encoded as samples of ) by the oscillatory Fourier integral (5).
The procedure described above was implemented in double-precision arithmetics using the standard open source GNU Scientific Library (GSL) (all algorithms were implemented on a laptop with Intel Core i7-2630QM processor at 2.0 GHz with 8 GB RAM. The actual computation of the Abel-type integrals is based on the GSL module gsl_integration_qaws.) [33].
The feasibility and accuracy of the algorithm were verified by the direct comparison of the obtained numerical results with the true Legendre coefficients for a variety of functions. We report some of them here.
Table 1 displays the absolute error in the computation of Legendre coefficients for four functions with different degrees of regularity: the discontinuous function (with being the sign function and being a constant), whose Legendre coefficients are , for ; the function , whose Legendre coefficients are [3] (p. 78)
the function with (with a singlarity for x outside the interval ; see (2)); and the -analytic function , with ( denoting the Bessel function of the first kind and zeroth order).

Table 1.
Absolute error of the computed Legendre coefficients for four different functions with different degrees of smoothness (see text). The reference “exact” values of were computed with 30 significant figures by standard quadrature with Mathematica [34].
The first observation from Table 1 is that the accuracy depends on the degree of smoothness of the function because of the computation of the Abel transform of , which, in order to obtain a given target precision, requires more quadrature knots for low regular functions. Concerning the smooth (within the interval ) functions and , which give similar results, the accuracy increases significantly to reach values comparable with the -machine.
The algorithm sources of error are the approximation of integral (5) by the discrete Fourier transform; the approximation of the Abel transform (6) by quadratures, and, finally, the limited accuracy of the floating-point arithmetic. The error associated with the discrete Fourier transform is ruled by N. This is clearly visible from Figure 1a, where the maximum error is plotted versus N. For the -function (asterisks), we see that for low values of N the maximum error is mainly ascribable to the error due to the approximation of the Fourier integral with the DFT and to the approximation of the Abel integral: it decreases according to up to and then starts increasing according to , as in the case of smooth functions. From the comparison with the plot of the maximum error for smooth functions (triangles), we can also say that it is not necessary to use a large number of points N in the DFT unless the function itself has low regularity.
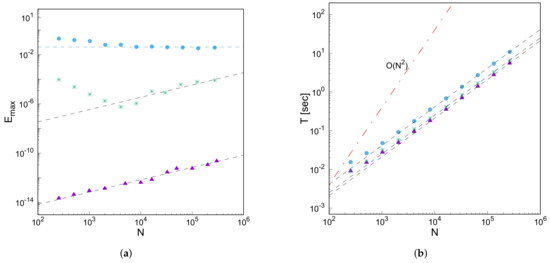
Figure 1.
(a) Maximum error versus the number N of computed Lagendre coefficients. The filled dots refer to the function , the asterisks refer to , and the filled triangles refer to (see text). (b) Execution time T versus N. The line is plotted just for reference.
The computation of N Legendre coefficients by ordinary quadrature produces a algorithm. The increment of performances of the algorithm presented here was verified by evaluating the speed of computation at (nearly) the same precision. The results of these tests are illustrated in Figure 1b, where the execution time T (in seconds) is plotted versus the number N of computed Legendre coefficients. The results show a execution time (at least in the N-interval we considered, up to ) independent of the regularity properties of the input function , confirming the expected great increase in computational speed (asymptotically, with the awaited improvement ratio being proportional to ). Such an increase in performances will become even more crucial for the efficient evaluation of multivariate Legendre transforms [5] and of spherical harmonic expansions [35], which will be the subject of a forthcoming paper.
3. Computation of Legendre Expansions
Let us now move on to consider the dual problem of computing the function from the set of N Legendre coefficients . In general, in the complex plane, the domain of convergence of the Legendre expansion (1) is the maximal ellipse with foci at within which the function f is analytic [36]. This rather restricted class of functions can be greatly enlarged when we limit ourselves to consider convergence issues on the segment . In Ref. [37], W. H. Young showed the tight connection between Legendre series and Fourier series when . In particular, he proved that in any internal closed interval of , the Legendre series (1) behaves, with respect to convergence (uniform or otherwise), divergence, and oscillation, exactly as the Fourier series of , where , assuming that the coefficients of Series (1) are such that
the latter being the natural necessary condition for the convergence of Series (1). More explicitly, E. W. Hobson [38] provided a test of convergence, stating that if the condition
is satisfied (the latter condition being equivalent to require that be integrable on ), then Series (1) is convergent for any near which f is of a bounded variation. Since the points are singular points of Legendre’s equation, the convergence at the end points of the interval requires somehow more stringent (than in the Fourier case) conditions, such as, e.g., being of bounded variation over the entire interval .
This parallelism between Legendre and Fourier expansions has already been exploited in the previous section, where we proved that the (normalized) Legendre coefficients of coincide with the Fourier coefficients of the function . In the next two subsections, we continue our analysis along this line, and present two algorithms for the computation of values of Legendre expansions.
3.1. An Algorithm for the Evaluation of Legendre Series
In the theorem that follows, we will prove that a Legendre expansion can be computed by calculating the (inverse) cosine transform of a sequence, which is obtained by a suitable linear transformation of the set of Legendre coefficients .
Theorem 2.
Proof.
Since is compactly supported on , the function () is a -periodic function of u. Hence, the latter can be represented as the Fourier series,
It is worth remarking that the linear transformation , which connects the Legendre coefficients of with the Fourier coefficients of , is independent of . Thus, it can be pre-computed with arbitrary precision and can be regarded as known. In the next proposition, some known facts on the structure of the matrix K are listed, along with the analytic expression of its entries as smooth functions of the indexes (see Ref. [10]) and an iterative procedure for computing its elements.
Proposition 1.
(i) The coefficients (defined in (13)) can be written as follows:
with denoting the Chebyshev polynomials of the first kind.
(ii) The matrix K is upper triangular, and its entries can be computed as follows:
where
with denoting the Euler gamma function.
(iii) The following recurrence relationship holds for and :
(iv) The diagonal elements can be written as follows:
(v) The elements of the first row can be written as follows:
Proof.
Formula (17) follows from Definition (13) by making the substitution into the integral and recalling the definition of the Chebyshev polynomials of the first kind: , (). Representation (ii) of the coefficients is well-known, and it is given, e.g., by Alpert and Rokhlin in [10] (Formula (20)) (where the matrix K is there named M). The recurrence relationship in Equation (19) follows from Representation (18) and from the following three-term recurrence relationships holding, respectively, for the Legendre polynomials and for Chebyshev polynomials :
and
The algorithmic prescription provided by Theorem 2 for the computation of the values of a (truncated) Legendre expansion is indeed very simple. It consists of a two-step procedure:
- From the N-vector of Legendre coefficients, compute the N-vector by , where the (known) upper triangular matrix is defined in (13) (see also Proposition 1);
- Compute the cosine transform of length N of the vector to obtain values of at N selected points of the interval .
The second step of the algorithm presents no difficulties. It is fast since it can be implemented by a single FFT of length N, which requires operations. The standard FFT procedure provides an output on a uniform grid of , so that, according to Formula (12), the final result consists of the set of function values at Chebyshev points.
The first step of the algorithm instead presents some aspects that deserve a few comments. The crux is that the matrix is dense, and the direct calculation of the matrix–vector product requires operations (precisely, multiplications). Therefore, this step can become a bottleneck for the algorithm when N becomes large. In some practical cases, the question is not critical, e.g., when the triangular structure of can be exploited on some computer architectures (e.g., vector machines or parallel GPU) to significantly decrease the complexity of the computation. Nevertheless, the reduction in the algorithmic complexity remains an issue. Approximate methods are the only tools to effectively handle the fast computation of the matrix–vector product when the matrix is not structured (e.g., when its entries depend only on parameters). The key to many of these fast methods is renouncing exactness and accepting the result of the computation within an a priori fixed level of accuracy. This enables using approximations of the kernel K which, combined with a suitable subdivision of the matrix into panels, can enormously reduce the computational cost. Among these algorithms, it is worth citing the celebrated fast multipole methods by L. Greengard and V. Rokhlin for the fast computation of N-body interactions [12,31,39], which are able to reduce the number of operations to (or even less, to , when the matrix has structure).
The specific problem we are dealing with here, that is, the fast computation of the matrix–vector product (where is given by Formula (17)) has been solved brilliantly by B. Alpert and V. Rokhlin in Ref. [10]. In that paper, the matrix is first properly divided in square submatrices, and then, the computation associated with each submatrix is performed efficiently, approximating each entry of the submatrix by its finite Chebyshev expansion. The computational cost brought by a submatrix is then reduced from order of the naive computation to , with being the fixed precision required in the Chebyshev interpolation of the submatrix entries. This basic building block can thus be assembled to construct an algorithm for the fast computation of the matrix–vector product with a order of complexity.
3.2. A Novel Algorithm
In this subsection, we present a novel algorithm for the inversion of the Legendre transform, which somewhat represents the natural dual algorithm of the one presented in Section 2 for the computation of the forward Legendre transform. In the next theorem, it will be proved that a Legendre expansion can be written as the Abel-type transform of a proper Fourier series, whose coefficients are the Legendre coefficients of (cf. Theorem 1).
Theorem 3.
Assume that the Legendre expansion in Equation (1) of converges uniformly on . Then, , where , can be represented as
with the function being given by
and where are the Legendre coefficients of (see (3)).
Proof.
The first step is to show that the Legendre polynomials can be represented by the following integral:
Theorem 3 suggests the following algorithm for the calculation of N values of a Legendre expansion.
- The N-term approximation of the function is computed by using (22) from the input N-vector of Legendre coefficients:
- The values of the N-term Legendre expansion at points ()are computed by the Abel-type integral (see (21))
The first step of the algorithm is fast. The N values of the function on a regular grid of can be computed in time with one FFT.
For what regards the second point of the algorithm, it should first be noted that the choice of the the nodes is unconstrained, and hence the approximation can be computed at any set of points using Formula (24). Concerning the computation of Integral (24), since the first step of the algorithm yields values of the integrand on a regular grid of , only quadrature formulae based on equally spaced knots can be implemented.
In general, the computation of at N points requires operations since the second step of the algorithm requires operations when all the N known values of the function are used for the computation of the integral in (24). However, it is important to note that, for this computation, it is not always necessary to implement a full N-knot quadrature procedure, particularly when N is large. Frequently, the computation with the a priori fixed precision of Integral (24) requires much less (than N) quadrature nodes, with the actual number of nodes depending either on the adopted quadrature algorithm or on the oscillatory behavior of the integrand, which, in turn, depends on the oscillatory characteristics of .
An instance of a suitable quadrature scheme is given in [25,26], where quadrature rules are proposed, which are based on modifications of the trapezoidal rule for integrands with end-point singularities of various types, including singularities of the form , . The convergence rate of these quadrature formulae is proved to be at least (that is, the approximation error is of the order of ), where denotes the order of the corrected quadrature rule [25,26]. Thus, in these cases, and for an N that is sufficiently large, the algorithm we propose for the evaluation of the Legendre expansion turns out to be particularly favourable since the number of operations in Step (2) of the algorithm is a constant that does not depend on N. Therefore, the algorithm’s complexity is ruled by the complexity of the FFT used in Step (1).
4. Conclusions
In summary, we have presented a new and rapid, i.e., , algorithm for the computation of Legendre coefficients. The algorithm is very easy to implement and computes the coefficients by employing only one FFT of the Abel-type transform of the input function. The dual problem of evaluating Legendre expansions has also been considered, and two algorithms have been described. In the first algorithm, the values of the expansion at appropriately chosen points of the interval are computed by simply performing a single (inverse) FFT of a sequence of coefficients, which are obtained by a suitable linear transformation of the given set of N Legendre coefficients. The rapid evaluation of the expansion values requires using approximate methods for the rapid calculation of the matrix–vector product. The second algorithm for the calculation of values of Legendre expansions is new and somehow inverts the logical steps of the algorithm we have proposed for the computation of the Legendre coefficients. Thus, the N-term Legendre expansion can be evaluated efficiently (for an N that is sufficiently large) at any point in the interval by computing the Abel transform of a proper Fourier series.
Future Work
The procedures described so far call for a number of natural generalizations to other orthogonal polynomial systems, such as the associated Legendre polynomials and the related spherical harmonics, with the aim of deriving an algorithm for a fast spherical harmonic transform with an analogous flavour to the present paper. Another challange is to go up the Legendre branch of the Askey scheme of hypergeometric orthogonal polynomials and generalize what was discussed in Section 2 to Jacobi polynomials in order to achieve an integral representation of the latter in terms of a composed Abel–Fourier transform.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors heartily acknowledge many illuminating discussions had with their friend and colleague, Giovanni Alberto Viano.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheney, C.W. Introduction to Approximation Theory; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Rainville, E.D. Special Functions; MacMillan: New York, NY, USA, 1960. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Davis, P.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Brunner, H.; Iserles, A.; Nørsett, S. The computation of the spectra of highly oscillatory Fredholm integral operators. J. Integral Equations Appl. 2011, 23, 467–519. [Google Scholar] [CrossRef]
- Gallagher, N.; Wise, G.; Allen, J. A novel approach for the computation of Legendre polynomial expansions. IEEE Trans. Acoustic Speech Signal Process. 1978, 26, 105–106. [Google Scholar] [CrossRef]
- Piessens, R. Algorithm 473, Computation of Legendre series coefficients. Comm. ACM 1974, 17, 25–26. [Google Scholar] [CrossRef]
- Delic, G. The Legendre series and a quadrature formula for its coefficients. J. Comp. Phys. 1974, 14, 254–268. [Google Scholar] [CrossRef]
- Orszag, S.A. Fast Eigenfunction Transforms. In Science and Computers; Academic Press: New York, NY, USA, 1986; pp. 13–30. [Google Scholar]
- Alpert, B.K.; Rokhlin, V. A fast algorithm for the evaluation of Legendre expansions. SIAM J. Sci. Stat. Comput. 1991, 12, 158–179. [Google Scholar] [CrossRef]
- O’Neil, M.; Woolfe, F.; Rokhlin, V. An algorithm for the rapid evaluation of special function transforms. Appl. Comput. Harmon. Anal. 2010, 28, 203–226. [Google Scholar] [CrossRef]
- Yarvin, N.; Rokhlin, V. An improved fast multipole method for potential fields on the line. SIAM J. Numer. Anal. 1999, 36, 629–666. [Google Scholar] [CrossRef]
- Hale, N.; Townsend, A. A fast, simple, and stable Chebyshev-Legendre transform using an asymptotic formula. SIAM J. Sci. Comput. 2014, 36, A148–A167. [Google Scholar] [CrossRef]
- Mori, A.; Suda, R.; Sugihara, M. An improvement on Orszag’s fast algorithm for Legendre polynomial transform. Trans. Info. Process. Soc. Japan 1999, 40, 3612–3615. [Google Scholar]
- Xiang, S. On fast algorithms for the evaluation of Legendre coefficients. Appl. Math. Lett. 2013, 26, 194–200. [Google Scholar] [CrossRef]
- Driscoll, J.R.; Healy, D.M., Jr. Computing Fourier transforms and convolutions on the 2-sphere. Adv. Appl. Math. 1994, 15, 202–250. [Google Scholar] [CrossRef]
- Potts, D.; Steidl, G.; Tasche, M. Fast algorithms for discrete polynomial transforms. Math. Comp. 1998, 67, 1577–1590. [Google Scholar] [CrossRef]
- Iserles, A. A fast and simple algorithm for the computation of Legendre coefficients. Numer. Math. 2011, 117, 529–553. [Google Scholar] [CrossRef]
- Gindikin, S. Abel Transform and Integral Geometry. In The Legacy of Niels Henrik Abel; Landal, O.A., Piene, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 585–596. [Google Scholar]
- Abd El-Hamid, H.A.; Rezk, H.M.; Ahmed, A.M.; AlNemer, G.; Zakarya, M.; El Saify, H.A. Dynamic inequalities in quotients with general kernels and measures. J. Funct. Spaces 2020, 2020, 5417084. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Saker, S.H.; Kenawy, M.R.; Rezk, H.M. Lower bounds on a generalization of Cesaro operator on time scales. Dyn. Contin. Discrete Impuls. Syst. A Math. Anal. 2021, 28, 345–355. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. (Eds.) Higher Transcendental Functions. In Bateman Manuscript Project; McGraw-Hill: New York, NY, USA, 1953; Volume 2. [Google Scholar]
- Vilenkin, N.I. Special Functions and the Theory of Group Representations; American Mathematical Society: Providence, RI, USA, 1968; Volume 22. [Google Scholar]
- Monegato, G.; Scuderi, L. Numerical integration of functions with boundary singularities. J. Comp. Appl. Math. 1999, 112, 201–214. [Google Scholar] [CrossRef]
- Alpert, B.K. High-order quadratures for integral operators with singular kernels. J. Comp. Appl. Math. 1995, 60, 367–378. [Google Scholar] [CrossRef]
- Rokhlin, V. End-point corrected trapezoidal quadrature rules for singular functions. Comput. Math. Appl. 1990, 20, 51–62. [Google Scholar] [CrossRef]
- Novak, E. Some Results on the Complexity of Numerical Integration. In Monte Carlo and Quasi-Monte Carlo Methods; Cools, R., Nuyens, D., Eds.; Springer: Cham, Switzerland, 2016; Volume 36. [Google Scholar]
- Calvetti, D. A stochastic roundoff error analysis for the fast Fourier transform. Math. Comp. 1991, 56, 755–774. [Google Scholar] [CrossRef]
- Kaneko, T.; Liu, B. Accumulation of round-off error in Fast Fourier Transforms. J. Assoc. Comp. Mach. 1970, 17, 637–654. [Google Scholar] [CrossRef]
- Song, J.; Mingotti, A.; Zhang, J.; Peretto, L.; Wen, H. Accurate damping factor and frequency estimation for damped real-valued sinusoidal signals. IEEE Trans. Instrum. and Meas. 2022, 71, 1–4. [Google Scholar] [CrossRef]
- Greengard, L. The Rapid Evaluation of Potential Fields in Particle Systems; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Gorenflo, R.; Vessella, S. Abel Integral Equations. In Lecture Notes in Math; Springer: Berlin/Heidelberg, Germany, 1991; Volume 1461. [Google Scholar]
- Galassi, M. GNU Scientific Library Reference Manual, 3rd ed.; Network Theory Ltd.: London, UK, 2009; ISBN 0954612078. [Google Scholar]
- Mathematica, Version 12.0; Software For Technical Computation; Wolfram Research, Inc.: Champaign, IL, USA, 2019.
- Mohlenkamp, M.J. A fast transform for spherical harmonics. J. Fourier Anal. Appl. 1999, 5, 159–184. [Google Scholar] [CrossRef]
- Hille, E. On the absolute convergence of polynomial series. Amer. Math. Monthly 1938, 45, 220–226. [Google Scholar] [CrossRef]
- Young, W.H. On the connexion between Legendre series and Fourier series. Proc. Lond. Math. Soc. 1920, 18, 141–162. [Google Scholar] [CrossRef]
- Hobson, E.W. The Theory of Spherical and Ellipsoidal Harmonics; Cambridge University Press: Cambridge, UK, 1931. [Google Scholar]
- Greengard, L.; Rokhlin, V. A fast algorithm for particle simulations. J. Comp. Phys. 1987, 73, 325–348. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).