Numerical Solution of Nonlinear Problems with Multiple Roots Using Derivative-Free Algorithms
Abstract
1. Introduction
2. Development of Method
3. Main Result
Some Special Cases
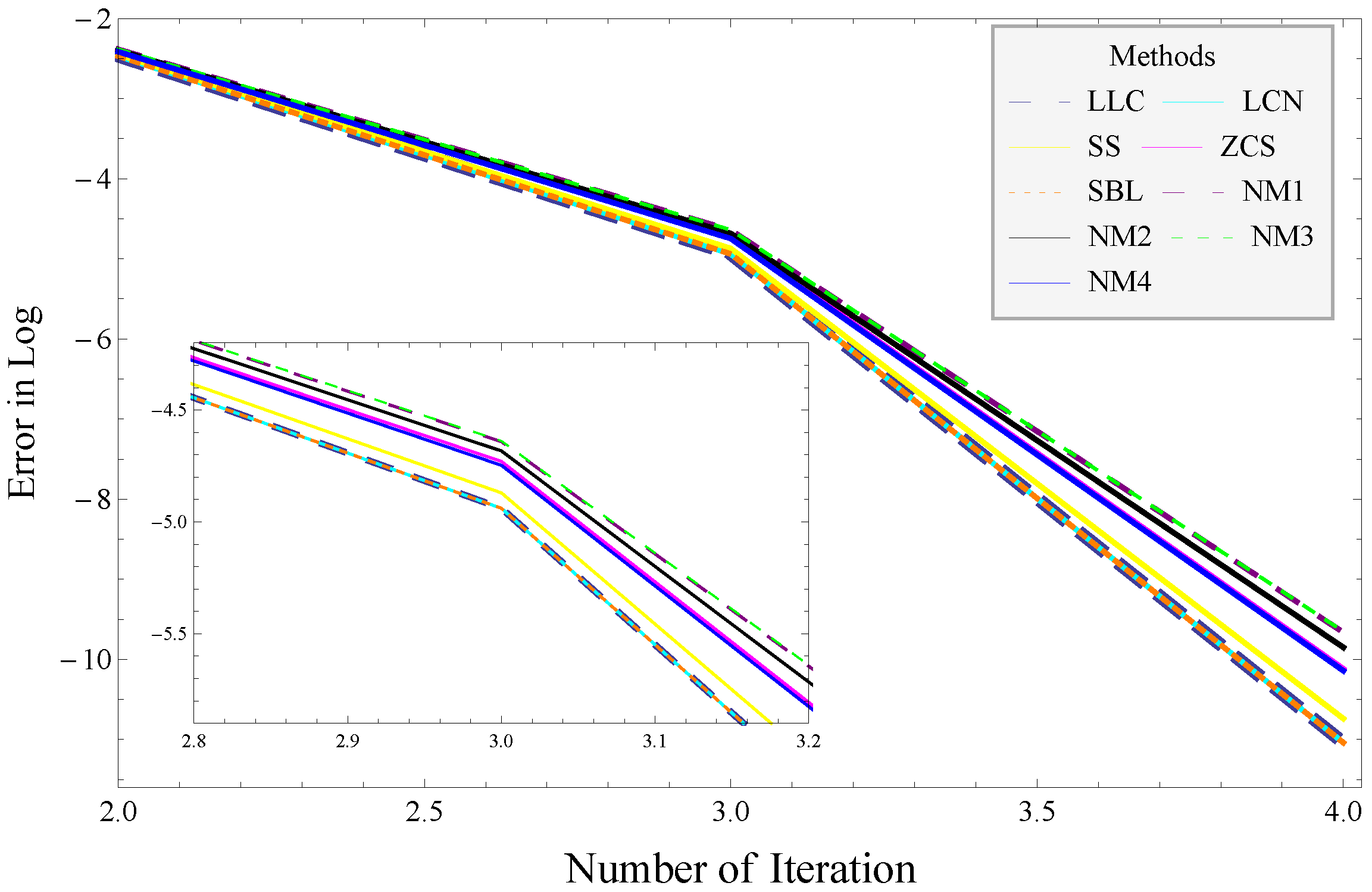
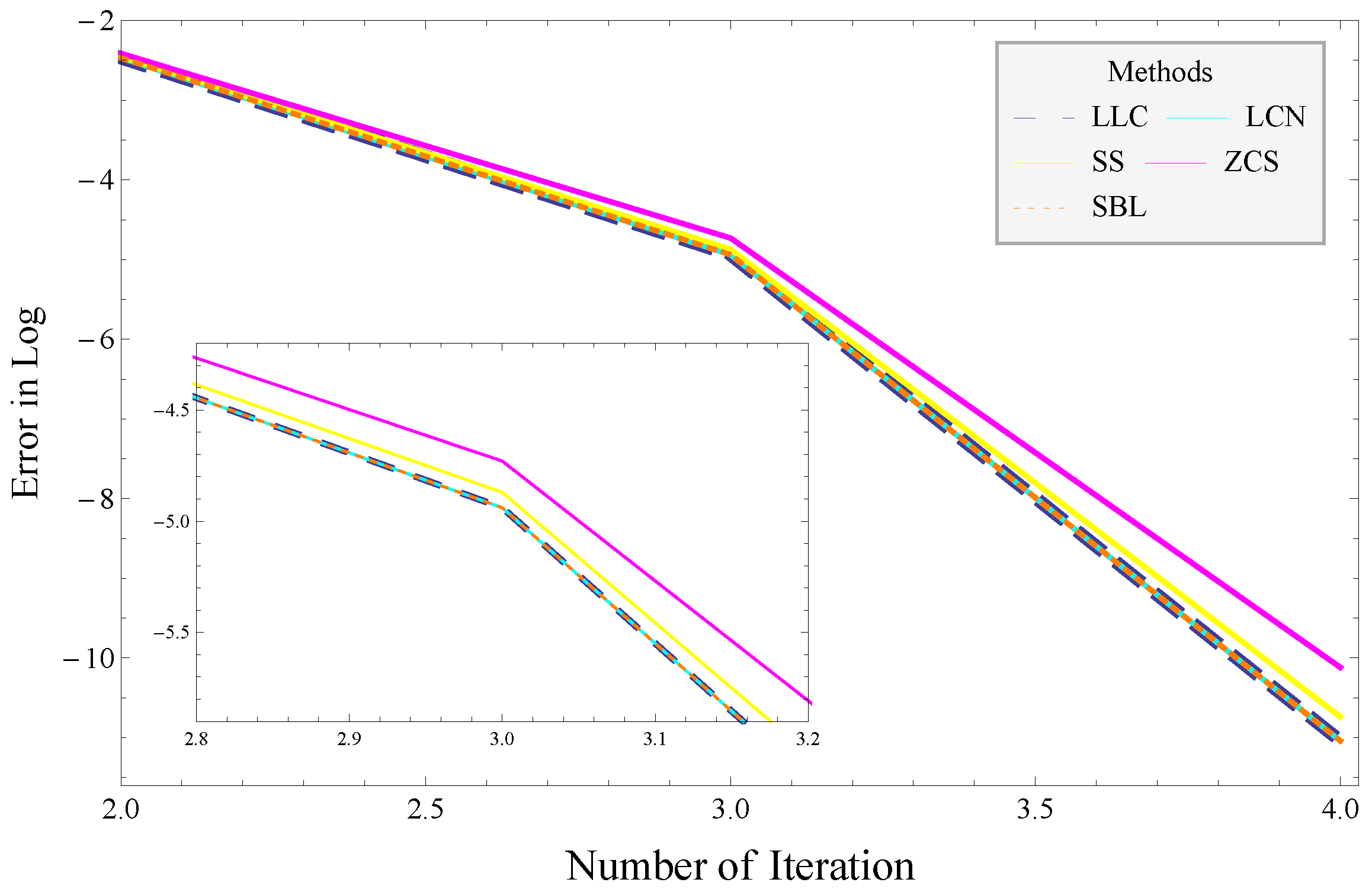
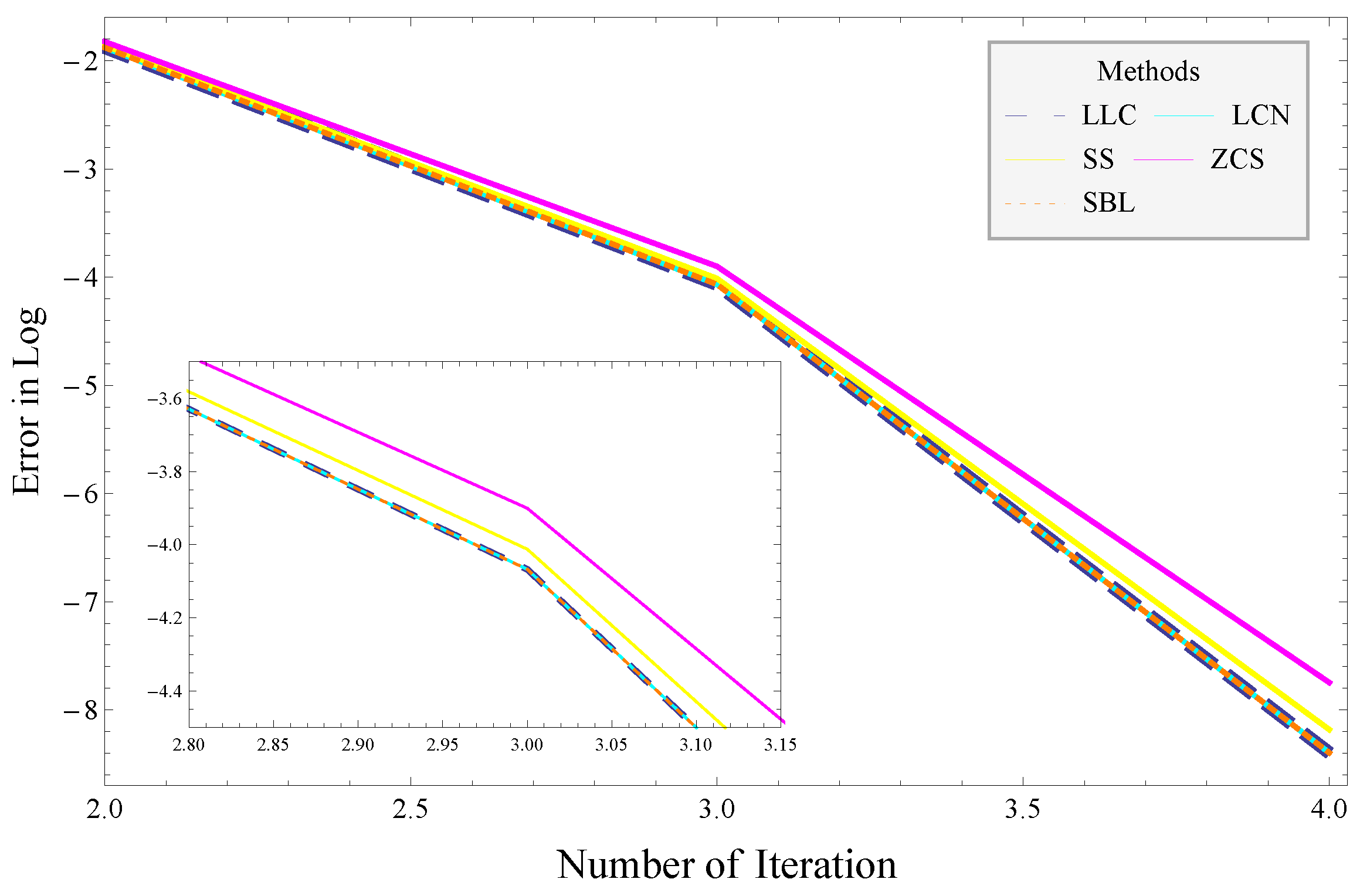
4. Numerical Results
- (i)
- The number of iterations taken by the algorithms and the satisfaction of the stopping criterion .
- (ii)
- The first three iterations’ error .
- (iii)
- The calculated convergence order (CCO).
- (iv)
- The total time (in seconds) consumed by the algorithms.
| Problem | Root | Multiplicity | Initial Guess | Results’ Table |
|---|---|---|---|---|
| 2: Isentropic supersonic flow problem [53] | ||||
| 1.8411… | 3 | 1.5 & 1.7 | Table 2 | |
| 3: Planck law of radiation problem [54] | ||||
| 4.9651… | 4 | 2.5 & 5.5 | Table 3 | |
| 4: Kepler’s problem [49] | ||||
| 0.8093… | 5 | 1 & 1.4 | Table 4 | |
| 5: Complex root problem | ||||
| i | 6 | 1.1 i & 1.3 i | Table 5 |
| Methods | CCO | CPU-Time | ||||
|---|---|---|---|---|---|---|
| LLC | 4 | 4 | 2.1224 | |||
| LCN | 4 | 4 | 2.4660 | |||
| SS | 4 | 4 | 2.4653 | |||
| ZCS | 4 | 4 | 2.4492 | |||
| SBL | 4 | 4 | 2.7765 | |||
| NM1 | 4 | 4 | 1.8522 | |||
| NM2 | 4 | 4 | 1.8878 | |||
| NM3 | 4 | 4 | 1.8867 | |||
| NM4 | 4 | 4 | 1.9042 | |||
| LLC | 4 | 4 | 2.6054 | |||
| LCN | 4 | 4 | 2.8556 | |||
| SS | 4 | 4 | 2.9173 | |||
| ZCS | 4 | 4 | 2.8868 | |||
| SBL | 4 | 4 | 3.2764 | |||
| NM1 | 4 | 4 | 2.4214 | |||
| NM2 | 4 | 4 | 2.5285 | |||
| NM3 | 4 | 4 | 2.5432 | |||
| NM4 | 4 | 4 | 2.4967 | |||
| Methods | CCO | CPU-Time | ||||
|---|---|---|---|---|---|---|
| LLC | 5 | 4 | 0.8893 | |||
| LCN | 5 | 4 | 1.2483 | |||
| SS | 5 | 4 | 1.2791 | |||
| ZCS | 5 | 4 | 1.2172 | |||
| SBL | 5 | 4 | 1.4986 | |||
| NM1 | 5 | 4 | 0.5946 | |||
| NM2 | 5 | 4 | 0.6385 | |||
| NM3 | 5 | 4 | 0.6843 | |||
| NM4 | 5 | 4 | 0.6682 | |||
| LLC | 4 | 4 | 0.6545 | |||
| LCN | 4 | 4 | 1.0772 | |||
| SS | 4 | 4 | 1.0301 | |||
| ZCS | 4 | 4 | 1.0142 | |||
| SBL | 4 | 4 | 1.2646 | |||
| NM1 | 3 | 0 | 4 | 0.4534 | ||
| NM2 | 3 | 0 | 4 | 0.5173 | ||
| NM3 | 3 | 0 | 4 | 0.5238 | ||
| NM4 | 3 | 0 | 4 | 0.4923 | ||
| Methods | CCO | CPU-Time | ||||
|---|---|---|---|---|---|---|
| LLC | 4 | 4 | 0.8422 | |||
| LCN | 4 | 4 | 0.9675 | |||
| SS | 4 | 4 | 0.9833 | |||
| ZCS | 4 | 4 | 0.9215 | |||
| SBL | 4 | 4 | 1.1863 | |||
| NM1 | 4 | 4 | 0.5865 | |||
| NM2 | 4 | 4 | 0.6246 | |||
| NM3 | 4 | 4 | 0.5934 | |||
| NM4 | 4 | 4 | 0.6440 | |||
| LLC | 4 | 4 | 0.8114 | |||
| LCN | 4 | 4 | 1.0320 | |||
| SS | 4 | 4 | 1.0146 | |||
| ZCS | 4 | 4 | 0.9998 | |||
| SBL | 4 | 4 | 1.1393 | |||
| NM1 | 4 | 4 | 0.6155 | |||
| NM2 | 4 | 4 | 0.6442 | |||
| NM3 | 4 | 4 | 0.6561 | |||
| NM4 | 4 | 4 | 0.6240 | |||
| Methods | CCO | CPU-Time | ||||
|---|---|---|---|---|---|---|
| LLC | 4 | 4 | 1.7604 | |||
| LCN | 4 | 4 | 2.4491 | |||
| SS | 4 | 4 | 2.4653 | |||
| ZCS | 4 | 4 | 2.5426 | |||
| SBL | 4 | 4 | 3.1042 | |||
| NM1 | 4 | 4 | 0.5311 | |||
| NM2 | 4 | 4 | 0.5380 | |||
| NM3 | 4 | 4 | 0.5935 | |||
| NM4 | 4 | 4 | 0.5468 | |||
| LLC | 4 | 4 | 1.6234 | |||
| LCN | 4 | 4 | 2.5432 | |||
| SS | 4 | 4 | 2.6216 | |||
| ZCS | 4 | 4 | 2.6217 | |||
| SBL | 4 | 4 | 3.1824 | |||
| NM1 | 4 | 4 | 0.5162 | |||
| NM2 | 4 | 4 | 0.6243 | |||
| NM3 | 4 | 4 | 0.5922 | |||
| NM4 | 4 | 4 | 0.5610 | |||
| Methods | CCO | CPU-Time | ||||
|---|---|---|---|---|---|---|
| LLC | 6 | 4 | 0.0787 | |||
| LCN | 6 | 4 | 0.0786 | |||
| SS | 6 | 4 | 0.1095 | |||
| ZCS | 6 | 4 | 0.0786 | |||
| SBL | 6 | 4 | 0.0938 | |||
| NM1 | 6 | 4 | 0.0753 | |||
| NM2 | 6 | 4 | 0.0821 | |||
| NM3 | 6 | 4 | 0.0778 | |||
| NM4 | 6 | 4 | 0.0782 | |||
| LLC | 6 | 4 | 0.0982 | |||
| LCN | 6 | 4 | 0.1102 | |||
| SS | 6 | 4 | 0.1096 | |||
| ZCS | 6 | 4 | 0.1145 | |||
| SBL | 6 | 4 | 0.0944 | |||
| NM1 | 6 | 4 | 0.0682 | |||
| NM2 | 6 | 4 | 0.0924 | |||
| NM3 | 6 | 4 | 0.0947 | |||
| NM4 | 6 | 4 | 0.0936 | |||
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haruo, H. Topological Index. A Newly Proposed Quantity Characterizing the Topological Nature of Structural Isomers of Saturated Hydrocarbons. Bull. Chem. Soc. Jpn. 1971, 44, 2332–2339. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bolboacă, S.D.; Furdui, C.M. Characteristic and counting polynomials: Modelling nonane isomers properties. Mol. Simulat. 2009, 35, 220–227. [Google Scholar] [CrossRef]
- Gander, W. On Halley’s iteration method. Am. Math. Mon. 1985, 92, 131–134. [Google Scholar] [CrossRef]
- Proinov, P.D. General local convergence theory for a class of iterative processes and its applications to Newton’s method. J. Complex. 2009, 25, 38–62. [Google Scholar] [CrossRef]
- Proinov, P.D.; Ivanov, S.I.; Petković, M.S. On the convergence of Gander’s type family of iterative methods for simultaneous approximation of polynomial zeros. Appl. Math. Comput. 2019, 349, 168–183. [Google Scholar] [CrossRef]
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint methods for solving nonlinear equations: A survey. Appl. Math. Comput. 2014, 226, 635–660. [Google Scholar] [CrossRef]
- McNamee, J.M.; Pan, V.Y. Numerical Methods for Roots of Polynomials—Part II; Elsevier Science: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Soleymani, F. Some optimal iterative methods and their with memory variants. J. Egypt. Math. Soc. 2013, 21, 133–141. [Google Scholar] [CrossRef]
- Hafiz, M.A.; Bahgat, M.S.M. Solving nonsmooth equations using family of derivative-free optimal methods. J. Egypt. Math. Soc. 2013, 21, 38–43. [Google Scholar] [CrossRef]
- Sihwail, R.; Solaiman, O.S.; Ariffin, K.A.Z. New robust hybrid Jarratt-Butterfly optimization algorithm for nonlinear models. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 8207–8220. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Galantai, A.; Hegedus, C.J. A study of accelerated Newton methods for multiple polynomial roots. Numer. Algorithms 2010, 54, 219–243. [Google Scholar] [CrossRef]
- Halley, E. A new exact and easy method of finding the roots of equations generally and that without any previous reduction. Philos. Trans. R. Soc. Lond. 1694, 18, 136–147. [Google Scholar] [CrossRef]
- Hansen, E.; Patrick, M. A family of root finding methods. Numer. Math. 1976, 27, 257–269. [Google Scholar] [CrossRef]
- Neta, B.; Johnson, A.N. High-order nonlinear solver for multiple roots. Comput. Math. Appl. 2008, 55, 2012–2017. [Google Scholar] [CrossRef]
- Victory, H.D.; Neta, B. A higher order method for multiple zeros of nonlinear functions. Int. J. Comput. Math. 1982, 12, 329–335. [Google Scholar] [CrossRef]
- Akram, S.; Zafar, F.; Yasmin, N. An optimal eighth-order family of iterative methods for multiple roots. Mathematics 2019, 7, 672. [Google Scholar] [CrossRef]
- Akram, S.; Akram, F.; Junjua, M.U.D.; Arshad, M.; Afzal, T. A family of optimal Eighth order iteration functions for multiple roots and its dynamics. J. Math. 2021, 5597186. [Google Scholar] [CrossRef]
- Ivanov, S.I. Unified convergence analysis of Chebyshev-Halley methods for multiple polynomial zeros. Mathematics 2022, 12, 135. [Google Scholar] [CrossRef]
- Sharifi, M.; Babajee, D.K.R.; Soleymani, F. Finding the solution of nonlinear equations by a class of optimal methods. Comput. Math. Appl. 2012, 63, 764–774. [Google Scholar] [CrossRef]
- Li, S.; Liao, X.; Cheng, L. A new fourth-order iterative method for finding multiple roots of nonlinear equations. Appl. Math. Comput. 2009, 215, 1288–1292. [Google Scholar] [CrossRef]
- Li, S.G.; Cheng, L.Z.; Neta, B. Some fourth-order nonlinear solvers with closed formulae for multiple roots. Comput. Math. Appl. 2010, 59, 126–135. [Google Scholar] [CrossRef]
- Sharma, J.R.; Sharma, R. Modified Jarratt method for computing multiple roots. Appl. Math. Comput. 2010, 217, 878–881. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, X.; Song, Y. Constructing higher-order methods for obtaining the multiple roots of nonlinear equations. J. Comput. Appl. Math. 2011, 235, 4199–4206. [Google Scholar] [CrossRef]
- Soleymani, F.; Babajee, D.K.R.; Lotfi, T. On a numerical technique for finding multiple zeros and its dynamics. J. Egypt. Math. Soc. 2013, 21, 346–353. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Neta, B. A class of two-point sixth-order multiple-zero finders of modified double-Newton type and their dynamics. Appl. Math. Comput. 2015, 270, 387–400. [Google Scholar] [CrossRef]
- Kansal, M.; Kanwar, V.; Bhatia, S. On some optimal multiple root-finding methods and their dynamics. Appl. Appl. Math. 2015, 10, 349–367. [Google Scholar]
- Behl, R.; Alsolami, A.J.; Pansera, B.A.; Al-Hamdan, W.M.; Salimi, M.; Ferrara, M. A new optimal family of Schröder’s method for multiple zeros. Mathematics 2019, 7, 1076. [Google Scholar] [CrossRef]
- Soleymani, F. Efficient optimal eighth-order derivative-free methods for nonlinear equations. Jpn. J. Ind. Appl. Math. 2013, 30, 287–306. [Google Scholar] [CrossRef]
- Larson, J.; Menickelly, M.; Wild, S. Derivative-free optimization methods. Acta Numer. 2019, 28, 287–404. [Google Scholar] [CrossRef]
- Moré, J.J.; Wild, S.M. Benchmarking Derivative-Free Optimization Algorithms. SIAM J. Optim. 2009, 20, 172–191. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S.; Jäntschi, L. On a class of optimal fourth order multiple root solvers without using derivatives. Symmetry 2019, 11, 1452. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S.; Argyros, I.K. Development of optimal eighth order derivative-free methods for multiple roots of nonlinear equations. Symmetry 2019, 11, 766. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Sharma, J.R.; Cesarano, C.; Agarwal, P.; Chu, Y.M. An optimal fourth order derivative-free numerical algorithm for multiple roots. Symmetry 2020, 12, 1038. [Google Scholar] [CrossRef]
- Kansal, M.; Alshomrani, A.S.; Bhalla, S.; Behl, R.; Salimi, M. One parameter optimal derivative-free family to find the multiple roots of algebraic nonlinear equations. Mathematics 2020, 8, 2223. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Torregrosa, J.R. A new higher-order optimal derivative free scheme for multiple roots. J. Comput. Appl. Math. 2022, 404, 113773. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Kumar, R. Development of cubically convergent iterative derivative free methods for computing multiple roots. SeMA J. 2022. [Google Scholar] [CrossRef]
- Kumar, D.; Sharma, J.R.; Cesarano, C. An Efficient Class of Traub–Steffensen-Type Methods for Computing Multiple Zeros. Axioms 2019, 8, 65. [Google Scholar] [CrossRef]
- Zafar, F.; Iqbal, S.; Nawaz, T. A Steffensen type optimal eighth order multiple root finding scheme for nonlinear equations. J. Comp. Math. Data Sci. 2023, 7, 100079. [Google Scholar] [CrossRef]
- Steffensen, J.F. Remarks on iteration. Scand. Actuar. J. 1933, 16, 64–72. [Google Scholar] [CrossRef]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Moriguchi, I.; Kanada, Y.; Komatsu, K. Van der Waals Volume and the Related Parameters for Hydrophobicity in Structure-Activity Studies. Chem. Phamaceut. Bull. 1976, 24, 1799–1806. [Google Scholar] [CrossRef]
- Quinlan, N.; Kendall, M.; Bellhouse, B.; Ainsworth, R.W. Investigations of gas and particle dynamics in first generation needle-free drug delivery devices. Shock Waves 2001, 10, 395–404. [Google Scholar] [CrossRef]
- Parrish, J.A. Photobiologic principles of phototherapy and photochemotherapy of psoriasis. Phamacol. Therapeut. 1981, 15, 439–446. [Google Scholar] [CrossRef]
- Balasubramanian, K. Integration of Graph Theory and Quantum Chemistry for Structure-Activity Relationships. SAR QSAR Environ. Res. 1994, 2, 59–77. [Google Scholar] [CrossRef]
- Basak, S.C.; Bertelsen, S.; Grunwald, G.D. Application of graph theoretical parameters in quantifying molecular similarity and structure-activity relationships. J. Chem. Inf. Comput. Sci. 1994, 34, 270–276. [Google Scholar] [CrossRef]
- Ivanciuc, O. Chemical Graphs, Molecular Matrices and Topological Indices in Chemoinformatics and Quantitative Structure-Activity Relationships. Curr. Comput. Aided Drug Des. 2013, 9, 153–163. [Google Scholar] [CrossRef]
- Matsuzaka, Y.; Uesawa, Y. Ensemble Learning, Deep Learning-Based and Molecular Descriptor-Based Quantitative Structure–Activity Relationships. Molecules 2023, 28, 2410. [Google Scholar] [CrossRef] [PubMed]
- Danby, J.M.A.; Burkardt, T.M. The solution of Kepler’s equation. I. Celest. Mech. 1983, 40, 95–107. [Google Scholar] [CrossRef]
- Wolfram, S. The Mathematica Book, 5th ed.; Wolfram Media: Champaign, IL, USA, 2003. [Google Scholar]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Hueso, J.L.; Martinez, E.; Teruel, C. Detemination of multiple roots of nonlinear equations and applications. J. Math. Chem. 2014, 53, 880–892. [Google Scholar] [CrossRef]
- Hoffman, J.D. Numerical Methods for Engineers and Scientists; McGraw-Hill Book Company: New York, NY, USA, 1992. [Google Scholar]
- Bradie, B. A Friendly Introduction to Numerical Analysis; Pearson Education Inc.: New Delhi, India, 2006. [Google Scholar]



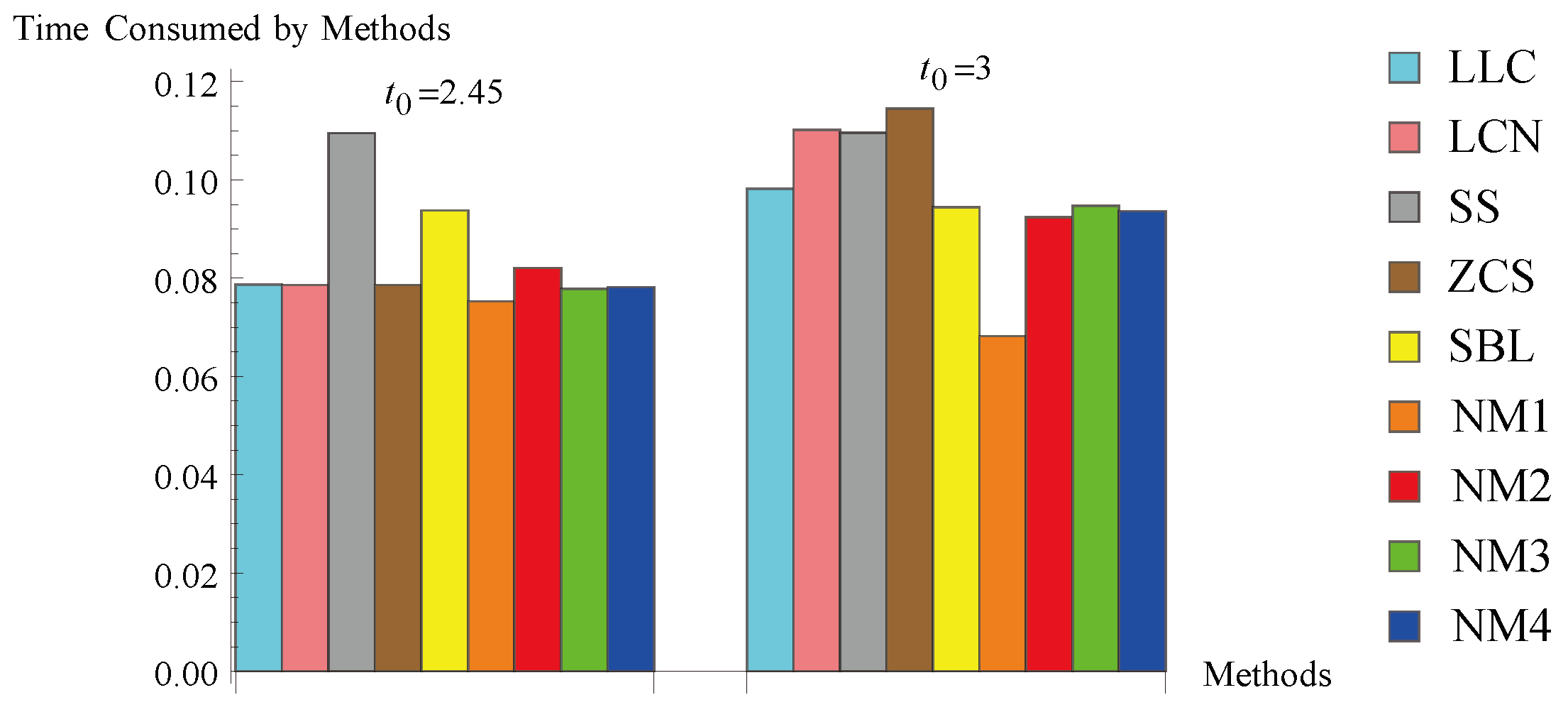


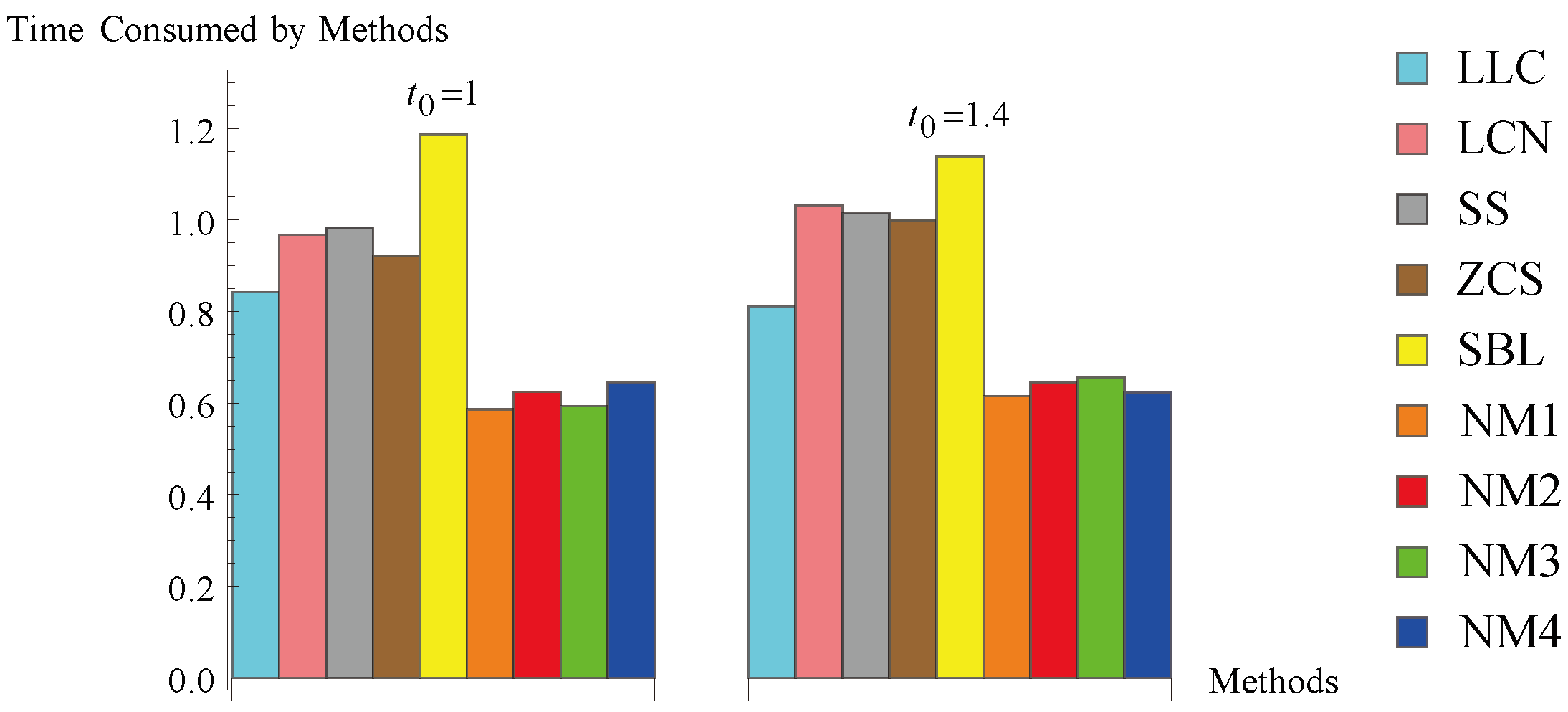
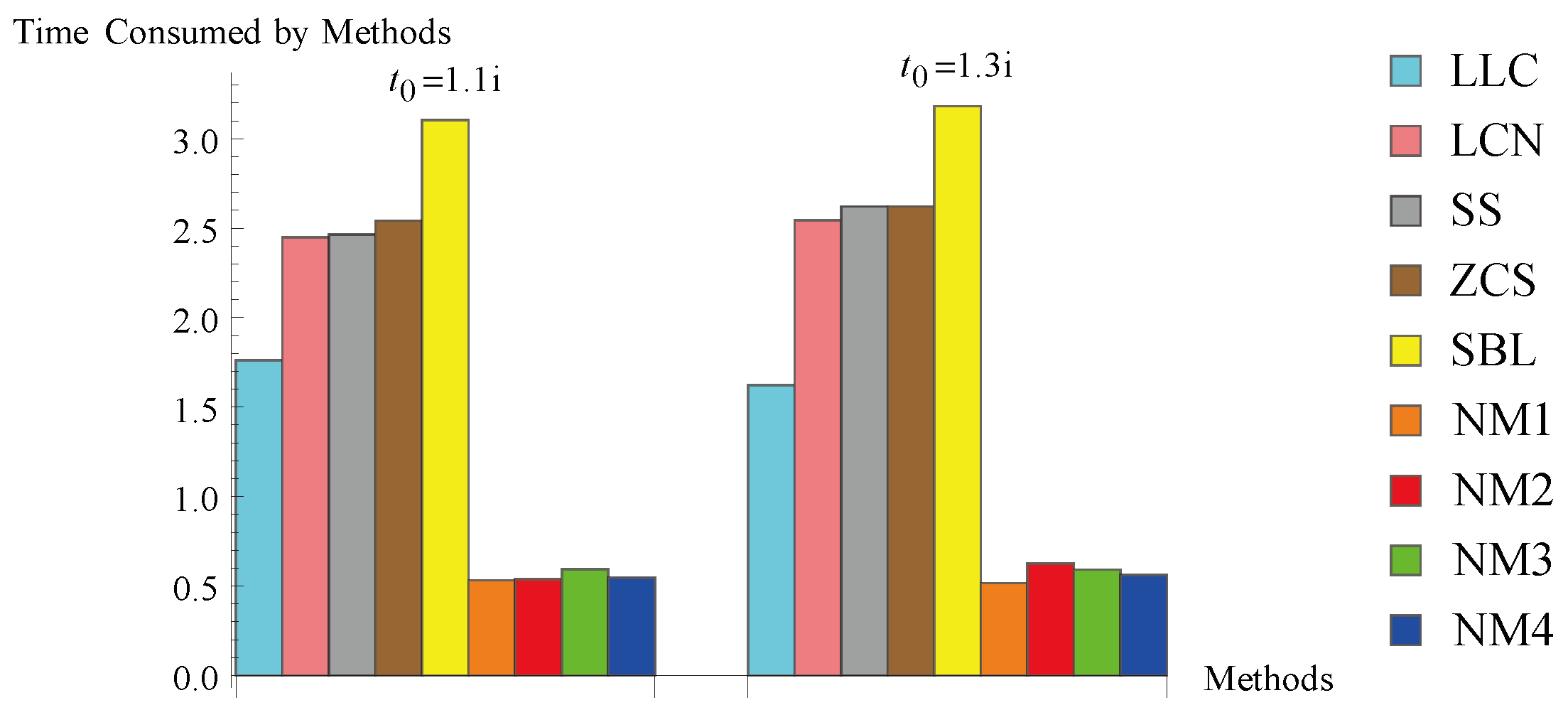
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Sharma, J.R.; Bhagwan, J.; Jäntschi, L. Numerical Solution of Nonlinear Problems with Multiple Roots Using Derivative-Free Algorithms. Symmetry 2023, 15, 1249. https://doi.org/10.3390/sym15061249
Kumar S, Sharma JR, Bhagwan J, Jäntschi L. Numerical Solution of Nonlinear Problems with Multiple Roots Using Derivative-Free Algorithms. Symmetry. 2023; 15(6):1249. https://doi.org/10.3390/sym15061249
Chicago/Turabian StyleKumar, Sunil, Janak Raj Sharma, Jai Bhagwan, and Lorentz Jäntschi. 2023. "Numerical Solution of Nonlinear Problems with Multiple Roots Using Derivative-Free Algorithms" Symmetry 15, no. 6: 1249. https://doi.org/10.3390/sym15061249
APA StyleKumar, S., Sharma, J. R., Bhagwan, J., & Jäntschi, L. (2023). Numerical Solution of Nonlinear Problems with Multiple Roots Using Derivative-Free Algorithms. Symmetry, 15(6), 1249. https://doi.org/10.3390/sym15061249







