Data-Driven RBFNN-Enhanced Model-Free Adaptive Traffic Symmetrical Signal Control for a Multi-Phase Intersection with Fast-Changing Traffic Flow
Abstract
1. Introduction
- (1)
- Based on the full-format dynamic linearization (FFDL), a novel MFAC traffic signal control scheme was proposed for multi-phase intersections. The raised scheme combines data-driven prediction technique with symmetrical queuing equalization rules in order to balance the pressure of each phase.
- (2)
- A two-layer parameters tuning framework was designed for the MFAC controller, aiming to deal with the fast-changing demand. In the first layer, radial basis function neural network (RBFNN) was used to just two key parameters in the second layer (i.e., η(k) and μ(k)) based on the error function. Then, the two adjusted parameters drove the projection algorithm to estimate pseudo partitioned Jacobian and give a prediction of queuing length.
- (3)
- A variable cycle mechanism was added to the above algorithm to make it work for different traffic patterns and further reduce the time loss of vehicles. Finally, the proposed method was tested on the micro traffic flow simulation platform compared with other three control methods. The simulation results showed the superiority of the proposed method.
2. Problem Formulation and Preliminaries
2.1. Signal Control Problem Formulation
2.2. Basic Assumptions
2.3. RBF Neural Network
3. Multi-Phase Traffic Signal Controller Design
3.1. FFDL-MFAC Symmetrical Controller Design
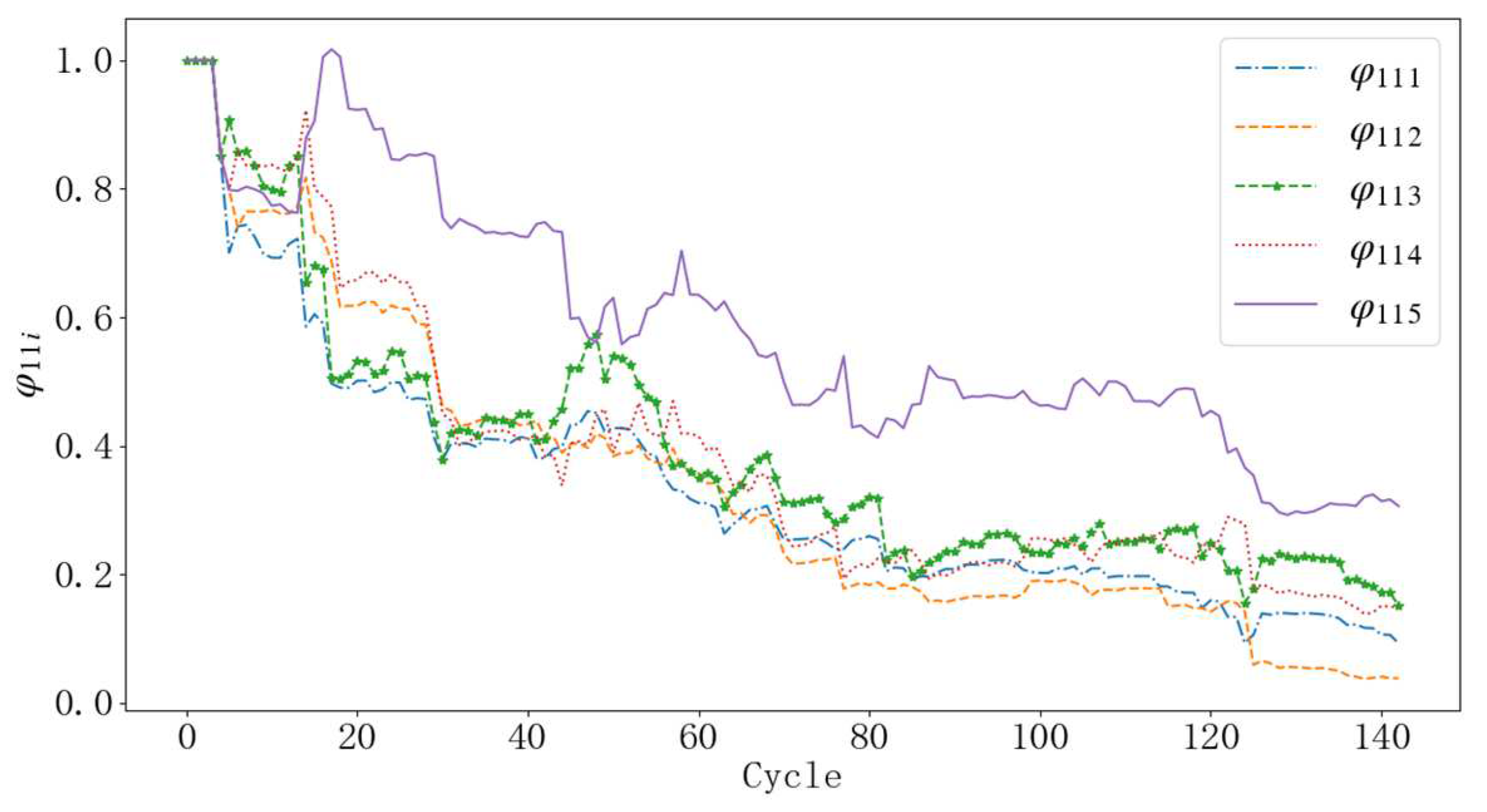
3.2. RBFNN-Enhanced Controller Design
4. Application Steps of the Proposed Algorithm
| Algorithm 1: RBFNN-FFDL algorithm for the intersection with fast-changing traffic flow | ||
| Import traci | ||
| Input: maximum control cycle number kmax, non-green time yy, minimum green time gmin, α, β; the initial values of l, , g, y, ,, C, W, η, μ, e, v and σ. | ||
| 1. Initialization: Q(k) = 0; | ||
| 2. for k = 2 to kmax | ||
| 3. The queuing lengths of each phase are obtained through the detectors. | ||
| li(k) = traci.lanearea.getJamLengthVehicle() | ||
| 4. If Q(k) < T | ||
| 5. , as Formula (14). The queuing lengths of k-period is predicted by the data of (k − 1)-period. | ||
| 6. , as Formula (21). The difference between the actual queuing lengths of k-period and the predicted queuing lengths are calculated. | ||
| 7. , as the input of RBFNN, as Formulas (22) and (23). | ||
| 8. Search for the negative gradient direction of the coefficient, as Formulas (24)–(28), to update weight coefficient W. | ||
| 9. Q(k) += 1 | ||
| 10. End if | ||
| 11. Select the η(k) and μ(k) that corresponds to the requirements when e(k) meet the requirements. | ||
| 12. , X(h) represents a function about h. | ||
| 13. , K(t) represents a function about t. | ||
| 14. The variable period C(k + 1) can be calculated from Formula (17). | ||
| 15. , predict the queuing lengths for the next cycle. | ||
| 16. , represents a function about θ, i represents phase. | ||
| 17. Set gi(k + 1) to traffic light. | ||
| SET: traci.trafficlight.setPhaseDuration(‘ ‘, g(k + 1)) | ||
| 18. k = k + 1 | ||
| 19. End for | ||
| Traci.simulationStep() | ||
5. Simulation
5.1. Simulation Platform
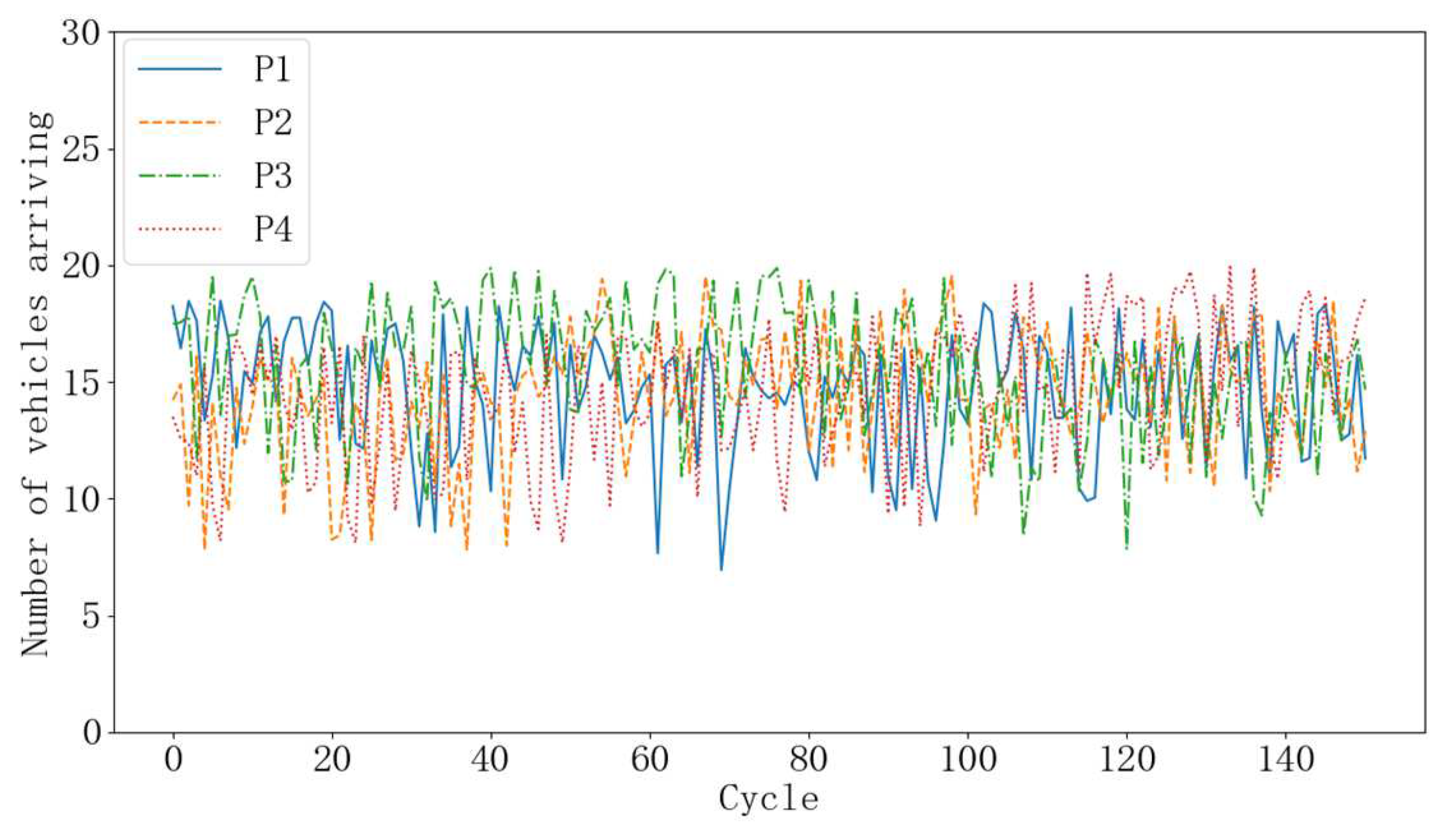
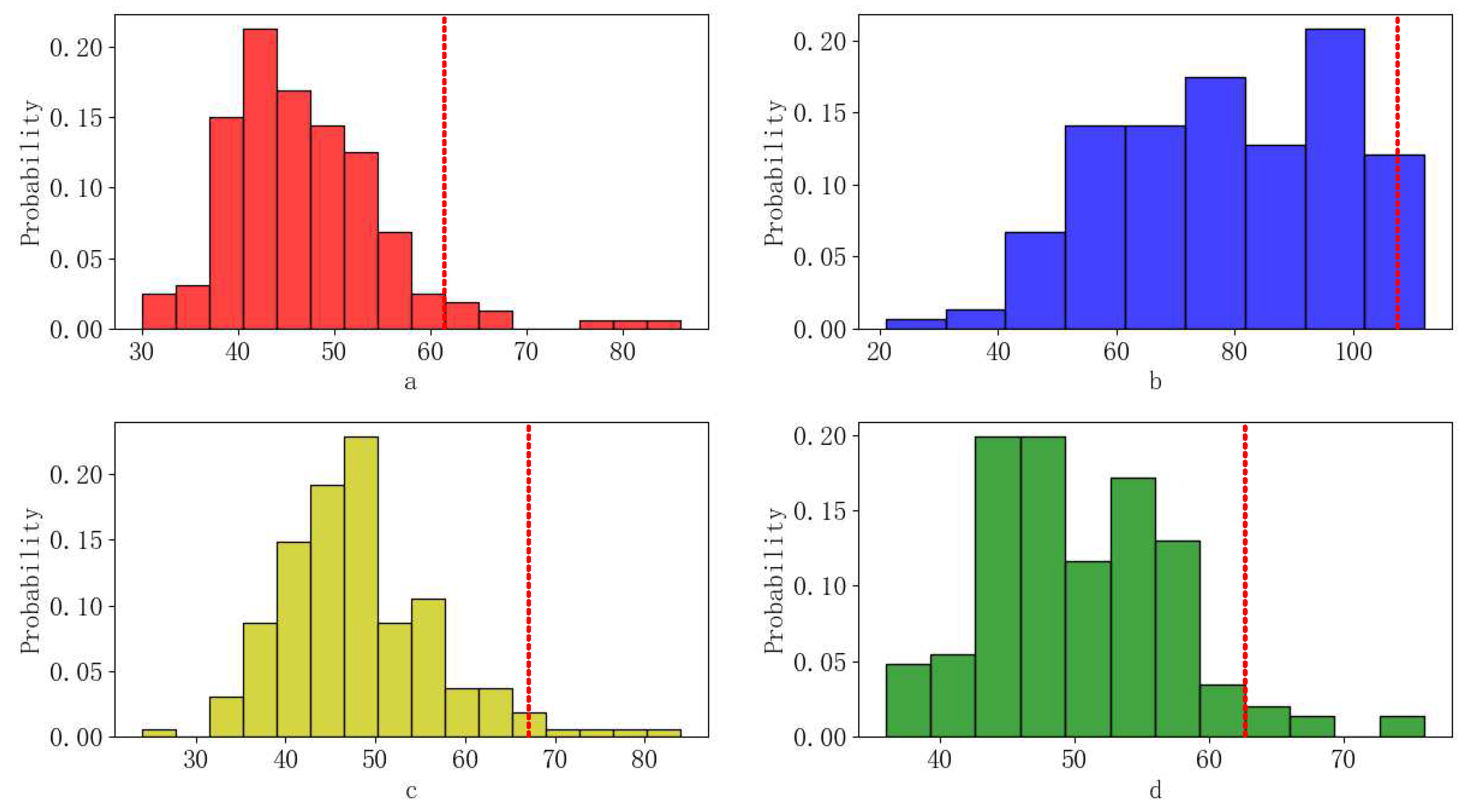
5.2. Low Traffic Demand
- (1)
- Fixed timing control (FC)
- (2)
- Linear control (LC)
- (3)
- Variable-period queuing feedback control (VQF)
- (4)
- FFDL control based on queuing feedback (FFDL-QF)
- (5)
- The proposed algorithm control (FFDL-RBFNN)
5.3. High Traffic Demand
- (1)
- Fixed timing control (FC)
- (2)
- Linear control (LC)
- (3)
- Variable-period queuing feedback control (VQF)
- (4)
- FFDL control based on queuing feedback (FFDL-QF)
- (5)
- The proposed algorithm control (FFDL-RBFNN)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, N.; Li, D.W.; Xi, Y.G. Distributed Weighted Balanced Control of Traffic Signals for Urban Traffic Congestion. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3710–3720. [Google Scholar] [CrossRef]
- Čubranić-Dobrodolac, M.; Švadlenka, L.; Čičević, S. A bee colony optimization (BCO) and type-2 fuzzy approach to measuring the impact of speed perception on motor vehicle crash involvement. Soft. Comput. 2022, 26, 4463–4486. [Google Scholar] [CrossRef]
- Dunne, M.C.; Potts, R.B. Algorithm for Traffic Control. Oper. Res. 1964, 12, 870–881. [Google Scholar] [CrossRef]
- Pascale, A.; Lam, H.T.; Nair, R. Characterization of Network Traffic Processes Under Adaptive Traffic Control Systems. Transp. Res. Procedia 2015, 9, 205–224. [Google Scholar] [CrossRef]
- Robertson, D.I.; Bretherton, R.D. Optimizing Networks of Traffic Signals in Real Time—The SCOOT Method. IEEE Trans. Veh. Technol. 1991, 40, 11–15. [Google Scholar] [CrossRef]
- Jin, J.; Ma, X.; Kosonen, I. An intelligent control system for traffic lights with simulation-based evaluation. Control. Eng. Pract. 2017, 58, 24–33. [Google Scholar] [CrossRef]
- Kenan, M.; Nezir, A.; Alper, Y. A Data Driven Approach to Forecasting Traffic Speed Classes Using Extreme Gradient Boosting Algorithm and Graph Theory. Phys. A Stat. Mech. Its Appl. 2023, 620, 128738. [Google Scholar]
- Ye, B.L.; Wu, W.M.; Ruan, K.Y. A survey of model predictive control methods for traffic signal control. IEEE CAA J. Autom. Sin. 2019, 6, 623–640. [Google Scholar] [CrossRef]
- Huang, Y.S.; Weng, Y.S.; Wu, W.M. Control strategies for solving the problem of traffic congestion. IET Intell. Transp. Syst. 2016, 10, 642–648. [Google Scholar] [CrossRef]
- Celtek, S.; Durdu, A.; Alı, M. Real-time traffic signal control with swarm optimization methods. Measurement 2020, 166, 108206. [Google Scholar] [CrossRef]
- Yuan, T.C.; Faisal, A.; Zhang, Y.H.; Petros, A.I. Evaluation of Integrated Variable Speed Limit and Lane Change Control for Highway Traffic Flow. IFAC Pap. 2021, 54, 107–113. [Google Scholar] [CrossRef]
- Baldi, S.; Michailidis, L.; Ntampasi, V. A Simulation-Based Traffic Signal Control for Congested Urban Traffic Networks. Transp. Sci. 2019, 53, 6–20. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, M.X.; Hong, W.S. Optimizing Signal Timing Control for Large Urban Traffic Networks Using an Adaptive Linear Quadratic Regulator Control Strategy. IEEE Trans. Intell. Transp. Syst. 2022, 23, 333–343. [Google Scholar] [CrossRef]
- Gao, P.; Yang, Z.S. Regional Traffic Control Evaluation Based on Genetic Neural Network. J. Beijing Univ. Technol. 2010, 36, 490–494. [Google Scholar]
- Molyneaux, N.; Scarinci, R.; Bierlaire, M. Design and analysis of control strategies for pedestrian flows. Transportation 2021, 48, 1767–1807. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.C.; Su, R. Pedestrian-Safety-Aware Traffic Light Control Strategy for Urban Traffic Congestion Alleviation. IEEE Trans. Intell. Transp. Syst. 2021, 22, 178–193. [Google Scholar] [CrossRef]
- Hou, Z.S.; Wang, Z. From model-based control to data-driven control: Survey, classification and perspective. Inf. Sci. 2013, 235, 3–35. [Google Scholar] [CrossRef]
- Hou, Z.S.; Jin, S.T. Data-driven model-free adaptive control for a class of MIMO nonlinear discrete-time systems. IEEE Trans. Neural Netw. 2011, 22, 2173–2188. [Google Scholar]
- Hou, Z.S.; Chi, R.H.; Gao, H.J. An Overview of Dynamic-Linearization-Based Data-Driven Control and Application. IEEE Trans. Ind. Electron. 2017, 64, 4076–4090. [Google Scholar] [CrossRef]
- Hou, Z.S.; Zhu, Y.M. Controller-Dynamic-Linearizati- on-Based Model Free Adaptive Control for Discrete-Time Nonlinear Systems. IEEE Trans. Ind. Inform. 2013, 9, 2301–2309. [Google Scholar] [CrossRef]
- Xiong, S.S.; Hou, Z.S. Model-Free Adaptive Control for Unknown MIMO Nonaffine Nonlinear Discrete-Time Systems With Experimental Validation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1727–1739. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Song, W.Z.; Zhang, H.G. Data-Driven Robust Iterative Learning Consensus Tracking Control for MIMO Multiagent Systems Under Fixed and Iteration-Switching Topologies. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1331–1344. [Google Scholar] [CrossRef]
- Xue, G.; Liu, Y.J.; Shi, Z.J. Research on Trajectory Tracking Control of Underwater Vehicle Manipulator System Based on Model-Free Adaptive Control Method. J. Mar. Sci. Eng. 2022, 10, 652. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Jin, S.T.; Liu, G.F. Model-Free Adaptive Direct Torque Control for the Speed Regulation of Asynchronous Motors. Processes 2020, 8, 333. [Google Scholar] [CrossRef]
- Jiang, Q.Q.; Li, Y.; Liao, Y.L. Information fusion model-free adaptive control algorithm and unmanned surface vehicle heading control. Appl. Ocean. Res. 2019, 90, 101851. [Google Scholar] [CrossRef]
- Liao, Y.L.; Du, T.P.; Jiang, Q.Q. Model-free adaptive control method with variable forgetting factor for unmanned surface vehicle control. Appl. Ocean. Res. 2019, 93, 101945. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Liu, L.F.; Yuan, M.X. A New Model-free Robust Adaptive Control of Cable-driven Robots. Int. J. Control Autom. Syst. 2021, 19, 3209–3222. [Google Scholar] [CrossRef]
- Ren, Y.; Hou, Z.S. Robust mode-free adaptive iterative learning formation for unknown heterogeneous non-linear multi-agent systems. IET Control. Theory Appl. 2020, 14, 654–663. [Google Scholar] [CrossRef]
- Hou, Z.S.; Lei, T. Constrained Model Free Adaptive Predictive Perimeter Control and Route Guidance for Multi-Region Urban Traffic Systems. IEEE Trans. Intell. Transp. Syst. 2022, 23, 912–924. [Google Scholar] [CrossRef]
- Ren, Y.; Hou, Z.S.; Sirmatel, I.I. Data driven model free adaptive iterative learning perimeter control for large-scale urban road networks. Transp. Res. Part C Emerg. Technol. 2020, 115, 102618. [Google Scholar] [CrossRef]
- Lei, T.; Hou, Z.S.; Ren, Y. Data-Driven Model Free Adaptive Perimeter Control for Multi-Region Urban Traffic Networks With Route Choice. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2894–2905. [Google Scholar] [CrossRef]
- Cui, X. Model Free Adaptive Control of Multi-Agent Systems and It’s Applications to Coordinated Signal Control of Intersections. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2015. [Google Scholar]
- Li, D.; De Schutter, B. Distributed Model-Free Adaptive Predictive Control for Urban Traffic Networks. IEEE Trans. Control. Syst. Technol. 2022, 30, 180–192. [Google Scholar] [CrossRef]
- Li, D.; Hou, Z.S. Data-driven urban traffic model-free adaptive iterative learning control with traffic data dropout compensation. IET Control. Theory Appl. 2021, 15, 1533–1544. [Google Scholar] [CrossRef]
- Han, H.G.; Ma, M.L.; Qiao, J.F. Accelerated gradient algorithm for RBF neural network. Neurocomputing 2021, 441, 237–247. [Google Scholar] [CrossRef]
- Xiong, S.S.; Hou, Z.S. Data-Driven Formation Control for Unknown MIMO Nonlinear Discrete-Time Multi-Agent Systems With Sensor Fault. IEEE Trans. Neural. Netw. Learn Syst. 2022, 33, 7728–7742. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.M.; Hou, Z.S.; Qian, F. Dual RBFNNs-Based Model-Free Adaptive Control With Aspen HYSYS Simulation. IEEE Trans. Neural. Netw. Learn Syst. 2017, 28, 759–765. [Google Scholar] [CrossRef]
- Hou, Z.S.; Jin, S.T. Model Free Adaptive Control Theory and Applications’; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2013; pp. 69–71. [Google Scholar]

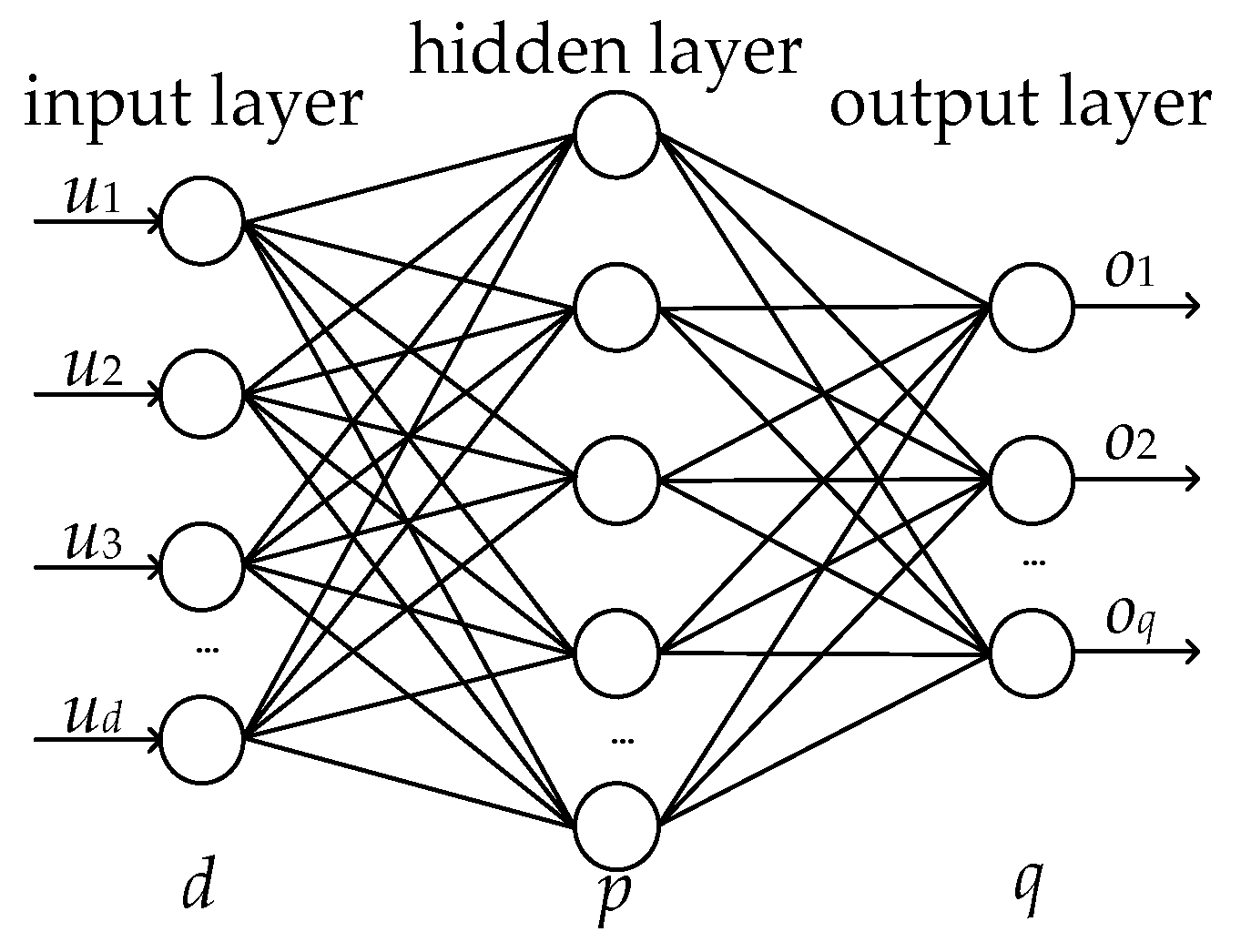







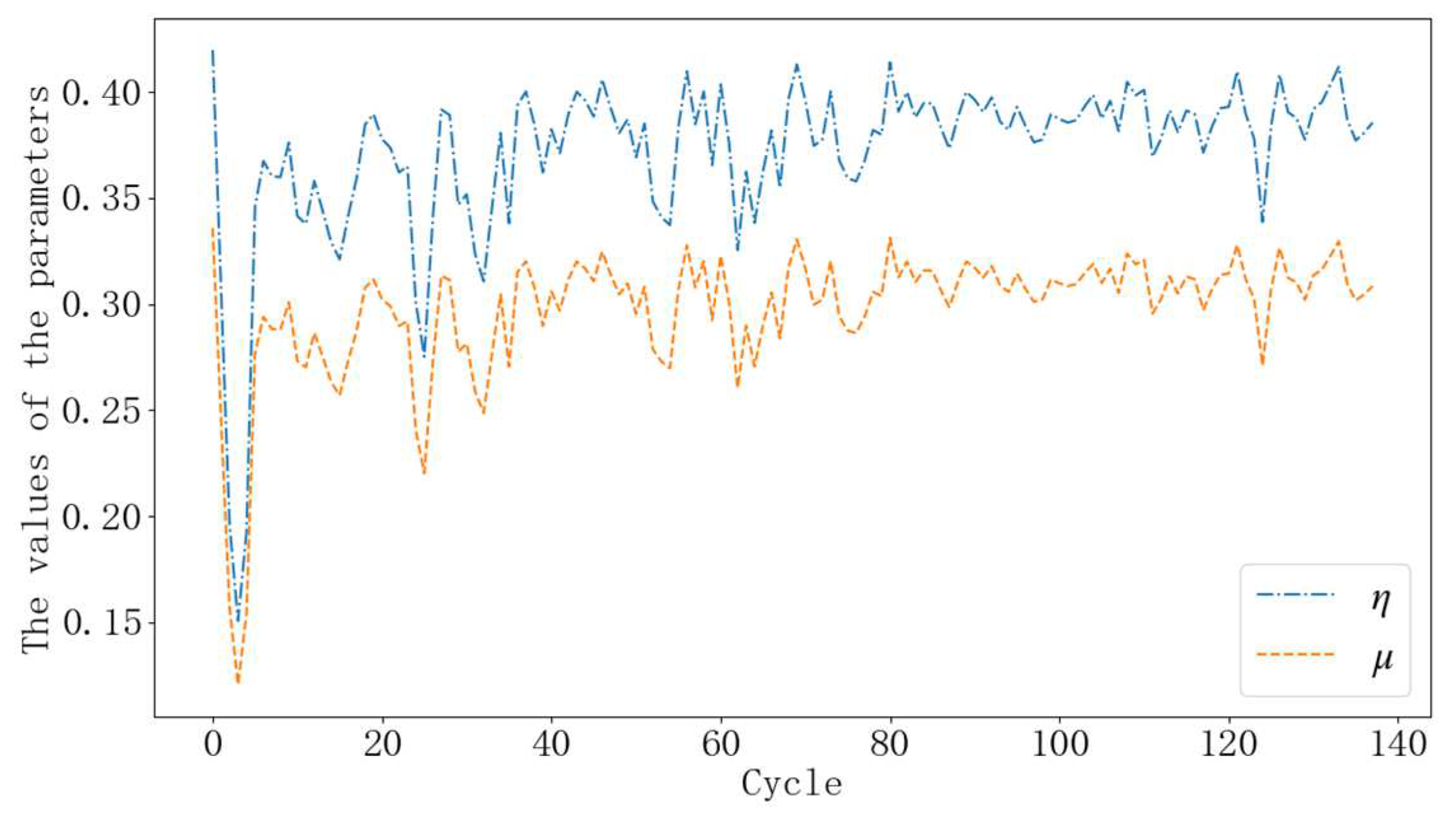
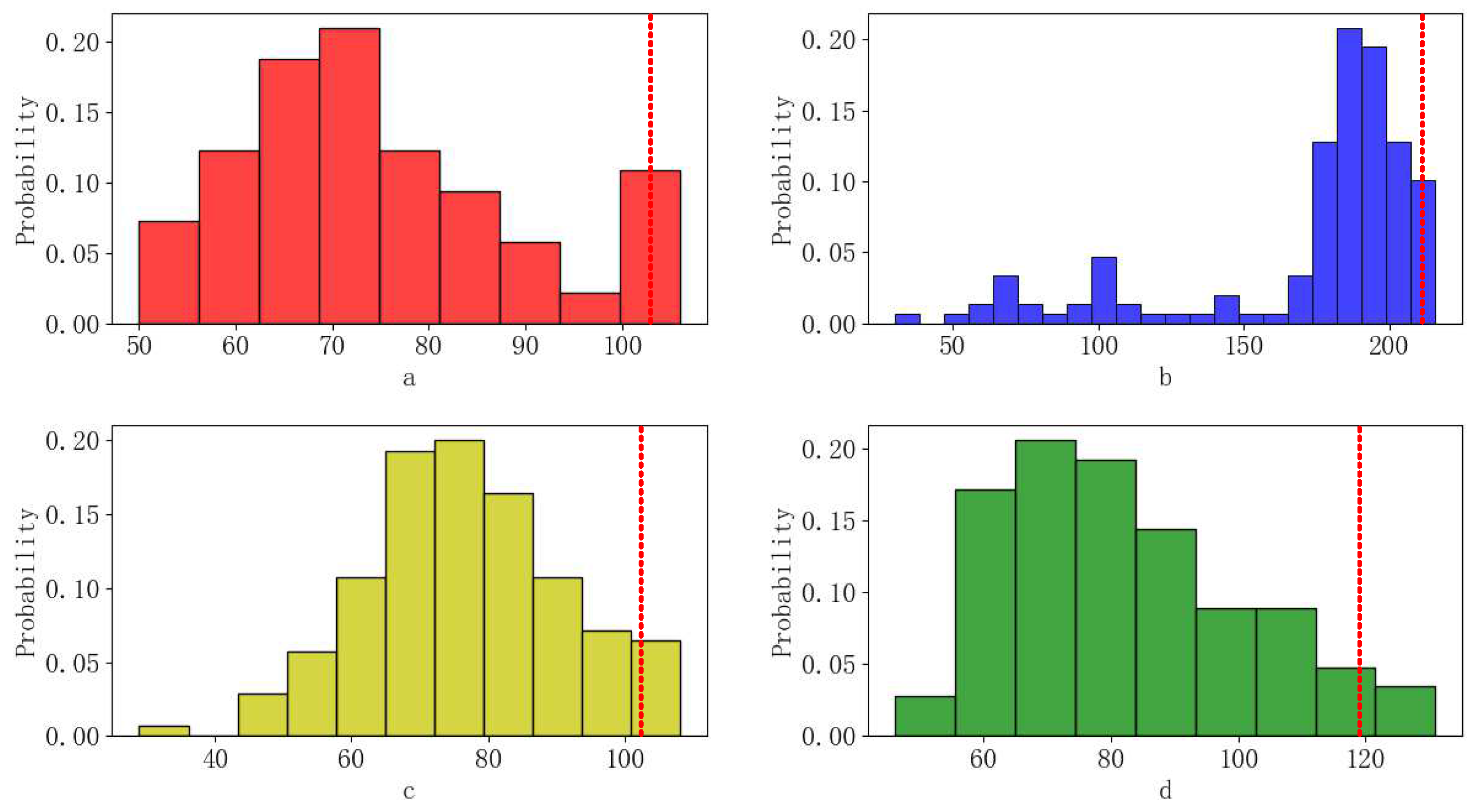
| Symbol | Meaning |
|---|---|
| l | The vector consisting of queuing lengths of each phase |
| The predicted values of l | |
| g | The vector consisting of green times of each phase |
| m | The number of phases |
| d | The number of input layer nodes of the RBFNN |
| p | The number of hidden layer nodes of the RBFNN |
| q | The number of output layer nodes of the RBFNN |
| u | The input vector of RBFNN |
| o | The output vector of RBFNN |
| Ψ | The basis function between input and hidden layer |
| Ψ | The vector consisting of Ψ |
| w | The weight coefficient between hidden and output layer |
| W | The vector consisting of w |
| v | The width matrix of RBFNN |
| σ | The center of RBFNN |
| Pseudo partitioned Jacobian matrix (PPJM) | |
| The vector consisting of corresponding output and input | |
| y | The vector consisting of the differences between l and |
| The desired values of y | |
| α, β | Inertia coefficient, learning rate |
| a, b | Weight coefficient |
| e | The vector consisting of the differences between y and |
| η | Step factor of MFAC |
| μ | Weighting factor of MFAC |
| Cbase | The basic cycle used in the intersection |
| Cmax | The max cycle used in the intersection |
| ls | The parameter used in the variable cycle algorithm |
| Period of Time (s) | Phase | |||
|---|---|---|---|---|
| Phase1 | Phase2 | Phase3 | Phase4 | |
| 0–6600 | 1/9 | 1/10 | 1/10 | 1/12 |
| 6601–13,200 | 1/9 | 1/10 | 1/11 | 1/9 |
| 13,201–19,800 | 1/11 | 1/9 | 1/10 | 1/10 |
| Control Strategies | FC | LC | FFDL-QF | VQF | FFDL-RBFNN | Improvement of FFDL-RBFNN Compared with FC |
|---|---|---|---|---|---|---|
| The average queuing lengths of each cycle (veh/cycle) | 78.81 | \ | 48.58 | 47.97(162 *) | 45.54(163 *) | 42.22% |
| Average time loss of vehicles (s/veh) | 93.41 | 65.39 | 68.01 | 65.53 | 64.26 | 31.21% |
| Period of Time (s) | Phase | |||
|---|---|---|---|---|
| Phase1 | Phase2 | Phase3 | Phase4 | |
| 0–6600 | 1/7.8 | 1/9 | 1/6 | 1/7 |
| 6601–13,200 | 1/7.8 | 1/7 | 1/6.7 | 1/9 |
| 13,201–19,800 | 1/7.5 | 1/7.7 | 1/7 | 1/7 |
| Control Strategies | FC | LC | FFDL-QF | VQF | FFDL-RBFNN | Improvement of FFDL-RBFNN Compared with FC |
|---|---|---|---|---|---|---|
| The average queuing lengths of each cycle (veh/cycle) | 173.63 | \ | 79.80 | 76.77(140 *) | 72.92(141 *) | 58.00% |
| Average time loss of vehicles (s/veh) | 208.12 | 298.20 | 102.65 | 97.39 | 94.11 | 54.78% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Yin, H.; Wang, L.; Ji, H. Data-Driven RBFNN-Enhanced Model-Free Adaptive Traffic Symmetrical Signal Control for a Multi-Phase Intersection with Fast-Changing Traffic Flow. Symmetry 2023, 15, 1235. https://doi.org/10.3390/sym15061235
Ren Y, Yin H, Wang L, Ji H. Data-Driven RBFNN-Enhanced Model-Free Adaptive Traffic Symmetrical Signal Control for a Multi-Phase Intersection with Fast-Changing Traffic Flow. Symmetry. 2023; 15(6):1235. https://doi.org/10.3390/sym15061235
Chicago/Turabian StyleRen, Ye, Hao Yin, Li Wang, and Honghai Ji. 2023. "Data-Driven RBFNN-Enhanced Model-Free Adaptive Traffic Symmetrical Signal Control for a Multi-Phase Intersection with Fast-Changing Traffic Flow" Symmetry 15, no. 6: 1235. https://doi.org/10.3390/sym15061235
APA StyleRen, Y., Yin, H., Wang, L., & Ji, H. (2023). Data-Driven RBFNN-Enhanced Model-Free Adaptive Traffic Symmetrical Signal Control for a Multi-Phase Intersection with Fast-Changing Traffic Flow. Symmetry, 15(6), 1235. https://doi.org/10.3390/sym15061235




