The D4/D8 Model and Holographic QCD
Abstract
1. Introduction
2. The D4/D8 Model
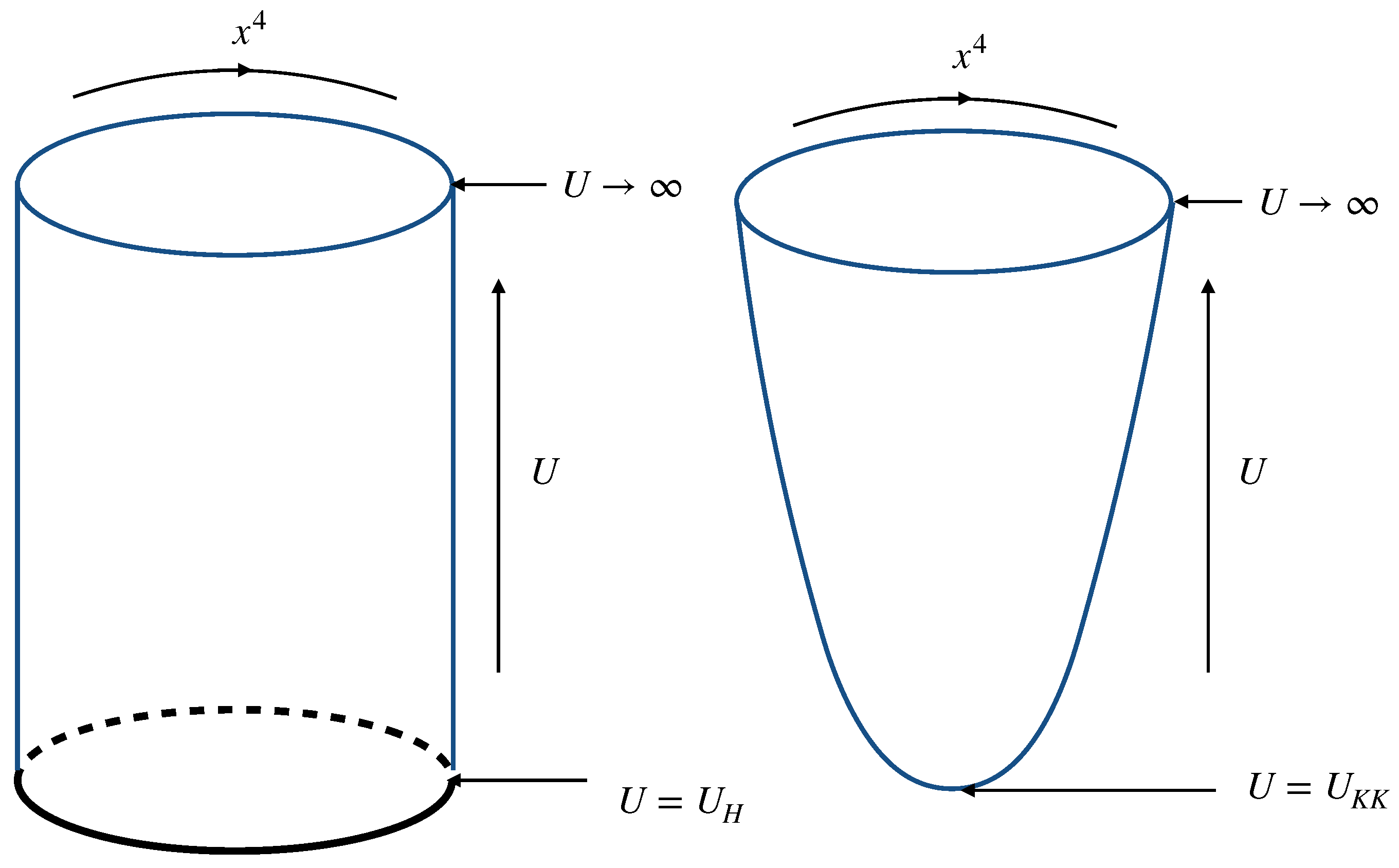
2.1. Eleven-Dimensional Supergravity and D4-Brane Background
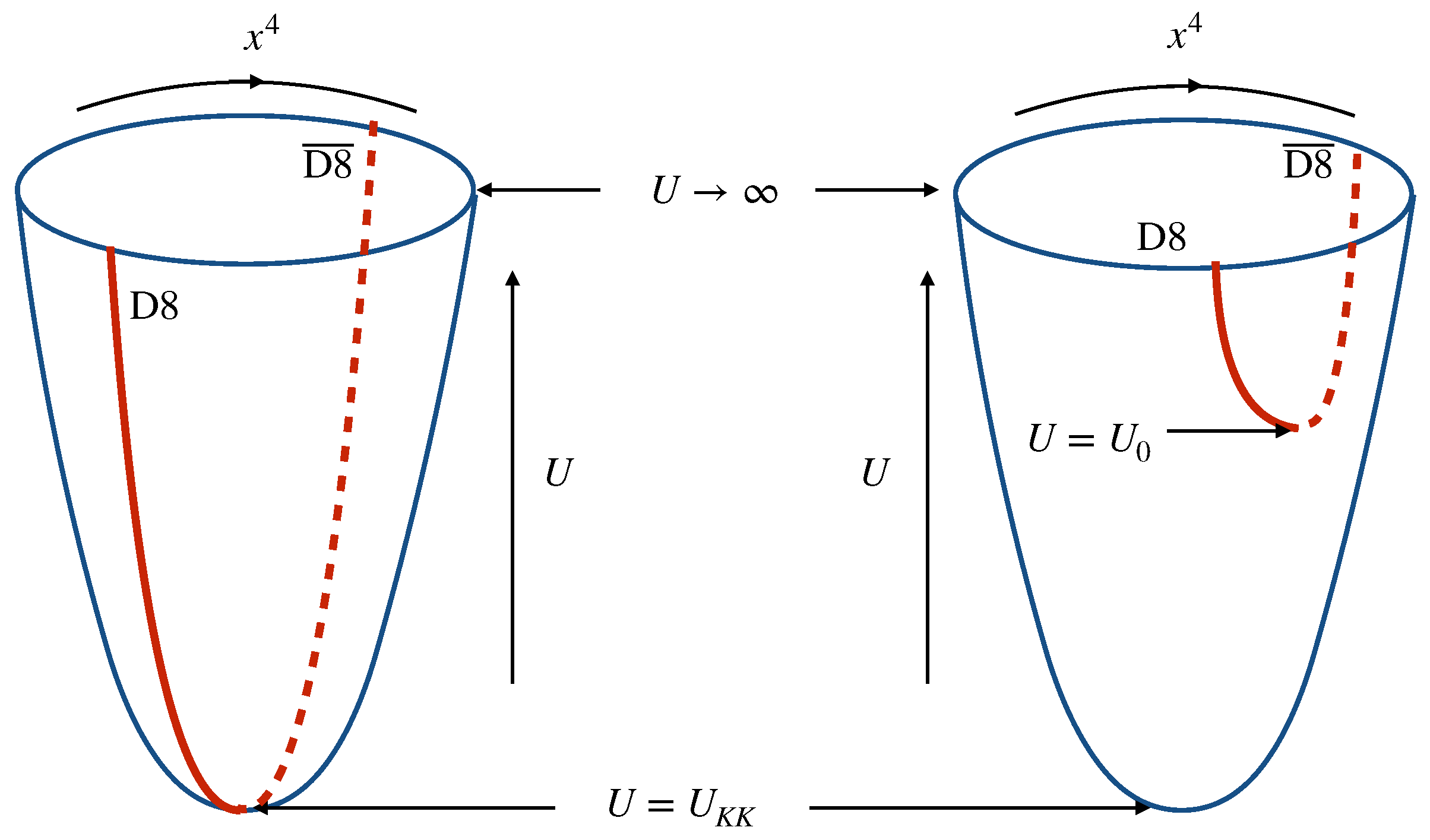
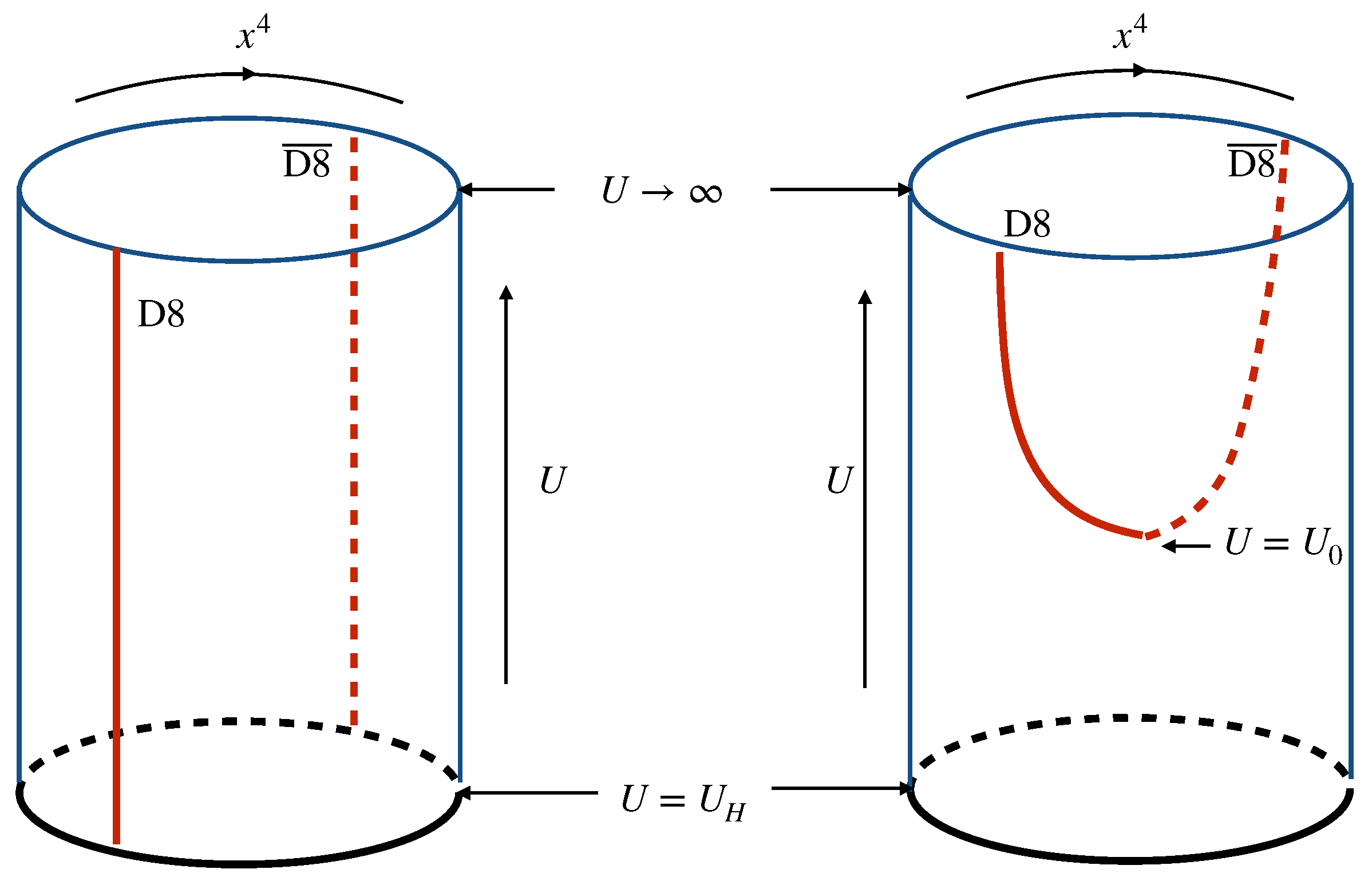
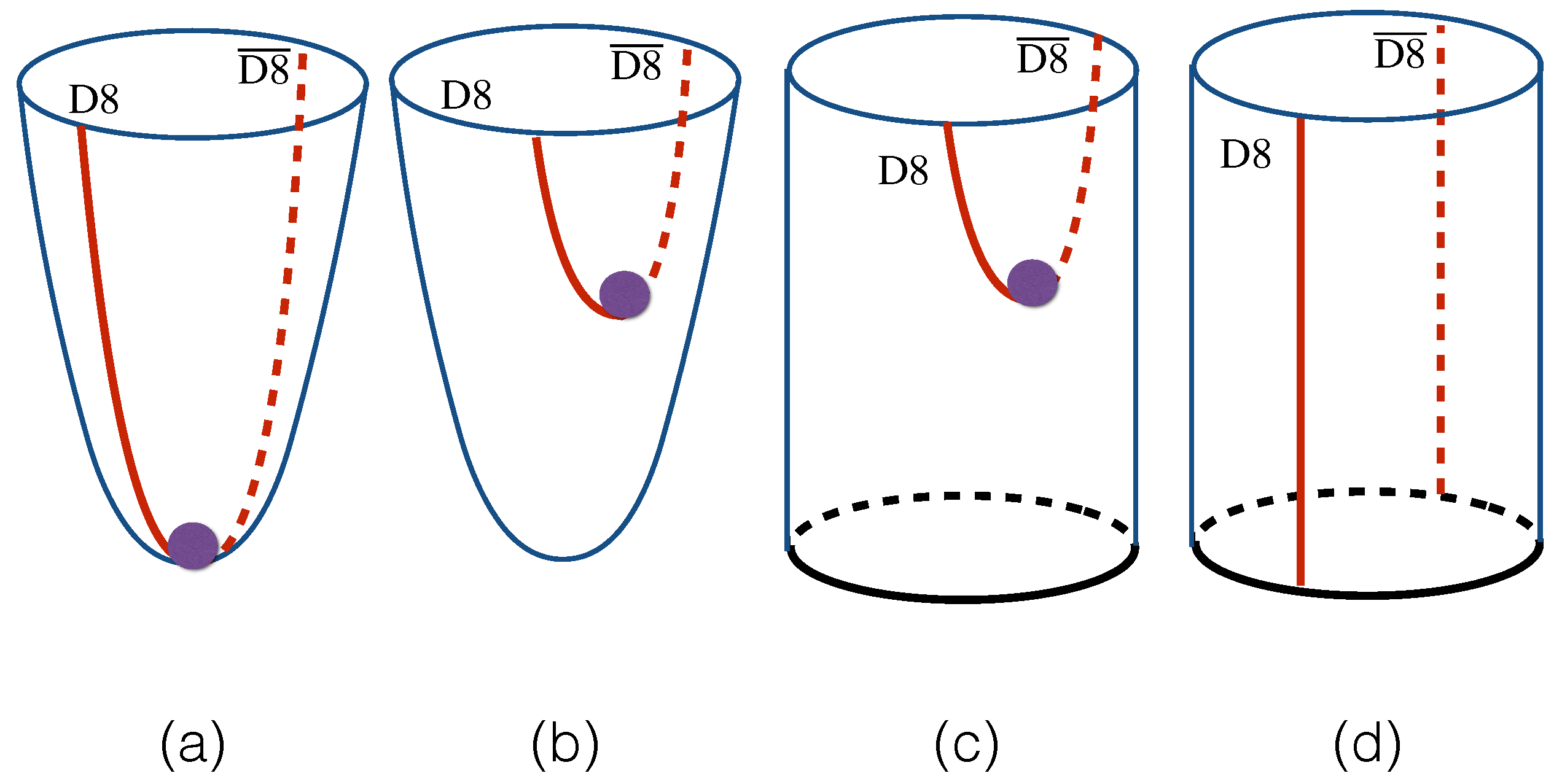
2.2. Embedding the Probe D8/-Branes
2.3. Gluon, Quark and Symmetries
2.4. Mesons on the Flavor Brane
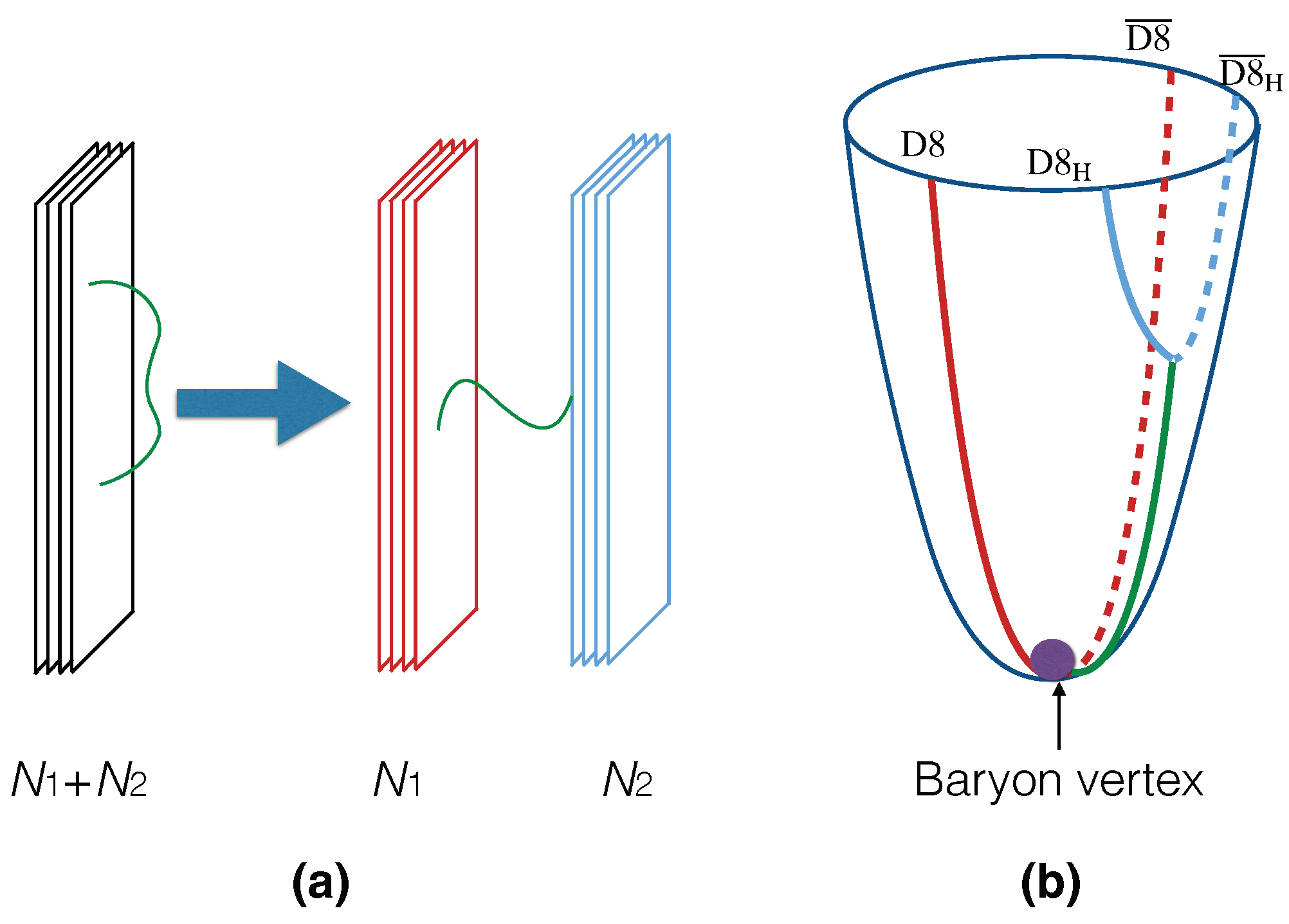
2.5. The Wrapped D4-Brane and Baryon Vertex
2.6. Gravitational Wave as Glueball
3. Developments and Holographic Approaches to QCD
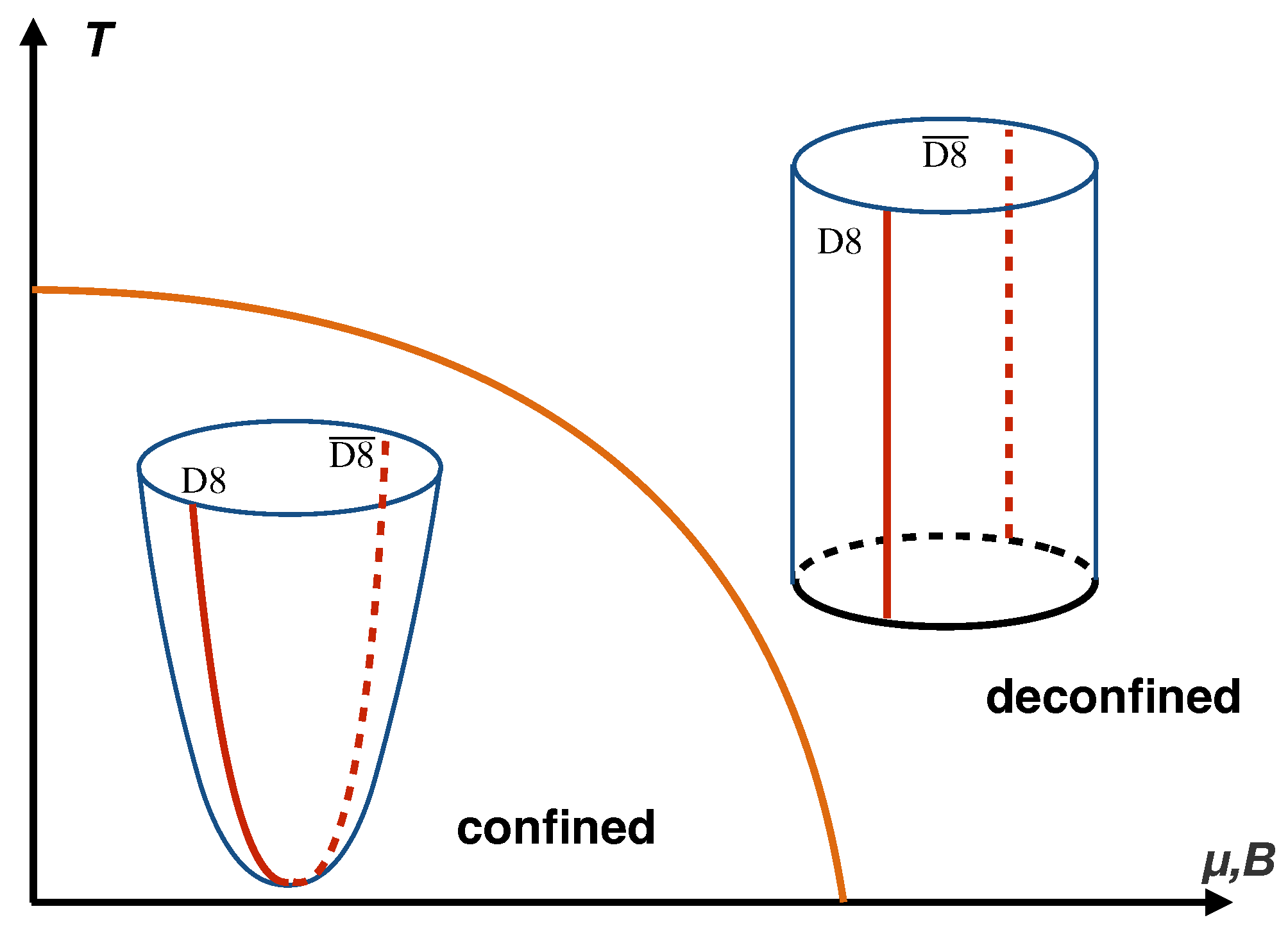
3.1. QCD Deconfinement Transition
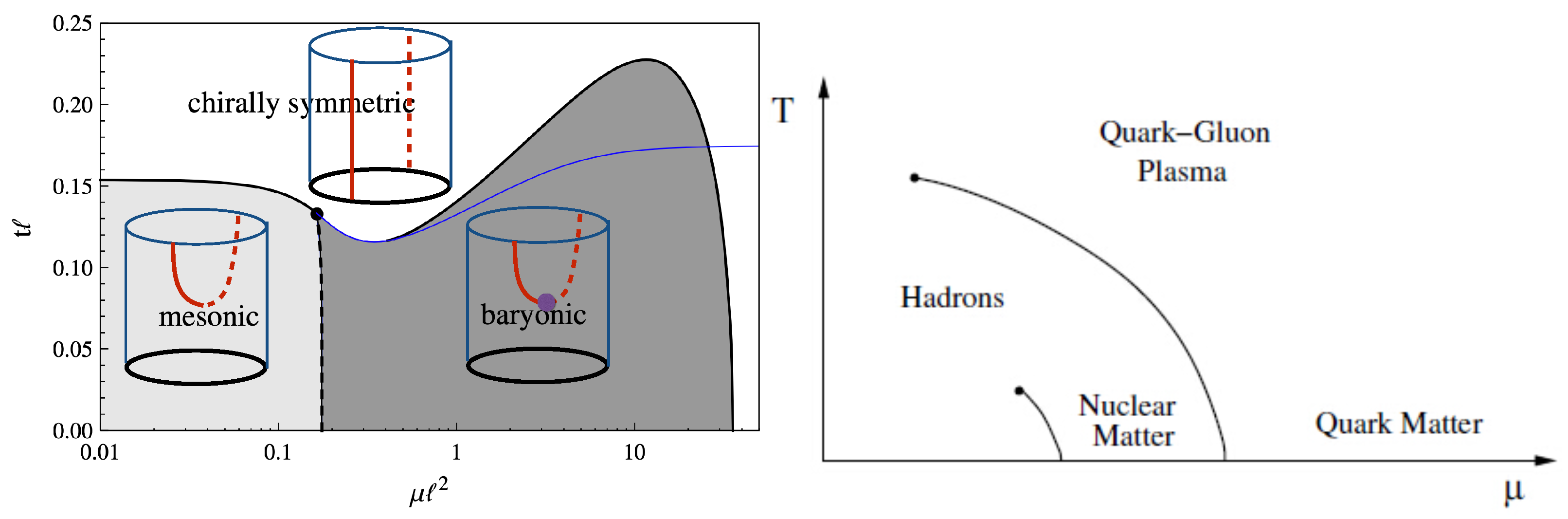
3.2. Phase Diagram with Chiral Transition
3.3. Higgs Mechanism and Heavy–Light Meson Field
3.4. Interactions of Hadrons and Glueballs
3.5. Theta Dependence in QCD
4. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Type II Supergravity Solution
Appendix B. Dimensional Reduction for Spinors
Appendix C. Supersymmetric Meson on the Flavor Brane
References
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Aharony, O.; Gubser, S.S.; Maldacena, J.M.; Ooguri, H. Large N field theories, string theory and gravity. Phys. Rept. 2000, 323, 183. [Google Scholar] [CrossRef]
- Maldacena, J. Wilson loops in large N field theories. Phys. Rev. Lett. 1998, 80, 4859–4862. [Google Scholar] [CrossRef]
- Rey, S.; Theisen, S.; Yee, J. Wilson-Polyakov loop at finite temperature in large N gauge theory and anti-de Sitter supergravity. Nucl. Phys. B 1998, 527, 171–186. [Google Scholar] [CrossRef]
- Brandhuber, A.; Itzhaki, N.; Sonnenschein, J.; Yankielowicz, S. Wilson loops in the large N limit at finite temperature. Phys. Lett. B 1998, 434, 36–40. [Google Scholar] [CrossRef]
- Policastro, G.; Son, D.T.; Starinets, A.O. From AdS/CFT correspondence to hydrodynamics. J. High Energy Phys. 2002, 9, 43. [Google Scholar] [CrossRef]
- Son, D.T.; Starinets, A.O. Minkowski space correlators in AdS/CFT correspondence: Recipe and applications. J. High Energy Phys. 2002, 9, 42. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef]
- Iqbal, N.; Liu, H. Real-time response in AdS/CFT with application to spinors. Fortsch. Phys. 2009, 57, 367–384. [Google Scholar] [CrossRef]
- Liu, H.; McGreevy, J.; Vegh, D. Non-Fermi liquids from holography. Phys. Rev. D 2011, 83, 065029. [Google Scholar] [CrossRef]
- Semenoff, G.W.; Zarembo, K. Holographic Schwinger Effect. Phys. Rev. Lett. 2011, 107, 171601. [Google Scholar] [CrossRef] [PubMed]
- Ryu, S.; Takayanagi, T. Holographic derivation of entanglement entropy from AdS/CFT. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef] [PubMed]
- Klebanov, I.R.; Kutasov, D.; Murugan, A. Entanglement as a probe of confinement. Nucl. Phys. B 2008, 796, 274–293. [Google Scholar] [CrossRef]
- Harlow, D. Jerusalem Lectures on Black Holes and Quantum Information. Rev. Mod. Phys. 2016, 88, 015002. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Erlich, J.; Katz, E.; Son, D.T.; Stephanov, M.A. QCD and a holographic model of hadrons. Phys. Rev. Lett. 2005, 95, 261602. [Google Scholar] [CrossRef]
- Karch, A.; Katz, E.; Son, D.T.; Stephanov, M.A. Linear Confinement and AdS/QCD. arXiv 2006, arXiv:hep-ph/0602229. [Google Scholar] [CrossRef]
- Rold, L.; Pomarol, A. Chiral symmetry breaking from five dimensional spaces. Nucl. Phys. B 2005, 721, 79–97. [Google Scholar] [CrossRef]
- Casalderrey-Solana, J.; Liu, H.; Mateos, D.; Rajagopal, K.; Wiedemann, U.A. Gauge/Gravity Duality, Hot QCD and Heavy Ion Collisions; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Kruczenski, M.; Mateos, D.; Myers, R.C.; Winters, D.J. Towards a holographic dual of large N(c) QCD. J. High Energy Phys. 2004, 5, 41. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys. 1998, 2, 505–532. [Google Scholar] [CrossRef]
- Sakai, T.; Sugimoto, S. Low energy hadron physics in holographic QCD. Prog. Theor. Phys. 2005, 113, 843–882. [Google Scholar] [CrossRef]
- Sakai, T.; Sugimoto, S. More on a holographic dual of QCD. Prog. Theor. Phys. 2005, 114, 1083–1118. [Google Scholar] [CrossRef]
- Witten, E. Baryons and branes in anti-de Sitter space. J. High Energy Phys. 1998, 7, 6. [Google Scholar] [CrossRef]
- Hata, H.; Sakai, T.; Sugimoto, S.; Yamato, S. Baryons from instantons in holographic QCD. Prog. Theor. Phys. 2007, 117, 1157. [Google Scholar] [CrossRef]
- Hata, H.; Murata, M. Baryons and the Chern-Simons term in holographic QCD with three flavors. Prog. Theor. Phys. 2008, 119, 461–490. [Google Scholar] [CrossRef]
- Constable, N.R.; Myers, R.C. Spin-two glueballs, positive energy theorems and the AdS/CFT correspondence. J. High Energy Phys. 1999, 9910, 37. [Google Scholar] [CrossRef]
- Brower, R.C.; Mathur, S.D.; Tan, C.-I. Glueball spectrum for QCD from AdS supergravity duality. Nucl. Phys. B 2000, 587, 249–276. [Google Scholar] [CrossRef]
- Hashimoto, K.; Tan, C.-I.; Terashima, S. Glueball Decay in Holographic QCD. Phys. Rev. 2008, D77, 086001. [Google Scholar] [CrossRef]
- Brünner, F.; Parganlija, D. Rebhan Glueball Decay Rates in the Witten-Sakai-Sugimoto Model. Phys. Rev. 2015, D91, 106002, Erratum in Phys. Rev. 2016, D93, 109903. [Google Scholar]
- Aharony, O.; Sonnenschein, J.; Yankielowicz, S. A Holographic model of deconfinement and chiral symmetry restoration. Ann. Phys. 2007, 322, 1420–1443. [Google Scholar] [CrossRef]
- Bigazzi, F.; Cotrone, A.L. Holographic QCD with Dynamical Flavors. J. High Energy Phys. 2015, 1501, 104. [Google Scholar] [CrossRef]
- Li, S.; Jia, T. Dynamically flavored description of holographic QCD in the presence of a magnetic field. Phys. Rev. D 2017, 96, 066032. [Google Scholar] [CrossRef]
- Bergman, O.; Lifschytz, G.; Lippert, M. Holographic Nuclear Physics. J. High Energy Phys. 2007, 11, 56. [Google Scholar] [CrossRef]
- Li, S.; Schmitt, A.; Wang, Q. From holography towards real-world nuclear matter. Phys. Rev. D 2015, 92, 026006. [Google Scholar] [CrossRef]
- Liu, Y.; Zahed, I. Heavy-light mesons in chiral AdS/QCD. Phys. Lett. B 2017, 769, 314–321. [Google Scholar] [CrossRef]
- Liu, Y.; Zahed, I. Holographic Heavy-Light Chiral Effective Action. Phys. Rev. D 2017, 95, 056022. [Google Scholar] [CrossRef]
- Kovensky, N.; Schmitt, A. Heavy Holographic QCD. J. High Energy Phys. 2020, 2, 96. [Google Scholar] [CrossRef]
- Wu, C.; Xiao, Z.; Zhou, D. Sakai-Sugimoto model in D0–D4 background. Phys. Rev. D 2013, 88, 026016. [Google Scholar] [CrossRef]
- Seki, S.; Sin, S. A New Model of Holographic QCD and Chiral Condensate in Dense Matter. J. High Energy Phys. 2013, 10, 223. [Google Scholar] [CrossRef]
- Bartolini, L.; Bigazzi, F.; Bolognesi, S.; Cotrone, A.L.; Manenti, A. Theta dependence in Holographic QCD. J. High Energy Phys. 2017, 2, 29. [Google Scholar] [CrossRef]
- Bigazzi, F.; Cotrone, A.L.; Sisca, R. Notes on Theta Dependence in Holographic Yang-Mills. J. High Energy Phys. 2015, 8, 90. [Google Scholar] [CrossRef]
- Bigazzi, F.; Caddeo, A.; Cotrone, A.L.; Vecchia, P.D.; Marzolla, A. The Holographic QCD Axion. J. High Energy Phys. 2019, 12, 56. [Google Scholar] [CrossRef]
- Hashimoto, K.; Sakai, T.; Sugimoto, S. Nuclear Force from String Theory. Prog. Theor. Phys. 2009, 122, 427–476. [Google Scholar] [CrossRef]
- Hashimoto, K.; Iizuka, N.; Yi, P. A Matrix Model for Baryons and Nuclear Forces. J. High Energy Phys. 2010, 10, 3. [Google Scholar] [CrossRef]
- Hashimoto, K.; Iizuka, N. Three-Body Nuclear Forces from a Matrix Model. J. High Energy Phys. 2010, 11, 58. [Google Scholar] [CrossRef]
- Hashimoto, K.; Matsuo, Y. Nuclear binding energy in holographic QCD. Phys. Rev. D 2021, 104, 026006. [Google Scholar] [CrossRef]
- Li, S.; Jia, T. Matrix model and Holographic Baryons in the D0–D4 background. Phys. Rev. D 2015, 92, 046007. [Google Scholar] [CrossRef]
- Li, S.; Jia, T. Three-body force for baryons from the D0–D4/D8 brane matrix model. Phys. Rev. D 2016, 93, 065051. [Google Scholar] [CrossRef]
- Kaplunovsky, V.; Sonnenschein, J. Searching for an Attractive Force in Holographic Nuclear Physics. J. High Energy Phys. 2011, 5, 58. [Google Scholar] [CrossRef]
- Becker, K.; Becker, M.; Schwarz, J.H. String Theory and M-Theory, A Modern Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Witten, E. String Theory Dynamics in Various Dimensions. Nucl. Phys. B 1995, 443, 197. [Google Scholar] [CrossRef]
- Sugimoto, S.; Takahashi, K. QED and string theory. J. High Energy Phys. 2004, 4, 51. [Google Scholar] [CrossRef]
- Antonyan, E.; Harvey, J.A.; Jensen, S.; Kutasov, D. NJL and QCD from String Theory. arXiv 2006, arXiv:hep-th/0604017. [Google Scholar]
- Freedman, D.Z.; Proeyen, A.V. Supergravity; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Mandal, G.; Morita, T. Gregory-Laflamme as the confinement/deconfinement transition in holographic QCD. J. High Energy Phys. 2011, 9, 73. [Google Scholar] [CrossRef]
- Mandal, G.; Morita, T. What is the gravity dual of the confinement/deconfinement transition in holographic QCD? J. Phys. Conf. Ser. 2012, 343, 012079. [Google Scholar]
- Johnson, C.V. D-Branes; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Zahed, I.; Brown, G.E. The Skyrme Model. Phys. Rept. 1986, 142, 1–102. [Google Scholar] [CrossRef]
- Witten, E. Global Aspects of Current Algebra. Nucl. Phys. B 1983, 223, 422. [Google Scholar] [CrossRef]
- Kaymakcalan, O.; Rajeev, S.; Schechter, J. Nonabelian Anomaly and Vector Meson Decays. Phys. Rev. D 1984, 30, 594. [Google Scholar] [CrossRef]
- Rey, S.-J.; Yee, J.-T. Macroscopic strings as heavy quarks in large N gauge theory and anti-de Sitter supergravity. Eur. Phys. J. C 2001, 22, 379–394. [Google Scholar] [CrossRef]
- Gross, D.J.; Ooguri, H. Aspects of large N gauge theory dynamics as seen by string theory. Phys. Rev. D 1998, 58, 106002. [Google Scholar] [CrossRef]
- Tong, D. TASI lectures on solitons: Instantons, monopoles, vortices and kinks. arXiv 2005, arXiv:hep-th/0509216. [Google Scholar]
- Witten, E. Current Algebra, Baryons, and Quark Confinement. Nucl. Phys. B 1983, 223, 433–444. [Google Scholar] [CrossRef]
- Seo, Y.; Sin, S.-J. Baryon Mass in medium with Holographic QCD. J. High Energy Phys. 2008, 4, 10. [Google Scholar] [CrossRef]
- Adkins, G.; Nappi, C.; Witten, E. Static Properties of Nucleons in the Skyrme Model. Nucl. Phys. B 1983, 228, 552. [Google Scholar] [CrossRef]
- Lau, P.; Sugimoto, S. Chern-Simons 5-form and Holographic Baryons. Phys. Rev. D 2017, 95, 126007. [Google Scholar] [CrossRef]
- Mateos, D.; Myers, R.C.; Thomson, R.M. Thermodynamics of the brane. J. High Energy Phys. 2007, 705, 67. [Google Scholar] [CrossRef]
- Bayona, A.B. Holographic deconfinement transition in the presence of a magnetic field. J. High Energy Phys. 2013, 1311, 168. [Google Scholar] [CrossRef]
- Bigazzi, F.; Cotrone, A.L.; Mas, J.; Mayerson, D.; Tarrio, J. D3–D7 Quark-Gluon Plasmas at Finite Baryon Density. J. High Energy Phys. 2011, 1104, 60. [Google Scholar] [CrossRef]
- Cotrone, A.L.; Tarrio, J. Consistent reduction of charged D3–D7 systems. J. High Energy Phys. 2012, 164, 1210. [Google Scholar] [CrossRef]
- Bigazzi, F.; Cotrone, A.L.; Tarrio, J. Charged D3–D7 plasmas: Novel solutions, extremality and stability issues. J. High Energy Phys. 2013, 1307, 74. [Google Scholar] [CrossRef]
- Benincasa, P. A note on Holographic Renormalization of Probe D-Branes. arXiv 2009, arXiv:0903.4356. [Google Scholar]
- Papadimitriou, I. Holographic renormalization as a canonical transformation. J. High Energy Phys. 2010, 1011, 14. [Google Scholar] [CrossRef]
- Papadimitriou, I. Holographic Renormalization of general dilaton-axion gravity. J. High Energy Phys. 2011, 1108, 119. [Google Scholar] [CrossRef]
- Giataganas, D.; Irges, N. Flavor Corrections in the Static Potential in Holographic QCD. Phys. Rev. D 2012, 85, 046001. [Google Scholar] [CrossRef]
- Deuzeman, A.; Lombardo, M.P.; Miura, K.; da Silva, T.N.; Pallante, E. Phases of many flavors QCD: Lattice results. arXiv 2012, arXiv:1304.3245. [Google Scholar]
- Braun, J.; Gies, H. Scaling laws near the conformal window of many-flavor QCD. J. High Energy Phys. 2010, 1005, 60. [Google Scholar] [CrossRef]
- Liao, J.; Shuryak, E. Effect of Light Fermions on the Confinement Transition in QCD-like Theories. Phys. Rev. Lett. 2012, 109, 152001. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Krieg, S.; Schafer, A.; Szabo, K.K. The QCD phase diagram for external magnetic fields. J. High Energy Phys. 2012, 2, 44. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrődi, G.; Katz, S.D.; Schäfer, A. The QCD equation of state in background magnetic fields. J. High Energy Phys. 2014, 8, 177. [Google Scholar] [CrossRef]
- Fukushima, K.; Hidaka, Y. Magnetic Catalysis Versus Magnetic Inhibition. Phys. Rev. Lett. 2013, 110, 031601. [Google Scholar] [CrossRef] [PubMed]
- Fraga, E.S.; Palhares, L.F. Deconfinement in the presence of a strong magnetic background: An exercise within the MIT bag model. Phys. Rev. D 2012, 86, 016008. [Google Scholar] [CrossRef]
- Sachan, S.; Siwach, S. Thermodynamics of soft wall AdS/QCD at finite chemical potential. Mod. Phys. Lett. A 2012, 27, 1250163. [Google Scholar] [CrossRef]
- Sachan, S. Study of confinement/deconfinement transition in AdS/QCD with generalized warp factors. Adv. High Energy Phys. 2014, 2014, 543526. [Google Scholar] [CrossRef]
- Sevrin, A.; Troost, J.; Troost, W. The non-Abelian Born-Infeld action at order F6. Nucl. Phys. B 2001, 603, 389–412. [Google Scholar] [CrossRef]
- Rozali, M.; Shieh, H.-H.; Raamsdonk, M.V.; Wu, J. Cold Nuclear Matter in Holographic QCD. J. High Energy Phys. 2008, 1, 53. [Google Scholar] [CrossRef]
- Ghoroku, K.; Kubo, K.; Tachibana, M.; Taminato, T.; Toyoda, F. Holographic cold nuclear matter as dilute instanton gas. Phys. Rev. D 2013, 87, 066006. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Pawlowski, J.M.; Wambach, J. The Phase Structure of the Polyakov–Quark–Meson Model. Phys. Rev. D 2007, 76, 074023. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wagner, M.; Wambach, J. Thermodynamics of (2 + 1)-flavor QCD: Confronting Models with Lattice Studies. Phys. Rev. D 2010, 81, 074013. [Google Scholar] [CrossRef]
- Nambu, Y.; Lasinio, G.J. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Lasinio, G.J. Dynamical model of elementary particles based on an analogy with superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. B 2004, 591, 277–284. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Ruester, S.B.; Werth, V.; Buballa, M.; Shovkovy, I.A.; Rischke, D.H. The Phase diagram of neutral quark matter: Self-consistent treatment of quark masses. Phys. Rev. D 2005, 72, 034004. [Google Scholar] [CrossRef]
- Walecka, J.D. A Theory of highly condensed matter. Ann. Phys. 1974, 83, 491–529. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. Relativistic Calculation of Nuclear Matter and the Nuclear Surface. Nucl. Phys. A 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Gallas, S.; Giacosa, F.; Pagliara, G. Nuclear matter within a dilatation-invariant parity doublet model: The role of the tetraquark at nonzero density. Nucl. Phys. A 2011, 872, 13–24. [Google Scholar] [CrossRef]
- Floerchinger, S.; Wetterich, C. Chemical freeze-out in heavy ion collisions at large baryon densities. Nucl. Phys. A 2012, 891, 11–24. [Google Scholar] [CrossRef]
- Myers, R.C. Dielectric-Branes. J. High Energy Phys. 1999, 22, 9912. [Google Scholar] [CrossRef]
- Liu, Y.; Nowak, M.A. Hyperons and θ s + in holographic QCD. Phys. Rev. D 2022, 105, 114021. [Google Scholar] [CrossRef]
- Liu, Y.; Zahed, I. Heavy Baryons and their Exotics from Instantons in Holographic QCD. Phys. Rev. D 2017, 95, 116012. [Google Scholar] [CrossRef]
- Liu, Y.; Zahed, I. Heavy and Strange Holographic Baryons. Phys. Rev. D 2017, 96, 056027. [Google Scholar] [CrossRef]
- Li, S. The interaction of glueball and heavy-light flavoured meson in holographic QCD. Eur. Phys. J. C 2020, 80, 881. [Google Scholar] [CrossRef]
- BESIII Collaboration. Measurement of yCP in D0−D0 oscillation using quantum correlations in e−e+→D0D0 at √s = 3.773 GeV. Phys. Lett. B 2015, 774, 339–346. [Google Scholar]
- CDF Collaboration. Observation of Bs-Bsbar Oscillations. Phys. Rev. Lett. 2006, 97, 242003. [Google Scholar] [CrossRef] [PubMed]
- Li, S.-W. Glueball–baryon interactions in holographic QCD. Phys. Lett. B 2017, 773, 142–149. [Google Scholar] [CrossRef]
- Li, S.-W. Holographic description of heavy-flavored baryonic matter decay involving glueball. Phys. Rev. D 2019, 99, 046013. [Google Scholar] [CrossRef]
- Vicari, E.; Panagopoulos, H. Theta dependence of SU(N) gauge theories in the presence of a topological term. Phys. Rept. 2009, 470, 93–150. [Google Scholar] [CrossRef]
- Debbio, L.D.; Manca, G.M.; Panagopoulos, H.; Skouroupathis, A.; Vicari, E. Theta-dependence of the spectrum of SU(N) gauge theories. J. High Energy Phys. 2006, 6, 5. [Google Scholar] [CrossRef]
- D’Elia, M.; Negro, F. Phase diagram of Yang-Mills theories in the presence of a θ term. Phys. Rev. D 2013, 88, 034503. [Google Scholar] [CrossRef]
- D’Elia, M.; Negro, F. θ dependence of the deconfinement temperature in Yang-Mills theories. Phys. Rev. Lett. 2012, 109, 072001. [Google Scholar] [CrossRef] [PubMed]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. The Chiral Magnetic Effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Kharzeev, D.E. The Chiral Magnetic Effect and Anomaly-Induced Transport. Prog. Part. Nucl. Phys. 2014, 75, 133–151. [Google Scholar] [CrossRef]
- Witten, E. Theta dependence in the large N limit of four-dimensional gauge theories. Phys. Rev. Lett. 1998, 81, 2862–2865. [Google Scholar] [CrossRef]
- Cai, W.; Wu, C.; Xiao, Z. Baryons in the Sakai-Sugimoto model in the D0–D4 background. Phys. Rev. D 2014, 90, 106001. [Google Scholar] [CrossRef]
- Cai, W.; Li, K.; Li, S. Electromagnetic instability and Schwinger effect in the Witten–Sakai–Sugimoto model with D0–D4 background. Eur. Phys. J. C 2019, 79, 904. [Google Scholar] [CrossRef]
- Hashimoto, K.; Oka, T.; Sonoda, A. Electromagnetic instability in holographic QCD. J. High Energy Phys. 2015, 6, 1. [Google Scholar] [CrossRef]
- Li, S.; Luo, S.; Li, H. Holographic Schwinger effect and electric instability with anisotropy. J. High Energy Phys. 2022, 8, 206. [Google Scholar] [CrossRef]
- Li, S. Holographic Schwinger effect in the confining background with D-instanton. Eur. Phys. J. C 2021, 81, 797. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Huang, M. Fluid/gravity correspondence: A nonconformal realization in compactified D4 branes. Phys. Rev. D 2016, 93, 066005. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Huang, M. Fluid/gravity correspondence: Second order transport coefficients in compactified D4-branes. J. High Energy Phys. 2017, 1, 118. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Huang, M. Chiral vortical effect from the compactified D4-branes with smeared D0-brane charge. J. High Energy Phys. 2017, 3, 82. [Google Scholar] [CrossRef]
- Cai, W.; Li, S. Sound waves in the compactified D0–D4 brane system. Phys. Rev. D 2016, 94, 066012. [Google Scholar] [CrossRef]
- Benincasa, P.; Buchel, A. Hydrodynamics of Sakai-Sugimoto model in the quenched approximation. Phys. Lett. B 2006, 640, 108–115. [Google Scholar] [CrossRef]
- Imaanpur, A. Correction to baryon spectrum in holographic QCD. Phys. Lett. B 2022, 832, 137233. [Google Scholar] [CrossRef]
- Li, S.; Li, H.; Luo, S. Corrections to the instanton configuration as baryon in holographic QCD. Phys. Rev. D 2022, 106, 126027. [Google Scholar] [CrossRef]
- Li, S.; Luo, S.; Hu, Y. Holographic QCD3 and Chern-Simons theory from anisotropic supergravity. J. High Energy Phys. 2022, 6, 40. [Google Scholar] [CrossRef]
- Li, S.; Luo, S.; Tan, M. Three-dimensional Yang-Mills-Chern-Simons theory from a D3-brane background with D-instantons. Phys. Rev. D 2021, 104, 066008. [Google Scholar] [CrossRef]
- Schmitt, A.; Shternin, P. Reaction rates and transport in neutron stars. Astrophys. Space Sci. Libr. 2018, 457, 455–574. [Google Scholar]
- Kovensky, N.; Poole, A.; Schmitt, A. Building a realistic neutron star from holography. Phys. Rev. D 2022, 105, 034022. [Google Scholar] [CrossRef]
- Heise, R.; Svendsen, H. A Note on fermions in holographic QCD. J. High Energy Phys. 2007, 8, 65. [Google Scholar] [CrossRef]
- Marolf, D.; Martucci, L.; Silva, P.J. Fermions, T-duality and effective actions for D-branes in bosonic backgrounds. J. High Energy Phys. 2003, 4, 51. [Google Scholar] [CrossRef]
- Marolf, D.; Martucci, L.; Silva, P.J. Actions and fermionic symmetries for D-branes in bosonic backgrounds. J. High Energy Phys. 2003, 7, 19. [Google Scholar] [CrossRef]
- Martucci, L.; Rosseel, J.; Van den Bleeken, D.; Van Proeyen, A. Dirac actions for D-branes on backgrounds with fluxes. Class. Quant. Grav. 2005, 22, 2745–2764. [Google Scholar] [CrossRef]
- Camporesi, R.; Higuchi, A. On the eigenfunctions of the Dirac operator on spheres and real hyperbolic spaces. J. Geom. Phys. 1996, 20, 1–18. [Google Scholar] [CrossRef]
- Nakas, T.; Rigatos, K.S. Fermions and baryons as open-string states from brane junctions. J. High Energy Phys. 2020, 12, 157. [Google Scholar] [CrossRef]

| 0 | 1 | 2 | 3 | 4 | 5(U) | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| D4-branes | - | - | - | - | - | |||||
| -branes | - | - | - | - | - | - | - | - | - |
| Fields | ||||
|---|---|---|---|---|
| adj. | 4 | 1 | (1, 1) | |
| fund. | 2+ | 1 | (fund., 1) | |
| fund. | 2− | 1 | (1, fund.) | |
| 1 | 1 | 1 | (1, 1) | |
| 1 | 1 | 5 | (1, 1) |
| Mode | ||||||
|---|---|---|---|---|---|---|
| 7.30835 | 22.0966 | 31.9853 | 53.3758 | 83.0449 | 115.002 | |
| 46.9855 | 55.5833 | 72.4793 | 109.446 | 143.581 | 189.632 | |
| 94.4816 | 102.452 | 126.144 | 177.231 | 217.397 | 227.283 | |
| 154.963 | 162.699 | 193.133 | 257.959 | 304.531 | 378.099 | |
| 228.709 | 236.328 | 273.482 | 351.895 | 405.011 | 492.171 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.-W.; Zhang, X.-T. The D4/D8 Model and Holographic QCD. Symmetry 2023, 15, 1213. https://doi.org/10.3390/sym15061213
Li S-W, Zhang X-T. The D4/D8 Model and Holographic QCD. Symmetry. 2023; 15(6):1213. https://doi.org/10.3390/sym15061213
Chicago/Turabian StyleLi, Si-Wen, and Xiao-Tong Zhang. 2023. "The D4/D8 Model and Holographic QCD" Symmetry 15, no. 6: 1213. https://doi.org/10.3390/sym15061213
APA StyleLi, S.-W., & Zhang, X.-T. (2023). The D4/D8 Model and Holographic QCD. Symmetry, 15(6), 1213. https://doi.org/10.3390/sym15061213





