Abstract
A review of several classical, algebraic models in nuclear structure physics, which use symmetries as an important tool, are presented. After a conceptual introduction to group theory, a selection of models is chosen to illustrate the methods and the power of the usage of symmetries. This enables us to describe very involved systems in a greatly simplified manner. Some problems are also discussed, when ignoring basic principles of nature, such as the Pauli exclusion principle. We also show that occasionally one can rescue these omissions. In a couple of representative models, applications of symmetries are explicitly applied in order to illustrate how extremely complicated systems can be treated. This contribution is meant as a review of the use of algebraic models in nuclear physics, leading to a better understanding of the articles in the same special volume.
1. Introduction
Symmetries play a primordial role in all fields of physics, just think of the cyclic variables in classical mechanics, which imply conserved generalized momenta. A cyclic variable thus exhibits a symmetry of the Lagrangian. Alternatively, take Noether’s theorem, which allows us to identify continuous symmetries, so it is essential not only in field theory. The rotational symmetry is one example of a continuous symmetry and the corresponding conserved quantum number is the angular momentum, which is in most models and theories a good quantum number.
A symmetry is related to a transformation that leaves the Lagrangian and Hamiltonian invariant, or in other words, that the Hamiltonian commutes with the operator, which generates the symmetry transformation.
Nuclear physics is no exception; here, the Hamiltonian commutes with the generators of the angular momentum group. However, there is more. The use of symmetries in nuclear physics is nearly as old as quantum mechanics. Remember the seminal work in 1931 of H. Weyl [1]. The first noticeable application of symmetries in nuclear physics is the shell model [2], recognizing that the special unitary group plays a central role. We will see in Section 2 that this is a trivial consequence, as it is nothing but counting the degrees of freedom of a system correctly. In fact, in Section 2, I will present a basic introduction to symmetry, also known as group theory (a less attractive word), resuming mainly well-known methods and facts that are very useful in understanding all models in nuclear theory based on symmetry. The content of Section 2 may seem to be too trivial for most physicists accustomed to the use of symmetry. This is intentional, because some points will be stressed that are often easily overlooked and taken as guaranteed.
Several years after the presentation of the shell model, J.P. Elliott [3,4] proposed a model for the description of deformed nuclei and we will see how this approach taught us to also describe nuclear clusters. Another advantage is that the method of using symmetry groups, such as the , provides very simple formulas for the spectrum of a nucleus.
The use of symmetries obtained an important boost in 1976 with the introduction of the Interacting Boson Approximation (IBA) [5,6]. This model is the first in a series of models and extensions where symmetry is a central part of the theory. In Section 3, we will resume all the historic achievements of these models, starting with the shell model, passing to the IBA, and finally, ending with the most involved model, which is a cluster model. Though I use the notion involved, with the help of Section 2, we will see that it can be readily understood, with no magic involved.
The mentioned group of models is referred frequently as algebraic models. One important feature is that, after having identified the number of degrees of freedom fixing the large group, the next steps are quite determined: the large group is reduced to the angular momentum group and several paths are possible, related to the so-called dynamical symmetries. Then, the Hamiltonian is constructed as a function in the generators of the large group. When restricted to a dynamical symmetry, the Hamiltonian can be written in terms of Casimir operators, which commute with each other. Thus, a basis can be constructed that is diagonal to the Hamiltonian, and analytic results are obtained. This is of huge advantage, because it allows us to describe the spectrum of certain nuclei in a very simple and concise manner.
However, when this path is chosen, this also exhibits some problems without further verifying the physics. For example, when two distinct models make use of the same large group, how do we differentiate between them? This will show that caution is required, i.e., one has to take into account the different physical assumptions both models use. This is sometimes ignored and results in jumping from one model to another. Moreover, when the standard path is used without observing basic physical principles, which one has to avoid, the results may be rendered useless. Although in some cases the spectra and transitions can be reproduced, the model itself should be abandoned. That there can be agreement is often related to too little experimental information available and/or to the use of too many parameters. Thus, the phrase “the model reproduces experiment, and therefore is correct” is an insufficient statement. For example, this part is related to the “and some of its problems” in the title of the present contribution.
Finally, it is clear that the use of symmetry (group theory) provides a powerful method to describe complicated systems, as is the case for a system of many nucleons (a nucleus).
This contribution is organized as follows: In Section 2, I will present the basic concepts of symmetries. It will contain mainly methods and tricks without proof, which can be retrieved in literature [7,8]. The main objective is to show that the methods used in nuclear physics can be understood via trivial manipulations. In Section 3, several classical models, which use symmetries, are presented, starting with the shell model and the Elliott’s model, and presenting several others that were created during the last 50 years. In Section 4, a discussion is presented on the related problems in relying only on the group structure, without taking into account basic principles of physics. Moreover, I will show how to correct errors, or at least what to do. Finally, in Section 5, conclusions will be drawn.
The objective and hope of the present contribution is that it provides an interesting and useful collection of information on symmetries in nuclear physics, which are not only useful for the experts but also for readers interested in this topic. Another motivation is to prepare the inexperienced reader such that the other contributions in this special issue can be understood.
It is also worth mentioning that this special issue has an overlap to other special issues, one of which is the journal Symmetries (Symmetry in Nuclear Physics: Model Calculations, Advances and Applications, Edts. Draayer, J.P.; Pan, F.; Martinou, A., in preparation). and the other one in [9], where will be available at approximately the same time. The emphasis, however, is different but provides additional useful information.
2. A Pedestrian Introduction to Symmetries
In this section, I will give a schematic and short review of how symmetries are exploited in nuclear physics. It is not meant to give a complete review but rather it will consist of a list of methods and useful tricks for handling symmetries and how to be able to construct in a direct manner a useful and effective model. For more, please consult [7,8] where a wealth of further information can be retrieved. The content of this section is also very useful for modeling particle physics as in Quantum Chromodynamics (QCD). I am sure that for many, the information at the start is trivial. It is kept so intentionally because little by little the main message will be surprisingly clear, not so well-known or ignored, i.e., I will indicate that the use of symmetries is direct and actually easy.
The language chosen is neutral, i.e., I will not restrict to a definite physical system, which is intentional as one will find out towards the end.
2.1. Algebras, Casimir Operators, and Group Structure
Let us start with a system with n degrees of freedom, where, as mentioned, no reference will be made as to what kind of degree of freedom is used, though the number of degrees of freedom is important information. I will restrict to bosons as particles, because the information presented can be readily extended to fermion systems too. Moreover, a mixture of bosons with fermions (i.e., supersymmetric models) can be made.
The bosons will be presented by boson creation () and annihilation () operators (), satisfying the commutation relations
where we use the notation of co- and contravariant indices in order to distinguish the different properties under unitary transformation. The is the Kronecker delta symbol. (In some models, the is denoted by , which I find quite confusing.)
One can construct operators, which conserve the number of bosons:
also called generators, which satisfy an algebra
One can introduce so-called raising and lowering operators. This definition is a bit arbitrary and different conventions exist. One possibility is to define a raising operator such that it lowers the index and the lowering operator raises the index, i.e.,
One can understand this definition by picturing a column vector with n entries and a 1 in the k’s row, where the index runs from above to below. A raising operator then moves the 1 up the column. The also defined weight operators just count the number of bosons in the state , with the number of bosons of type i. The can be cast into a Young diagram with boxes in the k’the row and [7]. The rank of a group is defined as the maximal number of operators that commute with each other. For the , this is just n, the number of weight operators.
The same as (3) is achieved when we consider bosons with a double index, separating in such a manner two distinct degrees of freedom. For example, , and summing over : = , but I keep it simple, for the moment. Further, below I will come back to discuss the consequences of it.
The algebra (3) is the one from . The form of the operators in (2) make it easy to construct Casimir operators, which commute with all generators of the group and allow the definition of quantum numbers. This is because the Casimir operators are functions in the generators of the group in question and, thus, also commute with each other.
Casimir operators are obtained by multiplying the generators and contracting over their indices:
which is a Casimir operator of l’th order. Two particular examples are the number operator and second-order Casimir operator
The selected form is ideal for calculating the eigenvalues of the Casimir operators, as shown in [8].
The Special Unitary Group, , is obtained by subtracting a trace from the generators:
The operators satisfy the relation , i.e., the number of generators in is one less, namely . The rank of is , because there is a relation between the operators. According to Racah’s theorem [8] the number of independent Casimir operators is equal to the rank of the group; therefore, for , there are n, and for independent Casimir operators. This limits the size of the sum in (5).
All other constructions, such as the Casimir operators of , are performed exactly the same as in , substituting the operators by . The eigenvalues of the weight operators, , however, change in terms of the , namely
In the notation used, it is particularly easy to determine the eigenvalue of a Casimir operator. This is illustrated for the case, when only. For that, we apply the second order Casimir operator onto the so-called maximum weight state, defined as
i.e., all raising operators give zero. For , there is only one independent weight operator, namely
Its eigenvalue is = L, which is abbreviated by L.
Applying the second-order Casimir operator of to the maximal weight state gives
Using the raising operator applied to the maximal weight state gives zero (when the lowering operator is applied first, one has to commute the raising operator from the left to the right), re-expressing the in terms of the and using the eigenvalues of the operators, results in
with the definition of L further above, we obtain the well-known eigenvalue of the angular momentum operator, apart from the factor of 2, which can be removed by redefining the Casimir operator by a convenient factor.
For , the path is exactly the same, with the complication that more indices appear now. Defining
the eigenvalue of the second-order Casimir operator of is given by
Note that this is valid for any , not having specified yet to what physical interpretation the refers to.
Another important concept is the direct product of groups: Let us consider bosons with a double index, in order to distinguish two kinds of degrees of freedom. The creation operator (analog to that for the annihilation operator) is expressed as . For example, the index may refer to the orbital degrees of freedom, and the index to the isospin degrees of freedom. However, at this stage, the meaning of the two degrees of freedom is not specified yet. In total, the bosons have degrees of freedom, which imply a group. Now, the generators of this group are
If one is interested only in one part of the degrees of freedom (one kind of property), one has to contract over the other part, which leads to
(here, one sees one of the advantages to using the notation of co- and contravariant indices). The operators in (16) are, respectively, the generators of and , which can be easily verified. The operators commute with the operators , but each of those is also a linear combination of generators of . Thus, and are subgroups of . All these properties are resumed in the group chain
The symbol ⊗ denotes a direct product. (17) implies that the two groups and are correlated and for a deeper source of information, please consult [7].
2.2. Dynamical Symmetries and Construction of Model Hamiltonians
With this small set of formulas, we are already able to construct models:
Let us consider Hamiltonians that are functions in the generators of (it can be also a function in the generators of ), i.e., the Hamiltonian conserves the number of bosons. This is not a necessary requirement and interactions that do not conserve the number of bosons can always be rewritten such that they conserve it. For example, of can be substituted by
where N is the total number of bosons considered and s refers to a scalar auxiliary boson introduced in order to lead to operators that conserve the total number of bosons. The total number of bosons is given by
with and are the number of b- and s-bosons, respectively. When , the can only vary between 0 and N, i.e., a cut-off is introduced. The in the denominator serves to erase the contribution of ∼ and s∼ to the matrix element when N is large ().
A particular form for the Hamiltonian is obtained when a so-called dynamical symmetry is present. A dynamical symmetry is defined by the group chain
where the group was chosen for the nuclear physics case because its generators have the commutation relations of the angular momentum operators. The is a possible group appearing between and within , etc. In general, there are several possible combinations corresponding to different chains of groups of the type (20). L is the angular momentum type quantum number and M is its projection. The represents the quantum numbers (there may be more than one) of . The states, describing the dynamical symmetry, can be cast into the Dirac notation as
which also contains multiplicities.
In the case of a dynamical symmetry, the Hamiltonian can be written in terms of the Casimir operators of the groups and one possible form (actually the simplest) is
where is the second-order Casimir operator of . More general formulas, with higher-order Casimir operators and powers of them, can be constructed at will. The important point is that when basis functions of (20) are used, the eigenvalue of is analytical and given by
where is the eigenvalue of the Casimir operator .
It is important to stress the observation that we were able to construct the Hamiltonian of a model without reference to a physical system. In general, one has to show that the generators correspond to the angular momentum components, a simple equivalence to the commutation relations is not enough. Moreover, the physical interpretation of the different quantum numbers has to be found.
2.3. An Example of Mathematically Two Equal Models
This lesson tells us that there must be more than just the number of degrees of a system. Knowing just n is sufficient to look at least for a basis to diagonalize a Hamiltonian, but not more.
Let me mention an example: the geometric model of the nucleus [10,11] and the Interacting Boson Approximation (IBA) [5]. In the first model, the lowest excitations of a nucleus are described via quadrupole surface motions. Because only quadrupole motion is considered (), there are five degrees of freedom, i.e., from what we have learned above there is a group involved. The basis states were constructed, for example, in [12], and applied to the geometric model in [11] to U and in [13] to the Os-, Pt-, and W-chain of isotopes with great success. Due to numerical and practical reasons, (one cannot diagonalize an infinite matrix), the number of quadrupole quanta are limited to a sufficient high maximal number of bosons. Alternatively, one can introduce a cut-off through the introduction of an auxiliary scalar s-boson, as described above, which will lead to .
The IBA is claimed to be different, because it uses (in its first version) basic degrees of freedom pairs of nucleons in the valence shell, coupled to spin 2 (d-bosons) and spin 0 (s-bosons). In total, there are six degrees of freedom, which also leads to . Therefore, one must find a manner to distinguish the IBA from the geometric model. There is a difference, while in the geometric model the bosons are real bosons (surface oscillations) without a substructure, the s- and d-bosons are composed of pairs of fermions. Moreover, the number of bosons in the IBA is limited to half of the number of nucleons in the valence shell. Therefore, there is a clear difference that one can exploit. Limiting to a fixed number of bosons still corresponds to the geometric model with a finite cut-off, both models on this level are still equivalent (both use ) as was proven in [14]. The main difference, however, is the sub-structure of each boson. When many bosons are present (in mid-shell the N is large), then, due to a large overlap of the pairs, this sub-structure should have an effect through the Pauli exclusion principle (PEP), also denoted as including exchange effects [15]. I will come back to this later in the article.
There are extensions of the IBA, for example, treating protons and neutrons separately. I will not go into this because the geometrical model also does it (isospin resonances [10]) and the discussion of the relation between the IBA-type models to the geometric-type models is still the same.
3. Examples of Models Using Symmetries: Algebraic Models
Models using symmetries are often called in nuclear physics algebraic models. This is not always a good notation because sometimes (as in the geometric model) the group structure is used for the construction of a basis, nothing more. The physics is in the basic assumptions (axioms) and in the Hamiltonian.
3.1. The Elliott Model
The first example is the shell model [2,16]. This approximates the interaction between the nucleons by a mean field, i.e., a harmonic oscillator in three dimensions (our space is three-dimensional), and adds some residual interactions to get the details right. Because it is a three-dimensional oscillator, the or groups pop up immediately. The basis states are easily constructed (known as a basic example to each physics student) and the matrix elements of the residual interactions of the Hamiltonian are calculated directly.
In nuclear physics, J. P. Elliott did raise the use of symmetry to a new level [3,4], really the first algebraic model in its true sense, i.e., that the Hamiltonian is a function of generators of and the basis states are the ones of the harmonic oscillator. The Hamiltonian has the form
The is the distance of the shells in energy, given approximately by MeV [10] (there are better formulas). The operator N counts the number of oscillation quanta. The -parameter describes the strength of the quadrupole–quadrupole interaction
The index a refers to the algebraic part of the quadrupole operator, which is a generator of as the number operator is of . The form of the algebraic part of the quadrupole operator is given by [17]
where the bracket denotes the angular momentum coupling of the creation with the annihilation operator, which creates (annihilate) an oscillator quantum.
As noted, the algebraic quadrupole operator does only act within a shell because it does not change the number of oscillation quanta. The great advantage is that (25) has an analytical solution because the quadrupole–quadrupole interaction can be written as a sum of Casimir operators [17]:
Thus, the eigenvalue of the Hamiltonian (24) is
The is the eigenvalue of the second-order Casimir operator, which is given by , where denotes a irreducible representation (irrep) of . The important feature is the analytical result of the energy and that deformed nuclei can be described by it. All that one has to do is to determine the content of the within a valence shell.
This is also performed in a straightforward manner, using the concept of a direct product group, as introduced in Section 2.1. Let us consider a particular oscillator shell . The number of orbitals in this shell (equal to the dimension of the Young diagram ) is . Considering spin (up and down) and isospin (proton and neutron), there are an additional four degrees of freedom to consider. The orbital part leads to and the spin-isospin content to . Thus, the group chain to consider is
The has to be reduced to and a library of programs exists [18,19], which also contains the determination of coupling coefficients of all possible kinds.
Let us take as an example Ne. It has four nucleons in the sd-shell (). Because nucleons are fermions, the irrep of = has to be completely anti-symmetric, i.e., . The irreps of the groups = and the spin-isospin group have to be, therefore, complementary. For example, when the one of is given by the one of is obtained by interchanging the rows and the columns of the Young diagram [8]. Considering that a nucleon system tends to couple to the “most anti-symmetric” irrep of , the irrep of is the . Thus, the one of is . Reducing this to , using the programs of [18,19] leads to the content of the sd-shell for Ne:
of which the has the largest eigenvalue of the second-order Casimir operator, and thus, is lowest in energy (for ). The Elliott model was able to describe the spectrum of Ne (see Figure 1) from first principles without explicit shell model calculations, and considering that it is a well-deformed nucleus, did lead to the great success of using algebraic models. To obtain the content (Hilbert space) was the most important step. In order to describe the scale of the spectrum, one has to apply the model Hamiltonian. The rotational band can be easily adjusted by any model, which adds by hand an term.
The largest irrep is (8, 0); thus, there is a band denoted by this irrep with the angular momentum content of . There is a maximal angular momentum, dictated by the (8, 0) irrep. The calculation of the matrix elements of the algebraic quadrupole operator is standard [6] and is used to calculate quadrupole transition matrix elements. The agreement to experiment is excellent.
The Elliott model is the first of its kind, proving that the use of algebraic models provides a powerful method to describe complicated many-particle systems in a simple manner.
In [20], the reader can find a complete review of the -model, its mathematical foundation, variations, and numerous applications, not only in nuclear physics.
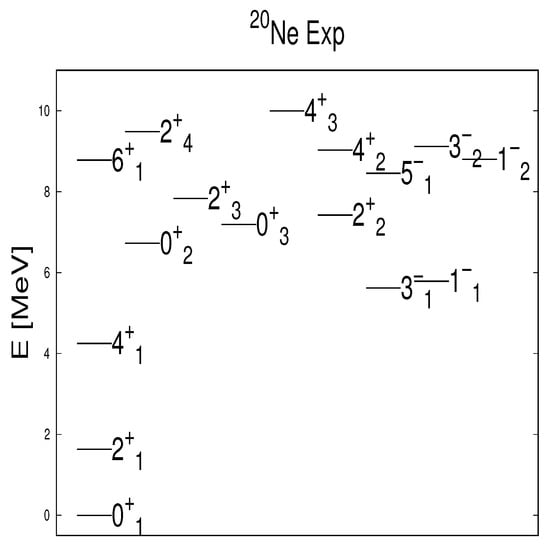
Figure 1.
Experimental spectrum of Ne [21]. The ground state band is plotted in the first column, which is well described by the Elliott model; however, also by any algebraic model with a term.
3.2. The Interacting Boson Approximation
The next huge step came in 1975 when A. Arima and F. Iachello proposed the Interacting Boson Approximation (IBA) [5]. The idea is very simple: Let us consider only the nucleons in the valence shell, not yet distinguishing protons and neutrons. In the valence shell, the pairing interaction favors that nucleon pairs are preferably coupled to spin zero. These nucleon pairs can be treated approximately as bosons (see next section). Thus, the number of boson pairs in the valence shell is given by N, which is the number of valence nucleons divided by 2. The lowest nucleon pairs in energy are the ones with angular momentum 0 and 2, the first denominated s-pairs and the latter as d-pairs.
Now, we can apply what we have learned. The total number of degrees of freedom is 1 (from the s-pair) plus 5 (from the d-pair), which gives 6. The particle creation and annihilation operators of the s-pair are , s and for the d-bosons they are and (). Here, we deviate a bit from the standard notation and make a difference between lower and upper indices, due to the different properties under unitary transformation. The annihilation operator with a lower index is related to the one with an upper index via .
Thus, the maximal group of importance is and the generators are
The number of the generators of is , as it should be. The last set of generators can be coupled to spin 0 (the d-number operator), to spin 1 (proportional to the angular momentum generators, spin 2 (proportional to the algebraic quadrupole operators) and, furthermore, to spin 3 and 4.
Because in nuclear physics the angular momentum is conserved (a “good quantum number”), which is described by a group, we have to look for a structure that contains this group. In fact, the generators are proportional to the components of the angular momentum, i.e., the angular momentum group is trivially contained in . In fact, there are three group chains, all starting from and ending up in :
Now, I will shortly describe these dynamical symmetry limits in terms of the Hilbert space (quantum numbers), model Hamiltonian, and spectrum. In the interpretation of the dynamical symmetries, of great help is the semi-classical description of algebraic models using coherent states [22]. It delivers classical potentials in terms of the deformation variables.
- The limit:
The generators of the are obtained by skipping in all generators containing s-boson operators. There are remaining operators. This is the simplest one. A model Hamiltonian and its eigenvalues are
where one can still add terms containing the angular momentum operators, serving to break the degeneracy of the five-dimensional harmonic oscillator. The spectrum is equidistant, as it is for a harmonic oscillator.
- The limit:
This was already discussed above and within the Elliott model and we do not need to repeat it. This dynamical symmetry describes well-deformed nuclei.
- The limit:
This dynamical symmetry describes -unstable nuclei [10] as can be appreciated when a geometrical mapping is applied. The geometric potential does not depend on the deformation variable .
A possible model Hamiltonian is
The eigenvalue is obtained in the same way as the example of discussed in Section 2. It is no surprise that is equivalent to L and instead of a 3 there is a 4 in the energy formula.
As is noted, with these algebraic methods, one can describe extremely complicated spectra without recurring to the standard shell model calculations, which would involve a Hilbert space of huge dimensions.
Each one of these chains can also be used as a basis in which a general Hamiltonian can be diagonalized. The most general Hamiltonian is just a function of the generators, i.e., the Hamiltonian also has to conserve the total number of bosons in the valence shell. However, there is a special class of Hamiltonians which are glued to each of the group chains in (32). To each group appearing in (32), there belong Casimir operators and the most general Hamiltonian can also be expressed in terms of functions in these Casimir operators. However, when a Hamiltonian is only a function of Casimir operators within one group chain, this Hamiltonian is said to have a dynamical symmetry. For example, one possible Hamiltonian with the dynamical group chain is
where denotes the second-order Casimir operator of . This looks pretty similar to the Elliott model, discussed further above. Moreover, the eigenvalue is analytical, which is of great advantage, because it is easier to fit into an experimental spectrum (experimentalists love analytic formulas).
For Hamiltonians in the other dynamical symmetry chains, equivalent analytical results for the energies are obtained. For their physical interpretation, please consult [5,22].
However, please note that all that is entered here is:
- Starting from a certain number of degrees of freedom;
- Constructing group chains;
- Setting up a model Hamiltonian.all of which are the result of a pure mathematical input. Some of the physics is yet to be included. This is achieved when we note that the bosons are nucleon pairs, information that we have still to exploit. This is especially important when there are other models, distinct from the IBA, with the same number of degrees of freedom.
3.3. The Nuclear Vibron Model
Another example is the Nuclear Vibron Model (NVM [23]. In its simplest form, this model describes the excitations of a two-cluster system, without any internal structure, such as for example + and +O. The excitations originate from the relative motion. Assuming clusters without internal structure (closed shell nuclei), the procedure is again the same:
- Identify the degrees of freedom. The relative vector is a spin-1 tensor and described by spin one p-bosons, i.e., there are three degrees of freedom. Add an auxiliary scalar boson s to it, such that the total number of bosons is constant. Here, adding the scalar boson is just a trick to introduce a cut-off. In this way, the p-bosons vary from zero to N.
- Construct a group chain, which contains the angular momentum group , where R refers to the relative motion degree of freedom. This leads to
- Construct a Model Hamiltonian. The simplest one is
- Its eigenvalue iswhere = is the irrep of the group and n the p-particle number operator, one of the generators of , together with the generators of .
3.4. The Semimicroscopic Algebraic Cluster Model (SACM)
The SACM was proposed in 1992 [24,25]. The main motivation was to construct a theory that is (i) algebraic with all the powerful methods applicable, (ii) describes clusters, as in the vibron model, and (iii) satisfies the PEP.
The first question is which basis to use. This is resolved, observing that the underlying group of the shell model is , at least for light nuclei, to which we will restrict here. Within the states, the nucleons are distributed such that the PEP is easily implemented. For that reason, in [24,25], the following procedure is used, restricting to two cluster systems with nuclei where (then no considerations have to be applied to the isospin).
In order to avoid a difficult, explicit anti-symmetrization of the cluster system, a method is designed to construct the Dirac states, i.e., a ket state with the allowed combination of quantum numbers. As was proposed in [24,25], first the cluster states, with definite quantum numbers, is coupled with the relative motion of the clusters, also given by a symmetric irrep. Here, one has to keep in mind that for A particles, the harmonic oscillator of the shell model can always be written in a sum of the harmonic oscillators for each cluster plus the relative motion [26]. Note that the clusters are defined within the united nucleus and, thus, move in the same harmonic oscillator.
The coupling of the cluster states with the relative motion irrep leads to
where is the number of relative oscillation quanta. The is limited from below by the Wildermuth condition [27], resulting in a lower limit of (see also Figure 2). The is the multiplicity of . The sum is overall irreps, which result in the coupling and, in general, still not all of them do satisfy the PEP.
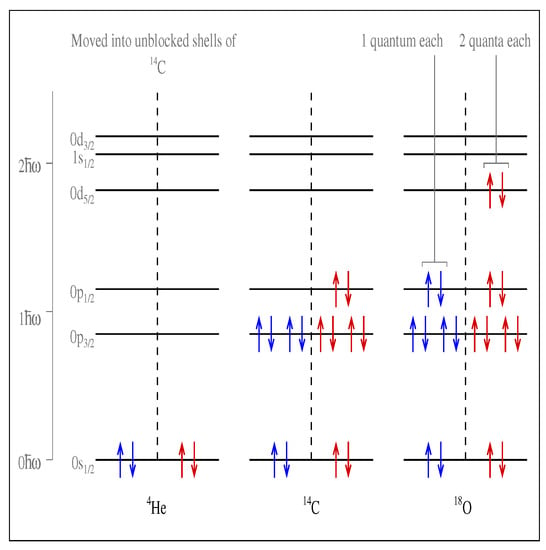
Figure 2.
Illustration of the Wildermuth condition with O →Ne. In their ground state, all four nucleons in the particle are in the s state and for the O-nucleus there are four in the s-shell and 12 in the p-shell. In order to satisfy the PEP, there must be four nucleons in the sd-shell for the Ne-nucleus. The particle contributes no oscillation quanta, but the O-nucleus has 12 quanta. The Ne-nucleus has a total of 20 quanta; thus, the difference of eight quanta must be in the relative motion. This computation results in a minimal number of relative oscillation quanta.
In the last step, the list of irreps in (39) is compared to the shell-model content (how to do it was indicated in Section 2, also see [24,25]). Only those thst have a counterpart in the shell model are included in the SACM model space. In this manner, the Pauli exclusion principle is observed and the model space can be called microscopic.
In the Dirac notation, the basis is denoted by the ket state
where , and are multiplicity labels. The cluster irreps are coupled first to , then with to the final irrep . The advantage of using the ket-formalism is the absence of the need for a coordinate space description, which suffices to obtain the quantum numbers describing Pauli allowed cluster states. Of course, the disadvantage is that no explicit space distribution of the clusters are depicted.
The Hamiltonian of the SACM is a function of the generators of the groups appearing in the groups of each cluster and the relative motion. This has a pretty similar form as described in the other examples. Due to the fact that the Hamiltonian is of phenomenological origin, the model contains the word semi, i.e., while the Hamiltonian is phenomenological, the basis states are microscopic.
The SACM was applied with success to many light cluster systems, such as in [28] (see Figure 3, were the date were retrieved from [21]), just to mention only one under many applications and its extensions.

Figure 3.
The C+→O, described within the SACM. [28]. Experimental data are from [21].
3.5. A Particular Application of Nuclear Physics Methods to Particle Physics
In this subsection, I will mention some use of symmetries in particle physics because the methods used are very much related to the ones in nuclear physics.
In [29], the spectrum of glue balls was described, recognizing that the Hamiltonian in QCD for gluons has a very similar structure as the collective microscopic Hamiltonian for the quadrupole excitations of nuclei [30]. This casual similarity did lead to an analytic formula, which was confirmed by lattice calculations.
The construction of the basis is equal to what we have learned in Section 2. A gluon in one level (no orbital degrees of freedom) has eight color components and three spin components (for a classification, it is important to also include the longitudinal part, which is excluded later on by an additional transversal condition). This leads to the group chain
where the labels are the corresponding quantum numbers. The irrep in the global group is completely symmetric (bosons). The , for the color degrees of freedom, and the group, for the spin degrees of freedom, are complementary and present the same symmetry . The color group is reduced to the standard color- (programs are available and can be sent on request) and the group on the right is reduced to the angular momentum group. This classification provides a complete set of quantum numbers for many gluon systems. An analytic formula for the energies is given in [29].
In [31], an effective algebraic Hamiltonian of QCD, for hadrons in general, was proposed and in [31,32,33] applied to describe hadron excitations, including gluons. Moreover, thermal excitations were considered in order to describe the physics of the Quark–Gluon Plasma, with quite a good agreement to the production of hadrons during the hadronization process.
The model Hamiltonian is composed of quark-antiquark elementary particles, treated as bosons. The PEP for the fermion part is approximately taken into account by adding factors , which simulate it. The Hamiltonian has the structure
where is the number of quark-antiquarks (particle-hole) pairs, the number of gluon pairs, , are the quark-antiquark pair creation and annihilation operators and , are gluon pair operators. The parameters, appearing in (42), model the interaction between the quark-antiquark and gluon pairs. The is the degeneracy of each quark level. The scale of energy for the level is chosen such that a quark level is approximately at one-third of the mass of a nucleon and the gluon level at twice the energy of a single gluon.
In [34], the catastrophe theory [35] was applied to a pure system of gluons in order to describe the phase transition from a non-interactive gluon system to a system of interactive gluons, which should describe the real physical state. As a Hamiltonian, the one of [31,32] was used. It was found that the transition is of first order.
As one can appreciate, the method of symmetries that originates from nuclear physics models can be easily extended to particle physics (QCD) with great insight and many applications. Thus, the methods described in this review can be applied in numerous situations.
3.6. Final Remarks
The examples presented are not exhaustive because a great wealth of algebraic models have been developed and the space available here is not sufficient to cover all these algebraic models and their applications. Nevertheless, the examples presented already give a sufficient list for the discussion of the characteristics of these models and what their respective advantages and powers are, as well as problems, as will be discussed in the next section.
4. Some Problems Which May Arise, Using Symmetries Without Critics
We start with the IBA. One problem was already mentioned in Section 3.2. It was shown that when two models have the same degrees of freedom, the recipe on how to construct a model Hamiltonian is not enough. In the relation of the IBA to the geometric model, this is just the case. The restriction to a finite number of bosons is one constraint, but it amounts to using a geometric model with a finite cut-off. Further, it was shown experimentally for the case of Pt, [36] that the geometric model works better due to the IBA having a low cut-off, while the geometric model has no cut-off. The other property, namely that the bosons are composed of fermion pairs, is never used. This leads to the following problem: In the limit, the lowest irrep is given by , which contains the ground state (gs) band with the states . The next irrep in energy is , which has a -band ( with ) and a -band ( with ). The problem consists in that the -band is in a different irrep than the gs-band, and, because the quadrupole operator is a generator of , there are no transitions between the - and the gs-band. This problem was proposed to be solved using g-bosons (hexadecupole modes, ). This produces a mixing and the transitions can be adjusted again. However, the use of g-bosons is not necessary when the PEP is taken into account, as shown by K. T. Hecht [37]. K. T.Hecht showed that in order to comply with the PEP, the lowest irrep are not those mentioned above, but have the form of with both values different from zero. Then, the gamma band is included in the lowest irrep and transitions are allowed. In conclusion, though the IBA seems to work, it does so due to its proximity in structure to the geometric model, but ignoring the exchange effects [15] leads to a transition to the geometric model.
The next example is the Vibron Model. The energy eigenvalues are given in (38) and may describe quite complicated spectra. For simplicity, put in Equation (38) . The term generates states that look like a rotational band; however, they are not, which will be discussed in what follows.
To see this, one has to look at the possible quantum numbers. The gives the relative excitation quanta, acquiring the values 0, 1, 2. The positive parity states (the parity is ) correspond to even and the negative parity states to odd. Further, each corresponds to the irrep and this is a problem. This is related to the definition of a band: given a nucleus with a definite deformation, a band is generated by rotating this deformed nucleus. In other words, all states in a band have to have the same internal (intrinsic) structure, and the states are only distinguished by their angular momentum. In contrast, the above states of the Vibron Model all have different internal structures described by (). Though, due to the -term, one can easily plot a “rotational band”, from , with , and all states in this “rotational band” have different internal structure and thus do not form a collective band. In [38], the number of p-quanta start from 0 and, thus, violate the Wildermuth condition [27] (see Figure 2, data are retrieved from [21]), which has to be satisfied minimally. This condition is not sufficient, as shown in [24,25], as will be discussed further below. The limit in the Vibron Model also poses a serious problem. When expanded in terms of the basis, an eigenstate of the -Hamiltonian includes components with all quantum numbers, i.e., all below the minimal number of p-quanta are required by the Wildermuth condition. Thus, in nuclear physics, the basis states partially violate the PEP. In other words, the limit in the nuclear Vibron Model is unphysical.
So, what is going wrong? The answer lies in the so-called Wildermuth condition [27], which includes the Pauli exclusion principle (PEP). To illustrate this, we take the system +O →Ne, also using the shell model with its symmetry (remember, it is the three-dimensional harmonic oscillator). All nucleons of the particle are in the s-shell, thus not contributing any oscillation quanta. The O nucleus has four nucleons in the s-shell and twelve in the p-shell. Each nucleon in the s-shell does not contribute to the oscillation number but each in the p-shell contributes 1, i.e., the oxygen nucleus contributes 12 oscillation numbers. In contrast to that, the Ne nucleons have four nucleons in the s-shell, twelve in the p-shell and four in the sd-shell, thus having a 4*0+12*1+4*2=20 oscillation number. Summing the ones from and O gives 12; thus, 8 are missing. Remember that the -particle and the oxygen are in the same mean field (oscillator potential) of the Ne-nucleus. In order to satisfy the PEP, the remaining eight oscillation quanta have to be deposited in the relative motion. This implies that the lowest number of quanta has to be eight. This corresponds to the irrep , identical to the Elliott model.
Note that the irrep contains and forms a band with the same internal -structure. Now, the description is complete, having included physical information, namely that the nucleons are fermions and all move in the same mean field.
This example shows how a pretty powerful mathematical method gives unphysical results, though by choosing the parameters adequately it can describe observation. Including the PEP results in a model that satisfies it and can also adjust the observational spectrum. This is meant as a warning, i.e., saying that “the model describes well the spectrum” does not necessarily imply that it is correct. In fact, there is a cluster model, which takes into account the PEP in the correct manner, also starting with counting the degrees of freedom and constructing the same type of Hamiltonian as the Vibron Model. This is the Semimicroscopic Algebraic Cluster Model (SACM) [24,25] presented in the last section.
This type of omission is continued in the Algebraic Cluster Model (ACM) [39] applied to C and O [40,41], described in terms of states consisting of three and four -particles, respectively. The relative motions of the -particles are described via Jacobi coordinates. With respect to setting up the degrees of freedom, this model is correct. However, the ACM does not anti-symmetrize between the -particles, though this is of utmost importance at low energy when the overlap of the -particles is significant. In Figure 4 (data are taken from [21]), the calculations of the ACM, in the case of C, is compared to the SACM. The content is given in Table 1, obtained from a microscopic construction. This space is opposed to the one used in the ACM. Considering the available data, both models seem to reproduce measurements. However, the ACM predicts too many states at low energy. For example, the state in the excited band is at too low energy compared to the results obtained within the SACM. In general, the ACM predicts more states at low energy than a model that takes into account the PEP. One may argue that the experiment has to decide; however, here we have another criterion: the PEP. Namely, any model that violates PEP is per definition wrong.
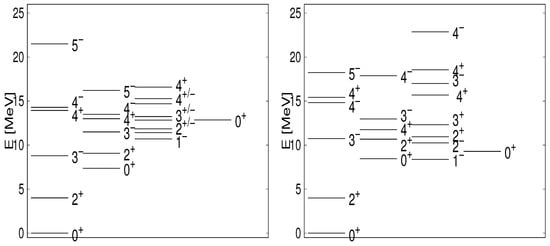
Figure 4.
In the (left) panel, the spectrum of C as a three -particle state, not considering the PEP, is plotted, and in the (right) panel figure, the same spectrum is plotted by taking into account the PEP. (Figure taken from [40].)

Table 1.
The model space of the C nucleus within the SACM up to 6 oscillation quanta, taken from [40,42,43].
5. Conclusions
In this contribution, we demonstrated the power and usefulness of symmetries in nuclear physics and presented several examples. First, a primary on the use of symmetries was presented, indicating how to construct an algebraic model. The construction of the Hamiltonian and the notion of dynamical symmetries was discussed.
Though the path in constructing an algebraic model is quite direct (of importance is to identify the correct number of degrees of freedom), problems are present in over-interpreting the model if important physical input is missing and the Hilbert space results can be incorrect.
I showed that two apparently different models may in fact be identical if different physical assumptions are not exploited. Moreover, when the PEP is not applied, though important, the results are wrong, even when the available experimental data seem to be reproduced. This may be the result of too many parameters and/or too few states known experimentally, the mathematical equivalence of the model to another correct model, etc. Thus, the argument “The model reproduces experimental data and, therefore, it is correct” is a logical fallacy. The model also has to comply with fundamental principles of nature, such as, for example, the PEP.
As mentioned in the introduction, the use of symmetries in algebraic models is not restricted to nuclear physics. There are many algebraic models in particle physics [8], derived in analogy from nuclear algebraic models, and of more recent applications, such as for gluon systems [29,31,32,33] or hadrons [44]. Some of these applications were discussed in Section 3.5.
We hope that the material presented is useful for the construction of algebraic models and also that it serves to advise caution to not over-interpret the use of symmetries.
Funding
This research was funded by PAPIIT-DGAPA grant number IN100421.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Weyl, H.; Robertson, H.P. The Theory of Groups and Quantum Mechanics; Martino Fine Books: Eastford, CT, USA, 2014; ISBN 978-1-61427-580-0. [Google Scholar]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Elliott, J.P. Collective motion in the nuclear shell model. I. Classification schemes for states of mixed configurations. Proc. R. Soc. Lond. A 1958, 245, 128. [Google Scholar]
- Elliott, J.P. Collective motion in the nuclear shell model II. The introduction of intrinsic wave-functions. Proc. R. Soc. Lond. A 1958, 245, 562. [Google Scholar]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambridge Univeristy Press: Cambridge, UK, 1987. [Google Scholar]
- Frank, A.; Van Isacker, P. Symmetry Methods in Molecules and Nuclei; SyG Editores: Coyoacan, Mexico, 2005. [Google Scholar]
- Coleman, A.J. The symmetric group made easy. Adv. Quant. Chem. 1968, 4, 83. [Google Scholar]
- Greiner, W.; Müller, B. Quantum Mechanics: Symmetries; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Kota, V.K.B.; Jain, A.K. Role of Symmetries in Nuclear Physics. Eur. Phys. J. Spec. Top. 2020, 229, 2349–2628. [Google Scholar] [CrossRef]
- Eisenberg, J.M.; Greiner, W. Nuclear Models I: Nuclear Theory, 3rd ed.; North-Holland: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Hess, P.O.; Seiwert, M.; Maruhn, J.; Greiner, W. General Collective Model and its Application to U. Z. Phys. 1980, 296, 147. [Google Scholar] [CrossRef]
- Chacón, E.; Moshinsky, M. Group theory of the collective model of the nucleus. J. Math. Phys. 1977, 18, 870. [Google Scholar] [CrossRef]
- Hess, P.O.; Maruhn, J.; Greiner, W. The general collective model applied to the chains of Pt, Os and W isotopes. J. Phys. G 1981, 7, 737. [Google Scholar] [CrossRef]
- Castaños, O.; Frank, A.; Hess, P.O.; Moshinsky, M. Confrontations between the interacting boson approximation and the Bohr-Mottelson model. Phys. Rev. C 1981, 24, 1367. [Google Scholar] [CrossRef]
- Draayer, J.P. Fermion models. In Algebraic Approaches to Nuclear Structure; Casten, R., Ed.; Harwood Academic Publisher: Reading, UK, 1993; p. 423. [Google Scholar]
- Goeppert-Mayer, M. Nuclear Configurations in the Spin-Orbit Coupling Model. I. Empirical Evidence. Phys. Rev. 1950, 78, 16. [Google Scholar] [CrossRef]
- Castaños, O.; Draayer, J.P. Contracted symplectic model with ds-shell applications. Nucl. Phys. A 1989, 491, 349. [Google Scholar] [CrossRef]
- Rowe, D.J.; Bahri, C. Clebsch–Gordan coefficients of SU(3) in SU(2) and SO(3) bases. J. Math. Phys. 2000, 41, 6544. [Google Scholar] [CrossRef]
- Bahri, C.; Rowe, D.J.; Draayer, J.P. Programs for generating Clebsch–Gordan coefficients of SU(3) in SU(2) and SO(3) bases. Comput. Phys. Commun. 2004, 159, 121. [Google Scholar] [CrossRef]
- Kota, V.K.B. SU(3) Symmetry in Atomic Nuclei; Springer Nature: Singapore, 2020. [Google Scholar]
- National Nuclear Data Center, Brookhaven. Available online: https://www.nndc.bnl.gov/ (accessed on 1 December 2011).
- Roosmalen, O.S.; Dieperink, A.E.L. The geometrical-classical limit of algebraic Hamiltonians for molecular vibrational spectra. Ann. Phys. N. Y. 1982, 139, 198. [Google Scholar]
- Iachello, F. Algebraic Approach to nuclear structure. Nucl. Phys. A 1983, 396, 233. [Google Scholar] [CrossRef]
- Cseh, J. Semimicroscopic algebraic description of nuclear cluster states. Vibron model coupled to the SU(3) shell model. Phys. Lett. B 1992, 281, 173. [Google Scholar] [CrossRef]
- Cseh, J.; Le’vai, G. Semimicroscopic Algebraic Cluster Model of Light Nuclei. I. Two-Cluster-Systems with Spin-Isospin-Free Interactions. Ann. Phys. N. Y. 1994, 230, 165. [Google Scholar] [CrossRef]
- Moshinsky, M.; Smirnov, Y.F. The Harmonic Oscillator in Modern Physics; Harwood Academic Publishers: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Wildermuth, K.; Tang, Y.C. A Unified Theory of the Nucleus; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Yépez-Martínez, H.; Ermamatov, M.J.; Fraser, P.R.; Hess, P.O. Application of the semimicroscopic algebraic cluster model to core+α nuclei in the p and sd shells. Phys. Rev. C 2012, 86, 034309. [Google Scholar] [CrossRef]
- Hess, P.O.; Weber, A.; Stephens, C.R.; Lerma-Hernández, S.; López, J.C. Glueball spectrum from an effective hamiltonian. Eur. Phys. J. C 1999, 9, 121. [Google Scholar] [CrossRef]
- Castaños, O.; Frank, A.; Chacón, E.; Hess, P.O.; Moshinsky, M. Complete set of states for microscopic nuclear collective models. J. Math. Phys. 1982, 23, 2537. [Google Scholar] [CrossRef]
- Lerma-Hernández, S.; Jesgarz, S.; Hess, P.O.; Civitarese, O.; Reboiro, M. Schematic model for QCD at finite temperature. Phys. Rev. C 2002, 66, 045207. [Google Scholar] [CrossRef]
- Lerma-Hernández, S.; Jesgarz, S.; Hess, P.O.; Civitarese, O.; Reboiro, M. Schematic model for QCD. I. Low energy meson states. Phys. Rev. C 2003, 67, 055209. [Google Scholar] [CrossRef]
- Jesgarz, S.; Lerma-Hernández, S.; Hess, P.O.; Civitarese, O.; Reboiro, M. Schematic model for QCD. II. Finite temperature regime. Phys. Rev. C 2003, 67, 055210. [Google Scholar] [CrossRef]
- Lohr-Robles, D.S.; López-Moreno, E.; Hess, P.O. Quantum phase transitions within a nuclear cluster model and an effective model of QCD. Nucl. Phys. A 2021, 1016, 122335. [Google Scholar] [CrossRef]
- Gilmore, R. Catastrophe Theory for Scientists and Engineers; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Mauthofer, A.; Stelzer, K.; Idzko, J.; Elze, H.W.; Wollersheim, H.J.; Emling, H.; Fuchs, P.; Grosse, F.; Schwalm, D. Triaxiality and -softness in 196Pt. Z. Phys. A 1990, 336, 263. [Google Scholar]
- Hecht, K.T. sp(6) and u(3) algebra of the fermion dynamical symmetry model. Notas Fis. 1985, 8, 165. [Google Scholar]
- Daley, H.J.; Iachello, F. Nuclear vibron model. I. The SU(3) limit. Ann. Phys. N. Y. 1986, 167, 73. [Google Scholar] [CrossRef]
- Bijker, R.; Iachello, F. The algebraic cluster model: Structure of 16O. Nucl. Phys. A 2017, 957, 154. [Google Scholar] [CrossRef]
- Hess, P.O. 12C within the Semimicroscopic Algebraic Cluster Model. Eur. Phys. J. A 2018, 54, 32. [Google Scholar] [CrossRef]
- Hess, P.O.; Berriel-Aguayo, J.R.M.; Chávez-Nuñez, L.J. 16O within the Semimicroscopic Algebraic Cluster Model and the importance of the Pauli Exclusion Principle. Eur. Phys. J. A 2019, 55, 71. [Google Scholar] [CrossRef]
- Horiuchi, H. Three-Alpha Model of 12C: Orthogonality Condition Model as an Approximation of Resonating Group Treatment. Prog. Theor. Phys. 1974, 51, 1266. [Google Scholar] [CrossRef]
- Katō, K.; Fukatsu, K.; Tanaka, H. Systematic Construction Method of Multi-Cluster Pauli-Allowed States. Prog. Theor. Phys. 1988, 80, 663. [Google Scholar]
- Ramirez-Soto, U.I.; Rico-Trejo, O.A.; Yépez-Martínez, T.; Hess, P.O.; Weber, A.; Civitarese, O. Schematic SO(4) model for the description of hadrons. J. Phys. G 2021, 48, 085013. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).