Classical and Bayesian Inference for the Kavya–Manoharan Generalized Exponential Distribution under Generalized Progressively Hybrid Censored Data
Abstract
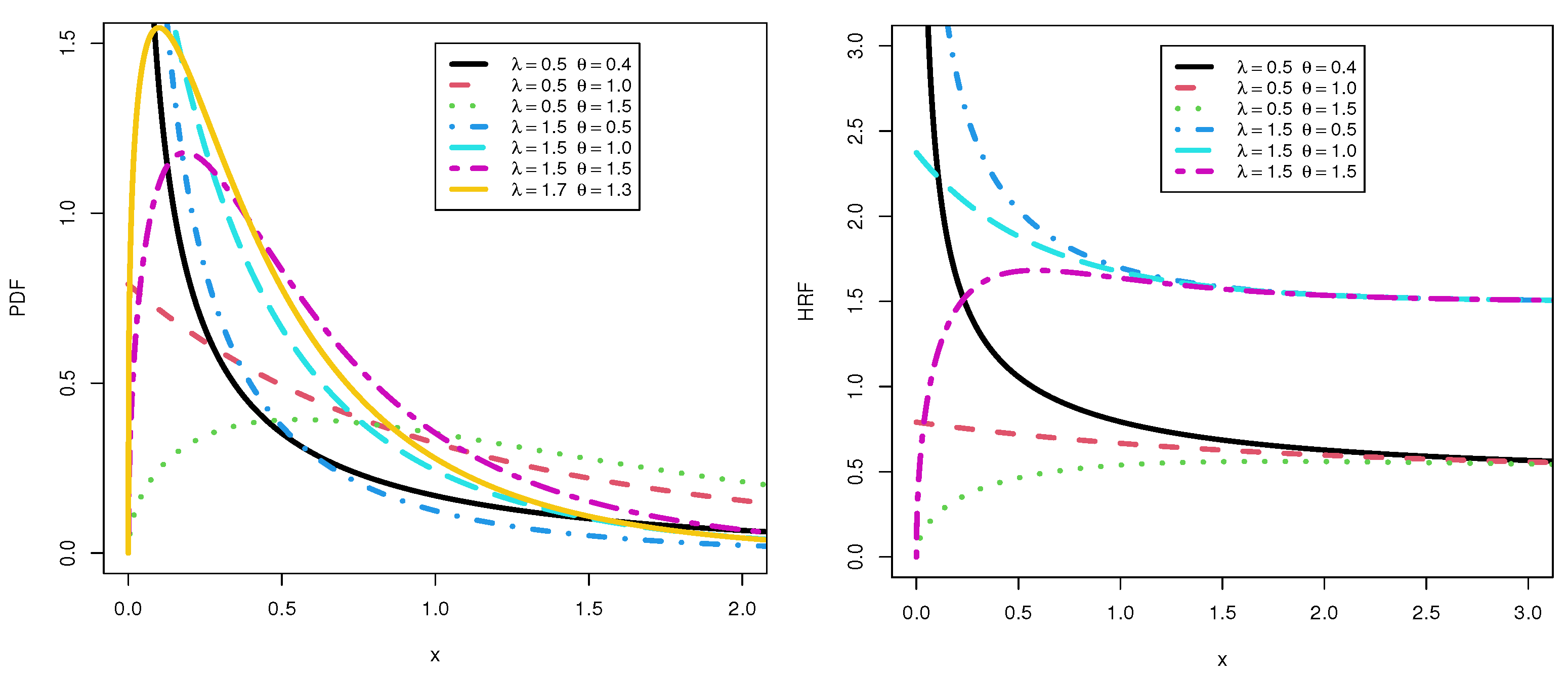
1. Introduction
- Discuss the point and interval statistical inference of the two unknown parameters and for the KMGE distribution using five classical estimation approaches such as ML, MPS, LS, WLS, and PE based on GTI-PHCS.
- Estimate the model’s parameters of the KMGE distribution in view of the Bayesian estimation strategy using symmetric and asymmetric loss functions.
- Using specific metrics of accuracy, a simulation study is run to look at how different estimates behave.
- A potential application based on GTI-PHCS has been explored for data from engineering and medical sciences.
2. Generalized Type-I Progressive Hybrid Censoring
- Assume that a random sample of n units undergoes a lifetime testing trial.
- Assume that before starting the experiment, the integers , the experimental time and () are assigned, so that , .
- The operational units are chosen at random and eliminated from the experiment at , the first failure time. At the subsequent failure time , operating units are randomly selected and eliminated from the experiment, and the procedure is repeated. Eventually, the experiment is completed when , and any remaining operational units are omitted from the experiment. Table 1 contains the values of the final censoring number .
- Assume that represents the number of units that fail prior to . The experiment’s end time is, therefore, provided byAny one of the subsequent six cases could be observed for the results:
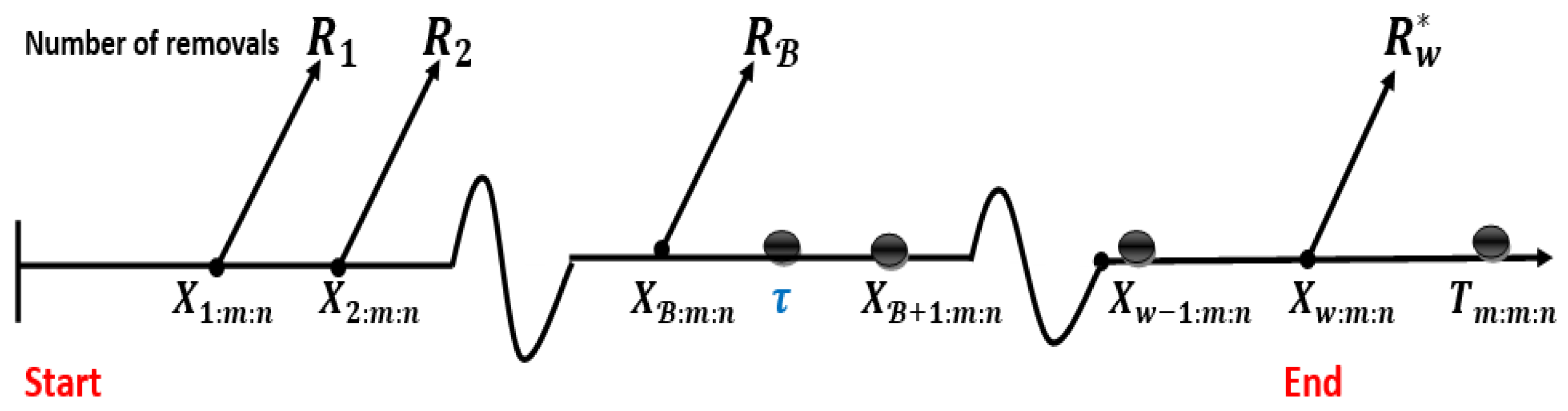
- Case I: If the observed time happens to occur before the wth failure time and failures occur up to time , . Afterward, we won’t remove any operating units from the experiment until the failure times, after which we will remove all of the remaining operating units from the experiment at the wth failure time, thereby stopping the experiment at , where , see Figure 2. In this case, we allow the experiment to continue after experimental time is reached to guarantee that at least the wth failure time happens. The following remarks, in this case, will be made:
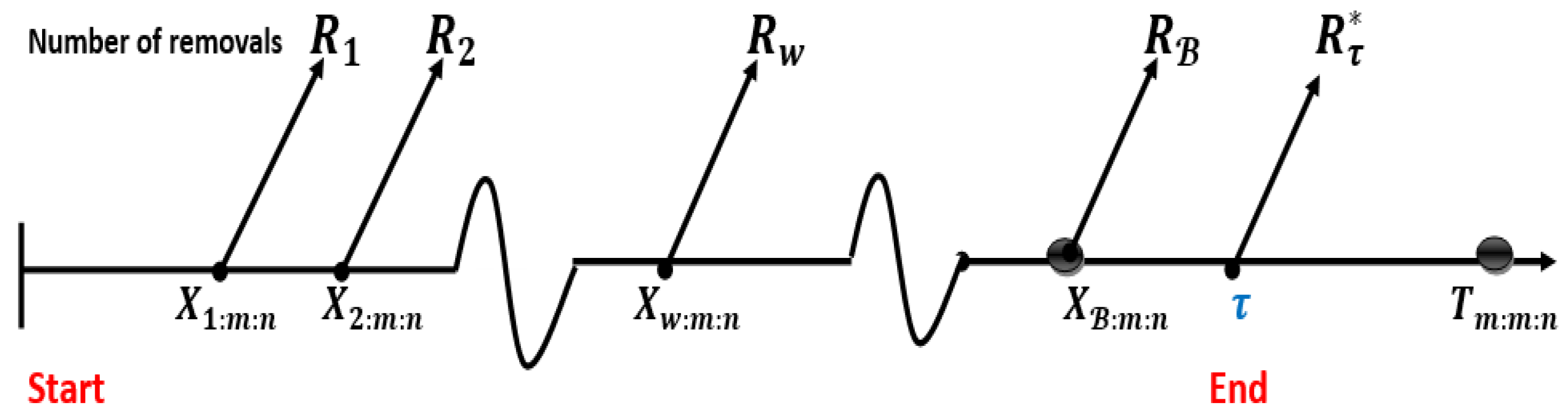
- Case II: When wth failure time happens before the , , and failures occur up to the time. The experiment is terminated at by removing all of the remaining operational units , as shown in Figure 3. The following observations will be made in this situation: .
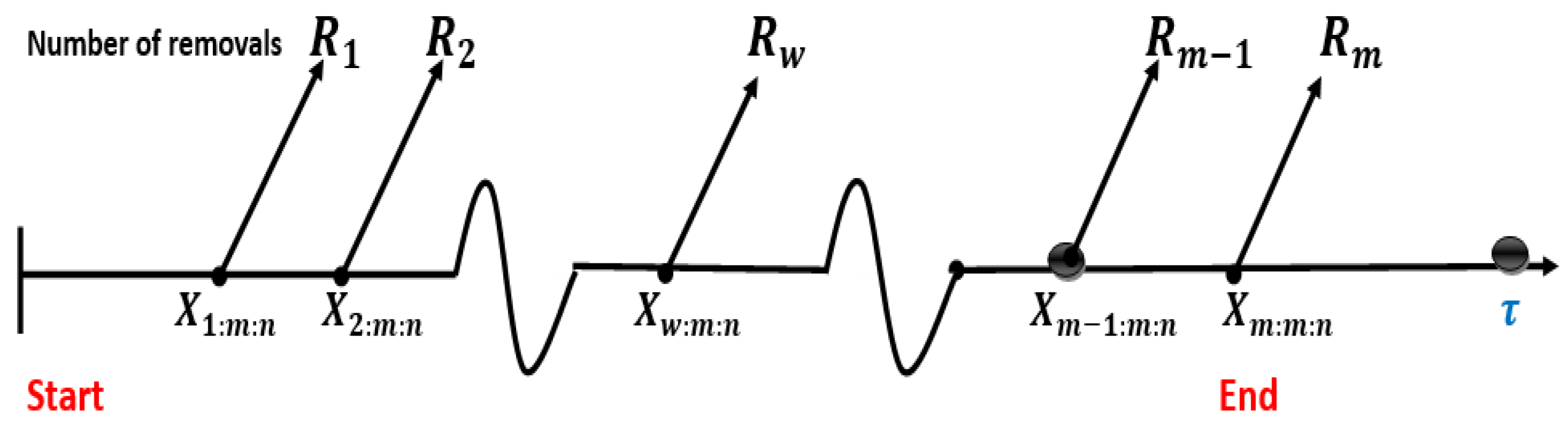
- Case III: When the mth failure time happens before the time , , then all the remaining operational units are deleted from the experiment, terminating it at , as shown in Figure 4. The following observations will be made in this situation:
3. Different Classical Approaches of Estimation
3.1. Approach of ML Estimation
3.2. Approach of Maximum Product of Spacing Estimation
3.3. Approaches of LS and WLS
3.4. Approach of Percentiles Estimation
4. Bayesian Estimation
- Set the starting values and .
- Set i = 1.
- Create and from and , respectively.
- Find , .
- Utilizing the uniform distribution, generate samples and .
- If both and are less than and , respectively, then set and , respectively. Otherwise, set and , respectively.
- Set i = i + 1.
- Redo steps 3–7 H times to get and for .
5. Results of Simulation
- Specify the sample size n and parameter values. Moreover, specify , , and values.
- Create n observations from the Uniform (0, 1) distribution .
- The observations may be obtained via CDF (3).
- As described in Section 2, employ GTI-PHCS to the random sample produced in Step 3.
- Compute the MLEs, MPSEs, LSEs, WLSEs, PEs, NACIs, and LTCIs of as mentioned in Section 3.
- Repeat the preceding steps = 1000 times.
- Determine the average of estimates, mean squared error (MSEr), and relative bias (RB) of across samples as described in the following:where is an estimate of .
- Determine the mean of the different estimates with their MSErs and RBs utilizing Step 9.
- Compute the average of the RBs (ARB) and MSErs (AMSEr) as below:
- Calculate the average lengths (ALs) and coverage probabilities (COVPs) of the parameters , then their 95% NACIs and LTCIs. Calculate also the average of the ALs (AAL) as below:
- CS.1:
- CS.2:
- CS.3:
- CS.4:
- The MPSEs are the best estimates through the AMSErs and ARBs.
- The MLEs are comparable to the LSEs, WLSEs, and PEs through the ARBs and AMSErs.
- The WLSEs are comparable to the LSEs and PEs through the ARBs and AMSErs.
- The LSEs are comparable to the PEs through the ARBs and AMSErs.
- The NACIs are comparable to the LTCIs through the AALs.
- For similar values of m and , and as n rises, the RBs, MSErs, ARBs, AMSErs, AL, and AAL decrease.
- For the same values of n, and , and as m increases, the RBs, MSErs, ARBs, AMSErs, AL, and AAL decrease.
- For similar values of n and m, by rising , the RBs, MSErs, ARBs, and AMSErs decrease for the MPSEs, MLEs, LSEs, and WLSEs, while the RBs, MSErs, ARBs, and AMSErs increase for the PEs.
- As increases, for the same values of n and m, the AL, and AAL decrease for CS.1 and CS.2, while the AL, and AAL increase for CS.3 and CS.4.
- As increases, for fixed values of n and m, the increases for CS.1 and CS.2, while the equals m for CS.3 and CS.4, where is the average number of observed failures when the experiment stops.
- The COVPs are close to 95%, as n, m, or increases.
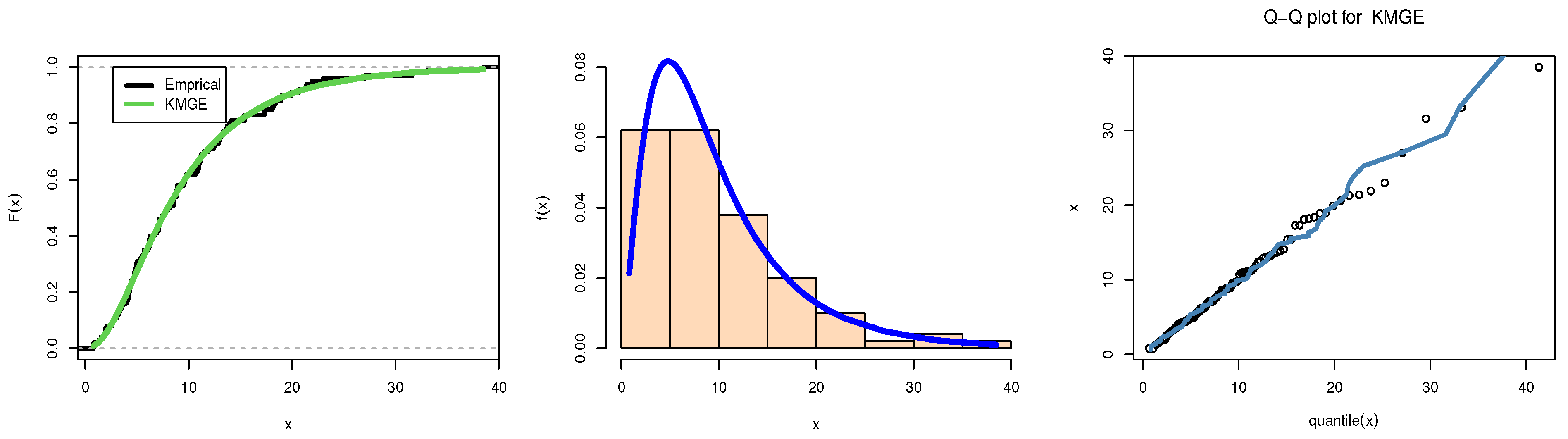
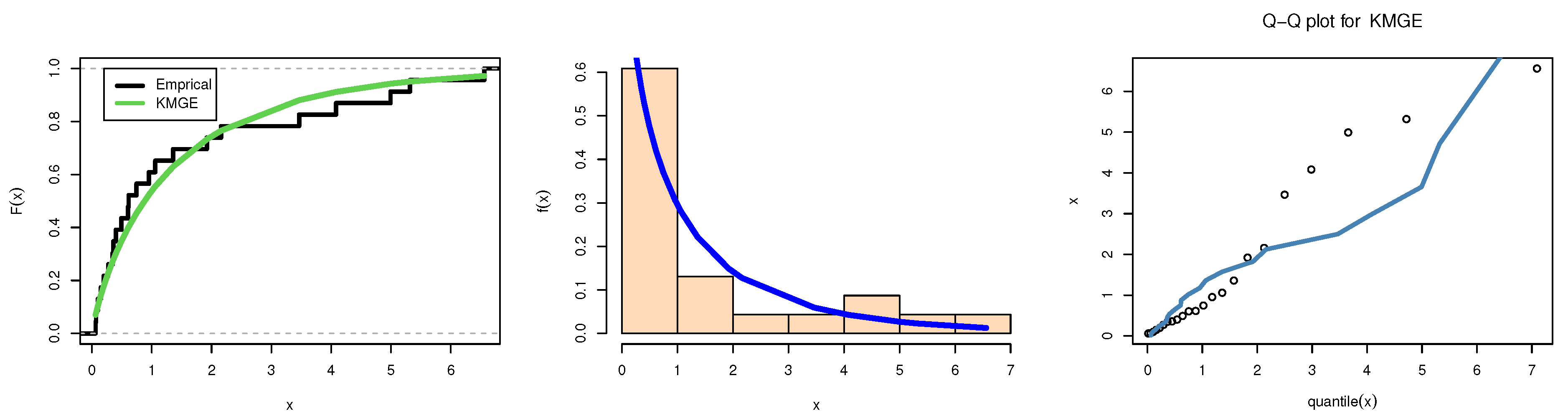
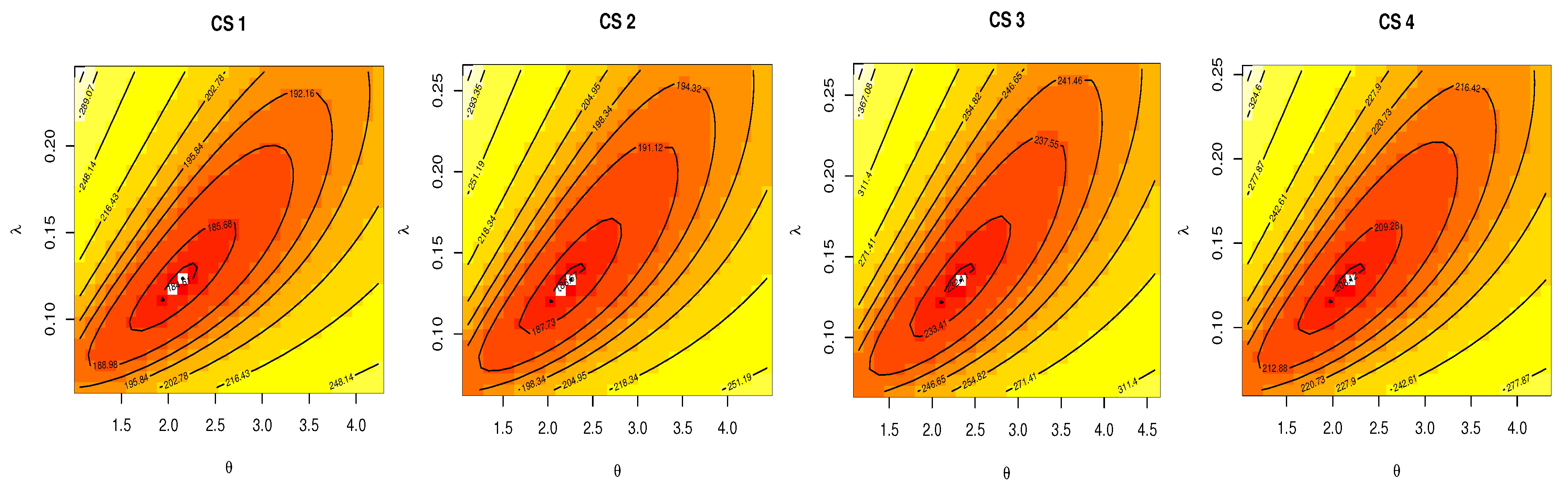
6. Applications
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Epstein, B. Truncated life-tests in the exponential case. Ann. Math. Statist. 1954, 25, 555–564. [Google Scholar] [CrossRef]
- Cohen, A.C. Progressively censored samples in life testing. Technometrics 1963, 5, 327–329. [Google Scholar] [CrossRef]
- Kundu, D.; Joarder, A. Analysis of type-II progressively hybrid censored data. Comput. Statist. Data Anal. 2006, 50, 2509–2528. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. Exact likelihood inference for an exponential parameter under generalized progressive hybrid CS. Statist. Method. 2015, 23, 18–34. [Google Scholar] [CrossRef]
- El-Sherpieny, E.S.A.; Almetwally, E.M.; Muhammed, H.Z. Progressive Type-II hybrid censored schemes based on maximum product spacing with application to Power Lomax distribution. Phys. A Stat. Mech. Its Appl. 2020, 553, 124251. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. Estimating the entropy of a Weibull distribution under generalized progressive hybrid censoring. Entropy 2015, 17, 102–122. [Google Scholar] [CrossRef]
- Salem, S.; Abo-Kasem, O.E.; Hussien, A. On Joint Type-II Generalized Progressive Hybrid Censoring Scheme. Comput. J. Math. Stat. Sci. 2023, 2, 123–158. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, Y. Statistical prediction of failure times under generalized progressive hybrid censoring in a simple step-stress accelerated competing risks model. J. Syst. Eng. Elect. 2017, 28, 282–291. [Google Scholar]
- Wang, L.; Tripathi, Y.M.; Lodhi, C. Inference for Weibull competing risks model with partially observed failure causes under generalized progressive hybrid censoring. J. Comput. Appl. Math. 2020, 368, 112537. [Google Scholar] [CrossRef]
- Koley, A.; Kundu, D. On generalized progressive hybrid censoring in presence of competing risks. Metrika 2017, 80, 401–426. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.H.; Hashem, A.F. Inference for the Exponential Distribution under Generalized Progressively Hybrid Censored Data from Partially Accelerated Life Tests with a Time Transformation Function. Mathematics 2021, 9, 1510. [Google Scholar] [CrossRef]
- Sayed-Ahmed, N.; Jawa, T.M.; Aloafi, T.A.; Bayones, F.S.; Elhag, A.A.; Bouslimi, J.; Abd-Elmougod, G.A. Generalized Type-I hybrid censoring scheme in estimation competing risks Chen lifetime populations. Math. Probl. Eng. 2021, 2021, 6693243. [Google Scholar] [CrossRef]
- Nagy, M.; Alrasheedi, A.F. The lifetime analysis of the Weibull model based on Generalized Type-I progressive hybrid censoring schemes. Math. Biosci. Eng. 2022, 19, 2330–2354. [Google Scholar] [CrossRef] [PubMed]
- Nagy, M.; Alrasheedi, A.F. Estimations of generalized exponential distribution parameters based on Type I generalized progressive hybrid censored data. Comput. Math. Methods Med. 2022, 2022, 8058473. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.C.; Gupta, P.L.; Gupta, R.D. Modeling failure time data by Lehman alternatives. Commun. Stat.-Theory Methods 1998, 27, 887–904. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K.; Freimer, M. The exponentiated Weibull family: A reanalysis of the bus-motor-failure data. Technometrics 1995, 37, 436–445. [Google Scholar] [CrossRef]
- Barreto-Souza, W.; Santos, A.H.; Cordeiro, G.M. The beta generalized exponential distribution. J. Stat. Comput. Simul. 2010, 80, 159–172. [Google Scholar] [CrossRef]
- Ristic, M.M.; Kundu, D. Marshall-Olkin generalized exponential distribution. Metron 2015, 73, 317–333. [Google Scholar] [CrossRef]
- Chaudhary, A.K.; Sapkota, L.P.; Kumar, V. Half-Cauchy Generalized Exponential Distribution: Theory and Application. J. Nepal Math. Soc. (JNMS) 2022, 5, 1–10. [Google Scholar] [CrossRef]
- Sapkota, L.P.; Kumar, V. Odd Lomax Generalized Exponential Distribution: Application to Engineering and COVID-19 data. Pak. J. Stat. Oper. Res. 2022, 18, 883–900. [Google Scholar] [CrossRef]
- Astorga, J.M.; Iriarte, Y.A.; Gómez, H.W.; Bolfarine, H. Modified slashed generalized exponential distribution. Commun. Stat.-Theory Methods 2019, 49, 4603–4617. [Google Scholar] [CrossRef]
- Alotaibi, N.; Elbatal, I.; Almetwally, E.M.; Alyami, S.A.; Al-Moisheer, A.S.; Elgarhy, M. Bivariate Step-Stress Accelerated Life Tests for the Kavya-Manoharan Exponentiated Weibull Model under Progressive Censoring with Applications. Symmetry 2022, 14, 1791. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Escobar, L.A. Statistical Method for Reliability Data; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Cheng, R.C.H.; Amin, N.A.K. Estimating parameters in continuous univariate distributions with a shifted origin. J. R. Stat. Soc. B 1983, 45, 394–403. [Google Scholar] [CrossRef]
- Ng, H.K.T.; Luo, L.; Hu, Y.; Duan, F. Parameter estimation of three-parameter Weibull distribution based on progressively type-II censored samples. J. Stat. Comput. Simul. 2012, 82, 1661–1678. [Google Scholar] [CrossRef]
- Alotaibi, N.; Hashem, A.F.; Elbatal, I.; Alyami, S.A.; Al-Moisheer, A.S.; Elgarhy, M. Inference for a Kavya–Manoharan Inverse Length Biased Exponential Distribution under Progressive-Stress Model Based on Progressive Type-II Censoring. Entropy 2022, 24, 1033. [Google Scholar] [CrossRef] [PubMed]
- Swain, J.J.; Venkatraman, S.; Wilson, J.R. Least-squares estimation of distribution function in Johnson’s translation system. J. Statist. Comput. Simul. 1988, 29, 271–297. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.H.; Hashem, A.F. A new lifetime distribution for a series-parallel system: Properties, applications and estimations under progressive type-II censoring. J. Statist. Comput. Simul. 2017, 87, 993–1024. [Google Scholar] [CrossRef]
- Hashem, A.F.; Alyami, S.A. Inference on a New Lifetime Distribution under Progressive Type-II Censoring for a Parallel-Series structure. Complexity 2021, 2021, 6684918. [Google Scholar] [CrossRef]
- Hashem, A.F.; Kuş, C.; Pekgör, A.; Abdel-Hamid, A.H. Poisson-logarithmic half-logistic distribution with inference under a progressive-stress model based on adaptive type-II progressive hybrid censoring. J. Egypt Math. Soc. 2022, 30, 15. [Google Scholar] [CrossRef]
- Aggarwala, R.; Balakrishnan, N. Some properties of progressive censored order statistics from arbitrary and uniform distributions with applications to inference and simulation. J. Stat. Plann. Inf. 1998, 70, 35–49. [Google Scholar] [CrossRef]
- Kao, J.H.K. A graphical estimation of mixed Weibull parameters in life testing electron tube. Technometrics 1959, 1, 389–407. [Google Scholar] [CrossRef]
- Dey, S.; Ali, S.; Park, C. Weighted exponential distribution: Properties and different methods of estimation. J. Stat. Comput. Simul. 2015, 85, 3641–3661. [Google Scholar] [CrossRef]
- Dey, S.; Singh, S.; Tripathi, Y.M.; Asgharzadeh, A. Estimation and prediction for a progressively censored generalized inverted exponential distribution. Stat. Methodol. 2016, 32, 185–202. [Google Scholar] [CrossRef]
- Hamdy, A.; Almetwally, E.M. Bayesian and Non-Bayesian Inference for The Generalized Power Akshaya Distribution with Application in Medical. Comput. J. Math. Stat. Sci. 2023, 2, 31–51. [Google Scholar] [CrossRef]
- Varian, H.R. Bayesian approach to real estate assessment. In Studies in Bayesian Econometrics and Statistics; Savage, L.J., Feinderg, S.E., Zellner, A., Eds.; North-Holland: Amsterdam, The Netherlands, 1975; pp. 195–208. [Google Scholar]
- Bantan, R.; Hassan, A.S.; Almetwally, E.; Elgarhy, M.; Jamal, F.; Chesneau, C.; Elsehetry, M. Bayesian analysis in partially accelerated life tests for weighted lomax distribution. Comput. Mater. Contin 2021, 68, 2859–2875. [Google Scholar] [CrossRef]
- Almongy, H.M.; Almetwally, E.M.; Alharbi, R.; Alnagar, D.; Hafez, E.H.; Mohie El-Din, M.M. The Weibull generalized exponential distribution with censored sample: Estimation and application on real data. Complexity 2021, 2021, 6653534. [Google Scholar] [CrossRef]
- Alotaibi, R.; Alamri, F.S.; Almetwally, E.M.; Wang, M.; Rezk, H. Classical and Bayesian Inference of a Progressive-Stress Model for the Nadarajah–Haghighi Distribution with Type II Progressive Censoring and Different Loss Functions. Mathematics 2022, 10, 1602. [Google Scholar] [CrossRef]
- Henningsen, A.; Toomet, O. maxLik: A package for maximum likelihood estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Atieh, B.; Nadarajah, S. Lindley distribution and its application. Math. Comput. Simul. 2008, 78, 493–506. [Google Scholar] [CrossRef]
- Suprawhardana, M.S.; Prayoto, S. Total time on test plot analysis for mechanical components of the RSG-GAS reactor. At. Indones 1999, 25, 81–90. [Google Scholar]



| Case I | Case II | Case III | |
|---|---|---|---|
| w | m | ||
| 0 | 1 | 0 | |
| n | m | CS | MLE | MPSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MSEr () | RB () | AMSEr | MSEr () | RB () | AMSEr | ||||||||
| MSEr () | RB () | ARB | MSEr () | RB () | ARB | ||||||||
| 40 | 16 | 20 | 2.5 | 1 | 2.8804 | 1.1209 | 0.2988 | 0.6393 | 2.3766 | 0.726 | 0.2544 | 0.4291 | 16.732 |
| 1.2278 | 0.1577 | 0.2679 | 0.2834 | 1.0381 | 0.1323 | 0.2609 | 0.2577 | ||||||
| 2 | 2.8653 | 1.0289 | 0.2923 | 0.5789 | 2.3734 | 0.7403 | 0.258 | 0.4351 | 16.142 | ||||
| 1.2106 | 0.1288 | 0.2485 | 0.2704 | 1.0524 | 0.1299 | 0.2474 | 0.2527 | ||||||
| 3 | 2.9135 | 1.179 | 0.3079 | 0.6588 | 2.4917 | 0.9366 | 0.2588 | 0.5507 | 20.00 | ||||
| 1.2282 | 0.1385 | 0.257 | 0.2825 | 1.0858 | 0.1649 | 0.2566 | 0.2577 | ||||||
| 4 | 2.8621 | 1.0522 | 0.2848 | 0.5893 | 2.4412 | 0.721 | 0.25 | 0.4227 | 20.00 | ||||
| 1.2128 | 0.1265 | 0.2416 | 0.2632 | 1.0688 | 0.1244 | 0.2373 | 0.2436 | ||||||
| 5.0 | 1 | 2.8546 | 1.0412 | 0.2803 | 0.5949 | 2.2576 | 0.5311 | 0.2333 | 0.3132 | 19.898 | |||
| 1.228 | 0.1486 | 0.2581 | 0.2692 | 0.9843 | 0.0954 | 0.2294 | 0.2314 | ||||||
| 2 | 2.8366 | 0.9224 | 0.2679 | 0.5204 | 2.2704 | 0.527 | 0.2308 | 0.3032 | 19.857 | ||||
| 1.2093 | 0.1184 | 0.2357 | 0.2518 | 1.001 | 0.0794 | 0.2115 | 0.2211 | ||||||
| 3 | 2.8998 | 1.0683 | 0.2957 | 0.6052 | 2.4648 | 1.1056 | 0.2691 | 0.6207 | 20.00 | ||||
| 1.2326 | 0.1421 | 0.2575 | 0.2766 | 1.0674 | 0.1358 | 0.2431 | 0.2561 | ||||||
| 4 | 2.8679 | 0.9591 | 0.2747 | 0.5383 | 2.4295 | 0.7659 | 0.251 | 0.4395 | 20.00 | ||||
| 1.2138 | 0.1174 | 0.2349 | 0.2548 | 1.0659 | 0.1132 | 0.2268 | 0.2389 | ||||||
| 30 | 2.5 | 1 | 2.7556 | 0.706 | 0.2398 | 0.3923 | 2.3457 | 0.5134 | 0.2226 | 0.2923 | 27.14 | ||
| 1.1623 | 0.0786 | 0.1953 | 0.2175 | 1.0212 | 0.0712 | 0.1949 | 0.2088 | ||||||
| 2 | 2.7441 | 0.7558 | 0.2509 | 0.4166 | 2.3415 | 0.4592 | 0.2102 | 0.2598 | 27.174 | ||||
| 1.1557 | 0.0773 | 0.1962 | 0.2235 | 1.034 | 0.0604 | 0.1797 | 0.1950 | ||||||
| 3 | 2.8041 | 0.7642 | 0.2525 | 0.4234 | 2.4078 | 0.4579 | 0.2094 | 0.2625 | 29.999 | ||||
| 1.1862 | 0.0825 | 0.2021 | 0.2273 | 1.058 | 0.0671 | 0.1890 | 0.1992 | ||||||
| 4 | 2.7505 | 0.6659 | 0.2341 | 0.3678 | 2.3988 | 0.4709 | 0.2117 | 0.2649 | 29.853 | ||||
| 1.1606 | 0.0697 | 0.1843 | 0.2092 | 1.0568 | 0.059 | 0.1743 | 0.1930 | ||||||
| 5.0 | 1 | 2.7696 | 0.6404 | 0.2325 | 0.3596 | 2.2886 | 0.4231 | 0.2111 | 0.2419 | 29.814 | |||
| 1.1928 | 0.0788 | 0.1937 | 0.2131 | 1.0091 | 0.0606 | 0.1829 | 0.1970 | ||||||
| 2 | 2.737 | 0.6555 | 0.2328 | 0.363 | 2.2971 | 0.4015 | 0.2046 | 0.2305 | 29.835 | ||||
| 1.1621 | 0.0706 | 0.1835 | 0.2081 | 1.0095 | 0.0595 | 0.1819 | 0.1932 | ||||||
| 3 | 2.8152 | 0.7046 | 0.2421 | 0.3902 | 2.4238 | 0.4827 | 0.2118 | 0.2730 | 30.0 | ||||
| 1.1929 | 0.0758 | 0.1922 | 0.2171 | 1.0625 | 0.0633 | 0.1824 | 0.1971 | ||||||
| 4 | 2.8301 | 0.801 | 0.2506 | 0.4424 | 2.3606 | 0.4078 | 0.1998 | 0.2336 | 30.0 | ||||
| 1.1961 | 0.0837 | 0.1992 | 0.2249 | 1.0524 | 0.0593 | 0.1757 | 0.1877 | ||||||
| — | 40 | — | — | 2.7524 | 0.5604 | 0.2173 | 0.3074 | 2.3033 | 0.3648 | 0.1921 | 0.2056 | 40.0 | |
| 1.1715 | 0.0544 | 0.1667 | 0.192 | 1.0174 | 0.0464 | 0.1616 | 0.1768 | ||||||
| n | m | CS | MLE | MPSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MSEr () | RB () | AMSEr | MSEr () | RB () | AMSEr | ||||||||
| MSEr () | RB () | ARB | MSEr () | RB () | ARB | ||||||||
| 80 | 32 | 40 | 2.5 | 1 | 2.6641 | 0.3329 | 0.1772 | 0.1984 | 2.3738 | 0.2768 | 0.1677 | 0.1655 | 34.219 |
| 1.1644 | 0.0639 | 0.1802 | 0.1787 | 1.0431 | 0.0542 | 0.1716 | 0.1696 | ||||||
| 2 | 2.6487 | 0.3428 | 0.183 | 0.1978 | 2.3542 | 0.3088 | 0.1811 | 0.18 | 33.95 | ||||
| 1.1478 | 0.0528 | 0.1634 | 0.1732 | 1.0452 | 0.0512 | 0.1663 | 0.1737 | ||||||
| 3 | 2.6412 | 0.3265 | 0.1763 | 0.1915 | 2.4423 | 0.3347 | 0.1826 | 0.1957 | 40.0 | ||||
| 1.1449 | 0.0566 | 0.1659 | 0.1711 | 1.0658 | 0.0566 | 0.1754 | 0.179 | ||||||
| 4 | 2.6641 | 0.3125 | 0.1703 | 0.1804 | 2.3894 | 0.2778 | 0.166 | 0.1608 | 40.0 | ||||
| 1.1551 | 0.0483 | 0.1558 | 0.1631 | 1.0586 | 0.0439 | 0.1524 | 0.1592 | ||||||
| 5.0 | 1 | 2.6492 | 0.2893 | 0.1645 | 0.1689 | 2.3671 | 0.2443 | 0.1578 | 0.1453 | 39.823 | |||
| 1.1483 | 0.0484 | 0.1545 | 0.1595 | 1.04 | 0.0463 | 0.1582 | 0.158 | ||||||
| 2 | 2.6501 | 0.3251 | 0.1782 | 0.1842 | 2.2782 | 0.2662 | 0.1727 | 0.153 | 39.755 | ||||
| 1.145 | 0.0434 | 0.1462 | 0.1622 | 1.0117 | 0.0398 | 0.1481 | 0.1604 | ||||||
| 3 | 2.6837 | 0.368 | 0.1866 | 0.2135 | 2.4183 | 0.2824 | 0.1714 | 0.1676 | 40.0 | ||||
| 1.1581 | 0.0589 | 0.1721 | 0.1794 | 1.0648 | 0.0527 | 0.1675 | 0.1694 | ||||||
| 4 | 2.6769 | 0.3382 | 0.176 | 0.1937 | 2.3818 | 0.294 | 0.1745 | 0.1713 | 40.0 | ||||
| 1.1645 | 0.0492 | 0.1577 | 0.1669 | 1.0503 | 0.0486 | 0.1633 | 0.1689 | ||||||
| 60 | 2.5 | 1 | 2.6142 | 0.248 | 0.1535 | 0.1415 | 2.4027 | 0.2352 | 0.1536 | 0.1343 | 54.537 | ||
| 1.132 | 0.0351 | 0.135 | 0.1443 | 1.0599 | 0.0334 | 0.1341 | 0.1439 | ||||||
| 2 | 2.5978 | 0.2471 | 0.1493 | 0.1388 | 2.3771 | 0.2256 | 0.153 | 0.1282 | 54.353 | ||||
| 1.1237 | 0.0306 | 0.1255 | 0.1374 | 1.0505 | 0.0309 | 0.1285 | 0.1407 | ||||||
| 3 | 2.6515 | 0.2771 | 0.1581 | 0.1563 | 2.4288 | 0.2229 | 0.1488 | 0.1272 | 60.0 | ||||
| 1.1445 | 0.0354 | 0.134 | 0.146 | 1.0645 | 0.0315 | 0.128 | 0.1384 | ||||||
| 4 | 2.6141 | 0.2527 | 0.1526 | 0.1427 | 2.4104 | 0.2234 | 0.1491 | 0.1275 | 59.914 | ||||
| 1.1394 | 0.0327 | 0.1267 | 0.1397 | 1.0677 | 0.0315 | 0.1273 | 0.1382 | ||||||
| 5.0 | 1 | 2.6078 | 0.2489 | 0.1501 | 0.1399 | 2.3797 | 0.1885 | 0.1427 | 0.1081 | 59.65 | |||
| 1.1314 | 0.0309 | 0.1228 | 0.1364 | 1.0508 | 0.0277 | 0.123 | 0.1329 | ||||||
| 2 | 2.6113 | 0.2428 | 0.1516 | 0.1359 | 2.3375 | 0.2147 | 0.1491 | 0.123 | 59.632 | ||||
| 1.1299 | 0.029 | 0.1236 | 0.1376 | 1.036 | 0.0313 | 0.1321 | 0.1406 | ||||||
| 3 | 2.6123 | 0.2459 | 0.1487 | 0.1384 | 2.412 | 0.2268 | 0.1517 | 0.1301 | 60.0 | ||||
| 1.1296 | 0.0309 | 0.1255 | 0.1371 | 1.0644 | 0.0333 | 0.1348 | 0.1432 | ||||||
| 4 | 2.628 | 0.2614 | 0.1563 | 0.1473 | 2.4015 | 0.2034 | 0.1456 | 0.1163 | 60.0 | ||||
| 1.1373 | 0.0333 | 0.1281 | 0.1422 | 1.0591 | 0.0291 | 0.1256 | 0.1356 | ||||||
| — | 80 | — | — | 2.6165 | 0.2002 | 0.1359 | 0.1112 | 2.3791 | 0.1664 | 0.1331 | 0.0941 | 80.0 | |
| 1.1321 | 0.0222 | 0.1049 | 0.1204 | 1.0515 | 0.0218 | 0.1105 | 0.1218 | ||||||
| n | m | CS | LSE | WLSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MSEr () | RB () | AMSEr | MSEr () | RB () | AMSEr | ||||||||
| MSEr () | RB () | ARB | MSEr () | RB () | ARB | ||||||||
| 40 | 16 | 20 | 2.5 | 1 | 2.9039 | 2.3725 | 0.378 | 1.294 | 2.8684 | 2.036 | 0.3419 | 1.1205 | 16.178 |
| 1.1533 | 0.2156 | 0.3173 | 0.3477 | 1.1473 | 0.205 | 0.3026 | 0.3222 | ||||||
| 2 | 2.8835 | 2.2141 | 0.3843 | 1.1954 | 2.9174 | 2.1381 | 0.3595 | 1.1522 | 16.036 | ||||
| 1.1144 | 0.1767 | 0.3024 | 0.3434 | 1.1291 | 0.1663 | 0.288 | 0.3238 | ||||||
| 3 | 2.7419 | 0.945 | 0.2747 | 0.5419 | 2.7432 | 0.8902 | 0.2651 | 0.5119 | 20.0 | ||||
| 1.1389 | 0.1389 | 0.2588 | 0.2667 | 1.1389 | 0.1335 | 0.2549 | 0.26 | ||||||
| 4 | 2.7329 | 1.0239 | 0.2933 | 0.5757 | 2.7389 | 0.8799 | 0.2741 | 0.5011 | 20.0 | ||||
| 1.1113 | 0.1274 | 0.2592 | 0.2763 | 1.117 | 0.1224 | 0.2532 | 0.2636 | ||||||
| 5.0 | 1 | 2.9529 | 2.3042 | 0.369 | 1.2491 | 2.9396 | 2.0888 | 0.3277 | 1.135 | 19.91 | |||
| 1.1687 | 0.1941 | 0.299 | 0.334 | 1.1726 | 0.1812 | 0.274 | 0.3008 | ||||||
| 2 | 3.0507 | 2.6596 | 0.39 | 1.4188 | 3.0943 | 2.3916 | 0.3695 | 1.2813 | 19.875 | ||||
| 1.1783 | 0.1781 | 0.2784 | 0.3342 | 1.1998 | 0.171 | 0.2639 | 0.3167 | ||||||
| 3 | 2.8121 | 1.1968 | 0.3054 | 0.6736 | 2.8099 | 1.0327 | 0.2881 | 0.5879 | 20.0 | ||||
| 1.1575 | 0.1504 | 0.2711 | 0.2882 | 1.1603 | 0.1432 | 0.2652 | 0.2767 | ||||||
| 4 | 2.7197 | 0.9559 | 0.2835 | 0.5375 | 2.7304 | 0.8217 | 0.2683 | 0.4665 | 20.0 | ||||
| 1.1041 | 0.119 | 0.2496 | 0.2665 | 1.1099 | 0.1114 | 0.2421 | 0.2552 | ||||||
| 30 | 2.5 | 1 | 3.6837 | 3.5841 | 0.4991 | 1.9219 | 3.8038 | 3.4262 | 0.5311 | 1.8567 | 27.303 | ||
| 1.4838 | 0.2596 | 0.3671 | 0.4331 | 1.5436 | 0.2871 | 0.4075 | 0.4693 | ||||||
| 2 | 3.4009 | 1.6959 | 0.3906 | 0.9392 | 3.622 | 2.0821 | 0.4573 | 1.1521 | 27.207 | ||||
| 1.4171 | 0.1826 | 0.3128 | 0.3517 | 1.4975 | 0.2221 | 0.3653 | 0.4113 | ||||||
| 3 | 2.6764 | 0.6708 | 0.2389 | 0.3761 | 2.6971 | 0.6359 | 0.2295 | 0.3581 | 29.999 | ||||
| 1.1059 | 0.0814 | 0.2045 | 0.2217 | 1.1134 | 0.0804 | 0.2014 | 0.2155 | ||||||
| 4 | 2.7726 | 0.7742 | 0.2482 | 0.4277 | 2.8001 | 0.7202 | 0.242 | 0.4004 | 29.858 | ||||
| 1.1503 | 0.0812 | 0.1995 | 0.2238 | 1.1631 | 0.0807 | 0.1978 | 0.2199 | ||||||
| 5.0 | 1 | 2.797 | 0.9503 | 0.2785 | 0.5227 | 2.8409 | 0.8232 | 0.2603 | 0.4538 | 29.815 | |||
| 1.1205 | 0.0934 | 0.2134 | 0.2468 | 1.138 | 0.0874 | 0.199 | 0.2282 | ||||||
| 2 | 3.5435 | 2.5167 | 0.4486 | 1.3732 | 3.7334 | 2.8315 | 0.5046 | 1.5468 | 27.225 | ||||
| 1.1271 | 0.0951 | 0.2187 | 0.2486 | 1.1477 | 0.0844 | 0.2042 | 0.2323 | ||||||
| 3 | 2.6505 | 0.6931 | 0.2454 | 0.3892 | 2.6506 | 0.596 | 0.2275 | 0.337 | 30.0 | ||||
| 1.1008 | 0.0853 | 0.2123 | 0.2289 | 1.1028 | 0.0781 | 0.201 | 0.2143 | ||||||
| 4 | 2.6562 | 0.6956 | 0.2428 | 0.389 | 2.6704 | 0.6202 | 0.2234 | 0.349 | 30.0 | ||||
| 1.0946 | 0.0824 | 0.2066 | 0.2247 | 1.1018 | 0.0777 | 0.1952 | 0.2093 | ||||||
| — | 40 | — | — | 2.6743 | 0.6288 | 0.2287 | 0.3466 | 2.7101 | 0.5719 | 0.2149 | 0.3144 | 40.0 | |
| 1.0994 | 0.0644 | 0.182 | 0.2054 | 1.1138 | 0.0569 | 0.1677 | 0.1913 | ||||||
| n | m | CS | LSE | WLSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MSEr () | RB () | AMSEr | MSEr () | RB () | AMSEr | ||||||||
| MSEr () | RB () | ARB | MSEr () | RB () | ARB | ||||||||
| 80 | 32 | 40 | 2.5 | 1 | 2.8428 | 0.8565 | 0.2717 | 0.4848 | 2.7992 | 0.5909 | 0.2308 | 0.3432 | 33.355 |
| 1.1972 | 0.113 | 0.243 | 0.2573 | 1.1934 | 0.0954 | 0.2221 | 0.2265 | ||||||
| 2 | 2.7256 | 0.8577 | 0.2636 | 0.4732 | 2.7318 | 0.6913 | 0.237 | 0.3852 | 32.071 | ||||
| 1.1186 | 0.0886 | 0.2154 | 0.2395 | 1.1257 | 0.079 | 0.2022 | 0.2196 | ||||||
| 3 | 2.6344 | 0.5065 | 0.2035 | 0.2907 | 2.6428 | 0.4439 | 0.1916 | 0.257 | 40.0 | ||||
| 1.1187 | 0.0749 | 0.1908 | 0.1972 | 1.1234 | 0.0702 | 0.1891 | 0.1904 | ||||||
| 4 | 2.6387 | 0.5235 | 0.2103 | 0.2956 | 2.6375 | 0.4217 | 0.1889 | 0.2408 | 40.0 | ||||
| 1.12 | 0.0677 | 0.1892 | 0.1998 | 1.1223 | 0.0598 | 0.1768 | 0.1829 | ||||||
| 5.0 | 1 | 2.6647 | 0.5786 | 0.2233 | 0.3281 | 2.6718 | 0.4412 | 0.1928 | 0.253 | 39.817 | |||
| 1.121 | 0.0776 | 0.2003 | 0.2118 | 1.1296 | 0.0647 | 0.1785 | 0.1856 | ||||||
| 2 | 2.7457 | 0.7031 | 0.2377 | 0.3865 | 2.7881 | 0.6164 | 0.2209 | 0.3399 | 39.785 | ||||
| 1.1314 | 0.0698 | 0.1861 | 0.2119 | 1.1496 | 0.0635 | 0.1722 | 0.1966 | ||||||
| 3 | 2.6489 | 0.5129 | 0.2083 | 0.2934 | 2.6529 | 0.4371 | 0.1925 | 0.2526 | 40.0 | ||||
| 1.1273 | 0.074 | 0.1914 | 0.1998 | 1.1311 | 0.068 | 0.1847 | 0.1886 | ||||||
| 4 | 2.6033 | 0.5044 | 0.2073 | 0.2861 | 2.6031 | 0.4149 | 0.1887 | 0.2376 | 40.0 | ||||
| 1.0937 | 0.0677 | 0.1858 | 0.1966 | 1.0957 | 0.0602 | 0.1745 | 0.1816 | ||||||
| 60 | 2.5 | 1 | 3.3965 | 1.3908 | 0.3674 | 0.7832 | 3.56 | 1.5802 | 0.4248 | 0.8977 | 54.382 | ||
| 1.454 | 0.1757 | 0.3252 | 0.3463 | 1.5268 | 0.2151 | 0.388 | 0.4064 | ||||||
| 2 | 3.3788 | 1.3606 | 0.362 | 0.7623 | 3.6484 | 1.8925 | 0.4599 | 1.0598 | 54.252 | ||||
| 1.4422 | 0.164 | 0.3153 | 0.3387 | 1.5394 | 0.2271 | 0.3994 | 0.4296 | ||||||
| 3 | 2.5861 | 0.3308 | 0.1727 | 0.1884 | 2.5978 | 0.2921 | 0.1604 | 0.168 | 60.0 | ||||
| 1.1069 | 0.046 | 0.1549 | 0.1638 | 1.112 | 0.0439 | 0.1492 | 0.1548 | ||||||
| 4 | 2.693 | 0.4485 | 0.1925 | 0.2489 | 2.7146 | 0.4577 | 0.1884 | 0.255 | 59.87 | ||||
| 1.1429 | 0.0492 | 0.1556 | 0.1741 | 1.1524 | 0.0522 | 0.1552 | 0.1718 | ||||||
| 5.0 | 1 | 2.6588 | 0.4155 | 0.1814 | 0.2292 | 2.6804 | 0.3298 | 0.1611 | 0.1839 | 59.651 | |||
| 1.1205 | 0.0428 | 0.1467 | 0.164 | 1.1337 | 0.038 | 0.1333 | 0.1472 | ||||||
| 2 | 2.6541 | 0.4281 | 0.1915 | 0.2359 | 2.7008 | 0.3911 | 0.1809 | 0.2155 | 59.628 | ||||
| 1.1138 | 0.0438 | 0.1489 | 0.1702 | 1.1327 | 0.0398 | 0.1384 | 0.1596 | ||||||
| 3 | 2.6026 | 0.3362 | 0.1785 | 0.1907 | 2.6195 | 0.3094 | 0.1655 | 0.1762 | 60.0 | ||||
| 1.1084 | 0.0451 | 0.1561 | 0.1673 | 1.1148 | 0.0431 | 0.148 | 0.1568 | ||||||
| 4 | 2.6025 | 0.3702 | 0.1814 | 0.2073 | 2.6215 | 0.3348 | 0.169 | 0.1884 | 60.0 | ||||
| 1.1014 | 0.0445 | 0.1531 | 0.1672 | 1.1086 | 0.042 | 0.1461 | 0.1576 | ||||||
| — | 80 | — | — | 2.5721 | 0.2718 | 0.1571 | 0.1509 | 2.5982 | 0.2592 | 0.1468 | 0.144 | 80.0 | |
| 1.0994 | 0.0299 | 0.1261 | 0.1416 | 1.1106 | 0.0289 | 0.1171 | 0.132 | ||||||
| n | m | CS | PE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MSEr () | RB () | AMSEr | |||||||
| MSEr () | RB () | ARB | |||||||
| 40 | 16 | 20 | 2.5 | 1 | 3.0511 | 1.4295 | 0.3503 | 0.7968 | 16.139 |
| 1.2304 | 0.1641 | 0.2834 | 0.3168 | ||||||
| 2 | 3.1193 | 1.7078 | 0.3912 | 0.9375 | 16.01 | ||||
| 1.2273 | 0.1671 | 0.2821 | 0.3366 | ||||||
| 3 | 3.0038 | 1.2282 | 0.3224 | 0.6908 | 20.0 | ||||
| 1.2288 | 0.1533 | 0.2719 | 0.2972 | ||||||
| 4 | 3.091 | 1.3674 | 0.3391 | 0.7528 | 20.0 | ||||
| 1.2351 | 0.1381 | 0.2583 | 0.2987 | ||||||
| 5.0 | 1 | 3.2972 | 2.2332 | 0.4447 | 1.2006 | 19.916 | |||
| 1.2615 | 0.168 | 0.2796 | 0.3621 | ||||||
| 2 | 3.3258 | 2.2933 | 0.45 | 1.2216 | 19.908 | ||||
| 1.2603 | 0.1499 | 0.2631 | 0.3565 | ||||||
| 3 | 3.0684 | 1.4316 | 0.3432 | 0.8077 | 20.0 | ||||
| 1.2555 | 0.1837 | 0.2943 | 0.3188 | ||||||
| 4 | 2.997 | 1.2712 | 0.3219 | 0.6971 | 20.0 | ||||
| 1.1998 | 0.1229 | 0.246 | 0.2839 | ||||||
| 30 | 2.5 | 1 | 3.2021 | 1.7333 | 0.3804 | 0.931 | 27.236 | ||
| 1.2489 | 0.1287 | 0.2493 | 0.3148 | ||||||
| 2 | 3.1476 | 1.7034 | 0.3831 | 0.9148 | 27.123 | ||||
| 1.233 | 0.1262 | 0.2526 | 0.3178 | ||||||
| 3 | 2.8463 | 0.8041 | 0.2631 | 0.4438 | 30.0 | ||||
| 1.1596 | 0.0836 | 0.2022 | 0.2327 | ||||||
| 4 | 2.8844 | 0.9053 | 0.2826 | 0.4944 | 29.831 | ||||
| 1.1688 | 0.0835 | 0.2042 | 0.2434 | ||||||
| 5.0 | 1 | 3.1889 | 1.8176 | 0.3963 | 0.9671 | 29.848 | |||
| 1.2275 | 0.1166 | 0.2323 | 0.3143 | ||||||
| 2 | 3.2246 | 1.8797 | 0.4083 | 0.993 | 29.826 | ||||
| 1.2286 | 0.1062 | 0.2288 | 0.3186 | ||||||
| 3 | 2.8633 | 0.8774 | 0.27 | 0.4809 | 30.0 | ||||
| 1.1628 | 0.0844 | 0.2048 | 0.2374 | ||||||
| 4 | 2.8472 | 0.9434 | 0.2839 | 0.5127 | 30.0 | ||||
| 1.1532 | 0.082 | 0.202 | 0.2429 | ||||||
| — | 40 | — | — | 2.8255 | 0.8312 | 0.2887 | 0.4467 | 40.0 | |
| 1.1447 | 0.0623 | 0.1793 | 0.234 | ||||||
| n | m | CS | PE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MSEr () | RB () | AMSEr | |||||||
| MSEr () | RB () | ARB | |||||||
| 80 | 32 | 40 | 2.5 | 1 | 2.7908 | 0.6698 | 0.2392 | 0.3776 | 32.907 |
| 1.1638 | 0.0855 | 0.2087 | 0.2239 | ||||||
| 2 | 2.8753 | 0.9004 | 0.2744 | 0.4898 | 32.827 | ||||
| 1.1673 | 0.0792 | 0.1971 | 0.2358 | ||||||
| 3 | 2.7379 | 0.5046 | 0.2059 | 0.29 | 40.0 | ||||
| 1.1552 | 0.0754 | 0.1897 | 0.1978 | ||||||
| 4 | 2.7708 | 0.5796 | 0.2209 | 0.3242 | 40.0 | ||||
| 1.1544 | 0.0688 | 0.1851 | 0.203 | ||||||
| 5.0 | 1 | 2.9592 | 1.0991 | 0.3044 | 0.594 | 39.81 | |||
| 1.1995 | 0.0889 | 0.2049 | 0.2547 | ||||||
| 2 | 2.9931 | 1.1295 | 0.3173 | 0.6019 | 39.772 | ||||
| 1.1872 | 0.0744 | 0.1895 | 0.2534 | ||||||
| 3 | 2.7365 | 0.4856 | 0.2099 | 0.2788 | 40.0 | ||||
| 1.1514 | 0.072 | 0.193 | 0.2014 | ||||||
| 4 | 2.7742 | 0.5613 | 0.2182 | 0.314 | 40.0 | ||||
| 1.1553 | 0.0667 | 0.1846 | 0.2014 | ||||||
| 60 | 2.5 | 1 | 2.8425 | 0.6556 | 0.2381 | 0.3574 | 54.355 | ||
| 1.1715 | 0.0591 | 0.1705 | 0.2043 | ||||||
| 2 | 2.8161 | 0.6145 | 0.2263 | 0.3335 | 54.098 | ||||
| 1.162 | 0.0526 | 0.1602 | 0.1933 | ||||||
| 3 | 2.6434 | 0.3439 | 0.1773 | 0.1921 | 60.0 | ||||
| 1.1255 | 0.0402 | 0.1448 | 0.161 | ||||||
| 4 | 2.6793 | 0.372 | 0.1842 | 0.2043 | 59.866 | ||||
| 1.1272 | 0.0366 | 0.1376 | 0.1609 | ||||||
| 5.0 | 1 | 2.8806 | 0.772 | 0.259 | 0.4106 | 59.648 | |||
| 1.168 | 0.0493 | 0.1532 | 0.2061 | ||||||
| 2 | 2.8851 | 0.7899 | 0.2676 | 0.4223 | 59.633 | ||||
| 1.173 | 0.0546 | 0.1622 | 0.2149 | ||||||
| 3 | 2.6653 | 0.3615 | 0.1775 | 0.2006 | 60.0 | ||||
| 1.1268 | 0.0396 | 0.1416 | 0.1596 | ||||||
| 4 | 2.6953 | 0.4076 | 0.1901 | 0.2244 | 60.0 | ||||
| 1.1321 | 0.0411 | 0.145 | 0.1675 | ||||||
| — | 80 | — | — | 2.6047 | 0.3859 | 0.2029 | 0.2099 | 80.0 | |
| 1.1059 | 0.0339 | 0.1369 | 0.1699 | ||||||
| n | m | CS | NACI | LTCI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CI () | AL () | COVP () | CI () | AL () | COVP () | ||||||
| CI () | AL () | COVP () | CI () | AL () | COVP () | ||||||
| 40 | 16 | 20 | 2.5 | 1 | {1.0681, 4.6926} | 3.6245 | 96.3 | {1.5378, 5.4128} | 3.875 | 94.8 | 16.057 |
| {0.5125, 1.9431} | 1.4306 | 95.4 | {0.6866, 2.2017} | 1.5151 | 93.5 | ||||||
| 2 | {1.0596, 4.671} | 3.6114 | 96.8 | {1.5278, 5.3886} | 3.8608 | 95.2 | 16.00 | ||||
| {0.5465, 1.8748} | 1.3283 | 95.2 | {0.7001, 2.0975} | 1.3974 | 94.2 | ||||||
| 3 | {1.0868, 4.7402} | 3.6534 | 96.6 | {1.5585, 5.4616} | 3.9031 | 94.2 | 20.0 | ||||
| {0.5557, 1.9007} | 1.345 | 95.5 | {0.7113, 2.1265} | 1.4152 | 92.1 | ||||||
| 4 | {1.1385, 4.5856} | 3.4471 | 96.9 | {1.5692, 5.233} | 3.6638 | 93.8 | 20.0 | ||||
| {0.5896, 1.836} | 1.2465 | 94.0 | {0.7261, 2.0294} | 1.3033 | 92.1 | ||||||
| 5.0 | 1 | {1.2269, 4.4822} | 3.2553 | 96.4 | {1.6163, 5.056} | 3.4397 | 93.1 | 19.909 | |||
| {0.6009, 1.8551} | 1.2542 | 94.1 | {0.7375, 2.0479} | 1.3104 | 91.0 | ||||||
| 2 | {1.1881, 4.4851} | 3.2971 | 96.5 | {1.5882, 5.0782} | 3.49 | 95.2 | 19.893 | ||||
| {0.6207, 1.7979} | 1.1772 | 95.1 | {0.7437, 1.9686} | 1.225 | 92.3 | ||||||
| 3 | {1.0867, 4.713} | 3.6264 | 96.8 | {1.5536, 5.4258} | 3.8721 | 95.1 | 20.0 | ||||
| {0.5572, 1.908} | 1.3509 | 96.2 | {0.7135, 2.1349} | 1.4214 | 92.7 | ||||||
| 4 | {1.1423, 4.5936} | 3.4512 | 97.8 | {1.5729, 5.2401} | 3.6672 | 95.5 | 20.0 | ||||
| {0.5904, 1.8371} | 1.2468 | 95.8 | {0.7269, 2.0303} | 1.3034 | 92.9 | ||||||
| 30 | 2.5 | 1 | {1.3288, 4.1823} | 2.8535 | 96.8 | {1.643, 4.6279} | 2.9848 | 94.7 | 27.169 | ||
| {0.6573, 1.6673} | 1.0100 | 94.3 | {0.7532, 1.7961} | 1.0429 | 93.2 | ||||||
| 2 | {1.2935, 4.1947} | 2.9012 | 95.1 | {1.6185, 4.6588} | 3.0403 | 93.0 | 27.083 | ||||
| {0.654, 1.6574} | 1.0034 | 93.6 | {0.7493, 1.7854} | 1.0361 | 92.8 | ||||||
| 3 | {1.3402, 4.268} | 2.9278 | 96.1 | {1.6648, 4.7296} | 3.0648 | 94.2 | 29.997 | ||||
| {0.6809, 1.6914} | 1.0106 | 95.7 | {0.7751, 1.817} | 1.0419 | 93.0 | ||||||
| 4 | {1.3343, 4.1667} | 2.8324 | 96.3 | {1.6446, 4.6057} | 2.9611 | 94.0 | 29.794 | ||||
| {0.6735, 1.6477} | 0.9741 | 95.8 | {0.7632, 1.7666} | 1.0034 | 94.4 | ||||||
| 5.0 | 1 | {1.3873, 4.1518} | 2.7644 | 96.1 | {1.6824, 4.5649} | 2.8825 | 95.2 | 29.854 | |||
| {0.7032, 1.6824} | 0.9791 | 95.4 | {0.7915, 1.7986} | 1.0072 | 93.0 | ||||||
| 2 | {1.3445, 4.1294} | 2.7849 | 96.9 | {1.6467, 4.5553} | 2.9086 | 94.3 | 29.815 | ||||
| {0.6855, 1.6387} | 0.9532 | 95.2 | {0.7713, 1.7518} | 0.9805 | 94.0 | ||||||
| 3 | {1.3452, 4.2851} | 2.9399 | 97.1 | {1.6712, 4.7486} | 3.0774 | 95.0 | 30.0 | ||||
| {0.6853, 1.7005} | 1.0152 | 95.9 | {0.7798, 1.8263} | 1.0466 | 94.2 | ||||||
| 4 | {1.3652, 4.2950} | 2.9298 | 96.9 | {1.6878, 4.7526} | 3.0647 | 93.4 | 30.0 | ||||
| {0.6995, 1.6927} | 0.9932 | 94.3 | {0.7900, 1.8123} | 1.0223 | 90.9 | ||||||
| — | 40 | — | — | {1.4824, 4.0224} | 2.54 | 96.0 | {1.7359, 4.3682} | 2.6323 | 93.3 | 40.0 | |
| {0.7518, 1.5912} | 0.8394 | 95.0 | {0.8189, 1.6765} | 0.8576 | 92.8 | ||||||
| n | m | CS | NACI | LTCI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CI () | AL () | COVP () | CI () | AL () | COVP () | ||||||
| CI () | AL () | COVP () | CI () | AL () | COVP () | ||||||
| 80 | 32 | 40 | 2.5 | 1 | {1.5301, 3.798} | 2.2679 | 97.2 | {1.7411, 4.079} | 2.3378 | 96.5 | 33.133 |
| {0.6835, 1.6453} | 0.9618 | 95.0 | {0.7708, 1.7606} | 0.9898 | 93.6 | ||||||
| 2 | {1.484, 3.8134} | 2.3294 | 95.9 | {1.707, 4.113} | 2.406 | 97.3 | 33.24 | ||||
| {0.7017, 1.594} | 0.8923 | 95.6 | {0.7784, 1.6937} | 0.9152 | 95.4 | ||||||
| 3 | {1.5093, 3.7731} | 2.2638 | 96.2 | {1.721, 4.0553} | 2.3343 | 96.7 | 40.0 | ||||
| {0.6899, 1.6} | 0.9101 | 95.7 | {0.7697, 1.7043} | 0.9346 | 94.8 | ||||||
| 4 | {1.5465, 3.7818} | 2.2353 | 96.8 | {1.7517, 4.0536} | 2.302 | 96.4 | 40.0 | ||||
| {0.7266, 1.5837} | 0.8571 | 96.6 | {0.7973, 1.6743} | 0.8771 | 95.4 | ||||||
| 5.0 | 1 | {1.6159, 3.6824} | 2.0665 | 97.2 | {1.794, 3.9138} | 2.1198 | 95.3 | 39.828 | |||
| {0.727, 1.5696} | 0.8425 | 95.9 | {0.7958, 1.6575} | 0.8617 | 94.3 | ||||||
| 2 | {1.5584, 3.7417} | 2.1833 | 96.5 | {1.7558, 4.002} | 2.2462 | 95.6 | 39.765 | ||||
| {0.7445, 1.5454} | 0.8009 | 95.5 | {0.8072, 1.6246} | 0.8174 | 94.2 | ||||||
| 3 | {1.5286, 3.8389} | 2.3103 | 96.9 | {1.7455, 4.1284} | 2.3829 | 96.0 | 40.0 | ||||
| {0.6998, 1.6164} | 0.9165 | 96.1 | {0.7799, 1.7209} | 0.941 | 93.8 | ||||||
| 4 | {1.5516, 3.8021} | 2.2505 | 97.7 | {1.7586, 4.0765} | 2.3179 | 95.7 | 40.0 | ||||
| {0.7329, 1.596} | 0.8631 | 96.4 | {0.804, 1.6872} | 0.8832 | 94.6 | ||||||
| 60 | 2.5 | 1 | {1.6769, 3.5516} | 1.8747 | 95.9 | {1.8268, 3.7421} | 1.9154 | 95.1 | 54.395 | ||
| {0.7808, 1.4833} | 0.7025 | 95.2 | {0.8302, 1.5442} | 0.714 | 94.8 | ||||||
| 2 | {1.6367, 3.5589} | 1.9222 | 95.5 | {1.7947, 3.7613} | 1.9666 | 94.4 | 54.273 | ||||
| {0.7749, 1.4725} | 0.6975 | 95.9 | {0.824, 1.5329} | 0.7089 | 95.5 | ||||||
| 3 | {1.6936, 3.6094} | 1.9158 | 96.3 | {1.8478, 3.8058} | 1.958 | 95.0 | 60.0 | ||||
| {0.7961, 1.4929} | 0.6968 | 94.5 | {0.8442, 1.5519} | 0.7077 | 93.8 | ||||||
| 4 | {1.6771, 3.5511} | 1.874 | 95.9 | {1.8269, 3.7415} | 1.9146 | 94.7 | 59.898 | ||||
| {0.7986, 1.4801} | 0.6816 | 95.1 | {0.8449, 1.5368} | 0.6918 | 94.2 | ||||||
| 5.0 | 1 | {1.7071, 3.5085} | 1.8014 | 95.9 | {1.8464, 3.6841} | 1.8377 | 94.3 | 59.654 | |||
| {0.7993, 1.4635} | 0.6641 | 94.5 | {0.8437, 1.5175} | 0.6738 | 93.4 | ||||||
| 2 | {1.6795, 3.543} | 1.8634 | 95.4 | {1.8279, 3.7313} | 1.9035 | 95.6 | 59.64 | ||||
| {0.7993, 1.4604} | 0.6612 | 96.4 | {0.8433, 1.514} | 0.6707 | 95.0 | ||||||
| 3 | {1.672, 3.5525} | 1.8805 | 95.9 | {1.8229, 3.7444} | 1.9216 | 95.0 | 60.0 | ||||
| {0.7843, 1.4748} | 0.6905 | 95.9 | {0.8322, 1.5336} | 0.7014 | 95.3 | ||||||
| 4 | {1.6853, 3.5707} | 1.8854 | 95.6 | {1.8361, 3.7625} | 1.9264 | 94.7 | 60.0 | ||||
| {0.7981, 1.4766} | 0.6786 | 94.6 | {0.8441, 1.5328} | 0.6888 | 93.2 | ||||||
| — | 80 | — | — | {1.7783, 3.4547} | 1.6764 | 96.1 | {1.8995, 3.6049} | 1.7054 | 94.2 | 80.0 | |
| {0.8429, 1.4213} | 0.5784 | 95.5 | {0.8769, 1.4617} | 0.5848 | 95.0 | ||||||
| SEL | LINEXL = −0.5 | LINEXL = 1.5 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RB () | MSEr () | ARB | RB () | MSEr () | ARB | RB () | MSEr () | ARB | ||||||||||
| CS | RB () | MSEr () | AMSEr | RB () | MSEr () | AMSEr | RB () | MSEr () | AMSEr | |||||||||
| 40 | 16 | 20 | 2.5 | 1 | 2.4920 | 0.0032 | 0.0221 | 0.0050 | 2.4948 | 0.0021 | 0.0220 | 0.0054 | 2.4837 | 0.0065 | 0.0224 | 0.0037 | 18.53 | |
| 1.1074 | 0.0067 | 0.0151 | 0.0186 | 1.1095 | 0.0087 | 0.0152 | 0.0186 | 1.1009 | 0.0008 | 0.0149 | 0.0186 | |||||||
| 2 | 2.4918 | 0.0033 | 0.0217 | 0.0021 | 2.4946 | 0.0022 | 0.0216 | 0.0025 | 2.4833 | 0.0067 | 0.0220 | 0.0059 | 18.143 | |||||
| 1.1010 | 0.0009 | 0.0150 | 0.0183 | 1.1032 | 0.0029 | 0.0150 | 0.0183 | 1.0944 | 0.0051 | 0.0150 | 0.0185 | |||||||
| 3 | 2.4964 | 0.0015 | 0.0208 | 0.0041 | 2.4991 | 0.0004 | 0.0208 | 0.0026 | 2.4883 | 0.0047 | 0.0211 | 0.0088 | 18.2365 | |||||
| 1.0925 | 0.0068 | 0.0162 | 0.0185 | 1.0948 | 0.0047 | 0.0162 | 0.0185 | 1.0858 | 0.0129 | 0.0162 | 0.0186 | |||||||
| 4 | 2.4921 | 0.0032 | 0.0221 | 0.0017 | 2.4949 | 0.0020 | 0.0220 | 0.0019 | 2.4837 | 0.0065 | 0.0226 | 0.0064 | 20 | |||||
| 1.0997 | 0.0003 | 0.0136 | 0.0178 | 1.1019 | 0.0017 | 0.0136 | 0.0178 | 1.0932 | 0.0062 | 0.0135 | 0.0180 | |||||||
| 5 | 1 | 2.4976 | 0.0010 | 0.0210 | 0.0012 | 2.5004 | 0.0001 | 0.0209 | 0.0003 | 2.4891 | 0.0043 | 0.0211 | 0.0058 | 19.892 | ||||
| 1.0984 | 0.0014 | 0.0150 | 0.0180 | 1.1006 | 0.0005 | 0.0151 | 0.0180 | 1.0920 | 0.0073 | 0.0150 | 0.0180 | |||||||
| 2 | 2.4944 | 0.0022 | 0.0213 | 0.0033 | 2.4972 | 0.0011 | 0.0229 | 0.0037 | 2.4859 | 0.0056 | 0.0236 | 0.0037 | 19.895 | |||||
| 1.1048 | 0.0044 | 0.0150 | 0.0190 | 1.1070 | 0.0064 | 0.0150 | 0.0190 | 1.0981 | 0.0017 | 0.0149 | 0.0192 | |||||||
| 3 | 2.4904 | 0.0038 | 0.0205 | 0.0024 | 2.4932 | 0.0027 | 0.0210 | 0.0018 | 2.4822 | 0.0071 | 0.0213 | 0.0070 | 20 | |||||
| 1.0989 | 0.0010 | 0.0137 | 0.0174 | 1.1010 | 0.0010 | 0.0137 | 0.0174 | 1.0925 | 0.0068 | 0.0137 | 0.0175 | |||||||
| 4 | 2.4921 | 0.0032 | 0.0221 | 0.0017 | 2.4949 | 0.0020 | 0.0220 | 0.0019 | 2.4837 | 0.0065 | 0.0226 | 0.0064 | 20 | |||||
| 1.0997 | 0.0003 | 0.0136 | 0.0178 | 1.1019 | 0.0017 | 0.0136 | 0.0178 | 1.0932 | 0.0062 | 0.0135 | 0.0180 | |||||||
| 30 | 2.5 | 1 | 2.4976 | 0.0010 | 0.0078 | 0.0010 | 2.4986 | 0.0006 | 0.0078 | 0.0012 | 2.4946 | 0.0022 | 0.0079 | 0.0018 | 27.292 | |||
| 1.1011 | 0.0010 | 0.0065 | 0.0072 | 1.1020 | 0.0018 | 0.0065 | 0.0072 | 1.0985 | 0.0014 | 0.0064 | 0.0072 | |||||||
| 2 | 2.4970 | 0.0012 | 0.0075 | 0.0007 | 2.4980 | 0.0008 | 0.0074 | 0.0009 | 2.4940 | 0.0024 | 0.0075 | 0.0023 | 27.105 | |||||
| 1.1002 | 0.0002 | 0.0066 | 0.0070 | 1.1011 | 0.0010 | 0.0066 | 0.0070 | 1.0976 | 0.0021 | 0.0066 | 0.0070 | |||||||
| 3 | 2.5007 | 0.0003 | 0.0083 | 0.0008 | 2.5018 | 0.0007 | 0.0083 | 0.0006 | 2.4975 | 0.0010 | 0.0083 | 0.0024 | 27.3564 | |||||
| 1.0985 | 0.0013 | 0.0072 | 0.0077 | 1.0994 | 0.0005 | 0.0071 | 0.0077 | 1.0958 | 0.0038 | 0.0072 | 0.0077 | |||||||
| 4 | 2.4956 | 0.0018 | 0.0087 | 0.0017 | 2.4966 | 0.0013 | 0.0086 | 0.0019 | 2.4925 | 0.0030 | 0.0088 | 0.0019 | 29.864 | |||||
| 1.1017 | 0.0016 | 0.0062 | 0.0074 | 1.1026 | 0.0024 | 0.0062 | 0.0074 | 1.0991 | 0.0009 | 0.0062 | 0.0075 | |||||||
| 5 | 1 | 2.5021 | 0.0008 | 0.0078 | 0.0016 | 2.5031 | 0.0012 | 0.0078 | 0.0022 | 2.4990 | 0.0004 | 0.0078 | 0.0003 | 29.831 | ||||
| 1.1027 | 0.0024 | 0.0063 | 0.0071 | 1.1035 | 0.0032 | 0.0063 | 0.0071 | 1.1001 | 0.0001 | 0.0063 | 0.0071 | |||||||
| 2 | 2.5008 | 0.0003 | 0.0074 | 0.0006 | 2.5019 | 0.0008 | 0.0087 | 0.0004 | 2.4976 | 0.0010 | 0.0087 | 0.0021 | 29.806 | |||||
| 1.0990 | 0.0009 | 0.0064 | 0.0076 | 1.0999 | 0.0001 | 0.0065 | 0.0076 | 1.0964 | 0.0033 | 0.0064 | 0.0075 | |||||||
| 3 | 2.4973 | 0.0011 | 0.0083 | 0.0006 | 2.4983 | 0.0007 | 0.0083 | 0.0008 | 2.4942 | 0.0023 | 0.0084 | 0.0023 | 30 | |||||
| 1.1001 | 0.0001 | 0.0062 | 0.0072 | 1.1010 | 0.0009 | 0.0062 | 0.0072 | 1.0975 | 0.0023 | 0.0062 | 0.0073 | |||||||
| 4 | 2.4958 | 0.0017 | 0.0075 | 0.0017 | 2.4968 | 0.0013 | 0.0075 | 0.0019 | 2.4927 | 0.0029 | 0.0076 | 0.0018 | 30 | |||||
| 1.1019 | 0.0018 | 0.0062 | 0.0069 | 1.1028 | 0.0025 | 0.0063 | 0.0069 | 1.0993 | 0.0006 | 0.0062 | 0.0069 | |||||||
| 40 | 40 | - | - | 2.4925 | 0.0030 | 0.0193 | 0.0016 | 2.4950 | 0.0020 | 0.0192 | 0.0019 | 2.4847 | 0.0061 | 0.0197 | 0.0056 | 39.76 | ||
| 1.1001 | 0.0001 | 0.0099 | 0.0146 | 1.1021 | 0.0019 | 0.0100 | 0.0146 | 1.0944 | 0.0051 | 0.0098 | 0.0147 | |||||||
| SEL | LINEXL = −0.5 | LINEXL = 1.5 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RB () | MSEr () | ARB | RB () | MSEr () | ARB | RB () | MSEr () | ARB | ||||||||||
| CS | RB () | MSEr () | AMSEr | RB () | MSEr () | AMSEr | RB () | MSEr () | AMSEr | |||||||||
| 80 | 32 | 40 | 2.5 | 1 | 2.5017 | 0.0007 | 0.0210 | 0.0018 | 2.5044 | 0.0018 | 0.0210 | 0.0032 | 2.4934 | 0.0026 | 0.0208 | 0.0025 | 37.081 | |
| 1.1032 | 0.0029 | 0.0110 | 0.0160 | 1.1051 | 0.0047 | 0.0110 | 0.0160 | 1.0975 | 0.0023 | 0.0109 | 0.0158 | |||||||
| 2 | 2.4936 | 0.0026 | 0.0229 | 0.0013 | 2.4963 | 0.0015 | 0.0229 | 0.0016 | 2.4852 | 0.0059 | 0.0232 | 0.0055 | 36.261 | |||||
| 1.1000 | 0.0000 | 0.0102 | 0.0166 | 1.1019 | 0.0017 | 0.0103 | 0.0166 | 1.0943 | 0.0052 | 0.0101 | 0.0167 | |||||||
| 3 | 2.4921 | 0.0032 | 0.0200 | 0.0037 | 2.4947 | 0.0021 | 0.0199 | 0.0040 | 2.4842 | 0.0063 | 0.0202 | 0.0034 | 40 | |||||
| 1.1047 | 0.0043 | 0.0094 | 0.0147 | 1.1065 | 0.0059 | 0.0095 | 0.0147 | 1.0994 | 0.0006 | 0.0093 | 0.0147 | |||||||
| 4 | 2.4980 | 0.0008 | 0.0188 | 0.0017 | 2.5006 | 0.0002 | 0.0188 | 0.0023 | 2.4904 | 0.0039 | 0.0188 | 0.0031 | 40 | |||||
| 1.1029 | 0.0027 | 0.0101 | 0.0144 | 1.1048 | 0.0043 | 0.0102 | 0.0145 | 1.0975 | 0.0023 | 0.0099 | 0.0144 | |||||||
| 5 | 1 | 2.4938 | 0.0025 | 0.0208 | 0.0017 | 2.4964 | 0.0014 | 0.0208 | 0.0020 | 2.4860 | 0.0056 | 0.0211 | 0.0048 | 39.828 | ||||
| 1.1011 | 0.0010 | 0.0095 | 0.0152 | 1.1029 | 0.0026 | 0.0096 | 0.0152 | 1.0956 | 0.0040 | 0.0094 | 0.0152 | |||||||
| 2 | 2.4954 | 0.0018 | 0.0203 | 0.0052 | 2.4980 | 0.0008 | 0.0204 | 0.0056 | 2.4875 | 0.0050 | 0.0204 | 0.0043 | 39.766 | |||||
| 1.1095 | 0.0086 | 0.0100 | 0.0158 | 1.1114 | 0.0103 | 0.0113 | 0.0158 | 1.1039 | 0.0035 | 0.0110 | 0.0157 | |||||||
| 3 | 2.4921 | 0.0032 | 0.0200 | 0.0037 | 2.4947 | 0.0021 | 0.0199 | 0.0040 | 2.4842 | 0.0063 | 0.0202 | 0.0034 | 40 | |||||
| 1.1047 | 0.0043 | 0.0094 | 0.0147 | 1.1065 | 0.0059 | 0.0095 | 0.0147 | 1.0994 | 0.0006 | 0.0093 | 0.0147 | |||||||
| 4 | 2.4980 | 0.0008 | 0.0188 | 0.0017 | 2.5006 | 0.0002 | 0.0188 | 0.0023 | 2.4904 | 0.0039 | 0.0188 | 0.0031 | 40 | |||||
| 1.1029 | 0.0027 | 0.0101 | 0.0144 | 1.1048 | 0.0043 | 0.0102 | 0.0145 | 1.0975 | 0.0023 | 0.0099 | 0.0144 | |||||||
| 60 | 2.5 | 1 | 2.4983 | 0.0007 | 0.0074 | 0.0010 | 2.4992 | 0.0003 | 0.0074 | 0.0011 | 2.4954 | 0.0018 | 0.0075 | 0.0014 | 54.419 | |||
| 1.1013 | 0.0012 | 0.0051 | 0.0063 | 1.1021 | 0.0019 | 0.0051 | 0.0063 | 1.0990 | 0.0009 | 0.0051 | 0.0063 | |||||||
| 2 | 2.4965 | 0.0014 | 0.0074 | 0.0013 | 2.4975 | 0.0010 | 0.0074 | 0.0015 | 2.4936 | 0.0026 | 0.0074 | 0.0017 | 54.21 | |||||
| 1.1013 | 0.0012 | 0.0051 | 0.0062 | 1.1021 | 0.0019 | 0.0051 | 0.0062 | 1.0990 | 0.0009 | 0.0051 | 0.0063 | |||||||
| 3 | 2.5015 | 0.0006 | 0.0080 | 0.0006 | 2.5025 | 0.0010 | 0.0080 | 0.0011 | 2.4985 | 0.0006 | 0.0079 | 0.0010 | 60 | |||||
| 1.1006 | 0.0006 | 0.0048 | 0.0064 | 1.1014 | 0.0013 | 0.0048 | 0.0064 | 1.0984 | 0.0015 | 0.0048 | 0.0063 | |||||||
| 4 | 2.5003 | 0.0001 | 0.0076 | 0.0017 | 2.5013 | 0.0005 | 0.0076 | 0.0023 | 2.4974 | 0.0011 | 0.0076 | 0.0011 | 59.853 | |||||
| 1.1037 | 0.0033 | 0.0051 | 0.0063 | 1.1045 | 0.0041 | 0.0051 | 0.0063 | 1.1013 | 0.0011 | 0.0051 | 0.0063 | |||||||
| 5 | 1 | 2.4997 | 0.0001 | 0.0081 | 0.0001 | 2.5007 | 0.0003 | 0.0081 | 0.0005 | 2.4967 | 0.0013 | 0.0081 | 0.0016 | 59.667 | ||||
| 1.1002 | 0.0001 | 0.0051 | 0.0066 | 1.1009 | 0.0008 | 0.0051 | 0.0066 | 1.0979 | 0.0019 | 0.0051 | 0.0066 | |||||||
| 2 | 2.4929 | 0.0028 | 0.0078 | 0.0018 | 2.4939 | 0.0024 | 0.0078 | 0.0020 | 2.4898 | 0.0041 | 0.0079 | 0.0027 | 59.589 | |||||
| 1.1009 | 0.0008 | 0.0051 | 0.0064 | 1.1016 | 0.0015 | 0.0051 | 0.0064 | 1.0985 | 0.0013 | 0.0051 | 0.0065 | |||||||
| 3 | 2.5015 | 0.0006 | 0.0080 | 0.0006 | 2.5025 | 0.0010 | 0.0080 | 0.0011 | 2.4985 | 0.0006 | 0.0079 | 0.0010 | 60 | |||||
| 1.1006 | 0.0006 | 0.0048 | 0.0064 | 1.1014 | 0.0013 | 0.0048 | 0.0064 | 1.0984 | 0.0015 | 0.0048 | 0.0063 | |||||||
| 4 | 2.5022 | 0.0009 | 0.0078 | 0.0015 | 2.5032 | 0.0013 | 0.0078 | 0.0021 | 2.4993 | 0.0003 | 0.0078 | 0.0002 | 60 | |||||
| 1.1024 | 0.0022 | 0.0050 | 0.0064 | 1.1032 | 0.0029 | 0.0050 | 0.0064 | 1.1001 | 0.0001 | 0.0050 | 0.0064 | |||||||
| 80 | 80 | - | - | 2.4980 | 0.0008 | 0.0182 | 0.0037 | 2.5006 | 0.0003 | 0.0182 | 0.0041 | 2.4903 | 0.0039 | 0.0182 | 0.0032 | 79.534 | ||
| 1.1072 | 0.0065 | 0.0065 | 0.0124 | 1.1086 | 0.0079 | 0.0066 | 0.0124 | 1.1029 | 0.0026 | 0.0064 | 0.0123 | |||||||
| Data | Estimates | SE | KS | p-Value | |
|---|---|---|---|---|---|
| I | 2.3358 | 0.3300 | 0.0366 | 0.9993 | |
| 0.1357 | 0.0162 | ||||
| II | 0.8571 | 0.2030 | 0.1198 | 0.8579 | |
| 0.4447 | 0.1460 |
| CS | Observation | |
|---|---|---|
| 1 | 0.8 0.8 1.3 1.5 1.8 1.9 1.9 2.1 2.6 2.7 2.9 3.1 3.2 3.3 4.1 4.2 4.3 4.4 4.4 4.6 4.7 4.7 4.8 4.9 4.9 5.5 5.7 5.7 6.1 6.2 6.2 6.3 6.7 6.9 7.1 7.1 7.1 7.1 7.6 7.7 8.2 8.6 8.6 8.8 8.8 9.5 9.6 9.7 10.7 10.9 11.0 11.1 11.2 11.2 11.5 | 55 |
| 2 | 0.8 0.8 1.3 1.5 1.8 1.9 1.9 2.6 2.9 3.1 3.2 3.3 3.6 4.0 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.6 4.8 4.9 4.9 5.0 5.5 5.7 5.7 6.1 6.2 6.2 6.3 6.7 6.9 7.1 7.1 7.4 7.6 7.7 8.0 8.6 8.6 8.8 8.8 8.9 9.5 9.6 9.7 9.8 10.7 10.9 11.0 11.0 11.1 11.2 11.9 | 57 |
| 3 | 0.8 0.8 1.3 1.5 1.8 1.9 1.9 2.1 2.6 2.7 2.9 3.1 3.2 3.3 3.5 3.6 4.0 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.6 4.7 4.7 4.8 4.9 4.9 5.0 5.3 5.5 5.7 5.7 6.1 6.2 6.2 6.2 6.3 6.7 6.9 7.1 7.1 7.1 7.1 7.4 7.6 7.7 8.0 8.2 8.6 8.6 8.6 8.8 8.8 8.9 8.9 9.5 9.6 9.7 9.8 10.7 10.9 11.0 11.0 11.1 11.2 11.2 11.5 11.9 | 71 |
| 4 | 0.8 0.8 1.3 1.5 1.8 1.9 1.9 2.1 2.6 2.7 2.9 3.1 3.2 3.3 3.6 4.0 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.6 4.7 4.8 4.9 4.9 5.0 5.5 5.7 5.7 6.1 6.2 6.2 6.2 6.3 6.7 6.9 7.1 7.1 7.4 7.6 7.7 8.0 8.6 8.6 8.8 8.8 8.9 8.9 9.5 9.6 9.7 9.8 10.7 10.9 11.0 11.0 11.1 11.2 11.5 11.9 | 63 |
| MLE | Bayesian | ||||
|---|---|---|---|---|---|
| CS | Estimates | SE | Bayes | SEBayes | |
| 1 | 2.1173 | 0.3615 | 2.3120 | 0.3444 | |
| 0.1213 | 0.0210 | 0.1322 | 0.0191 | ||
| 2 | 2.2197 | 0.3847 | 2.3149 | 0.3347 | |
| 0.1312 | 0.0218 | 0.1366 | 0.0184 | ||
| 3 | 2.2943 | 0.3722 | 2.3563 | 0.3424 | |
| 0.1331 | 0.0199 | 0.1366 | 0.0181 | ||
| 4 | 2.1549 | 0.3594 | 2.2909 | 0.3154 | |
| 0.1261 | 0.0203 | 0.1345 | 0.0181 | ||
| CS | Observation | |
|---|---|---|
| 1 | 0.062 0.070 0.101 0.150 0.199 0.273 0.347 0.358 0.402 0.491 0.605 0.614 0.746 0.954 1.060 | 15 |
| 2 | 0.062 0.070 0.101 0.150 0.199 0.273 0.347 0.358 0.402 0.491 0.605 0.614 0.746 0.954 1.921 | 15 |
| 3 | 0.062 0.070 0.101 0.150 0.199 0.273 0.347 0.358 0.402 0.491 0.605 0.614 0.746 0.954 1.060 1.359 1.921 | 17 |
| 4 | 0.062 0.070 0.101 0.150 0.199 0.273 0.347 0.358 0.402 0.491 0.491 0.605 0.614 0.746 0.954 1.060 1.921 | 16 |
| MLE | Bayesian | ||||
|---|---|---|---|---|---|
| CS | Estimates | SE | Bayes | SEBayes | |
| 1 | 0.9451 | 0.2726 | 0.9307 | 0.2508 | |
| 0.6276 | 0.2843 | 0.6267 | 0.2656 | ||
| 2 | 0.9151 | 0.2605 | 0.8824 | 0.2362 | |
| 0.5770 | 0.2640 | 0.5357 | 0.2342 | ||
| 3 | 0.9283 | 0.2576 | 0.9225 | 0.2466 | |
| 0.5299 | 0.2265 | 0.5372 | 0.2047 | ||
| 4 | 0.9514 | 0.2679 | 0.9306 | 0.2599 | |
| 0.6075 | 0.2623 | 0.5903 | 0.2378 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelwahab, M.M.; Ghorbal, A.B.; Hassan, A.S.; Elgarhy, M.; Almetwally, E.M.; Hashem, A.F. Classical and Bayesian Inference for the Kavya–Manoharan Generalized Exponential Distribution under Generalized Progressively Hybrid Censored Data. Symmetry 2023, 15, 1193. https://doi.org/10.3390/sym15061193
Abdelwahab MM, Ghorbal AB, Hassan AS, Elgarhy M, Almetwally EM, Hashem AF. Classical and Bayesian Inference for the Kavya–Manoharan Generalized Exponential Distribution under Generalized Progressively Hybrid Censored Data. Symmetry. 2023; 15(6):1193. https://doi.org/10.3390/sym15061193
Chicago/Turabian StyleAbdelwahab, Mahmoud M., Anis Ben Ghorbal, Amal S. Hassan, Mohammed Elgarhy, Ehab M. Almetwally, and Atef F. Hashem. 2023. "Classical and Bayesian Inference for the Kavya–Manoharan Generalized Exponential Distribution under Generalized Progressively Hybrid Censored Data" Symmetry 15, no. 6: 1193. https://doi.org/10.3390/sym15061193
APA StyleAbdelwahab, M. M., Ghorbal, A. B., Hassan, A. S., Elgarhy, M., Almetwally, E. M., & Hashem, A. F. (2023). Classical and Bayesian Inference for the Kavya–Manoharan Generalized Exponential Distribution under Generalized Progressively Hybrid Censored Data. Symmetry, 15(6), 1193. https://doi.org/10.3390/sym15061193








