Lumped Element Method Based Conductivity Reconstruction Algorithm for Localization Using Symmetric Discrete Operators on Coarse Meshes
Abstract
1. Introduction
2. Related Work
3. The Basics of Self-Developed Algorithms
3.1. The Direct Problem
- Discretization: the continuous PDE is transformed into its discrete counterpart;
- Approximation: the unknown potential values are obtained by solving the discrete linear system of equations.
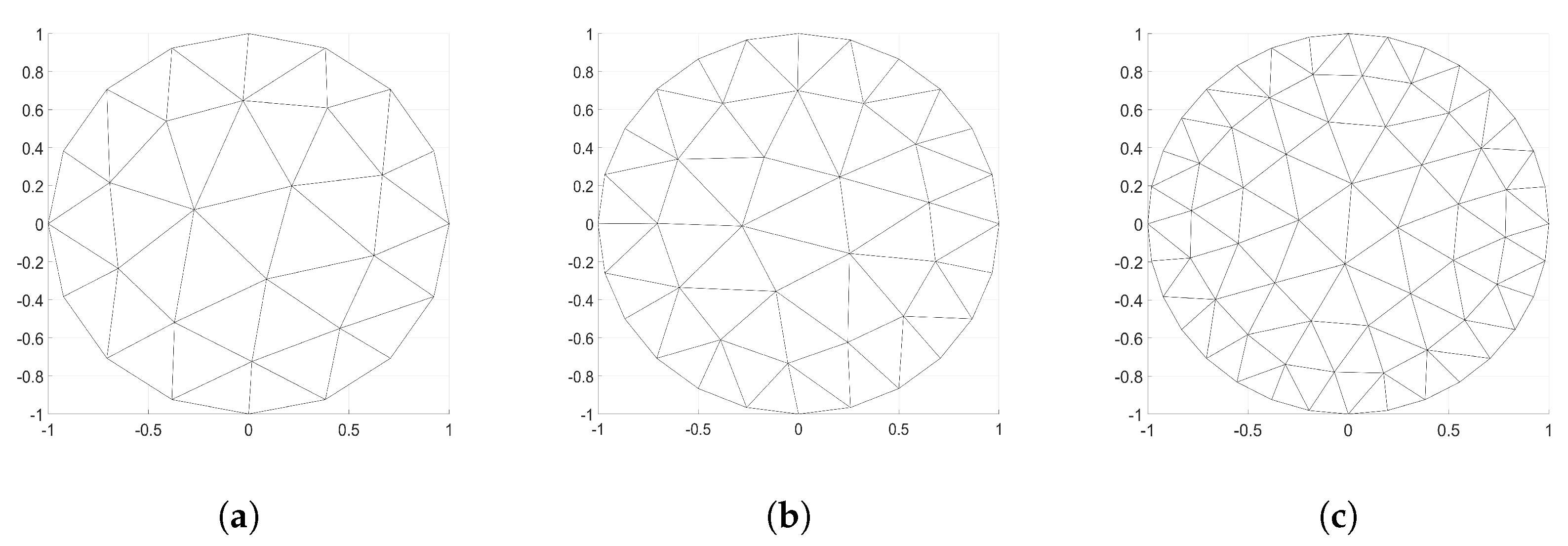
- Spatial discretization of the investigated domain: here in the proposed method it is the triangulation, using the Distmesh algorithm by Delunay triangulation [52], with the following properties:
- : mesh;
- : nodes;
- : branches (sides);
- : triangles.
- is the area of segment of the triangle, defined by connecting the center of the circumcircle with the middle points of the edges;
- is the radius of the circumcircle of the triangle;
- h is the height.
Since i and j denote the local numbering of the triangle vertices, the elements are placed in the matrix based on the branches connecting the and vertices in the triangle. Furthermore, (in Equation (2)) is the vector of average values calculated for triangles, which is determined from the average values of taken at the vertices in the triangle. Finally, is the vector of weights (concentrated parameters) resulting from the novel discretization method. The geometric transformation proposed by Vizvari et al. [6] is based on the matrix in Equation (2), whose elements are determined using Equation (3). This matrix transforms the continuous physical domain into the graph, on which further calculations take place. The calculation of the values in is based on simple geometric manipulations on the elements of the triangular mesh. As a result of the work, the geometric transformation can be performed as follows:- (a)
- For each triangle, three values can be calculated on the basis of the element segments, which are produced by connecting the midpoints of the sides and the center of the circumcircle.
- (b)
- The discretization error occurs when these segments are replaced by their equivalent subdomains with a constant cross-section.
- (c)
- At this point, a graph corresponding to a star connection can be created from the triangle, which can be transformed into a delta triangle using the star–delta transformation [1]. Thus, the derived symmetric weighted graph replaces the original triangle.
- (d)
- Triangle connections are considered using the matrix in Equation (2).
- (e)
- The elements of the vector can be obtained by simple averaging, where the coordinates of the triangle vertices and the center of the circumcircle are substituted into the function. Next, the arithmetic mean of the resulting values is calculated.
Further detailed descriptions illustrated with figures can be found in the relevant publication summarizing the results of the work by Vizvari et al. [6].- Based on Vizvari et al. [6], the following system of linear equations, considering , is as follows:where
- is the symmetric weighted Laplacian graph constructed by LumEM;
- is the branch-node incidence matrix;
- is the admittance matrix (based on Equation (3): );
- is the conductance vector (based on Equation (3): );
- is the capacitance vector (based on Equation (3): );
- is the potential vector;
- is the node current vector;
- is the angular frequency;
- .
3.2. Data Collection Strategy
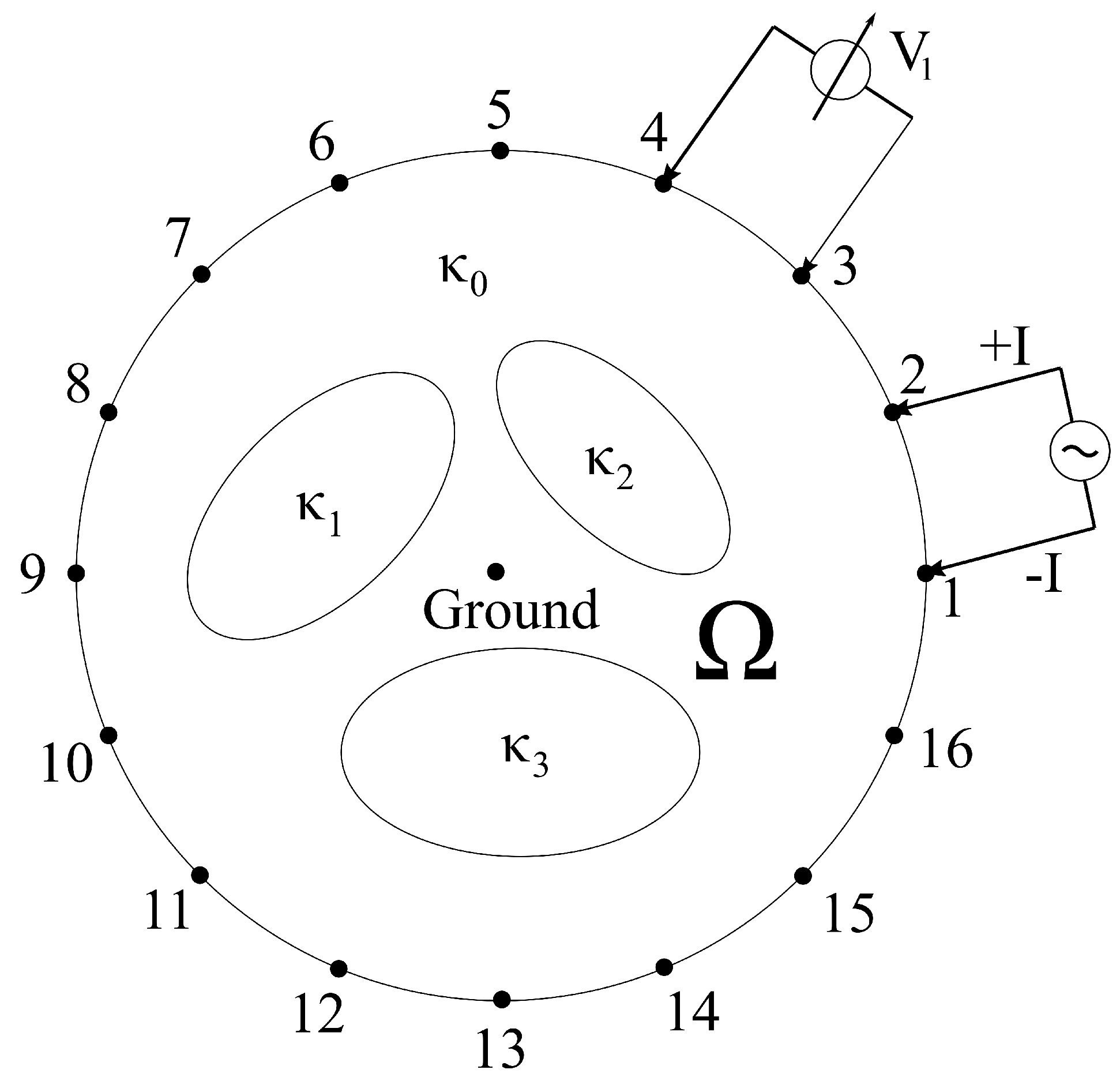
- Place the generator on the first two electrodes (points 1 and 2 in Figure 1), then take the measurements of the remaining 14 electrodes.
- Then place the generator on the next adjacent pair of electrodes (points 3 and 4 in Figure 1) and take the measurements of the remaining 14 electrodes again.
- All of this is repeated until the generator returns to the starting position [1].
- is number of equations;
- n is number of nodes constructed by LumEM [6];
- is number of frequencies applied for each measurement;
- is number of measurements applied for each generator position.
3.3. The Inverse Problem
- number of unknown values in the concatenated system;
- number of branches in graph;
- number of nodes placed in domain ().
3.4. Algorithms for Solving Inverse Problems
3.4.1. Newton Method
- is the solution vector in the step of the iteration;
- is the solution vector in the k step of the iteration;
- is the Moore–Penrose inverse of Jacobian which, due to the quadratic system of equations, can be calculated symbolically as follows:
3.4.2. Singular Value Decomposition
- is an orthogonal matrix;
- is an orthogonal matrix;
- is an diagonal matrix with non-negative elements that are called singular values.
3.4.3. Tikhonov Regularization
- is the regularization parameter;
- is the solution vector in case of optimal value;
- is the residual norm;
- is solution seminorm in the case of an prior solution vector.
3.5. Visualization Methods
- is the relative error of conductivity value corresponding to the triangle;
- is the relative error of dielectric constant value corresponding to the triangle.
4. Reconstruction Algorithm for Inverse Conductivity Problem
| Algorithm 1: The LumEM solver function. |
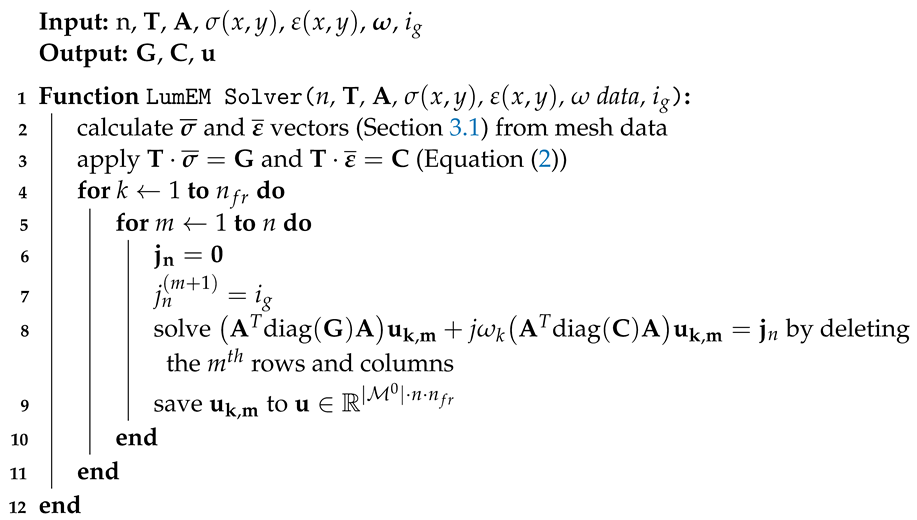 |
- The vectors and consist of homogeneous values on the triangles, and they are generated from the functions and by averaging, where the utilized values were taken at the vertices of each triangle and at the center of their circumcircle (row 2 in Algorithm 1) [6].
- Then, Equation (2) calculates the values of the weights (, ) taken on the edges of the graph formed from the triangular mesh. The matrix shown in the input of the procedure is generated using Equation (3). Then, everything is prepared to start calculating the potential values taken at the nodes using Equation (4).
- For this, a “for” loop is started in the first step, where the elements of the angular frequency vector are selected with the k parameter.
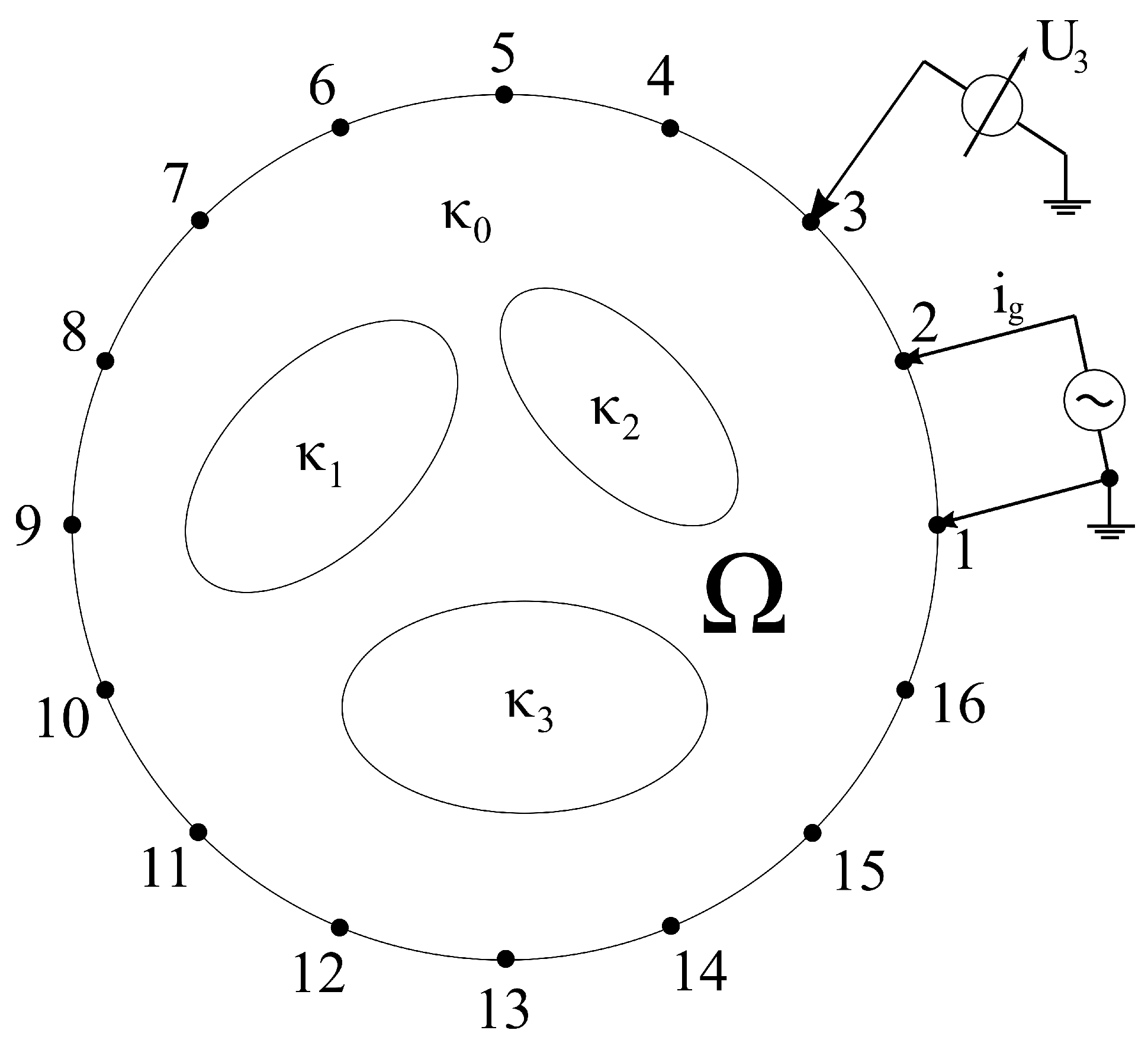
- Then another “for” loop starts, which selects the position of the ground point (m in Algorithm 1) on the graph in the case of the modified adjacent pattern shown in Figure 2.
- When applying the LumEM solver function, the following operations are performed for each frequency value and for each generator position:
- (a)
- The vector is created as a null vector, and then the generator current value is entered in the element (rows 6–7 in Algorithm 1);
- (b)
- Obtaining the solution, the equation system provides the potential vector for the entire graph (row 8 in Algorithm 1). Naturally, the previously presented calculation takes place at the generator position and the angular frequency value.
- The resulting data are built from all angular frequency values and n generator positions. This structure is defined as a solution to the direct problem.
| Algorithm 2: Direct problem solver. |
| Input: n, mesh data, , , , |
| Output: , , |
| 1 build from mesh data |
| 2 build from mesh data (Equation (3)) |
| 3 , , = LumEM Solver(n, , , , , , ) |
| 4 = |
- In the first step, the solver calculates the branch-node incidence matrix.
- In the second step (based on Equation (4)), the transformation matrix is constructed.
- Then, using these matrices and all the other input parameters, the LumEM solver function is run, which generates the , matrices and the potential data structure.
- For further calculations, the values taken from the data are only needed at boundary nodes; therefore, during the generation of the structure, these are extracted from the dataset. Thus, the structure only contains values taken at the boundary nodes for all generator positions and angular frequencies.
- The handling of the initial condition is fully consistent with the procedure described in Algorithm 2, since the LumEM solver function (Algorithm 1) is used in the same way. However, in this case, the , matrices are calculated from the function (row 3 in Algorithm 3).
- Nevertheless, here the potential structure is not extracted for boundary vertices only, as it is extracted for all the other nodes too.
- After these steps, and before starting the Newton iteration, the vector is generated by rearranging and concatenating the , and structures.
- Entering the Newton iteration (after step ), and are extracted from the vector (rows 7–9 in Algorithm 3).
- Then, two “for” loops are started, where angular frequencies are selected by k and generator positions are parameterized by m (rows 10–11 in Algorithm 3).
- The generator vector is handled in exactly the same way as in the case of the LumEM solver function (Algorithm 1).
- Next, the potential vector for the actual angular frequency and generator position is extracted from the vector.
- The driving force of the reconstruction algorithm comes from the fact that the calculated from function and taken from boundary points is concatenated with , calculated from the , rather than taken at non-boundary points at all present frequencies and generator positions (row 15 in Algorithm 3).
- The residual of the equation system (calculated from the potential vector , matrices , , , the current angular frequency value, and the vector) is no longer zero in Algorithm 3 (row 16 in Algorithm 3).
- At each angular frequency value and generator position (and naturally, at each step in the Newton iteration (Section 3.4.1)), a new and updated Jacobian matrix is applied. The Jacobian matrix (based on Section 3.4.1) can be determined by simple derivation, since now the represents a system of quadratic equations.
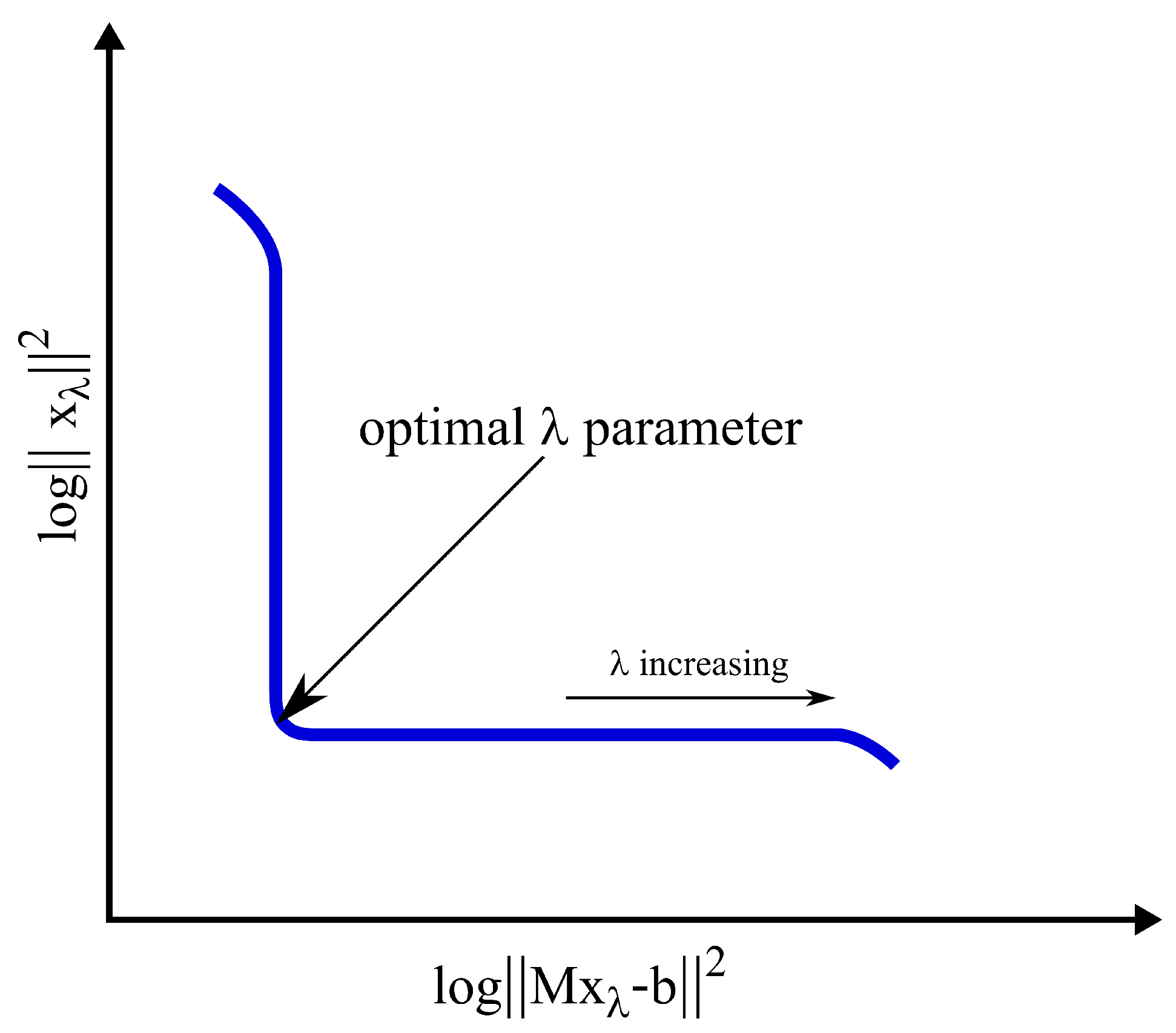
- The generalized inverse Jacobian required for the method is approximated using SVD (Section 3.4.2) [55] and Tikhonov regularization (Section 3.4.3) [55] in each step of the iteration (at each angular frequency value and generator position). The optimal parameter, based on the L-curve (Figure 3) [57], is generated using the MATLAB Regularization Toolbox at each step of the iteration (rows 18–19 in Algorithm 3) [57].
- As the product of the residual vector and the generalized inverse of the Jacobian at the actual angular frequency and generator position, the vector is calculated and then concatenated to all elements of the frequency vector and the generator position into a general vector.
- Next, a Newton step [36] is performed by (row 24 in Algorithm 3).
- The Newton iteration continues until the defined stop condition is achieved. The value of the stop condition is defined as one of the inputs in Algorithm 3. Actually, this is how the solution method of the quadratic system of equations (considering the unknown , matrices and vectors) is implemented in Algorithm 3. This system is an overdetermined system of equations, where the number of equations can be calculated using Equation (6), while the number of unknowns can be calculated using Equation (7).
- After the optimal solution is determined, the and vectors are extraxted from and transformed into and vectors using Equation (17) (rows 27–30 in Algorithm 3).
| Algorithm 3: Inverse problem solver. |
 |
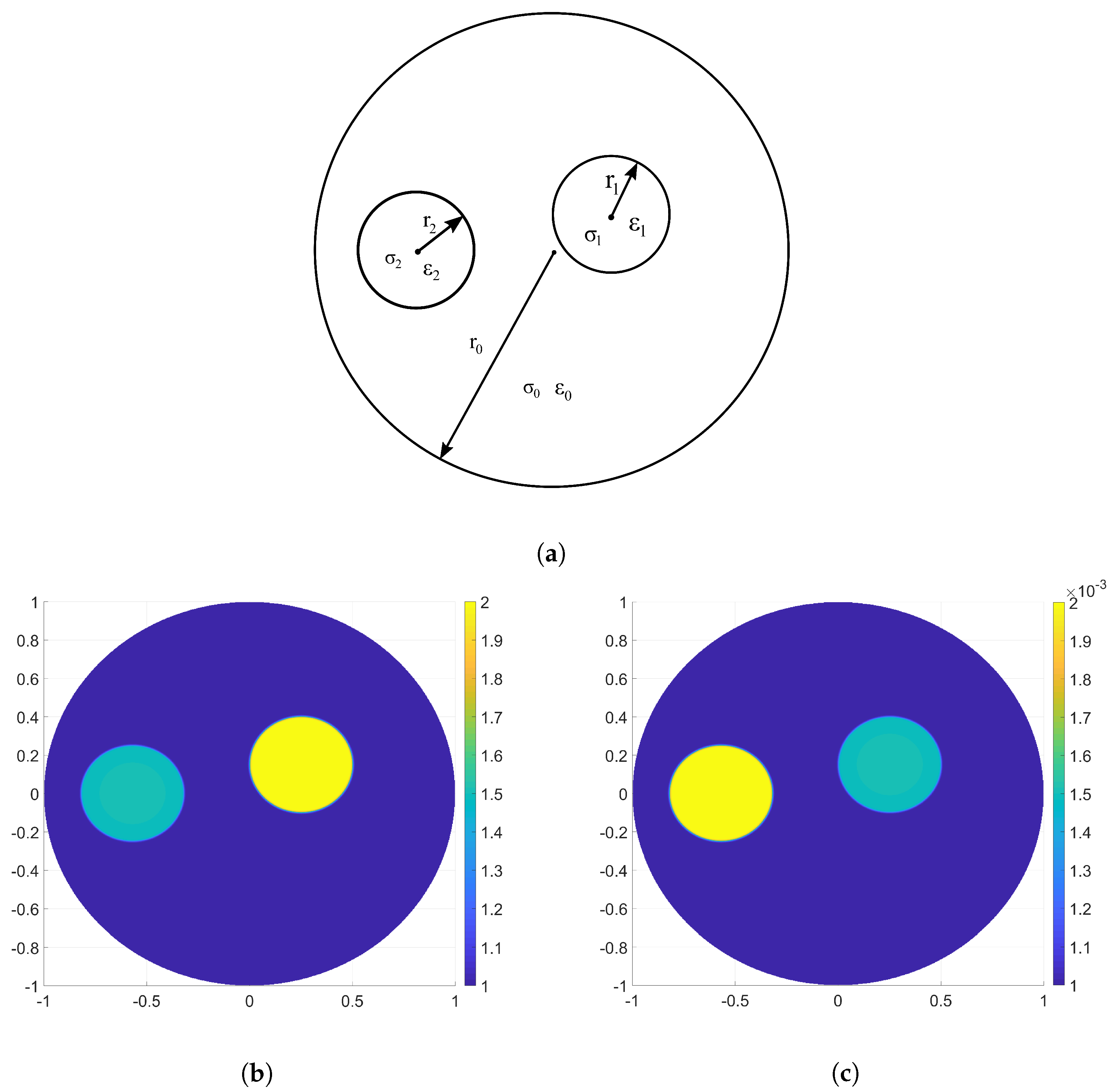
5. Case Studies
- Triangular mesh with 16 electrodes: , , , ;
- Triangular mesh with 24 electrodes: , , , ;
- Triangular mesh with 32 electrodes: , , , .
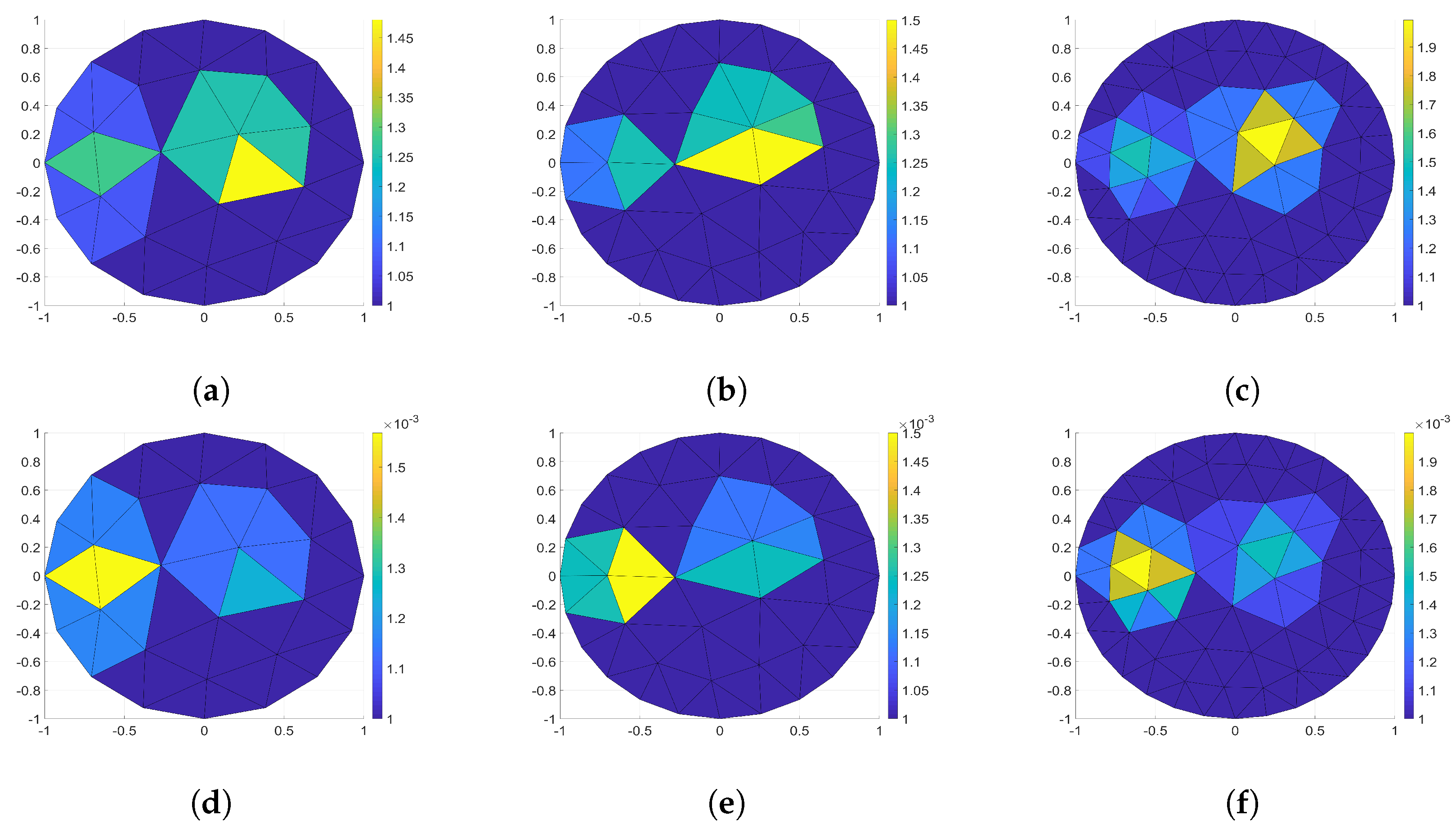
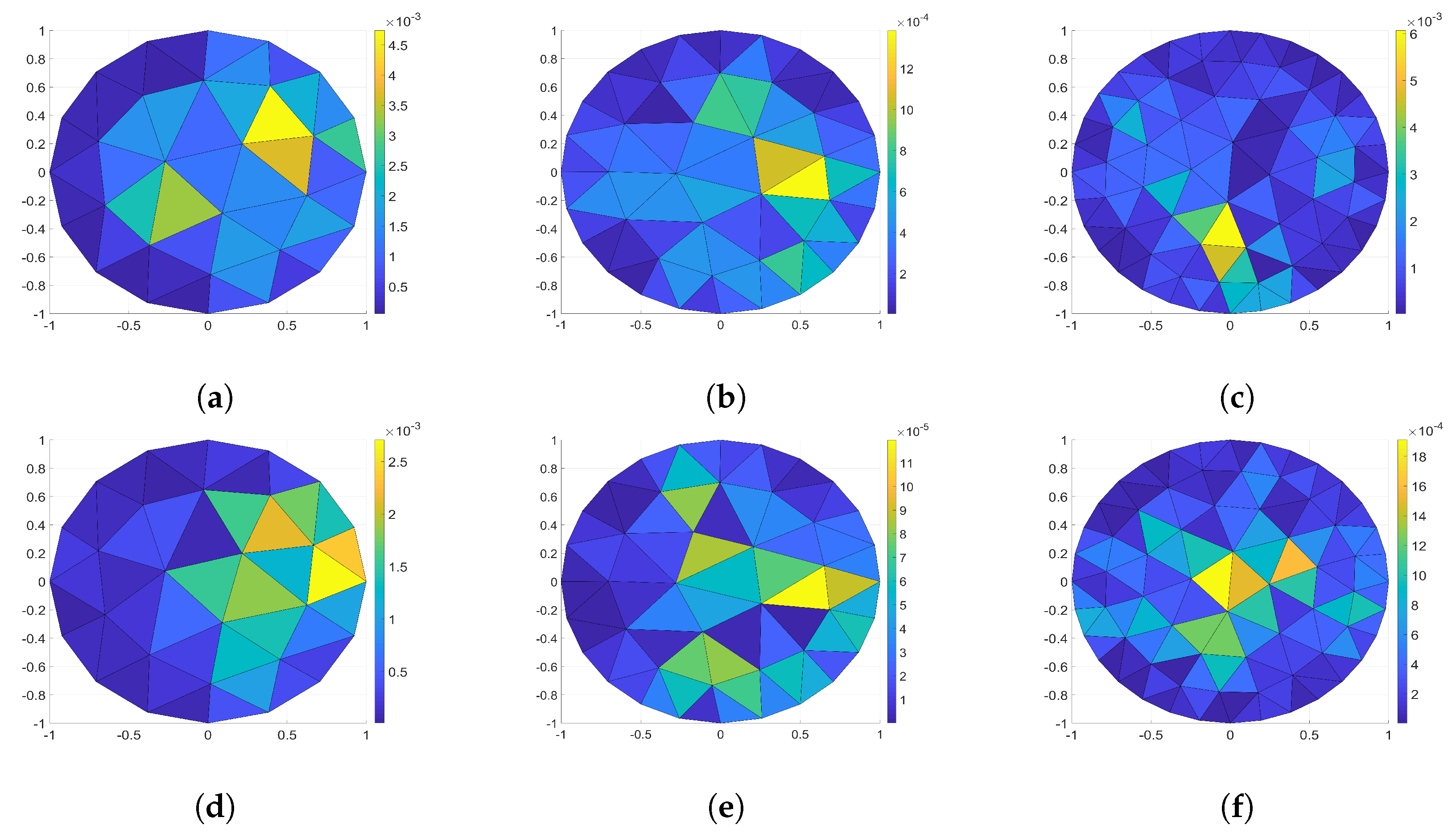
- The maximum relative error values of the 16-electrode solution were and ;
- For the 24-electrode solution, they were and ;
- For the 32-electrode solution, they were , and .
6. Conclusions
7. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holder, D. Electrical Impedance Tomography: Methods, History, and Applications; Institute of Physics Pub: Bristol, PA, USA, 2005; ISBN 9780750309523. [Google Scholar]
- Amalia, I. Continuous and Discrete Simulation in Electrodynamics; Akademiai Kiado: Budapest, Hungary, 2003; ISBN 9630579987. (In Hungarian) [Google Scholar]
- Cardoso, J. Electromagnetics through the Finite Element Method: A Simplified Approach Using Maxwell’s Equations; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Oxfordshire, UK, 2017; ISBN 1498783570. [Google Scholar]
- Jin, J.M. The Finite Element Method in Electromagnetics, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2014; ISBN 1118571363. [Google Scholar]
- Calderón, A.P. On an inverse boundary value problem. Comput. Appl. Math. Braz. Soc. Comput. Appl. Math. (SBMAC) 2006, 25, 2–3. [Google Scholar] [CrossRef]
- Vizvari, Z.; Klincsik, M.; Sari, Z.; Odry, P. Lumped Element Method—A Discrete Calculus Approach for Solving Elliptic and Parabolic PDEs. Acta Polytech. Hung. 2021, 18, 201–223. [Google Scholar] [CrossRef]
- Uhlmann, G. 30 Years of Calderón’s Problem, Seminaire Laurent Schwartz—EDP et Applications, Cellule MathDoc/CEDRAM, 2012, Séminaire Laurent Schwartz—EDP et Applications, 1–25. Available online: https://slsedp.centre-mersenne.org/item/SLSEDP_2012-2013____A13_0/ (accessed on 27 April 2023).
- Uhlmann, G. Electrical Impedance Tomography and Calderón’s Problem. Inverse Probl. 2009, 25, 123011. [Google Scholar] [CrossRef]
- Siltanen, S.; Mueller, J.L.; Isaacson, D. Reconstruction of high contrast 2-D conductivities by the algorithm of A. Nachman. Am. Math. Soc. 2001, 278, 241–254. [Google Scholar]
- Mueller, J.; Siltanen, S.; Isaacson, D. A direct reconstruction algorithm for electrical impedance tomography. IEEE Trans. Med Imaging Inst. Electr. Electron. Eng. 2002, 21, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Isaacson, D.; Newell, J.C.; Saulnier, G.J. Studies of an Adaptive Kaczmarz Method for Electrical Impedance Imaging. J. Physics: Conf. Ser. 2013, 434, 012075. [Google Scholar] [CrossRef]
- Li, T.; Kao, T.J.; Isaacson, D.; Newell, J.C.; Saulnier, G.J. Adaptive Kaczmarz Method for Image Reconstruction in Electrical Impedance Tomography. Physiol. Meas. 2013, 34, 595–608. [Google Scholar] [CrossRef]
- Chen, Z.Q. Reconstruction Algorithms for Electrical Impedance Tomography. Ph.D. Thesis, Department of Electrical and Computer Engineering, University of Wollongong, Hong Kong, China, 1990. Available online: http://ro.uow.edu.au/theses/1348 (accessed on 29 March 2023).
- Ahn, S.; Oh, T.I.; Jun, S.C.; Seo, J.K.; Woo, J.E.J. Validation of Weighted Frequency-Difference EIT Using a Three-Dimensional Hemisphere Model and Phantom. Physiol. Meas. 2011, 32, 1663–1680. [Google Scholar] [CrossRef] [PubMed]
- Boverman, G.; Isaacson, D.; Newell, J.C.; Saulnier, G.J.; Kao, T.J.; Amm, B.C.; Wang, X.; Davenport, D.; Chong, D.H.; Sahni, R.; et al. Efficient Simultaneous Reconstruction of Time-Varying Images and Electrode Contact Impedances in Electrical Impedance Tomography. IEEE Trans. Biomed. Eng. Inst. Electr. Electron. Eng. 2017, 64, 795–806. [Google Scholar] [CrossRef] [PubMed]
- Jerbi, K.; Lionheart, W.R.B.; Vauhkonen, P.J.; Vauhkonen, M. Sensitivity matrix and reconstruction algorithm for EIT assuming axial uniformity. Physiol. Meas. 2000, 21, 61–66. [Google Scholar] [CrossRef]
- Lionheart, W.R. Reconstruction Algorithms for Permittivity and Conductivity Imaging. In Proceedings of the 2nd World Congress on Industrial Process Tomography, Hannover, Germany, 29–31 August 2001; pp. 4–11. [Google Scholar]
- Graham, B.M.; Adler, A. Electrode placement configurations for 3D EIT. Physiol. Meas. 2007, 28, S29–S44. [Google Scholar] [CrossRef] [PubMed]
- Paridis, K.; Lionheart, W.R.B. Shape corrections for 3D EIT. J. Phys. Conf. Ser. 2010, 224, 012049. [Google Scholar] [CrossRef]
- Polydorides, N. Image Reconstruction Algorithms for Soft-Field Tomography. Ph.D. Thesis, University of Manchester Institute of Science and Technology, Manchester, UK, 2002. [Google Scholar]
- Akhtari-Zavare, M.; Latiff, L.A. Electrical Impedance Tomography as a Primary Screening Technique for Breast Cancer Detection, Asian Pacific Journal of Cancer Prevention. Asian Pac. Organ. Cancer Prev. 2015, 16, 5595–5597. [Google Scholar] [CrossRef] [PubMed]
- Karpov, A.; Korotkova, M.; Shiferson, G.; Kotomina, E. Electrical Impedance Mammography: Screening and Basic Principles, Breast Cancer and Breast Reconstruction; IntechOpen: London, UK, 2020; Available online: https://www.intechopen.com/chapters/69046 (accessed on 29 March 2023). [CrossRef]
- Spatenkova, V.; Teschner, E.; Jedlicka, J. Evaluation of regional ventilation by electric impedance tomography during percutaneous dilatational tracheostomy in neurocritical care: A pilot study. BMC Neurol. 2020, 20, 374. [Google Scholar] [CrossRef]
- Zhang, N.; Jiang, H.; Zhang, C.; Li, Q.; Li, Y.; Zhang, B.; Deng, J.; Niu, G.; Yang, B.; Frerichs, I.; et al. The influence of an electrical impedance tomography belt on lung function determined by spirometry in sitting position. Physiol. Meas. 2020, 41, 044002. [Google Scholar] [CrossRef]
- Luo, Y.; Abiri, P.; Chang, C.C.; Tai, Y.C.; Hsiai, T.K. Epidermal EIT Electrode Arrays for Cardiopulmonary Application and Fatty Liver Infiltration. Interfacing Bioelectron. Biomed. Sens. 2020, 163–184. [Google Scholar]
- Humplik, P.; Cermak, P.; Zid, T. Electrical impedance tomography for decay diagnostics of Norway spruce (Picea abies): Possibilities and opportunities. Silva Fenn. Finn. Soc. For. Sci. 2016, 50, 1341. [Google Scholar] [CrossRef]
- Proto, A.R.; Cataldo, M.F.; Costa, C.; Papandrea, S.F.; Zimbalatti, G. A tomographic approach to assessing the possibility of ring shake presence in standing chestnut trees. Eur. J. Wood Wood Prod. 2020, 78, 1137–1148. [Google Scholar] [CrossRef]
- Hong, L.E.; Yunos, Y.B.M. Application of FPGA in Process Tomography Systems. Engineering 2020, 12, 790–809. [Google Scholar] [CrossRef]
- Sahovic, B.; Atmani, H.; Sattar, M.A.; Garcia, M.M.; Schleicher, E.; Legendre, D.; Climent, E.; Zamansky, R.; Pedrono, A.; Babout, L.; et al. Controlled Inline Fluid Separation Based on Smart Process Tomography Sensors. Chem. Ing. Tech. 2020, 92, 554–563. [Google Scholar] [CrossRef]
- Boyle, A. Geophysical Applications of Electrical Impedance Tomography. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2016. [Google Scholar]
- Molyneux, J.E.; Witten, A. Impedance tomography: Imaging algorithms for geophysical applications. Inverse Probl. 1994, 10, 655–667. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. A posteriori error estimates for the adaptivity technique for the Tikhonov functional and global convergence for a coefficient inverse problem. Inverse Probl. 2010, 26, 045012. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. Reconstruction of dielectrics from experimental data via a hybrid globally convergent/adaptive inverse algorithm. Inverse Probl. 2010, 26, 125009. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. Approximate Global Convergence and Adaptivity for Coefficient Inverse Problems. Springer: New York, NY, USA, 2010; ISBN 9781441978059. [Google Scholar]
- Mueller, J.L.; Siltanen, S. Linear and Nonlinear Inverse Problems with Practical Applications; SIAM: Philadelphia, PA, USA, 2012; ISBN 9781611972337. [Google Scholar]
- Isakov, V. Inverse Problems for Partial Differential Equations; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; ISBN 9783319516578. [Google Scholar]
- Koyunbakan, H. Inverse nodal problem for p-Laplacian energy-dependent Sturm-Liouville equation. Bound. Value Probl. 2013, 2013, 272. [Google Scholar] [CrossRef]
- Koyunbakan, H. Reconstruction of Potential in Discrete Sturm–Liouville Problem. Qual. Theory Dyn. Syst. 2022, 21, 13. [Google Scholar] [CrossRef]
- Khaled, D.E.; Novas, N.; Gazquez, J.A.; Manzano-Agugliaro, F. Dielectric and Bioimpedance Research Studies: A Scientometric Approach Using the Scopus Database. Publications 2018, 6, 6. [Google Scholar] [CrossRef]
- Naranjo-Hernández, D.; Reina-Tosina, J.; Min, M. Fundamentals, Recent Advances, and Future Challenges in Bioimpedance Devices for Healthcare Applications. J. Sens. 2019, 2019, 9210258. [Google Scholar] [CrossRef]
- Liu, D.; Wang, J.; Shan, Q.; Smyl, D.; Deng, J.; Du, J. DeepEIT: Deep Image Prior Enabled Electrical Impedance Tomography. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 1–12. [Google Scholar] [CrossRef]
- Wang, W.; Yousaf, M.; Liu, D.; Sohail, A. A Comparative Study of the Genetic Deep Learning Image Segmentation Algorithms. Symmetry 2022, 14, 1977. [Google Scholar] [CrossRef]
- Colibazzi, F.; Lazzaro, D.; Morigi, S.; Samore, A. Learning Nonlinear Electrical Impedance Tomography. J. Sci. Comput. 2022, 90, 58. [Google Scholar] [CrossRef]
- Wang, G.; Feng, D.; Tang, W. Electrical Impedance Tomography Based on Grey Wolf Optimized Radial Basis Function Neural Network. Micromachines 2022, 13, 1120. [Google Scholar] [CrossRef] [PubMed]
- Bibi, K. Particular Solutions of Ordinary Differential Equations Using Discrete Symmetry Groups. Symmetry 2020, 12, 180. [Google Scholar] [CrossRef]
- Jauhiainen, J.; Seppänen, A.; Valkonen, T. Mumford–Shah regularization in electrical impedance tomography with complete electrode model. Inverse Probl. 2022, 38, 065004. [Google Scholar] [CrossRef]
- Chen, Z.; Xiang, J.; PBagnaninchi, P.-O.; Yang, Y. MMV-Net: A Multiple Measurement Vector Network for Multifrequency Electrical Impedance Tomography. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Benoit, B.; Yassine, H.; Nabil, Z. Robust imaging using electrical impedance tomography: Review of current tools. Proc. R. Soc. Math. Phys. Eng. Sci. 2022, 478, 2258. [Google Scholar]
- Perot, J.; Subramanian, V. Discrete calculus methods for diffusion. J. Comput. Phys. 2007, 224, 59–81. [Google Scholar] [CrossRef]
- Leo, J.; Grady, J.P. Discrete Calculus; Springer: London, UK, 2010; ISBN 1849962898. [Google Scholar]
- Subramanian, V. Discrete Calculus Methods and Their Implementation. Ph.D. Thesis, Mechanical Engineering, University of Massachusetts, Amherst, MA, USA, 2007. [Google Scholar]
- Persson, P.O.; Strang, G. A Simple Mesh Generator in MATLAB. Siam Rev. Soc. Ind. Appl. Math. (SIAM) 2004, 46, 329–345. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Ganie, H.A.; Shang, Y. Bounds for the Generalized Distance Eigenvalues of a Graph. Symmetry 2019, 11, 1529. [Google Scholar] [CrossRef]
- Garde, H.; Hyvönen, N. Mimicking relative continuum measurements by electrode data in two-dimensional electrical impedance tomography. Numer. Math. 2021, 147, 579–609. [Google Scholar] [CrossRef]
- Aster, R.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems; Elsevier Academic Press: Amsterdam, The Netherlands, 2005; ISBN 9780080470559. [Google Scholar]
- Hanka, L. An efficient quadratic programming optimization method for deconvolution of gamma-ray spectra. AARMS Technol. 2010, 9, 47–66. [Google Scholar]
- Hansen, P.C. Regularization Tools Version 4.0 for Matlab 7.3. Numer. Algorithms 2007, 46, 189–194. [Google Scholar] [CrossRef]
- Gramacki, A. Nonparametric Kernel Density Estimation and Its Computational Aspects; Springer: Cham, Switzerland, 2018; ISBN 9783319716879. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sari, Z.; Klincsik, M.; Odry, P.; Tadic, V.; Toth, A.; Vizvari, Z. Lumped Element Method Based Conductivity Reconstruction Algorithm for Localization Using Symmetric Discrete Operators on Coarse Meshes. Symmetry 2023, 15, 1008. https://doi.org/10.3390/sym15051008
Sari Z, Klincsik M, Odry P, Tadic V, Toth A, Vizvari Z. Lumped Element Method Based Conductivity Reconstruction Algorithm for Localization Using Symmetric Discrete Operators on Coarse Meshes. Symmetry. 2023; 15(5):1008. https://doi.org/10.3390/sym15051008
Chicago/Turabian StyleSari, Zoltan, Mihaly Klincsik, Peter Odry, Vladimir Tadic, Attila Toth, and Zoltan Vizvari. 2023. "Lumped Element Method Based Conductivity Reconstruction Algorithm for Localization Using Symmetric Discrete Operators on Coarse Meshes" Symmetry 15, no. 5: 1008. https://doi.org/10.3390/sym15051008
APA StyleSari, Z., Klincsik, M., Odry, P., Tadic, V., Toth, A., & Vizvari, Z. (2023). Lumped Element Method Based Conductivity Reconstruction Algorithm for Localization Using Symmetric Discrete Operators on Coarse Meshes. Symmetry, 15(5), 1008. https://doi.org/10.3390/sym15051008











