Numerical Approximation of a Time-Fractional Modified Equal-Width Wave Model by Using the B-Spline Weighted Residual Method

Abstract

Fractional calculus (FC) is an important mathematical tool in modeling many dynamical processes. Therefore, some analytical and numerical methods have been proposed, namely, those based on symmetry and spline schemes. This paper proposed a numerical approach for finding the solution to the time-fractional modified equal-width wave (TFMEW) equation. The fractional derivative is described in the Caputo sense. Indeed, the B-spline Galerkin scheme combined with functions with different weights was employed to discretize TFMEW. The $L_2$ and $L_{\infty }$ error norm values and the three invariants $I_1, I_2$, and $I_3$ of the numerical example were calculated and tabulated. A comparison of these errors and invariants was provided to confirm the efficiency and accuracy of the proposed method.

1. Introduction

The study of fractional calculus has become increasingly suitable for the formulation of natural phenomena [1,2]. This is because fractional differential equations rather than integer-order differential equations can better model natural physics processes and dynamic system processes. Numerous scientific fields such as control and electromagnetism, dynamical systems, computer and electrical engineering, biological tissues, physical systems, electrical networks, computer vision, and signal processing rely heavily on fractional calculus, which has been successfully formulated by nonlinear or linear non-integer differential equations [3,4,5,6,7,8,9,10]. Fractional differential equations (FDEs) represent the whole function in a weighted form, unlike integer differential equations, which depend exclusively on the local function’s behavior [11,12,13,14].

Nonlinear partial differential equations (NPDEs) have a large effect on the investigation of nonlinear physical processes. Therefore, developing efficient numerical approaches for these equations is important [15,16,17,18,19,20,21,22]. The modified equal-width wave (MEW) model is based on the equal-width wave (EW) model developed by Morrison et al. [23]. This equation can be formulated as a PDE (partial differential equation) used to simulate one-dimensional (1D) wave propagation through nonlinear media when dispersion is present. This model is based on the modified Korteweg-de Vries (MKdV) model [24] and the modified regularized long-wave (MRLW) equation [25]. These modified equations have cubic nonlinearities, and all have soliton wave solutions in the form of pulses or packets of waves. In nonlinear media, these waves propagate by maintaining their waveform and velocity even after interaction with other waves. There are only a few analytic solutions to the MEW equation. Therefore, approximate solutions to the MEW equation can be useful and can be compared with analytical solutions. Using the Petrov–Galerkin finite element (FE) technique with cubic B-spline element shape functions and quadratic weight functions, Geyikli and Battal Gazi Karakoc ([26,27]) addressed the MEW equation using a collocation technique with septic B-spline finite elements and cubic B-spline finite elements. The MEW and EW equations were solved using a lumped Galerkin technique implemented by quadratic B-spline FE applied by Esen ([28,29]). The tanh and sine–cosine methods were used by Wazwaz to study the MEW equation and two of its related variants [30]. The MEW equation was solved using a variational iteration method described in [31]. Moreover, solving the MEW equation with linearized implicit finite differences was studied by Esen and Kutluay [32]. According to [33], the regularized long-wave (RLW) equation and the EW equation have only three such conditions, and this is likely to apply to the MEW equation as well. Through a Fourier analysis based on linear stability, it can be demonstrated that the numerical scheme formed by exponentially traveling waves is unconditionally stable.

In this work, we investigated the approximated solution of the time-fractional modified equal-width wave (TFMEW) equation [23] with the interval $\left[a,b\right]$ as

$$\frac{{\partial }^{\gamma }U\left(x,t\right)}{\partial t^{\gamma }}+3U^2\left(x,t\right)U_x\left(x,t\right)-\mu U_{xxt}\left(x,t\right)=0.$$

(1)

The following boundary conditions (BCs) and the initial condition (IC) are prescribed as

$$\begin{gathered} U \left(a,t\right)=0, U\left(b,t\right)=0 \\ {U}_x\left(a,t\right)=0, U_x\left(b,t\right)=0, \\ {U}_{xx}\left(a,t\right)=U_{xx}\left(b,t\right)=0,\hspace{1em}t>0, \end{gathered}$$

(2)

$$U\left(x,0\right)=f\left(x\right),\hspace{1em}\hspace{1em}a\le x\le b,$$

(3)

where the parameter $\mu$ denotes a positive constant and $f\left(x\right)$ stands for localized disturbance inside domain $\left[a,b\right]$ with physical BC $U\to 0$ as $x\to \pm \infty .$

Definition 1.1:

Letting m be the smallest integer exceeding$\gamma$, the Caputo time fractional derivative operator of order$\gamma >0$is defined as follows [34]:

$$C{D}_{0,t}^{\gamma }u\left(x,t\right)=\{\begin{array}{cc}\frac{{\partial }^{m}u\left(x,t\right)}{\partial t^m}\hfill & \hfill \gamma =m\in N\\ \frac{1}{\Gamma \left(m-\gamma \right)}{{\displaystyle \int }}_0^t{\left(t-\omega \right)}^{m-\gamma -1} \frac{{\partial }^{m}u\left(x,\omega \right)}{\partial {\omega }^m}d\omega ,\hfill & \hfill m-1<\gamma <m, m\in N,\end{array}$$

(4)

where $u\left(x,t\right)$ is the unknown function that is continuously differentiable $\left(m-1\right)$ times and $\Gamma (.)$ denotes the usual gamma function.

Symmetry plays a crucial role in computational science, and symmetry analysis can lead to the systematic determination of exact solutions. Numerical methods are adopted either when no analytic solution can be found, or as a computationally efficient alternative to find an approximate solution. In what follows, we use the quadratic B-spline Galerkin method with linear B-spline as a weight to approximate TFMEW.

This paper is organized as follows. Section 2 provides an overview of the quadratic B-spline base functions and then uses the B-spline Galerkin scheme combined with the functions with different weights to discretize TFMEW. Numerical results are provided in Section 3 to clarify the numerical accuracy and performance of the proposed method. Furthermore, it is shown that the results of numerical test problems are in excellent agreement with other methods accessible in the literature. Finally, Section 4 is devoted to a brief conclusion.

2. Implementation of the Proposed Method for TFMEW Model

For TFMEW, we first define the quadratic B-spline base functions. To do this, let the interval $\left[a,b\right]$ be the solution domain to Equation (1), and it is divided into $M$ uniformly spaced nodes $x_m$ so that $a=x_0<x_1<\cdots <x_{N-1}<x_M=b$ and $h=\left(x_{m+1}-x_m\right)$; then, the quadratic B-spline $Q_m\left(x\right)$, at the nodal point $x_m$, which is a form based on the solution interval $\left[a,b\right]$, is defined as follows [35]:

$$Q_m\left(x\right)=\frac{1}{h^2}\{\begin{array}{cc}{\left(x_{m+2}-x\right)}^2-3{\left(x_{m+1}-x\right)}^2+3{\left(x_m-x\right)}^2,\hfill & \mathrm{if} x\in \left[x_{m-1},x_m\right],\hfill \\ {\left(x_{m+2}-x\right)}^2-3{\left(x_{m+1}-x\right)}^2,\hfill & \mathrm{if} x\in \left[x_m,x_{m+1}\right],\hfill \\ {\left(x_{m+2}-x\right)}^2,\hfill & \mathrm{if} x\in \left[x_{m+1},x_{m+2}\right],\hfill \\ \hspace{1em}0,\hfill & \mathrm{otherwise},\hfill \end{array}$$

(5)

where splines $(Q_{-1}\left(x\right),Q_0\left(x\right),\dots ,Q_M\left(x\right))$ represent the basis for functions introduced on the interval $\left[a,b\right]$ and the approximate solution is

$$U_M\left(x,t\right)={\displaystyle \sum }_{m=-1}^M{\delta }_m\left(t\right)Q_m\left(x\right),$$

(6)

where ${\delta }_m$ are unknown time-dependent parameters to be determined from the initial, boundary, and weighted residual conditions. The value of $U$ and its first derivative $U^{\prime }$ at the knot $x_m$ is determined in terms of ${\delta }_m$ by

$$\begin{gathered} U_m={\delta }_{m-1}+{\delta }_m, \\ {U^{\prime }}_m=\frac{2}{h}\left({\delta }_{m-1}-{\delta }_m\right), \end{gathered}$$

(7)

Based on local coordinate transformation [36],

$$\xi h=x-x_m, 0\le \xi \le 1$$

(8)

the quadratic B-spline shape functions will be

$$\begin{gathered} Q_{m-1}={\left(1-\xi \right)}^2 \\ {Q}_m=1+2\xi -2{\xi }^2 \\ {Q}_{m+1}={\xi }^2 \end{gathered}$$

(9)

and the variation of $U\left(\xi ,t\right)$ on each element [$x_m,x_{m+1}$] can be represented by

$$U_M\left(\xi ,t\right)={\displaystyle \sum }_{j=m-1}^{m+1}{\delta }_j\left(t\right)Q\left(\xi \right),$$

(10)

where B-splines $Q_{m-1}\left(\xi \right),Q_m\left(\xi \right)$ and $Q_{m+1}\left(\xi \right)$ are the element shape functions while ${\delta }_{m-1}\left(t\right), {\delta }_m\left(t\right)$ and ${\delta }_{m+1}\left(t\right)$ act as element parameters. The Galerkin formulation in spatial and temporal directions for Equation (1) can be described as

$$\underset{a}{\overset{b}{{\displaystyle \int }}}W(U_t+3U^2{U}_x-\mu U_{xxt})dx=0,$$

(11)

where $W\left(x\right)>0$ is a weight function, by (8), we obtain

$$\underset{0}{\overset{1}{{\displaystyle \int }}}W(U_t+\frac{3}{h}{\mathsf{Ա}}^2{U}_{\xi }-\frac{\mu }{h^2}{U}_{\xi \xi t})d\xi =0,$$

(12)

where $\mathsf{Ա}=\left(\xi ,t\right)$ is taken to be a constant to simplify the integral [37], we apply partial integration to obtain

$$\underset{0}{\overset{1}{{\displaystyle \int }}}(W{U}_t+\lambda W{U}_{\xi }+\yen W_{\xi }{U}_{\xi t})d\eta =\yen W{U}_{\xi t}{\mid }_0^1,$$

(13)

where,

$$\lambda =\frac{3}{h}{\mathsf{Ա}}^2 \mathrm{and} \yen =\mu /h^2$$

By taking linear B-spline $L_m\left(x\right), m=0,\dots ,M$ as a substitute for the weight function $W$ at the node $x_m$ can be defined as follows [35]:

$$L_m\left(x\right)=\frac{1}{h}\{\begin{array}{c}\left(x-x_{m-1}\right), \mathrm{if} x \in \left[x_{m-1},x_m\right],\\ \left(x_{m+1}-x\right), \mathrm{if} x \in \left[x_m,x_{m+1}\right],\\ 0, \mathrm{otherwise}. \end{array}$$

(14)

where $L_m\left(x\right),$ forms the basis on the interval $\left[a,b\right]$. The approximate solution $U_M\left(x,t\right)$ can be illustrated by

$$U_N\left(x,t\right)={\displaystyle \sum }_{m=0}^M{L}_m\left(x\right){\omega }_m\left(t\right),$$

(15)

where using local coordinate Equation (8), a linear B-spline shape functions in terms of $\eta$ on the element [$x_m,x_{m+1}$] can be defined as

$$L_m=1-\xi , L_{m+1}=\xi$$

(16)

the variation of the function $U\left(\xi ,t\right)$ on the sub-domain [$x_m,x_{m+1}$] can be expanded by

$$U_M\left(\xi ,t\right)={\displaystyle \sum }_{i=m}^{m+1}{L}_i\left(\xi \right){\omega }_i\left(t\right),$$

(17)

where ${\omega }_m\left(t\right)$ and ${\omega }_{m+1}\left(t\right)$, and B-splines $L_m\left(\xi \right)$ and $L_{m+1}\left(\xi \right)$ act as element parameters and element shape functions, respectively.

Now, we can write Equation (13) as follows:

$${\displaystyle \sum }_{j=m-1}^{m+1}[(\underset{0}{\overset{1}{{\displaystyle \int }}}{L}_i{Q}_j+\yen L_i^{\prime }{Q}_j^{\prime })d\xi -\yen L_i{Q}_j^{\prime }{\mid }_0^1]{\delta }_{\mathrm{j}}^{·e}+{\displaystyle \sum }_{\mathrm{j}=m-1}^{m+1}(\lambda \underset{0}{\overset{1}{{\displaystyle \int }}}{L}_i{Q}_j^{\prime }d\xi ){\delta }_{\mathrm{j}}^e=0,\hspace{1em}\hspace{1em}i=m, m+1$$

where $\dot{\delta }$ denotes the $\delta \mathrm{th}$ fractional derivative concerning time, which in matrix form is as follows:

$$\left[X_{ij}^e+\yen \left(Y_{ij}^e-R_{ij}^e\right)\right]{\delta }^e+\lambda Q_{ij}^e{\delta }^e=0$$

(18)

where ${\delta }^e={({\delta }_{m-1},{\delta }_m,{\delta }_{m+1})}^T$ are the element parameters. The element matrices $X_{ij}^e,Y_{ij}^e,Q_{ij}^e$ and $R_{ij}^e$ are rectangular $2\times 3$ and are given by the following integrals:

$$\begin{gathered} X_{ij}^e=\underset{0}{\overset{1}{{\displaystyle \int }}}{A}_i{Q}_{j}d\eta =\frac{1}{12}\left[\begin{array}{ccc}3& 8& 1\\ 1& 8& 3\end{array}\right], \\ {Y}_{ij}^e=\underset{0}{\overset{1}{{\displaystyle \int }}}{A^{\prime }}_i{Q}_j^{\prime }d\eta =\left[\begin{array}{ccc}1& 0& -1\\ -1& 0& 1\end{array}\right], \\ {Q}_{ij}^e=\underset{0}{\overset{1}{{\displaystyle \int }}}{A}_i{Q}_j^{\prime }d\eta =\frac{1}{3}\left[\begin{array}{ccc}-2& 1& 1\\ -1& -1& 2\end{array}\right]. \\ {R}_{ij}^e=A_i{Q}_j^{\prime }{\mid }_0^1=\left[\begin{array}{ccc}2& -2& 0\\ 0& -2& 2\end{array}\right], \end{gathered}$$

The lumped value of λ can be obtained as

$$\mathsf{\lambda }=\frac{3}{4h}{\left({\delta }_{m-1}+2{\delta }_m+{\delta }_{m+1}\right)}^2$$

Assembling all contributions from all elements, we obtain the matrix equation as

$$\left[X+\yen \left(\mathrm{Y}-\mathrm{R}\right)\right]{\delta }^{·}+\lambda \mathrm{Q}\delta =0$$

(19)

where $\delta ={\left({\delta }_{-1},{\delta }_0,{\delta }_1,\dots ,{\delta }_N\right)}^T$ represents a global element parameter. The matrices $X, Y,$ and $\lambda Q$ denote rectangular and penta-diagonal, and row m of each contains the following form:

$$\begin{gathered} X=\frac{1}{12}\left(1, 11, 11, 1, 0\right) \\ Y=\left(-1 ,1, 1,-1, 0\right) \\ \lambda Q=\left(-{\lambda }_1,-{\lambda }_1-2{\lambda }_2,2{\lambda }_1+{\lambda }_2,{\lambda }_2,0\right) \end{gathered}$$

where

$$\begin{gathered} {\lambda }_1=\frac{3}{4h}{\left({\delta }_{m-2}+2{\delta }_{m-1}+{\delta }_m\right)}^2 \\ {\lambda }_2=\frac{3}{4h}{\left({\delta }_{m-1}+2{\delta }_m+{\delta }_{m+1}\right)}^2 \end{gathered}$$

Following [38], the Caputo derivative is approximated with the help of the $L1$ formula:

$$\frac{d^{\gamma }f\left(t\right)}{d{t}^{\gamma }}{\mid }_{t_f}=\frac{{\left(\Delta t\right)}^{-\gamma }}{\Gamma \left(2-\gamma \right)} {\displaystyle \sum }_{k=0}^{m-1}{b}_k^{\gamma }[f(t_{m-k}-f\left(t_{m-1k}\right)]+O{(\Delta t)}^{2-\gamma },$$

where $b_k^{\gamma }={(k+1)}^{1-\gamma }-k^{1-\gamma },$ $\Delta t=\frac{t_f-0}{N}$, $t_f=n\left(\Delta t\right), n=0,1,\dots N, N$ is a positive integer and uses the following lemma:

Lemma 2.1:

([39]) Assume that $0<\gamma <1 and b_k^{\gamma }={(k+1)}^{1-\gamma }-k^{1-\gamma }, k=0,1, \dots$ Then, we have the following:

$1=b_0^{\gamma }>b_1^{\gamma }>\cdots >b_k^{\gamma }\to 0, as k\to \infty$;

We can write the parameter ${\delta }_m^{{}^{·}}$ as

$${\delta }_m^{{}^{·}}=\frac{d^{\gamma }\sigma }{d{t}^{\gamma }}=\frac{{\left(\Delta t\right)}^{-\gamma }}{\Gamma \left(2-\gamma \right)} {\displaystyle \sum }_{k=0}^{m-1}{b}_k^{\gamma }[\left({\delta }_{m-1}^{n-k+1}-{\delta }_{m-1}^{n-k}\right)+\left({\delta }_m^{n-k+1}-{\delta }_m^{n-k}\right)]+O{(\Delta t)}^{2-\gamma },$$

$$b_k^{\gamma }={(k+1)}^{1-\gamma }-k^{1-\gamma },$$

and the parameter$\delta$is based on the Crank–Nicolson scheme:

$${\delta }_m=\frac{1}{2}\left({\delta }_m^n+{\delta }_m^{n+1}\right)$$

Substituting both parameters above into Equation (18), we have

$$\begin{array}{cc}[[X+\yen (Y-R)]& +\left[\frac{{\left(\Delta t\right)}^{-\gamma }\Gamma \left(2-\gamma \right)+\lambda Q_7}{2}\right]]{\delta }^{n+1}\\ & =\left[\left[X+\yen \left(Y-R\right)\right]-\left[\frac{{\left(\Delta t\right)}^{-\gamma }\Gamma \left(2-\gamma \right)+\lambda Q_7}{2}\right]\right]{\delta }^n\\ & -\left[X+\yen \left(Y-R\right)\right]{\displaystyle {\displaystyle \sum }_{k=1}^n}{b}_k^{\gamma }\left[\left({\delta }_{m-1}^{n-k+1}-{\delta }_{m-1}^{n-k}\right)+\left({\delta }_m^{n-k+1}-{\delta }_m^{n-k}\right)\right],\end{array}$$

(20)

where $\delta ={\left({\delta }_{m-2}+{\delta }_{m-1}+{\delta }_m+{\delta }_{m+1}+{\delta }_{m+1}+{\delta }_{m+2}\right)}^T$. Equation (20) contains$M+2$linear equations that contain$M+2$unknown parameters. To obtain a unique solution, we require two extra restrictions. These are computed from the BCs to eliminate${\delta }_{-1}$and${\delta }_N$from the system to make (20) a$M\times M$solvable system of equations.

The initial vector${\delta }^0={\left( {\delta }_{0,}, {\delta }_{1,}, \dots , {\delta }_{M-1,}\right)}^T$can be calculated by the IC and BCs. Therefore, Equation (6) can be restated over the interval$\left[a,b\right]$as

$$U_M\left(x,0\right)={\displaystyle \sum }_{m=-1}^M{\delta }_m\left(0\right)Q_m\left(x\right),$$

where the${\delta }_m\left(0\right)$’s denote unknown parameters.$U_M\left(x,0\right)$is implemented to fulfill the following expressions at the nodes$x_m$:

$$\begin{gathered} U_M\left(x,0\right)=U\left(x_m,0\right),\hspace{1em}m=0,\dots ,M, \\ {U}_M^{\prime }\left(x_0,0\right)=U^{\prime }\left(x_0,0\right)=0, \end{gathered}$$

So, we will obtain the following matrix system:

$$Z{\delta }^0=b,$$

where

$$Z=\left[\begin{array}{cccccc}\frac{2}{h}& \frac{-2}{h}& & & & \\ 1& 1& & & & \\ & 1& 1& & & \\ & & & \ddots & & \\ & & & & 1& 1\\ & & & & 1& 1\end{array}\right]$$

and$b={\left(U^{\prime }\left(x_0,0\right), U\left(x_0,0\right), U\left(x_1,0\right), \dots ,U\left(x_{M-2},0\right), U\left(x_{M-1},0\right)\right)}^T$.

3. Numerical Example

In the TFMEW Equation (1), there is a solitary wave solution [40] with the form

$$U\left(x,t\right)=\mathsf{Ʈ} \mathrm{sech}\left(\mathcal{K}\left[x-x_0-\mathsf{ʋ}t\right]\right).$$

(21)

In this equation, ${\mathcal{K}}^2=1/ \mu$, and the wave velocity ʋ equals $\mathsf{ʋ}=\frac{{\mathsf{Ʈ}}^2}{2}$. Based on the equation, the amplitude Ʈ represents one solitary wave with an initial center of $x_0$. We consider the IC to be

$$U\left(x,0\right)=\mathsf{Ʈ} \mathrm{sech}\left(\mathcal{K}\left[x-x_0\right]\right)$$

The magnitude of the solitary waves may be positive or negative, but their velocity is proportional to the square of the wave amplitude. Moreover, in the RLW equation, all solitary waves have the same wave number $\mathcal{K}=\sqrt{\left(1/\mu \right)}$, so the width of all of them is the same too. Unlike the RLW equation, the TFMEW equation does not prohibit positive velocities. As TFMEW Equation (1) is defined with BCs, there are three invariant conditions given as follows [40]:

$$\begin{gathered} I_1=\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}Udx, \\ {I}_2=\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}\left(U^2+\mu U_x{}^2\right)dx, \\ {I}_3=\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}{U}^{4}dx, \end{gathered}$$

which are computed as [41]

$$I_1=\frac{2\mathsf{Ʈ}}{\mathcal{K}}, I_2=\frac{12{\mathsf{Ʈ}}^2}{\mathcal{K}}+\frac{48\mathcal{K}{\mathsf{Ʈ}}^2\mu }{5}, I_3=\frac{144{\mathsf{Ʈ}}^2}{5\mathcal{K}}.$$

The $L_{\infty }$ and $L_2$ error norms to measure the difference between the numerical and analytic solutions are defined as [42]

$$\begin{gathered} L_{\infty }=║U-U_N{║}_{\infty }\cong \underset{j}{\mathit{max}}\left|U_J^{}-{\left(U_N\right)}_j\right|, \\ {L}_2=║U-U_N{║}_2\cong \sqrt{h{\displaystyle \sum }_{J=0}^N{\left|U_J^{}-{\left(U_N\right)}_j\right|}^2} \end{gathered}$$

where $U_N$ and $U$ represent the approximate and exact solutions, respectively.

The proposed strategy here was adopted for computing the solutions of the TFMEW equation to show the motion of a single solitary wave and conservation laws. Therefore, Equation (21) was employed as IC with domain $\left[0, 80\right],$ spatial step $h=0.1$, temporal step $\Delta t=0.05$, $\mu =1, A=0.25,$ and the simulation was run to time $t=20.$ The conservative $I_1, I_2, I_3$ quantities calculated for different $t$ values and $\gamma =0.5, 0.75$ are shown in Table 1 and Table 2, respectively. The values of $I_1, I_2, I_3$ at various final times indicated that the proposed method is conservative for mass and energy. We see that the numerical results of the proposed strategy are in excellent agreement with both their exact values and all of the compared ones. Figure 1 shows the motion of a single solitary wave with various values of times.

Table 1. Error norms and invariants of a single solitary wave with $\mathsf{Ʈ}=0.1, x_0=30, \mu =1, \gamma =0.5$.

Time (t)	Comparative Studies	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_3$	${\mathit{L}}_2$	${\mathit{L}}_{\mathit{\infty }}$
0.00		0.19796010	0.01983155	0.00012916	0.000000	0.000000
0.01		0.19796010	0.01983155	0.00012916	1.33 × 10−15	0.58 × 10−16
0.02		0.19796010	0.01983155	0.00012916	1.11 × 10−15	0.41 × 10−16
0.03		0.19796010	0.01983155	0.00012916	1.20 × 10−15	0.49 × 10−16
0.04		0.19796010	0.01983155	0.00012916	1.34 × 10−15	0.55 × 10−16
0.05		0.19796007	0.01983155	0.00012916	1.55 × 10−15	0.63 × 10−16
0.06		0.19796007	0.01983156	0.00012916	2.00 × 10−15	0.71 × 10−16
0.07		0.19796006	0.01983156	0.00012916	2.10 × 10−15	0.79 × 10−16
0.08		0.19796005	0.01983156	0.00012916	2.15 × 10−15	0.89 × 10−16
0.09		0.19796003	0.01983157	0.00012916	2.24 × 10−15	1.02 × 10−16
0.10		0.19796003	0.01983157	0.00012916	2.33 × 10−15	1.15 × 10−16
0.10	[40]	0.7854000	0.12500000	0.00520000	1.99 × 10−15	5.82 × 10−16
0.10	[43]	0.7853967	0.16666633	0.00520830	0.0800980	0.0460618
0.10	[29]	0.7849545	0.16647652	0.00519955	0.29051667	0.24989254

Table 2. Error norms and invariants of a single solitary wave with $\mathsf{Ʈ}=0.1, x_0=30, \mu =1, \gamma =0.75$.

Time (t)	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_3$	${\mathit{L}}_2$	${\mathit{L}}_{\mathit{\infty }}$
0.00	0.19796016	0.01983155	0.00012916	0.000000	0.000000
0.01	0.19796016	0.01983155	0.00012916	1.52 × 10−15	1.98 × 10−16
0.02	0.19796015	0.01983155	0.00012916	1.38 × 10−15	1.73 × 10−16
0.03	0.19796015	0.01983155	0.00012916	1.55 × 10−15	1.88 × 10−16
0.04	0.19796015	0.01983155	0.00012916	1.34 × 10−15	1.94 × 10−16
0.05	0.19796014	0.01983155	0.00012916	1.55 × 10−15	2.01 × 10−16
0.06	0.19796013	0.01983156	0.00012916	1.89 × 10−15	2.12 × 10−16
0.07	0.19796013	0.01983156	0.00012916	2.18 × 10−15	2.19 × 10−16
0.08	0.19796013	0.01983156	0.00012916	2.15 × 10−15	2.28 × 10−16
0.09	0.19796012	0.01983157	0.00012916	2.53 × 10−15	2.40 × 10−16
0.10	0.19796011	0.01983157	0.00012916	2.45 × 10−15	2.55 × 10−16

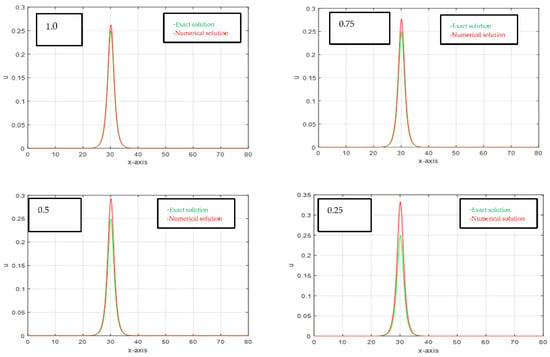
Figure 1. Motion of a single solitary wave with various values of times $\mathsf{Ʈ}$ (1.0, 0.75, 0.50, 0.25).

4. Conclusions

This paper used the B-spline weighted residual Galerkin finite element method with a weight function different in degrees from the spline function to obtain high-precision numerical solutions of the TFMEW. To demonstrate the efficiency and accuracy of the approach, $L_2$ and $L_{\infty }$ error norms were calculated using the motion of a single solitary wave. It is evident that in all computer runs, the error norms were relatively small and the invariants remained relatively constant. Additionally, the method can be used to solve a large number of physically critical nonlinear problems by utilizing the MATLAB 2022 software package.