p-Numerical Semigroups of Generalized Fibonacci Triples
Abstract
1. Introduction
2. Preliminaries
3. Main Results
3.1. The Case
3.2. The Case
3.3. The Case
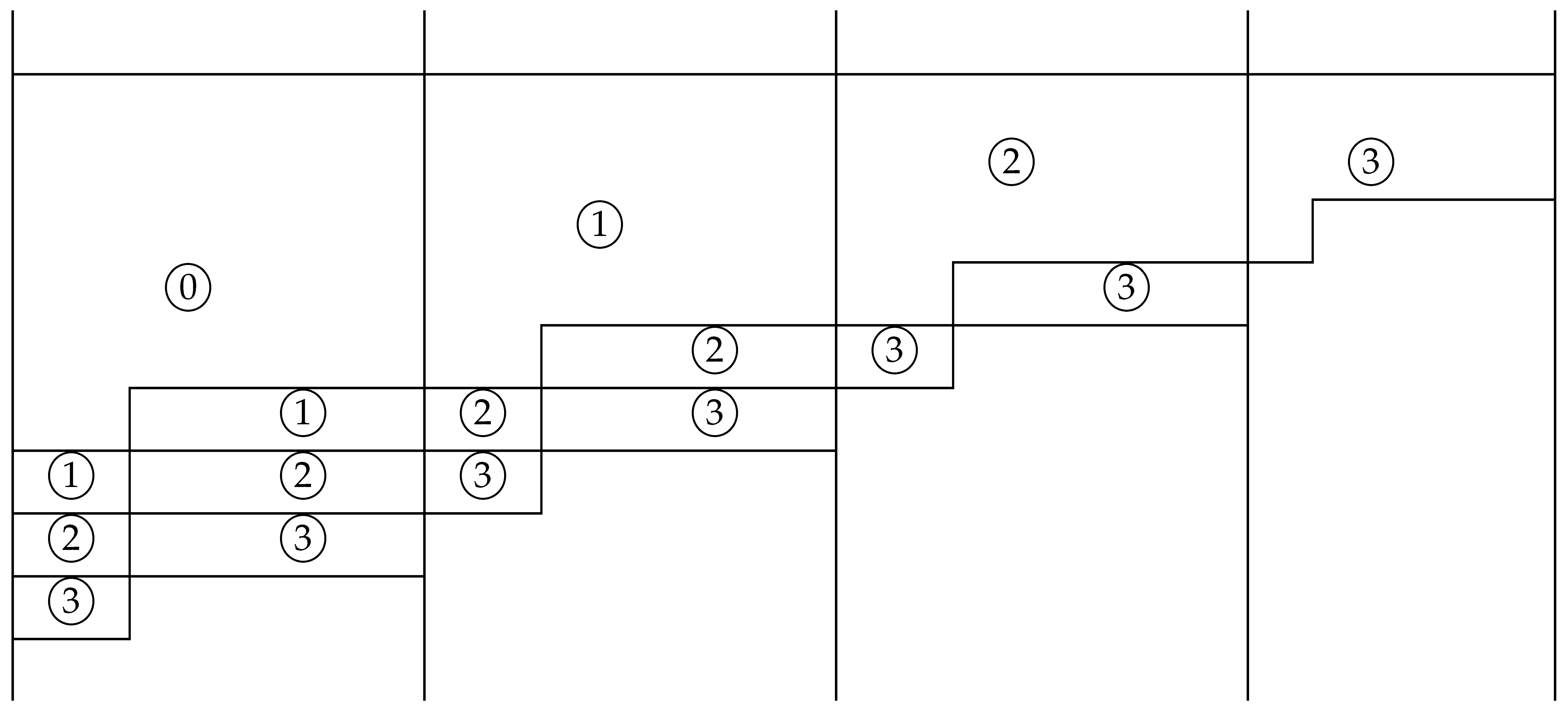
 denotes the area of elements in Apn(A). Here, each , satisfying , can be expressed in at least n + 1 ways but in at most n ways. Each element of Ap3(A) existing in the second block to the fourth block corresponds to each element having the same residue of Ap2(A) existing in the block immediately to the left thereof in a form of shifting up one step. The Jk(v) elements of Ap3(A) existing over two rows (or one row) at the bottom of the first block correspond to the Jk(v) elements with the same residue of Ap2(A) at the top of the third block. Therefore, since all the elements in Ap2(A) form a complete remainder system, so is Ap3(A). It can be shown that all the elements of Ap3(A) have exactly four ways of being expressed in terms of a, va + b and vaJk−1(v) + bJk(v). Within each region of Ap3(A), one of the two leftmost (lower left) elements tr−1,q+3 and tJk(v)−1,q+2 is the largest so, by comparing these elements, the largest element of Ap3(A) can be determined.
denotes the area of elements in Apn(A). Here, each , satisfying , can be expressed in at least n + 1 ways but in at most n ways. Each element of Ap3(A) existing in the second block to the fourth block corresponds to each element having the same residue of Ap2(A) existing in the block immediately to the left thereof in a form of shifting up one step. The Jk(v) elements of Ap3(A) existing over two rows (or one row) at the bottom of the first block correspond to the Jk(v) elements with the same residue of Ap2(A) at the top of the third block. Therefore, since all the elements in Ap2(A) form a complete remainder system, so is Ap3(A). It can be shown that all the elements of Ap3(A) have exactly four ways of being expressed in terms of a, va + b and vaJk−1(v) + bJk(v). Within each region of Ap3(A), one of the two leftmost (lower left) elements tr−1,q+3 and tJk(v)−1,q+2 is the largest so, by comparing these elements, the largest element of Ap3(A) can be determined.4. -Genus
p-Sylvester Sum
5. Jacobsthal–Lucas Polynomials
6. -Hilbert Series
7. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Binner, D.S. The number of solutions to ax+by+cz=n and its relation to quadratic residues. J. Integer Seq. 2020, 23, 20.6.5. [Google Scholar]
- Cayley, A. On a problem of double partitions. Philos. Mag. 1860, 20, 337–341. [Google Scholar] [CrossRef]
- Komatsu, T. On the number of solutions of the Diophantine equation of Frobenius–General case. Math. Commun. 2003, 8, 195–206. [Google Scholar]
- Sylvester, J.J. On the partition of numbers. Quart. J. Pure Appl. Math. 1857, 1, 141–152. [Google Scholar]
- Tripathi, A. The number of solutions to ax+by=n. Fibonacci Quart. 2000, 38, 290–293. [Google Scholar]
- Sylvester, J.J. On subinvariants, i.e., semi-invariants to binary quantics of an unlimited order. Am. J. Math. 1882, 5, 119–136. [Google Scholar] [CrossRef]
- Ramirez Alfonsin, J.L. The Diophantine Frobenius Problem; Oxford Lecture Series in Mathematics and Its Applications 30; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Sylvester, J.J. Mathematical questions with their solutions. Educ. Times 1884, 41, 21. [Google Scholar]
- Assi, A.; D’Anna, M.; Garcia-Sanchez, P.A. Numerical Semigroups and Applications, 2nd ed.; RSME Springer Series 3; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Rosales, J.C.; Garcia-Sanchez, P.A. Finitely Generated Commutative Monoids; Nova Science Publishers, Inc.: Commack, NY, USA, 1999. [Google Scholar]
- Rosales, J.C.; Garcia-Sanchez, P.A. Numerical Semigroups. In Developments in Mathematics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Brown, A.; Dannenberg, E.; Fox, J.; Hanna, J.; Keck, K.; Moore, A.; Robbins, Z.; Samples, B.; Stankewicz, J. On a generalization of the Frobenius number. arXiv 2010, arXiv:1001.0207. [Google Scholar]
- Fukshansky, L.; Schurmann, A. Bounds on generalized Frobenius numbers. Eur. J. Comb. 2011, 32, 361–368. [Google Scholar] [CrossRef]
- Matthews, G.L. Frobenius numbers of generalized Fibonacci semigroups. In Proceedings of the 3rd Integers Conference 2007, Carrollton, GA, USA, 24–27 October 2007. [Google Scholar]
- Johnson, S.M. A linear diophantine problem. Can. J. Math. 1960, 12, 390–398. [Google Scholar] [CrossRef]
- Marin, J.M.; Ramirez Alfonsin, J.L.; Revuelta, M.P. On the Frobenius number of Fibonacci numerical semigroups. Integers 2007, 7, A14. [Google Scholar]
- Koshy, T. Fibonacci and Lucas Numbers with Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; Volume 2. [Google Scholar]
- Komatsu, T.; Pita-Ruiz, C. The Frobenius number for Jacobsthal triples associated with number of solutions. Axioms 2023, 12, 98. [Google Scholar] [CrossRef]
- Komatsu, T.; Ying, H. The p-Frobenius and p-Sylvester numbers for Fibonacci and Lucas triplets. Math. Biosci. Eng. 2023, 20, 3455–3481. [Google Scholar] [CrossRef] [PubMed]
- Brown, T.C.; Shiue, P.J. A remark related to the Frobenius problem. Fibonacci Quart. 1993, 31, 32–36. [Google Scholar]
- Rødseth, ∅J. A note on Brown and Shiue’s paper on a remark related to the Frobenius problem. Fibonacci Quart. 1994, 32, 407–408. [Google Scholar]
- Curtis, F. On formulas for the Frobenius number of a numerical semigroup. Math. Scand. 1990, 67, 190–192. [Google Scholar] [CrossRef]
- Fel, L.G. Frobenius problem for semigroups S(d1,d2,d3). Funct. Anal. Other Math. 2006, 1, 119–157. [Google Scholar] [CrossRef]
- Rosales, J.C.; Garcia-Sanchez, P.A. Numerical semigroups with embedding dimension three. Arch. Math. 2004, 83, 488–496. [Google Scholar] [CrossRef]
- Tripathi, A. Formulae for the Frobenius number in three variables. J. Number Theory 2017, 170, 368–389. [Google Scholar] [CrossRef]
- Robles-Pérez, A.M.; Rosales, J.C. The Frobenius number for sequences of triangular and tetrahedral numbers. J. Number Theory 2018, 186, 473–492. [Google Scholar] [CrossRef]
- Rosales, J.C.; Branco, M.B.; Torrão, D. The Frobenius problem for Thabit numerical semigroups. J. Number Theory 2015, 155, 85–99. [Google Scholar] [CrossRef]
- Rosales, J.C.; Branco, M.B.; Torrão, D. The Frobenius problem for Mersenne numerical semigroups. Math. Z. 2017, 286, 741–749. [Google Scholar] [CrossRef]
- Komatsu, T. The Frobenius number for sequences of triangular numbers associated with number of solutions. Ann. Comb. 2022, 26, 757–779. [Google Scholar] [CrossRef]
- Komatsu, T. The Frobenius number associated with the number of representations for sequences of repunits. C. R. Math. Acad. Sci. Paris 2023, 361, 73–89. [Google Scholar] [CrossRef]
- Albano, A. The Fibonacci sequence and the golden section in a lunette decoration of the medieval church of San Nicola in Pisa. Territ. Cult. 2015, 21, 48–59. [Google Scholar]
- Antoniotti, A.; Caldarola, F.; d’Atri, G.; Pellegrini, M. New Approaches to Basic Calculus: An Experimentation via Numerical Computation. In Numerical Computations: Theory and Algorithms: Third International Conference, NUMTA 2019, Crotone, Italy, 15–21 June 2019; Sergeyev, Y.D., Kvasov, D.E., Eds.; Springer: Cham, Switzerland, 2020; pp. 329–342. [Google Scholar]
- Caldarola, F.; d’Atri, G.; Maiolo, M.; Pirillo, G. New algebraic and geometric constructs arising from Fibonacci numbers. Soft Comput. 2020, 24, 17497–17508. [Google Scholar] [CrossRef]
- Apéry, R. Sur les branches superlinéaires des courbes algébriques. C. R. Acad. Sci. Paris 1946, 222, 1198–1200. [Google Scholar]
- Komatsu, T. Sylvester power and weighted sums on the Frobenius set in arithmetic progression. Discrete Appl. Math. 2020, 315, 110–126. [Google Scholar] [CrossRef]
- Komatsu, T. On p-Frobenius and related numbers due to p-Apéry set. arXiv 2023, arXiv:2111.11021v3. [Google Scholar]
- Komatsu, T.; Zhang, Y. Weighted Sylvester sums on the Frobenius set. Irish Math. Soc. Bull. 2021, 87, 21–29. [Google Scholar] [CrossRef]
- Komatsu, T.; Zhang, Y. Weighted Sylvester Sums on the Frobenius Set in More Variables. Kyushu J. Math. 2022, 76, 163–175. [Google Scholar] [CrossRef]
- Brauer, A.; Shockley, B.M. On a problem of Frobenius. J. Reine. Angew. Math. 1962, 211, 215–220. [Google Scholar]
- Selmer, E.S. On the linear diophantine problem of Frobenius. J. Reine Angew. Math. 1977, 293–294, 1–17. [Google Scholar]
- Tripathi, A. On sums of positive integers that are not of the form ax+by. Amer. Math. Monthly 2008, 115, 363–364. [Google Scholar] [CrossRef]
- Punyani, P.; Tripathi, A. On changes in the Frobenius and Sylvester numbers. Integers 2018, 18B, A8. [Google Scholar]
- Batra, S.S.; Kumar, N.; Tripathi, A. On a linear Diophantine problem involving the Fibonacci and Lucas sequences. Integers 2015, 15, A26. [Google Scholar]
| ⋯ | ⋯ | ⋯ | ||
| ⋯ | ⋯ | ⋯ | ||
| ⋮ | ⋮ | |||
| ⋯ | ⋯ | ⋯ | ||
| ⋯ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komatsu, T.; Laishram, S.; Punyani, P. p-Numerical Semigroups of Generalized Fibonacci Triples. Symmetry 2023, 15, 852. https://doi.org/10.3390/sym15040852
Komatsu T, Laishram S, Punyani P. p-Numerical Semigroups of Generalized Fibonacci Triples. Symmetry. 2023; 15(4):852. https://doi.org/10.3390/sym15040852
Chicago/Turabian StyleKomatsu, Takao, Shanta Laishram, and Pooja Punyani. 2023. "p-Numerical Semigroups of Generalized Fibonacci Triples" Symmetry 15, no. 4: 852. https://doi.org/10.3390/sym15040852
APA StyleKomatsu, T., Laishram, S., & Punyani, P. (2023). p-Numerical Semigroups of Generalized Fibonacci Triples. Symmetry, 15(4), 852. https://doi.org/10.3390/sym15040852







