Abstract
An investigation has been carried out on a reconfigured form of the Einstein-Hilbert action, denoted by , where represents the energy-momentum tensor trace of the scalar field under consideration. The study has focused on how the structural behavior of the scalar field changes based on the potential’s shape, which has led to the development of a new set of Friedmann equations. In the context of modified theories, researchers have extensively explored the range of gravitational wave polarization modes associated with relevant fields. In addition to the two transverse-traceless tensor modes that are typically observed in general relativity, two additional scalar modes have been identified: a massive longitudinal mode and a massless transverse mode, also known as the breathing mode.
1. Introduction
It is well known that the Friedmann-Lemaître-Robertson-Walker (FLRW) metric, which represents the exact solution of Einstein’s equations obtained under the presumption of homogeneity and isotropy of space, has successfully clarified several additional observational facts about our Universe, including the distribution of large-scale galaxies and the close uniformity of the CMB temperature [1]. The existing accepted cosmological model, which is very good at fitting the most recent observational data sets and explaining observed cosmic acceleration, is embraced by the FLRW metric. Strong evidence that the cosmological space-time metric differs from the FLRW metric would significantly affect fundamental physics and inflation theory.
Alternative theories of gravity have long been recognized as a way to get around some of the inconsistencies in standard cosmology [2,3,4]. One of the viable alternative approaches is the gravity, which has been recently introduced by Harko et al [5]. The gravitational field equations in the metric formalism and the covariant divergence of a stress-energy tensor lead to the equations of motion for test particles. The type of matter source generally impacts the equations governing the gravitational field.
In the context of quantum gravity, higher derivative theories are a natural fit. Due to standard power-counting arguments, it is prominent that general relativity (GR) appears to be non renormalizable [6]. These theories become renormalizable when quadratic terms of the curvature are added to the Einstein-Hilbert action [7]. Unfortunately, higher derivative models have a significant drawback: according to Ostrogradsky’s theorem [8], unbounded kinetic terms are incorporated into field equations with higher-order time derivatives than second-order, leading to disorders in both classical and quantum theory. The Ostrogradsky instability can appear at the classical level through exponentially increasing modes. If the theory is conversing, the vacuum field configurations may become unstable in the presence of small perturbations.
The Advanced LIGO team’s recent detection [9,10,11] of gravitational waves (GWs) has introduced an enormous window to observe the Universe. The high classification accuracy expected for some events, such as the one detected (black hole–black hole merger, neutron star–neutron star merger), combined with some electromagnetic counterparts, may help us better understand physics at extreme regimes gravitational fields, densities, and other parameters.
Aside from using LIGO/VIRGO interferometers to detect GWs directly, it is possible to employ the indirect detection of GWs by analysing the considerable reduction in the orbital period of stellar binary systems. It is the perfect situation for testing modified gravity theories because the orbital period has decreased, and the GR prediction can be tested with high precision. Several tests have been carried out to put modified gravity theories to the test.
Hagiara et al. [12] examine a superposition of the two null streams to demonstrate that any of the three modes (one cumulative spin-0 and two spin-1 modes) can be excluded by appropriately adapting a weighted superposition of the null streams, allowing for the experimental testing of the remaining polarization modes. According to the findings of the study, by analysing the polarization states of the detected GW, it is feasible to verify numerous assumptions of the scalar-tensor theories of gravitation [13]. The signals from the multiple detector LIGO-Virgo network alone present a challenge for recognizing the polarization content of such GWs [14,15]. Three GW detectors cannot resolve all polarization mode degeneracies and characterize the GW polarization content for such transient GW signals [16,17]. Assuming that all polarizations are purely GR, all observations of GWs from CBCs to date agree with GR’s assumptions [18].
The GW spectrum, as well as its polarization modes, are dependent on theory. Reconfigured theories of gravity, which have initially been motivated by the drawbacks in the standard cosmological scenario, can now contribute to the study of GWs by generating observables that can be verified by experiment.
The polarization, as well as dispersion of GWs in a vacuum, are two significant characteristics of GWs that differentiate the validity of gravity theories in the radiative regime. Alternative metric theories allow for six possible polarization states for GW, four more than GR have. The propagation speed of GW can differ from GR’s estimation that GW propagates at light speed in vacuum, implying that the effective graviton mass is zero. Plus mode and cross mode of polarization is very normal in the Einstein’s GR. In general, in terms of Riemman tensor , the plus mode is represented by , the cross mode by , the transverse breathing mode by , the vector-x mode by , the vector-y mode by , and the longitudinal mode by .
Detailed studies of the polarization mode for such theories as the Horndeski theory have been conducted by Hou et al. [19]. Alves et al. [20] studied the formalism through GWs polarization. As in other gravity models, the model shows the existence of scalar degrees of freedom for such gravity models in the metric formalism. The theory contains a scalar mode of polarization of GWs. Extension of the non linear form of is also extensively studied with the correction terms. The polarization mode exists in a mixed state, with one being a massive longitudinal mode and the other being a transverse massless breathing mode with non-vanishing trace [21]. The potential and mass of scalar gravitons in both Jordan and Einstein frames have been analyzed to understand better the particular form of the model with the corrective terms [22]. Due to the mistaken notion that applying the Lorenz gauge suggests solutions for transverse-traceless waves, the massive longitudinal and massless transverse modes have frequently been overlooked. In the recent works [23,24], on modified gravity and gravitational waves, the different modified gravity techniques for obtaining gravitational waves tensor modes has also been reviewed.
Nevertheless, Kausar et al. [25], show that it is not possible in general and, specifically, the traceless condition cannot be enforced because a Minkowski background metric is no longer available. In the context of quantum gravity, a broad category of higher derivative gravity models, the degrees of freedom of the metric is (super) renormalizable, which makes them interesting. In the massive tensor field in D-dimensions, only the transverse modes are stimulated in the appearance of a matter source, and the harmonic gauge condition is dynamically induced [26].
The energy-momentum squared gravity theory, applied on a homogeneous and isotropic spacetime, the optimum energy density and, consequently, the least length can be found in the expanding Universe. According to the implication, a bounce in the early Universe prevents an early-time singularity from existing [27]. According to the theories, the gravitational component of the action depends on a general function of R and a function of . The dependence on results from taking into account exotic fluids or quantum effects. The energy-momentum tensor’s variation concerning the metric [28] is represented by the model’s source term.
Although non-Einsteinian polarizations can be identified by laser interferometric gravity wave detectors, their specification is not preferable for the position. On the other hand, due to the angular distribution of pulsars in the sky, pulsar timing is a versatile tool for detecting all polarizations. In order to detect nano-Hertz GWs, a method known as a pulsar timing array involves timing multiple millisecond pulsars, which seem to be extraordinarily sustainable celestial clocks [29]. For widely spaced pulsars, a stochastic GW background turns out to leave an angular dependent correlation in pulsar timing residuals. In this random GW background, the timing residuals of pulsar pairs are correlated. According to Lee [30], this correlation, , is influenced by the angular separation () between the two pulsars, the polarization of the graviton mass, and other factors. For the breathing mode, we need 40 pulsars, for the longitudinal mode 100 pulsars, and for the shear mode 500 pulsars to differentiate between the non-Einsteinian modes and the Einsteinian modes [31,32].
The spectral configuration of the stochastic gravitational-wave background, which is developed by the superposition of cosmological as well as individually unaddressed astrophysical references, encodes the polarization of GWs. Abbott et al. [33] look for a stochastic background of conceptually polarized GWs using data collected by aLIGO during the first observing run [34]. The evaluation is not dependent on any particular theory of gravity and is sensitive to continuous signals of scalar, vector, or tensor polarizations. Although LIGO and Virgo are restricted in differentiating the polarization of GWs transients, subsequent detectors such as KAGRA [35], and LIGO-India [36] will assist in reducing existing degeneracies and enable more precise polarization mode detection.
The purpose of the present study is to explore the physical features of the gravity as well as the GWs signature of the following gravity and the dependence of the structure on the functional form of gravity potential. The basic structure and field equation is developed in Section 2. Corresponding scalar field and properties are discussed in Section 3 based on the potentials. We discuss the Friedmann equation in Section 4. In order to characterize the polarization modes, we evaluate the Newman-Penrose (NP) quantities in Section 5. We discuss the polarization modes from different observations that corresponds to our model in Section 6.
2. Basic Outline of the Modified Gravity
The total action including the scalar field for the modified theory of gravity [5] can be structured in the following manner,
The Ricci scalar is represented by R, and represents the trace of the energy-momentum tensor of the scalar field. Furthermore, K is the coupling constant.
The action of the field, where g is the factor that determines the signature of the metric (−, +, +, +). We employ the natural units in this article such that . Hereafter, we presumed . Where the conventional Lagrangian density for a real scalar field () is , [37], namely over,
Here, is a self-interacting potential. The matter fields in this theory have a minimal coupling with gravity and have no coupling with the scalar field.
The stress-energy tensor can define as
and its trace by , respectively. We considered that the Lagrangian density L depends only on the metric tensor components , and is independent of its derivatives.
Consequently, the energy-momentum tensor corresponding to the scalar field is
and the corresponding trace is as follows,
We consider the system in the absence of matter, and therefore, = 0 [27].
The following relationship is provided by by varying the gravitational field’s action S against the metric tensor components.
Where, and denotes and , respectively, and are hereafter considered as and , respectively.
After integrating, we obtain the generalized form of the Einstein field equation in vacuum in the presence of scalar field, which is as follows
We presume that is the modified gravity function, and that it is defined as .
is a freely chosen function of the stress-energy tensor trace of a scalar field, and is a freely chosen constant. Immediately, the field equation adopts the following form:
3. Scalar Field
The Ricci scalar of the Equation (7) can be obtained by contraction and simplification as shown in the followinfg:
According to covariant divergence of the field Equation (8), it is feasible to derive the equation of motion for the scalar field as follows,
Using the subsequent mathematical identity,
3.1. Case-I
Let the scalar field expand around the constant scalar curvature as follows,
We assume that is the steady minimum for the effective potential, say, around the minimum potential . The potential as a function of the effective scalar field, near the minimum , can be as follows
where is a constant, in the dimension of mass.
Let us consider , following Moraes and Santos [37]. Based on the following consideration, Equation (10) reduces to
with . Explorations into the linear region of the field equations result in the following solution:
where, is the small amplitude and is the wave vector, which obeys the following equation,
The effective cosmological constant is,
3.2. Case-II
One interesting notion is that the trace of the energy-momentum tensor of the scalar field has a non linear function, i.e., , where and n both are constant. Linearity can be easily achieved by considering .
Based on this Equation (10) reduces to
Let us consider the potential in the following manner
where, are real constants.
We restricted to the terms of first order in . On such approximation, the third term of Equation (18) vanishes. Expanding V around the non null minimum value . We can expand the field as . Following the relative methodology as before, we find that with such a presumption and first order constraints,
The equation that represents the scalar field’s solution conforms to the following relation as in Equation (15),
and
Correlated energy of the system can be defined as
Introduction of the minimally coupled scalar field included at the first order introduces an effective cosmological constant, as follows,
With being a positive constant, there are two possible outcomes for the potential in Equation (19): (i) , and (ii) . The steady minimum scalar field value for is zero, and as a result, the effective cosmological constant () is also zero. Figure 1 depicts the propagation of the perturbation of the vacuum scalar field for various . The transition of colour from light brown to deep blue shows the amplitude variation from crest to trough.
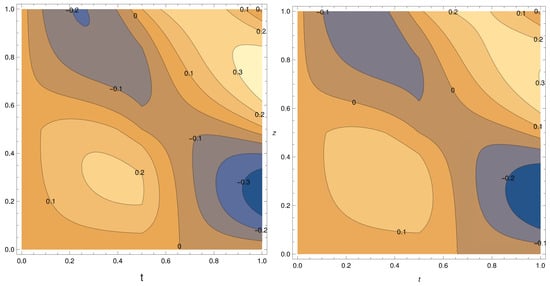
Figure 1.
Propagation for the perturbation of the vacuum scalar field. The left panel shows the variation for , and the right panel shows the variation for ; considered .
This stands to steady the universe. Although the minimum scalar field is non zero for , this consideration results in non zero because of the effective cosmological constant. Effectively, there is a cosmological constant.
4. The Friedmann-Lemaître-Robertson-Walker Universe
We assess the four-dimensional, curved, isotropic, spatially statistically homogeneous spacetime with Jordan frame FLRW metric as
Here, stands for the scale factor (in the unit of [length]). The cosmic curvature parameter is coupled to the dimensionless curvature k as , where signifies the Hubble constant (in [time]) and is the present value of the scale factor.
The scale factor determines the Hubble parameter .
For the observational purpose hereafter, we considered the flat FLRW metric.
5. Polarization Modes of the Modified Gravity
Newman-Penrose Formalism
Extra polarization modes are found using the Newman-Penrose (NP) [38] formalism; more details can be found in the references [39,40]. The system of four linearly independent vectors at any point of space, which are called tetrads, can be used to define the NP quantities that correspond to each of the six polarization modes of GWs. Such vectors can be represented as the NP tetrads as . The real null vectors are,
and the other two complex null vectors are,
While all other dot product vanishes.
In the algebraically unbiased NP representation, the fundamental components of the Riemann tensor are depicted by ten constituents of the Wely tensor (’s), nine constituents of the traceless Ricci tensor (’s), and just a curvature scalar (). Some symmetrical and differential properties reduce them to six: real and complex. The following Riemann tensor elements in the null tetrad basis have the following relationships with these NP measurements:
The remaining nonzero NP variables are defined in terms of the above-mentioned variables; , and , respectively.
Based on the characteristics of their transformations, these four NP variables and can be grouped into the group E(2), the Lorentz group for massless particles. These transformations show that the four NP variables’ amplitudes are not observer-independent and that only is invariant. On the other hand, some of the four NP variables’ absence (zero amplitude) is independent of the observer.
The following relations for the Ricci tensor and the Ricci scalar hold:
Following Equation (7), the Ricci tensor can be written as,
The corresponding non-null components are as follows,
Using Equations (30) and (31), one finds the following NP quantities:
; ; and
This results in the GW having four polarization modes: breathing scalar mode, longitudinal scalar mode, +, tensorial mode.
6. Detection of GWs’ Polarization Modes
The experimental detection of GWs polarization modes is essential for understanding the proper mechanism of GWs and, as a result, determining the viability of modified gravity theories. The Pulsar Timing Arrays (PTAs) are discussed in this section as a method for differentiating between polarization modes. We also explain the model’s findings. In the indirect identification of GWs, PTAs play an important role. They are also used in a variety of astronomical applications.
We calculate the GW-induced correlation functional relations between the timing residuals of two pulsars for each of the six polarizations. There are two groups for the polarizations. Analytical calculations of the GW-induced correlation functions for primarily transverse polarizations in the GR and breathing modes are feasible. Monte Carlo simulations must be used to evaluate the correlation function for shear and longitudinal polarization, not just transverse polarization.
The correlation functional relations [30] of the tensor and breathing modes are not dependent on the individual models, but the correlation functional relation of massive longitudinal modes is not, since the scalar graviton mass determines it.
For the tensor modes, the correlation functional relation is as follows
where is the angular separation between two pulsars
The correlation functional relation for the corresponding scalar modes is defined as
where, is the angular separation between two pulsars
The normalized correlation functional relation is explained as
The time residual induced by GW can be expressed in terms of the dispersion relation, as
where the mass () of the polarization mode is defined as , and . are the unit vectors pointing the pulsars, respectively, and is the displacement vector. The corresponding correlation coefficient [30,41,42] between the pulsars is
Correlation functions of some selected pulsars obtained from PPTA [43,44], NANOGrav [45,46] and IPTA [47,48] data are shown in Figure 2.
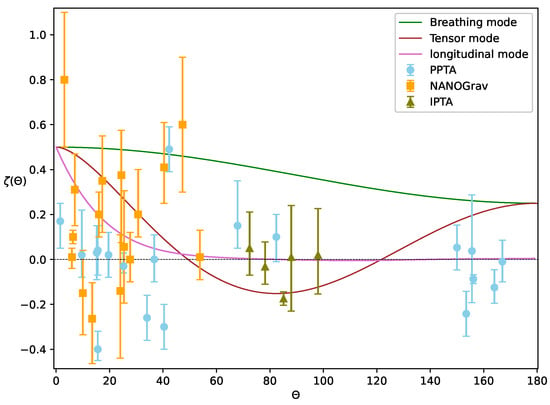
Figure 2.
Variation of the correlation functions with .
7. Conclusions and Outlook
For the considered spontaneous symmetry-breaking potential in our system, the scalar field’s structural characteristics depend on the nature of the potential. A phase transition can be thought of as the behaviour of the scalar field changing depending on the sign of the critical parameter . When , the system is independent of degree order, whereas leads to the dependency on order. The variation of the wave is very minute on varying the coupling constant . The variation of the field also varies with the order of the variation. However, the variation is almost stagnant for the higher-order. The variation of the propagation based on the coupling constant and order parameter is shown in Figure 3 and Figure 4, respectively.
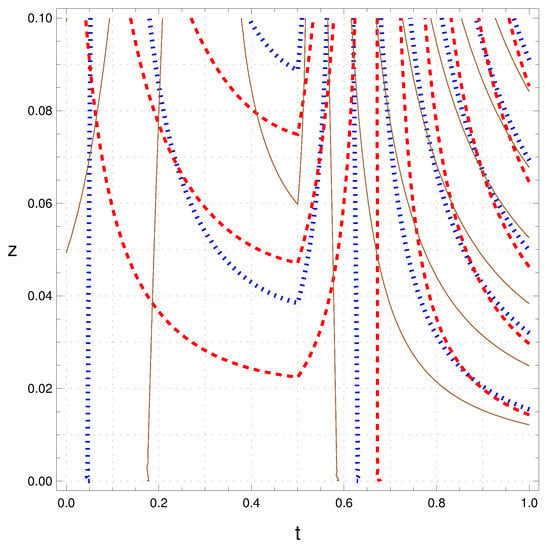
Figure 3.
Variation of the field based on the coupling constant . Blue dotted line for = 1.1, Red dashed line for = 0, and Black solid line for = .
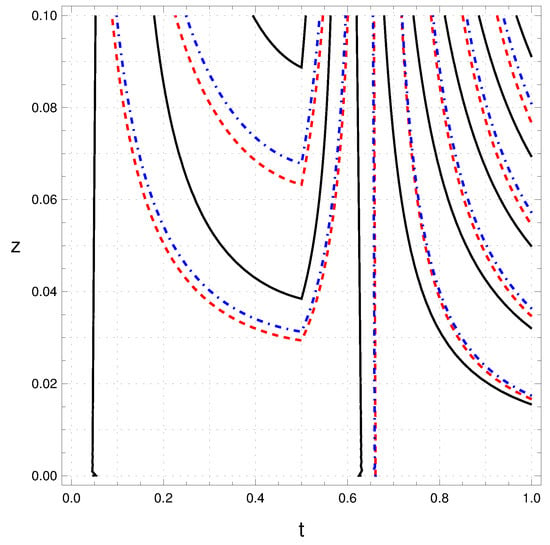
Figure 4.
Variation of the field based on order parameter n with = 1.1. For n = 3, we use Blue dash-dotted line, where Red dashed line is used to define n = 2, and Black solid line for n = 1.
An analyzed signal, such as a stochastic cosmological background of GWs, would be an integration of all of those modes if GWs have the nontensorial polarization modes discussed above. If there are only tensorial polarizations, the appearance of scalar and/or vector modes helps distinguish between different theories of gravity that go beyond general relativity and places limits on the relative intensities of each mode. When we can recognize the polarization states, we may establish a considerable framework for determining the theory of gravity [49]. It is also already clear that the polarization modes are independent of the characteristics of the cosmological constant. The relationship between the cosmological constant and the mass of the graviton is noteworthy. The amplitude, on the other hand, is modified by terms depending on the cosmological constant. Furthermore, if a source emits a regular waveform, the periodicity of the waveform, as observed by a distant observer, changes. These effects, however, are incredibly tiny and, thus, far below the identification [50].
For pulsars close together in the sky, the correlation curve for such waves reaches a maximum of 0.5. It has decreased from 1.0 because the same GW background passing over the pulsars produces a statistically equal but uncorrelated modulation in their residuals that goes negative for pulsars separated by about 90° and favourable again for pulsars separated by 180°.
Author Contributions
Conceptualization, M.K.; methodology, S.R.C.; writing—original draft preparation, M.K. and S.R.C.; writing—review and editing, M.K. and S.R.C.; supervision, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work of S.R.C was supported by the Southern Federal University (SFedU) (grant no. P-VnGr/21-05-IF). The research by M.K. was carried out in Southern Federal University with financial support of the Ministry of Science and Higher Education of the Russian Federation (State contract GZ0110/23-10-IF).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
SRC is thankful to Ranjini Mondol of IISc, Bangalore, for the fruitful discussion to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results-XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Padmanabhan, T. Cosmological constant—The weight of the vacuum. Phys. Rep. 2003, 380, 235. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1. [Google Scholar] [CrossRef]
- Kehagias, A. A conical tear drop as a vacuum-energy drain for the solution of the cosmological constant problem. Phys. Lett. B 2004, 600, 133. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Deser, S.; van Nieuwenhuizen, P. One-loop divergences of quantized Einstein-Maxwell fields. Phys. Rev. D 1974, 10, 401. [Google Scholar] [CrossRef]
- Stelle, K.S. Renormalization of higher-derivative quantum gravity. Phys. Rev. D 1977, 16, 953. [Google Scholar] [CrossRef]
- Ostrogradsky, M. Mémoires sur les équations différentielles, relatives au problème des isopérimètres. Mem. Acad. St. Petersbourg 1850, 6, 385. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Hagihara, Y.; Era, N.; Iikawa, D.; Asada, H. Probing gravitational wave polarizations with Advanced LIGO, Advanced Virgo and KAGRA. Phys. Rev. D 2018, 98, 064035. [Google Scholar] [CrossRef]
- Fesik, L. Polarization states of gravitational waves detected by LIGO-Virgo antennas. arXiv 2017, arXiv:1706.09505. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- Baker, T.; Bellini, E.; Ferreira, P.G.; Lagos, M.; Noller, J.; Sawicki, I. Strong Constraints on Cosmological Gravity from GW170817 and GRB 170817A. Phys. Rev. Lett. 2017, 119, 251301. [Google Scholar] [CrossRef] [PubMed]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2017, 17, 4. [Google Scholar] [CrossRef]
- Chatziioannou, K.; Yunes, N.; Cornish, N. Model-independent test of general relativity: An extended post-Einsteinian framework with complete polarization content. Phys. Rev. D 2012, 86, 022004. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Tests of general relativity with the binary black hole signals from the LIGO-Virgo catalog GWTC-1. Phys. Rev. D 2019, 100, 104036. [Google Scholar] [CrossRef]
- Hou, S.; Gong, Y.; Liu, Y. Polarizations of gravitational waves in Horndeski theory. Eur. Phys. J. C 2018, 78, 378. [Google Scholar] [CrossRef]
- Alves, M.E.S.; Miranda, O.D.; de Araujo, J.C.N. Probing the f(R) formalism through gravitational wave polarizations. Phys. Lett. B 2009, 679, 401. [Google Scholar] [CrossRef]
- Chowdhury, S.R.; Khlopov, M. Gravitational waves in the extended theory of gravity. Int. J. Mod. Phys. D 2021, 30, 2140011. [Google Scholar] [CrossRef]
- Gogoi, D.J.; Dev Goswami, U. A new f(R) gravity model and properties of gravitational waves in it. Eur. Phys. J. C 2020, 80, 1101. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Amplification of the primordial gravitational waves energy spectrum by a kinetic scalar in f(R) gravity. Astropart. Phys. 2023, 144, 102777. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Myrzakulov, R. Spectrum of Primordial Gravitational Waves in Modified Gravities: A Short Overview. Symmetry 2022, 14, 729. [Google Scholar] [CrossRef]
- Kausar, H.R.; Philippoz, L.; Jetzer, P. Gravitational wave polarization modes in f(R) theories. Phys. Rev. D 2016, 93, 124071. [Google Scholar] [CrossRef]
- Hölscher, P. Gravitational waves and degrees of freedom in higher derivative gravity. Phys. Rev. D 2019, 99, 064039. [Google Scholar] [CrossRef]
- Roshan, M.; Shojai, F. Energy-momentum squared gravity. Phys. Rev. D 2016, 94, 044002. [Google Scholar] [CrossRef]
- Alves, M.E.S.; Moraes, P.H.R.S.; de Araujo, J.C.N.; Malheiro, M. Gravitational waves in f(R,T) and f(R,Tϕ) theories of gravity. Phys. Rev. D 2016, 94, 024032. [Google Scholar] [CrossRef]
- Jenet, F.A.; Hobbs, G.B.; Lee, K.J.; Manchester, R.N. Detecting the Stochastic Gravitational Wave Background Using Pulsar Timing. Astrophys. J. 2017, 625, L123. [Google Scholar] [CrossRef]
- Lee, K.J.; Jenet, F.A.; Price, R.H. Pulsar Timing as a Probe of Non-Einsteinian Polarizations of Gravitational Waves. Astrophys. J. 2008, 685, 1304. [Google Scholar] [CrossRef]
- Lee, K.J.; Wex, N.; Kramer, M.; Stappers, B.W.; Bassa, C.G.; Janssen, G.H.; Karuppusamy, R.; Smits, R. Gravitational wave astronomy of single sources with a pulsar timing array. Mon. Not. R. Astron. Soc. 2011, 414, 3251. [Google Scholar] [CrossRef]
- Burke-Spolaor, S.; Taylor, S.R.; Charisi, M.; Dolch, T.; Hazboun, J.S.; Holgado, A.M.; Kelley, L.Z.; Lazio, T.J.W.; Madison, D.R.; McMann, N.; et al. The astrophysics of nanohertz gravitational waves. Astron. Astrophys. Rev. 2019, 27, 5. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. First Search for Nontensorial Gravitational Waves from Known Pulsars. Phys. Rev. Lett. 2018, 120, 031104. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Search for Tensor, Vector, and Scalar Polarizations in the Stochastic Gravitational-Wave Background. Phys. Rev. Lett. 2018, 120, 201102. [Google Scholar] [CrossRef]
- Aso, Y.; Michimura, Y.; Somiya, K.; Ando, M.; Miyakawa, O.; Sekiguchi, T.; Tatsumi, D.; Yamamoto, H.; Kagra Collaboration. Interferometer design of the KAGRA gravitational wave detector. Phys. Rev. D 2013, 88, 043007. [Google Scholar] [CrossRef]
- Iyer, B.; Souradeep, T.; Unnikrishnan, C.S.; Dhurandhar, S.; Raja, S.; Sengupta, A. LIGO-India: A Critical Element of the International Network of Gravitational Wave Detectors; Technical Report No. LIGO-M1100296; Indian Initiative in Gravitational-wave Observations: Dughala, India, 2011. [Google Scholar]
- Moraes, P.H.R.S.; Santos, J.R.L. A complete cosmological scenario from f(R,Tϕ) gravity theory. Eur. Phys. J. C 2016, 76, 60. [Google Scholar] [CrossRef]
- Newman, E.; Penrose, R. An Approach to Gravitational Radiation by a Method of Spin Coefficients. J. Math. Phys. 1962, 4, 566, Erratum in J. Math. Phys. 1963, 3, 998. [Google Scholar] [CrossRef]
- Eardley, D.M.; Lee, D.L.; Lightman, A.P. Gravitational-Wave Observations as a Tool for Testing Relativistic Gravity. Phys. Rev. D 1973, 8, 3308. [Google Scholar] [CrossRef]
- Eardley, D.M.; Lee, D.L.; Lightman, A.P.; Wagoner, R.V.; Will, C.M. Gravitational-wave observations as a tool for testing relativistic gravity. Phys. Rev. Lett. 1973, 30, 884–886. [Google Scholar] [CrossRef]
- Lee, K.; Jenet, F.A.; Price, R.H.; Wex, N.; Kramer, M. Detecting massive gravitons using Pulsar timing arrays. Astrophys. J. 2010, 722, 1589. [Google Scholar] [CrossRef]
- Lee, K.J. Pulsar timing arrays and gravity tests in the radiative regime. Class. Quantum Gravit. 2013, 30, 224016. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.; Bailes, M.; Coles, W.A.; Van Straten, W.; Keith, M.J.; Shannon, R.M.; Bhat, N.D.; Brown, A.; Burke-Spolaor, S.G.; et al. The Parkes Pulsar Timing Array Project. Publ. Astron. Soc. Aust. 2013, 30, E017. [Google Scholar] [CrossRef]
- Tiburzi, C.; Hobbs, G.; Kerr, M.; Coles, W.A.; Dai, S.; Manchester, R.N.; Possenti, A.; Shannon, R.M.; You, X.P. A study of spatial correlations in pulsar timing array data. Mon. Not. R. Astron. Soc. 2015, 455, 4339. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.; Crowter, K.; Demorest, P.B.; et al. The Nanograv Nine-Year Data Set: Observations, Arrival Time Measurements, and Analysis of 37 Millisecond Pulsars. Astrophys. J. 2015, 813, 65. [Google Scholar]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision Timing of 45 Millisecond Pulsars. Astrophys. J. 2018, 235, 37. [Google Scholar] [CrossRef]
- Verbiest, J.P.W.; Lentati, L.; Hobbs, G.; van Haasteren, R.; Demorest, P.B.; Janssen, G.H.; Wang, J.B.; Desvignes, G.; Caballero, R.N.; Keith, M.J.; et al. The International Pulsar Timing Array: First data release. Mon. Not. R. Astron. Soc. 2016, 458, 1267. [Google Scholar] [CrossRef]
- Perera, B.B.P.; DeCesar, M.E.; Demorest, P.B.; Kerr, M.; Lentati, L.; Nice, D.J.; Osłowski, S.; Ransom, S.M.; Keith, M.J.; Arzoumanian, Z.; et al. The International Pulsar Timing Array: Second data release. Mon. Not. R. Astron. Soc. 2019, 490, 4666. [Google Scholar] [CrossRef]
- Corda, C. Interferometric detection of gravitational waves: The definitive test for General Relativity. Int. J. Mod. Phys. D 2009, 18, 2275. [Google Scholar] [CrossRef]
- Joachim, N.; Philippe, J.; Mauro, S. On gravitational waves in spacetimes with a nonvanishing cosmological constant. Phys. Rev. D 2009, 79, 024014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).