Geometric Aggregation Operators for Solving Multicriteria Group Decision-Making Problems Based on Complex Pythagorean Fuzzy Sets
Abstract
1. Introduction
2. Preliminaries
 with condition, such that
with condition, such that 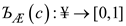 , and then is called the CMeG of with and be the function of the real value.
, and then is called the CMeG of with and be the function of the real value.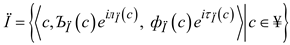 , where , are called the CMeG and the CNMeG of , respectively, with situation, such as . Moreover, and with restriction, such as, ,
, where , are called the CMeG and the CNMeG of , respectively, with situation, such as . Moreover, and with restriction, such as, , 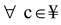 .
.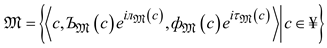 , , , are called the CMeG and the CNMeG of, respectively, with condition, such as . Moreover, and with ,
, , , are called the CMeG and the CNMeG of, respectively, with condition, such as . Moreover, and with , 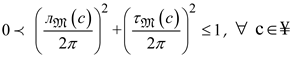 .
.- (1)
- If,
- (2)
- If,, then
- (3)
- If,, then there are three conditions:
- (i)
- If,
- (ii)
- If,
- (iii)
- If,
3. Basic Operations under CPyFNs
- (i)
- (ii)
- (iii)
- (iv)
- 1.
- Symmetry property of score function: Let be a group of CPyFNs, and let be their corresponding complements, then .
- 2.
- Monotonicity property of score functions: If be a CPyFN, then is monotonically decreasing when are increasing and monotonically increasing with and decreasing.
- 3.
- Symmetry property of accuracy function: If be a CPyFN and be their corresponding complement function, then .
- 4.
- Monotonicity property of accuracy functions: If be a CPyFN, then the accuracy function is monotonically increasing with the terms and are increasing.
- (1)
- Commutative laws:
- (i)
- (ii)
- (2)
- Associative laws:
- (i)
- (ii)
- (3)
- Distributive laws:
- (i)
- (ii)
- (i)
- (ii)
- .
- (i)
- (ii)
- (iii)
- (iv)
- (i)
- By Definition 6, we have
- (ii)
- Using Definition 6, with , we have□
- (i)
- (ii)
- (iii)
- (iv)
- (v)
- (vi)
- (vii)
- (viii)
- (iii)
- Since are CPyFNs, then
- (i)
- (ii)
- (iii)
- (iv)
- (i)
- Since and are CPyFNs, then□
- (i)
- (ii)
- (iii)
- (iv)
- (i)
- Since, and are CPyFNs, then□
- (i)
- (ii)
- (iii)
- (iv)
- (v)
- (vi)
4. Complex Pythagorean Fuzzy Geometric Aggregation Operators
- Step 1: For n = 2, we haveThus, we haveThus, for n = 2, Equation (2) is true.
- Step 2: Suppose Equation (2) is true for n = k, where k is any positive integer.
- Step 3: Assume that Equation (2) true for n = k, we show that it is true for n = k + 1.Thus, by principle of mathematical induction, Equation (2) holds for all positive integer. □
5. Application of the Novel Approaches
| Algorithm 1. Complex Pythagorean Fuzzy Geometric Aggregation Operators |
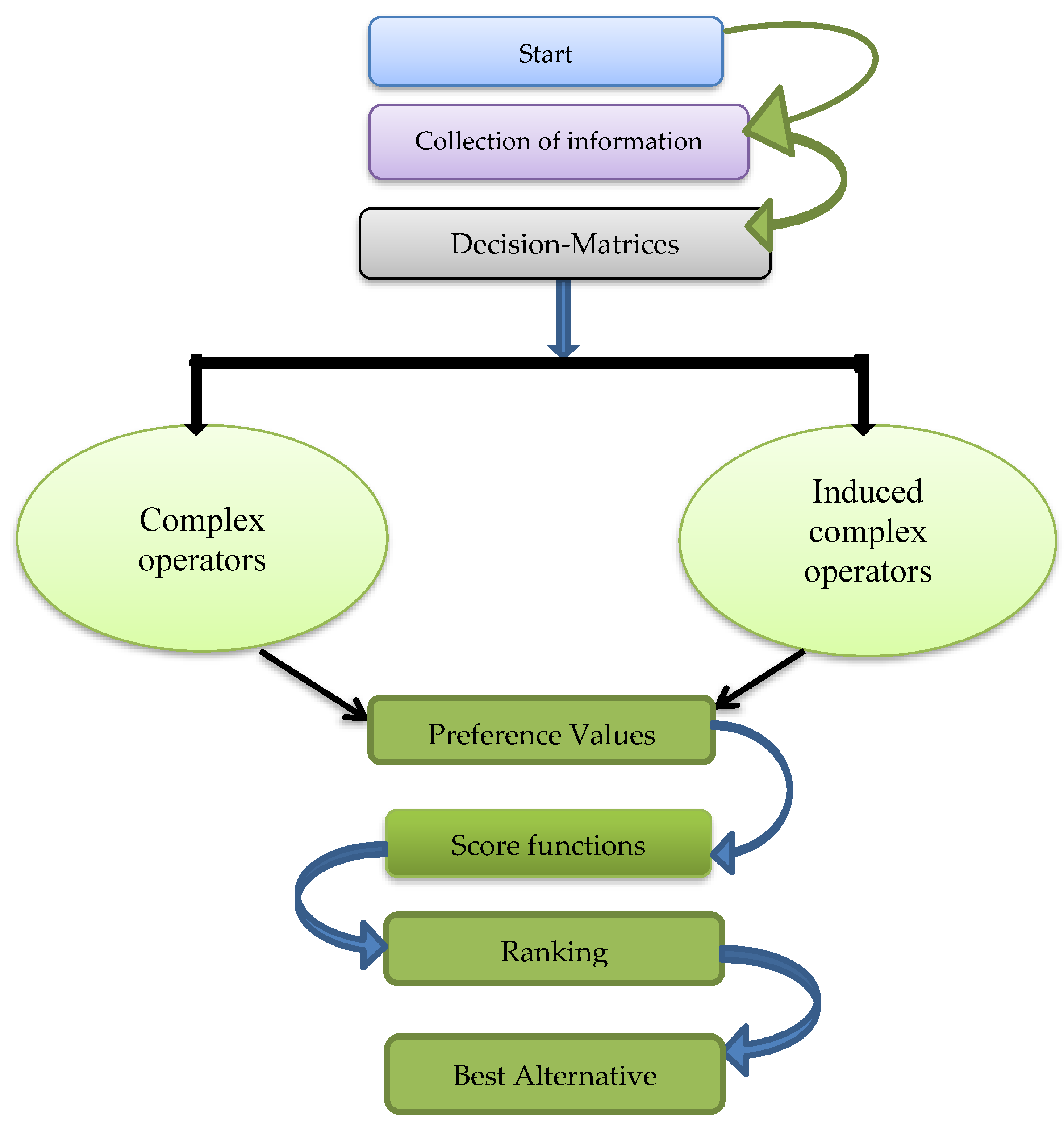
| Let be the set of m alternatives and be the set of n criteria whose associated vector is with restriction, such as and . . Let be a group of k experts whose weighted vector is with settings, such as and . The main steps are as follows (Figure 1 for explanation):
Step 1: Develop matrices based on the expertise of experts. Step 2: Make a single matrix out of all the separate matrices by combining them using the specified operators. Step 3: Again, compute all of the preference values using the specified techniques. Step 4: Calculate the scores using all preference values. Step 5: Choose the one with the highest score value. |
6. Illustrative Example
6.1. By Algebraic Operators
- Step 1: The decision matrices can be constructed according to the ideas of experts as:
- Step 2: Combine all the individual matrices into one matrix using the CPyFWG operator, where .
- Step 3: Again, using CPyFWG operator with , and obtain
- Step 4: Computing the score functions as:
- Step 5: Thus, the best option is .
6.2. By Induced Aggregation Operators
- Step 1: Construct the following same matrices based on experts’ ideas:
- Step 2: Combine all the individual matrices into a single matrix using 1-CPFOWG aggregation operator, where .
- Step 3: Again, using I-CPyFOWG operator, where , and obtain all the preference values as below:
- Step 4: Again, computing the score functions as below.
- Step 5: Thus, the best option is .
7. Comparative Analysis
8. Sensitivity Analysis
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Trans. Fuzzy Syst. 2013, 22, 958–965. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R.R. Fermatean fuzzy sets. J. Ambient. Intell. Humaniz. Comput. 2019, 11, 663–674. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic Fuzzy Aggregation Operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Intuitionistic fuzzy geometric aggregation operators based on einstein operations. Int. J. Intell. Syst. 2011, 26, 1049–1075. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Intuitionistic Fuzzy Information Aggregation Using Einstein Operations. IEEE Trans. Fuzzy Syst. 2012, 20, 923–938. [Google Scholar] [CrossRef]
- Rahman, K.; Abdullah, S.; Jamil, M.; Khan, M.Y. Some Generalized Intuitionistic Fuzzy Einstein Hybrid Aggregation Operators and Their Application to Multiple Attribute Group Decision Making. Int. J. Fuzzy Syst. 2018, 20, 1567–1575. [Google Scholar] [CrossRef]
- Rahman, K. Some new logarithmic aggregation operators and their application to group decision making problem based on t-norm and t-conorm. Soft Comput. 2022, 26, 2751–2772. [Google Scholar] [CrossRef]
- Ahmmad, J.; Mahmood, T.; Mehmood, N.; Urawong, K.; Chinram, R. Intuitionistic Fuzzy Rough Aczel-Alsina Average Aggregation Operators and Their Applications in Medical Diagnoses. Symmetry 2022, 14, 2537. [Google Scholar] [CrossRef]
- Rahman, K.; Khan, M.S.A.; Ullah, M.; Fahmi, A. Multiple Attribute Group Decision Making for Plant Location Selection with Pythagorean Fuzzy Weighted Geometric Aggregation Operator. Nucleus 2017, 54, 66–74. [Google Scholar]
- Rahman, K.; Abdullah, S.; Hussain, F.; Khan, M.S.A.; Shakeel, M. Pythagorean Fuzzy Ordered Weighted Geometric Aggregation Operator and Their Application to Multiple Attribute Group Decision Making. J. Appl. Environ. Biol. Sci. 2017, 7, 67–83. [Google Scholar]
- Rahman, K.; Abdullah, S.; Khan, M.S.A.; Shakeel, M. Pythagorean fuzzy hybrid geometric operator and their application to multiple attribute decision making. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 837–854. [Google Scholar]
- Rahman, K.; Khan, M.S.A.; Ullah, M. New Approaches to Pythagorean Fuzzy Averaging Aggregation Operators. Math. Lett. 2017, 3, 29. [Google Scholar] [CrossRef]
- Garg, H. A New Generalized Pythagorean Fuzzy Information Aggregation Using Einstein Operations and Its Application to Decision Making. Int. J. Intell. Syst. 2016, 31, 886–920. [Google Scholar] [CrossRef]
- Garg, H. Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int. J. Intell. Syst. 2017, 32, 597–630. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Siddique, I.; Ahmad, S.; Iampan, A.; Jovanov, G.; Vranješ, D.; Vasiljević, J. Pythagorean Fuzzy Soft Einstein Ordered Weighted Average Operator in Sustainable Supplier Selection Problem. Math. Probl. Eng. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Siddique, I.; Ei-Morsy, S. Einstein-Ordered Weighted Geometric Operator for Pythagorean Fuzzy Soft Set with Its Application to Solve MAGDM Problem. Math. Probl. Eng. 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Siddique, I.; Jarad, F.; Hamed, Y.S.; Abualnaja, K.M.; Iampan, A. Einstein Aggregation Operators for Pythagorean Fuzzy Soft Sets with Their Application in Multiattribute Group Decision-Making. J. Funct. Spaces 2022, 2022, 1–21. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Dayan, F. Selection of Best Alternative for An Automotive Company by Intuitionistic Fuzzy TOPSIS Method. Int. J. Sci. Technol. Res. 2017, 6, 126–132. [Google Scholar]
- Ramot, D.; Milo, R.; Friedman, M.; Kandel, A. Complex fuzzy sets. IEEE Trans Fuzzy Syst. 2002, 10, 171–186. [Google Scholar] [CrossRef]
- Alkouri, A.S.; Salleh, A.R. Complex intuitionistic fuzzy sets. AIP Conf. Proc. 2012, 1482, 464–470. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, G.; Lu, J. A Method for Multiple Periodic Factor Prediction Problems Using Complex Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2011, 20, 32–45. [Google Scholar] [CrossRef]
- Dick, S.; Yager, R.R.; Yazdanbakhsh, O. On Pythagorean and Complex Fuzzy Set Operations. IEEE Trans. Fuzzy Syst. 2015, 24, 1009–1021. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X. Comment on Pythagorean and Complex Fuzzy Set Operations. IEEE Trans. Fuzzy Syst. 2018, 26, 3902–3904. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Some Generalized Complex Intuitionistic Fuzzy Aggregation Operators and Their Application to Multicriteria Decision-Making Process. Arab. J. Sci. Eng. 2018, 44, 2679–2698. [Google Scholar] [CrossRef]
- Kumar, T.; Bajaj, R.K. On Complex Intuitionistic Fuzzy Soft Sets with Distance Measures and Entropies. J. Math. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Rani, D.; Garg, H. Complex intuitionistic fuzzy power aggregation operators and their applications in multicriteria decision-making. Expert Syst. 2018, 35, e12325. [Google Scholar] [CrossRef]
- Greenfield, S.; Chiclana, F.; Dick, S. Interval-valued complex fuzzy logic. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar]
- Garg, H.; Rani, D. A robust correlation coefficient measure of complex intuitionistic fuzzy sets and their applications in decision-making. Appl. Intell. 2018, 49, 496–512. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Ali, Z.; Jan, N. On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex Intell. Syst. 2019, 6, 15–27. [Google Scholar] [CrossRef]
- Liu, P.; Mahmood, T.; Ali, Z. Complex q-Rung Orthopair Fuzzy Aggregation Operators and Their Applications in Multi-Attribute Group Decision Making. Information 2019, 11, 5. [Google Scholar] [CrossRef]
- Zhou, X.; Deng, Y.; Huang, Z.; Yan, F.; Li, W. Complex Cubic Fuzzy Aggregation Operators with Applications in Group Decision-Making. IEEE Access 2020, 8, 223869–223888. [Google Scholar] [CrossRef]
- Akram, M.; Naz, S. A Novel Decision-Making Approach under Complex Pythagorean Fuzzy Environment. Math. Comput. Appl. 2019, 24, 73. [Google Scholar] [CrossRef]
- Qiyas, M.; Naeem, M.; Abdullah, L.; Riaz, M.; Khan, N. Decision Support System Based on Complex Fractional Orthotriple Fuzzy 2-Tuple Linguistic Aggregation Operator. Symmetry 2023, 15, 251. [Google Scholar] [CrossRef]
- Bi, L.; Dai, S.; Hu, B. Complex Fuzzy Geometric Aggregation Operators. Symmetry 2018, 10, 251. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Ullah, K.; Khan, Q. Einstein Geometric Aggregation Operators using a Novel Complex Interval-valued Pythagorean Fuzzy Setting with Application in Green Supplier Chain Management. Rep. Mech. Eng. 2021, 2, 105–134. [Google Scholar] [CrossRef]
- Rahman, K.; Khan, H.; Abdullah, S. Mathematical calculation of COVID-19 disease in Pakistan by emergency response modeling based on complex Pythagorean fuzzy information. J. Intell. Fuzzy Syst. 2022, 43, 3411–3427. [Google Scholar] [CrossRef]
- Rahman, K.; Iqbal, Q. Multi-attribute group decision-making problem based on some induced Einstein aggregation operators under complex fuzzy environment. J. Intell. Fuzzy Syst. 2023, 44, 421–453. [Google Scholar] [CrossRef]
| Methods | Scores | Ranking |
|---|---|---|
| CPyFWG | ||
| CPyFOWG | ||
| CPyFHG | ||
| I-CPyFOWG | ||
| I-CPyFHG |
| Model | Uncertainty | Falsity | Hesitation | Periodicity | 2-D Information | Square in Power |
|---|---|---|---|---|---|---|
| FSs | ✓ | ✕ | ✕ | ✕ | ✕ | ✕ |
| IFSs | ✓ | ✓ | ✓ | ✕ | ✕ | ✕ |
| PyFSs | ✓ | ✓ | ✓ | ✕ | ✕ | ✕ |
| FeFSs | ✓ | ✓ | ✓ | ✕ | ✕ | ✕ |
| CFSs | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ |
| CIFSs | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| CPyFSs | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hezam, I.M.; Rahman, K.; Alshamrani, A.; Božanić, D. Geometric Aggregation Operators for Solving Multicriteria Group Decision-Making Problems Based on Complex Pythagorean Fuzzy Sets. Symmetry 2023, 15, 826. https://doi.org/10.3390/sym15040826
Hezam IM, Rahman K, Alshamrani A, Božanić D. Geometric Aggregation Operators for Solving Multicriteria Group Decision-Making Problems Based on Complex Pythagorean Fuzzy Sets. Symmetry. 2023; 15(4):826. https://doi.org/10.3390/sym15040826
Chicago/Turabian StyleHezam, Ibrahim M., Khaista Rahman, Ahmad Alshamrani, and Darko Božanić. 2023. "Geometric Aggregation Operators for Solving Multicriteria Group Decision-Making Problems Based on Complex Pythagorean Fuzzy Sets" Symmetry 15, no. 4: 826. https://doi.org/10.3390/sym15040826
APA StyleHezam, I. M., Rahman, K., Alshamrani, A., & Božanić, D. (2023). Geometric Aggregation Operators for Solving Multicriteria Group Decision-Making Problems Based on Complex Pythagorean Fuzzy Sets. Symmetry, 15(4), 826. https://doi.org/10.3390/sym15040826








