Confidence Interval Estimation for the Ratio of the Percentiles of Two Delta-Lognormal Distributions with Application to Rainfall Data

Abstract

The log-normal distribution (skewed distribution or asymmetry distribution) is used to describe random variables comprising positive real values. It is well known that the logarithm values of these are normally distributed (symmetry distribution). Positively right-skewed data applicable to the log-normal distribution are frequently observed in the fields of environmental studies, biology, and medicine. The number of zero observations follows a binomial distribution. However, problems can arise in the analysis of data containing zero observations along with log-normally distributed data, for which the delta-lognormal distribution is often referred to for using the analysis of the data. In statistics, the percentile provides the relative standing of a numerical data point when compared to all of the others in a distribution with reference to the observations at or below it. In this study, estimates for the confidence interval for the ratio of the percentiles of two delta-lognormal distributions are constructed using fiducial generalized confidence interval approaches based on the fiducial quantity and the optimal generalized fiducial quantity, the Bayesian approach, and the parametric bootstrap method. As assessed by Monte Carlo simulations using the RStudio programming in terms of the coverage probability and the average length, the Bayesian approach performed quite well by providing adequate coverage probabilities along with the shortest average lengths in all of the scenarios tested. Daily rainfall data contain both zero and positive values. The daily rainfall data can usually be fitted to the delta-lognormal distribution. Their application to rainfall data is also provided to illustrate their efficacies with real data. The efficacy of the approach is used to compare two rainfall dispersion populations.

1. Introduction

The quantile, decile, and percentile can be used to investigate the central tendency and spread of a distribution. The difference between the third quartile and the first quartile is the interquartile range, which can be used as a measure of the spread of a distribution. The percentile has been utilized in many applications, such as in insurance and environmental science. For example, it has been used to compare the same-strength properties in the wood industry [1,2], to set premiums in the insurance industry [3], to compute rainfall amounts [4], and to estimate rainfall dispersion [5]. The ratio of the same-strength properties to compare two sources of lumber in terms of dimensions, grade, or species is commonly used as a comparison measure in the wood industry [1], for which the US lumber standards use the fifth percentile. Moreover, using the ratio of the fifth percentiles of two strength distributions is more meaningful than using the ratio of their means [2]. In addition, the ratio of percentiles is scale-free and easily interpretable. Thailand is an agricultural country, for which water is essential. Since the amount of water available depends on rainfall, predicting the latter is of interest, which is a particularly difficult task. Motivated by the application of the ratio of percentiles used in the lumber industry, we applied this approach in this study to compare two rainfall dispersion populations.

For environmental data, meteorology and climatology studies are often the positive values or the right-skewed data. The data follow the normal, log-normal, gamma, and exponential distributions. However, the log-normal distribution is commonly used in analysis of the right-skewed data. The delta-lognormal distribution can be used to investigate populations comprising a combination of zero and positive values [6]. The number of zero observations has a binomial distribution with probability ${\delta }^{\prime }=1-\delta$, whereas the positive observations follow a log-normal distribution with probability $\delta$. The log-normal distribution (asymmetry distribution) is used to describe random variables comprising positive real values. It is well known that the logarithm values of the random variables are normal distributions (symmetry distribution). The delta-lognormal distribution has been utilized in many fields, including medical and environmental science. For example, it has been used to study the diagnostic test charge data for older adults with depression [7] and to estimate rainfall dispersion [5].

Several researchers have studied interval estimation for the parameters of the delta-lognormal distribution, such as the mean, variance, coefficient of variation, and percentile. For instance, Hasan and Krishnamoorthy [8] estimated the confidence interval for the mean and the percentile of a delta-lognormal distribution. Moreover, Thangjai et al. [5] estimated the confidence interval for the common percentile of several delta-lognormal distributions.

Interval estimation about the ratio of percentiles of two delta-lognormal distributions are of practical and theoretical importance. To the best of our knowledge, the interval estimation for the ratio of the percentiles of two delta-lognormal distributions has not previously been studied. Therefore, the confidence interval for the ratio of the percentiles of two delta-lognormal distributions is of interest. The fiducial generalized confidence interval (FGCI), the Bayesian (BS), and the parametric bootstrap (PB) have been widely used to estimate confidence intervals for the parameter of interest [5]. The FGCI, BS, and PB approaches are based on simulated data. The FGCI approach uses simulation based on the fiducial generalized pivotal quantity (FGPQ). The BS approach uses simulation based on the prior distribution. The PB approach uses simulation based on the sampling distribution. This paper focuses on developing an approach for estimating the ratio of the percentiles of two delta-lognormal distributions. Herein, estimates for the confidence interval for the ratio of the percentiles of two delta-lognormal distributions are provided using several methods: two FGCI approaches based on the fiducial quantity and the optimal generalized fiducial quantity, one based on the BS approach, and one based on the PB approach. The confidence interval estimates were investigated via a Monte Carlo simulation study and then used to compare the percentiles of rainfall dispersion datasets from two regions in Thailand.

The rest of the paper is organized as follows. Several methods to construct the confidence intervals for the ratio of the percentiles of two delta-lognormal distributions are demonstrated in Section 2. The simulation studies are presented in Section 3. Application is given to illustrate the proposed approaches of constructing confidence intervals in Section 4. Some conclusions are given in Section 5.

2. Methods

For $i=1,2$, let $n_{i\left(0\right)}$ be the number of true zero observed value and let $n_{i\left(1\right)}$ be the number of positive observed values. Additionally, let $n_i=n_{i\left(0\right)}+n_{i\left(1\right)}$ be the number of the sample size. Let $X_i=(X_{i1},X_{i2},...,X_{i{n}_i})$ be a non-negative random sample of size $n_i$ from the delta-lognormal distribution with parameters mean ${\mu }_i$, variance ${\sigma }_i^2$, and probability of obtaining the positive observation ${\delta }_i$. Moreover, let ${\delta }_i^{\prime }=1-{\delta }_i$ be the probability of zero observation. The density function of delta-lognormal distribution is

$$f(x_{ij};{\mu }_i,{\sigma }_i^2,{\delta }_i)=(1-{\delta }_i)I_0\left[x_{ij}\right]+{\delta }_i\frac{1}{x_{ij}{\sigma }_i\sqrt{2\pi }}exp\left[-\frac{1}{2}{\left(\frac{ln\left(x_{ij}\right)-{\mu }_i}{{\sigma }_i}\right)}^2\right]I_{(0,\infty )}\left[x_{ij}\right],$$

(1)

where $I_0\left[x_{ij}\right]$ is an indicator function for which the values are equal to 1 when $x_{ij}=$0 and 0 otherwise, and $I_{(0,\infty )}\left[x_{ij}\right]$ are equal to 0 when $x_{ij}=$0 and 1 when $x_{ij}>$0.

The distribution function of delta-lognormal distribution is

$$G(x_{ij};{\mu }_i,{\sigma }_i^2,{\delta }_i)=\{\begin{array}{cc}{\delta }_i^{\prime };& x_{ij}=0\\ {\delta }_i^{\prime }+{\delta }_{i}F(x_{ij};{\mu }_i,{\sigma }_i^2);& x_{ij}>0\end{array},$$

(2)

where $F(x_{ij};{\mu }_i,{\sigma }_i^2)$ is the log-normal cumulative distribution function and $j=1,2,...,n_i$.

Let $Y_i=ln\left(X_i\right)$ be the normal distribution with parameters mean ${\mu }_i$ and variance ${\sigma }_i^2$. Let ${\overline{Y}}_i$ and $S_i$ be the estimators of mean and standard deviation, respectively. Suppose that ${\overline{y}}_i$ and $s_i$ are the observed values of ${\overline{Y}}_i$ and $S_i$, respectively. Moreover, let ${\overline{Y}}_{i\left(1\right)}$ and $S_{i\left(1\right)}$ be the estimators of mean and standard deviation based on the log-transformed positive observations, respectively. Suppose that ${\overline{y}}_{i\left(1\right)}$ and $s_{i\left(1\right)}$ are the observed values of ${\overline{Y}}_{i\left(1\right)}$ and $S_{i\left(1\right)}$, respectively.

Let $q_{p_i}$ be the $p_i$-th quantile of the delta-lognormal distribution. From the distribution function, that is $G(q_{p_i};{\mu }_i,{\sigma }_i^2,{\delta }_i)=p_i$. Therefore, the $q_{p_i}$ is

$$q_{p_i}=\{\begin{array}{cc}0;& p_i<{\delta }_i^{\prime }\\ exp\left({\mu }_i+{\Phi }^{-1}\left(\frac{p_i-{\delta }_i^{\prime }}{1-{\delta }_i^{\prime }}\right){\sigma }_i\right);& p_i>{\delta }_i^{\prime }\end{array},$$

(3)

where $\Phi$ is the standard normal distribution function.

Suppose that ${\lambda }_{p_i}={\mu }_i+{\Phi }^{-1}\left(\frac{p_i-{\delta }_i^{\prime }}{1-{\delta }_i^{\prime }}\right){\sigma }_i$. The estimator of the $q_{p_i}$ is

$${\widehat{q}}_{p_i}=exp\left({\widehat{\lambda }}_{p_i}\right)=exp\left({\overline{Y}}_{i\left(1\right)}+{\Phi }^{-1}\left(\frac{p_i-{\delta }_i^{\prime }}{1-{\delta }_i^{\prime }}\right)S_{i\left(1\right)}\right).$$

(4)

Let $\theta$ be the ratio of two percentiles of delta-lognormal distributions. The estimator of $\theta$ is

$$\widehat{\theta }=\frac{{\widehat{q}}_{p_1}}{{\widehat{q}}_{p_2}}=\frac{exp\left({\widehat{\lambda }}_{p_1}\right)}{exp\left({\widehat{\lambda }}_{p_2}\right)}=\frac{exp\left({\overline{Y}}_{1\left(1\right)}+{\Phi }^{-1}\left(\frac{p_1-{\delta }_1^{\prime }}{1-{\delta }_1^{\prime }}\right)S_{1\left(1\right)}\right)}{exp\left({\overline{Y}}_{2\left(1\right)}+{\Phi }^{-1}\left(\frac{p_2-{\delta }_2^{\prime }}{1-{\delta }_2^{\prime }}\right)S_{2\left(1\right)}\right)}.$$

(5)

2.1. Fiducial Generalized Confidence Interval Approach

We proposed the FGCI approach based on the fiducial quantity and the FGCI approach based on optimal generalized fiducial quantity. First, the FGCI approach based on the fiducial quantity uses the FGPQ of $\widehat{\theta }$. The FGPQ of $\widehat{\theta }$ is based on the FGPQs of ${\mu }_1$, ${\mu }_2$, ${\sigma }_1^2$, ${\sigma }_2^2$, ${\delta }_1^{\prime }$, ${\delta }_2^{\prime }$, ${\lambda }_{p_1}$, and ${\lambda }_{p_2}$.

Let $Z_1$ and $Z_2$ be the standard normal distributions. Additionally, let $U_{1\left(1\right)}$ and $U_{2\left(1\right)}$ be the chi-squared distributions with $n_{1\left(1\right)}-1$ and $n_{2\left(1\right)}-1$ degrees of freedom, respectively. The FGPQs for ${\mu }_1$, ${\mu }_2$, ${\sigma }_1^2$, and ${\sigma }_2^2$ are given by

$$R_{{\mu }_1}={\overline{y}}_{1\left(1\right)}-\frac{Z_1}{\sqrt{U_{1\left(1\right)}}}\sqrt{\frac{(n_{1\left(1\right)}-1)s_{1\left(1\right)}^2}{n_{1\left(1\right)}}}$$

(6)

$$R_{{\mu }_2}={\overline{y}}_{2\left(1\right)}-\frac{Z_2}{\sqrt{U_{2\left(1\right)}}}\sqrt{\frac{(n_{2\left(1\right)}-1)s_{2\left(1\right)}^2}{n_{2\left(1\right)}}}$$

(7)

$$R_{{\sigma }_1^2}=\frac{(n_{1\left(1\right)}-1)s_{1\left(1\right)}^2}{U_{1\left(1\right)}}$$

(8)

and

$$R_{{\sigma }_2^2}=\frac{(n_{2\left(1\right)}-1)s_{2\left(1\right)}^2}{U_{2\left(1\right)}}.$$

(9)

According to Thangjai et al. [5], let $B_{n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5}$ be the beta random variable with shape parameters $n_{1\left(0\right)}+0.5$ and $n_{1\left(1\right)}+0.5$. Additionally, let $B_{n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5}$ be the beta random variable with shape parameters $n_{2\left(0\right)}+0.5$ and $n_{2\left(1\right)}+0.5$. Let $V_1$ and $V_2$ be the standard uniform distributions. Let $p_1$ and $p_2$ be the percentiles. Let $H(p_1;n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5)$ and $H(p_2;n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5)$ be the beta distribution functions. Moreover, let $H^{-1}(V_{1}H(p_1;n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5);n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5)$ and $H^{-1}(V_{2}H(p_2;n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5);n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5)$ be the quartile functions of the beta distributions. The FGPQs for ${\delta }_1^{\prime }$ and ${\delta }_2^{\prime }$ are given by

$$R_{{\delta }_1^{\prime }}=H^{-1}(V_{1}H(p_1;n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5);n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5)$$

(10)

and

$$R_{{\delta }_2^{\prime }}=H^{-1}(V_{2}H(p_2;n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5);n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5).$$

(11)

The FGPQs for ${\mu }_1$, ${\sigma }_1^2$, and ${\delta }_1^{\prime }$ are used to compute the FGPQ for ${\lambda }_{p_1}$. Additionally, the FGPQs for ${\mu }_2$, ${\sigma }_2^2$, and ${\delta }_2^{\prime }$ are used to calculate the FGPQ for ${\lambda }_{p_2}$. The FGPQs for ${\lambda }_{p_1}$ and ${\lambda }_{p_2}$ are given by

$$R_{{\lambda }_{p_1}}=R_{{\mu }_1}+\frac{\sqrt{R_{{\sigma }_1^2}}}{\sqrt{n_{1\left(1\right)}}}\left(\frac{Z_1+{\Phi }^{-1}\left(\frac{p_1-R_{{\delta }_1^{\prime }}}{1-R_{{\delta }_1^{\prime }}}\right)\sqrt{n_{1\left(1\right)}}}{\sqrt{U_{1\left(1\right)}}}\right)$$

(12)

and

$$R_{{\lambda }_{p_2}}=R_{{\mu }_2}+\frac{\sqrt{R_{{\sigma }_2^2}}}{\sqrt{n_{2\left(1\right)}}}\left(\frac{Z_2+{\Phi }^{-1}\left(\frac{p_2-R_{{\delta }_2^{\prime }}}{1-R_{{\delta }_2^{\prime }}}\right)\sqrt{n_{2\left(1\right)}}}{\sqrt{U_{2\left(1\right)}}}\right),$$

(13)

where ${\Phi }^{-1}(•)$ is the quartile function.

The FGPQ for $\theta$ is

$$R_{\theta }=\frac{exp\left(R_{{\lambda }_{p_1}}\right)}{exp\left(R_{{\lambda }_{p_2}}\right)},$$

(14)

where $R_{{\lambda }_{p_1}}$ and $R_{{\lambda }_{p_2}}$ are defined in Equation (12) and Equation (13), respectively.

Therefore, the $100(1-\alpha )\%$ two-sided confidence interval for the ratio of two percentiles based on the FGCI approach using fiducial quantity is

$$C{I}_{FGCI1}=[L_{FGCI1},U_{FGCI1}]=[R_{\theta }(\alpha /2),R_{\theta }(1-\alpha /2)],$$

(15)

where $R_{\theta }(\alpha /2)$ and $R_{\theta }(1-\alpha /2)$ are the $100(\alpha /2)$-th and $100(1-\alpha /2)$-th percentiles of $R_{\theta }$, respectively.

Algorithm 1: Confidence interval based on FGCI approach using fiducial quantity

Step 1: Calculate the values of $R_{{\mu }_1}$, $R_{{\mu }_2}$, $R_{{\sigma }_1^2}$, and $R_{{\sigma }_2^2}$ as given in Equations (6)–(9). Step 2: Calculate the values of $R_{{\delta }_1^{\prime }}$, $R_{{\delta }_2^{\prime }}$, $R_{{\lambda }_{p_1}}$, and $R_{{\lambda }_{p_2}}$ as given in Equations (10)–(13). Step 3: Calculate the value of $R_{\theta }$ as given in Equation (14). Step 4: Repeat the step 1–step 3 for q times. Step 5: Calculate the values of $L_{FGCI1}$ and $U_{FGCI1}$ as given in Equation (15).

Second, the concept of the FGCI approach based on the optimal generalized fiducial quantity is similar to the concept of the FGCI approach based on the fiducial quantity. The FGCI approach based on optimal generalized fiducial quantity uses the FGPQ of $\widehat{\theta }$, which is given by

$$R_{\theta .m}=\frac{exp\left(R_{{\lambda }_{p.m1}}\right)}{exp\left(R_{{\lambda }_{p.m2}}\right)},$$

(16)

where

$$R_{{\lambda }_{p.m1}}=R_{{\mu }_1}+\frac{\sqrt{R_{{\sigma }_1^2}}}{\sqrt{n_{1\left(1\right)}}}\left(\frac{Z_1+{\Phi }^{-1}\left(\frac{p_1-R_{{\delta }_{m1}^{\prime }}}{1-R_{{\delta }_{m1}^{\prime }}}\right)\sqrt{n_{1\left(1\right)}}}{\sqrt{U_{1\left(1\right)}}}\right),$$

$$R_{{\lambda }_{p.m2}}=R_{{\mu }_2}+\frac{\sqrt{R_{{\sigma }_2^2}}}{\sqrt{n_{2\left(1\right)}}}\left(\frac{Z_2+{\Phi }^{-1}\left(\frac{p_2-R_{{\delta }_{m2}^{\prime }}}{1-R_{{\delta }_{m2}^{\prime }}}\right)\sqrt{n_{2\left(1\right)}}}{\sqrt{U_{2\left(1\right)}}}\right),$$

$$R_{{\delta }_{m1}^{\prime }}=\frac{H^{-1}(V_{1}H(p_1;n_{1\left(0\right)},n_{1\left(1\right)}+1);n_{1\left(0\right)}+1,n_{1\left(1\right)})}{2},$$

and

$$R_{{\delta }_{m2}^{\prime }}=\frac{H^{-1}(V_{2}H(p_2;n_{2\left(0\right)},n_{2\left(1\right)}+1);n_{2\left(0\right)}+1,n_{2\left(1\right)})}{2}.$$

Therefore, the $100(1-\alpha )\%$ two-sided confidence interval for the ratio of two percentiles based on the FGCI approach using the optimal generalized fiducial quantity is

$$C{I}_{FGCI2}=[L_{FGCI2},U_{FGCI2}]=[R_{\theta .m}(\alpha /2),R_{\theta .m}(1-\alpha /2)],$$

(17)

where $R_{\theta .m}(\alpha /2)$ and $R_{\theta .m}(1-\alpha /2)$ are the $100(\alpha /2)$-th and $100(1-\alpha /2)$-th percentiles of $R_{\theta .m}$, respectively.

Algorithm 2: Confidence interval based on FGCI approach using optimal generalized fiducial quantity

Step 1: Calculate the values of $R_{{\mu }_1}$, $R_{{\mu }_2}$, $R_{{\sigma }_1^2}$, and $R_{{\sigma }_2^2}$ as given in Equations (6)–(9). Step 2: Calculate the values of $R_{{\lambda }_{p.m1}}$, $R_{{\lambda }_{p.m2}}$, $R_{{\delta }_{m1}^{\prime }}$, $R_{{\delta }_{m2}^{\prime }}$, and $R_{\theta .m}$ as given in Equation (16). Step 3: Repeat steps 1–2 for q times. Step 4: Calculate the values of $L_{FGCI2}$ and $U_{FGCI2}$ as given in Equation (17).

2.2. Bayesian Approach

The prior distribution is based on the experimenter’s belief and is updated with the sample information. The posterior distribution is used to update the prior distribution with Bayes’ rule. The Bayesian approach is based on the likelihood function and the prior distributions. The Jeffreys independence priors are

$$p({\mu }_1,{\sigma }_1^2)\propto \frac{1}{{\sigma }_1^2}$$

(18)

and

$$p({\mu }_2,{\sigma }_2^2)\propto \frac{1}{{\sigma }_2^2}.$$

(19)

The posterior distributions for ${\sigma }_1^2$, ${\sigma }_2^2$, ${\mu }_1$, and ${\mu }_2$ are

$${\sigma }_1^2|y_1\sim IG\left(\frac{n_{1\left(1\right)}-1}{2},\frac{(n_{1\left(1\right)}-1)s_{1\left(1\right)}^2}{2}\right)$$

(20)

$${\sigma }_2^2|y_2\sim IG\left(\frac{n_{2\left(1\right)}-1}{2},\frac{(n_{2\left(1\right)}-1)s_{2\left(1\right)}^2}{2}\right)$$

(21)

$${\mu }_1|{\sigma }_1^2,y_1\sim N\left({\overline{y}}_{1\left(1\right)},\frac{{\sigma }_1^2}{n_{1\left(1\right)}}\right)$$

(22)

and

$${\mu }_2|{\sigma }_2^2,y_2\sim N\left({\overline{y}}_{2\left(1\right)},\frac{{\sigma }_2^2}{n_{2\left(1\right)}}\right).$$

(23)

Let $Q_{{\delta }_1^{\prime }}$ and $Q_{{\delta }_2^{\prime }}$ be the probability distributions. The probability distributions are defined by

$$Q_{{\delta }_1^{\prime }}=H^{-1}(V_{1}H(p_1;n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5);n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5)$$

(24)

and

$$Q_{{\delta }_2^{\prime }}=H^{-1}(V_{2}H(p_2;n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5);n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5).$$

(25)

The posterior distributions of ${\lambda }_{p_1}$ and ${\lambda }_{p_2}$ are

$${\lambda }_{BS.p_1}={\mu }_1+\frac{\sqrt{{\sigma }_1^2}}{\sqrt{n_{1\left(1\right)}}}\left(\frac{Z_1+{\Phi }^{-1}\left(\frac{p_1-Q_{{\delta }_1^{\prime }}}{1-Q_{{\delta }_1^{\prime }}}\right)\sqrt{n_{1\left(1\right)}}}{\sqrt{U_{1\left(1\right)}}}\right)$$

(26)

and

$${\lambda }_{BS.p_2}={\mu }_2+\frac{\sqrt{{\sigma }_2^2}}{\sqrt{n_{2\left(1\right)}}}\left(\frac{Z_2+{\Phi }^{-1}\left(\frac{p_2-Q_{{\delta }_2^{\prime }}}{1-Q_{{\delta }_2^{\prime }}}\right)\sqrt{n_{2\left(1\right)}}}{\sqrt{U_{2\left(1\right)}}}\right),$$

(27)

where ${\sigma }_1^2$, ${\sigma }_2^2$, ${\mu }_1$, ${\mu }_2$, $Q_{{\delta }_1^{\prime }}$, and $Q_{{\delta }_2^{\prime }}$ are defined in Equations (20)–(25).

Therefore, the posterior distribution for $\theta$ is

$${\theta }_{BS}=\frac{exp\left({\lambda }_{BS.p_1}\right)}{exp\left({\lambda }_{BS.p_2}\right)},$$

(28)

where ${\lambda }_{BS.p_1}$ and ${\lambda }_{BS.p_2}$ are defined in Equation (26) and Equation (27), respectively.

Therefore, the $100(1-\alpha )\%$ two-sided credible interval for the ratio of two percentiles based on the BS approach is

$$C{I}_{BS}=[L_{BS},U_{BS}],$$

(29)

where $L_{BS}$ and $U_{BS}$ are the lower limit and the upper limit of the shortest $100(1-\alpha )\%$ highest posterior density interval of ${\theta }_{BS}$, respectively.

Algorithm 3: Credible interval based on BS approach

Step 1: Generate the values of ${\sigma }_1^2|y_1$, ${\sigma }_2^2|y_2$, ${\mu }_1|{\sigma }_1^2,y_1$, and ${\mu }_2|{\sigma }_2^2,y_2$ as given in Equations (20)–(23). Step 2: Calculate the values of $Q_{{\delta }_1^{\prime }}$, $Q_{{\delta }_2^{\prime }}$, ${\lambda }_{BS.p_1}$, and ${\lambda }_{BS.p_2}$ as given in Equations (24)–(27). Step 3: Calculate the value of ${\theta }_{BS}$ as given in Equation (28). Step 4: Repeat the step 1–step 3 for q times. Step 5: Calculate the values of $L_{BS}$ and $U_{BS}$ as given in Equation (29).

2.3. Parametric Bootstrap Approach

For $i=1,2$, let $X_i^{*}=(X_{i1}^{*},X_{i2}^{*},...,X_{i{n}_i}^{*})$ be the sample with replacement from $X_i=(X_{i1},X_{i2},...,X_{i{n}_i})$. Let $x_i^{*}=(x_{i1}^{*},x_{i2}^{*},...,x_{i{n}_i}^{*})$ be the observed values of $X_i^{*}=(X_{i1}^{*},X_{i2}^{*},...,X_{i{n}_i}^{*})$. Moreover, let $Y_i^{*}=ln\left(X_i^{*}\right)$ be the normal distribution with parameters mean ${\mu }_i^{*}$ and variance ${\sigma }_i^{2*}$. Let ${\overline{Y}}_i^{*}$ and $S_i^{2*}$ be the estimators of mean and variance, respectively. Let ${\overline{Y}}_{i\left(1\right)}^{*}$ and $S_{i\left(1\right)}^{2*}$ be the estimators of mean and variance based on the log-transformed positive observations, respectively. Let ${\overline{y}}_i^{*}$, ${\overline{y}}_{i\left(1\right)}^{*}$, $s_i^{2*}$, and $s_{i\left(1\right)}^{2*}$ be observed values of ${\overline{Y}}_i^{*}$, ${\overline{Y}}_{i\left(1\right)}^{*}$, $S_i^{2*}$, and $S_{i\left(1\right)}^{2*}$, respectively.

Let $W_1$ and $W_2$ be the standard uniform distributions. Let $Q_{{\delta }_1^{\prime }}^{*}$ and $Q_{{\delta }_2^{\prime }}^{*}$ be the probability distributions, which are given by

$$Q_{{\delta }_1^{\prime }}^{*}=H^{-1}(W_{1}H(p_1;n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5);n_{1\left(0\right)}+0.5,n_{1\left(1\right)}+0.5)$$

(30)

and

$$Q_{{\delta }_2^{\prime }}^{*}=H^{-1}(W_{2}H(p_2;n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5);n_{2\left(0\right)}+0.5,n_{2\left(1\right)}+0.5).$$

(31)

The estimators of ${\lambda }_{p_1}$ and ${\lambda }_{p_2}$ are

$${\widehat{\lambda }}_{p_1}^{*}={\overline{Y}}_{1\left(1\right)}^{*}+{\Phi }^{-1}\left(\frac{p_1-Q_{{\delta }_1^{\prime }}^{*}}{1-Q_{{\delta }_1^{\prime }}^{*}}\right)S_{1\left(1\right)}^{*}$$

(32)

and

$${\widehat{\lambda }}_{p_2}^{*}={\overline{Y}}_{2\left(1\right)}^{*}+{\Phi }^{-1}\left(\frac{p_2-Q_{{\delta }_2^{\prime }}^{*}}{1-Q_{{\delta }_2^{\prime }}^{*}}\right)S_{2\left(1\right)}^{*}.$$

(33)

Let ${\theta }^{*}$ be the ratio of two percentiles of delta-lognormal distributions. The estimator of ${\theta }^{*}$ is

$${\widehat{\theta }}^{*}=\frac{exp\left({\widehat{\lambda }}_{p_1}^{*}\right)}{exp\left({\widehat{\lambda }}_{p_2}^{*}\right)},$$

(34)

where ${\widehat{\lambda }}_{p_1}^{*}$ and ${\widehat{\lambda }}_{p_2}^{*}$ are defined in Equation (32) and Equation (33), respectively.

Let ${\overline{\widehat{\theta }}}^{*}$ and $sd\left({\widehat{\theta }}^{*}\right)$ be the mean and standard deviation of ${\widehat{\theta }}^{*}$, respectively. The lower and upper bounds for ${\theta }^{*}$ are defined by

$$L_{PB}={\overline{\widehat{\theta }}}^{*}-z_{1-\alpha /2}sd\left({\widehat{\theta }}^{*}\right)$$

(35)

and

$$U_{PB}={\overline{\widehat{\theta }}}^{*}+z_{1-\alpha /2}sd\left({\widehat{\theta }}^{*}\right),$$

(36)

where $z_{1-\alpha /2}$ is the $100(1-\alpha /2)$-th percentile of the standard normal distribution.

Therefore, the $100(1-\alpha )\%$ two-sided confidence interval for the ratio of two percentiles based on the PB approach is

$$C{I}_{PB}=[L_{PB},U_{PB}]$$

(37)

where $L_{PB}$ and $U_{PB}$ are defined in Equation (35) and Equation (36), respectively.

Algorithm 4: Confidence interval based on PB approach

Step 1: Generate the value of $x_1^{*}=(x_{11}^{*},x_{12}^{*},...,x_{1n_1}^{*})$ with replacement from $x_1=(x_{11},x_{12},...,x_{1n_1})$ and generate the value of $x_2^{*}=(x_{21}^{*},x_{22}^{*},...,x_{2n_2}^{*})$ with replacement from $x_2=(x_{21},x_{22},...,x_{2n_2})$. Step 2: Calculate the values of $y_1^{*}=ln\left(x_1^{*}\right)$, $y_2^{*}=ln\left(x_2^{*}\right)$, ${\overline{y}}_1^{*}$, ${\overline{y}}_2^{*}$, ${\overline{y}}_{1\left(1\right)}^{*}$, ${\overline{y}}_{2\left(1\right)}^{*}$, $s_1^{2*}$, $s_2^{2*}$, $s_{1\left(1\right)}^{2*}$, and  $s_{2\left(1\right)}^{2*}$. Step 3: Calculate the values of $Q_{{\delta }_1^{\prime }}^{*}$, $Q_{{\delta }_2^{\prime }}^{*}$, ${\widehat{\lambda }}_{p_1}^{*}$, and ${\widehat{\lambda }}_{p_2}^{*}$ as given in Equations (30)–(33). Step 4: Calculate the value of ${\widehat{\theta }}^{*}$ as given in Equation (34). Step 5: Repeat the step 1–step 4 for q times. Step 6: Calculate the values of $L_{PB}$ and $U_{PB}$ as given in Equations (35) and (36).

3. Results

Monte Carlo simulation was used to investigate the efficacies of the proposed approaches in terms of the coverage probability (the percentage of times the true parameter of interest falls within the confidence interval) and the average length of the estimate via the RStudio programming. The nominal confidence level was set as 95%. The best-performing confidence interval estimates for each scenario provided a coverage probability greater than or equal to the nominal confidence level of 0.95 and the shortest average length. To generate the data, the sample sizes were set as $(n_1,n_2)=$ (30,30), (50,50), (30,50), (100,100), or (50,100); the population means were fixed as $({\mu }_1,{\mu }_2)=$ (1.00,1.00); the population variances were set as $({\sigma }_1^2,{\sigma }_2^2)=$ (0.50,0.50), (0.50,1.00), or (1.00,1.00); and the probabilities of zero observations were set as $({\delta }_1^{\prime },{\delta }_2^{\prime })=$ (0.3,0.3), (0.3,0.5), or (0.5,0.5). 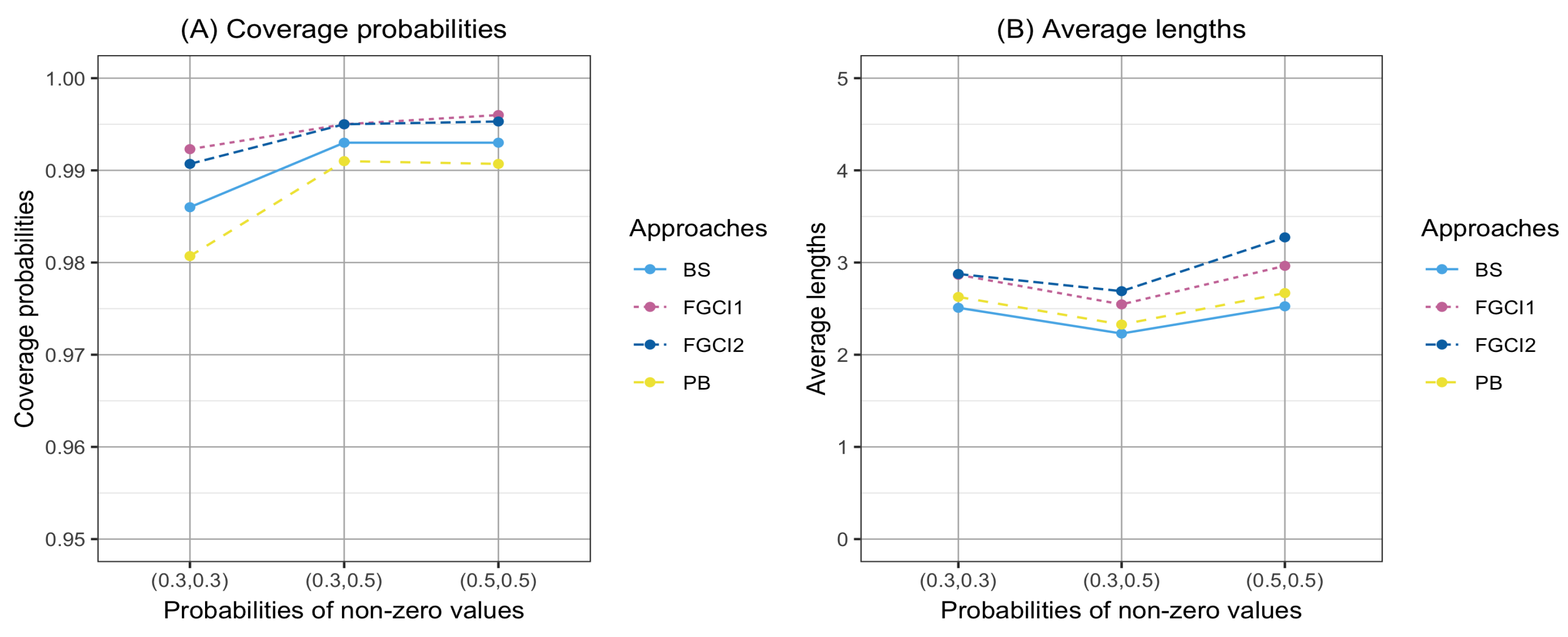For each simulation, 3000 runs were made together with 1500 replications.  

Algorithm 5: Coverage probability and average length of the confidence intervals

For a given $n_1$, $n_2$, ${\mu }_1$, ${\mu }_2$, ${\delta }_1^{\prime }$, ${\delta }_2^{\prime }$, ${\sigma }_1^2$, ${\sigma }_2^2$, and $\theta$ Step 1: Generate the values of $x_1=(x_{11},x_{12},...,x_{1n_1})$ and $x_2=(x_{21},x_{22},...,x_{2n_2})$ from the delta-lognormal distributions. Step 2: Calculate the values of $y_1=ln\left(x_1\right)$, $y_2=ln\left(x_2\right)$, ${\overline{y}}_1$, ${\overline{y}}_2$, ${\overline{y}}_{1\left(1\right)}$, ${\overline{y}}_{2\left(1\right)}$, $s_1^2$, $s_2^2$, $s_{1\left(1\right)}^2$, and $s_{2\left(1\right)}^2$. Step 3: Construct $C{I}_{FGCI1\left(h\right)}=[L_{FGCI1\left(h\right)},U_{FGCI1\left(h\right)}]$ using the Algorithm 1. Step 4: Construct $C{I}_{FGCI2\left(h\right)}=[L_{FGCI2\left(h\right)},U_{FGCI2\left(h\right)}]$ using the Algorithm 2. Step 5: Construct $C{I}_{BS\left(h\right)}=[L_{BS\left(h\right)},U_{BS\left(h\right)}]$ using the Algorithm 3. Step 6: Construct $C{I}_{PB\left(h\right)}=[L_{PB\left(h\right)},U_{PB\left(h\right)}]$ using the Algorithm 4. Step 7: If $L_{\left(h\right)}⩽\theta ⩽U_{\left(h\right)}$ set $p_{\left(h\right)}=$ 1, else $p_{\left(h\right)}=$ 0. Step 8: Calculate $U_{\left(h\right)}-L_{\left(h\right)}$. Step 9: Repeat the step 1–step 8 for a large number of times (say, M times) and calculate coverage probability and average length.

The coverage probabilities and average lengths of each confidence interval are presented in

Table 1. The coverage probabilities (CPs) and average lengths (ALs) of 95% two-sided confidence intervals for the ratio of the percentiles of two delta-lognormal distributions.

$({\mathit{n}}_1,{\mathit{n}}_2)$	$({\mathit{\mu }}_1,{\mathit{\mu }}_2)$	$({\mathit{\delta }}_1^{\prime },{\mathit{\delta }}_2^{\prime })$	$({\mathit{\sigma }}_1^2,{\mathit{\sigma }}_2^2)$	CP (AL)
				${\mathit{C}\mathit{I}}_{\mathit{F}\mathit{G}\mathit{C}\mathit{I}1}$	${\mathit{C}\mathit{I}}_{\mathit{F}\mathit{G}\mathit{C}\mathit{I}2}$	${\mathit{C}\mathit{I}}_{\mathit{B}\mathit{S}}$	${\mathit{C}\mathit{I}}_{\mathit{P}\mathit{B}}$
(30,30)	(1.0,1.0)	(0.3,0.3)	(0.5,0.5)	0.9950	0.9950	0.9930	0.9910
				(2.5460)	(2.6894)	(2.2299)	(2.3273)
			(0.5,1.0)	0.9943	0.9953	0.9920	0.9920
				(2.0245)	(2.0671)	(1.7386)	(1.9352)
			(1.0,1.0)	0.9927	0.9947	0.9907	0.9887
				(4.5295)	(4.8314)	(3.6130)	(4.3502)
		(0.3,0.5)	(0.5,0.5)	0.9923	0.9907	0.9860	0.9807
				(2.8673)	(2.8758)	(2.5092)	(2.6268)
			(0.5,1.0)	0.9937	0.9910	0.9860	0.9860
				(2.4029)	(2.2886)	(2.0468)	(2.3110)
			(1.0,1.0)	0.9950	0.9943	0.9913	0.9870
				(5.2764)	(5.3124)	(4.1935)	(5.0920)
		(0.5,0.5)	(0.5,0.5)	0.9960	0.9953	0.9930	0.9907
				(2.9642)	(3.2731)	(2.5253)	(2.6688)
			(0.5,1.0)	0.9967	0.9957	0.9933	0.9923
				(2.4995)	(2.6089)	(2.0791)	(2.3692)
			(1.0,1.0)	0.9937	0.9943	0.9880	0.9860
				(5.6224)	(6.4502)	(4.3045)	(5.5863)
(50,50)	(1.0,1.0)	(0.3,0.3)	(0.5,0.5)	0.9930	0.9943	0.9907	0.9883
				(1.6773)	(1.7432)	(1.5578)	(1.5834)
			(0.5,1.0)	0.9940	0.9953	0.9940	0.9953
				(1.3285)	(1.3390)	(1.2167)	(1.2822)
			(1.0,1.0)	0.9927	0.9917	0.9900	0.9893
				(2.6586)	(2.7784)	(2.3229)	(2.5554)
		(0.3,0.5)	(0.5,0.5)	0.9943	0.9913	0.9857	0.9843
				(1.9112)	(1.8864)	(1.7737)	(1.8024)
			(0.5,1.0)	0.9927	0.9883	0.9877	0.9873
				(1.6139)	(1.5126)	(1.4709)	(1.5735)
			(1.0,1.0)	0.9923	0.9903	0.9857	0.9850
				(3.1755)	(3.0862)	(2.7680)	(3.0512)
		(0.5,0.5)	(0.5,0.5)	0.9943	0.9937	0.9937	0.9910
				(1.8877)	(2.0385)	(1.7256)	(1.7624)
			(0.5,1.0)	0.9947	0.9950	0.9920	0.9910
				(1.5758)	(1.6069)	(1.4184)	(1.5152)
			(1.0,1.0)	0.9933	0.9917	0.9903	0.9877
				(3.1608)	(3.4810)	(2.6977)	(2.9972)
(30,50)	(1.0,1.0)	(0.3,0.3)	(0.5,0.5)	0.9953	0.9943	0.9913	0.9847
				(2.3111)	(2.4502)	(2.0192)	(2.0532)
			(0.5,1.0)	0.9957	0.9963	0.9923	0.9900
				(1.7212)	(1.7609)	(1.4965)	(1.5918)
			(1.0,1.0)	0.9917	0.9913	0.9887	0.9820
				(4.0489)	(4.3732)	(3.2471)	(3.7715)
		(0.3,0.5)	(0.5,0.5)	0.9920	0.9907	0.9860	0.9763
				(2.5849)	(2.5940)	(2.2673)	(2.3035)
			(0.5,1.0)	0.9937	0.9890	0.9867	0.9843
				(2.1018)	(1.9964)	(1.8207)	(1.9397)
			(1.0,1.0)	0.9947	0.9933	0.9880	0.9837
				(4.7258)	(4.6993)	(3.7844)	(4.4954)
		(0.5,0.5)	(0.5,0.5)	0.9963	0.9963	0.9963	0.9930
				(2.7961)	(3.1043)	(2.3796)	(2.4386)
			(0.5,1.0)	0.9960	0.9957	0.9910	0.9907
				(2.1357)	(2.2267)	(1.8044)	(1.9514)
			(1.0,1.0)	0.9950	0.9950	0.9963	0.9930
				(5.2021)	(5.9882)	(3.9804)	(4.8729)
(100,100)	(1.0,1.0)	(0.3,0.3)	(0.5,0.5)	0.9960	0.9953	0.9927	0.9910
				(1.0621)	(1.0968)	(1.0194)	(1.0323)
			(0.5,1.0)	0.9943	0.9937	0.9917	0.9917
				(0.8466)	(0.8481)	(0.8073)	(0.8323)
			(1.0,1.0)	0.9923	0.9930	0.9907	0.9887
				(1.5956)	(1.6469)	(1.4855)	(1.5559)
		(0.3,0.5)	(0.5,0.5)	0.9940	0.9887	0.9907	0.9907
				(1.2290)	(1.2023)	(1.1794)	(1.1939)
			(0.5,1.0)	0.9960	0.9827	0.9887	0.9910
				(1.0472)	(0.9689)	(0.9952)	(1.0338)
			(1.0,1.0)	0.9940	0.9880	0.9890	0.9867
				(1.9285)	(1.8404)	(1.7952)	(1.8889)
		(0.5,0.5)	(0.5,0.5)	0.9933	0.9933	0.9917	0.9903
				(1.1822)	(1.2580)	(1.1272)	(1.1401)
			(0.5,1.0)	0.9907	0.9907	0.9897	0.9907
				(0.9819)	(0.9850)	(0.9294)	(0.9624)
			(1.0,1.0)	0.9957	0.9947	0.9937	0.9933
				(1.7969)	(1.9312)	(1.6575)	(1.7492)
(50,100)	(1.0,1.0)	(0.3,0.3)	(0.5,0.5)	0.9943	0.9933	0.9917	0.9877
				(1.4553)	(1.5199)	(1.3477)	(1.3457)
			(0.5,1.0)	0.9913	0.9917	0.9913	0.9890
				(1.0928)	(1.1063)	(1.0094)	(1.0336)
			(1.0,1.0)	0.9923	0.9927	0.9887	0.9837
				(2.3210)	(2.4394)	(2.0415)	(2.1534)
		(0.3,0.5)	(0.5,0.5)	0.9933	0.9893	0.9890	0.9830
				(1.6587)	(1.6297)	(1.5360)	(1.5401)
			(0.5,0.5)	0.9933	0.9823	0.9870	0.9803
				(1.3195)	(1.2287)	(1.2155)	(1.2523)
			(0.5,1.0)	0.9933	0.9893	0.9883	0.9820
				(2.7516)	(2.6548)	(2.4220)	(2.5710)
		(0.5,0.5)	(0.5,0.5)	0.9930	0.9930	0.9910	0.9873
				(1.6779)	(1.8074)	(1.5302)	(1.5300)
			(0.5,1.0)	0.9930	0.9907	0.9893	0.9870
				(1.3099)	(1.3329)	(1.1930)	(1.2194)
			(1.0,1.0)	0.9927	0.9917	0.9907	0.9860
				(2.7363)	(2.9991)	(2.3541)	(2.5189)

and shown in Figure 1, Figure 2 and Figure 3. It can be seen that the coverage probabilities of all of the methods were greater than the nominal confidence level of 0.95, while the BS approach performed better than the others by providing the shortest average lengths for all of the scenarios tested.

4. Empirical Application of the Methods to Rainfall Data from Two Regions in Thailand

The confidence intervals for the ratio of percentiles discussed in the previous section were subsequently applied to estimate the confidence interval for the ratio of percentiles for two rainfall datasets. The calculations were conducted using RStudio.

Of the six geographical regions in Thailand, the northern and northeastern regions are the most agrarian, and since water is essential for agriculture, estimating the amount of rainfall is paramount. Rainfall data for 1 September 2021 from the northern and northeastern regions of Thailand obtained from the Thai Meteorological Department were previously reported by Thangjai et al. [5]. The rainfall data of northern and northeastern regions contain the zero and positive values. From Thangjai et al. [5], the minimum Akaike information criterion (AIC) values of the positive rainfall data for northern and northeastern regions are fitted to the log-normal distributions. Therefore, the rainfall data of the northern and northeastern regions follow delta-lognormal distributions. The summary statistics for the rainfall data from the northern region are $n_1=$ 29, $n_{1\left(1\right)}=$ 23, $n_{1\left(0\right)}=$ 6, ${\overline{y}}_{1\left(1\right)}=$ 0.56, and $s_{1\left(1\right)}^2=$ 2.28, while those for the northeastern region are $n_2=$ 28, $n_{2\left(1\right)}=$ 18, $n_{2\left(0\right)}=$ 10, ${\overline{y}}_{2\left(1\right)}=$ 1.10, and $s_{2\left(1\right)}^2=$ 3.26. The 95% confidence interval for the ratio of the percentiles of the two populations based on the four approaches was $C{I}_{FGCI1}=$ [0.0418,4.6082] with an interval length of 4.5664, $C{I}_{FGCI2}=$ [0.0270, 3.3244] with an interval length of 3.2974, $C{I}_{BS}=$ [0.0026, 3.1862] with an interval length of 3.1836, and $C{I}_{PB}=$ [−0.8686, 2.3793] with an interval length of 3.2479. The results show that the BS credible interval estimate provided the shortest length. The trace plot of the BS estimate is shown in Figure 4. Therefore, the empirical results are in accordance with the simulation study results.

5. Discussion and Conclusions

The percentile is used to describe the dispersion of a probability distribution. Moreover, the ratio of percentiles is used to compare the dispersion of two populations. In addition, the data comprising the positively right-skewed data and zero observation are also often encountered in many fields. The positively right-skewed data conform to the log-normal distribution, whereas the number of zero observations conforms to the binomial distribution. The distribution of data consists of positively right-skewed data, and zero observations correspond to the delta-lognormal distribution. Therefore, the ratio of percentiles of the delta-lognormal data plays an important part in statistics. The confidence interval estimation is recommended for estimating the ratio of percentiles of the delta-lognormal data. Herein, we present the four approaches to estimate the confidence interval for the ratio of the percentiles of two delta-lognormal distributions based on the FGCI approach using the fiducial quantity, the optimal generalized fiducial quantity, the BS approach, or the PB approach. The main advantage of using the four approaches is that they can be used to estimate the confidence intervals for complex parameters, whereas the main disadvantage is that a simulation study is required to determine their values for a particular scenario. Comparatively, the FGCI approach requires numerical simulation based on the fiducial generalized pivotal quantity, the BS approach requires simulation with the prior distribution, and the PB approach is based on the sampling distribution. The performance results of the proposed confidence intervals were compared to obtain the precise interval estimator.

Nevertheless, the simulation study results indicate that while the coverage probabilities of all of the approaches were suitable, the average lengths of the BS approach were the shortest for all of the scenarios tested. Thus, the BS approach is the best for constructing an estimate for the confidence interval for the ratio of the percentiles of two delta-lognormal distributions, albeit the other methods being suitable alternatives. This conclusion is similar to those presented elsewhere [5]. The BS approach can be used to construct the estimate of the credible interval for complex parameters. Moreover, the BS approach can be easily extended to infer the percentiles of other distributions. In future research, statistical inference using the percentiles of other distributions will be considered. For the delta-lognormal distribution, the proposed approach can be applied to compare rainfall dispersion in other two areas. Moreover, it can be used in many applications, such as insurance and PM2.5 dispersion.