Exact (1 + 3 + 6)-Dimensional Cosmological-Type Solutions in Gravitational Model with Yang–Mills Field, Gauss–Bonnet Term and Λ Term
Abstract
1. Introduction
2. The 10-Dimensional Model
2.1. The Action and Equations of Motion
2.2. Cosmological Ansatz
3. Cosmological Solutions
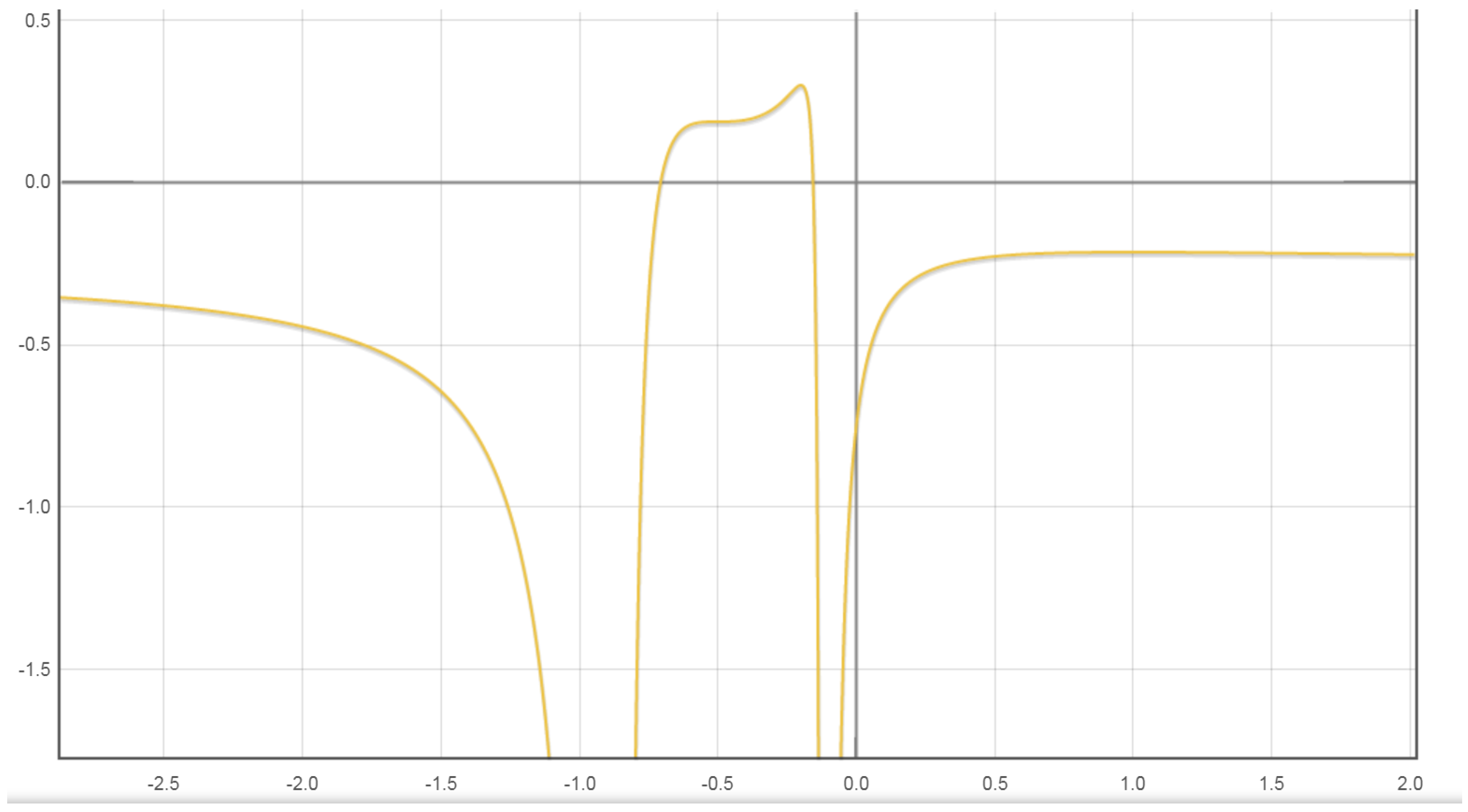
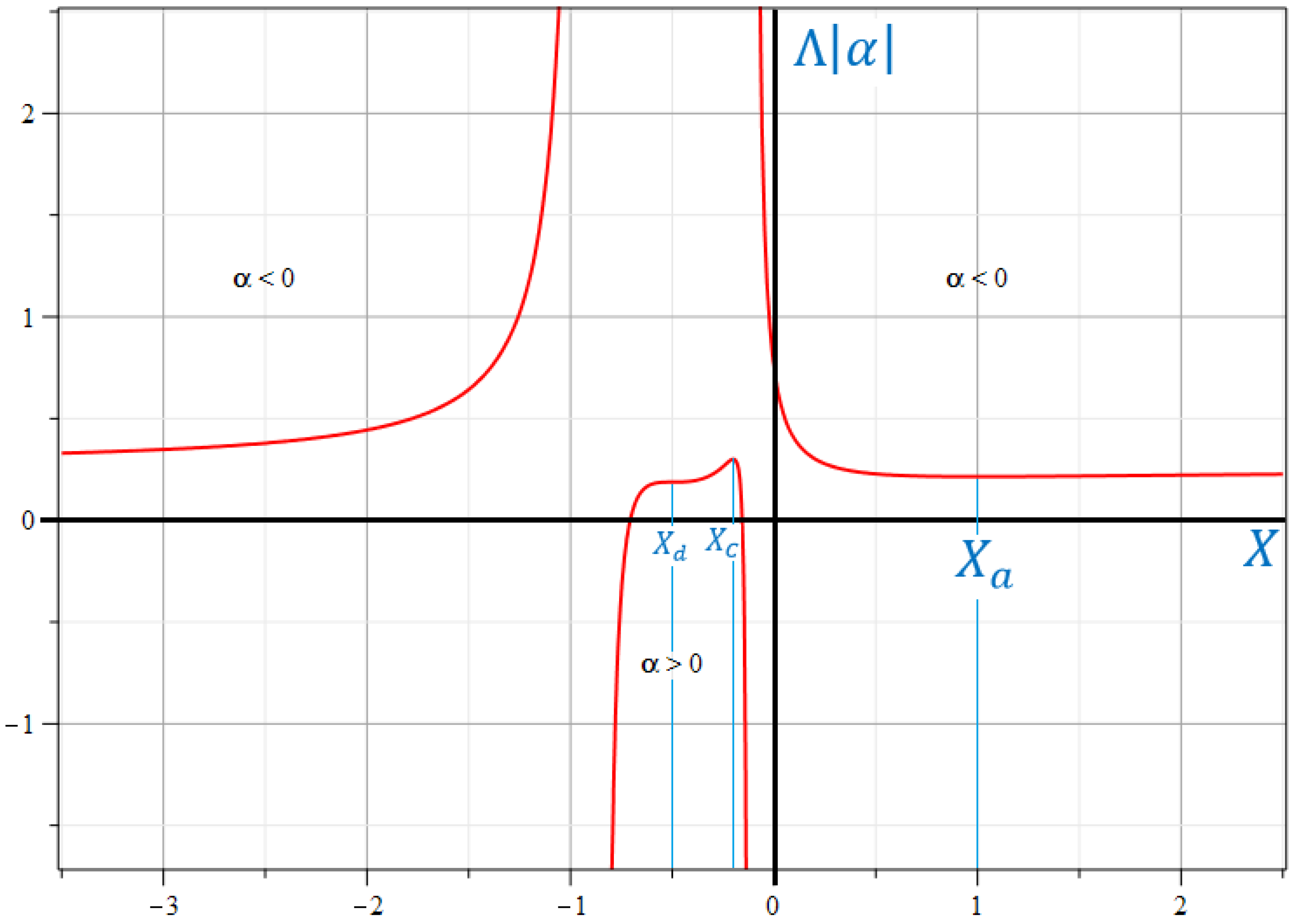
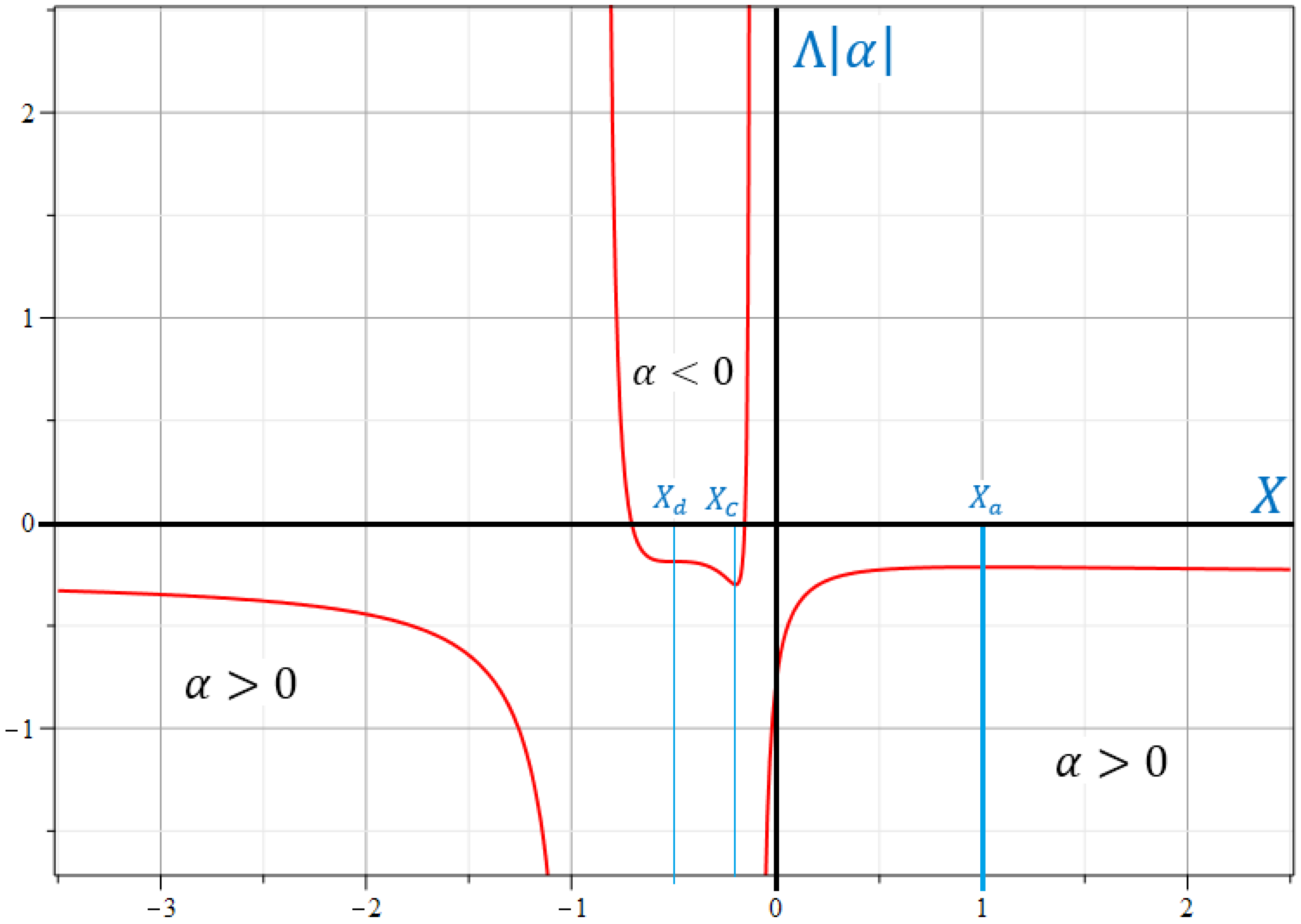
4. Static Analogs of Cosmological Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zwiebach, B. Curvature squared terms and string theories. Phys. Lett. B 1985, 156, 315. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Effective action approach to superstring theory. Phys. Lett. B 1985, 160, 69–76. [Google Scholar] [CrossRef]
- Gross, D.; Witten, E. Superstring modifications of Einstein’s equations. Nucl. Phys. B 1986, 277, 1. [Google Scholar] [CrossRef]
- Gross, D.; Harvey, J.; Martinec, E.; Rohm, R. Heterotic String. Phys. Rev. Lett. 1984, 54, 502. [Google Scholar] [CrossRef] [PubMed]
- Ishihara, H. Cosmological solutions of the extended Einstein gravity with the Gauss-Bonnet term. Phys. Lett. B 1986, 179, 217. [Google Scholar] [CrossRef]
- Deruelle, N. On the approach to the cosmological singularity in quadratic theories of gravity: The Kasner regimes. Nucl. Phys. B 1989, 327, 253–266. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to Modified Gravity and Gravitational Alternative for Dark Energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115–146. [Google Scholar] [CrossRef]
- Elizalde, E.; Makarenko, A.; Obukhov, V.; Osetrin, K.; Filippov, A. Stationary vs. singular points in an accelerating FRW cosmology derived from six-dimensional Einstein–Gauss–Bonnet gravity. Phys. Lett. B 2007, 644, 1–6. [Google Scholar] [CrossRef]
- Bamba, K.; Guo, Z.-K.; Ohta, N. Accelerating Cosmologies in the Einstein-Gauss-Bonnet Theory with a Dilaton. Prog. Theor. Phys. 2007, 118, 879–892. [Google Scholar] [CrossRef]
- Toporensky, A.; Tretyakov, P. Power-law anisotropic cosmological solution in 5+1 dimensional Gauss–Bonnet gravity. Grav. Cosmol. 2007, 13, 207–210. [Google Scholar]
- Pavluchenko, S.A.; Toporensky, A.V. A note on differences between (4+1)- and (5+1)-dimensional anisotropic cosmology in the presence of the Gauss-Bonnet term. Mod. Phys. Lett. A 2009, 24, 513–521. [Google Scholar] [CrossRef]
- Pavluchenko, S.A. General features of Bianchi-I cosmological models in Lovelock gravity. Phys. Rev. D 2009, 80, 107501. [Google Scholar] [CrossRef]
- Kirnos, I.; Makarenko, A.; Pavluchenko, S.; Toporensky, A. The nature of singularity in multidimensional anisotropic Gauss-Bonnet cosmology with a perfect fluid. Gen. Rel. Grav. 2010, 42, 2633–2641. [Google Scholar] [CrossRef]
- Ivashchuk, V.D. On anisotropic Gauss-Bonnet cosmologies in (n + 1) dimensions, governed by an n-dimensional Finslerian 4-metric. Grav. Cosmol. 2010, 16, 118–125. [Google Scholar] [CrossRef]
- Ivashchuk, V.D. On cosmological-type solutions in multi-dimensional model with Gauss-Bonnet term. Int. J. Geom. Meth. Mod. Phys. 2010, 7, 797–819. [Google Scholar] [CrossRef]
- Maeda, K.-I.; Ohta, N. Cosmic acceleration with a negative cosmological constant in higher dimensions. J. High Energy Phys. 2014, 2014, 95. [Google Scholar] [CrossRef]
- Chirkov, D.; Pavluchenko, S.; Toporensky, A. Exact exponential solutions in Einstein–Gauss–Bonnet flat anisotropic cosmology. Mod. Phys. Lett. A 2014, 29, 1450093. [Google Scholar] [CrossRef]
- Chirkov, D.; Pavluchenko, S.; Toporensky, A. Non-constant volume exponential solutions in higher-dimensional Lovelock cosmologies. Gen. Rel. Grav. 2015, 47, 137. [Google Scholar] [CrossRef]
- Pavluchenko, S.A. Stability analysis of exponential solutions in Lovelock cosmologies. Phys. Rev. D 2015, 92, 104017. [Google Scholar] [CrossRef]
- Pavluchenko, S.A. Cosmological dynamics of spatially flat Einstein-Gauss-Bonnet models in various dimensions: Low-dimensional Λ-term case. Phys. Rev. D 2016, 94, 084019. [Google Scholar] [CrossRef]
- Canfora, F.; Giacomini, A.; Pavluchenko, S.; Toporensky, A. Friedmann Dynamics Recovered from Compactified Einstein–Gauss–Bonnet Cosmology. Grav. Cosmol. 2018, 24, 28–38. [Google Scholar] [CrossRef]
- Ivashchuk, V.D. On stability of exponential cosmological solutions with non-static volume factor in the Einstein–Gauss–Bonnet model. Eur. Phys. J. C 2016, 76, 431. [Google Scholar] [CrossRef]
- Fomin, I.; Chervon, S. A new approach to exact solutions construction in scalar cosmology with a Gauss–Bonnet term. Mod. Phys. Lett. A 2017, 32, 1750129. [Google Scholar] [CrossRef]
- Ivashchuk, V.D.; Kobtsev, A.A. Stable exponential cosmological solutions with 3- and l-dimensional factor spaces in the Einstein–Gauss–Bonnet model with a Λ-term. Eur. Phys. J. C 2018, 78, 100. [Google Scholar] [CrossRef]
- Ivashchuk, V.D.; Kobtsev, A.A. Exponential cosmological solutions with two factor spaces in EGB model with Λ = 0 revisited. Eur. Phys. J. C 2019, 79, 824. [Google Scholar] [CrossRef]
- Ivashchuk, V.D. On Stability of Exponential Cosmological Type Solutions with Two Factor Spaces in the Einstein–Gauss–Bonnet Model with a Λ-Term. Grav. Cosmol. 2020, 20, 16–21. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Abbas, G.; Momeni, D.; Ali, M.A.; Myrzakulov, R.; Qaisar, S. Anisotropic compact stars in f(G) gravity. Astrophys. Space Sci. 2015, 357, 158. [Google Scholar]
- Benetti, M.; da Costa, S.S.; Capozziello, S.; Alcaniz, J.; De Laurentis, M. Various characteristics of transition energy for nearly symmetric colliding nuclei. Int. J. Mod. Phys. 2018, 27, 1850084. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Unifying Inflation with Early and Late-time Dark Energy in F(R) Gravity. Phys. Dark Universe 2020, 29, 100602. [Google Scholar] [CrossRef]
- Vasilev, T.B.; Bouhmadi-Lopez, M.; Martin-Moruno, P. Classical and Quantum f(R) Cosmology: The Big Rip, the Little Rip and the Little Sibling of the Big Rip. Universe 2021, 7, 288. [Google Scholar] [CrossRef]
- Vasilev, T.B.; Bouhmadi-Lopez, M.; Martin-Moruno, P. f(G,TαβTαβ) theory and complex cosmological structures. Phys. Dark Universe 2022, 36, 101015. [Google Scholar]
- Fazlollahi, H.R. Energy–momentum squared gravity and late-time Universe. Eur. Phys. J. Plus 2023, 138, 211. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. String Generated Gravity Models. Phys. Rev. Lett. 1985, 55, 2656. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, J.T. Symmetric Solutions to the Gauss-Bonnet Extended Einstein Equations. Nucl. Phys. B 1986, 268, 737. [Google Scholar] [CrossRef]
- Wheeler, J.T. Symmetric Solutions to the Maximally Gauss-Bonnet Extended Einstein Equations. Nucl. Phys. B 1986, 273, 732. [Google Scholar] [CrossRef]
- Wiltshire, D.L. Spherically Symmetric Solutions of Einstein-maxwell Theory With a Gauss-Bonnet Term. Phys. Lett. B 1986, 169, 36–40. [Google Scholar] [CrossRef]
- Cai, R.-G. Gauss-Bonnet black holes in AdS spaces. Phys. Rev. D 2002, 65, 084014. [Google Scholar] [CrossRef]
- Cvetic, M.; Nojiri, S.; Odintsov, S. Black hole thermodynamics and negative entropy in de Sitter and anti-de Sitter Einstein-Gauss-Bonnet gravity. Nucl. Phys. B 2002, 628, 295. [Google Scholar] [CrossRef]
- Garraffo, C.; Giribet, G. The Lovelock Black Holes. Mod. Phys. Lett. A 2008, 23, 1801. [Google Scholar] [CrossRef]
- Charmousis, C. Higher order gravity theories and their black hole solutions. Lect. Notes Phys. 2009, 769, 299. [Google Scholar]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Black-Hole Solutions with Scalar Hair in Einstein-Scalar-Gauss-Bonnet Theories. Phys. Rev. D 2018, 97, 084037. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Kononogov, S.A.; Melnikov, V.N. Brane world corrections to Newton’s law. Gen. Rel. Grav. 2006, 38, 1215–1232. [Google Scholar] [CrossRef]
- Tavakoli, Y.; Ardabili, A.K.; Bouhmadi-Lopez, M.; Moniz, P.V. Role of Gauss-Bonnet corrections in a DGP brane gravitational collapse. Phys. Rev. D 2022, 105, 084050. [Google Scholar] [CrossRef]
- Kanti, P.; Kleihaus, B.; Kunz, J. Wormholes in Dilatonic Einstein-Gauss-Bonnet Theory. Phys. Rev. Lett. 2011, 107, 271101. [Google Scholar] [CrossRef]
- Barton, S.; Kiefer, C.; Kleihaus, B.; Kunz, J. Symmetric wormholes in Einstein-vector–Gauss–Bonnet theory. Eur. Phys. J. C 2022, 82, 802. [Google Scholar] [CrossRef]
- Wu, Y.-S.; Wang, Z. Time variation of Newton’s gravitational constant in superstring theories. Phys. Rev. Lett. B 1986, 57, 1978. [Google Scholar] [CrossRef]
- Ivashchuk, V.D.; Melnikov, V.N. On time variations of gravitational and Yang-Mills constants in a cosmological model of superstring origin. Grav. Cosmol. 2014, 20, 26–29. [Google Scholar] [CrossRef]
- Candelas, P.; Horowitz, G.T.; Strominger, A.; Witten, E. Vacuum configurations for superstrings. Nucl. Phys. B 1985, 256, 46. [Google Scholar] [CrossRef]
- Duff, M. Architecture of Fundamental Interactions at Short Distances; Ramond, P., Stora, R., Eds.; Les Houches Lectures: Les Houches, France, 1985; p. 819. [Google Scholar]
- Cadavid, A.; Ceresole, A.; D’Auria, R.; Ferrara, S. Eleven-dimensional supergravity compactified on Calabi-Yau threefolds. Phys. Lett. B 1995, 357, 76–80. [Google Scholar] [CrossRef]
- Duff, M.J.; Lu, H.; Pope, C.N.; Sezgin, E. Supermembranes with fewer supersymmetries. Phys. Lett. B 1996, 371, 206–214. [Google Scholar] [CrossRef]
- Golubtsova, A.A.; Ivashchuk, V.D. Triple M-brane configurations and preserved supersymmetries. Nucl. Phys. B 2013, 872, 289–312. [Google Scholar] [CrossRef]
- Ivashchuk, V.D. On Supersymmetric M-brane configurations with an /Z2 submanifold. Grav. Cosmol. 2016, 22, 32–35. [Google Scholar] [CrossRef]
- Witten, L.; Witten, E. Large Radius Expansion of Superstring Compactifications. Nucl. Phys. B 1987, 281, 109. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivashchuk, V.D.; Ernazarov, K.K.; Kobtsev, A.A. Exact (1 + 3 + 6)-Dimensional Cosmological-Type Solutions in Gravitational Model with Yang–Mills Field, Gauss–Bonnet Term and Λ Term. Symmetry 2023, 15, 783. https://doi.org/10.3390/sym15040783
Ivashchuk VD, Ernazarov KK, Kobtsev AA. Exact (1 + 3 + 6)-Dimensional Cosmological-Type Solutions in Gravitational Model with Yang–Mills Field, Gauss–Bonnet Term and Λ Term. Symmetry. 2023; 15(4):783. https://doi.org/10.3390/sym15040783
Chicago/Turabian StyleIvashchuk, V. D., K. K. Ernazarov, and A. A. Kobtsev. 2023. "Exact (1 + 3 + 6)-Dimensional Cosmological-Type Solutions in Gravitational Model with Yang–Mills Field, Gauss–Bonnet Term and Λ Term" Symmetry 15, no. 4: 783. https://doi.org/10.3390/sym15040783
APA StyleIvashchuk, V. D., Ernazarov, K. K., & Kobtsev, A. A. (2023). Exact (1 + 3 + 6)-Dimensional Cosmological-Type Solutions in Gravitational Model with Yang–Mills Field, Gauss–Bonnet Term and Λ Term. Symmetry, 15(4), 783. https://doi.org/10.3390/sym15040783





