The Space-Time Properties of Three Static Black Holes
Abstract
1. Introduction
2. Space-Time Metric and Equations of Motion
2.1. TBH Space-Time Metric
2.2. Test Particle Motion Equation
2.3. Contact and Curvature
2.4. Hamiltonian Canonical Equation
2.5. Horizon of Space-Time
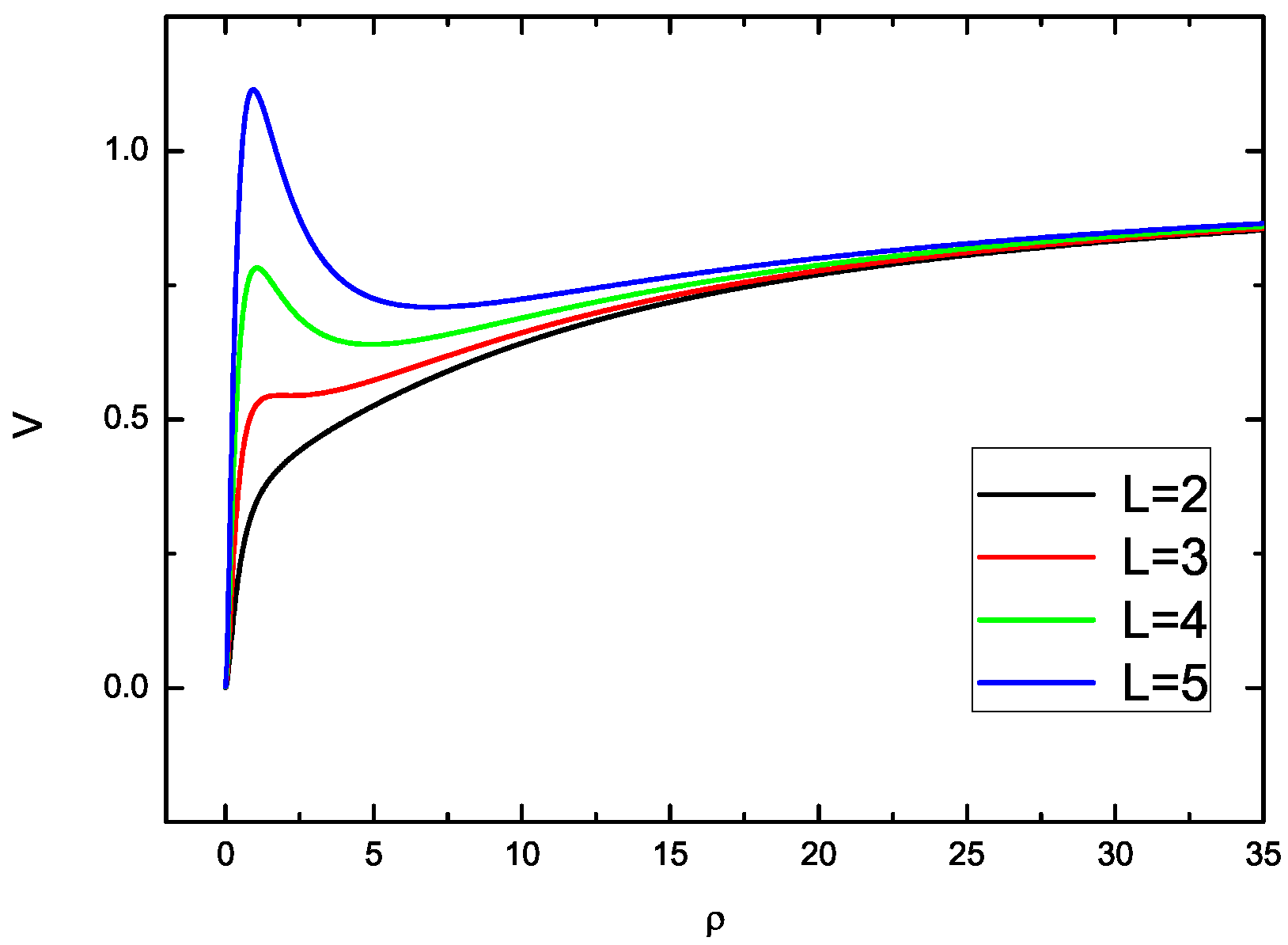
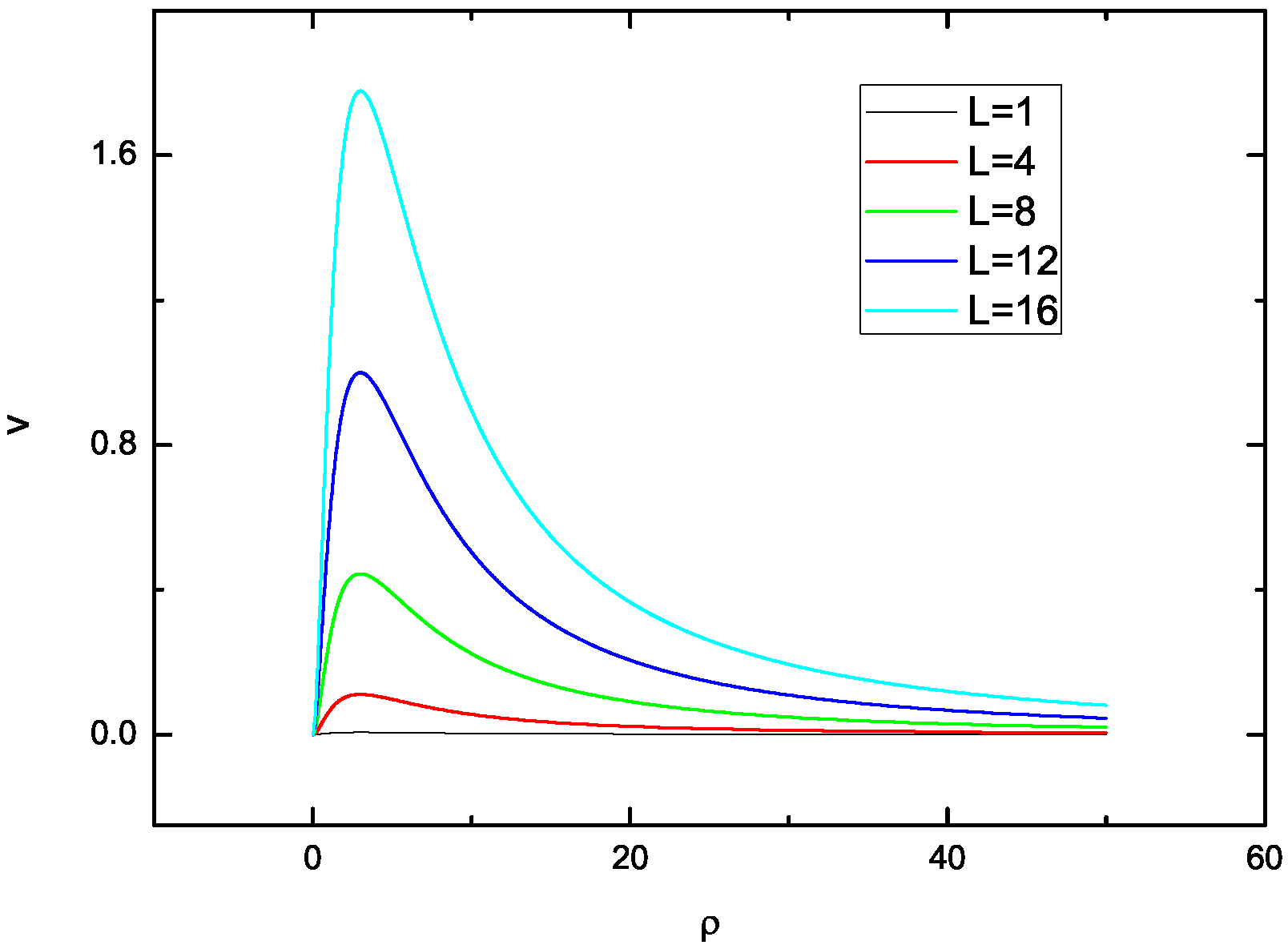
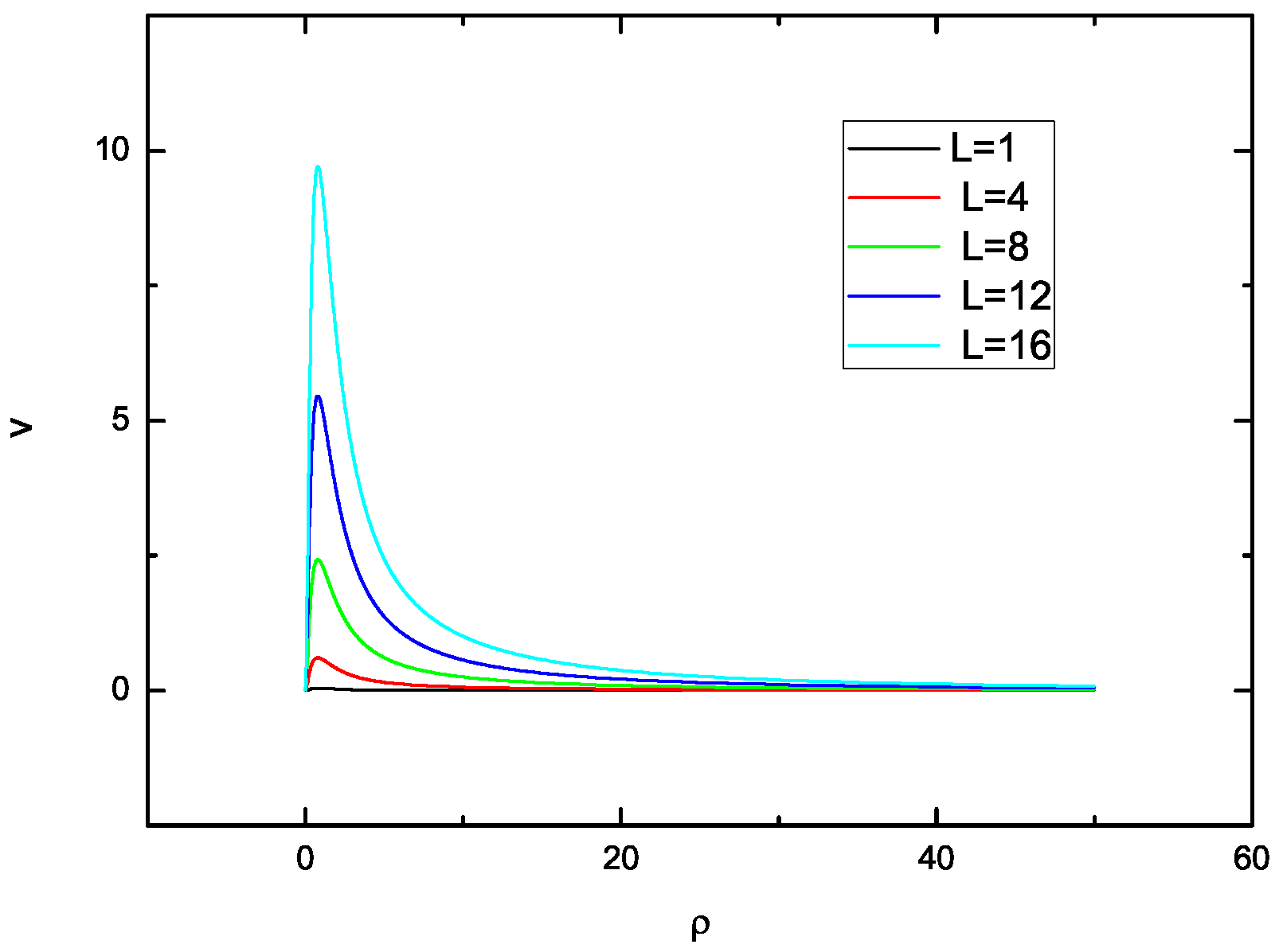
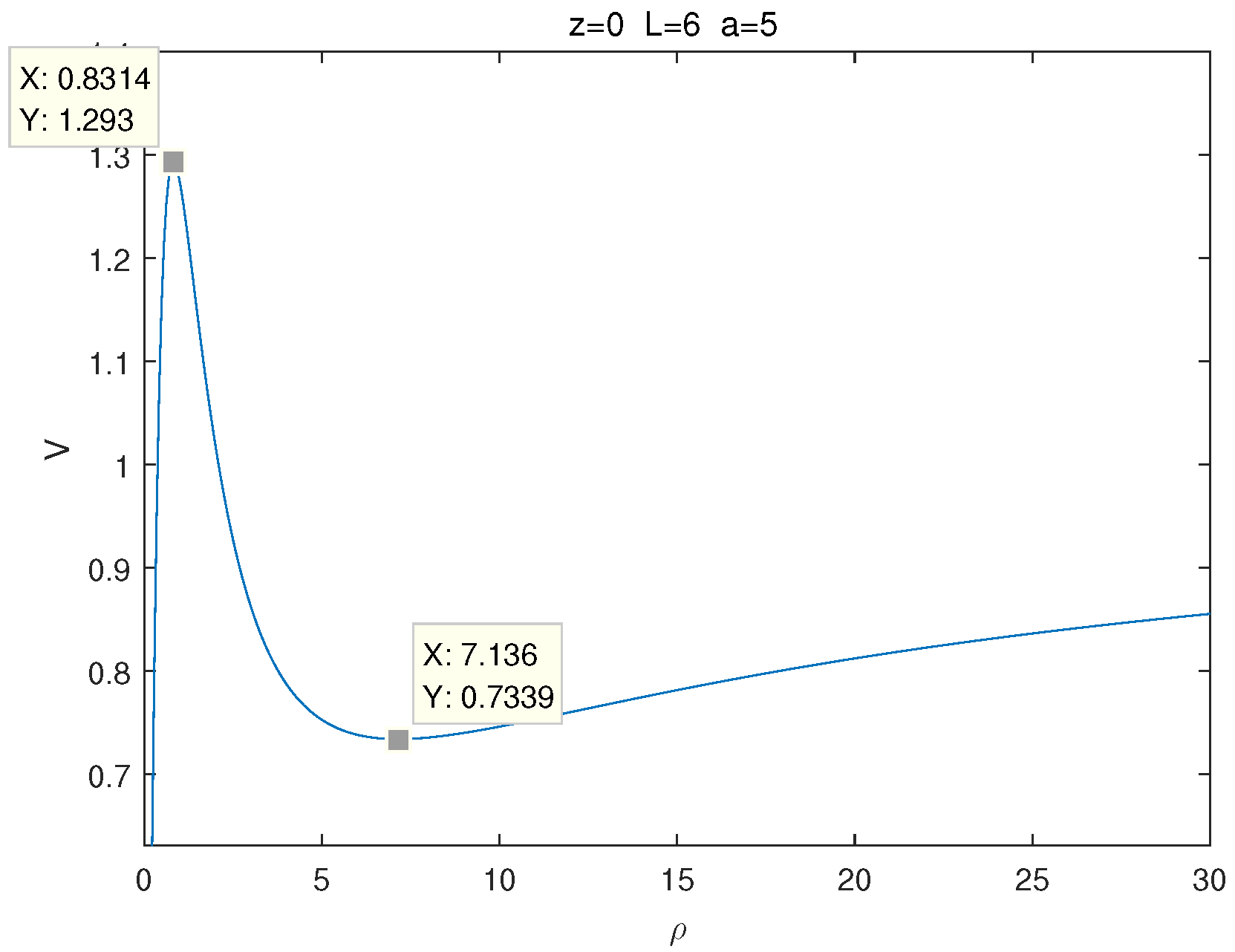
2.6. One-Dimensional Effective Potential
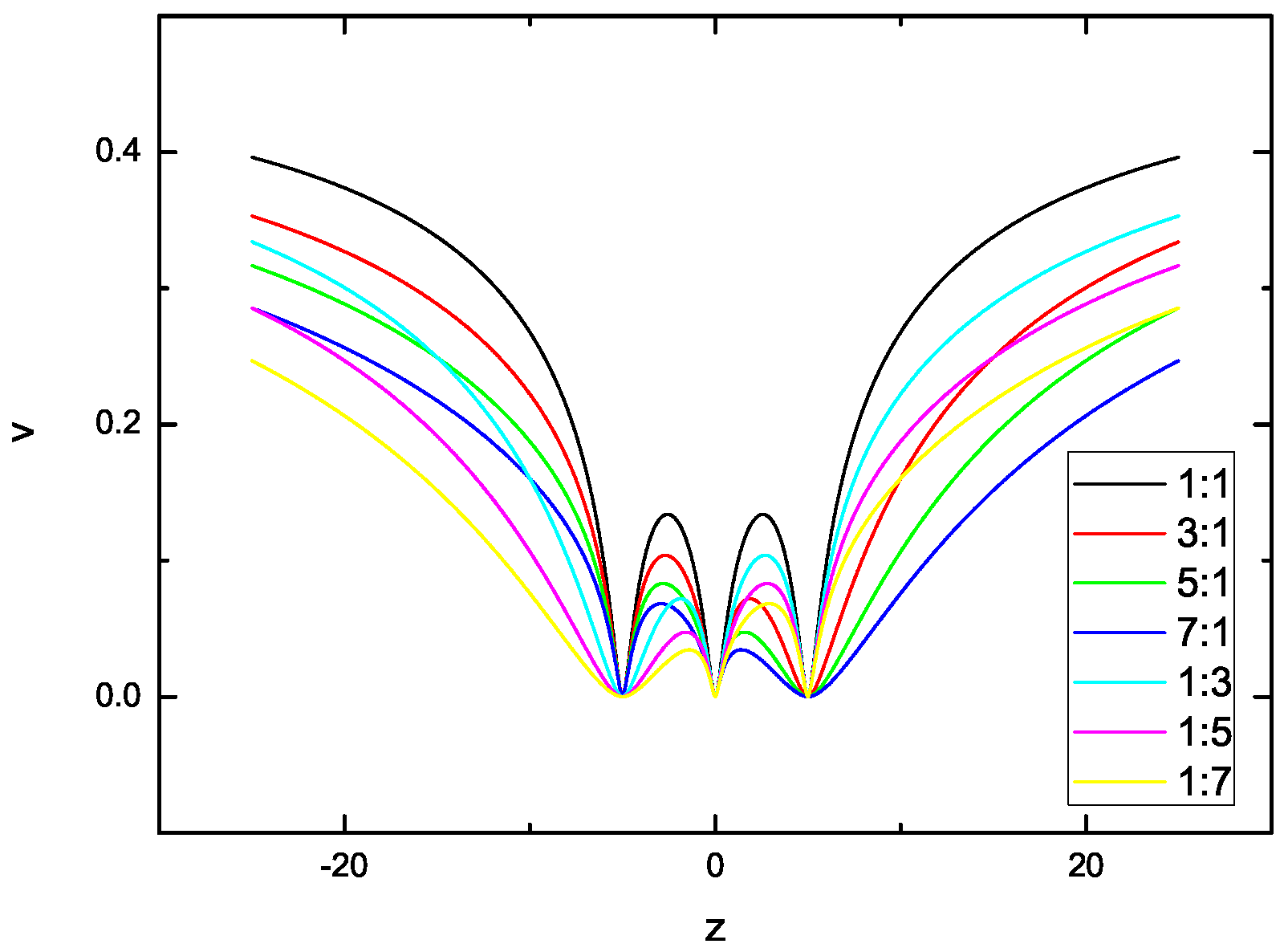
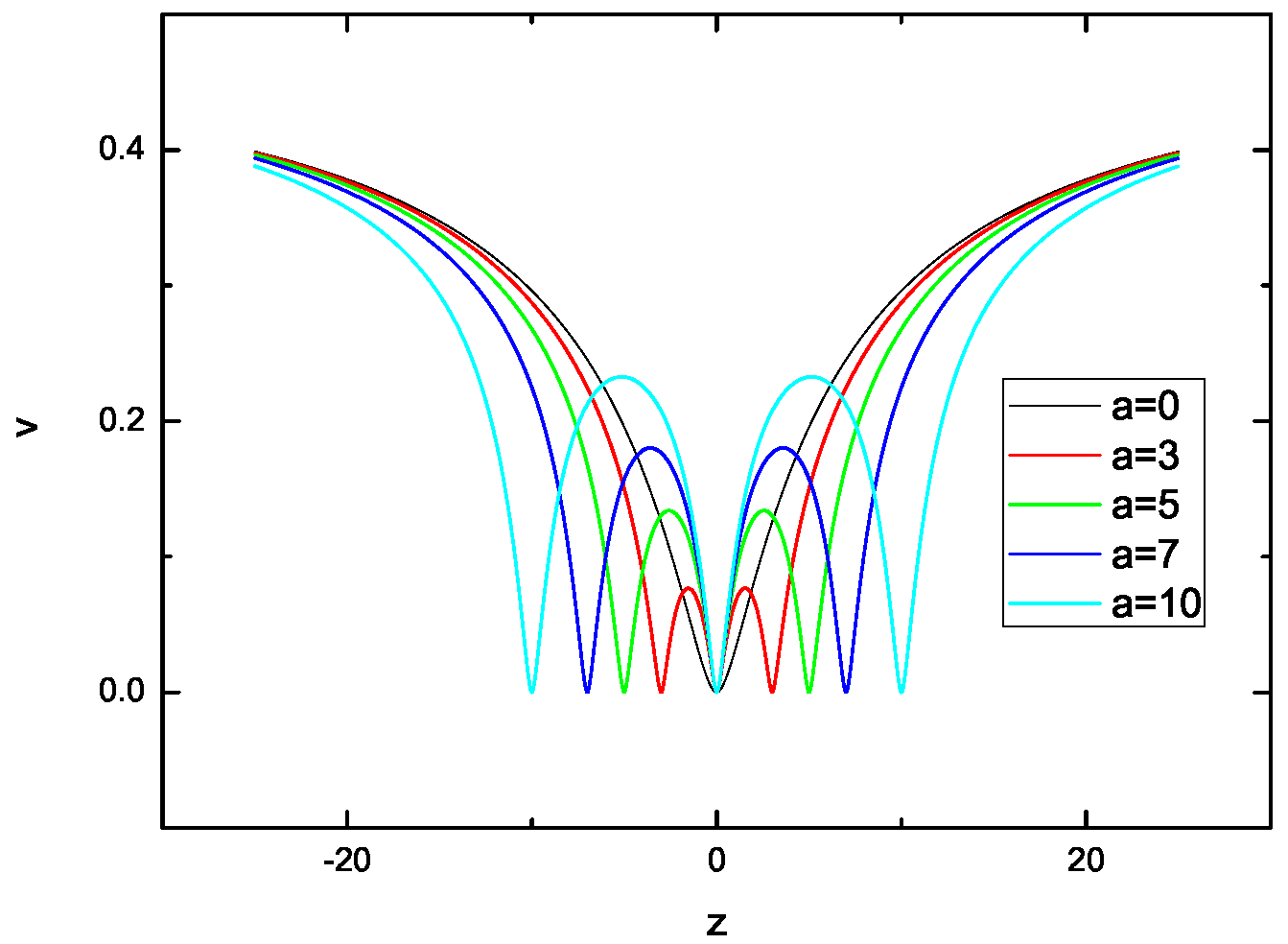
3. The Effect of on the Equilibrium Position
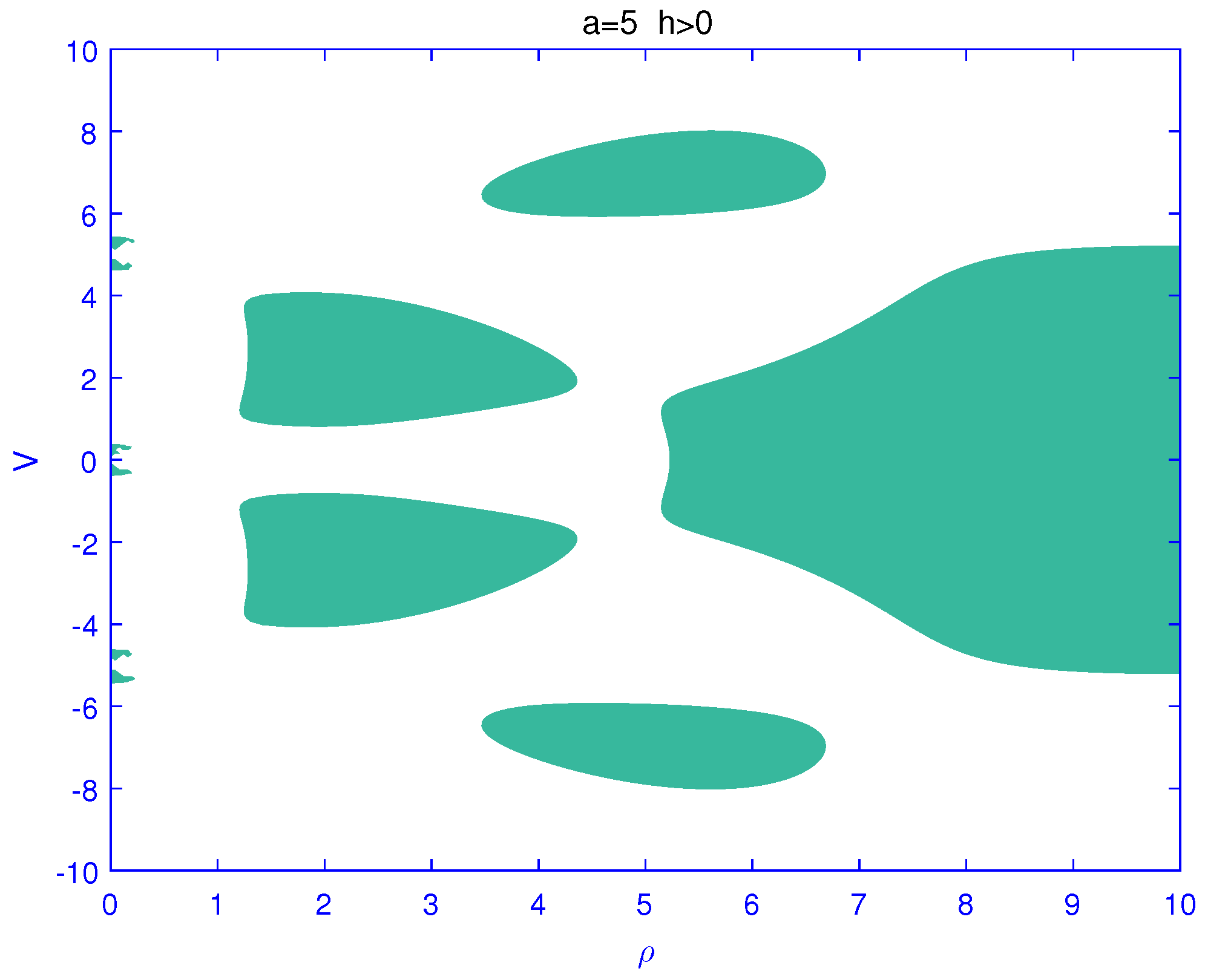
4. The Stability of Symmetric Plane Orbits Is Discussed by Phase Plane Analysis
5. Stability Conditions for Test Particle Circular Orbit in TBH Space-Time
6. Coordinate Quantities and Intrinsic Quantities in TBH Spacetime
6.1. Coordinate Distance and Proper Distance
6.2. Coordinate Time and Proper Time
6.3. The Natural Velocity of Light and the Coordinate Velocity of Light
6.4. Red Shift in TBH Space-Time
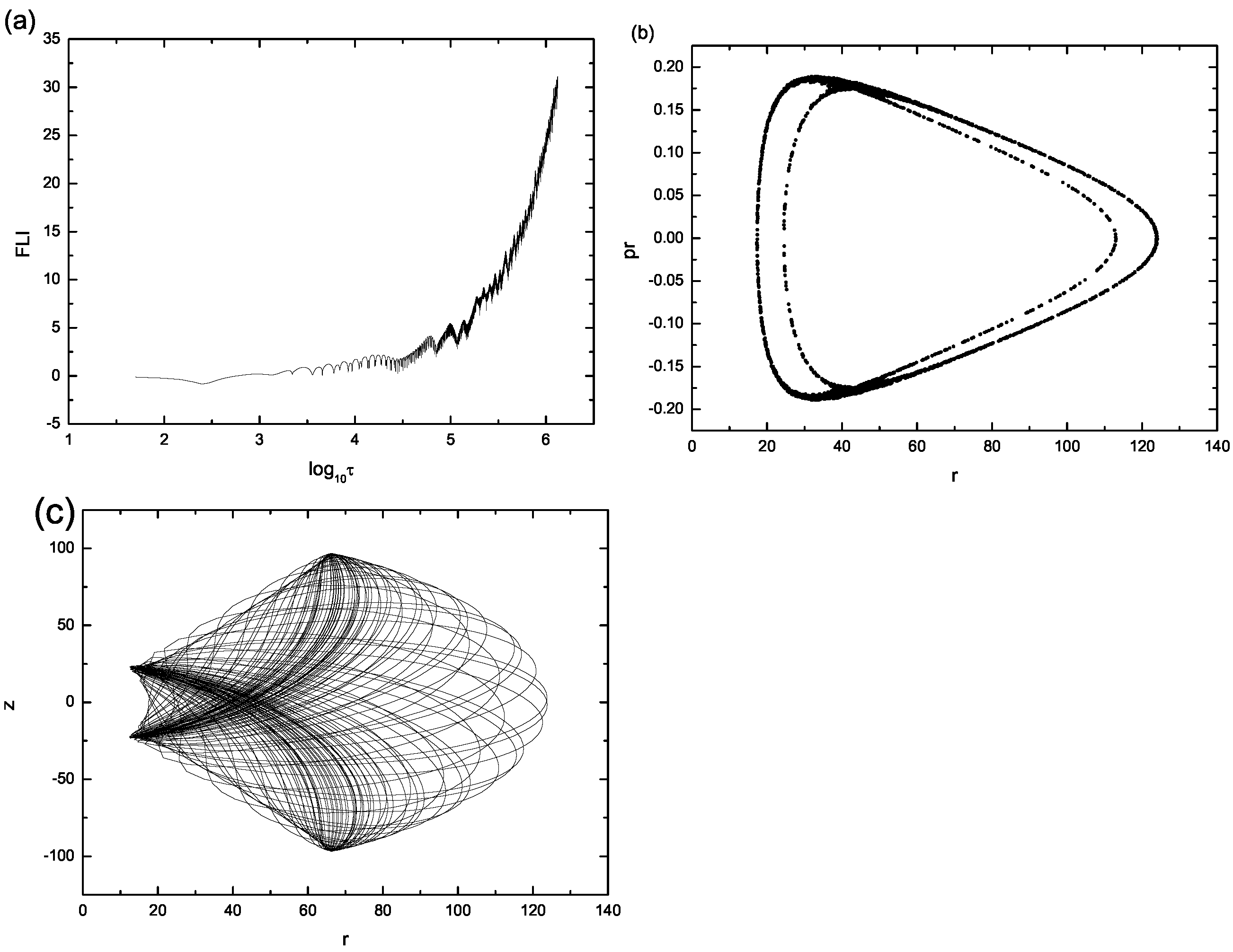
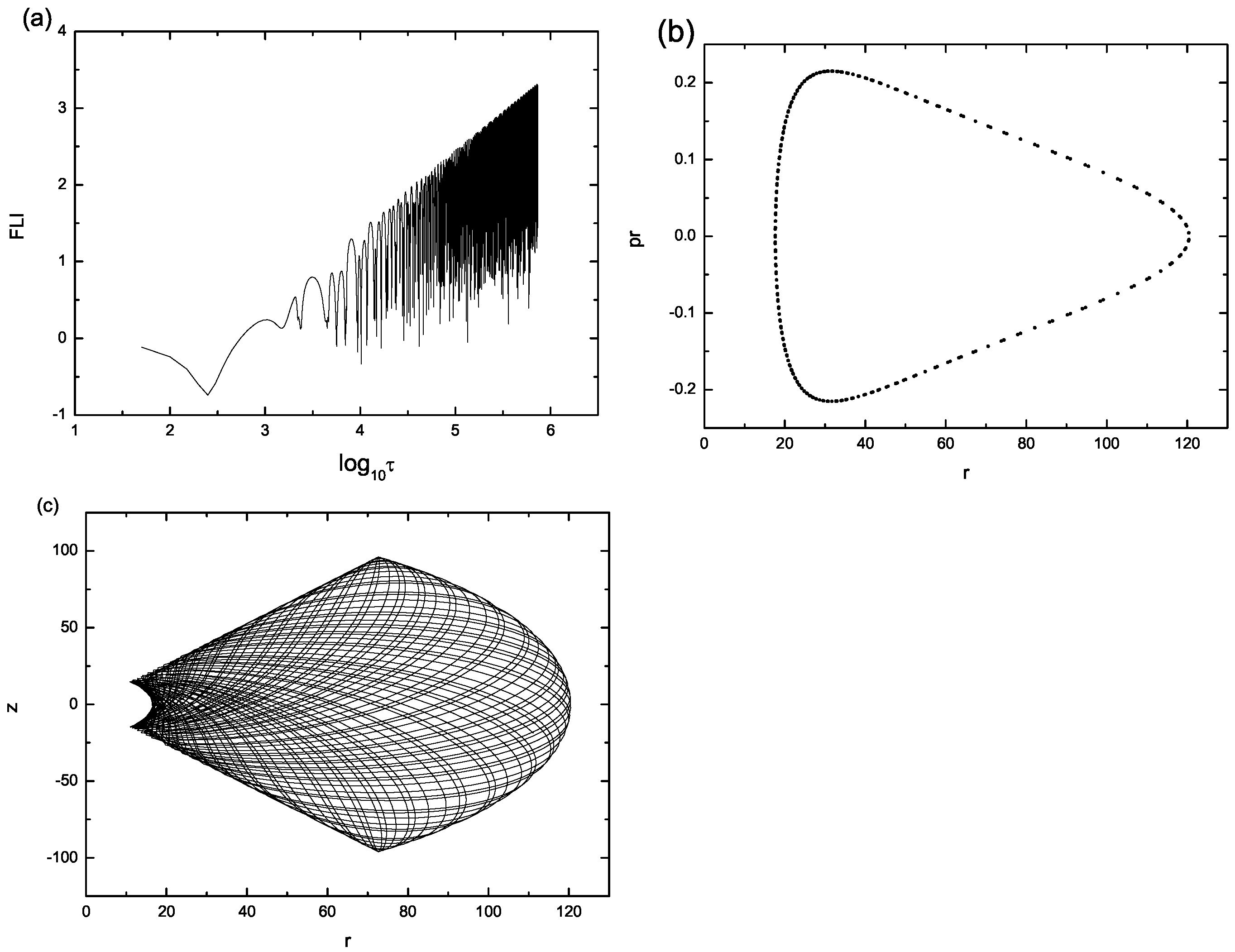
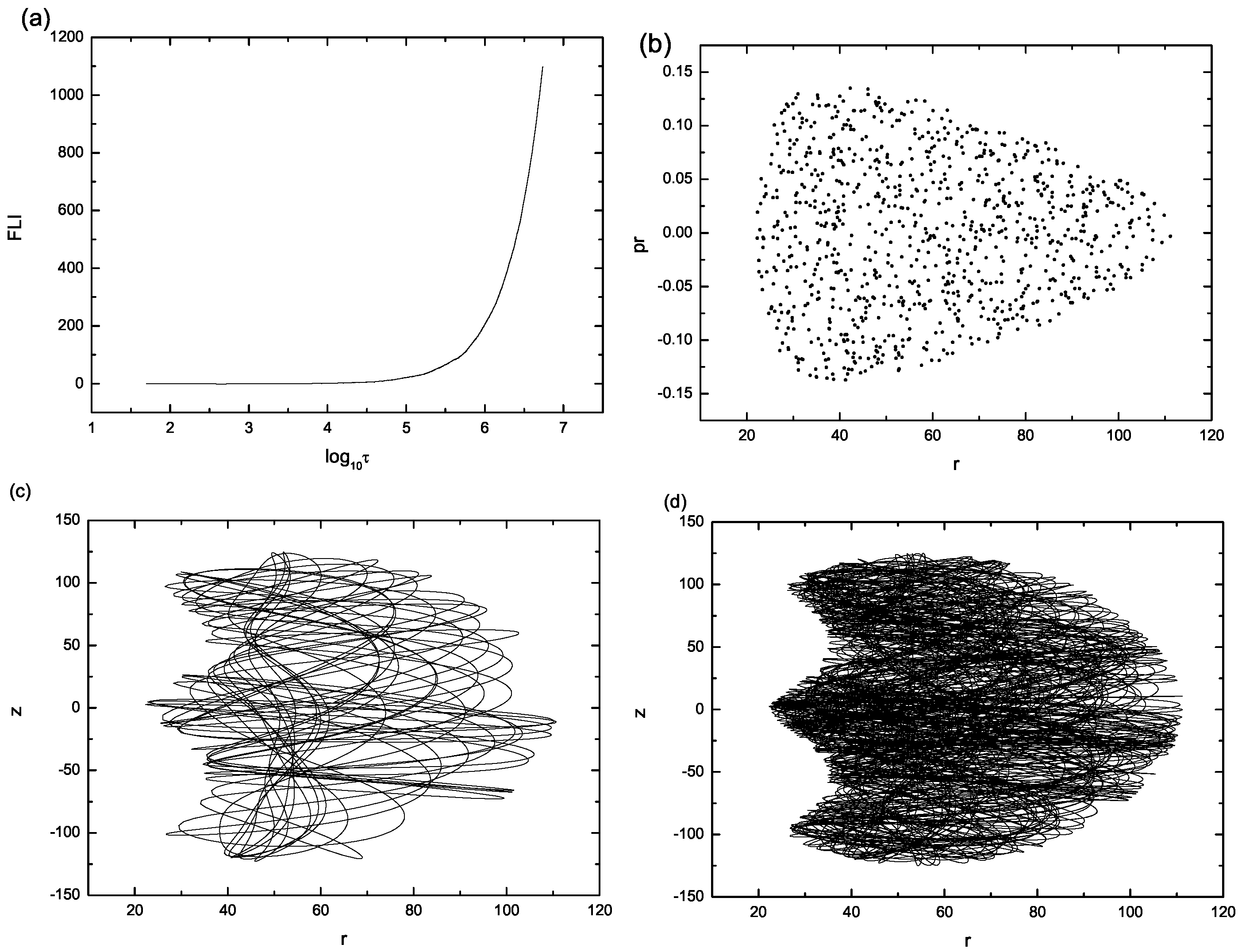
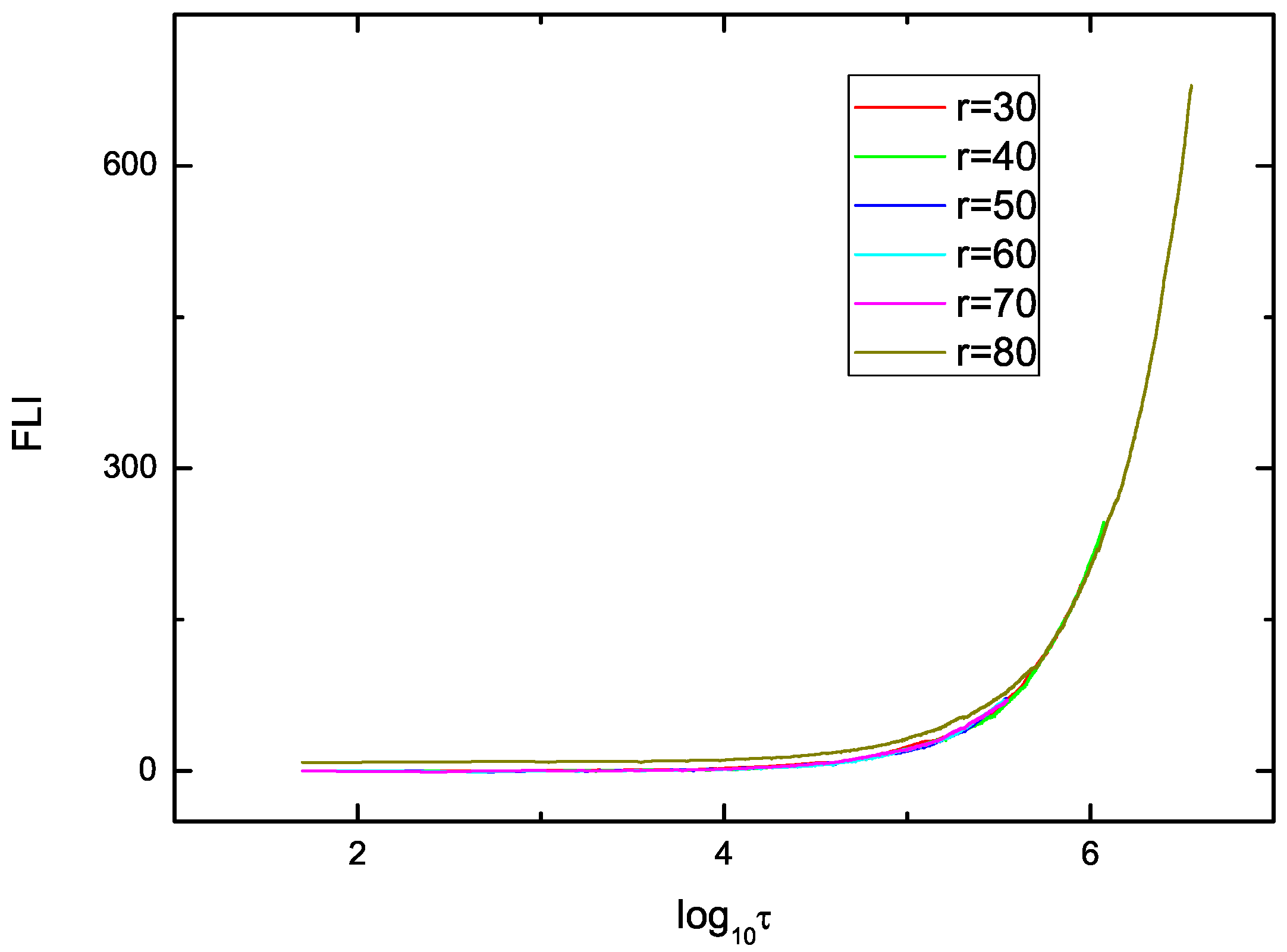
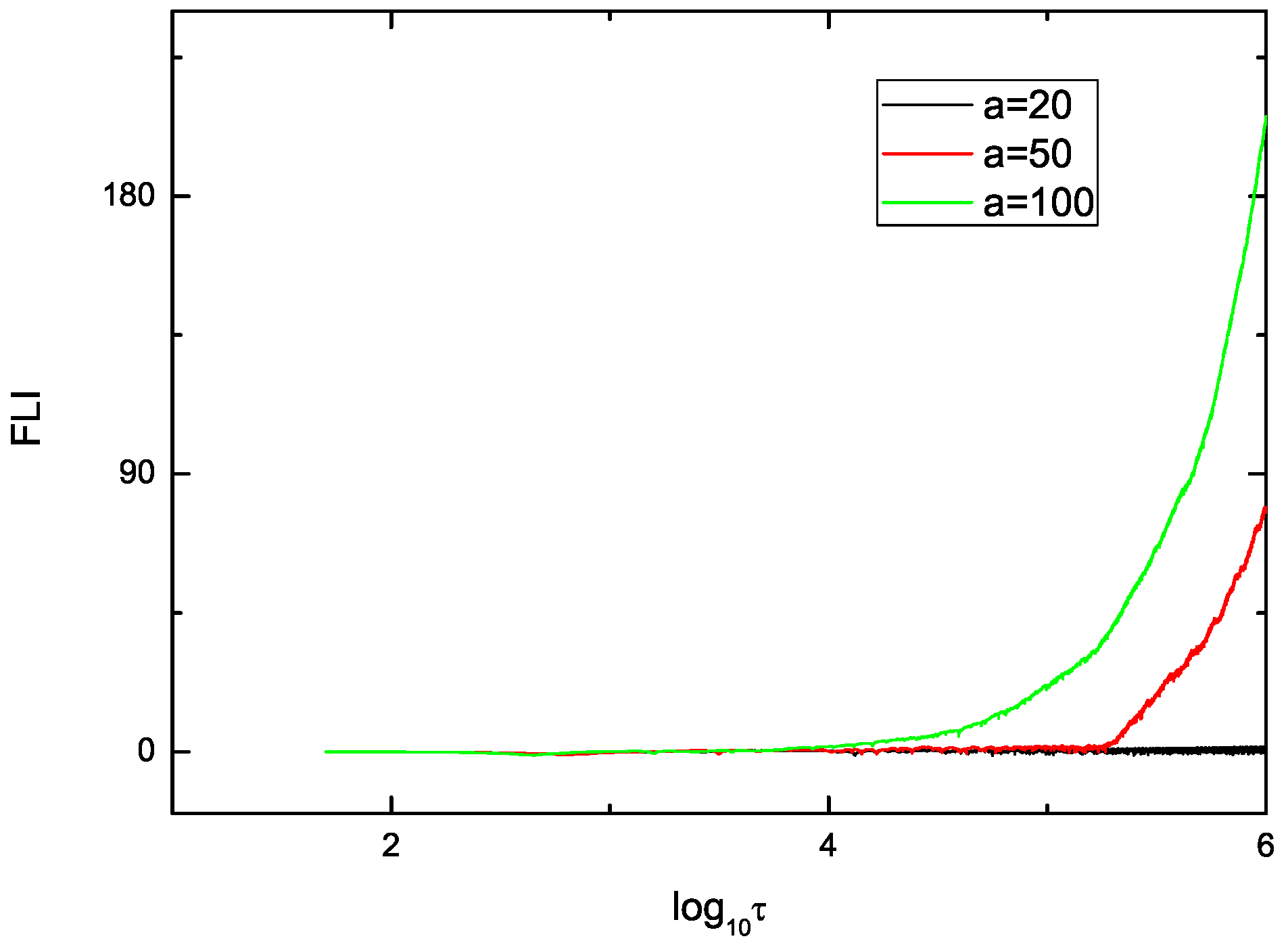
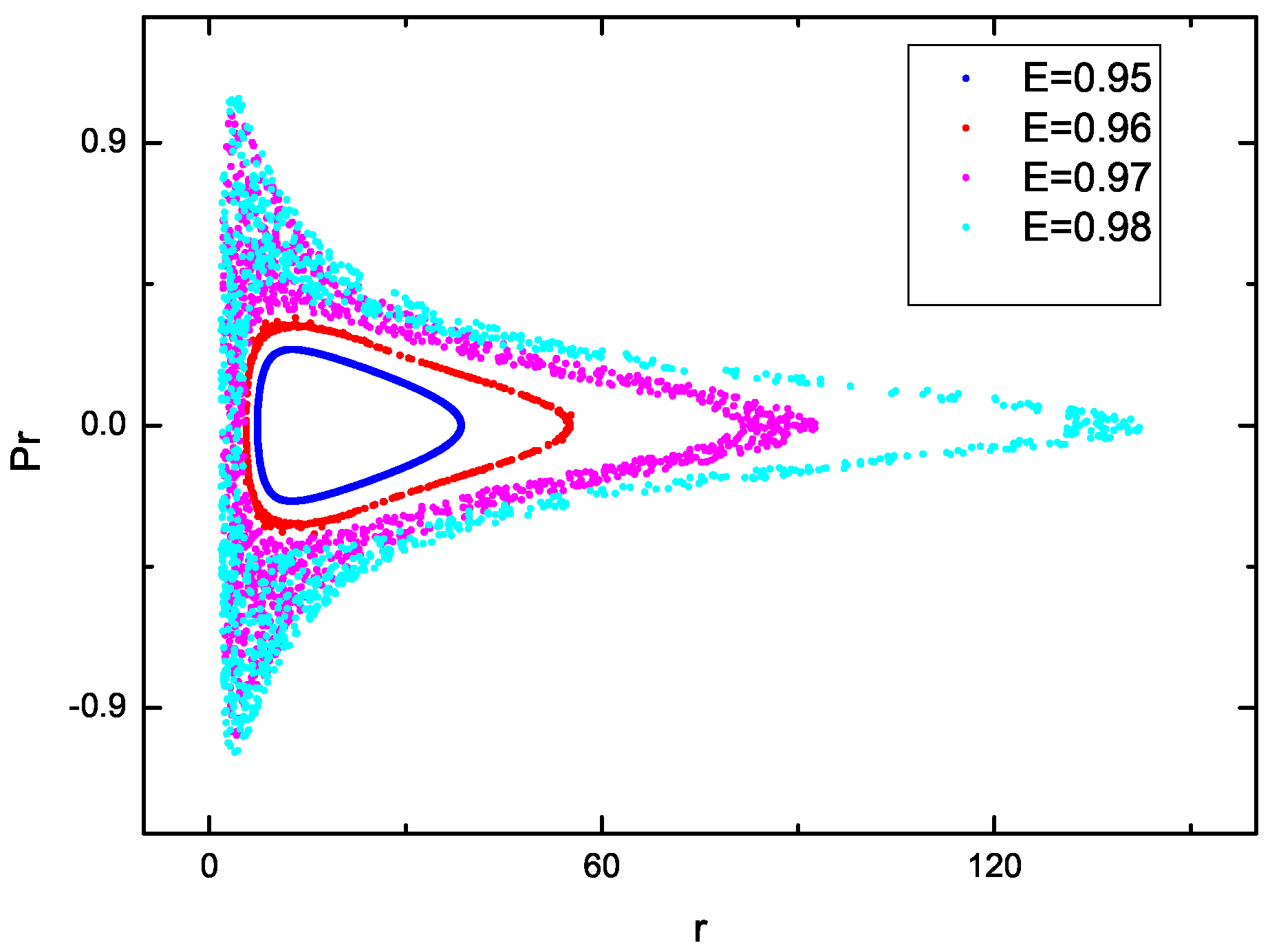
7. The Order and Chaos Orbits of Particle
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Properties of the Binary Black Hole Merger GW150914. Phys. Rev. Lett. 2016, 116, 241102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger observations of a binary neutron star merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo During the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Weyl, H. The theory of gravitation. Ann. Phys. 1917, 359, 117. [Google Scholar] [CrossRef]
- Majumdar, S.D. A class of exact solutions of Einstein’s field equations. Phys. Rev. 1947, 72, 390. [Google Scholar] [CrossRef]
- Papaetrou, A. A static solution of the equations of the gravitational field for an arbitrary charge distribution. Proc. R. Ir. Acad. Sect. A 1947, 51, 191. [Google Scholar]
- Hartle, J.B.; Hawking, S.W. Solutions of the Einstein-Maxwell equations with many black holes. Commun. Math. Phys. 1972, 26, 87. [Google Scholar] [CrossRef]
- Kramer, D.; Neugebauer, G. The superposition of two Kerr solutions. Phys. Lett. A 1980, 75, 259. [Google Scholar] [CrossRef]
- Nitta, D.; Chiba, T.; Sugiyama, N. Shadows of colliding black holes. Phys. Rev. D 2011, 84, 063008. [Google Scholar] [CrossRef]
- Bohn, A.; Throwe, W.; Hébert, F.; Henriksson, K.; Bunandar, D.; Scheel, M.A.; Taylor, N.W. What does a binary black hole merger look like? Class. Quantum Gravity 2015, 32, 065002. [Google Scholar] [CrossRef]
- Patil, M.; Mishra, P.; Narasimha, D. Curious case of gravitational lensing by binary black holes: A tale of two photon spheres, new relativistic images and caustics. Phys. Rev. D 2017, 95, 024026. [Google Scholar] [CrossRef]
- Assumpcao, T.; Cardoso, V.; Ishibashi, A.; Richartz, M.; Zilhao, M. Black hole binaries: Ergoregions, photon surfa-ces, wave scattering, and quasinormal modes. Phys. Rev. D 2018, 98, 064036. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Rodriguez, M.J. Shadows of exact binary black holes. Phys. Rev. D 2018, 98, 044053. [Google Scholar] [CrossRef]
- Psaltis, Dimitrios and Talbot, Colm and Payne, Ethan and Mandel, Ilya, Probing the black hole metric: Black hole shadows and binary black-hole inspirals. Phys. Rev. D 2021, 103, 106036.
- Campanelli, M.; Dettwyler, M.; Hannam, M.; Lousto, C.O. Relativistic three-body effects in black hole coa-lescence. Phys. Rev. D 2006, 74, 087503. [Google Scholar] [CrossRef]
- Torigoe, Y.; Hattori, K.; Asada, H. Gravitational Wave- forms for Two- and Three-Body Gravitating Systems. Phys. Rev. Lett. 2009, 102, 251101. [Google Scholar] [CrossRef] [PubMed]
- Seto, N. Relativistic resonant relations between massive black hole binary and extreme mass ratio inspiral. Phys. Rev. D 2012, 85, 064037. [Google Scholar] [CrossRef]
- Yamada, K.; Asada, H. Nonchaotic evolution of triangu- lar configuration due to gravitational radiation reaction in the three-body problem. Phys. Rev. D 2016, 93, 084027. [Google Scholar] [CrossRef]
- Hayasaki, K.; Mineshige, S.; Sudou, H. Binary black hole accretion flows in merged galactic nuclei. Publ. Astron. Soc. Jpn. 2007, 59, 427. [Google Scholar] [CrossRef]
- Kimitake, H.; Mineshige, S.; Ho, L.C. A supermassive binary black hole with triple disks. Astrophys. J. 2008, 682, 1134. [Google Scholar]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occus); DeWitte, C., DeWitt, B., Eds.; Gordon and Breach: New York, NY, USA, 1973; p. 343. [Google Scholar]
- Clark, J.P.A.; Eardley, D.M. Evolution of close neutron star binaries. Astrophys. J. 1977, 215, 311. [Google Scholar] [CrossRef]
- Kidder, L.E.; Will, C.M.; Wiseman, A.G. Coalescing binary systems of compact objects to to (post)5/2-Newtonian order. III. Transition from inspiral to plunge. Phys. Rev. D 1993, 47, 3281. [Google Scholar] [CrossRef]
- Penrose, R. Chandrasekhar, black holes, and singularities. J. Astrophys. Astron. 1996, 17, 213–231. [Google Scholar] [CrossRef]
- Contoplous, G. Periodic Orbits and Chaos around Two Fixed Black Holes. Proc. R. Soc. A 1990, 413, 183–202. [Google Scholar]
- Contoplous, G. Periodic Orbits and Chaos around Two Fixed Black Holes. II. Proc. R. Soc. A 1991, 435, 551–562. [Google Scholar]
- Wunsch, A.; Muller, T.; Weiskopf, D.; Wunner, G. Circular orbits in the extreme Reissner-Nordström dihole metric. Phys. Rev. D 2013, 87, 024007. [Google Scholar] [CrossRef]
- Camps, J.; Hadar, S.; Manton, N.S. Exact gravitational wave signatures from colliding extreme black holes. Phys. Rev. D 2017, 96, 061501. [Google Scholar] [CrossRef]
- Igata, T.; Ishihara, H.; Takamori, Y. Constants of motion for constrained Hamiltonian systems: A particle around a charged rotating black hole. Phys. Rev. D 2011, 83, 047501. [Google Scholar] [CrossRef]
- Igata, T.; Ishihara, H.; Takamori, Y. Stable Bound Orbits of Massless Particles around a Black Ring. Phys. Rev. D 2013, 87, 104005. [Google Scholar] [CrossRef]
- Wald, R. General Relativity; University Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Ellis, J.; Fairbairn, M.; Hütsi, G.; Raidal, M.; Urrutia, J.; Vaskonen, V.; Veermäe, H. Prospects for Future Binary Black Hole GW Studies in Light of PTA Measurements. arXiv 2013, arXiv:2301.13854. [Google Scholar]
- Abbott, B.P.; Abe, H.; Acernese, F.; Ackley, K.; Adhicary, S.; Adhikari, N.; Adhikari, R.X.; Adkins, V.K.; Adya, V.B.; Affeldt, C.; et al. Observation of gravitational waves from a 22-solar-mass bi-nary black hole coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Page, D.N.; Thorne, K.S. Disk-accretion onto a black hole. Time-averaged structure of accretion disk. Astrophys. J. 1974, 191, 499–506. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Thorne, K.S. The mathematical theory of black holes. Int. Ser. Monogr. Phys. 1985, 53, 1013. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Circular motion of neutral test particles in Reissner-Nordstrom spacetime. Phys. Rev. D 2011, 83, 024021. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Lee, D.-S.; Lin, C.-Y. Geodesic motion of neutral particles around a Kerr-Newman black hole. Class. Quantum Gravity 2017, 34, 235008. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A.; Kaiser, D.I. Gravitation; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular motion in Kerr space-time. Phys. Rev. D 2011, 84, 044030. [Google Scholar] [CrossRef]
- Faraji, S. Circular Geodesics in a New Generalization of q-Metric. Universe 2022, 8, 195. [Google Scholar] [CrossRef]
- Narayan, R.; McClintock, J.E. Observational evidence for a correlation between jet power and black hole spin. Mon. Not. R. Astron. Soc. Lett. 2012, 419, L69–L73. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. Lett. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Zahrani, A.M.A. Escape of charged particles moving around a weakly magne-tized Kerr black hole. Phys. Rev. D 2014, 90, 044012. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Ahmedov, B. Charged particle motion around rotating black hole in braneworld immersed in magnetic field. Phys. Rev. D 2010, 81, 044022. [Google Scholar] [CrossRef]
- Akcay, S.; Barack, L.; Damour, T.; Sago, N. Gravitational self-force and the effective-one-body formalism between the innermost stable circular orbit and the light ring. Phys. Rev. D 2012, 86, 104041. [Google Scholar] [CrossRef]
- Asano, K.; Maszros, P. Ultrahigh-energy cosmic ray production by turbulence in gamma-ray burst jets and cosmogenic neutrinos. Phys. Rev. D 2016, 94, 023005. [Google Scholar] [CrossRef]
- Cabanac, C.; Fender, R.P.; Dunn, R.J.H.; Koerding, E.G. On the variation of black hole accretion disc radii as a function of state and accretion rate. Mon. Not. R. Astron. Soc. Lett. 2009, 396, 1415. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C.O.; Zlochower, Y. The last orbit of binary black holes. Phys. Rev. D 2006, 73, 061501. [Google Scholar] [CrossRef]
- Chakraborty, C. Inner-most stable circular orbits in extremal and non-extremal Kerr-Taub-NUT spacetimes. Eur. Phys. J. C 2014, 74, 2759. [Google Scholar] [CrossRef]
- Delsate, T.; Rocha, J.V.; Santarelli, R. Geodesic motion in equal angular momenta Myers-Perry-AdS spacetimes. Phys. Rev. D 2015, 92, 084028. [Google Scholar] [CrossRef]
- Hadar, S.; Kol, B.; Berti, E.; Cardoso, V. Comparing numerical and analytical cal- culations of post-ISCO ringdown amplitudes. Phys. Rev. D 2011, 84, 047501. [Google Scholar] [CrossRef]
- Harms, E.; Lukes-Gerakopoulos, G.; Bernuzzi, S.; Nagar, A. Spinning test body or-biting around a Schwarzschild black hole: Circular dynamics and gravitational-wave fluxes. Phys. Rev. D 2016, 94, 104010. [Google Scholar] [CrossRef]
- Hod, S. Analytic toy model for the innermost stable circular orbit shift. Phys. Rev. D 2013, 87, 024036. [Google Scholar] [CrossRef]
- Hod, S. Self-gravitating ring of matter in orbit around a black hole: The in- nermost stable circular orbit. Eur. Phys. J. C 2014, 74, 2840. [Google Scholar] [CrossRef]
- Isoyama, S.; Barack, L.; Dolan, S.R.; Tiec, A.L.; Nakano, H.; Shah, A.G.; Tanaka, T.; Warburton, N. Gravitational self-force correction to the innermost stable circular equatorial orbit of a Kerr black hole. Phys. Rev. Lett. 2014, 113, 161101. [Google Scholar] [CrossRef]
- Lukes-Gerakopoulos, G.; Harms, E.; Bernuzzi, S.; Nagar, A. Spinning test-body orbiting around a Kerr black hole: Circular dynamics and gravitational-wave fluxes. Phys. Rev. D 2017, 96, 064051. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Innermost stable circular orbit near dirty black holes in mag- netic field and ultra-high energy particle collisions. Eur. Phys. J. C 2015, 75, 403. [Google Scholar] [CrossRef]
- Shiose, R.; Kimura, M.; Chiba, T. Motion of charged particles around a weakly magnetized rotating black hole. Phys. Rev. D 2014, 90, 124016. [Google Scholar] [CrossRef]
- Hussain, S.; Hussain, I.; Jamil, M. Dynamics of a charged particle around a slowly rotating Kerr black hole immersed in magnetic field. Eur. Phys. J. C 2014, 74, 3210. [Google Scholar] [CrossRef]
- Takahashi, M.; Koyama, H. Chaotic motion of charged particles in an elec- tromagnetic field surrounding a rotating black hole. Astrophys. J. 2009, 693, 472–485. [Google Scholar] [CrossRef]
- Frolov, V.P.; Shoom, A.A. Motion of charged particles near weakly magnetized Schwarzschild black hole. Phys. Rev. D 2010, 82, 084034. [Google Scholar] [CrossRef]
- Frolov, V.P. Weakly magnetized black holes as particle accelerators. Phys. Rev. D 2012, 85, 024020. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular orbits of neutral test particles in the Kerr-Newman spacetime. Phys. Rev. D 2013, 88, 024042. [Google Scholar] [CrossRef]
- Corinaldesi, E.; Papapetrou, A. Spinning test particles in general relativity. II. Proc. R. Soc. Lond. Ser. A 1951, 209, 259–268. [Google Scholar]
- Rasband, S. Black holes and spinning test bodies. Phys. Rev. Lett. 1973, 30, 111. [Google Scholar] [CrossRef]
- Tod, K.P.; de Felice, F.; Calvani, M. Spinning test particles in the field of a black hole. Nuovo C. B Ser. 1976, 34, 365. [Google Scholar] [CrossRef]
- Zhang, Y.-P.; Wei, S.-W.; Guo, W.-D.; Sui, T.-T.; Liu, Y.-X. Innermost stable circular orbit of spinning particle in charged spinning black hole background. Phys. Rev. D 2018, 97, 084056. [Google Scholar] [CrossRef]
- Schroven, K.; Hackmann, E.; Lämmerzahl, C. Relativistic dust accretion of charged particles in Kerr-Newman spacetime. Phys. Rev. D 2017, 96, 063015. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, J.; Liu, Y.; Liu, W.-B. Collisional Penrose process of charged spinning particles. Phys. Rev. D 2018, 98, 044006. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shen, G.; Sun, X. The Space-Time Properties of Three Static Black Holes. Symmetry 2023, 15, 702. https://doi.org/10.3390/sym15030702
Wang Y, Shen G, Sun X. The Space-Time Properties of Three Static Black Holes. Symmetry. 2023; 15(3):702. https://doi.org/10.3390/sym15030702
Chicago/Turabian StyleWang, Yu, Gangqi Shen, and Xin Sun. 2023. "The Space-Time Properties of Three Static Black Holes" Symmetry 15, no. 3: 702. https://doi.org/10.3390/sym15030702
APA StyleWang, Y., Shen, G., & Sun, X. (2023). The Space-Time Properties of Three Static Black Holes. Symmetry, 15(3), 702. https://doi.org/10.3390/sym15030702




