The Impact of Increasing the Length of the Conical Segment on Cyclone Performance Using Large-Eddy Simulation
Abstract
:1. Introduction
2. Numerical Setup
2.1. The Governing Equation
2.2. Modeling the Discrete Phase
3. Description of the Model, Validation, and Methodology
3.1. The Details of Cyclone Geometry
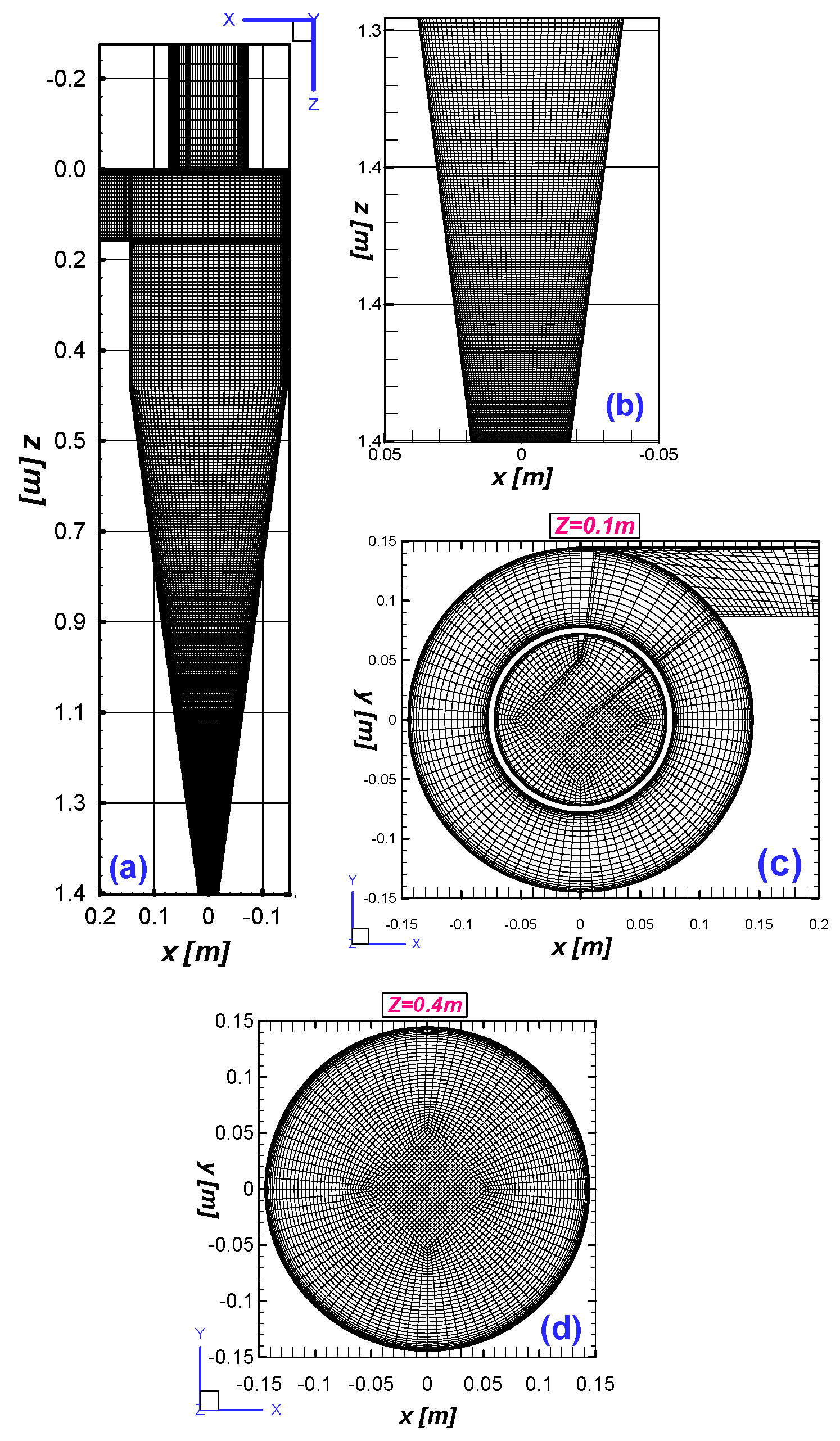
3.2. Mesh Generation
3.3. CFD Methodology
3.4. Numerical Settings and Boundary Conditions
3.4.1. Continuous Phase
3.4.2. Discrete Phase
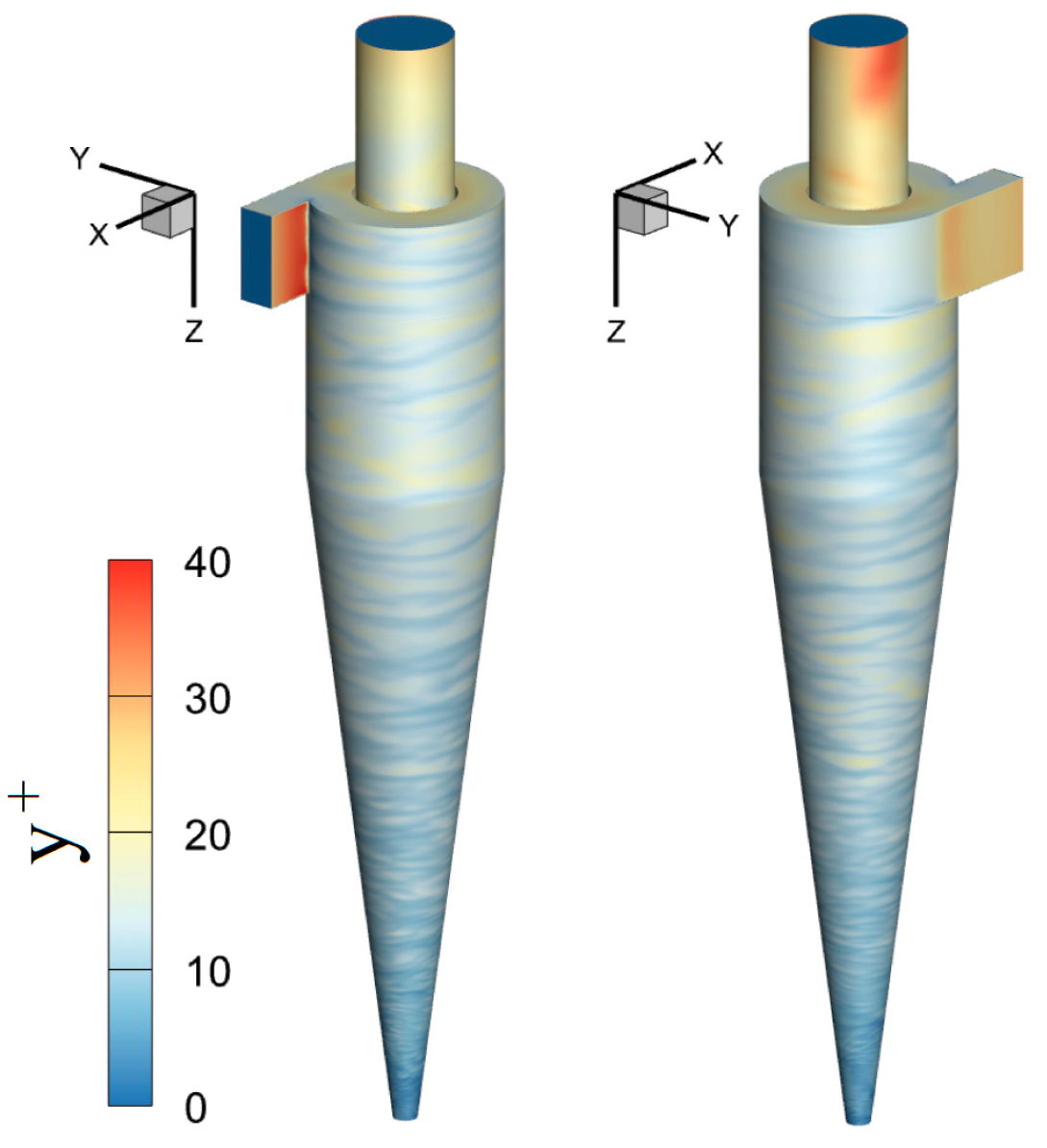
3.4.3. Near-Wall Treatment
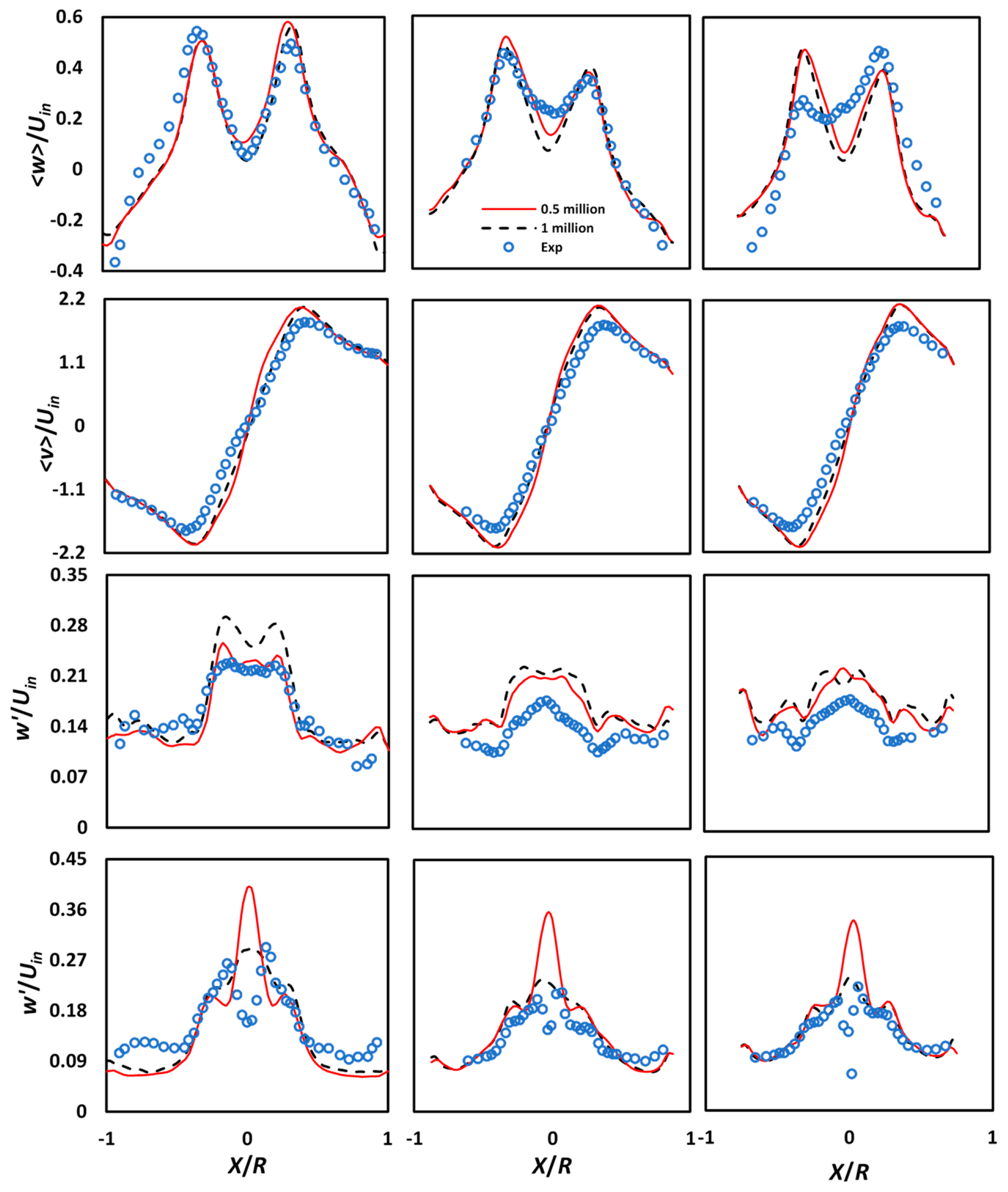
3.5. Validation and Methodology
4. Results and Discussion
4.1. The Quality of LES
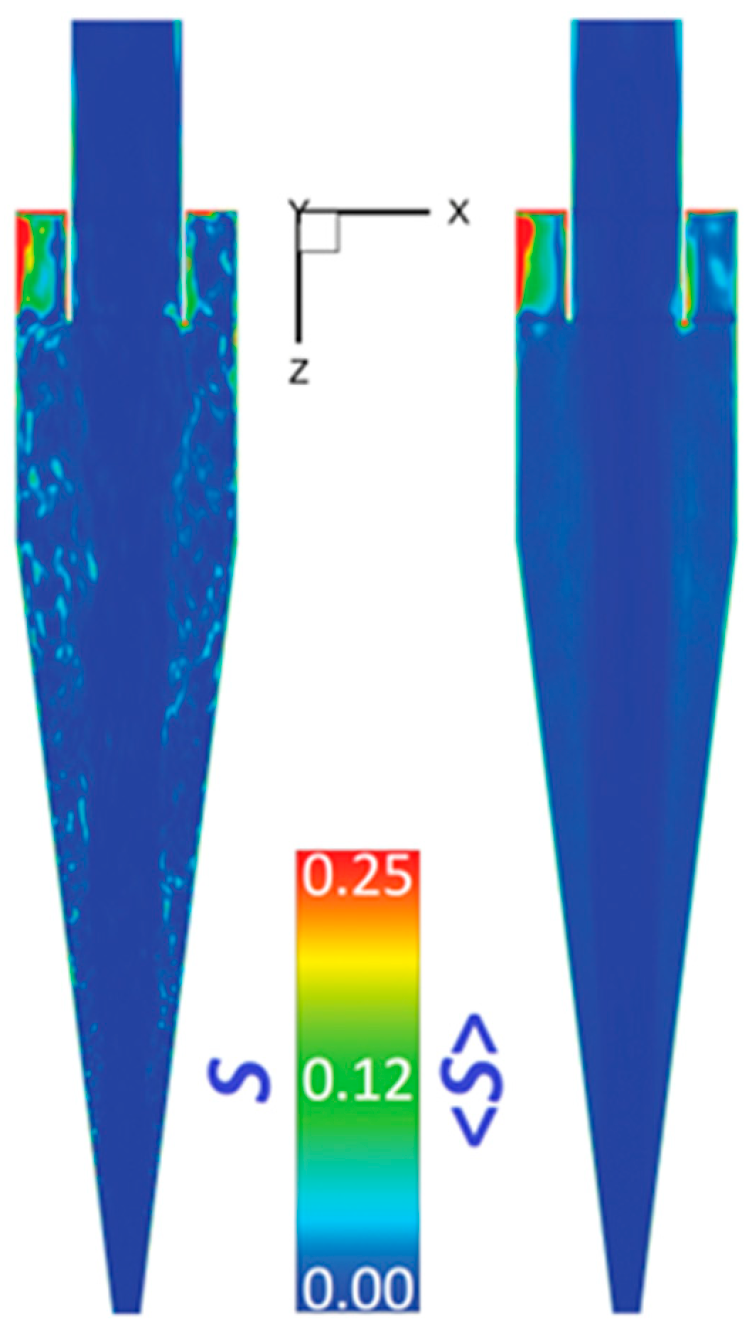
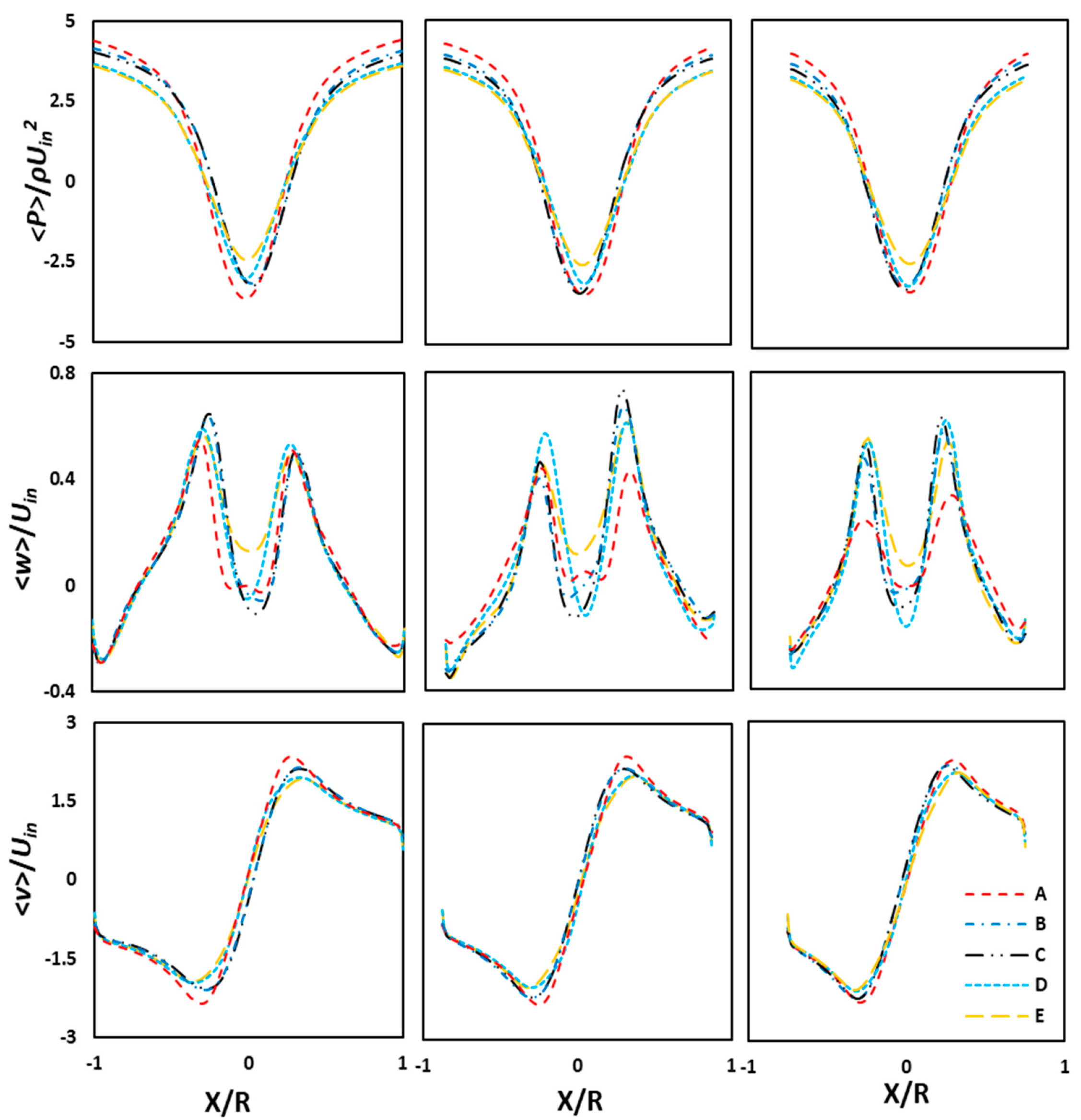
4.2. The Mean Flow Field
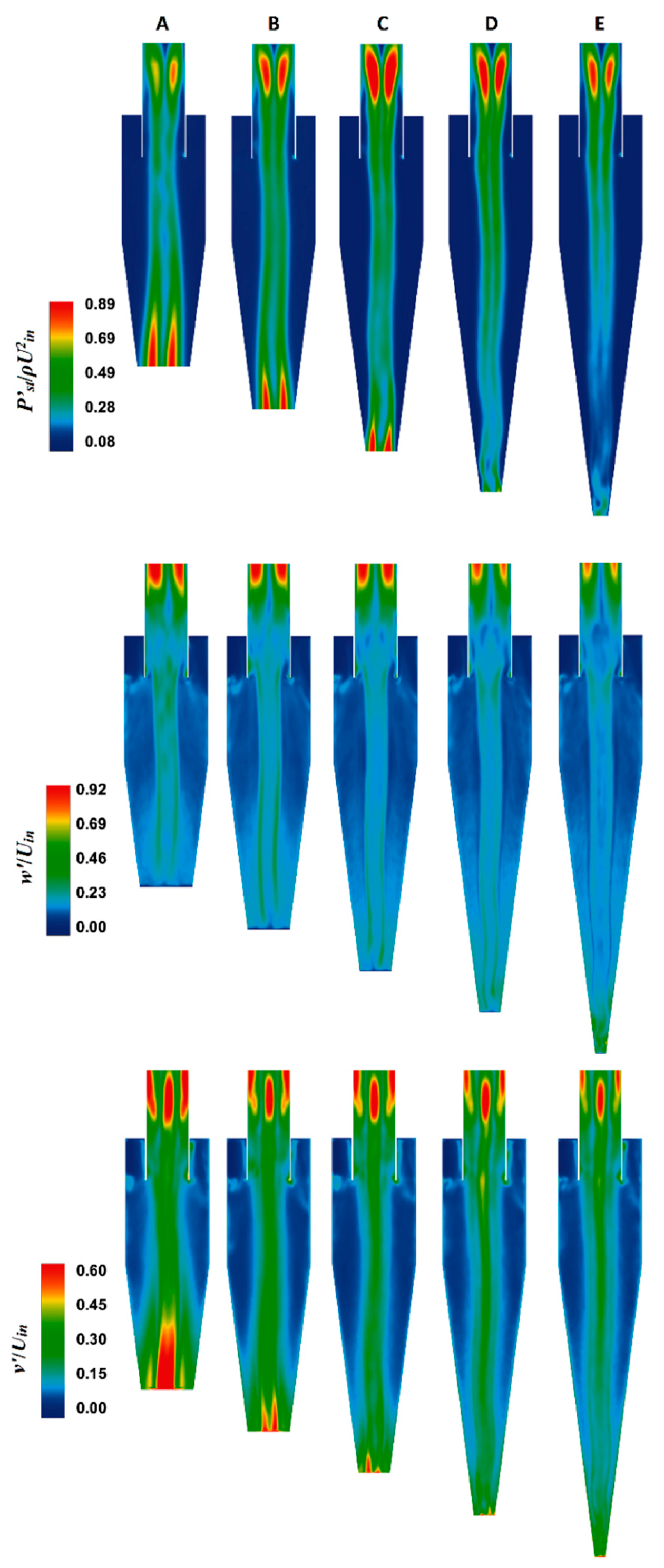
4.3. The Fluctuating Flow Field
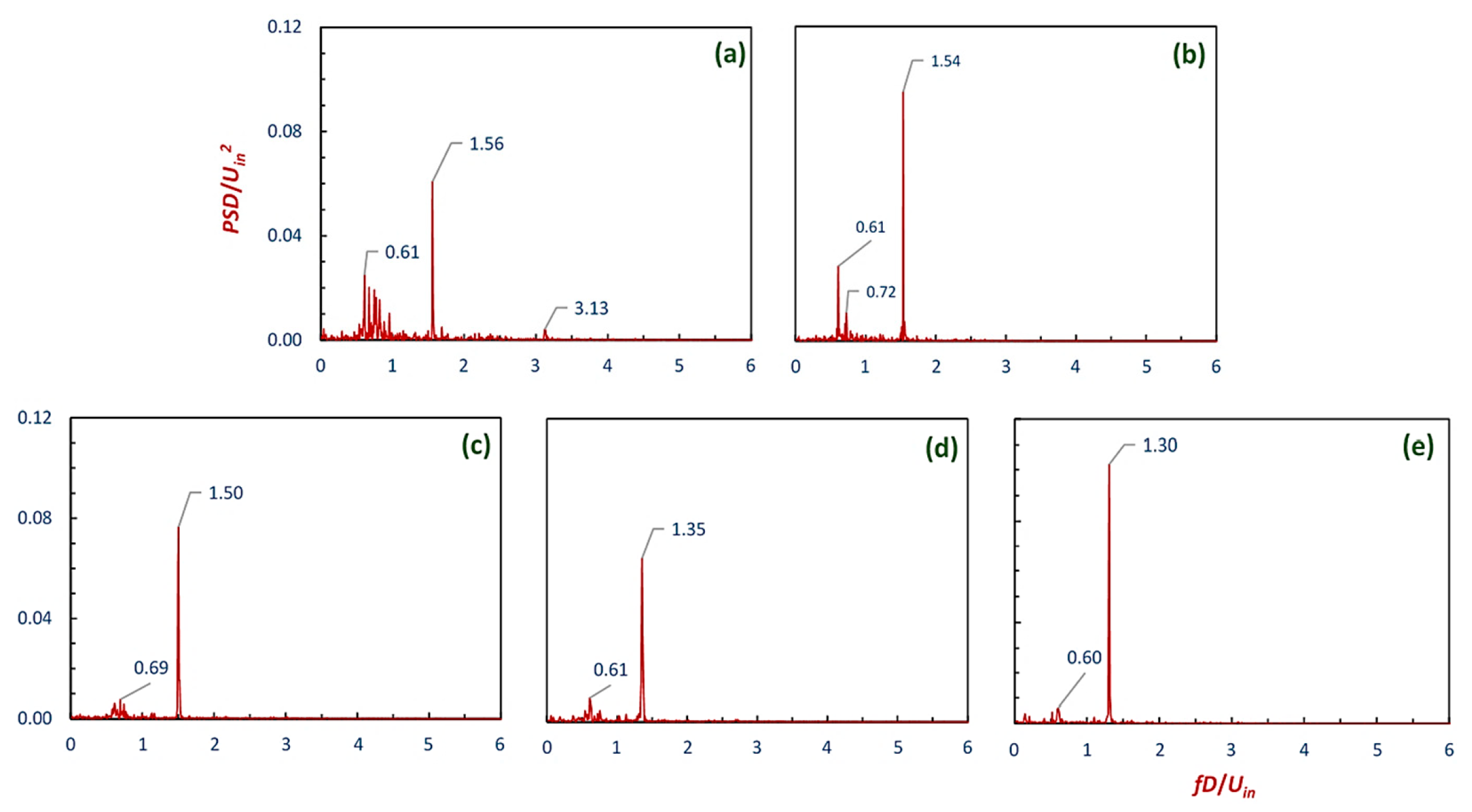
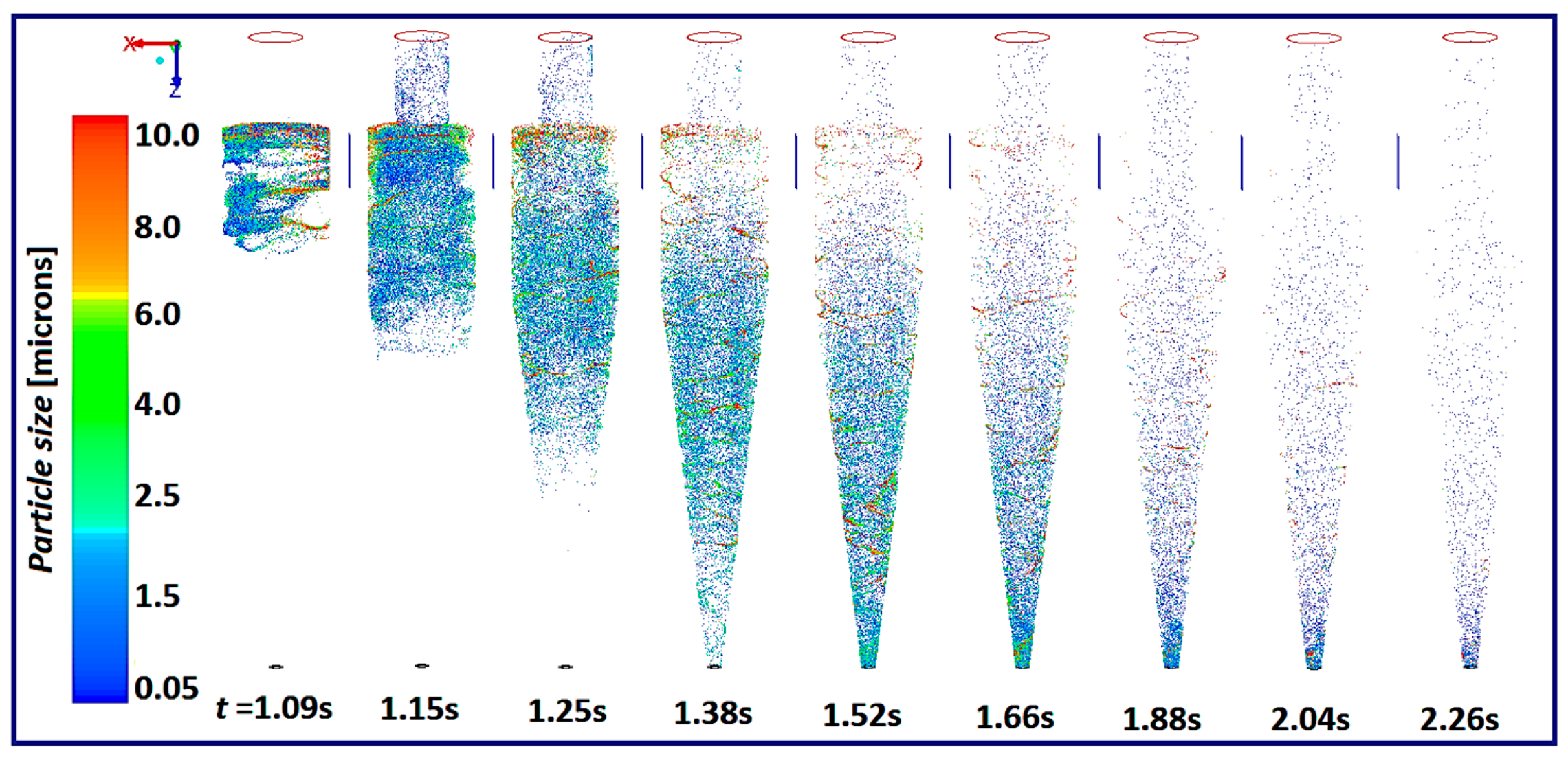
4.4. The Representation of the Vortex Core
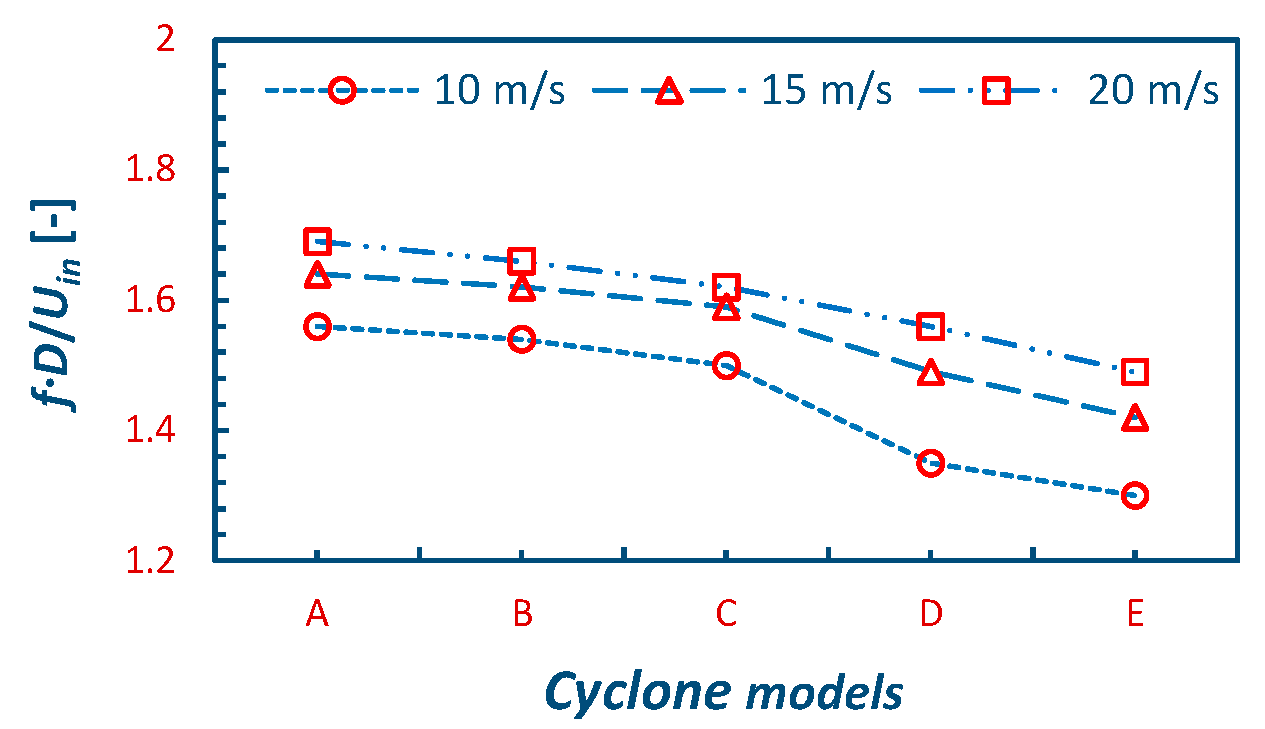
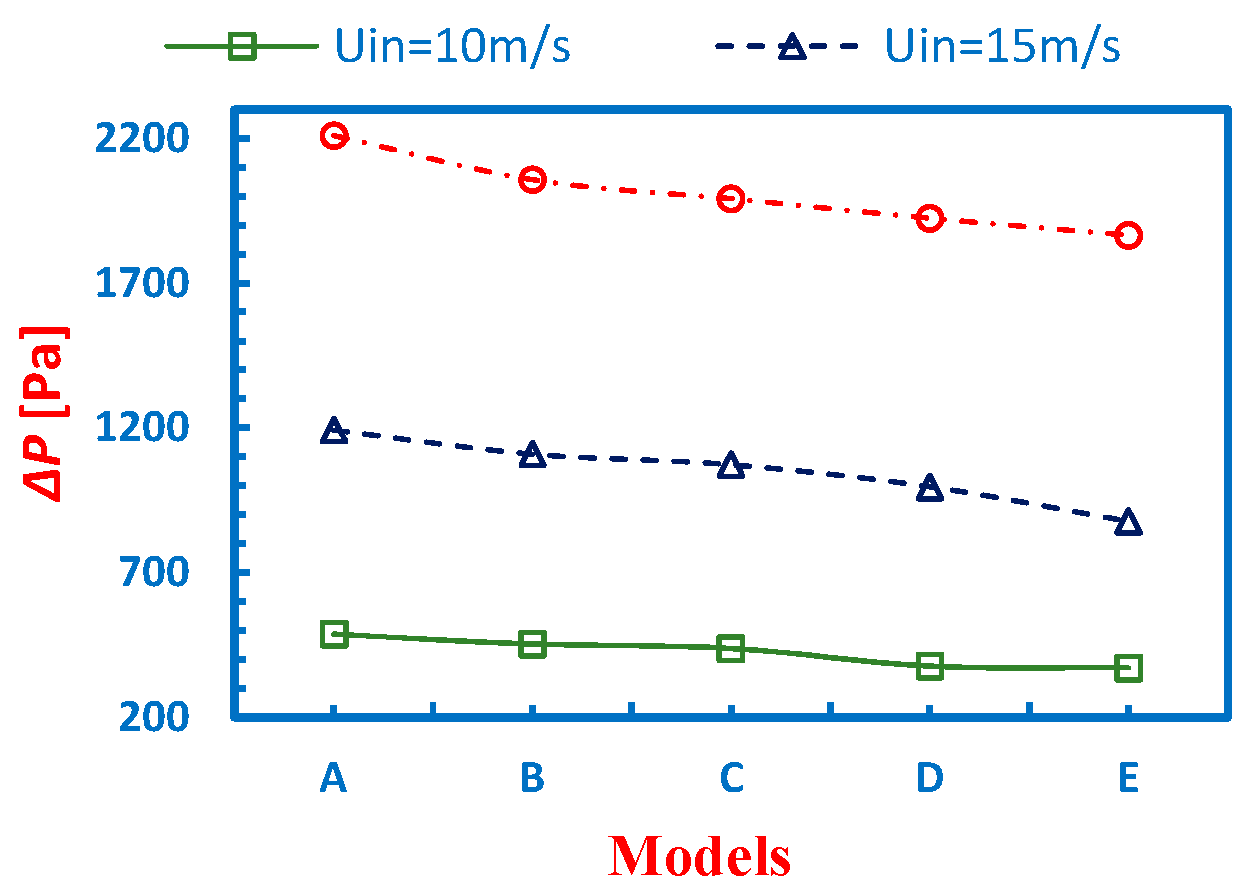
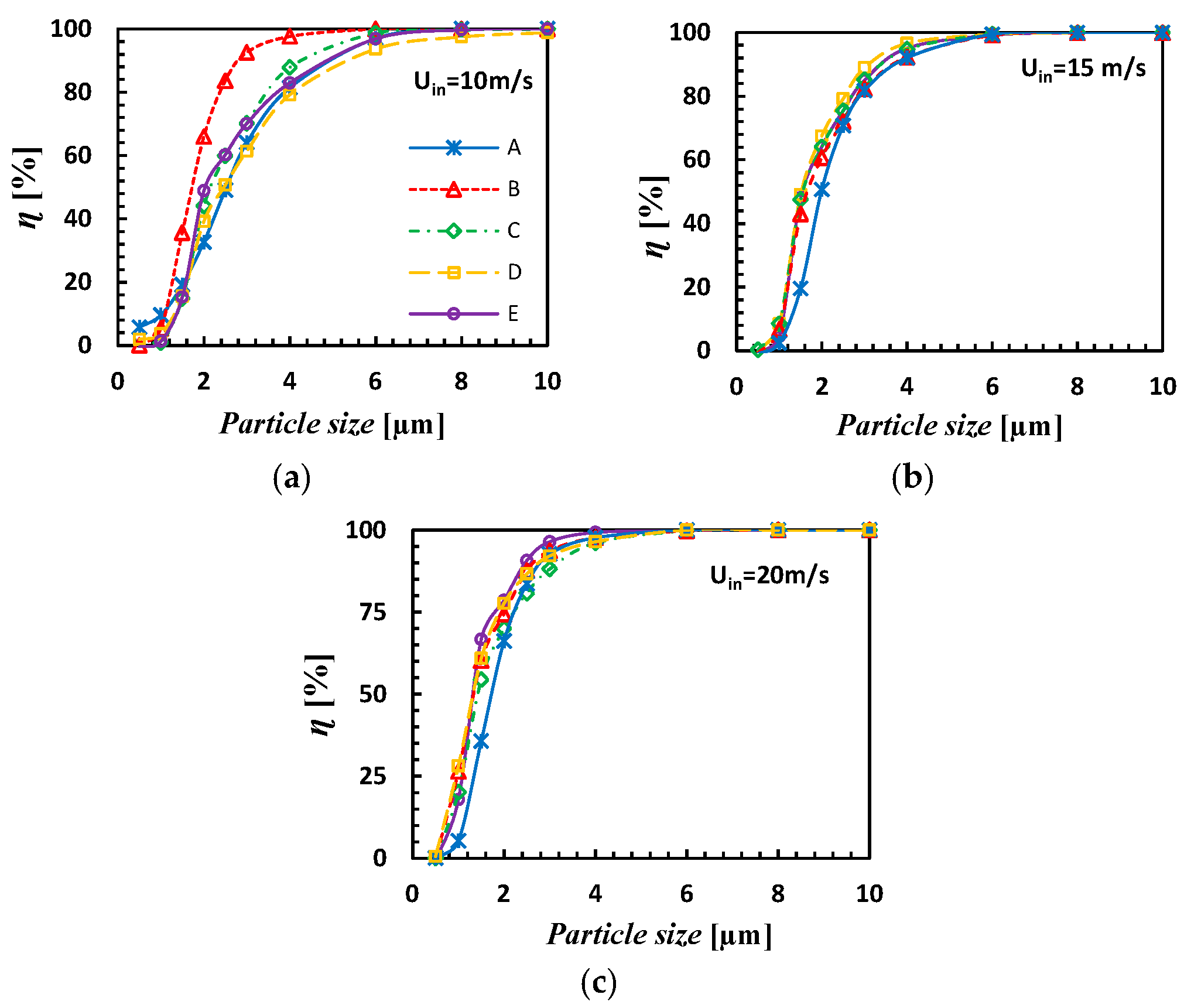
4.5. Performance of the Cyclone
5. Conclusions
- The pressure drop decreases by increasing the conical height of the cyclone separator and decreasing the cone-tip diameter.
- The magnitude of the tangential velocity decreases as the length of the cyclone separator increases along with the diameter of the cone tip.
- The velocity fluctuations were suppressed in models A–E.
- The frequency with which the vortex core precesses about the geometrical axis was lowest in model A and it decreased gradually from cyclone models A–E.
- The pressure drop reduced from 1017 Pa to 877 Pa.
- The collection efficiency increased from 59.63% to 63.90%.
- The cut-off size reduced from 2 μm to 1.54 μm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Flagan, R.C.; Seinfeld, J.H. Fundamentals of Air Pollution Engineering; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1988; ISBN 0-13-332537-7. Available online: http://resolver.caltech.edu/CaltechBOOK:1988.001 (accessed on 25 November 2022).
- Hoekstra, A.J. Gas Flow Field and Collection Efficiency of Cyclone Separators. Ph.D. Thesis, Technical University Delft, Delft, The Netherlands, 2000. Available online: http://resolver.tudelft.nl/uuid:67b8f405-eef0-4c2d-9646-80200e5274c6 (accessed on 2 May 2022).
- Ficici, F.; Ari, V. The influence of diameter of vortex finder on cyclone collection efficiency. Environ. Prog. Sustain. Energy 2014, 34, 669–673. [Google Scholar] [CrossRef]
- Wasilewski, M.; Brar, L.S.; Ligus, G. Experimental and numerical investigation on the performance of square cyclones with different vortex finder configurations. Sep. Purif. Technol. 2020, 239, 116588. [Google Scholar] [CrossRef]
- Elsayed, K. Design of a novel gas cyclone vortex finder using the adjoint method. Sep. Purif. Technol. 2015, 142, 274–286. [Google Scholar] [CrossRef]
- Parvaz, F.; Hosseini, S.H.; Ahmadi, G.; Elsayed, K. Impacts of the vortex finder eccentricity on the flow pattern and performance of a gas cyclone. Sep. Purif. Technol. 2017, 187, 1–13. [Google Scholar] [CrossRef]
- Brar, L.S.; Elsayed, K. Analysis and optimization of cyclone separators with eccentric vortex finders using large eddy simulation and artificial neural network. Sep. Purif. Technol. 2018, 207, 269–283. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. The effect of cyclone inlet dimensions on the flow pattern and performance. Appl. Math. Model. 2011, 35, 1952–1968. [Google Scholar] [CrossRef] [Green Version]
- Wasilewski, M.; Brar, L.S. Effect of the inlet duct angle on the performance of cyclone separators. Sep. Purif. Technol. 2019, 213, 19–33. [Google Scholar] [CrossRef]
- Yoshida, H.; Ono, K.; Fukui, K. The effect of a new method of fluid flow control on submicron particle classification in gas-cyclones. Powder Technol. 2005, 149, 139–147. [Google Scholar] [CrossRef]
- Bernardo, S.; Mori, M.; Peres, A.; Dionísio, R. 3-D computational fluid dynamics for gas and gas-particle flows in a cyclone with different inlet section angles. Powder Technol. 2006, 162, 190–200. [Google Scholar] [CrossRef]
- Qian, F.P.; Zhang, M.Y. Effects of the Inlet Section Angle on the Flow Field of a Cyclone. Chem. Eng. Technol. 2007, 30, 1564–1570. [Google Scholar] [CrossRef]
- Qian, F.; Wu, Y. Effects of the inlet section angle on the separation performance of a cyclone. Chem. Eng. Res. Des. 2009, 87, 1567–1572. [Google Scholar] [CrossRef]
- Misiulia, D.; Andersson, A.G.; Lundström, T.S. Computational Investigation of an Industrial Cyclone Separator with Helical-Roof Inlet. Chem. Eng. Technol. 2015, 38, 1425–1434. [Google Scholar] [CrossRef]
- Misiulia, D.; Andersson, A.G.; Lundström, T.S. Effects of the inlet angle on the flow pattern and pressure drop of a cyclone with helical-roof inlet. Chem. Eng. Res. Des. 2015, 102, 307–321. [Google Scholar] [CrossRef]
- Misiulia, D.; Andersson, A.G.; Lundström, T.S. Effects of the inlet angle on the collection efficiency of a cyclone with helical-roof inlet. Powder Technol. 2017, 305, 48–55. [Google Scholar] [CrossRef]
- Demir, S.; Karadeniz, A.; Aksel, M. Effects of cylindrical and conical heights on pressure and velocity fields in cyclones. Powder Technol. 2016, 295, 209–217. [Google Scholar] [CrossRef]
- Brar, L.; Sharma, R. Effect of varying diameter on the performance ofindustrial scale gas cyclone dust separators. Mater. Today Proc. 2015, 2, 3230–3237. [Google Scholar] [CrossRef]
- Gimbun, J.; Chuah, T.; Choong, T.S.; Fakhru’L-Razi, A. Prediction of the effects of cone tip diameter on the cyclone performance. J. Aerosol Sci. 2005, 36, 1056–1065. [Google Scholar] [CrossRef]
- Wang, L.; Buser, M.D.; Parnell, C.B., Jr.; Shaw, B.W. Effect of Air Density on Cyclone Performance and System Design. Trans. ASAE 2003, 46, 1193–1201. [Google Scholar] [CrossRef]
- Wang, L. Theoretical Study of Cyclone Design. Ph.D. Thesis, Texas A & M University, College Station, Texas, USA, 2004. [Google Scholar] [CrossRef]
- Shastri, R.; Brar, L.S. Numerical investigations of the flow-field inside cyclone separators with different cylinder-to-cone ratios using large-eddy simulation. Sep. Purif. Technol. 2020, 249, 117149. [Google Scholar] [CrossRef]
- Stern, A.C.; Caplan, K.J.; Bush, P.D. Cyclone Dust Collectors; American Petroleum Institute: New York, NY, USA, 1955. [Google Scholar]
- Wang, L. A New Engineering Approach to Cyclone Design for Cotton Gins. Master’s Thesis, Texas A&M University, College Station, Texas, USA, 2000. Available online: https://hdl.handle.net/1969.1/ETD-TAMU-2000-THESIS-W264 (accessed on 14 November 2022).
- Pandey, S.; Saha, I.; Prakash, O.; Mukherjee, T.; Iqbal, J.; Roy, A.K.; Wasilewski, M.; Brar, L.S. CFD Investigations of Cyclone Separators with Different Cone Heights and Shapes. Appl. Sci. 2022, 12, 4904. [Google Scholar] [CrossRef]
- Pandey, S.; Brar, L.S. On the performance of cyclone separators with different shapes of the conical section using CFD. Powder Technol. 2022, 407, 1–17. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Pericć, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer-Verlag: Berlin, Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Crowe, C.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Stairmand, C.J. The design and performance of cyclone separators. Ind. Eng. Chem. 1951, 29, 356–383. [Google Scholar]
- Derksen, J.J. Separation performance predictions of a Stairmand high-efficiency cyclone. AIChE J. 2003, 49, 1359–1371. [Google Scholar] [CrossRef]
- Gronald, G.; Derksen, J. Simulating turbulent swirling flow in a gas cyclone: A comparison of various modeling approaches. Powder Technol. 2011, 205, 160–171. [Google Scholar] [CrossRef]
- De Souza, F.J.; Salvo, R.D.V.; Martins, D.A.D.M. Large Eddy Simulation of the gas–particle flow in cyclone separators. Sep. Purif. Technol. 2012, 94, 61–70. [Google Scholar] [CrossRef]
- Kumar, M.; Vanka, S.P.; Banerjee, R.; Mangadoddy, N. Dominant Modes in a Gas Cyclone Flow Field Using Proper Orthogonal Decomposition. Ind. Eng. Chem. Res. 2022, 61, 2562–2579. [Google Scholar] [CrossRef]
- Brar, L.S.; Derksen, J. Revealing the details of vortex core precession in cyclones by means of large-eddy simulation. Chem. Eng. Res. Des. 2020, 159, 339–352. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Yazdabadi, P.A.; Griffiths, A.J.; Syred, N. Characterization of the PVC phenomena in the exhaust of a cyclone dust separator. Exp. Fluids 1994, 17, 84–95. [Google Scholar] [CrossRef]
- Derksen, J.J.; Akker, H.E.A.V.D. Simulation of vortex core precession in a reverse-flow cyclone. AIChE J. 2000, 46, 1317–1331. [Google Scholar] [CrossRef]
- Derksen, J.J.; Akker, H.E.A.V.D.; Sundaresan, S. Two-way coupled large-eddy simulations of the gas-solid flow in cyclone separators. AIChE J. 2008, 54, 872–885. [Google Scholar] [CrossRef]

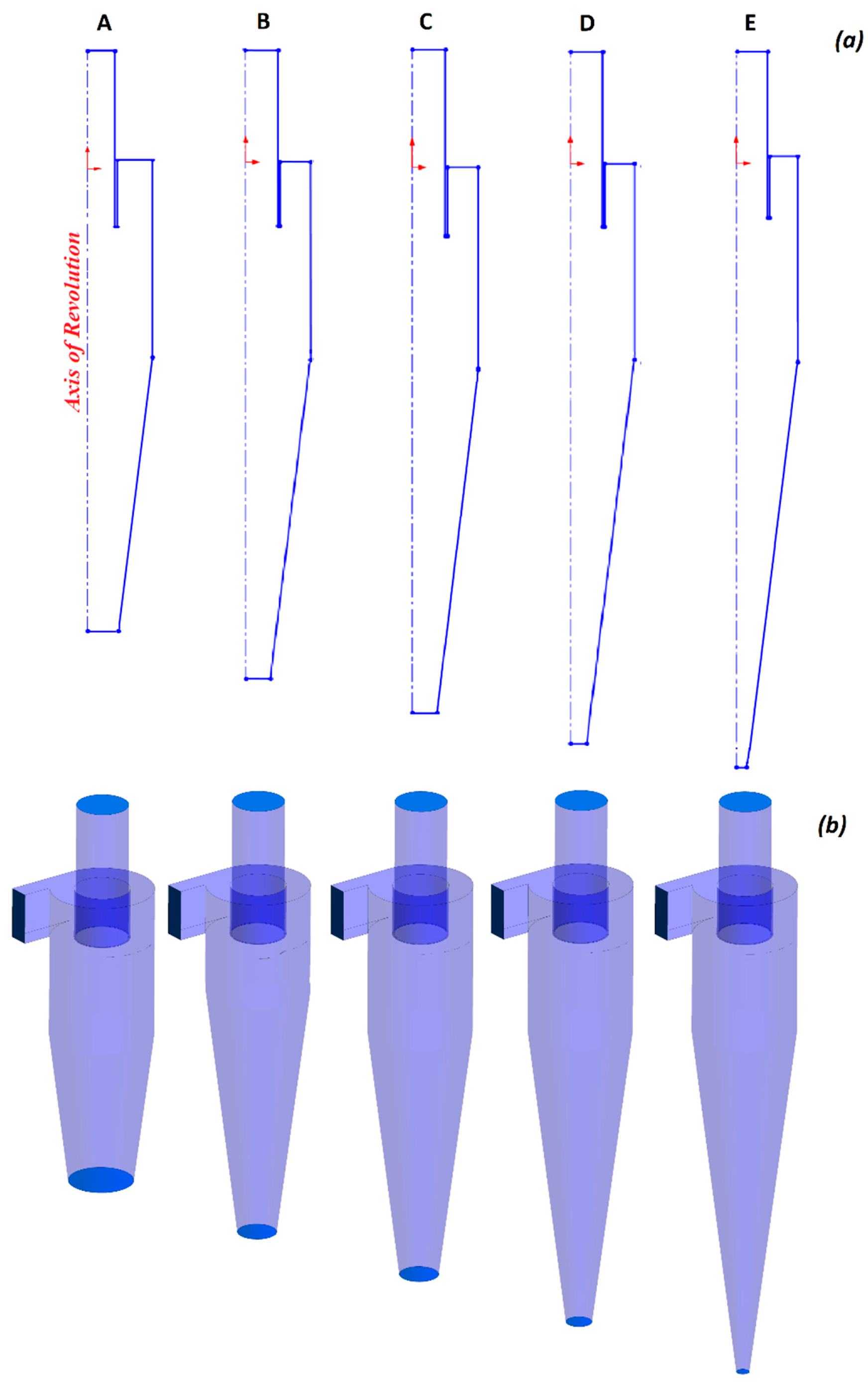




| Cyclone Geometry | Cyclone Model | Symbols (Normalized with D) | Dimensions [-] |
|---|---|---|---|
| Vortex finder diameter | De/D | 0.5 | |
| Inlet duct height | a/D | 0.5 | |
| Inlet duct width | b/D | 0.2 | |
| Vortex finder insertion length | Lv/D | 0.5 | |
| Height of cylindrical section | H/D | 1.5 | |
| Height of conical segment | A | Hc/D | 1.5 |
| B | 2.0 | ||
| C | 2.5 | ||
| D | 3.0 | ||
| E | 3.5 | ||
| Cone-tip diameter | A | Bc/D | 0.3125 |
| B | 0.2500 | ||
| C | 0.1875 | ||
| D | 0.1250 | ||
| E | 0.0625 |
| Model | A | B | C | D | E |
|---|---|---|---|---|---|
| Mesh count | 0.685 M | 0.880 M | 1.5 M | 1.6 M | 1.8 M |
| LES (Coarse) | LES (Fine) | |
|---|---|---|
| Mesh count | 0.5 million | 1.0 million |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, S.; Brar, L.S. The Impact of Increasing the Length of the Conical Segment on Cyclone Performance Using Large-Eddy Simulation. Symmetry 2023, 15, 682. https://doi.org/10.3390/sym15030682
Pandey S, Brar LS. The Impact of Increasing the Length of the Conical Segment on Cyclone Performance Using Large-Eddy Simulation. Symmetry. 2023; 15(3):682. https://doi.org/10.3390/sym15030682
Chicago/Turabian StylePandey, Satyanand, and Lakhbir Singh Brar. 2023. "The Impact of Increasing the Length of the Conical Segment on Cyclone Performance Using Large-Eddy Simulation" Symmetry 15, no. 3: 682. https://doi.org/10.3390/sym15030682
APA StylePandey, S., & Brar, L. S. (2023). The Impact of Increasing the Length of the Conical Segment on Cyclone Performance Using Large-Eddy Simulation. Symmetry, 15(3), 682. https://doi.org/10.3390/sym15030682







