Gravitational Waves and Electromagnetic Radiation from Charged Black Hole Binaries

Abstract

In this manuscript, we investigate the electromagnetic radiation of a binary system of electrically charged black holes. Using the results of previous works, we compute the analytical expression for the waveform, the phase, and the Fourier transform during the inspiral phase for both the electromagnetic and gravitational radiations. To do so, we consider the quasi-circular approximation and small values for the charge-to-mass ratio in each black hole. In the case of electromagnetic radiation, we focus on the dipole contribution, but we also include the quadrupole term to complete our discussion. We found that the gravitational and electromagnetic waveforms contain two terms, and so does the Fourier transform. However, the behavior is dominated only by one of them. In the frequency-domain waves, for example, the dipole and quadrupole contributions and the gravitational wave are dominated by terms proportional to f^−3/6, f^−1/6, and f^−7/6, respectively. As expected, the gravitational radiation and the quadrupole contribution have the same phase, in contrast to the dipole contribution. Moreover, the electromagnetic wave is more sensitive to changes in the charge-to-mass ratio than the gravitational wave.

1. Introduction

The detection of gravitational waves by LIGO and Virgo scientific collaborations [1,2,3] has opened the possibility of exploring and understanding the nature of gravity in the strong-field regime, giving us the occasion to test general relativity (GR) and compare its predictions with alternative theories and observations [4]. Nowadays, the observation of gravitational waves (GWs) is constrained to the frequency range of $10-{10}^3$ Hz. Nonetheless, space-based observatories, such as LISA [5], TianQin [6] and Taiji [7], will improve the accuracy and range of observations, allowing for the detection of GWs at low frequencies.

One of the sources of GW signals detectable using space-based observatories is a binary system formed by a stellar-mass compact object, such as black holes (BHs) or neutron stars (NS), orbiting a supermassive black hole (SMBH). When the mass ratio of these systems is between ${10}^{-7}$ and ${10}^{-4}$, we refer to them as extreme mass ratio inspirals (EMRIs). It is well-known that EMRIs are suitable for investigating the mass, the spin, the electric charge, and the strong-field physics in the vicinity of BHs [8,9,10,11,12]. On the other hand, according to GR, any astrophysical black hole can be described by three external parameters: mass, angular momentum, and electric charge. This is a consequence of the well-known no-hair theorem [13,14,15]. Hence, from the observational point of view, one expects that the reason behind the multi-messenger (this term refers to observations of electromagnetic radiation, gravitational waves, neutrinos, and cosmic rays [16]) experiments is to determine these external parameters. Nevertheless, only the black hole mass and its angular momentum have been taken into account, while the electric charge, on the other hand, is usually neglected and set equal to zero. As claimed by M. Zajaček and A. Tursunov, “this assumption is supported by arguing that the presence of plasma around astrophysical black holes leads to prompt discharging ” [16].

The presence of charge in compact objects is still in debate, and the question how could black holes get charged? has been considered by several authors [17,18,19,20,21,22]. In Ref. [17], for example, to prevent the separation of electrons and protons in the stellar atmosphere, Eddington suggested that stars should have a small amount of positive charge. In Ref. [18], Wald proposed a relativistic mechanism that supports the existence of charged black holes. According to Wald, when one immerses a rotating black hole in a uniform magnetic field, an electric field is induced due to the twisting of magnetic field lines, implying that a non-zero charge is conceivable. The value of the induced electric charge is proportional not only to the strength of the magnetic field, but also to the black hole’s spin [16,21,22]. The sign of the electric charge induced via the Wald mechanism depends on the orientation of magnetic field lines relative to the black hole’s spin. For example, the black hole would have a positive charge if the magnetic field is parallel to the rotation axis of the black hole. In this sense, since a certain degree of alignment between the accretion flow angular momentum and the black hole spin is expected, the charge of astrophysical black holes tends to be positive [16]. Later, in 1978, Bally and Harrison showed that any macroscopic body in the universe, such as stars, galaxies, and black holes, is positively charged with a charge-to-mass ratio of approximately 100 Coulombs per solar mass [20].

Recently, there has been an increasing interest in charged black holes: see Refs. [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39] and references therein. In Ref. [22], M. Zajaček et al. used observations of the galactic center black hole Sgr A* to constrain its charge. They also used their results to analyze two of the most interesting astrophysical consequences of slightly charged black holes: the effect on the gamma-ray bursts (also called X-ray bremsstrahlung by M. Zajaček et al. in Ref. [22]) (GRBs) profiles and the effect on the position of the innermost stable circular orbit (ISCO). Although a small amount of charge does not affect the space–time structure drastically, the authors showed that it could be relevant for the plasma dynamics close to the galactic center black hole or supermassive black holes. Moreover, the authors concluded that the electric charge and the associated electromagnetic (EM) signal could be crucial for plunges of neutron stars into supermassive black holes or black hole–neutron star mergers [32,35,36,37].

In Refs. [23,24], Kim and Lee investigated the charge and the magnetic flux on rotating black holes. The results show that black holes and magnetars carry a similar amount of electric charge (and the same sign). Furthermore, in the collapsar/hypernova scenario of gamma-ray bursts, the results indicate that the central object charge and the corresponding magnetic flux remain continuous. On the other hand, regarding the extraction of rotational energy, the authors found that this process will continue, provided the magnetic field remains supported by the surrounding magnetized matter.

In Refs. [25,26,27,28,29,30,31,32,33,34], the authors consider charged black holes to investigate gravitational-wave physics. In Ref. [25], for example, G. Bozzola and V. Paschalidis developed an initial data formalism valid for general relativistic simulations of binary systems with electric charge and linear and angular momenta. As claimed by the authors, the formalism is useful for simulating the dynamical evolution of the ultrarelativistic head-on collision, the quasicircular or eccentric inspiral, and the merger of two black holes [30,31].

L. Liu et al. studied the case of BH binaries with electric and magnetic charges in circular and elliptical orbits on a cone in Refs. [26,27,28]. First, the authors considered a BH binary system formed by non-rotating dyonic black holes. Then, using the Newtonian approximation with radiation reactions, they calculated the total emission rate of the energy and angular momentum generated by the gravitational and EM radiation. In the case of circular orbits, they showed that electric and magnetic charges significantly suppress the merger times of binaries. On the other hand, when considering elliptical orbits, they showed that the emission rates of energy and angular momentum produced by the gravitational and EM radiation have the same dependence on the conic angle for different orbits.

Finally, in Ref. [29], Christiansen et al. investigated the emission of GWs by systems involving charged BHs whose charge corresponds to some dark-charge. The authors explain that this kind of BH can be created in the early universe by self-interacting dark matter (DM) models. The main idea of their work is to “investigate some observational consequences of compact objects beyond those well-captured by the employed templates” [29]. To do so, they begin by considering Keplerian orbits, where the emission comes mainly from the EM dark-charge dipole contribution, which they use later to obtain the time evolution of the orbital parameters in the Newtonian approximation. In that work, the authors show that a good approximation for both EM and GW-dominated emissions (in the LIGO/Virgo sensitivity range) can be obtained by considering circular orbits at the time of the merger.

In the manuscript, we investigate the EM radiation of a binary system formed by charged black holes. In a previous paper [40], we studied the EM radiation of a binary system immersed in a uniform magnetic field using a toy model proposed by C. Palenzuela et al. in Ref. [41]. Following a similar philosophy, we obtain the EM waveform radiated by the system during the inspiral phase using the quasicircular approximation derived in Ref. [29] by Christiansen et al. We organized the paper as follows: in Section 2, we follow Ref. [42] to discuss and obtain the Keplerian orbits for a system of two-point masses with electric charges. In Section 3 and Section 4, we review the gravitational and EM radiation, the angular momentum emission, and the evolution of the orbital parameters, following previous results in the literature. The GW and EM waves are computed in Section 5. Then, in Section 7, we obtain the Fourier transform of the EM wave. Finally, we discuss our results in Section 8.

In the manuscript, we use bold and normal letters to denote vectors and scalars, respectively. We denote the time average of a quantity A by $\overline{A}$, and we use CGS units with the electric constant $k_e=1$. Following Refs. [43,44], we keep G, c, and $k_e$ in the expressions, with the exception of Section 5 and figures, where we use dimensionless units; see Appendix A.

2. Keplerian Motion

The problem of two bodies moving under the influence of a central force can be analyzed using the Lagrangian formulation [42]. Therefore, we devote this section to the Keplerian orbits of two point particles with masses $m_1$ and $m_2$ and charges $Q_1$ and $Q_2$, respectively. To obtain the equations of motion, we consider a central force given by a function $\mathcal{U}$ containing the gravitational and electric potentials. It is worth noting that $\mathcal{U}$ is only affected by the vectors separating the two masses, ${\mathbf{r}}_1-{\mathbf{r}}_2$, their relative velocity, ${\dot{\mathbf{r}}}_2-{\dot{\mathbf{r}}}_1$, or any higher derivative of ${\mathbf{r}}_1-{\mathbf{r}}_2$. This Newtonian approximation of the problem will help model the motion of a binary system during the inspiral phase and before the merger.

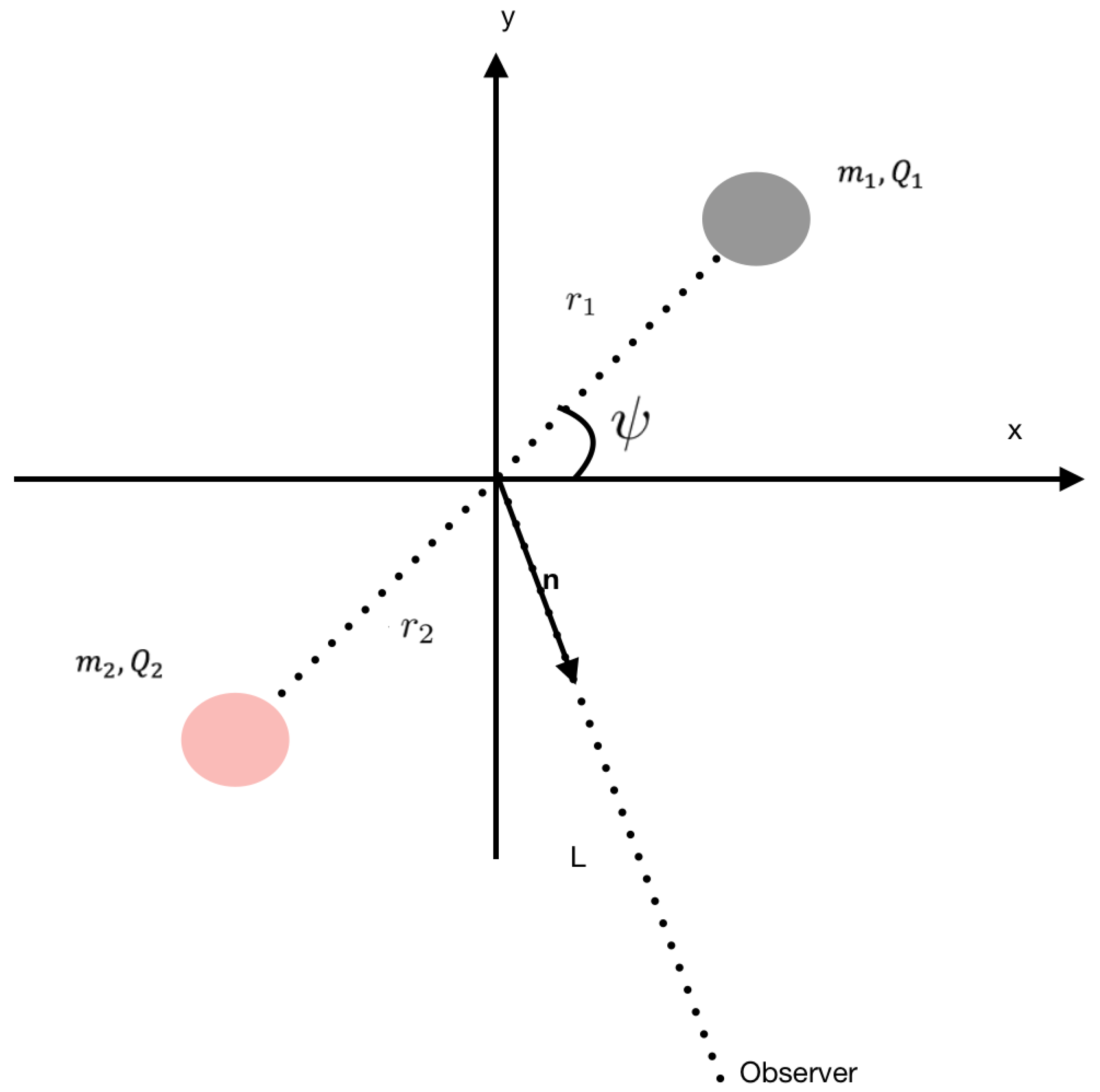
Let us start by defining the separation between the charged black holes as $\mathbf{R}={\mathbf{r}}_1-{\mathbf{r}}_2$. Therefore, each black hole has coordinates [26,45]

$$\begin{array}{ccc}{\mathbf{r}}_1=r_1(cos\psi ,sin\psi ),& \mathrm{and}& {\mathbf{r}}_2=-r_2(cos\psi ,sin\psi ).\end{array}$$

(1)

See the scheme in Figure 1, where $|{\mathbf{r}}_{\mathbf{1}}|=r_1$ and $|{\mathbf{r}}_{\mathbf{2}}|=r_2$ are measured with respect to the origin of coordinates. The separation between the black holes is $R=\left|\mathbf{R}\right|$, and the center of mass of the system is defined by

$${\mathbf{r}}_{CM}=\sum _{i=1}^2\frac{{\mathbf{r}}_i{m}_i}{M},$$

(2)

with $M=m_1+m_2$ being the total mass of the binary system. Hence, from Equation (2), we obtain that

$${\mathbf{r}}_{CM}=\frac{(r_1{m}_1-r_2{m}_2)}{M}\left(cos\psi ,sin\psi \right).$$

(3)

Since we choose the origin of coordinates at the point (0, 0), it is clear that

$$\begin{array}{cc}\hfill 0& =r_1{m}_1-r_2{m}_2\hfill \\ \hfill R& =r_1+r_2.\hfill \end{array}$$

(4)

Therefore,

$$\begin{array}{ccc}{r}_1=\frac{m_2}{M}R& \mathrm{and}& r_2=\frac{m_1}{M}R.\end{array}$$

(5)

From the last expressions, we can conclude that $r_1=r_2$ if $m_1=m_2$. The Lagrangian of the system is given by

$$\mathcal{L}=\mathcal{T}-\mathcal{U},$$

(6)

where $\mathcal{T}$ and $\mathcal{U}$ denote kinetic and potential energies, respectively. Moreover, $\mathcal{U}$ has two contributions: the gravitational and electric potentials. Therefore, we have

$$\mathcal{U}=-\frac{G{m}_1{m}_2}{R}+\frac{k_e{Q}_1{Q}_2}{R}.$$

(7)

On the other hand, from Figure 1, the kinetic energy is given by

$$\mathcal{T}=\frac{1}{2}{m}_1{\dot{r}}_1^2+\frac{1}{2}{m}_2{\dot{r}}_2^2.$$

(8)

Hence, with the help of Equations (5) and (8), it reduces to

$$\mathcal{T}=\frac{1}{2}\mu {\dot{R}}^2.$$

(9)

Here, $\mu$ is known as the reduced mass, defined by the expression

$$\mu =\frac{m_1{m}_2}{M}.$$

(10)

From the physical point of view, Equation (9) allows us to interpret the problem as the motion of a single particle with reduced mass $\mu$ and radial separation R. Hence, after using polar coordinates $(r,\psi )$, the Lagrangian in Equation (6) takes the form

$$\mathcal{L}=\frac{1}{2}\mu ({\dot{R}}^2+R^2{\dot{\psi }}^2)-\mathcal{U}\left(R\right).$$

(11)

Since the Lagrangian only depends on the radial separation, R, the system has spherical symmetry. Therefore, the solution is invariant under rotations about any fixed axis. This particular fact simplifies the problem considerably because the system’s angular momentum is a constant of motion. Furthermore, R is always perpendicular to the fixed direction of the angular momentum L, implying that central force motion always takes place on a plane perpendicular to the polar axis. In this sense, by orienting the polar axis in the direction of the angular momentum, we can limit the discussion to the equatorial plane $\theta =\pi /2$. We can understand this conclusion by considering the canonical momentum $P_{\psi }$, given by the following relation:

$$P_{\psi }=\frac{\partial \mathcal{L}}{\partial \dot{\psi }}=\mu R^2\dot{\psi }.$$

(12)

Then, after using the Euler–Lagrange equation, given by

$$\frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial {\dot{x}}^i}\right)-\frac{d\mathcal{L}}{d{x}^i}=0,$$

Where $x^i=\psi$ or R, we obtain that

$${\dot{P}}_{\psi }=\frac{d}{dt}\left(\mu R^2\dot{\psi }\right)=0.$$

(13)

According to Equation (13), the canonical momentum is a constant of motion: the well-known angular momentum of the system. Hence,

$$P_{\psi }=L=\mu R^2\dot{\psi }.$$

(14)

Note that the Kepler’s second law can be obtained from Equation (13) by considering the areal velocity [42]

$$\frac{dA}{dt}=\frac{1}{2}{R}^2\dot{\psi },$$

(15)

from which

$$\frac{d}{dt}\left(\frac{dA}{dt}\right)=\frac{d}{dt}\left(\frac{1}{2}{R}^2\dot{\psi }\right)=0.$$

(16)

Therefore, the conservation of angular momentum is equivalent to the constancy of the areal velocity. In other words: “The radius vector sweeps out equal areas in equal times” [42].

On the other hand, after considering the Euler–Lagrange equation for the radial separation and taking into account the conservation of the angular momentum, we can obtain the differential equation

$$\mu \ddot{R}+\frac{d}{dR}\left(\mathcal{U}+\frac{1}{2}\frac{L^2}{\mu R^2}\right)=0,$$

(17)

which reduces to

$$\frac{d}{dt}\left(\frac{1}{2}\mu {\dot{R}}^2+\frac{1}{2}\frac{L^2}{\mu R^2}+\mathcal{U}\right)=0$$

(18)

after multiplying Equation (17) by R. Expressed in that way, we can easily see that the quantity inside the brackets is a constant of motion: the energy of the system

$$E=\frac{1}{2}\mu {\dot{R}}^2+\frac{1}{2}\frac{L^2}{\mu R^2}+\mathcal{U}.$$

(19)

Now, if the forces are derivable from a potential, the kinetic energy and the potential energy are related by the following relation (Equation (20) is a consequence of the virial theorem when one applies it to the particular case of central force motion):

$$\mathcal{T}=-\frac{1}{2}\mathcal{U}.$$

(20)

The last equation is valid when the forces follow the inverse square law, such as the gravitational and electric forces. Therefore, we can express the total energy as

$$E=\mathcal{T}+\mathcal{U}=\frac{1}{2}\mathcal{U}=-\frac{G{m}_1{m}_2}{2R}+k_e\frac{Q_1{Q}_2}{2R},$$

(21)

where G is the Newton’s constant and $k_e$ the electric constant (in CGS units $k_e=1$). Since the total energy is constant for any value of R, it has the same value at the semi-major axis, a, of the Keplerian orbit, i.e., when $R=a$. In this sense, the total energy (the energy of the Keplerian orbit) reduces to [26]

$$E_{\mathrm{Orbit}}=-\frac{G{m}_1{m}_2}{2a}+k_e\frac{Q_1{Q}_2}{2a}=-\frac{G{m}_1{m}_2}{2a}(1-\lambda ),$$

(22)

where

$$\lambda =k_e\frac{Q_1{Q}_2}{G{m}_1{m}_2}=\frac{k_e{\lambda }_1{\lambda }_2}{G}.$$

(23)

with

$$\begin{array}{cc}{\lambda }_i=\frac{Q_i}{m_i},& i=1,2.\end{array}$$

(24)

Since the point masses conform a bound system, we have that $\lambda <1$ [26].

The system’s trajectory can be obtained by solving both the radial separation R and the angular velocity $\psi$ in terms of $\psi$; i.e., R($\psi$) and $\dot{\psi }$($\psi$), respectively. Hence, it is necessary to establish a relationship between d/dt and $d/d\psi$. Consider the function $f\left(\psi \right(t\left)\right)$ as an example. Its first derivative takes the form

$$\frac{df}{dt}=\frac{df}{d\psi }\dot{\psi }.$$

(25)

Then, from the conservation of the angular momentum in Equation (14), we obtain the following relation:

$$\frac{d}{dt}=\frac{L}{\mu R^2}\frac{d}{d\psi }.$$

(26)

In a similar way, the second derivative reduces to

$$\frac{d^2}{d{t}^2}=\frac{L}{\mu R^2}\frac{d}{d\psi }\left(\frac{L}{\mu R^2}\frac{d}{d\psi }\right),$$

(27)

and Equation (17) takes the form

$$\frac{L}{R^2}\frac{d}{d\psi }\left(\frac{L}{\mu R^2}\frac{dR}{d\psi }\right)-\frac{L^2}{\mu R^3}=-\frac{\partial \mathcal{U}}{\partial R}.$$

(28)

Now, after changing the variable to $u=1/R$, we obtain the following equation [42]

$$\frac{d^{2}u}{d{\psi }^2}+u=\frac{\mu \kappa }{L^2},$$

(29)

where we defined $\kappa \equiv G{m}_1{m}_2(1-\lambda )$. Finally, by changing the variable $y=u-\mu \kappa /L^2$, Equation (29) takes the form [42]

$$\frac{d^{2}y}{d{\psi }^2}+y=0.$$

(30)

The solution of Equation (30) has the form $y=Ccos(\psi -{\psi }_0)$, with C and ${\psi }_0\equiv \psi \left(0\right)$ constants of integration. Therefore, after returning to the original variable R, we obtain the following expression [42]

$$R=\frac{L^2}{\mu \kappa [1+ϵcos(\psi -{\psi }_0)]},$$

(31)

where the eccentricity $ϵ$ is defined by (see Appendix B)

$$ϵ=\frac{C{L}^2}{\mu \kappa }=\sqrt{1+\frac{2E{L}^2}{\mu {\kappa }^2}}.$$

(32)

Note that the factor $L^2/\left(\mu \kappa \right)$ in Equation (31) can be expressed in terms of the eccentricity using Equations (32) and (22). We obtain [42]

$$\frac{L^2}{\mu \kappa }=-\frac{\kappa (1-{ϵ}^2)}{2E}=a(1-{ϵ}^2).$$

(33)

As a consequence, the radial separation R can be expressed in terms of the orbital parameters a, $ϵ$, and $\psi$. Hence, Equation (31) reduces to

$$R=\frac{a(1-{ϵ}^2)}{[1+ϵcos(\psi -{\psi }_0)]}.$$

(34)

Finally, using Equation (32), we have that

$$\frac{L}{\mu }=\sqrt{G(m_1+m_2)a(1-{ϵ}^2)(1-\lambda )},$$

(35)

From which Equation (14) takes the form

$$\dot{\psi }=\frac{\sqrt{G(m_1+m_2)a(1-{ϵ}^2)(1-\lambda )}}{R^2}.$$

(36)

Equations (34) and (36) give the values of R and $\dot{\psi }$ for particles in a Keplerian orbit. Moreover, depending on the eccentricity, one could obtain different trajectories. For example, the orbit would be a circle if $ϵ=0$, an ellipse if $0<ϵ<1$, a parabola if $ϵ=1$, and a hyperbola if $ϵ>1$. In this work, we want to investigate the EM radiation of binary systems formed by charged black holes during the inspiral phase. Therefore, we focus on cases where the trajectory is a circular orbit ($ϵ=0$).

3. Gravitational and Electromagnetic Radiation

In this section, we focus on gravitational and electromagnetic radiation. The mathematical expressions were obtained for the non-charge and charge binary systems in Refs. [26,45], respectively. Nevertheless, intending to have a clear discussion and a self-contained manuscript, we review and analyze the most crucial aspects.

3.1. Gravitational Radiation

We start by first considering gravitational radiation. According to Ref. [45], the total radiation (over all directions of emission) is given by the formula:

$$P_{GW}=\frac{G}{5c^5}\left({\stackrel{⃛}{M}}_{ij}{\stackrel{⃛}{M}}_{ij}-\frac{1}{3}{\stackrel{⃛}{M}}_{ii}{\stackrel{⃛}{M}}_{jj}\right).$$

(37)

Here the dot denotes the time derivative, and $M_{ij}$ is the mass moment. In the reference frame of an orbit laying on the $(x,y)$ plane (the equatorial plane), $M_{ij}$ takes the form [44]

$$M_{ij}=\mu R^2\left(\begin{array}{cc}{cos}^2\psi & sin\psi cos\psi \\ sin\psi cos\psi & {sin}^2\psi \end{array}\right),$$

(38)

where $\mu$ and R are the reduced mass and the radial separation between the charged black holes, respectively. Therefore, after using Equation (34), we obtain (from now on, we set ${\psi }_0=0$).

$$\begin{array}{cc}\hfill M_{11}& =\frac{\mu a^2{(1-{ϵ}^2)}^2}{{[1+ϵcos\psi ]}^2}{cos}^2\psi ,\hfill \\ \hfill M_{12}& =M_{21}=\frac{\mu a^2{(1-{ϵ}^2)}^2}{{[1+ϵcos\psi ]}^2}sin\psi cos\psi ,\hfill \\ \hfill M_{22}& =\frac{\mu a^2{(1-{ϵ}^2)}^2}{{[1+ϵcos\psi ]}^2}{sin}^2\psi .\hfill \end{array}$$

(39)

According to Equation (37), to obtain the total radiation $P_{GW}$, it is necessary to compute the third derivative of $M_{ij}$. Nevertheless, since the components $M_{ij}$ depend on $\psi$, the easiest way to compute their derivatives is using Equation (36), which can be expressed as

$$\dot{\psi }={\omega }_s=\sqrt{\frac{G(m_1+m_2)(1-\lambda )}{a^3}}{(1-{ϵ}^2)}^{-\frac{3}{2}}{(1+ϵcos\psi )}^2.$$

(40)

Therefore, after using the chain rule, ${\dot{M}}_{ij}$ in terms of $\dot{\psi }$ is given by the expression

$${\dot{M}}_{ij}=\frac{d{M}_{ij}}{d\psi }\dot{\psi }.$$

(41)

The same idea can be extended to the second and third derivatives. We then obtain

$$\begin{array}{cc}\hfill {\stackrel{⃛}{M}}_{11}& =\beta {(1+ϵcos\psi )}^2[2sin2\psi +3ϵsin\psi {cos}^2\psi ],\hfill \\ \hfill {\stackrel{⃛}{M}}_{22}& =\beta {(1+ϵcos\psi )}^2[-2sin2\psi -ϵsin\psi (1+3{cos}^2\psi )],\hfill \\ \hfill {\stackrel{⃛}{M}}_{12}& =\beta {(1+ϵcos\psi )}^2[-2cos2\psi +ϵcos\psi (1-3{cos}^2\psi )],\hfill \end{array}$$

(42)

where we define

$$\beta =\frac{2\mu {\left[G(m_1+m_2)(1-\lambda )\right]}^{\frac{3}{2}}}{{\left[a(1-{ϵ}^2)\right]}^{\frac{5}{2}}}.$$

(43)

Note that Equation (42) reduces to Equations (4.68)–(4.70) reported in Ref. [44] when $\lambda =0$, i.e., when $Q_1=Q_2=0$. Now, from Equation (37), the total gravitational radiation is

$$P_{GW}=\frac{G}{5c^5}\left[{\stackrel{⃛}{M}}_{11}^2+{\stackrel{⃛}{M}}_{22}^2+2{\stackrel{⃛}{M}}_{12}^2-\frac{1}{3}{({\stackrel{⃛}{M}}_{11}+{\stackrel{⃛}{M}}_{22})}^2\right].$$

(44)

Hence, after using Equation (42), one obtains [26]

$$\begin{array}{cc}\hfill P_{GW}& =\frac{8G^4{(m_1+m_2)}^3{(1-\lambda )}^3{\mu }^2}{15a^5{c}^5{(1-{ϵ}^2)}^5}{(1+ϵcos\psi )}^4\hfill \\ \hfill & [12{(1+ϵcos\psi )}^2+{ϵ}^2{sin}^2\psi ],\hfill \end{array}$$

(45)

which reduces to that of Refs. [44,45] when $\lambda =0$.

Usually, the energy of GWs is well defined by considering a temporal average over several periods of a wave [44]. This can be done by computing the time average integral

$${\overline{P}}_{GW}=\frac{1}{T}{\int }_0^{2\pi }\frac{P_{GW}\left(\psi \right)}{\dot{\psi }}d\psi .$$

(46)

After using Equations (36) and (45), the last expression reduces to

$$\begin{array}{cc}\hfill {\overline{P}}_{GW}& =\frac{8G^4{(m_1+m_2)}^3{(1-\lambda )}^3{\mu }^2}{15a^5{c}^5}{(1-{ϵ}^2)}^{-\frac{7}{2}}\hfill \\ \hfill & {\int }_0^{2\pi }\frac{1}{2\pi }[12{(1+ϵcos\psi )}^4+{ϵ}^2{sin}^2\psi {(1+ϵcos\psi )}^2]d\psi ,\hfill \end{array}$$

(47)

where we had into account that [26]

$$T=2\pi \sqrt{\frac{a^3}{G(m_1+m_2)(1-\lambda )}}.$$

(48)

After integration, we obtain

$${\overline{P}}_{GW}=\frac{32G^4{(m_1+m_2)}^3{(1-\lambda )}^3{\mu }^2}{5a^5{c}^5{(1-{ϵ}^2)}^{\frac{7}{2}}}\left(1+\frac{73}{24}{ϵ}^2+\frac{37}{96}{ϵ}^4\right),$$

(49)

Which reduces to the expression obtained by P.C. Peters and J. Mathews in Ref. [45] when $\lambda =0$. Finally, the average energy loss due to gravitational radiation over an orbital period T is given by

$$\overline{\frac{d{E}_{GW}}{dt}}=-{\overline{P}}_{GW}.$$

(50)

3.2. Electromagnetic Radiation

The rate of emission due to electromagnetic radiation is given by [43]

$$\frac{d{E}_{EM}}{dt}=-\frac{2{\ddot{p}}^2}{3c^3}$$

(51)

where $p=\left|\mathbf{p}\right|$ is the electric dipole moment, which is defined by

$$\mathbf{p}=\sum _{i=1}^2{Q}_i{\mathbf{r}}_i.$$

(52)

In our case, the electric dipole moment of a binary system formed by charged black holes is

$$\mathbf{p}=Q_1{\mathbf{r}}_1+Q_2{\mathbf{r}}_2.$$

(53)

Now, from Equations (1) and (5), the electric dipole moment reduces to

$$\mathbf{p}=\frac{Q_1{m}_2-Q_2{m}_1}{m_1+m_2}R(cos\psi ,sin\psi ),$$

(54)

From which, after taking into account Equations (34) and (40), we obtain

$$\ddot{\mathbf{p}}=-\frac{G(Q_1{m}_2-Q_2{m}_1)(1-\lambda )}{a^2{(1-{ϵ}^2)}^2}{(1+ϵcos\psi )}^2(cos\psi ,sin\psi ).$$

(55)

Hence, ${\ddot{p}}^2$ is given by

$${\ddot{p}}^2=\ddot{\mathbf{p}}·\ddot{\mathbf{p}}=\frac{G^2{(Q_1{m}_2-Q_2{m}_1)}^2{(1-\lambda )}^2{(1+ϵcos\psi )}^4}{a^4{(1-{ϵ}^2)}^4},$$

(56)

and

$$\frac{d{E}_{EM}}{dt}=-\frac{2G^2{(Q_1{m}_2-Q_2{m}_1)}^2{(1-\lambda )}^2{(1+ϵcos\psi )}^4}{3c^3{a}^4{(1-{ϵ}^2)}^4}$$

(57)

Since we are interested in the average energy loss over an orbital period T, it is necessary to compute the integral

$$\overline{\frac{d{E}_{EM}}{dt}}=\frac{1}{T}{\int }_0^{2\pi }\frac{d{E}_{EM}}{dt}{\dot{\psi }}^{-1}d\psi .$$

(58)

With the help of Equations (40) and (48), the last integral reduces to

$$\begin{array}{c}\hfill -{\int }_0^{2\pi }\frac{G^2{(Q_1{m}_2-Q_2{m}_1)}^2{(1-\lambda )}^2{(1+ϵcos\psi )}^2}{3\pi c^3{a}^4{(1-{ϵ}^2)}^{\frac{5}{2}}}d\psi ,\end{array}$$

(59)

From which [26]

$$\overline{\frac{d{E}_{EM}}{dt}}=-\frac{G^2{(Q_1{m}_2-Q_2{m}_1)}^2(2+{ϵ}^2){(1-\lambda )}^2}{3c^3{a}^4{(1-{ϵ}^2)}^{\frac{5}{2}}}.$$

(60)

4. Evolution of the Orbital Parameters

From the physical point of view, a binary system in Keplerian motion radiates energy and angular momentum. On the other hand, under the approximation of point-like bodies without an intrinsic spin, those quantities are drained from the orbital motion. In this sense, the orbit experiences changes in its semi-major axis and eccentricity until the system reaches the merging phase and collapses. As shown in Ref. [26], the emission of angular momentum has two contributions. The first one is due to the gravitational interaction of the masses. The second one comes as a consequence of the electric interaction of the charges. Once again, intending to have a clear discussion and a self-contained manuscript, in this section, we review Refs. [26,44] to compute the evolution of the Keplerian orbit as the binary system realizes energy and angular momentum.

In the quadrupole approximation, the angular momentum radiated by an orbit on the equatorial plane (see Figure 1) is given by [26,44]

$$\overline{\frac{d{L}_{GW}}{dt}}=\frac{4G}{5c^5}\frac{1}{T}{\int }_0^{2\pi }\frac{{\ddot{M}}_{12}({\stackrel{⃛}{M}}_{11}-{\stackrel{⃛}{M}}_{22})}{\dot{\psi }}d\psi .$$

(61)

Hence, from Equation (39) and the chain rule, one obtains

$$\begin{array}{cc}\hfill {\ddot{M}}_{12}& =\dot{\psi }\frac{d}{d\psi }\left(\dot{\psi }\frac{d{M}_{12}}{d\psi }\right)=-\frac{G(m_1+m_2)(1-\lambda )\mu }{a(1-{ϵ}^2)}\hfill \\ \hfill & \times sin\psi \left[4cos\psi +ϵ(3+cos2\psi )\right].\hfill \end{array}$$

(62)

After integration, the radiation of angular momentum (the average over one period) due to the gravitational interaction is therefore [26]

$$\overline{\frac{d{L}_{GW}}{dt}}=-\frac{32}{5}\frac{G^{\frac{7}{2}}{\mu }^2{(m_1+m_2)}^{\frac{5}{2}}{(1-\lambda )}^{\frac{5}{2}}}{c^5{a}^{\frac{7}{2}}{(1-{ϵ}^2)}^2}\left(1+\frac{7}{8}{ϵ}^2\right).$$

(63)

Now, let us consider the emission of angular momentum due to the electromagnetic interaction. In Refs. [26,43], it was shown that the rate of angular momentum carried by the electromagnetic waves is given by

$$\frac{d{J}_{EM}}{dt}=-\frac{2}{3c^3}{ϵ}^{ikl}{\dot{p}}_k{\ddot{p}}_l.$$

(64)

Hence, the last expression takes the form

$$\frac{d{J}_{EM}}{dt}=-\frac{2}{3c^3}({\dot{p}}_y{\ddot{p}}_x-{\dot{p}}_x{\ddot{p}}_y).$$

(65)

The first derivative of $\mathbf{p}$ can be computed with the help of Equation (40). One obtains

$$\dot{\mathbf{p}}=\frac{G^{\frac{1}{2}}(m_2{Q}_1-m_1{Q}_2){(1-\lambda )}^{\frac{1}{2}}}{{(m_1+m_2)}^{\frac{1}{2}}{a}^{\frac{1}{2}}{(1-{ϵ}^2)}^{\frac{1}{2}}}(-sin\psi ,(ϵ+cos\psi )).$$

(66)

Therefore, Equation (65) takes the form

$$\frac{d{J}_{EM}}{dt}=\frac{G^{\frac{3}{2}}{(m_2{Q}_1-m_1{Q}_2)}^2{(1-\lambda )}^{\frac{3}{2}}{(1+ϵcos\psi )}^3}{6\pi a^{\frac{5}{2}}{(m_1+m_2)}^{\frac{1}{2}}{(1-{ϵ}^2)}^{\frac{5}{2}}}.$$

(67)

The average emission of angular momentum in one period is given by

$$\overline{\frac{d{L}_{EM}}{dt}}=\frac{1}{T}{\int }_0^{2\pi }\frac{d{J}_{EM}}{dt}{\dot{\psi }}^{-1}d\psi .$$

(68)

From which,

$$\begin{array}{cc}\hfill \overline{\frac{d{L}_{EM}}{dt}}& =\frac{2G^{\frac{3}{2}}{(m_2{Q}_1-m_1{Q}_2)}^2{(1-\lambda )}^{\frac{3}{2}}}{3a^{\frac{5}{2}}{c}^2(1-{ϵ}^2){(m_1+m_2)}^{\frac{1}{2}}}.\hfill \end{array}$$

(69)

In Section 2, we showed that the total energy of the Keplerian orbit is given by Equation (22). Therefore, the semi-major axis can be expressed by

$$a=\frac{G\mu (m_1+m_2)(1-\lambda )}{2|E_{\mathrm{Orbit}}|}.$$

(70)

After computing the derivative with respect to time t, one obtains

$$\frac{da}{dt}=-\frac{G\mu (m_1+m_2)(1-\lambda )}{2}\frac{E_{\mathrm{Orbit}}}{|E_{\mathrm{Orbit}}{|}^3}\frac{d{E}_{\mathrm{Orbit}}}{dt}.$$

(71)

According to Refs. [44,45], in the case of a binary system formed by two non-charged black holes, the emission of GWs costs energy. Therefore, the variation in $E_{\mathrm{Orbit}}$ must be equal to the power radiated by GWs. In the case of two charged black holes, on the other hand, the variation in the total energy ($E_{\mathrm{Orbit}}$) has two contributions: the power radiated by both the gravitational wave, $\overline{d{E}_{GW}/dt}$, and the electromagnetic wave, $\overline{d{E}_{EM}/dt}$. Hence, we have the following relationship:

$$\frac{d{E}_{\mathrm{Orbit}}}{dt}=\overline{\frac{d{E}_{GW}}{dt}}+\overline{\frac{d{E}_{EM}}{dt}}.$$

(72)

After replacing into Equation (71), we obtain the following expression [26]

$$\begin{array}{cc}\hfill \frac{da}{dt}& =-\frac{2G^3{(m_1+m_2)}^2{(1-\lambda )}^2\mu }{15a^3{c}^5{(1-{ϵ}^2)}^{\frac{7}{2}}}(96+292{ϵ}^2+37{ϵ}^4)\hfill \\ \hfill & -\frac{2({ϵ}^2+2)G(m_1+m_2)(1-\lambda ){({\lambda }_1-{\lambda }_2)}^2\mu }{3c^3{a}^2{(1-ϵ)}^{\frac{5}{2}}}.\hfill \end{array}$$

(73)

On the other hand, from Equation (35), we have that

$$\frac{d{L}_{\mathrm{Orbit}}}{dt}=\mu \sqrt{G(m_1+m_2)(1-\lambda )}\left[(1-{ϵ}^2)\frac{da}{dt}-2aϵ\frac{dϵ}{dt}\right].$$

(74)

Then, after solving for $dϵ/dt$, we obtain

$$\frac{dϵ}{dt}=\frac{(1-{ϵ}^2)}{2aϵ}\frac{da}{dt}-\frac{\sqrt{a(1-{ϵ}^2)}}{aϵ\mu \sqrt{G(m_1+m_2)(1-\lambda )}}\frac{d{L}_{\mathrm{Orbit}}}{dt}.$$

(75)

Using Equation (74) and taking into account that

$$\frac{d{L}_{\mathrm{Orbit}}}{dt}=\overline{\frac{d{L}_{GW}}{dt}}+\overline{\frac{d{L}_{\mathrm{EM}}}{dt}},$$

(76)

Equation (75) reduces to [26]

$$\begin{array}{cc}\hfill \frac{dϵ}{dt}& =-\frac{ϵ(121{ϵ}^2+304)G^3{(1-\lambda )}^2{m}_1{m}_2(m1+m2)}{15a^2{c}^5{(1-{ϵ}^2)}^{\frac{5}{2}}}\hfill \\ \hfill & -\frac{ϵG(1-\lambda )(m_2{Q}_1-m_1{Q}_2)}{4\pi a^3{(1-{ϵ}^2)}^{\frac{3}{2}}{m}_1{m}_2}.\hfill \end{array}$$

(77)

The system of differential Equations (73) and (77) describes the evolution due to gravitational and electrical interactions in the binary system. Note that the system is coupled. Therefore, any variation on the eccentricity $ϵ$ has a repercussion on the evolution of the semi-major axis a. In the next section, we discuss the particular case of circular orbits.

5. Quasi-Circular Approximation

It is known that a binary system circularizes its orbit after some time. In this sense, during the inspiral phase, the system loses energy in such a way that the motion of the binary system remains circular. That can be seen from Equation (77). When the orbit reaches the value $ϵ=0$ (circular orbit), the binary system will continue moving in a circular orbit because $\dot{ϵ}=0$. Therefore, if the initial conditions of the binary system are those of a circular orbit, the system will continue its circular motion with a variation of dR/dt given by (when $ϵ=0$, the semi-major axis a and the separation R are the same. See Equation (34)).

$$\begin{array}{cc}\hfill \frac{dR}{dt}& =-\frac{64G^3{(m_1+m_2)}^2{(1-\lambda )}^2\mu }{5R^3{c}^5}\hfill \\ \hfill & -\frac{4G(m_1+m_2)(1-\lambda ){({\lambda }_1-{\lambda }_2)}^2\mu }{3c^3{R}^2}.\hfill \end{array}$$

(78)

From the last equation, we can identify several situations. First, if ${\lambda }_1={\lambda }_2=0$, Equation (78) reduces to that obtained by M. Maggiore in Ref. [44]. Second, if the two black holes have the same charge-to-mass ratio, ${\lambda }_1={\lambda }_2$, the second term in the right-hand side of Equation (78) vanishes. Therefore, the electric dipole vanishes, and it is necessary to consider the next order, whose term decomposes into the charge quadrupole and current dipole that generate electric quadrupolar and magnetic dipolar radiation, respectively, as the leading order contributions. Finally, if the charge-to-mass-ratio difference is small, both the GW quadrupole and the EM dipole emissions can be important [29]. In this manuscript, we focus on the dipole order of EM waves.

Before continuing our discussion, it is worth expressing Equation (78) in dimensionless quantities. To do so, we follow Ref. [44] and define the dimensionless variables by the relations:

$$\begin{array}{ccc}R\to \frac{R}{R_{*}}& \mathrm{and}& t\to \frac{ct}{R_{*}},\end{array}$$

(79)

with

$$R_{*}^3={\left(\frac{2GM}{c^2}\right)}^2\left(\frac{G\mu }{c^2}\right).$$

(80)

Thus, Equation (78) takes the form

$$\frac{dR}{dt}=-\frac{\alpha }{R^3}-\frac{\beta }{R^2},$$

(81)

With $\alpha$ and $\beta$ dimensionless constants, see Appendix A.

The solution of Equation (81) can be expressed as

$$\alpha t={\int }_R^{R_0}\frac{R^{\prime 3}d{R}^{\prime }}{1+\gamma R^{\prime }},$$

(82)

where

$$\gamma =\frac{\beta }{\alpha }=\frac{5}{48}\frac{{({\lambda }_1-{\lambda }_2)}^2}{(1-\lambda )}{\left(\frac{4\mu }{M}\right)}^{1/3}.$$

(83)

Hence, after integration, the solution can be represented as $\alpha t=f\left(R_0\right)-f\left(R\right)$, where the function $f\left(R\right)$ is defined by [29]

$$f\left(R\right)=-\frac{log(1+\gamma R)}{{\gamma }^4}+\frac{R}{{\gamma }^3}-\frac{R^2}{2{\gamma }^2}+\frac{R^3}{3\gamma }.$$

(84)

One can use the function $f\left(R\right)$ to define the time to coalescence as $\tau \left(R\right)=f\left(R\right)/\alpha$, from which

$$t={\tau }_0-\tau \left(R\right).$$

(85)

Note that $R=R_0$ when $t=0$. Therefore, ${\tau }_0$ corresponds to the time at the coalescence $t_{\mathrm{coal}}$ and Equation (85) reduces to the well-known definition $\tau =t_{\mathrm{coal}}-t$ [44].

On the other hand, the form of $f\left(R\right)$ makes it difficult to investigate the dynamics of the binary system analytically due to the term with the log function. Nevertheless, by considering a small charge-to-mass ratio, it is possible to obtain a simple expression for $f\left(R\right)$ when $\gamma R<<1$ [29]. In this sense, after expanding the $log(1+\gamma R)$ up to the sixth order, the time to the coalescence $\tau$ takes the following form:

$$\tau \left(R\right)\approx \frac{R^4}{4\alpha }\left(1-\frac{4\gamma R}{5}\right).$$

(86)

Note that Equation (86) reduces to Equation (4.26) of Ref. [44] when $\gamma =0$. Using this approximation and defining $u=\tau /{\tau }_0$, it is possible to obtain the following expressions for R, $R_0$, ${\omega }_s$, ${\omega }_0$, and $\Phi$ (See Appendix C for details)

$$\begin{array}{cc}\hfill \frac{R}{R_0}& =u^{1/4}\left[1-\frac{\gamma R_0}{5}\left(1-u^{1/4}\right)\right],\hfill \\ \hfill \frac{{\omega }_s}{{\omega }_0}& =u^{-3/8}\left[1+\frac{3}{10}\delta {\omega }_0^{-2/3}(1-u^{1/4})\right],\hfill \\ \hfill \Phi & =\frac{16{\tau }_0}{5}{\left(\frac{8{\tau }_0}{3\sigma }\right)}^{-3/8}\left[1-u^{5/8}-\frac{3\delta }{14}{\left(\frac{8{\tau }_0}{3\sigma }\right)}^{1/4}(1-u^{7/8})\right].\hfill \end{array}$$

(87)

and

$$\begin{array}{cc}\hfill R_0& ={\left(4\alpha {\tau }_0\right)}^{1/4}\left[1+\frac{\gamma {\left(4\alpha {\tau }_0\right)}^{1/4}}{5}\right],\hfill \\ \hfill {\omega }_0& ={\left(\frac{3\sigma }{8{\tau }_0}\right)}^{3/8}\left[1-\frac{3}{10}\delta {\left(\frac{8{\tau }_0}{3\sigma }\right)}^{1/4}\right].\hfill \end{array}$$

(88)

Christiansen et al. obtained similar expressions in Ref. [29], where the charge is not the usual electric charge, but a dark sector charge.

From the Kepler law in Equation (40), one can obtain the following relation [44]

$$\dot{R}=-\frac{2}{3}R{\omega }_s\frac{{\dot{\omega }}_s}{{\omega }_s^2}.$$

(89)

Note that $|\dot{R}|$ is smaller than the tangential velocity ${\omega }_{s}R$ if ${\dot{\omega }}_s<<{\omega }_s^2$. Therefore, we can use circular orbits with a slowly varying radius to model the dynamics of the binary system, the well-known quasi-circular approximation. Nevertheless, in the case of the binary system formed by charged black holes, the quasi-circular approximation must include the condition $\gamma R<<1$ so that we can use Equations (87) and (88) to model the inspiral phase.

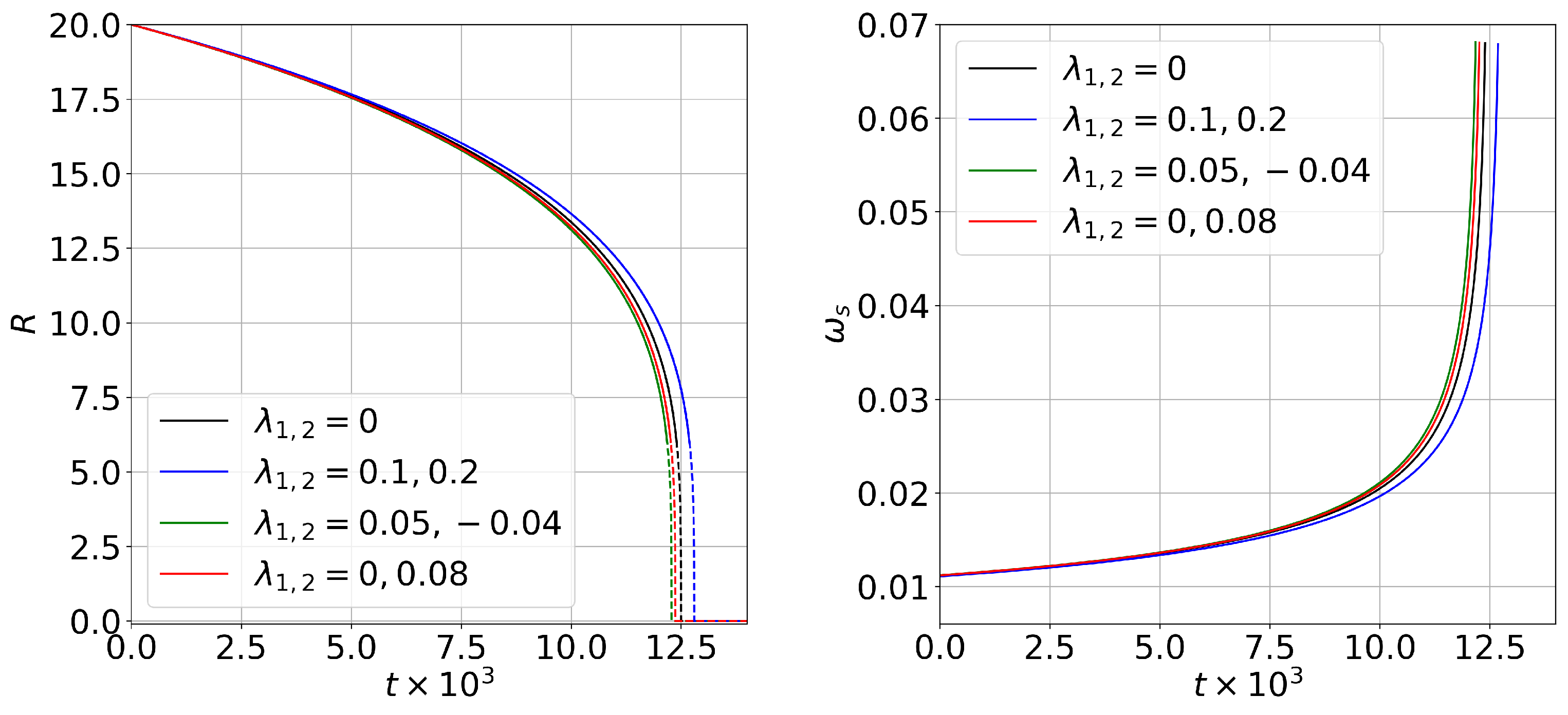
In Figure 2, we plot the analytical expressions for R, ${\omega }_s$, and $\Phi$ as a function of t for different values of ${\lambda }_1$ and ${\lambda }_2$. We also show the numerical solution of Equation (78). See the dashed lines in the left panel. On the other hand, since the quasi-circular approximation cannot describe the motion of the binary system when the radial separation is too small, the analytical solution for R (as well as ${\omega }_s$ and $\Phi$) is plotted until a certain value: see the continuous lines in the left panel of the figure. In this sense, and following Wang et al., we choose the innermost stable circular orbit (ISCO) as the moment of coalescence [32]. For example, when ${\lambda }_1={\lambda }_2=0$, $R_{ISCO}=6{(4\mu /M)}^{-1/3}$. Nevertheless, when ${\lambda }_1={\lambda }_2\ne 0$, it is not straightforward to exactly know the final values of $\lambda$ and M for the remnant black hole. Therefore, we use the following expression (in dimensionless units) to compute $R_{ISCO}$ [32] (see Appendix A).

$$R_{ISCO}=\frac{4{\lambda }_{*}^2}{3+\frac{1}{C}+C}{\left(\frac{4\mu }{M}\right)}^{-1/3},$$

(90)

where

$$C=-{\left(9-8{\lambda }_{*}^2-4\sqrt{4{\lambda }_{*}^4-9{\lambda }_{*}^2+5}\right)}^{1/3},$$

(91)

and

$${\lambda }_{*}=\min \left[\left|\frac{m_1{\lambda }_1+m_2{\lambda }_2}{M}\right|,\left|\frac{m_2{\lambda }_1+m_1{\lambda }_2}{M}\right|\right].$$

(92)

In

Table 1. The radial separation at the coalescence, $R_{ISCO}$, for different values of ${\lambda }_1$ and ${\lambda }_2$. We consider dimensionless units with $m_1=m_2=1/2$, $M=1$, and $\mu =1/4$.

${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_{*}$	${\mathit{R}}_{\mathit{ISCO}}$
0.0	0.0	—	6.0
0.05	−0.04	0.005	5.999
0.0	0.08	0.075	5.998
0.1	0.2	0.15	5.966

, we show some values for $R_{ISCO}$.

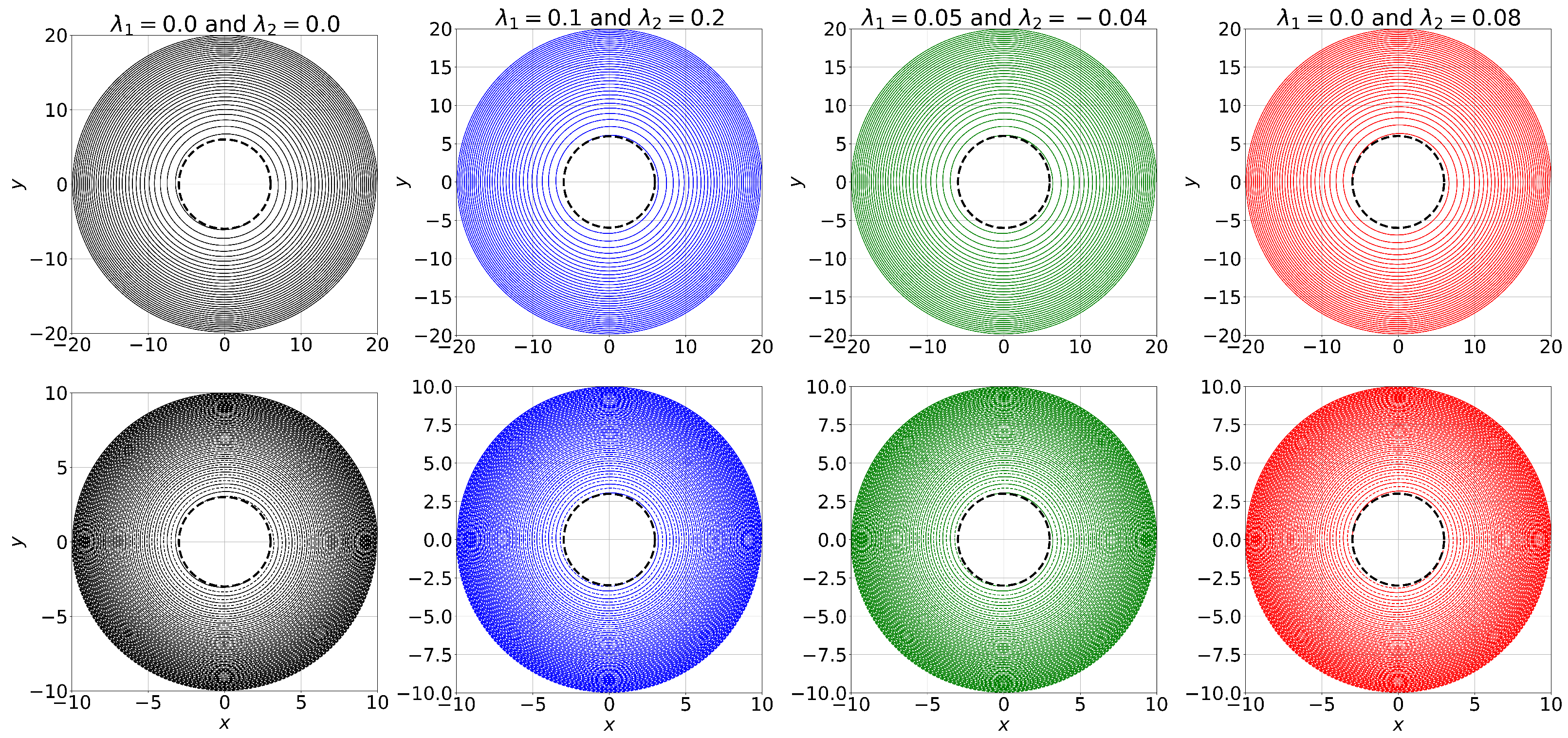
The left panel of Figure 2 shows how the radial separation between the charged black holes reduces in a way that resembles an inspiral: see Figure 3, where we plot the reduced mass and the black holes’ trajectories in the binary system, upper and lower panels, respectively. Note that, depending on the values of ${\lambda }_1$ and ${\lambda }_2$, the duration of the inspiral phase is longer or shorter. For example, when we consider a binary system formed by positively charged black holes (${\lambda }_1=0.1$ and ${\lambda }_2=0.2$), the inspiral phase is longer than the other three cases. See the continuous blue line in the left panel of Figure 2. In the case of two black holes with opposite signs (${\lambda }_1=0.05$ and ${\lambda }_2=-0.04$), the inspiral phase takes less time than in the cases in which the binary system is formed by non-charged black holes or by only one charged black hole (${\lambda }_1=0.0$ and ${\lambda }_2=0.08$). This is plotted with a continuous red line in the figure. Therefore, the presence of charge in the binary system does affect the coalescence time.

From the physical point of view, this behavior agrees with the phenomenological interaction between electric charges. As shown in Figure 1, we have considered each black hole in the binary system as a charged-point mass. In this sense, the electric and gravitational interactions become stronger as the black holes get closer. Nevertheless, the presence of an electric charge produces attraction or repulsion depending on its sign, in contrast to the gravitational interaction, which is always attractive. Hence, in the case of the binary system formed by black holes with opposite signs, the gravitational interaction will encounter an additional attraction that makes the separation R change faster than in the case of a binary system formed by charged black holes with the same sign, where the gravity “competes” against the repulsion of the electric charges.

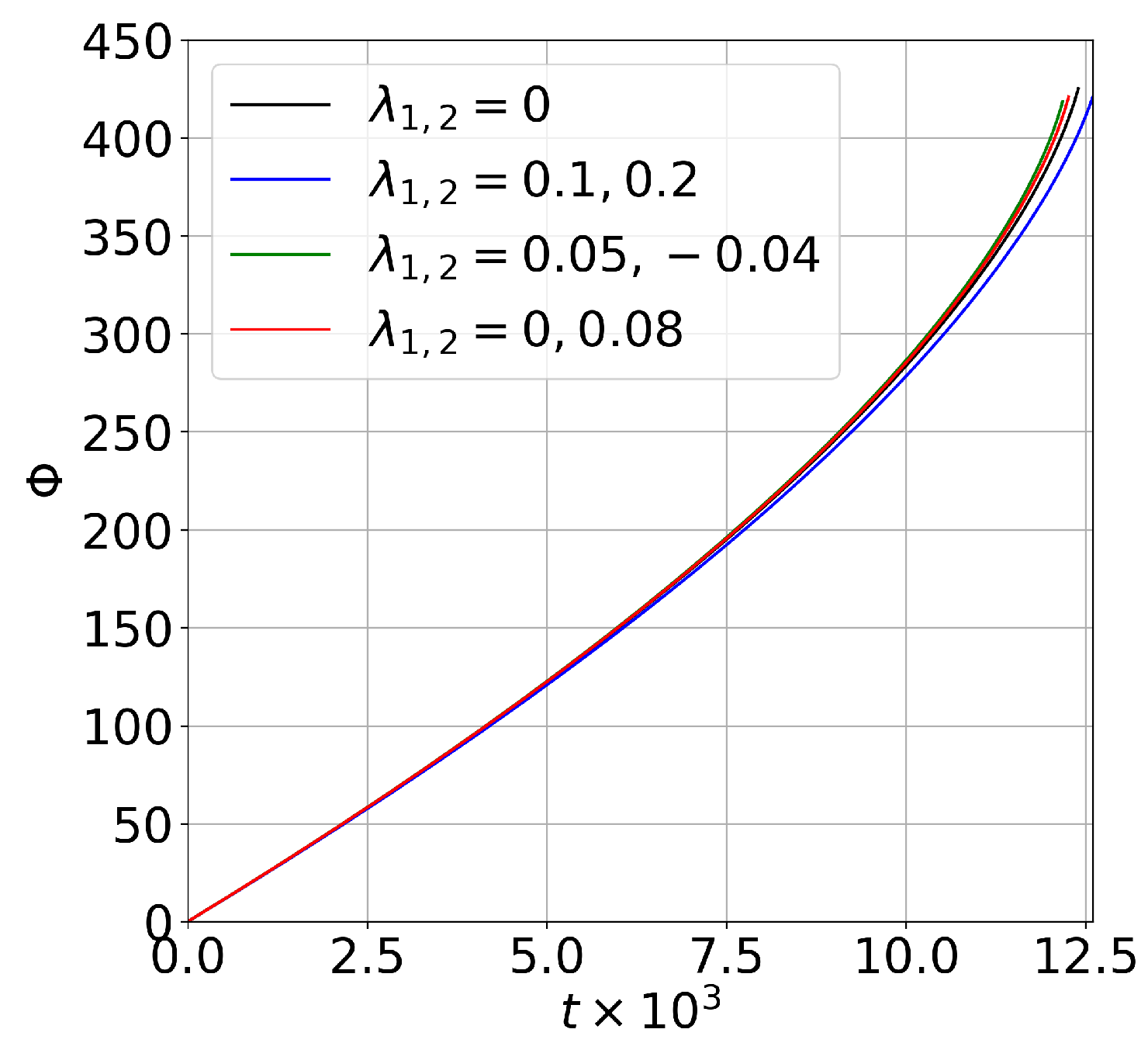
Finally, in the central and left panels of Figure 2, we show the behavior of ${\omega }_s$ and $\Phi$, respectively, as a function of time t. From the figures, it is possible to see how ${\omega }_s$ increases by time. This is in agreement with Kepler’s law $\gamma R=\delta {\omega }_s^{-2/3}$, where ${\omega }_s$ increases as the radial separation R decreases. Moreover, because the inspiral phase takes more time when ${\lambda }_1=0.1$ and ${\lambda }_2=0.2$, the value of ${\omega }_s$ is smaller than in the other cases; see the continuous blue line. On the other hand, when ${\lambda }_1=0.05$ and ${\lambda }_2=-0.04$, the inspiral phase is the shortest. Therefore, the values for ${\omega }_s$ are larger. See the continuous green line. Moreover, note that ${\omega }_s$ will diverge as $R\to 0$. This is in contrast to $\Phi$, which has a similar behavior, but reaches a finite value when $R\to 0$.

6. The Gravitational and Electromagnetic Waves

In this section, we will investigate the electromagnetic and gravitational radiation under the approximation $\gamma R<<1$. Therefore, we shall use the expressions obtained in Equation (86) along with the electrodynamics theory to compute an analytical expression for the electromagnetic field. In this way, and from a phenomenological point of view, we will be able to understand the electromagnetic counterpart of a binary system formed by charged black holes.

6.1. The Electromagnetic Wave

To compute the EM field generated by the binary system, an observer must reckon that the fields have a retarded value due to the motion of the charges. Hence, if the observer is located at a distance L far from the source (with $L>>R$), the potentials take the form [43]

$$\begin{array}{cc}\hfill \phi & =\frac{1}{L}\int {\rho }_{t-L/c}dV,\hfill \\ \hfill \mathbf{A}& =\frac{1}{cL}\int {\mathbf{J}}_{t-L/c}dV,\hfill \end{array}$$

(93)

also known as the Liénard–Wiechert potentials. In the last equation, $\rho$ and $\mathbf{J}$ are the charge and current densities evaluated at the retarded time $t_r=t-L/c$, respectively. Note that the potentials in Equation (93) reduce to the static case when $\rho$ and $\mathbf{J}$ do not depend on time.

At large distances, the EM field can be considered like a wave plane if one takes small regions of space. Therefore, it is possible to relate the electric and magnetic fields using the following relation [43]:

$$\mathbf{E}=\mathbf{B}\times \mathbf{n},$$

(94)

where $\mathbf{n}$ is a unit vector in the direction of L; see the scheme in Figure 4. From the last equation, one concludes that $\mathbf{E}$ and $\mathbf{B}$ are perpendicular to each other. Therefore, since $\mathbf{B}=\nabla \times \mathbf{A}$, one only needs to compute the vector potential $\mathbf{A}$ for a complete determination of the EM field in the wave zone, which is the name of the region where the wave plane approximation takes place. In this zone, the vector potential takes the form [43]

$$\mathbf{A}=\frac{\dot{\mathbf{p}}}{cL}+\frac{\ddot{\mathbf{D}}}{6c^{2}L}+\frac{\dot{\mathbf{\mu }}\times \mathbf{n}}{cL},$$

(95)

where $\mathbf{p}$ is the dipole moment of the system defined in Equation (52). $\mathbf{D}$ is the quadrupole moment of the system with components ($D_{\alpha \beta }$ are the components of the quadrupole moment tensor with null trace $D_{\alpha \alpha }=0$.) $D_{\alpha }=D_{\alpha \beta }{n}_{\beta }$ [43]

$$D_{\alpha \beta }=\sum _i{Q}_i(3x_{\alpha }{x}_{\beta }-{\delta }_{\alpha \beta }{r}_i^2),$$

(96)

and $\mathbf{\mu }$ is the magnetic moment, given by the relation [43]

$$\mathbf{\mu }=\frac{1}{2c}\sum _i{Q}_i{\mathbf{r}}_i\times \mathbf{n}.$$

(97)

In Equations (96) and (97), the sum goes over all charges, the dot $\dot{}$ denotes time derivative, and $x_{\alpha }$ are the components of $\mathbf{r}$ for each charge. Hence, after computing $\nabla \times \mathbf{A}$, we have that the EM field is given by the following expression (see Ref. [43] for details)

$$\begin{array}{cc}\hfill \mathbf{B}& =\frac{1}{c^{2}L}\left\{\ddot{\mathbf{p}}\times \mathbf{n}+\frac{1}{6c}\stackrel{⃛}{\mathbf{D}}\times \mathbf{n}+(\ddot{\mathbf{\mu }}\times \mathbf{n})\times \mathbf{n}\right\},\hfill \end{array}$$

(98)

evaluated at the retarded time. From Equation (98), we identify the contributions to the EM field of the dipole (first term), quadrupole (second term), and magnetic moment (third term). In this manuscript, we only consider the dipole contribution in the results, but we compute the quadrupole contribution for completeness. In this sense, we only use the first two terms of Equation (98).

According to Figure 4, the observer locates at a distance L along the direction of the unit vector $\mathbf{n}$, which forms an angle $\iota$ with the Z-axis. Hence,

$$\mathbf{n}=(sin\iota ,0,cos\iota ),$$

(99)

From the first term in Equations (98) and (55), the dipole contribution is given by

$${\mathbf{B}}_{\mathrm{dipole}}=\frac{1}{c^{2}L}\ddot{\mathbf{p}}\times \mathbf{n}.$$

(100)

In dimensionless units, the last expression reduces to

$$\begin{array}{cc}\hfill {\mathbf{B}}_{\mathrm{dipole}}& =\frac{m_1{m}_2({\lambda }_1-{\lambda }_2)(1-\lambda )}{R^{2}L}\hfill \\ \hfill & \times (-sin\psi cos\iota ,cos\psi cos\iota ,sin\psi sin\iota ),\hfill \end{array}$$

(101)

See Appendix A. Note that for ${\lambda }_1={\lambda }_2$, the dipole contribution vanishes and it is necessary to consider the quadrupole contribution. The quadrupole radiation is given by

$${\mathbf{B}}_{\mathrm{quadrupole}}=\frac{1}{6c^{3}L}\stackrel{⃛}{\mathbf{D}}\times \mathbf{n}.$$

(102)

As mentioned before, the vector $\mathbf{D}$ can be computed as the projection of the tensor $D_{\alpha \beta }$ along the unit vector $\mathbf{n}$. Since we assume that the motion of the binary system occurs on the equatorial plane, the third derivative of the quadrupole moment has the form $\stackrel{⃛}{\mathbf{D}}=({\stackrel{⃛}{D}}_x,{\stackrel{⃛}{D}}_y,{\stackrel{⃛}{D}}_z)$. Therefore, the quadrupole contribution to the magnetic field reduces to

$${\mathbf{B}}_{\mathrm{quadrupole}}=\frac{1}{6c^{3}L}({\stackrel{⃛}{D}}_{y}cos\iota ,{\stackrel{⃛}{D}}_{z}sin\iota -{\stackrel{⃛}{D}}_{x}cos\iota ,-{\stackrel{⃛}{D}}_{y}sin\iota ).$$

(103)

Using Equations (3) and (5) and the relation $D_{\alpha }=D_{\alpha \beta }{n}_{\beta }$, it is straightforward to compute ${\stackrel{⃛}{D}}_{\alpha }$. Nevertheless, because the third derivatives of $D_x$, $D_y$, and $D_z$ involve the first and higher derivatives of R and $\psi$, it is important to note that we use the quasi-circular approximation to simplify the expressions. Therefore, in dimensionless units, the quadrupole contribution reduces to (see Appendix A)

$$\begin{array}{cc}\hfill {\mathbf{B}}_{\mathrm{quadrupole}}& =\frac{{\mu }^2{R}^2{\omega }_s^3}{L}\left(\frac{{\lambda }_1}{m_1}+\frac{{\lambda }_2}{m_2}\right)\hfill \\ \hfill & \times (sin2\iota cos2\psi ,-sin2\iota sin2\psi ,2{sin}^2\iota cos2\psi ).\hfill \end{array}$$

(104)

For simplicity, we consider an observer located along the X-axis with a distance $L>>R$. Therefore, $\iota =\pi /2$, and Equations (103) and (104) reduce to

$$\begin{array}{cc}\hfill {\mathbf{B}}_{\mathrm{dipole}}& =\frac{m_1{m}_2({\lambda }_1-{\lambda }_2)(1-\lambda )}{R^{2}L}sin\frac{\Phi }{2}\widehat{\mathbf{k}},\hfill \\ \hfill {\mathbf{B}}_{\mathrm{quadrupole}}& =\frac{2{\mu }^2{R}^2{\omega }_s^3}{L}\left(\frac{{\lambda }_1}{m_1}+\frac{{\lambda }_2}{m_2}\right)cos\Phi \widehat{\mathbf{k}},\hfill \end{array}$$

(105)

where we take into account the relation $\Phi =2\psi$ in the expression for ${\mathbf{B}}_{\mathrm{quadrupole}}$. Then, the total magnetic field is given by

$${\mathbf{B}}_{\mathrm{Total}}={\mathbf{B}}_{\mathrm{dipole}}+{\mathbf{B}}_{\mathrm{quadrupole}}.$$

(106)

According to Equation (105), both contributions lay along the Z-axis. Moreover, note that ${\mathbf{B}}_{\mathrm{dipole}}$ is proportional to $sin\Phi /2$, while ${\mathbf{B}}_{\mathrm{quadrupole}}$ is proportional to $cos\Phi$. On the other hand, it is important to point out that ${\mathbf{B}}_{\mathrm{dipole}}$ is inversely proportional to the second power of the radial separation, $R^2$, and the observer distance L, while the quadrupole contribution to the magnetic field ${\mathbf{B}}_{\mathrm{quadrupole}}$ is proportional not only to $R^2$, but also to the third power of the angular frequency of the source ${\omega }_s^3$. Equation (105) also shows that the dipole contribution vanishes when ${\lambda }_1={\lambda }_2$. Hence, as mentioned before, it is necessary to consider higher contributions to the magnetic field, i.e., the quadrupole contribution.

From the phenomenological point of view, it is possible to investigate the behavior of the EM field during the inspiral phase of a binary system formed by charged black holes by replacing the analytical expressions of Equation (87) in Equation (105). In this sense, in Figure 5, we plot the behavior of ${\mathbf{B}}_{\mathrm{dipole}}$ as a function of time for different values of ${\lambda }_1$ and ${\lambda }_2$. We consider an observer at a distance $L=5.644\times {10}^{20}$ (see Appendix A) along the X-axis. From the figure, we can see that the order of magnitude of the EM field is small, ${10}^{-24}$. The figure also shows how the EM field increases as the binary system approaches coalescence at the ISCO. In the case of ${\lambda }_1=0.1$ and ${\lambda }_2=0.2$, shown in the continuous blue line, ${\mathbf{B}}_{\mathrm{dipole}}$ oscillates between $-1\times {10}^{-24}$ and $1\times {10}^{-24}$. When ${\lambda }_1=0.05$ and ${\lambda }_2=-0.04$, the behavior is similar; see the continuous green line. When one of the black holes does not have an electric charge, i.e., ${\lambda }_1=0.0$ and ${\lambda }_2=0.08$, the dipole contribution to the magnetic field oscillates between $-0.5\times {10}^{-24}$ and $0.5\times {10}^{-24}$.

In Figure 5, we can see how the presence of electric charge affects the duration of the signal. For example, when the two black holes have $Q_1>0$ and $Q_2>0$, the inspiral phase is longer than in the other two cases: two black holes with opposite charges (green line) and a binary system in which one of the black holes is uncharged (red line). As mentioned above, the fact that the same-sign electric charges repel each other enables the binary system to interact for more time before the coalescence at the ISCO. This contrasts the case in which the black holes have an opposite electric charge, where the attraction makes the interaction shorter.

6.2. The Gravitational Wave

The plus and cross-polarization of the gravitational wave of a point particle with reduced mass $\mu$ are given in dimensionless units by [44]

$$\begin{array}{cc}\hfill h_{+}& =\frac{4\mu {\omega }_s^2{R}^2}{L}\left(\frac{1+{cos}^2\iota }{2}\right)cos\Phi ,\hfill \\ \hfill h_{\times }& =\frac{4\mu {\omega }_s^2{R}^2}{L}cos\iota sin\Phi .\hfill \end{array}$$

(107)

where $L\to L/R_{*}$, $\mu \to G\mu /c^2/R_{*}$, ${\omega }_s\to {\omega }_s{R}_{*}/c$, and $R\to R/R_{*}$. See Appendix A. In the case of an observer located along the X-axis at a distant L, $h_{\times }$ vanishes, and $h_{+}$ takes the form

$$h_{+}=\frac{2(1-\lambda )}{\sqrt{2}L}\frac{M_c^{5/4}}{R}cos\Phi .$$

(108)

where we have considered the Keplerian law in Equation (A9) and defined the chirp mass, $M_c$, in dimensionless units by

$$M_c^5=\frac{1}{64}{\left(\frac{4\mu }{M}\right)}^{4/3}.$$

(109)

In Figure 6, we plot the GW form in the plus polarization for different values of ${\lambda }_1$ and ${\lambda }_2$ using the data from the numerical solution of Equation (81) and considering $L=5.644\times {10}^{20}$. The figure shows how $h_{+}$ oscillates between $-1\times {10}^{-22}$ and $1\times {10}^{-22}$. Therefore, the value of $h_{+}$ is greater than the corresponding EM wave. Furthermore, the figure also shows that the magnitude of $h_{+}$ increases slowly in the last part of the inspiral phase (when $10\times {10}^3<t<12\times {10}^3$) in contrast to the EM waveform, which increases its magnitude faster than $h_{+}$ in the same interval of time.

On the other hand, similar to the EM waveform, the electric charge affects the duration of the inspiral time before coalescence. Hence, in the case of a binary system formed by non-charged black holes, the coalescence time is longer than in those cases in which ${\lambda }_1=0.05$ and ${\lambda }_2=-0.04$, or ${\lambda }_1=0.0$ and ${\lambda }_2=0.08$. Nevertheless, when ${\lambda }_1=0.1$ and ${\lambda }_2=0.2$, the coalescence time is longer than in the other cases. Once again, this behavior is due to the attraction/repulsion between electric charges.

7. Fourier Transform

Under certain conditions, it is possible to express a function $g\left(t\right)$ (the “signal”) as a linear combination of sines and cosines with the help of the Fourier series. Furthermore, one can also represent the signal in the frequency domain, which shows the collection of frequencies constituting the function $g\left(t\right)$. The representation of $g\left(t\right)$ in the frequency domain, denoted by $\tilde{g}\left(f\right)$, is known as the Fourier transform and is a powerful tool used to analyze and obtain information regarding the evolution and behavior of the signal. In this sense, the central purpose of this section is to calculate the Fourier transform of the EM wave. To do so, we follow the ideas of Ref. [44].

7.1. Gravitational Wave

In the last section, we discussed the behavior of $h_{+}$ as a function of time using Equation (108) and the data from the numerical solution of Equation (81). Nevertheless, to compute the Fourier transform, it is necessary to find an analytical expression. For that purpose, it is necessary to use the approximation for R and $\Phi$ obtained in Section 5. Hence, after replacing Equation (87) in Equation (108), we obtain the following expression:

$$h_{+}=A\left(t\right)cos\Phi \left(t\right),$$

(110)

with

$$A\left(\tau \right)=\frac{{(1-\lambda )}^{1/2}}{2L}{M}_c^{5/4}{\left(\frac{5}{\tau }\right)}^{1/4}-\frac{{({\lambda }_1-{\lambda }_2)}^2}{12L}{M}_c^{5/2},$$

(111)

where we have considered the approximation $\gamma R<<1$. It is straightforward to show that Equation (110) reduces to the Equation (4.361) of Ref. [44] when ${\lambda }_1$ and ${\lambda }_2$ vanish.

Following Ref. [44], the Fourier transform of Equation (110) is given by

$${\tilde{h}}_{+}\left(f\right)={\int }_{-\infty }^{\infty }dtA\left(t_{\mathrm{r}}\right)cos\Phi \left(t_{\mathrm{r}}\right)e^{2\pi fti}.$$

(112)

Note that the integrand is evaluated at the retarded time $t_r=t-L$ (dimensionless units). Hence, after taking into account that $dt=d{t}_r$ and Euler’s formula, the last expression reduces to

$${\tilde{h}}_{+}\left(f\right)=\frac{1}{2}{e}^{2\pi fLi}{\int }_{-\infty }^{\infty }d{t}_{r}A\left(t_r\right)\left[e^{i\Phi \left(t_r\right)}+e^{-i\Phi \left(t_r\right)}\right]e^{2\pi f{t}_{r}i}.$$

(113)

According to Ref. [44], because $\dot{\Phi }={\omega }_{\mathrm{GW}}>0$, only the term proportional to $e^{[-\Phi \left(t_{\mathrm{r}}\right)+2\pi f{t}_{\mathrm{r}}]i}$ has a stationary point, while the term proportional to $e^{[\Phi \left(t_{\mathrm{r}}\right)+2\pi f{t}_{\mathrm{r}}]i}$ is oscillating fast and integrates to a negligible value. Hence, the Fourier transformation reduces to [44]

$${\tilde{h}}_{+}\simeq \frac{1}{2}{e}^{2\pi fLi}{\int }_{-\infty }^{\infty }d{t}_{r}A\left(t_r\right)e^{i[2\pi f{t}_r-\Phi \left(t_r\right)]}.$$

(114)

We can compute the last integral using the stationary phase method. Hence, because $A\left(t_{\mathrm{r}}\right)$ varies slowly in contrast to $\dot{\Phi }$, the stationary point $t_{*}\left(f\right)$ can be obtained by the condition $2f\pi =\dot{\Phi }\left(t_{*}\right)={\omega }_{\mathrm{Gw}}$. This means that the highest contribution to the Fourier transform with a given f is obtained for the values of t for which ${\omega }_{\mathrm{GW}}$ is equal to $2\pi f$. Therefore, after expanding the exponential in the integrand up to the second order in $(t-t_{*})$, one obtains [44]

$${\tilde{h}}_{+}\left(f\right)=\frac{1}{2}{e}^{i{\Psi }_{+}\left(t_{*}\right)}A\left(t_{*}\right){\left(\frac{2\pi }{\ddot{\Phi }\left(t_{*}\right)}\right)}^{1/2},$$

(115)

where [44]

$${\Psi }_{+}\left(t_{*}\right)=2\pi f(L+t_{*})-\Phi \left(t_{*}\right)-\frac{\pi }{4}.$$

(116)

From Equation (A57), it is straightforward to show that

$$\begin{array}{cc}\hfill \Phi \left(\tau \right)& ={\Phi }_0-2{(1-\lambda )}^{-1/4}{\left(5M_c\right)}^{-5/8}{\tau }^{5/8}\hfill \\ \hfill & +\frac{{(1-\lambda )}^{-3/4}{({\lambda }_1-{\lambda }_2)}^2}{14\sqrt{5}}{\left(5M_c\right)}^{5/8}{\tau }^{7/8}.\hfill \end{array}$$

(117)

To obtain the analytical expression for ${\tilde{h}}_{+}$, it is necessary to obtain $t_{*}$. To do so, we start by considering the condition $\dot{\Phi }\left(t_{*}\right)={\omega }_{\mathrm{GW}}$. Hence, from Equation (117), we obtain the following relation:

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{GW}}& =2{(1-\lambda )}^{-1/4}{\left(\frac{5}{256}\frac{1}{{\tau }_{*}}\right)}^{3/8}{M}_c^{-5/8}\hfill \\ \hfill & -\frac{1}{8}{(1-\lambda )}^{-3/4}{({\lambda }_1-{\lambda }_2)}^2{\left(\frac{5}{256}\frac{1}{{\tau }_{*}}\right)}^{1/8}{M}_c^{5/8}.\hfill \end{array}$$

(118)

Nevertheless, since ${({\lambda }_1-{\lambda }_2)}^2<<1$, the second term of Equation (118) is small, and we can use the approximation

$${\omega }_{\mathrm{GW}}\approx 2{(1-\lambda )}^{-1/4}{\left(\frac{5}{256}\frac{1}{{\tau }_{*}}\right)}^{3/8}{M}_c^{-5/8}.$$

(119)

Therefore, the stationary point is given by

$${\tau }_{*}=\frac{5}{256}{(1-\lambda )}^{-2/3}{M}_c^{-5/3}{\left(\pi f\right)}^{-8/3},w$$

(120)

which reduces to Equation (4.19) of Ref. [44] when $\lambda =0$ and solving for $\tau$. After replacing in Equations (116) and (117), we obtain the following expression for the phase [29,46]

$$\begin{array}{cc}\hfill {\Psi }_{+}\left(f\right)& =2\pi f(L+t_{\mathrm{coal}})+\frac{3}{4}{(1-\lambda )}^{-2/3}{\left(M_{c}8\pi f\right)}^{-5/3}\hfill \\ \hfill & -\frac{5}{14}{(1-\lambda )}^{-4/3}{({\lambda }_1-{\lambda }_2)}^2{M}_c^{3/2}{\left(M_{c}8\pi f\right)}^{-7/3}\hfill \\ \hfill & -\frac{\pi }{4}-{\Phi }_0.\hfill \end{array}$$

(121)

Finally, from Equation (119), the second time derivative is given by

$$\ddot{\Phi }\left(\tau \right)=\frac{192}{5}{(1-\lambda )}^{-1/4}{\left(\frac{5}{256}\frac{1}{\tau }\right)}^{11/8}{M}_c^{-5/8},$$

(122)

From which

$$\ddot{\Phi }\left({\tau }_{*}\right)=\frac{192}{5}{(1-\lambda )}^{2/3}{M}_c^{5/3}{\left(\pi f\right)}^{11/3}.$$

(123)

Hence, after replacing in Equation (115), the analytical expression for the Fourier transform ${\tilde{h}}_{+}$ is given by

$$\begin{array}{c}\hfill {\tilde{h}}_{+}\left(f\right)=\frac{1}{2L}\left[{\left(\frac{5}{24}\right)}^{1/2}\frac{1}{{\pi }^{2/3}}\right]{(1-\lambda )}^{1/3}{M}_c^{5/6}{f}^{-7/6}{e}^{i{\Psi }_{+}}-\frac{1}{48L}\left[{\left(\frac{5}{24}\right)}^{1/2}\frac{1}{{\pi }^{4/3}}\right]{(1-\lambda )}^{-1/3}{({\lambda }_1-{\lambda }_2)}^2{M}_c^{5/12}{f}^{-11/6}{e}^{i{\Psi }_{+}}.\end{array}$$

(124)

Note that the last expression reduces to Equation (4.34) of Ref. [44] when ${\lambda }_1$ and ${\lambda }_2$ vanish.

In Figure 7, we plot the Fourier transform for the electromagnetic and gravitational waves for different values of ${\lambda }_1$ and ${\lambda }_2$. In particular, the first-row left panel of the figure shows the behavior of ${\tilde{h}}_{+}$ as a function of f. The figure shows that ${\tilde{h}}_{+}$ behaves similarly to the Fourier transform of a binary system formed by non-charged black holes. According to Equation (124), this behavior is expected by noticing that the term proportional to $f^{-7/6}$ dominates over the term proportional to $f^{-11/6}$ when ${({\lambda }_1-{\lambda }_2)}^2<<1$.

7.2. Electromagnetic Wave

From Equations (87), (105), and (A44) and the approximation $\gamma R<<1$, the dipole contribution takes the form

$$B_{\mathrm{dipole}}=B\left(\tau \right)cos\left(\frac{\Phi }{2}-\frac{\pi }{2}\right),$$

(125)

where

$$\begin{array}{cc}\hfill B\left(\tau \right)& =\frac{m_1{m}_2({\lambda }_1-{\lambda }_2)}{8L}{\left(\frac{5}{\tau }\right)}^{1/2}\hfill \\ \hfill & -\frac{m_1{m}_2{({\lambda }_1-{\lambda }_2)}^3{(1-\lambda )}^{-1/2}}{24L}{M}_c^{5/4}{\left(\frac{5}{\tau }\right)}^{1/4}.\hfill \end{array}$$

(126)

The Fourier transform is given by

$${\tilde{B}}_{\mathrm{dipole}}={\int }_{-\infty }^{\infty }dtB\left(t_r\right)cos\left(\frac{\Phi \left(t_r\right)}{2}-\frac{\pi }{2}\right)e^{2\pi fti}.$$

(127)

Once again, note that the integrand is evaluated at the retarded time $t_r=t-L$. Hence, after taking into account that $dt=d{t}_r$ and Euler’s formula, the last expression reduces to (we use the relation $\tau =t_{\mathrm{coal}}-t$).

$${\tilde{B}}_{\mathrm{dipole}}\simeq \frac{e^{i(2\pi fL+\pi /2)}}{2}{\int }_{-\infty }^{\infty }d{t}_{r}B\left(t_r\right)e^{i\rho \left(tr\right)}.$$

(128)

where we take into account that only the term proportional to $e^{[-\Phi \left(t_{\mathrm{r}}\right)+2\pi f{t}_{\mathrm{r}}]i}$ has a stationary point and define

$$\rho =2\pi f{t}_r-\frac{\Phi \left(t_r\right)}{2}.$$

(129)

Expanding $\rho$ up to second order around the stationary point $t_{*}$, we obtain the following relation

$$\begin{array}{cc}\hfill \rho & \approx 2\pi f{t}_{*}-\frac{\Phi \left(t_{*}\right)}{2}+\left[2\pi f-\frac{\dot{\Phi }\left(t_{*}\right)}{2}\right](t_r-t_{*})\hfill \\ \hfill & -\frac{\ddot{\Phi }\left(t_{*}\right)}{4}{(t_r-t_{*})}^2.\hfill \end{array}$$

(130)

Hence, the stationary point for the dipole contribution can be obtained by the condition

$$2\pi f=\frac{\dot{\Phi }\left(t_{*}\right)}{2}=\frac{{\omega }_{\mathrm{GW}}}{2},$$

(131)

From which

$$\rho \left(t_r\right)\approx 2\pi f{t}_{*}-\frac{\Phi \left(t_{*}\right)}{2}-\frac{\ddot{\Phi }\left(t_{*}\right)}{4}{(t_r-t_{*})}^2,$$

(132)

and

$${\tilde{B}}_{\mathrm{dipole}}=\frac{e^{i[2\pi f(L+t_{*})+\pi /2-\Phi \left(t_{*}\right)/2]}}{\sqrt{\ddot{\Phi }\left(t_{*}\right)}}{\int }_{-\infty }^{\infty }dx{e}^{-i{x}^2}.$$

(133)

In the last expression, we consider the change of variable

$$x=\sqrt{\frac{4}{\ddot{\Phi }\left(t_{*}\right)}}(t_r-t_{*}).$$

(134)

Therefore, after integration, we obtain

$${\tilde{B}}_{\mathrm{dipole}}=e^{i{\Psi }_{\mathrm{dipole}}}B\left(t_{*}\right){\left(\frac{\pi }{\ddot{\Phi }\left(t_{*}\right)}\right)}^{1/2},$$

(135)

where

$${\Psi }_{\mathrm{dipole}}=2\pi f(L+t_{\mathrm{coal}})-2\pi f{\tau }_{*}+\frac{\pi }{4}-\frac{\Phi \left({\tau }_{*}\right)}{2}.$$

(136)

To obtain the last expression, we consider the relation $t_{*}=t_{\mathrm{coal}}-{\tau }_{*}$. Now, from Equation (131), we obtain

$${\tau }_{*}=5{(1-\lambda )}^{-2/3}{M}_c^{-5/3}{\left(16\pi f\right)}^{-8/3}.$$

(137)

From which, after replacing in Equation (136), we obtain

$$\begin{array}{cc}\hfill {\Psi }_{\mathrm{dipole}}& =2\pi f(L+t_{\mathrm{coal}})+\frac{3}{8}{(1-\lambda )}^{-2/3}{\left(M_{c}16\pi f\right)}^{-5/3}\hfill \\ \hfill & -\frac{5}{28}{(1-\lambda )}^{-4/3}{({\lambda }_1-{\lambda }_2)}^2{M}_c^{3/2}{\left(M_{c}16\pi f\right)}^{-7/3}\hfill \\ \hfill & +\frac{\pi }{4}-\frac{{\Phi }_0}{2}.\hfill \end{array}$$

(138)

Now, from Equations (126), (135), and (137), we get

$$\begin{array}{c}{\tilde{B}}_{\mathrm{dipole}}=\frac{1}{2L}{\left(\frac{5}{24}\right)}^{1/2}{m}_1{m}_2({\lambda }_1-{\lambda }_2)f^{-3/6}{e}^{i{\Psi }_{\mathrm{dipole}}}-\frac{1}{24L}{\left(\frac{5}{24}\frac{1}{{\pi }^{4/3}}\right)}^{1/2}\\ m_1{m}_2{({\lambda }_1-{\lambda }_2)}^3{\left(2(1-\lambda )\right)}^{-2/3}{M}_c^{5/6}{f}^{-7/6}{e}^{i{\Psi }_{\mathrm{dipole}}}.\end{array}$$

(139)

Finally, in the case of the quadrupole contribution, Equation (105) reduces to

$$B_{\mathrm{quadrupole}}=C\left(\tau \right)cos\Phi \left(\tau \right),$$

(140)

where we define

$$\begin{array}{cc}\hfill C\left(\tau \right)& =\frac{1}{8L}{(1-\lambda )}^{1/4}\left(\frac{{\lambda }_1}{m_1}+\frac{{\lambda }_2}{m_2}\right)M_c^{25/8}{\left(\frac{5}{\tau }\right)}^{5/8}\hfill \\ \hfill & -\frac{5}{96L}\frac{{({\lambda }_1-{\lambda }_2)}^2}{{(1-\lambda )}^{1/4}}\left(\frac{{\lambda }_1}{m_1}+\frac{{\lambda }_2}{m_2}\right)M_c^{35/8}{\left(\frac{5}{\tau }\right)}^{3/8}.\hfill \end{array}$$

(141)

Once again, we considered the Keplerian law in Equation (A9) and the approximation $\gamma R<<1$.

From Equations (110) and (140), it is possible to see that $h_{+}$ and $B_{\mathrm{quadrupole}}$ have the same behavior. The only difference lies in the value of the amplitudes $A\left(\tau \right)$ and $C\left(\tau \right)$. In this sense, the GW and the quadrupole contribution of the magnetic field will have the same phase, i.e., ${\Psi }_{\mathrm{quadrupole}}={\Psi }_{+}$. Therefore, the Fourier transform is given by the relation:

$${\tilde{B}}_{\mathrm{quadrupole}}\left(f\right)=\frac{1}{2}{e}^{i{\Psi }_{+}\left({\tau }_{*}\right)}C\left({\tau }_{*}\right){\left(\frac{2\pi }{\ddot{\Phi }\left({\tau }_{*}\right)}\right)}^{1/2},$$

(142)

From which

$$\begin{array}{c}{\tilde{B}}_{\mathrm{quadrupole}}\left(f\right)=\frac{1}{2L}{\left(\frac{5\pi }{6}\right)}^{1/2}\left(\frac{{\lambda }_1}{m_1}+\frac{{\lambda }_2}{m_2}\right)e^{i{\Psi }_{+}\left({\tau }_{*}\right)}\\ \left[{(1-\lambda )}^{1/3}{M}_c^{10/3}{\left(\pi f\right)}^{-1/6}-\frac{{(1-\lambda )}^{-1/3}}{48}{({\lambda }_1-{\lambda }_2)}^2{M}_c^{25/6}{\left(\pi f\right)}^{-17/6}\right].\end{array}$$

(143)

In the first row and second panel of Figure 7, we plot the Fourier transform of the dipole contribution as a function of f for different values of ${\lambda }_1$ and ${\lambda }_2$. The figure shows that $|{\tilde{B}}_{\mathrm{dipole}}|$ is between ${10}^{-26}$ and ${10}^{-25}$, in contrast to that of the gravitational wave, where the order of magnitude goes between ${10}^{-24}$ and ${10}^{-23}$. Furthermore, similarly to $|{\tilde{h}}_{+}|$, $|{\tilde{B}}_{\mathrm{dipole}}|$ decreases as the frequency f increases. This behavior is shown clearly in the second row of Figure 7, where we plot the Fourier transform of $h_{+}$ and $B_{\mathrm{dipole}}$ together. It is important to point out that the rate at which $|{\tilde{B}}_{\mathrm{dipole}}|$ decreases is less than that of $|{\tilde{h}}_{+}|$, i.e., while the Fourier transform in the case of $h_{+}$ is dominated by a term proportional to $f^{-7/6}$, the Fourier transform of $B_{\mathrm{dipole}}$ is dominated by a term proportional to $f^{-3/6}$; see Equations (124) and (139), respectively. Hence, while $|{\tilde{h}}_{+}|$ decreases with a slope of $-7/6$, $|B_{\mathrm{dipole}}|$ decreases with a smaller slope of $-3/6$; see the dashed gray lines in the figure.

8. Results and Discussion

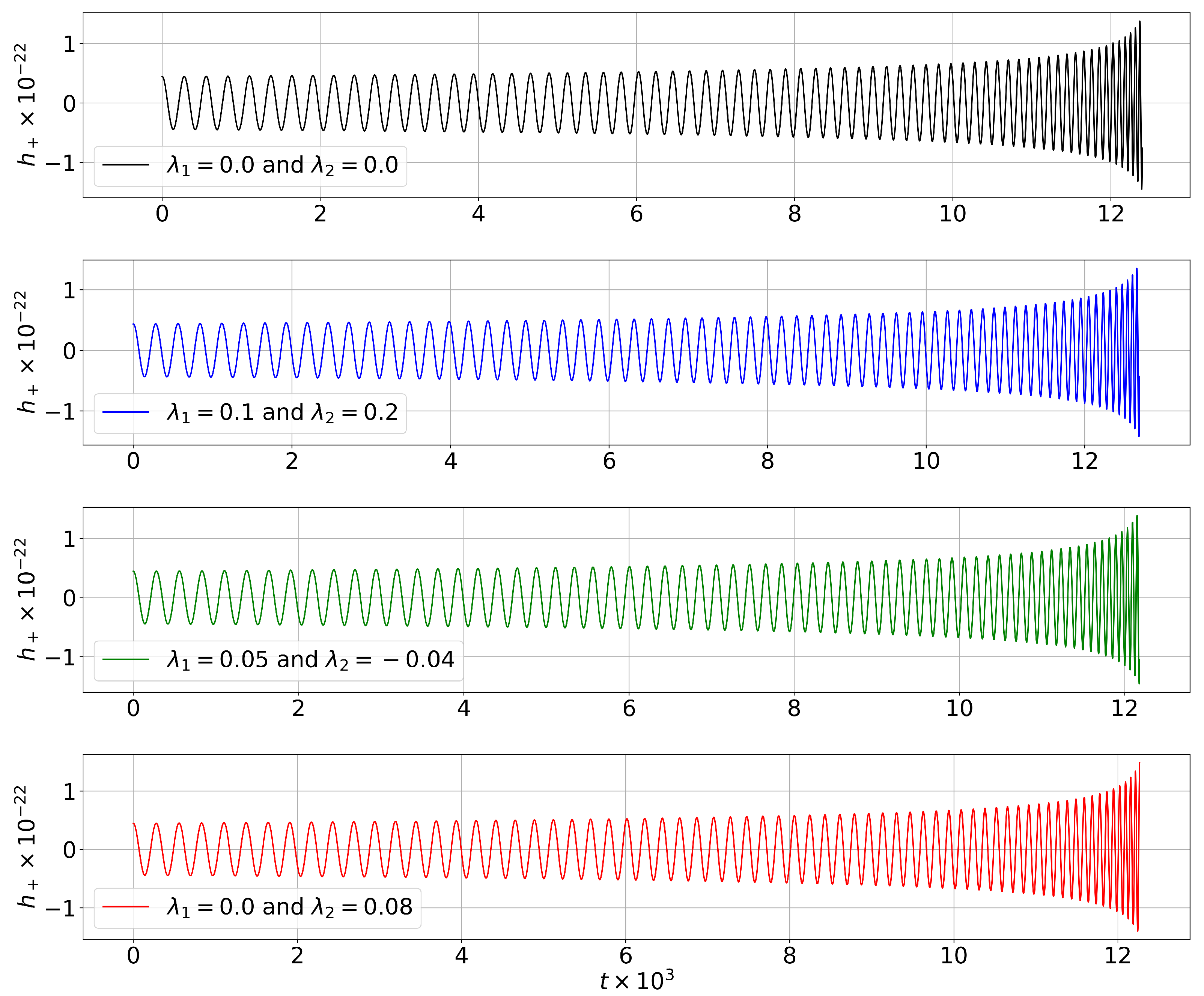
Our results show that $h_{+}$ contains two terms: one term proportional to ${(5/\tau )}^{1/4}$ and a small constant proportional to ${({\lambda }_1-{\lambda }_2)}^2$. The latter is a small contribution if ${({\lambda }_1-{\lambda }_2)}^2<<1$. When the binary system does not have an electric charge, $h_{+}$ reduces to the well-known relation; see Ref. [44]. However, the presence of electric charge in the binary system does affect the Keplerian orbit during the inspiral phase. For example, when the two black holes in the binary system have a positive charge, the inspiral phase will last longer than the other cases, i.e., ${\lambda }_1={\lambda }_2=0$, ${\lambda }_1>0$ and ${\lambda }_2<0$, and ${\lambda }_1=0$ and ${\lambda }_2>0$: see Figure 4 (left panel) and Figure 6. As mentioned above, this behavior results from the phenomenological interaction between the charges, which repel/attract when they have the same/opposite signs.

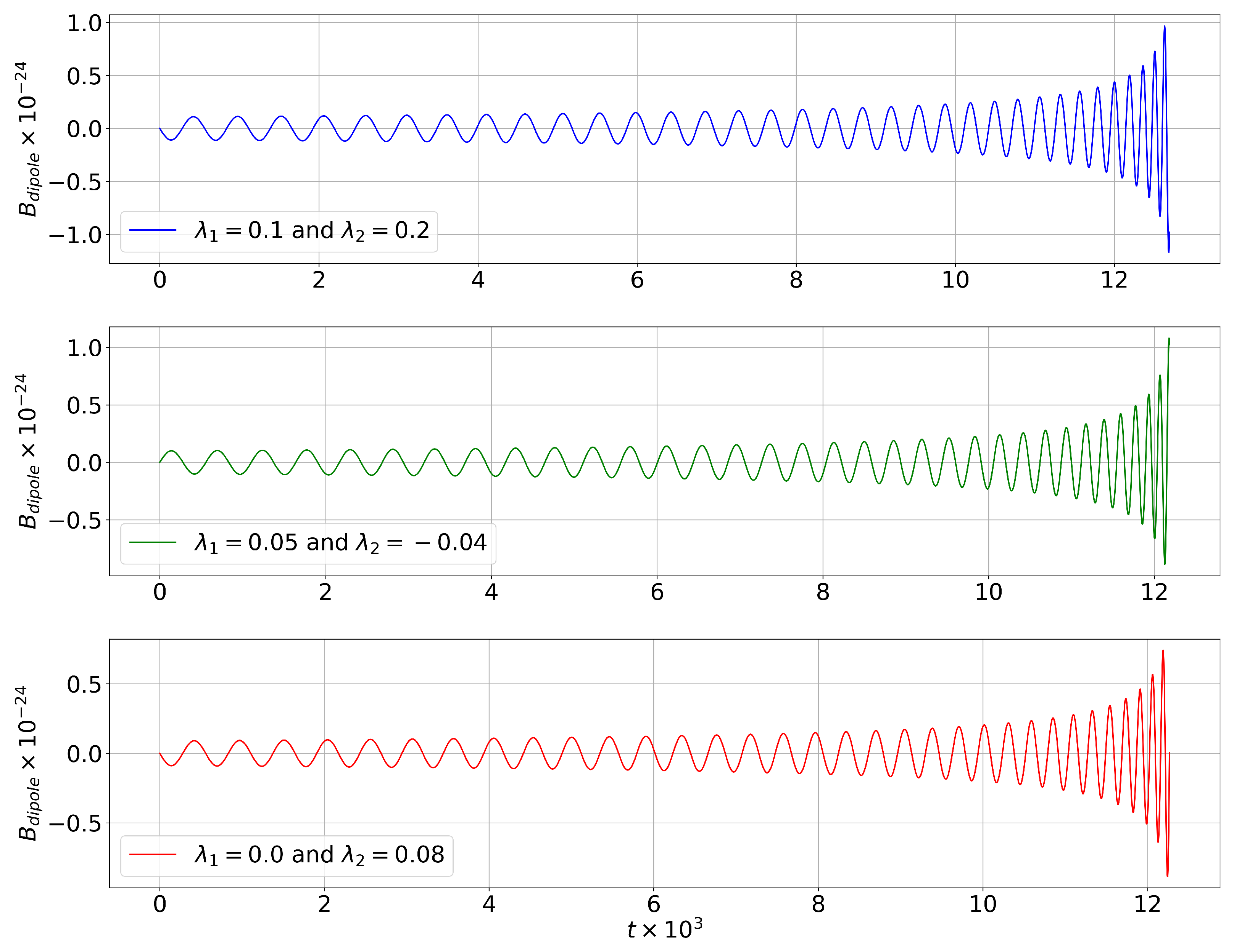
We found similar behavior for the EM waves. Nevertheless, while the magnitude of $h_{+}$ oscillates between $\pm 1\times {10}^{-22}$, the magnitude of the dipole contribution to the magnetic field oscillates between $\pm 1\times {10}^{-24}$. Therefore, the magnetic field detected by the observer will be of order $3.932\times {10}^{-15}\mathrm{Gauss}$. Moreover, it is important to remark that $|{\mathbf{B}}_{\mathrm{dipole}}|$ is proportional to $sin(\Phi /2)$, while $|{\mathbf{B}}_{\mathrm{quadrupole}}|$ is proportional to $cos\Phi$. Hence, the quadrupole contribution of the magnetic field will have the same phase as the GW. From the analytical point of view, we found that ${\mathbf{B}}_{\mathrm{dipole}}$ also has two contributions: one proportional to ${(5/\tau )}^{1/2}$ and the other proportional to ${(5/\tau )}^{1/4}$. Once again, the former will dominate because the second one, proportional to ${({\lambda }_1-{\lambda }_2)}^3$, is much smaller: see Equation (125). The same situation occurs for ${\mathbf{B}}_{\mathrm{quadrupole}}$. There, we have two contributions proportional to ${(5/\tau )}^{5/8}$ and ${(5/\tau )}^{3/8}$, where the former also dominates. See Equation (140).

Finally, following the ideas of Ref. [44], we compute the Fourier transform for $h_{+}$, ${\mathbf{B}}_{\mathrm{dipole}}$, and ${\mathbf{B}}_{\mathrm{quadrupole}}$. In all the cases, we found two contributions. For example, in the GWs, we obtain two terms proportional to $f^{-7/6}$ and $f^{-11/6}$ respectively: see Equation (124). However, the former term dominates if ${({\lambda }_1-{\lambda }_2)}^2<<1$. Note that the exponent of the dominant term is the same as that of the binary system formed by non-charged black holes, and its behavior is similar even if we change the values of ${\lambda }_1$ and ${\lambda }_2$. Hence, the frequencies constituting the GW signal during the inspiral phase belong to the same interval in all the cases (different values of ${\lambda }_1$ and ${\lambda }_2$), and they increase as the magnitude of ${\tilde{h}}_{+}$ decreases.

In the case of the dipole contribution to the magnetic field, we also found that its Fourier transform has two terms proportional to $f^{-3/6}$ and $f^{-7/6}$, respectively. See Equation (139). Once again, as in the case of ${\tilde{h}}_{+}$, the former term dominates. Furthermore, it is important to remark that $|{\tilde{\mathbf{B}}}_{\mathrm{dipole}}|$ is more sensitive to the change in the values of ${\lambda }_1$ and ${\lambda }_2$, but the frequencies constituting the EM wave always belong to the same interval. Therefore, the presence of electric charge affects the magnitude of the Fourier transform, but it does not affect the distribution of frequencies during the inspiral phase; this will be the same in all cases (different values of ${\lambda }_1$ and ${\lambda }_2$). On the other hand, note that the frequency interval in the dipole contribution of the magnetic field is different from that of the GW; this is due to the different phases; see Equations (121) and (138) and Figure 7. Nevertheless, the behavior of $|{\tilde{\mathbf{B}}}_{\mathrm{dipole}}|$ as a function of f is the same as in the Fourier transform of the GW, i.e., Its magnitude decreases as f increases.

We also consider the quadrupole contribution. Nevertheless, as mentioned above, we include it to complete our discussion since our focus is the dipole contribution. As expected, the quadrupole contribution to the magnetic field has the same phase as the GW. That is a consequence of its proportionality of $cos\Phi$. Furthermore, similar to the Fourier transform of the dipole and the gravitational wave, the quadruple contribution contains two terms proportional to $f^{-1/6}$ and $f^{-17/6}$, where the former is the dominant term. See Equation (143). The results show that the lowest contribution occurs when ${\lambda }_1=0.05$ and ${\lambda }_2=-0.04$ (when the binary system contains black holes with opposite signs). It is followed by the cases where ${\lambda }_1=0.0$ and ${\lambda }_2=0.08$, and ${\lambda }_1=0.1$ and ${\lambda }_2=0.2$, respectively. See the first row, right panel of Figure 7. When compared with the $|{\tilde{\mathbf{B}}}_{\mathrm{dipole}}|$, we found that the quadrupole contribution has the same order in the latter case, i.e., when ${\lambda }_1=0.1$ and ${\lambda }_2=0.2$.

9. Conclusions

The main goal of this work was to obtain the waveform, the phase, and the Fourier transform of the EM wave radiated by a binary system of charged black holes without spin, constraining our discussion to the Newtonian limit and the inspiral phase. To do so, we first discuss the Keplerian motion of two-point masses with electric charges, where we consider the gravitational and electrical interactions to obtain the equations of motion. In particular, we consider the radial separation, R, and the angular velocity, ${\omega }_s$, as functions of $\psi$. These equations reduce the problem from two-point masses to a single point mass particle with a reduced mass, $\mu$, under the influence of a central force (the Newton and Coulomb laws).

From the phenomenological point of view, the gravitational and electrical interactions of the binary system generate gravitational and electromagnetic radiation. In the first case, the presence of electric charge modifies the expressions to model the GW by including a parameter $\lambda$, defined as the product of the charge-to-mass ratio in each black hole. On the other hand, electromagnetic radiation arises from the system’s dynamics and from the fact that accelerated charges radiate EM waves.

Since the system loses energy by radiation, we need to obtain the differential equations for the evolution of the Keplerian orbit. In particular, during the inspiral phase, it is known that the binary system circularizes. This phenomenological trait allows us to model the inspiral phase as the evolution of circular orbits. This approximation is possible if we assume that ${\dot{\omega }}_s<<{\omega }_s^2$: this is the quasi-circular approximation. Moreover, due to the presence of electric charges in the binary system, the charge-to-mass ratio in each black hole must be small so that $\lambda <<1$ (this is the reason behind the selection of small values for ${\lambda }_1$ and ${\lambda }_2$ in all the figures; see Table 1).

The description of the inspiral phase is complete by setting the limit within which it is valid. On the one hand, the Newtonian limit breaks when the two black holes get closer, i.e., when the strong-field regime plays a crucial role. On the other hand, it is hard to know the final values of $\lambda$ and M for the remnant black hole. Therefore, we use the innermost stable circular orbit (ISCO) as the range of validity of the model because the numerical solution of the equation of motion coincides with the analytical expressions obtained from the approximations ${\dot{\omega }}_s<<{\omega }_s^2$ and $\lambda <<1$.

Once we establish the model for the inspiral phase, we use the analytical solutions for R, ${\omega }_s$, and $\psi$ to compute the electromagnetic waveform, the waveform phase, and its Fourier transform. We did so by considering the electrodynamics of the binary system and focusing our attention on the dipole and quadrupole contributions. These contributions contain two terms. The Fourier transform also contains two terms. In the case of the dipole contribution, we found that one of the terms is proportional to $f^{-3/6}$, while the other is proportional to $f^{-7/6}$. Nevertheless, the behavior is dominated by the former. Something similar occurs for the quadrupole contribution; the Fourier transform shows two terms proportional to $f^{-1/6}$ and $f^{-17/6}$, respectively. The behavior in the quadrupole contribution is dominated by $f^{-1/6}$. Therefore, we found that the power law is −3/6 and −1/6 for the dipole and quadrupole contributions, respectively.

The gravitational and electromagnetic radiations during the inspiral phase of a binary system formed by electrically charged black holes have similar behavior. When we consider the quasi-circular approximation and small values of the charge-to-mass ratio, the magnitude of the Fourier transform decreases as the frequency increases. Nevertheless, in contrast to the GW, the dipole contribution to the EM wave seems more sensitive to changes in the charge-to-mass ratio in each black hole. The same is true for the quadrupole contribution; however, when compared with the dipole contribution and the GW, the variation of its Fourier transform is slight as the frequency increases.