Semilocal Convergence of a Multi-Step Parametric Family of Iterative Methods

Abstract

In this paper, we deal with a new family of iterative methods for approximating the solution of nonlinear systems for non-differentiable operators. The novelty of this family is that it is a m-step generalization of the Steffensen-type method by updating the divided difference operator in the first two steps but not in the following ones. This procedure allows us to increase both the order of convergence and the efficiency index with respect to that obtained in the family that updates divided differences only in the first step. We perform a semilocal convergence study that allows us to fix the convergence domain and uniqueness for real applied problems, where the existence of a solution is not known a priori. After this study, some numerical tests are developed to apply the semilocal convergence theoretical results obtained. Finally, mediating the dynamic planes generated by the different numerical methods that compose the family, we study the symmetry of the basins of attraction generated by each solution, the shape of these basins, and the convergence to each root of a polynomial function.

1. Introduction

Using iterative methods for solving nonlinear systems is the most common technique to solve a great variety of applied nonlinear problems. Nowadays, iterative methods with a high order of convergence are being developed because the use of variable precision arithmetic in the existing software allows us to obtain approximated solutions with high accuracy. In addition, other approximation techniques have been developed in recent years, such as hybrid algorithms, schemes that use iterative methods together with optimization algorithms [1,2].

In this sense, we deal, in the present work, with high-order iterative methods for solving the system $F(x)=0,$ with F, a nonlinear operator between Banach spaces X and Y [3,4].

It is well known that the iteration function for solving the problem involves the operator F and probably its Fréchet derivative, $F^{\prime }(x),$ as is the case of Newton’s method [5]. However, in real applications, it is highly probable to find non-differentiable operators modeling the problem. In these cases, the secant-type or Steffensen-type iterative methods are used [6,7,8] since the derivative has been approximated by divided differences, mainly first-order forward or backward divided differences or second-order symmetric divided differences [9]. For this reason, we concentrate on high-order iterative methods for non-differentiable problems [10]. Let us consider the composition of a generalized Steffensen method with itself by performing m steps, whose iterative expression is as follows:

$$\left\{\begin{array}{ccc}{z}_1^{(k)}\hfill & =& x^{(k)}-{[w^{(k)},x^{(k)};F]}^{-1}F(x^{(k)})\hfill \\ z_2^{(k)}\hfill & =& z_1^{(k)}-{[w^{(k)},x^{(k)};F]}^{-1}F(z_1^{(k)})\hfill \\ \hfill & ⋮& \\ z_j^{(k)}\hfill & =& z_{j-1}^{(k)}-{[w^{(k)},x^{(k)};F]}^{-1}F(z_{j-1}^{(k)})j=1,2,\dots ,m\hfill \\ \hfill & ⋮& \\ z_{m-1}^{(k)}\hfill & =& z_{m-2}^{(k)}-{[w^{(k)},x^{(k)};F]}^{-1}F(z_{m-2}^{(k)})\hfill \\ x^{(k+1)}\hfill & =& z_{m-1}^{(k)}-{[w^{(k)},x^{(k)};F]}^{-1}F(z_{m-1}^{(k)}),k=0,1,\dots \hfill \end{array}\right.$$

(1)

where $x^{(0)}$ is the starting point, $w^{(k)}=x^{(k)}+\beta F(x^{(k)})$, and $\beta$ is an arbitrary constant such that $\beta \ne 0$. The number of steps selected is denoted by m, and k denotes which iteration we are computing. Ref. [11] proved that this iterative method reaches convergence order $m+1$ (see [12,13,14]).

In order to increase the convergence order without losing the efficiency index, we introduce a new family of iterative methods, consisting in performing m-steps per iteration, but we will perform two first steps of the Steffensen method updating all data. After that, we reuse the divided differences of the second step in the remaining ones. The iterative expression is as follows:

$$\left\{\begin{array}{ccc}{z}_1^{(k)}\hfill & =& x^{(k)}-{[w^{(k)},x^{(k)};F]}^{-1}F(x^{(k)})\hfill \\ z_2^{(k)}\hfill & =& z_1^{(k)}-{[z_1^{(k)},v^{(k)};F]}^{-1}F(z_1^{(k)})\hfill \\ \hfill & ⋮& \\ z_j^{(k)}\hfill & =& z_{j-1}^{(k)}-{[z_1^{(k)},v^{(k)};F]}^{-1}F(z_{j-1}^{(k)}),j=2,\dots ,m\hfill \\ \hfill & ⋮& \\ z_{m-1}^{(k)}\hfill & =& z_{m-2}^{(k)}-{[z_1^{(k)},v^{(k)};F]}^{-1}F(z_{m-2}^{(k)})\hfill \\ x^{(k+1)}\hfill & =& z_{m-1}^{(k)}-{[z_1^{(k)},v^{(k)};F]}^{-1}F(z_{m-1}^{(k)}),k=0,1,\dots \hfill \end{array}\right.$$

(2)

where $w^{(k)}=x^{(k)}+\beta F(x^{(k)})$ and $v^{(k)}=z_1^{(k)}+\beta F(z_1^{(k)})$. The number of steps selected is denoted by m, and k denotes which iteration we are computing. That is, we perform two steps of the Steffensen type. From then, by using the divided difference obtained in the second step, we perform $m-2$ new steps.

Our family of methods coincides with the family studied in [15] for the weight function $H(t)=t^{-1}$ and for the parameters $\beta =\delta$. Moreover, in this article, the complex dynamics is studied in depth. From this study, we can deduce the dynamics of our family (for example, see [16,17]).

The paper is organized as follows: Section 2 is devoted to set a semilocal convergence study for this new family of iterative methods. Next, in Section 3, we perform some numerical tests in order to apply the theoretical results obtained previously. Finally, we expose some conclusions.

2. Semilocal Convergence

In this section, we analyze the semilocal convergence of the iterative method (2), that is, we impose the necessary conditions so that, given a starting point $x^{(0)}$, the iterative method (2) converges to a solution. Moreover, we determine the existence and uniqueness convergence domains [18].

For this, we consider $x^{(0)}\in \mathsf{\Omega }$, and we assume the following:

(I)

There exists $L_0^{-1}=L{(x^{(0)})}^{-1}={[w^{(0)},x^{(0)};F]}^{-1}$ such that $\parallel L_0^{-1}\parallel \le \gamma$. Furthermore, $\parallel F(x^{(0)})\parallel \le {\eta }_0$ such that $\parallel L_0^{-1}F(x^{(0)})\parallel \le \gamma {\eta }_0=b$.

(II)

$\parallel F(x)-F(y)\parallel \le {\mu }_0\left(\parallel x-y\parallel \right)$, $x,y\in \mathsf{\Omega }$ where ${\mu }_0:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ is a continuous non-decreasing function.

(III)

We suppose that there exists $[x,y;F]$ for each pair $x,y\in \mathsf{\Omega }$, $x\ne y$ such that the divided differences operator satisfies the following:

$$∥[x,y;F]-[u,v;F]∥\le {\mu }_1\left(∥x-u∥,∥y-v∥\right);\mathrm{for}\mathrm{all}x,y,u,v\in \mathsf{\Omega },$$

where ${\mu }_1:{\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ is a continuous non-decreasing function with respect to both arguments.

Note that since F is non-differentiable, ${\mu }_1\left(0,0\right)>0.$ Then, we will give a generalized result of the semilocal convergence. We will do so by fixing the radius r of the domain of existence and we will try to calculate it so that the sequence $\left\{x^{(n)}\right\}$ is contained in the ball of convergence $B(x^{(0)},r)$ whose center is the initial iteration and whose radius is our fixed r.

Theorem 1.

Under conditions (I)–(III), we consider the following functions and parameters:

$$\begin{array}{cc}\hfill & l(t)={\mu }_1(t,\beta {\eta }_0),\hfill \\ \hfill & m(t)=\gamma {\mu }_1(t,t+\beta {\eta }_0(t)),\hfill \\ \hfill & \lambda (t)={\displaystyle \frac{\gamma }{1-m(t)}}l(t),\hfill \end{array}$$

with $t\in {\mathbb{R}}^{+}$. Suppose the following equation has at least one positive real root:

$$t-{\displaystyle \frac{b}{1-\lambda (t)}}=0,$$

(3)

where r is the smallest positive real root that satisfies Equation (3) and the conditions $l(r)\gamma <1$, $m(r)<1$ and $\lambda (r)<1$. Then, the sequence $\left\{x_n\right\}$ given by the iterative method (2) is well defined, remains on the semilocal ball of convergence $B(x_0,r)$ and converges to the solution α of the equation $F(x)=0$.

Proof. 

To simplify the notation, we denote

$$L_i=L(x^{(i)})=[x^{(i)}+\beta F(x^{(i)}),x^{(i)};F].$$

We start from the fact that $z_1^{(0)}$ is well defined since by the condition $(\mathrm{I})$, we have the following:

$$\parallel z_1^{(0)}-x^{(0)}\parallel =\parallel L_0^{-1}F(x^{(0)})\parallel \le \gamma {\eta }_0=b<r.$$

Let us see that there exists ${[z_1^{(0)},v^{(0)};F]}^{-1}$. To do this, we denote $S_0={[z_1^{(0)},v^{(0)};F]}^{-1}$ and apply Banach’s lemma:

$$\begin{array}{cc}\hfill \parallel I-L_0^{-1}{S}_0\parallel & \le \parallel L_0^{-1}\parallel \parallel L_0-S_0\parallel \hfill \\ \hfill & \le \gamma ∥[x^{(0)},x^{(0)}+\beta F(x^{(0)});F]-[z_1^{(0)},z_1^{(0)}+\beta F(z_1^{(0)});F]∥\hfill \\ \hfill & \le \gamma \left(\parallel x^{(0)}-z_1^{(0)}\parallel ,\parallel x^{(0)}-z_1^{(0)}+\beta (F(x^{(0)})-F(z_1^{(0)})\parallel \right))\hfill \\ \hfill & \le \gamma {\mu }_1\left(r,r+\beta {\mu }_0(r)\right)=m(r)<1.\hfill \end{array}$$

So, by applying Banach’s lemma, there exists $S_0^{-1}$ and

$$\begin{array}{cc}\hfill \parallel S_0^{-1}\parallel & \le {\displaystyle \frac{\gamma }{1-m(r)}}.\hfill \end{array}$$

Since F is Fréchet differentiable, one has

$$\begin{array}{cc}\hfill F(z_1^{(0)})& =F(z_1^{(0)})+F(x^{(0)})-F(x^{(0)})=F(x^{(0)})+[z_1^{(0)},x^{(0)};F]\left(z_1^{(0)}-x^{(0)}\right).\hfill \end{array}$$

By the first step,

$$F(x^{(0)})=-[w^{(0)},x^{(0)};F](z_1^{(0)}-x^{(0)}).$$

Therefore,

$$F(z_1^{(0)})=\left([z_1^{(0)},x^{(0)};F]-[x^{(0)},w^{(0)};F]\right)(z_1^{(0)}-x^{(0)}).$$

Taking the rules in the above expression and taking into account conditions (I)–(III), one has

$$\begin{array}{cc}\hfill \parallel F(z_1^{(0)})\parallel & \le {\mu }_1\left(\parallel z_1^{(0)}-x^{(0)}\parallel ,\parallel w^{(0)}-x^{(0)}\parallel \right)\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & \le {\mu }_1\left(r,\beta {\eta }_0\right)\parallel z_1^{(0)}-x^{(0)}\parallel \le l(r)\gamma {\eta }_0<{\eta }_0,\hfill \end{array}$$

where we denote $l(r)={\mu }_1\left(r,\beta {\eta }_0\right)$ to simplify the notation. Moreover, thanks to the condition of the theorem $l(r)\gamma <1$, we can say that $l(r)\gamma {\eta }_0<{\eta }_0$. With this bound, we can determine

$$\begin{array}{cc}\hfill \parallel z_2^{(0)}-z_1^{(0)}\parallel =\parallel S_0^{-1}F(z_1^{(0)})\parallel & \le {\displaystyle \frac{\gamma }{1-m(r)}}l(r)\parallel z_1^{(0)}-x^{(0)}\parallel =\lambda (r)\parallel z_1^{(0)}-x^{(0)}\parallel <r,\hfill \end{array}$$

where we denote $\lambda (r)={\displaystyle \frac{\gamma }{1-m(r)}}l(r)$. Moreover, in the previous equation, we applied the fact that $\lambda (r)<1$. Thus,

$$\begin{array}{cc}\hfill \parallel z_2^{(0)}-x^{(0)}\parallel & =\parallel z_2^{(0)}-z_1^{(0)}\parallel +\parallel z_1-x^{(0)}\parallel \le \lambda (r)\parallel z_1^{(0)}-x^{(0)}\parallel +\parallel z_1-x^{(0)}\parallel \hfill \\ & =\left(\lambda (r)+1\right)\parallel z_1^{(0)}-x^{(0)}\parallel \le (1+\lambda (r))b<r.\hfill \end{array}$$

Therefore, since $\parallel z_2^{(0)}-x^{(0)}\parallel <r$, one has $z_2\in B(x^{(0)},r)$. To prove that $z_3$ resides inside $B(x^{(0)},r)$, we must first bound

$$\parallel z_3^{(0)}-z_2^{(0)}\parallel =\parallel S_0^{-1}F(z_2^{(0)})\parallel \le {\displaystyle \frac{\gamma }{1-m(r)}}\parallel F(z_2^{(0)})\parallel .$$

As the value of $\parallel F(z_2^{(0)})\parallel$ is unknown, we are going to develop the expression

$$\begin{array}{cc}\hfill F(z_2^{(0)})& =F(z_2^{(0)})+F(z_1^{(0)})-F(z_1^{(0)})\hfill \\ \hfill & =F(z_1^{(0)})+[z_1^{(0)},z_2^{(0)};F](z_2^{(0)}-z_1^{(0)})\hfill \\ \hfill & =-[z_1^{(0)},v^{(0)};F]\left(z_2^{(0)}-z_1^{(0)}\right)+[z_2^{(0)},z_1^{(0)};F](z_2^{(0)}-z_1^{(0)}).\hfill \end{array}$$

By taking norms,

$$\begin{array}{cc}\hfill \parallel F(z_2^{(0)})\parallel & \le \parallel z_2^{(0)}-z_1^{(0)}\parallel {\mu }_1\left(\parallel z_2^{(0)}-z_1^{(0)}\parallel ,\parallel v^{(0)}-z_1^{(0)}\parallel \right)\hfill \\ \hfill & \le {\mu }_1\left(r,\beta \parallel F(z_1^{(0)})\parallel \right)\parallel z_2^{(0)}-z_1^{(0)}\parallel \hfill \\ \hfill & \le {\mu }_1\left(r,\beta {\eta }_0\right)\parallel z_2^{(0)}-z_1^{(0)}\parallel =l(r)\parallel z_2^{(0)}-z_1^{(0)}\parallel =l(r)\gamma {\eta }_0<{\eta }_0.\hfill \end{array}$$

Now, we can bound the following $\parallel z_3^{(0)}-z_2^{(0)}\parallel$:

$$\begin{array}{cc}\hfill \parallel z_3^{(0)}-z_2^{(0)}\parallel & \le {\displaystyle \frac{\gamma }{1-m(r)}}\parallel F(z_2^{(0)})\parallel \le {\displaystyle \frac{\gamma }{1-m(r)}}l(r)\parallel z_2^{(0)}-z_1^{(0)}\parallel \hfill \\ \hfill & \le \lambda (r)\parallel z_2^{(0)}-z_1^{(0)}{\parallel \le \lambda (r)}^2\parallel z_1^{(0)}-x^{(0)}\parallel <r.\hfill \end{array}$$

It is therefore easy to obtain that

$$\begin{array}{cc}\hfill \parallel z_3^{(0)}-x^{(0)}\parallel & \le \parallel z_3^{(0)}-z_2^{(0)}\parallel +\parallel z_2^{(0)}-z_1^{(0)}\parallel +\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & \le \lambda {(r)}^2\parallel z_1^{(0)}-x^{(0)}\parallel +\lambda (r)\parallel z_1^{(0)}-x^{(0)}\parallel +\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & =\left(\lambda {(r)}^2+\lambda (r)+1\right)\parallel z_1^{(0)}-x^{(0)}\parallel <r.\hfill \end{array}$$

This proves that $z_3\in B(x^{(0)},r)$. We are going to induce the number of steps m to finally obtain that the iteration $x^{(1)}$ is also inside the convergence ball. To do so, we assume that for $q\ge 3$, the following are satisfied:

(1)

$\parallel F(z_q^{(0)})\parallel \le l(r)\parallel z_q^{(0)}-z_{q-1}^{(0)}\parallel <{\eta }_0.$

(2)

$\parallel z_q^{(0)}-z_{q-1}^{(0)}\parallel \le \lambda (r)\parallel z_{q-1}^{(0)}-z_{q-2}^{(0)}{\parallel \le \lambda (r)}^{q-1}\parallel z_1^{(0)}-x^{(0)}\parallel <r.$

(3)

$\parallel z_q^{(0)}-x^{(0)}\parallel \le {\displaystyle \frac{1-\lambda {(r)}^q}{1-\lambda (r)}}b<r$ and, therefore, $z_q^{(0)}\in B(x^{(0)},r).$

Let us see that, since it is true for q, it is also true for $q+1$.

• We start by proving (2) for $q+1$, using (1), (2) and (3) for q:

  $$\begin{array}{cc}\hfill \parallel z_{q+1}^{(0)}-z_q^{(0)}\parallel & =∥{[z_1^{(0)},v^{(0)};F]}^{-1}F(z_q^{(0)})∥\le {\displaystyle \frac{\gamma }{1-m(r)}}l(r)\parallel z_q^{(0)}-z_{q-1}^{(0)}\parallel \hfill \\ \hfill & \le \lambda (r)\parallel z_q^{(0)}-z_{q-1}^{(0)}{\parallel \le \lambda (r)}^q\parallel z_1^{(0)}-x^{(0)}\parallel <r.\hfill \end{array}$$
  It is, therefore, proven.
• Using the hypothesis on q, we prove (3) for $q+1$:

  $$\begin{array}{cc}\hfill \parallel z_{q+1}^{(0)}-x^{(0)}\parallel & =\parallel z_{q+1}^{(0)}-z_q^{(0)}\parallel +\parallel z_q^{(0)}-x^{(0)}{\parallel \le \lambda (r)}^q\parallel z_1^{(0)}-x^{(0)}\parallel +{\displaystyle \frac{1-\lambda {(r)}^q}{1-\lambda (r)}}b\hfill \\ \hfill & \le \left(\lambda {(r)}^q+{\displaystyle \frac{1-\lambda {(r)}^q}{1-\lambda (r)}}\right)b={\displaystyle \frac{1-\lambda {(r)}^{q+1}}{1-\lambda (r)}}b<r.\hfill \end{array}$$
  With this, it is proved that $z_{q+1}\in B(x^{(0)},r)$ and (3) is satisfied for $q+1$.
• Finally we prove (1) for $q+1$ provided that $q<m$:

  $$\begin{array}{cc}\hfill F(z_{q+1}^{(0)})& =F(z_{q+1}^{(0)})+F(z_q^{(0)})-F(z_q^{(0)})\hfill \\ \hfill & =[z_{q+1}^{(0)},z_q^{(0)};F](z_{q+1}^{(0)}-z_q^{(0)})+F(z_q^{(0)})\hfill \\ \hfill & =[z_{q+1}^{(0)},z_q^{(0)};F](z_{q+1}^{(0)}-z_q^{(0)})-[z_1^{(0)},v^{(0)};F](z_{q+1}^{(0)}-z_q^{(0)}).\hfill \end{array}$$
  Applying the rules, we obtain

  $$\begin{array}{cc}\hfill \parallel F(z_{q+1}^{(0)})\parallel & \le {\mu }_1\left(\parallel z_{q+1}^{(0)}-z_1^{(0)}\parallel ,\parallel z_q^{(0)}-v^{(0)}\parallel \right)\parallel z_{q+1}^{(0)}-z_q^{(0)}\parallel \hfill \\ \hfill & \le {\mu }_1\left(\parallel z_{q+1}^{(0)}-x^{(0)}\parallel +\parallel x^{(0)}-z_1^{(0)}\parallel ,\parallel z_q^{(0)}-z_1^{(0)}\parallel +\beta \parallel F(z_1^{(0)})\parallel \right)\parallel z_{q+1}^{(0)}-z_q^{(0)}\parallel \hfill \\ \hfill & \le {\mu }_1\left({\displaystyle \frac{1-\lambda {(r)}^{q+1}}{1-\lambda (r)}}b+b,{\displaystyle \frac{1-\lambda {(r)}^q}{1-\lambda (r)}}b+b+\beta {\eta }_0\right)\parallel z_{q+1}^{(0)}-z_q^{(0)}\parallel \hfill \\ \hfill & \le l(r)\parallel z_{q+1}^{(0)}-z_q^{(0)}\parallel ,\hfill \end{array}$$

  where

  $$l(r)=max\left\{{\mu }_1\left(r,\beta {\eta }_0\right),{\mu }_1\left({\displaystyle \frac{2b-b\lambda (r)\left(\lambda {(r)}^q+1\right)}{1-\lambda (r)}},{\displaystyle \frac{2b-b\lambda (r)\left(\lambda {(r)}^{q-1}+1\right)}{1-\lambda (r)}}+\beta {\eta }_0\right)\right\},$$

  for $q=2,\dots ,m-1.$ Therefore, it is proved (3) for $q+1$.

If $q=m-1$, we have that $z_m^{(0)}=x^{(1)}$ and, therefore, the first iteration generated by the method is inside $B(x^{(0)},r)$. Now we want to prove that $x^{(2)}\in B(x^{(0)},r)$. To do so, we have to see that $z_1^{(1)},\dots ,z_m^{(1)}$ are well defined and inside the convergence ball. Since $z_m^{(0)}=x^{(1)}\in B(x^{(0)},r)$, we go to the first step of the method. In this step, we want to bound $∥z_1^{(1)}-x^{(1)}∥$ to prove that $x^{(1)}$ is inside $B(x^{(0)},r).$ By the method, one has

$$\begin{array}{c}\hfill \parallel z_1^{(1)}-x^{(1)}\parallel \le ∥{[w^{(1)},x^{(1)};F]}^{-1}∥\parallel F(x^{(1)})\parallel \le \parallel L_1^{-1}\parallel \parallel F(x^{(1)})\parallel .\end{array}$$

Since by induction we saw that (3) is satisfied for $q\ge 3$, then

$$\parallel z_1^{(1)}-x^{(1)}\parallel \le \parallel L_1^{-1}\parallel l(r)\parallel z_m^{(0)}-z_{m-1}^{(0)}\parallel .$$

Now, let us see that $L_1^{-1}$ exists. To do this, we use Banach’s lemma:

$$\begin{array}{cc}\hfill \parallel I-L_0^{-1}{L}_1\parallel & \le \parallel L_0^{-1}\parallel \parallel L_0-L_1\parallel \le \gamma ∥[w^{(0)},x^{(0)};F]-[w^{(1)},x^{(1)};F]∥\hfill \\ \hfill & \le \gamma {\mu }_1\left(\parallel w^{(1)}-w^{(0)}\parallel ,\parallel x^{(1)}-x^{(0)}\parallel \right)\hfill \\ \hfill & \le \gamma {\mu }_1\left(\parallel x^{(1)}-x^{(0)}\parallel +\beta \parallel (F(x^{(1)})-F(x^{(0)})\parallel ,\parallel x^{(1)}-x^{(0)}\parallel \right)\hfill \\ \hfill & \le \gamma {\mu }_1\left(\parallel x^{(1)}-x^{(0)}\parallel +\beta {\mu }_0\left(\parallel x^{(1)}-x^{(0)}\parallel \right),\parallel x^{(1)}-x^{(0)}\parallel \right)\hfill \\ \hfill & \gamma {\mu }_1\left(r+\beta {\mu }_0(r),r\right)=m(r)<1.\hfill \end{array}$$

Therefore, by Banach’s lemma,

$$\parallel L_1^{-1}\parallel \le {\displaystyle \frac{\gamma }{1-m(r)}}.$$

Therefore,

$$\begin{array}{cc}\hfill \parallel z_1^{(1)}-x^{(1)}\parallel & \le {\displaystyle \frac{\gamma }{1-m(r)}}l(r)\parallel z_m^{(0)}-z_{m-1}^{(0)}\parallel \le \lambda (r)\parallel z_m^{(0)}-z_{m-1}^{(0)}\parallel \hfill \\ \hfill & \le \lambda (r)\lambda {(r)}^{m-1}\parallel z_1^{(0)}-x^{(0)}{\parallel \le \lambda (r)}^m\parallel z_1^{(0)}-x^{(0)}\parallel <r.\hfill \end{array}$$

To see if it is part of the convergence ball,

$$\begin{array}{cc}\hfill \parallel z_1^{(1)}-x^{(0)}\parallel & \le \parallel z_1^{(1)}-x^{(1)}\parallel +\parallel x^{(1)}-x^{(0)}\parallel \hfill \\ \hfill & \le \lambda {(r)}^m\parallel z_1^{(0)}-x^{(0)}\parallel +\parallel z_m^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & \le \left(\lambda {(r)}^m+{\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}\right)\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & ={\displaystyle \frac{1-\lambda {(r)}^{m+1}}{1-\lambda (r)}}b<r.\hfill \end{array}$$

It is therefore established that $z_1^{(1)}\in B(x^{(0)},r).$ To continue with induction, we are going to prove that $z_2^{(1)}$ is inside the convergence ball. To do this, we want to bound

$$\parallel z_2^{(1)}-z_1^{(1)}\parallel \le ∥{[z_1^{(1)},v^{(1)};F]}^{-1}∥\parallel F(z_1^{(1)})\parallel \le \parallel S_1^{-1}\parallel \parallel F(z_1^{(1)})\parallel .$$

Let see that there exists $S_1^{-1}$ using Banach’s lemma

$$\begin{array}{cc}\hfill \parallel I-L_0^{-1}{S}_1\parallel & \le \parallel L_0^{-1}\parallel ∥L_0-S_1∥\le \gamma ∥[w^{(0)},x^{(0)};F]-[v^{(1)},z_1^{(1)};F]∥\hfill \\ \hfill & \le \gamma {\mu }_1\left(\parallel z_1^{(1)}-x^{(0)}\parallel +\beta \parallel F(z_1^{(1)})-F(x^{(0)})\parallel ,\parallel z_1^{(1)}-x^{(0)}\parallel \right)\hfill \\ \hfill & \le \gamma {\mu }_1\left(r+\beta {\mu }_0(r),r\right)=m(r)<1.\hfill \end{array}$$

Therefore, there exists $S_1^{-1}$ and $\parallel S_1^{-1}\parallel \le {\displaystyle \frac{\gamma }{1-m(r)}}.$ Now we develop

$$F(z_1^{(1)})=F(z_1^{(1)})+F(x^{(1)})-F(x^{(1)})=[z_1^{(1)},x^{(1)};F](z_1^{(1)}-x^{(1)})+F(x^{(1)}).$$

By taking the norms, we obtain

$$\begin{array}{cc}\hfill \parallel F(z_1^{(1)})\parallel & \le ∥[z_1^{(1)},x^{(1)};F](z_1^{(1)}-x^{(1)})-[x^{(1)},w^{(1)};F](z_1^{(1)}-x^{(1)})∥\hfill \\ \hfill & \le {\mu }_1\left(\parallel z_1^{(1)}-x^{(1)}\parallel ,\beta \parallel F(x^{(1)})\parallel \right)\parallel z_1^{(1)}-x^{(1)}\parallel \hfill \\ \hfill & \le {\mu }_1\left(\parallel z_1^{(1)}-x^{(1)}\parallel ,\beta {\eta }_0\right)\parallel z_1^{(1)}-x^{(1)}\parallel \le S\parallel z_1^{(1)}-x^{(1)}\parallel <{\eta }_0.\hfill \end{array}$$

Therefore, we calculate the difference

$$\begin{array}{cc}\hfill \parallel z_2^{(1)}-z_1^{(1)}\parallel & \le {\displaystyle \frac{\gamma }{1-m(r)}}l(r)\parallel z_1^{(1)}-x^{(1)}\parallel \le \lambda (r)\parallel z_1^{(1)}-x^{(1)}\parallel \hfill \\ \hfill & \le \lambda (r)\lambda {(r)}^m\parallel z_1^{(0)}-x^{(0)}{\parallel \le \lambda (r)}^{m+1}\parallel z_1^{(0)}-x^{(0)}\parallel <r.\hfill \end{array}$$

Finally, we would have that $z_2^{(1)}\in B(x^{(0)},r)$, since

$$\begin{array}{cc}\hfill \parallel z_2^{(1)}-x^{(0)}\parallel & \le \parallel z_2^{(1)}-z_1^{(1)}\parallel +\parallel z_1^{(1)}-x^{(0)}\parallel \hfill \\ \hfill & \le \lambda {(r)}^{m+1}\parallel z_1^{(0)}-x^{(0)}\parallel +{\displaystyle \frac{1-\lambda {(r)}^{m+1}}{1-\lambda (r)}}\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & \le {\displaystyle \frac{1-\lambda {(r)}^{m+2}}{1-\lambda (r)}}b<r.\hfill \end{array}$$

Again, by induction on the number of steps to reach the iteration $x^{(2)}$, we can argue analogously (1), (2) and (3) and we obtain for $q=3,\dots ,m$:

(4)

$\parallel F(z_q^{(1)})\parallel \le l(r)\parallel z_q^{(1)}-z_{q-1}^{(1)}\parallel \le {\eta }_0.$

(5)

$\parallel z_q^{(1)}-z_{q-1}^{(1)}\parallel \le \lambda (r)\parallel z_{q-1}^{(1)}-z_{q-2}^{(1)}{\parallel \le \lambda (r)}^{m+q-1}\parallel z_1^{(0)}-x^{(0)}\parallel <r$.

(6)

$\parallel z_q^{(1)}-x^{(0)}\parallel \le {\displaystyle \frac{1-\lambda {(r)}^{m+q}}{1-\lambda (r)}}b<r$ and, therefore, $z_q^{(1)}\in B(x^{(0)},r)$.

By induction, we would see that (4), (5) and (6) are satisfied for $q=m$. Therefore, $x^{(2)}=z_m^{(1)}$ is well defined, and it holds that $x^{(2)}\in B(x^{(0)},r).$ Suppose we repeat the process to see that there exist $x^{(1)}$ and $x^{(2)}$ for all the iterations $x^{(i)}$ with $i=3,\dots ,n-1$. Then, we would obtain the following:

(7)

$\parallel F(z_q^{(n-1)})\parallel \le l(r)\parallel z_q^{(n-1)}-z_{q-1}^{(n-1)}\parallel \le {\eta }_0$ for $q=2,\dots ,m$ and $\parallel F(z_1^{(n-1)})\parallel \le l(r)\parallel z_1^{(n-1)}-x^{(n-1)}\parallel \le {\eta }_0.$

(8)

$\parallel z_q^{(n-1)}-z_{q-1}^{(n-1)}\parallel \le \lambda (r)\parallel z_{q-1}^{(n-1)}-z_{q-2}^{(n-1)}{\parallel \le \lambda (r)}^{(n-1)m+q-1}\parallel z_1^{(0)}-x^{(0)}\parallel <r$ for $q=1,\dots ,m$.

(9)

$\parallel z_q^{(n-1)}-x^{(0)}\parallel \le {\displaystyle \frac{1-\lambda {(r)}^{(n-1)m+q}}{1-\lambda (r)}}b<r$ and $z_q^{(n-1)}\in B(x^{(0)},r)$ for $q=1,\dots ,m$ where $z_m^{(n-1)}=x^{(n)}.$

Assuming that (7), (8) and (9) are satisfied for $n-1$, then let us prove that they are also satisfied for n, and, furthermore, $x^{(n+1)}$ is well defined and belongs to $B(x^{(0)},r)$. We start with the same aim as always. We want to bound

$$\parallel z_1^{(n)}-x^{(n)}\parallel \le ∥{[w^{(n)},x^{(n)};F]}^{-1}F(x^{(n)})∥\le \parallel L_n^{-1}\parallel \parallel F(x^{(n)})\parallel .$$

To do this, we must prove that there exists $L_n^{-1}$:

$$\begin{array}{cc}\hfill \parallel I-L_0^{-1}{L}_n\parallel & \le \parallel L_0^{-1}\parallel \parallel L_0-L_n\parallel \le \gamma ∥[w^{(0)},x^{(0)};F]-[w^{(n)},x^{(n)};F]∥\hfill \\ \hfill & \le \gamma {\mu }_1\left(\parallel w^{(0)}-w^{(n)}\parallel ,\parallel x^{(n)}-x^{(0)}\parallel \right)\hfill \\ \hfill & \le \gamma {\mu }_1\left(\parallel x^{(n)}-x^{(0)}\parallel +\beta \parallel F(x^{(n)})-F(x^{(0)})\parallel ,r\right)\hfill \\ \hfill & \le \gamma {\mu }_1\left(r+\beta {\mu }_0(r),r\right)=m(r)<1.\hfill \end{array}$$

Therefore, applying Banach’s lemma again, we obtain that there exists $L_n^{-1}$ and $\parallel L_n^{-1}\parallel \le {\displaystyle \frac{\gamma }{1-m(r)}}.$ As we have seen in induction,

$$\parallel F(x^{(n)})\parallel \le l(r)\parallel z_m^{(n-1)}-z_{m-1}^{(n-1)}\parallel <{\eta }_0.$$

Thus,

$$\begin{array}{cc}\hfill \parallel z_1^{(n)}-x^{(n)}\parallel & \le \frac{\gamma }{1-m(r)}l(r)\parallel z_m^{(n-1)}-z_{m-1}^{(n-1)}\parallel \le \lambda (r)\parallel z_m^{(n-1)}-z_{m-1}^{(n-1)}\parallel \hfill \end{array}$$

By applying (8), we obtain

$$\parallel z_1^{(n)}-x^{(n)}{\parallel \le \lambda (r)\lambda (r)}^{(n-1)m+m-1}\parallel z_1^{(0)}-x^{(0)}{\parallel \le \lambda (r)}^{nm}\parallel z_1^{(0)}-x^{(0)}\parallel <r.$$

From this, we deduce

$$\begin{array}{c}\hfill \parallel z_1^{(n)}-x^{(0)}\parallel \le \parallel z_1^{(n)}-x^{(n)}\parallel +\parallel x^{(n)}-x^{(0)}{\parallel \le \lambda (r)}^{nm}\parallel z_1^{(0)}-x^{(0)}\parallel +\parallel x^{(n)}-x^{(0)}\parallel .\end{array}$$

By applying (9), we easily obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel z_1^{(n)}-x^{(0)}\parallel & \le \lambda {(r)}^{nm}\parallel z_1^{(0)}-x^{(0)}\parallel +{\displaystyle \frac{1-\lambda {(r)}^{m(n-1)+m}}{1-\lambda (r)}}\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & \le \frac{1-\lambda {(r)}^{nm+1}}{1-\lambda (r)}\parallel z_1^{(0)}-x^{(0)}\parallel \le \frac{1-\lambda {(r)}^{nm+1}}{1-\lambda (r)}b<r,\hfill \end{array}\end{array}$$

(4)

that is, $z_1^{(n)}\in B(x^{(0)},r)$. Let us see that $z_2^{(n)}\in B(x^{(0)},r).$ To do this, we first bound

$$\parallel z_2^{(n)}-z_1^{(n)}\parallel \le ∥{[z_1^{(n)},v^{(n)};F]}^{-1}∥\parallel F(z_1^{(n)})\parallel \le \parallel S_n^{-1}\parallel \parallel F(z_1^{(n)})\parallel .$$

Let see that $S_n^{-1}$ exists, using Banach’s lemma:

$$\begin{array}{cc}\hfill \parallel I-L_0^{-1}{S}_n\parallel & \le \parallel L_0^{-1}\parallel \parallel L_0-S_n\parallel \le \gamma ∥[w^{(0)},x^{(0)};F]-[v^{(n)},z_1^{(n)};F]∥\hfill \\ \hfill & \le \gamma {\mu }_1\left(\parallel z_1^{(n)}-x^{(0)}\parallel ,\parallel z_1^{(n)}-x^{(0)}\parallel +\beta \parallel F(z_1^{(n)})-F(x^{(0)})\parallel \right)\hfill \\ \hfill & \le \gamma {\mu }_1\left(r,r+\beta {\mu }_0(r)\right)=m(r)<1.\hfill \end{array}$$

Therefore, there exists $S_n^{-1}$, and $\parallel S_n^{-1}\parallel \le {\displaystyle \frac{\gamma }{1-m(r)}}$. Now, we calculate

$$F(z_1^{(n)})=F(x^{(n)})+[z_1^{(n)},x^{(n)};F](z_1^{(n)}-x^{(n)})=\left([x^{(n)},z_1^{(n)};F]-[w^{(n)},x^{(n)};F]\right)(z_1^{(n)}-x^{(n)}),$$

and by applying rules

$$\begin{array}{cc}\hfill \parallel F(z_1^{(n)})\parallel & \le \parallel z_1^{(n)}-x^{(n)}\parallel {\mu }_1\left(\beta \parallel F(x^{(n)})\parallel ,\parallel z_1^{(n)}-x^{(n)}\parallel \right)\le \parallel z_1^{(n)}-x^{(n)}\parallel {\mu }_1\left(r,\beta {\eta }_0\right)\le l(r)\parallel z_1^{(n)}-x^{(n)}\parallel <{\eta }_0.\hfill \end{array}$$

Therefore, we calculate the distance between iterations

$$\begin{array}{c}\hfill \parallel z_2^{(n)}-z_1^{(n)}\parallel \le \frac{\gamma }{1-m(r)}l(r)\parallel z_1^{(n)}-x^{(n)}{\parallel \le \lambda (r)}^{mn+1}\parallel z_1^{(0)}-x^{(0)}\parallel <r.\end{array}$$

Then, we have that $z_2^{(n)}\in B(x^{(0)},r)$, since

$$\begin{array}{cc}\hfill \parallel z_2^{(n)}-x^{(0)}\parallel & \le \parallel z_2^{(n)}-z_1^{(n)}\parallel +\parallel z_1^{(n)}-x^{(0)}{\parallel \le \lambda (r)}^{mn+1}\parallel z_1^{(0)}-x^{(0)}\parallel +{\displaystyle \frac{1-\lambda {(r)}^{mn+1}}{1-\lambda (r)}}b\hfill \\ \hfill & \lambda {(r)}^{mn+1}b+\frac{1-\lambda {(r)}^{mn+1}}{1-\lambda (r)}b\le \frac{1-\lambda {(r)}^{mn+2}}{1-\lambda (r)}b<r.\hfill \end{array}$$

By induction on the number of steps in iteration number $n+1$ of the method, we can reason analogously to the other iterations and obtain

(A)

$\parallel F(z_m^{(n)})\parallel \le l(r)\parallel z_m^{(n)}-z_{m-1}^{(n)}\parallel <{\eta }_0.$

(B)

$\parallel z_m^{(n)}-z_{m-1}^{(n)}{\parallel \le \lambda (r)}^{m(n+1)-1}\parallel z_1^{(0)}-x^{(0)}\parallel <r.$

(C)

$\parallel z_m^{(n)}-x^{(0)}\parallel \le {\displaystyle \frac{1-\lambda {(r)}^{m(n+1)}}{1-\lambda (r)}}b<r$ and $z_m^{(n)}\in B(x^{(0)},r)$, $\forall n\in \mathbb{N}$.

Since $x^{(n+1)}=z_m^{(n)}$, we obtain that the iteration $x^{(n+1)}$ belongs to the convergence ball $B(x_0,r)$, where

$$\begin{array}{c}\hfill \parallel x^{(n+1)}-x^{(0)}\parallel \le {\displaystyle \frac{b}{1-\lambda (r)}}=r,\end{array}$$

being that r is the radius of convergence. Now, using (A), (B) and (C), we are going to prove that the sequence of iterations $\left\{x_n\right\}$ is a Cauchy sequence in the ball $B(x_0,r)$. We want to bound $\parallel x^{(n)}-x^{(n-1)}\parallel$ in relation to $\parallel z_1^{(n-1)}-x^{(n-1)}\parallel$.

$$\begin{array}{cc}\hfill \parallel x^{(n)}-x^{(n-1)}\parallel & =\parallel z_m^{(n-1)}-x^{(n-1)}\parallel \hfill \\ \hfill & =\parallel z_m^{(n-1)}-z_{m-1}^{(n-1)}+z_{m-1}^{(n-1)}-z_{m-2}^{(n-1)}+z_{m-2}^{(n-1)}+\dots -z_2^{(n-1)}+z_2^{(n-1)}-z_1^{(n-1)}+z_1^{(n-1)}-x^{(n-1)}\parallel \hfill \\ \hfill & \le \parallel z_m^{(n-1)}-z_{m-1}^{(n-1)}\parallel +\parallel z_{m-1}^{(n-1)}-z_{m-2}^{(n-1)}\parallel +\dots +\parallel z_2^{(n-1)}-z_1^{(n-1)}\parallel +\parallel z_1^{(n-1)}-x^{(n-1)}\parallel \hfill \end{array}$$

By condition $(8)$, it follows that

$$\parallel z_q^{(n-1)}-z_{q-1}^{(n-1)}{\parallel \le \lambda (r)}^{q-1}\parallel z_1^{(n-1)}-x^{(n-1)}\parallel .$$

Therefore, by applying this,

$$\begin{array}{cc}\parallel x^{(n)}-x^{(n-1)}\parallel \hfill & =\parallel z_m^{(n-1)}-x^{(n-1)}\parallel \hfill \\ & \le \parallel z_m^{(n-1)}-z_{m-1}^{(n-1)}\parallel +\parallel z_{m-1}^{(n-1)}-z_{m-2}^{(n-1)}\parallel +\dots +\parallel z_2^{(n-1)}-z_1^{(n-1)}\parallel +\parallel z_1^{(n-1)}-x^{(n-1)}\parallel \hfill \\ & \le \lambda {(r)}^{m-1}\parallel z_1^{(n-1)}-x^{(n-1)}{\parallel +\lambda (r)}^{m-2}\parallel z_1^{(n-1)}-x^{(n-1)}\parallel +\dots +\lambda (r)\parallel z_1^{(n-1)}-x^{(n-1)}\parallel +\parallel z_1^{(n-1)}-x^{(n-1)}\parallel \hfill \\ & \le (\lambda {(r)}^{m-1}+\lambda {(r)}^{m-2}+\dots +\lambda (r)+1)\parallel z_1^{(n-1)}-x^{(n-1)}\parallel \hfill \\ & \le {\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}\parallel z_1^{(n-1)}-x^{(n-1)}\parallel .\hfill \end{array}$$

We therefore calculate

$$\begin{array}{cc}\parallel x^{(n+k)}-x^{(n-1)}\parallel \hfill & \le \parallel x^{(n+k)}-x^{(n+k-1)}\parallel +\parallel x^{(n+k-1)}-x^{(n+k-2)}\parallel +\dots +\parallel x^{(n+1)}-x^{(n)}\parallel +\parallel x^{(n)}-x^{(n-1)}\parallel \hfill \\ & \le {\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}\parallel z_1^{(n+k-1)}-x^{(n+k-1)}\parallel +{\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}\parallel z_1^{(n+k-2)}-x^{(n+k-2)}\parallel +\dots +{\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}\parallel z_1^{(n-1)}-x^{(n-1)}\parallel \hfill \\ & \le {\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}(\parallel z_1^{(n+k-1)}-x^{(n+k-1)}\parallel +\parallel z_1^{(n+k-2)}-x^{(n+k-2)}\parallel +\dots +\parallel z_1^{(n-1)}-x^{(n-1)}\parallel )\hfill \end{array}$$

Furthermore, from the property $(8)$ it also follows that

$$\parallel z_1^{(n-1)}-x^{(n-1)}{\parallel \le \lambda (r)}^{mk}\parallel z_1^{(n-1-k)}-x^{(n-1-k)}\parallel .$$

In this way,

$$\begin{array}{cc}\hfill \parallel x^{(n+k)}-x^{(n-1)}\parallel & \le {\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}(\parallel z_1^{(n+k-1)}-x^{(n+k-1)}\parallel +\parallel z_1^{(n+k-2)}-x^{(n+k-2)}\parallel +\dots +\parallel z_1^{(n-1)}-x^{(n-1)}\parallel )\hfill \\ \hfill & \le {\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}{(\lambda (r)}^{mk}\parallel z_1^{(n-1)}-x^{(n-1)}{\parallel +\lambda (r)}^{m(k-1)}\parallel z_1^{(n-1)}-x^{(n-1)}\parallel +\dots +\parallel z_1^{(n-1)}-x^{(n-1)}\parallel )\hfill \\ \hfill & \le {\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}(\lambda {(r)}^{mk}+\lambda {(r)}^{m(k-1)}+\dots +\lambda {(r)}^m+1)\parallel z_1^{(n-1)}-x^{(n-1)}\parallel \hfill \\ \hfill & \le {\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}{\displaystyle \frac{1-\lambda {(r)}^{m(k+1)}}{1-\lambda {(r)}^m}}\parallel z_1^{(n-1)}-x^{(n-1)}\parallel \hfill \\ \hfill & \le {\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda (r)}}{\displaystyle \frac{1-\lambda {(r)}^{m(k+1)}}{1-\lambda {(r)}^m}}\lambda {(r)}^{m(n-1)}\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & \le {\displaystyle \frac{1-\lambda {(r)}^{m(k+1)}}{1-\lambda (r)}}{\displaystyle \frac{1-\lambda {(r)}^m}{1-\lambda {(r)}^m}}\lambda {(r)}^{m(n-1)}\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & \le {\displaystyle \frac{1-\lambda {(r)}^{m(k+1)}}{1-\lambda (r)}}\lambda {(r)}^{m(n-1)}\parallel z_1^{(0)}-x^{(0)}\parallel \hfill \\ \hfill & <{\displaystyle \frac{1}{1-\lambda (r)}}\lambda {(r)}^{m(n-1)}\parallel z_1^{(0)}-x^{(0)}\parallel .\hfill \end{array}$$

By condition (A), $\parallel F(z_m^{(n)})\parallel \le l(r)\parallel z_m^{(n)}-z_{m-1}^{(n)}\parallel <{\eta }_0.$

Therefore, by applying condition (B), $\parallel F(x^{(n+1)})\parallel =\parallel F(z_m^{(n)})\parallel \le l(r)\parallel z_m^{(n)}-z_{m-1}^{(n)}\parallel \le l(r)\lambda {(r)}^{m-1}\parallel z_1^{(n)}-x^{(n)}\parallel$.

Moreover, by taking limits when $n⟶\infty$, as $\parallel z_1^{(n)}-x^{(n)}\parallel ⟶0$, and thus, by the continuity of the operator F, $F(x^{*})=0$. □

Theorem 2.

Under the conditions (I)–(III), we suppose that the equation

$$\gamma {\mu }_1(t,t+\beta {\mu }_0(t))-1=0$$

(5)

has at least one positive real root, where R is the smallest positive real root of this equation. Then, the solution α is the only solution of the equation $H(x)=0$ in $\overline{B(\alpha ,R)}\cap \mathsf{\Omega }$

Proof. 

To see the uniqueness of the solution, we assume by the reduction to the absurd that another solution exists $\tilde{\alpha }\in \overline{B(x_0,R)}\cup \mathsf{\Omega }$, and we consider the operator $P=[\alpha ,\tilde{\alpha };F]$. Then, since $P(\tilde{\alpha }-\alpha )=F(\tilde{\alpha })-F(\alpha )=0$, if we prove that P is an inverse operator, we will have that $\tilde{\alpha }=\alpha$. Then, to apply Banach’s lemma, we prove

$$\begin{array}{cc}\hfill \parallel I-L_0^{-1}P\parallel & \le \parallel L_0^{-1}\parallel \parallel L_0-P\parallel \hfill \\ \hfill & \le \gamma \parallel [x^{(0)},x^{(0)}+\beta F(x^{(0)});F]-[\alpha ,\tilde{\alpha };F]\parallel \hfill \\ \hfill & \le \gamma {\mu }_1(\parallel x^{(0)}-\alpha \parallel ,\parallel x^{(0)}+\beta F(x^{(0)})-\tilde{\alpha }\parallel )\hfill \\ \hfill & \le \gamma {\mu }_1(\parallel x^{(0)}-\alpha \parallel ,\parallel x^{(0)}-\tilde{\alpha }\parallel +\beta \parallel F(x^{(0)})\parallel )\hfill \\ \hfill & \le \gamma {\mu }_1(\parallel x^{(0)}-\alpha \parallel ,\parallel x^{(0)}-\tilde{\alpha }\parallel +\beta {\mu }_0(\parallel x^{(0)}-\alpha \parallel ))\hfill \\ \hfill & <\gamma {\mu }_1(R,R+\beta {\mu }_0(R))=1.\hfill \end{array}$$

In the last inequality, we used the hypothesis that there is at least one positive real root of Equation (5) since this implies that at least one of the functions ${\mu }_0(t)$ or ${\mu }_1(t)$ is strictly increasing. So, the uniqueness follows. □

3. Numerical Experiments

In this section, we study numerically our family of methods (2) for different values of $\beta$. In doing so, we highlight the best methods of the family from two essential points of view in numerical analysis: semi-local and dynamic convergence.

For the calculations and dynamical planes, we used MATLAB R2022a with 100-digit variable precision arithmetic.

3.1. Numerical Study of Semilocal Convergence

In this subsection, we apply the theoretical results obtained in previous sections for obtaining the convergence and uniqueness domain of the solution of a nonlinear and non-differentiable integral equation. These kinds of equations play an important role in the study of nonlinear physical phenomena that appear in various scientific and engineering fields, such as chemical physics, fluid mechanics, plasma physics, biology, etc.

We consider the equation

$$x(s)=f(s)+\frac{1}{2}{\int }_a^{b}K(s,t)\varphi (x(t))dt,a\le s\le b,$$

(6)

where $K:[a,b]\times [a,b]\to \mathbb{R}$ is the Green’s function. We transform the equation by discretization into

$$F(x)(s)=x(s)-f(s)-\frac{1}{2}{\int }_a^{b}K(s,t)\varphi (x(t))dt=0.$$

(7)

This problem is finite dimensional if we approximate the integral by the Gauss–Legendre quadrature formula

$${\int }_a^{b}q(t)dt\simeq \sum _{i=1}^p{\omega }_{i}q(t_i)$$

where the nodes $t_i$ and the weights ${\omega }_i$ are known.

If we denote the approximations of $x(t_i)$ and $f(t_i)$ by $x_i$ and $f_i$, respectively, with $i=1,\cdots ,p,$ then Equation (7) is equivalent to the following nonlinear system:

$$x_i=f_i+\frac{1}{2}\sum _{j=1}^p{a}_{ij}\varphi (x_j),j=1,\dots ,p,$$

(8)

where

$$a_{ij}={\omega }_{j}K(t_i,t_j)=\left\{\begin{array}{cc}{\omega }_j\frac{(b-t_i)(t_j-a)}{b-a},\hfill & j\le i\hfill \\ {\omega }_j\frac{(b-t_j)(t_i-a)}{b-a},\hfill & j\le i.\hfill \end{array}\right.$$

Now, the system (8) can be written as

$$F(x)\equiv x-f-\frac{1}{2}Az=0,F:{\mathbb{R}}^p\to {\mathbb{R}}^p,$$

(9)

where

$$x={(x_1,\cdots ,x_p)}^T,f={(f_1,\cdots ,f_p)}^T,A={(a_{ij})}_{i,j=1}^p,z={(\varphi (x_1),\cdots ,\varphi (x_p))}^T.$$

We choose $a=0$, $b=1$, $K(s,t)$ as the Green’s function in $[0,1]\times [0,1]$ and $\varphi (x(t))={(x(t))}^3+\left|x(t)\right|$ in (6). Then, the nonlinear equation system given in (9) is of the form

$$F(x)\equiv x-f-\frac{1}{2}A(x_1^3+|x_1|,\dots ,x_p^3+|x_p|)=0.$$

(10)

It is obvious that the function F defined in (10) is non-linear and non-differentiable. Therefore, we can apply our method which dispenses with derivatives and uses divided differences. We can consider the first-order divided differences that do not require F to be differentiable (see [11]), defined by the following expression:

$$\begin{array}{cc}\hfill [u,v;F]=& {({[u,v,F]}_{ij})}_{i,j=1}^p\in \mathcal{L}({\mathbb{R}}^p,{\mathbb{R}}^p),\mathrm{where}\hfill \\ \hfill {[u,v;F]}_{i,j}& =\frac{1}{u_j-v_j}(F_i(u_1,\cdots ,u_j,v_{j+1},\cdots ,v_p)-F_i(u_1,\cdots ,u_{j-1},v_j,\cdots ,v_p)),\mathrm{where}\hfill \\ \hfill u& ={(u_1,\cdots ,u_p)}^T\mathrm{and}v={(v_1,\cdots ,v_p)}^T.\hfill \end{array}$$

To simplify the problem, we consider $f=0$ in (10). Obviously, in this case, $\alpha =0$ is a solution of $F(x)=0$, and it is the solution on which we study the semilocal convergence. Although for this study it is not necessary to know the solution, we use this information to take the $\mathsf{\Omega }=B(0,\xi )$ as the domain.

Taking $f=0$, the nonlinear equation system given by (10) is of the form

$$F(x)=x-\frac{1}{2}Az,z_j=x_j^3+\left|x_j\right|,j=1,\cdots ,p.$$

(11)

We now calculate $[x,y;F]$, first calculating ${[x,y,F]}_{ij}$ for $i,j=1,\cdots ,p$:

$$\begin{array}{cc}\hfill {[x,y,F]}_{ij}& =\frac{1}{x_j-y_j}\left[F_i(x_1,\cdots ,x_j,y_{j+1},\cdots ,y_p)-F_i(x_1,\cdots ,x_{j-1},y_j,\cdots ,y_p)\right]\hfill \\ \hfill =& -\frac{1}{2(x_j-y_j)}(a_{i1},\cdots ,a_{in})\left(x_1^3+|x_1|,\cdots ,x_j^3+|x_j|,y_{j+1}^3+|y_{j+1}|,\cdots ,y_p^3+\left|y_p\right|\right)\hfill \\ \hfill & +\frac{1}{2(x_j-y_j)}(a_{i1},\cdots ,a_{in})\left(x_1^3+|x_1|,\cdots ,x_{j-1}^3+|x_{j-1}|,y_j^3+|y_j|,\cdots ,y_p^3+\left|y_p\right|\right)\hfill \end{array}$$

Since j is the only component that does not cancel out,

$$\begin{array}{cc}\hfill {[x,y,F]}_{ij}& =-a_{ij}\frac{1}{2(x_j-y_j)}\left[\left(x_j^3+\left|x_j\right|\right)-\left(y_j^3+\left|y_j\right|\right)\right]=-\frac{a_{ij}}{2}\left(\left(\frac{x_j^3-y_j^3}{x_j-y_j}\right)+\left(\frac{|x_j|-|y_j|}{x_j-y_j}\right)\right)\hfill \\ \hfill & =-\frac{a_{ij}}{2}\left((x_j^2+x_j{y}_j+y_j^2)+\frac{|x_j|-|y_j|}{x_j-y_j}\right).\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill [x,y,F]& =I-\frac{1}{2}A·Diag\left(\left(\begin{array}{c}{x}_1^2+x_1{y}_1+y_1^2\\ \cdots \\ x_p^2+x_p{y}_p+y_p^2\end{array}\right)+\left(\begin{array}{c}\frac{|x_1|-|y_1|}{x_1-y_1}\\ \cdots \\ \frac{|x_p|-|y_p|}{x_p-y_p}\end{array}\right)\right).\hfill \end{array}$$

If we consider $\mathsf{\Omega }=B(0,\xi ),$ then

$$\parallel F(x)-F(y)\parallel \le \parallel x-y-\frac{1}{2}A(x^3-y^3)-\frac{1}{2}A(|x|-|y|)\parallel \le \parallel x-y\parallel +\frac{1}{2}\parallel A\parallel \parallel x^3-y^3\parallel +\frac{1}{2}\parallel A\parallel \parallel \left|x\right|-\left|y\right|\parallel .$$

(12)

As we know that $\parallel x^3-y^3\parallel \le \parallel x-y\parallel \parallel x^2+xy+y^2\parallel$ and $\parallel \left|x\right|-\left|y\right|\parallel \le \parallel x-y\parallel$ is satisfied, then

$$\begin{array}{cc}\hfill \parallel F(x)-F(y)\parallel & \le \parallel x-y\parallel +\frac{1}{2}\parallel A\parallel \left(\parallel x-y\parallel \parallel x^2+xy+y^2\parallel +\parallel x-y\parallel \right)\hfill \\ & \le \parallel x-y\parallel +\frac{1}{2}\parallel A\parallel \left(3{\xi }^2\parallel x-y\parallel +\parallel x-y\parallel \right)\le {\mu }_0(\parallel x-y\parallel ),\hfill \end{array}$$

with ${\mu }_0(t)=t+\frac{1}{2}\parallel A\parallel (3{\xi }^2+1)t.$

On the other hand, we develop

$$\begin{array}{cc}\hfill \parallel [x,y;F]-[u,v;F]\parallel & =∥I-\frac{1}{2}A\left((x^2+xy+y^2)+\frac{\left|x\right|-\left|y\right|}{x-y}\right)-I+\frac{1}{2}A\left((u^2+uv+v^2)+\frac{\left|u\right|-\left|v\right|}{u-v}\right)∥\hfill \\ \hfill & \le \frac{1}{2}\parallel A\parallel \left(\parallel x^2+xy+y^2-u^2-uv-v^2\parallel +∥\frac{\left|x\right|-\left|y\right|}{x-y}-\frac{\left|u\right|-\left|v\right|}{u-v}∥\right)\hfill \\ \hfill & \le \frac{1}{2}\parallel A\parallel \left(\parallel x^2-u^2\parallel +\parallel y^2-v^2\parallel +\parallel xy-uv\parallel \right)+2\parallel A\parallel \hfill \\ \hfill & \le \frac{1}{2}\parallel A\parallel \left(\parallel x-u\parallel \parallel x+u\parallel +\parallel y-v\parallel \parallel y+v\parallel +\parallel xy-xv+xv-uv\parallel \right)+2\parallel A\parallel \hfill \\ \hfill & \le \frac{1}{2}\parallel A\parallel \left(2\xi \parallel x-u\parallel +2\xi |y-v\parallel +\parallel x\parallel \parallel y-v\parallel +\parallel v\parallel \parallel x-u\parallel \right)+2\parallel A\parallel \hfill \\ \hfill & \le \frac{1}{2}\parallel A\parallel \left(2+3\xi (\parallel x-u\parallel +\parallel y-v\parallel )\right).\hfill \end{array}$$

Therefore, we have

$${\mu }_1(s,t)=\frac{1}{2}\parallel A\parallel (2+3\xi (s+t)).$$

(13)

Under these conditions, $\alpha =0$ is a solution of the problem. Furthermore, assuming that the dimension of the problem is $p=8$, we have

$$\parallel I-L\parallel \le \parallel I-[w^{(0)},x^{(0)};F]\parallel \le \frac{1}{2}\parallel A\parallel (3{\xi }^2+1)$$

since

$$\begin{array}{cc}\hfill [w^{(0)},x^{(0)},F]& =I-\frac{1}{2}A·Diag\left(\left(\begin{array}{c}{(x_1^{(0)})}^2+x_1^{(0)}{w}_1^{(0)}+{(w_1^{(0)})}^2\\ \cdots \\ {(x_p^{(0)})}^2+x_p^{(0)}{w}_p^{(0)}+{(w_p^{(0)})}^2\end{array}\right)+\left(\begin{array}{c}\frac{|x_1^{(0)}|-|w_1^{(0)}|}{x_1^{(0)}-w_1^{(0)}}\\ \cdots \\ \frac{|x_p^{(0)}|-|w_p^{(0)}|}{x_p^{(0)}-w_p^{(0)}}\end{array}\right)\right).\hfill \end{array}$$

and $w^{(0)},x^{(0)}\in B(0,\xi )$. Then, if ${\displaystyle \frac{1}{2}}\parallel A\parallel (3{\xi }^2+1)<1$, by the Banach’s lemma, $L^{-1}$ exists and

$$\parallel L^{-1}\parallel <\frac{2}{2-\parallel A\parallel (3{\xi }^2+1)}=\gamma .$$

For this experiment, we consider that $\xi =1$ and, therefore, we take an initial estimate belonging to the ball $B(0,1)$. For example,

$$x^{(0)}={(0.1,\dots ,0.1)}^T.$$

In this case, $w^{(0)}=x^{(0)}+F(x^{(0)})$ also remains inside $B(0,1)$ because

$$\parallel w^{(0)}\parallel =\parallel x^{(0)}\parallel +\parallel F(x^{(0)})\parallel \le \parallel x^{(0)}\parallel +\parallel x^{(0)}\parallel +\frac{1}{2}\parallel A\parallel (\parallel x^{(0)}{\parallel }^3+\parallel x^{(0)}\parallel )\le 0.2063.$$

In addition, in the previous bound, we used that

$$\parallel F(x^{(0)})\parallel \le \parallel x^{(0)}\parallel +\frac{1}{2}\parallel A\parallel (\parallel x^{(0)}{\parallel }^3+\parallel x^{(0)}\parallel ),$$

which allows us to deduce the parameter ${\eta }_0$ as $\parallel F(x^{(0)})\parallel \le 0.1063={\eta }_0$. The rest of the bounds and parameters are deduced for particular $\beta$, and that is the reason that in the following table, we present the radius of convergence and uniqueness that we obtain by changing $\beta$, and, in turn, we check the values of $m(r)$, $\lambda (r)$, b and $l(r)\gamma$ to verify that the conditions of the semilocal convergence existence theorem are fulfilled.

As we can see in

Table 1. Numerical results with different values of $\beta$.

$\mathit{\beta }$	r	R	$\mathit{m}(\mathit{r})$	$\mathit{\lambda }(\mathit{r})$	b	$\mathit{l}(\mathit{r})\mathit{\gamma }$
$0.01$	$0.2016$	$1.6563$	$0.2681$	$0.2970$	$0.1417$	$0.2173$
$0.02$	$0.2018$	$1.6461$	$0.2688$	$0.2977$	$0.1417$	$0.2177$
$0.03$	$0.2020$	$1.6360$	$0.2696$	$0.2984$	$0.1417$	$0.2180$
⋯	⋯	⋯	⋯	⋯	⋯	⋯
$0.1$	$0.2036$	$1.5686$	$0.2748$	$0.3037$	$0.1417$	0.2202
$0.2$	$0.2059$	$1.4815$	$0.2825$	$0.3114$	$0.1417$	$0.2234$
$0.3$	$0.2083$	$1.4035$	$0.2903$	$0.3195$	$0.1417$	$0.2267$
⋯	⋯	⋯	⋯	⋯	⋯	⋯
$1.0$	$0.2324$	$1.0256$	$0.3555$	$0.3899$	$0.1417$	$0.2513$
$1.1$	$0.2376$	$0.9877$	$0.3671$	$0.4034$	$0.1417$	$0.2553$
$1.2$	$0.2438$	$0.9524$	$0.3800$	$0.4185$	$0.1417$	$0.2595$

, the best semilocal convergence results are obtained for the smallest values of $\beta$. Moreover, for this value of $x_0$, we also obtain a larger uniqueness radius than for the rest of the values, which implies that we can ensure the uniqueness of the solution in a larger set. On the other hand, it is interesting to note that for $\beta =1$, i.e., for the Steffensen multistep method with second frozen divided difference, we do not obtain the best results in terms of semilocal convergence, and this fact implies that we have better options in this new family. Finally, it is important to point out that the optimal existence and uniqueness radii are obtained when $\beta ⟶0$ since the symmetric divided difference operators, $[x^{(k)},x^{(k)};F]$ and $[z_1^{(k)},z_1^{(k)};F]$, are the best approximations to the derivatives in the (2) scheme.

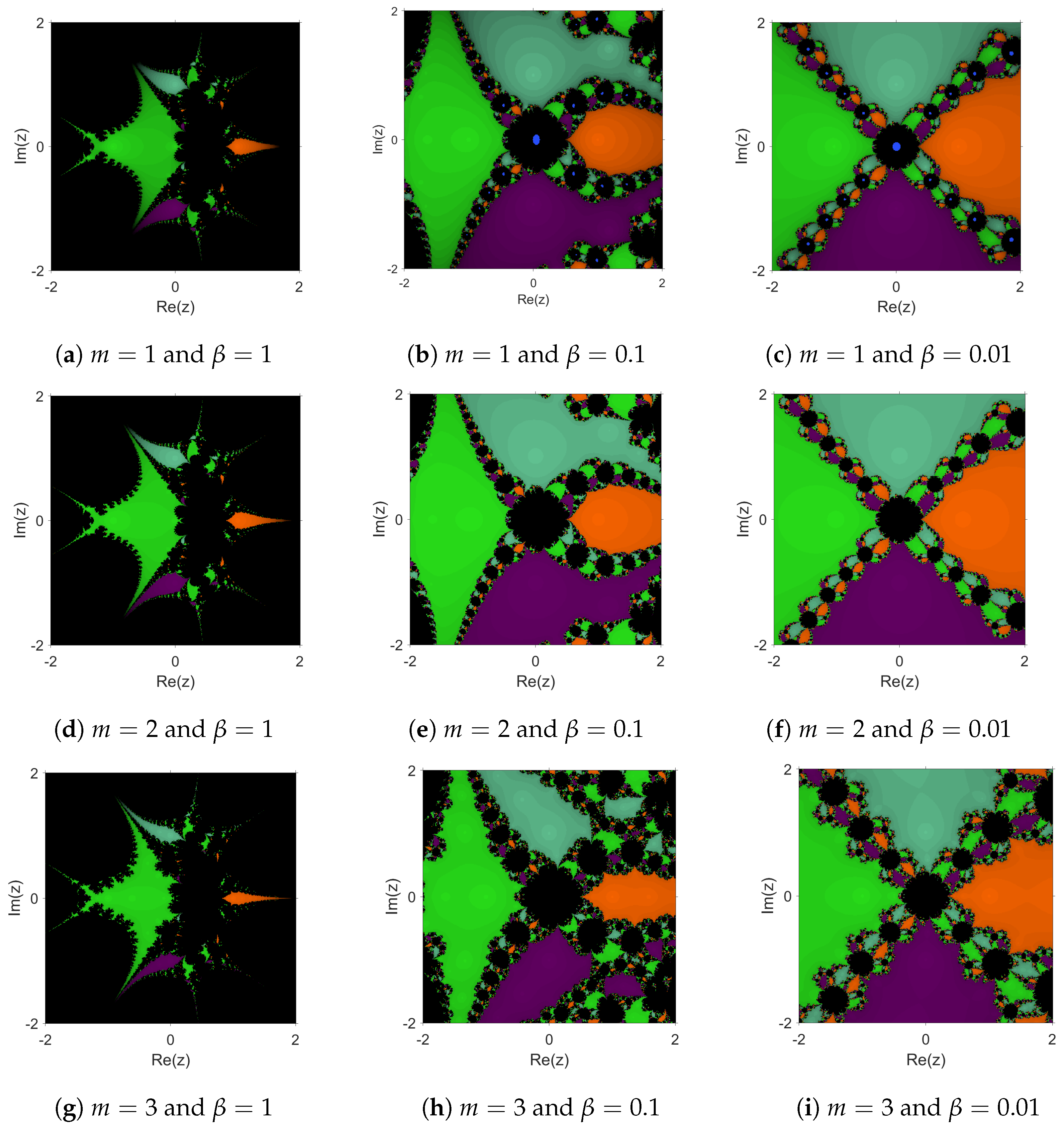
3.2. Dynamical Planes for Different Steps

In this section, we compare the different dynamical planes that are generated by varying the parameter $\beta$ and the number of steps m of the family of numerical methods. For dynamical planes, we choose a mesh of $400\times 400$ points, and what we do is apply our family of methods to each of these points, taking the point as the method’s initial estimate z. We consider z as a complex number, and represent their real part in the abscissa axis and their imaginary part in the ordinate axis. We define that the maximum number of iterations that we must carry out with each initial estimate is 50 and we consider that the initial points of the mesh converge to one of the solutions of the function if the distance to that solution is less than ${10}^{-3}$.

The function to which we apply the family of methods is

$$f(x)=x^4-1.$$

We represent in orange the initial points that converge to the root 1, in green the initial points that converge to the root $-1$, in blue the initial points that converge to the root i, in purple the initial points that converge to the root $-i$ and in black the initial points that do not converge to any root in fewer than 50 iterations.

As is illustrated in the dynamic planes, Figure 1, we observe a behavior similar to what happened in the numerical example of the semilocal convergence since, as the value of parameter $\beta$ decreases, the basins of attraction of the roots increase. Note that when $\beta =0.01$, in the dynamic planes we can observe that the basins of attraction of the four roots of the function present a symmetry, that is to say, the same amount of initial points converge to the roots within the chosen mesh.

On the other hand, regarding the number of steps, using one or two steps does not apparently change the number of points that converge to a solution but it does decrease when the number of steps increases. However, by employing more steps, convergence is realized in a smaller number of iterations as we see in the figures since the intensity of color determines the number of iterations needed to satisfy the stopping criterion.

Therefore, if we had to choose between the illustrated methods, which of them is more convenient in this simple polynomial case, dynamically speaking, we would choose the method using $m=2$ and $\beta =0.01$ since it obtains a large number of points converging to one of the solutions in a few iterations.

4. Conclusions

In this work, a new family of Steffensen-type methods was introduced, and a semilocal convergence study of this family was developed. Theoretical studies of the semilocal convergence were verified by applying the method to a Hammerstein-type nonlinear integral equation. Finally, we analyzed some dynamical planes of the method applied to a nonlinear equation in order to conclude which number of steps and which $\beta$ is more convenient from the dynamic point of view.

In conclusion, it is important to emphasize that, although working with methods with many steps is not convenient to study simple numerical examples, it is necessary to use these methods for problems in which we work on very large systems. This is because the more steps there are in the method used, the fewer iterations it performs to find the solution, and, therefore, this means less execution time.