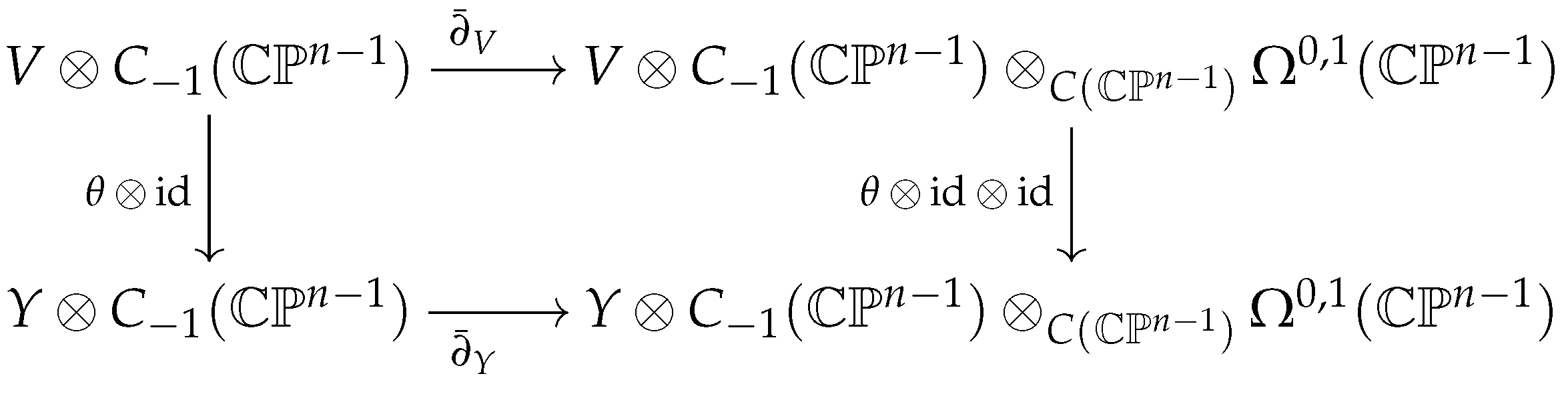Differentiating the State Evaluation Map from Matrices to Functions on Projective Space

Abstract

The pure state evaluation map from $M_n\left(\mathbb{C}\right)$ to $C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ is a completely positive map of $C^{*}$-algebras intertwining the $U_n$ symmetries on the two algebras. We show that it extends to a cochain map from the universal calculus on $M_n\left(\mathbb{C}\right)$ to the holomorphic $\overline{\partial }$ calculus on $\mathbb{C}{\mathbb{P}}^{n-1}$. The method uses connections on Hilbert $C^{*}$-bimodules.

1. Introduction

For a subset X of the state space S of a $C^{*}$-algebra A we have a positive “state evaluation map” $\delta :A\to C\left(X\right)$ given by $\delta \left(a\right)\left(\varphi \right)=\varphi \left(a\right)$ for $a\in A$ and $\varphi \in X$. For $M_n\left(\mathbb{C}\right)$ the result of Choi [1] gave the pure state space as $\mathbb{C}{\mathbb{P}}^{n-1}$. We use the KSGNS construction [2] to analyse the case $A=M_n\left(\mathbb{C}\right)$ and $X=\mathbb{C}{\mathbb{P}}^{n-1}$ and then consider the differentiability of the state evaluation map. To do this, we begin by constructing the Hilbert $C^{*}$-bimodule giving the state evaluation map. Then, we use the methods of connections on bimodules to connect the differential structure on $M_n\left(\mathbb{C}\right)$ (we take the universal calculus) to that on $\mathbb{C}{\mathbb{P}}^{n-1}$ (the usual calculus). Here, we follow the methods in [3] but then find that the conditions required there do not apply, so in Section 5.1 we consider a more general theory extending the results in [3]. As a result, Proposition 12 on an induced functor from left $M_n$-modules to holomorphic bundles on $\mathbb{C}{\mathbb{P}}^{n-1}$ is phrased in terms of holomorphic bundles rather than flat bundles on $\mathbb{C}{\mathbb{P}}^{n-1}$. For brevity, we often refer to $M_n\left(\mathbb{C}\right)$ just as $M_n$. Additionally, our main result Theorem 1 on extending the state evaluation map to a cochain map uses the $\overline{\partial }$ calculus on projective space.

The main reason why we chose to do this construction with $M_n$ is the concrete construction of the state space. More generally, it might be possible to put a differential structure on the pure state space of a $C^{*}$-algebra, even if we know little about the state space. For this one thing, it is important to remember that there is a very general idea of calculus on infinite dimensional spaces [4] using directional derivatives. It would be interesting to see whether the constraint of having bimodule connections, similar to the one in this paper, for smooth subalgebras of more general $C^{*}$-algebras would shed light on possible calculi on the algebras.

Apart from the concrete description of the state space, another reason why we are interested in the calculi on matrix algebras and the link with representations and states is Connes’ noncommutative derivation of the standard model [5]. The fact is that from a relatively simple noncommutative beginning involving matrices Connes constructs the standard model indicates that there probably something very interesting in the geometry of the initial noncommutative space. Most gauge theories in physics are described in terms of calculi, so we are naturally led to questions about calculi on matrices and how they relate to states. The unitary symmetry described in Section 3.1 is then related to gauge transformations.

The construction of the state evaluation map and its associated bimodule implies the existence of various functors between categories of modules, including one from $M_n\left(\mathbb{C}\right)$ modules to holomorphic bundles on $\mathbb{C}{\mathbb{P}}^{n-1}$, which is described in Section 6.

We use the notation that $h_i\in {\mathrm{Col}}^n\left(\mathbb{C}\right)$ is the column vector with 1 in position i and zero elsewhere, and that $E_{ij}\in M_n\left(\mathbb{C}\right)$ in the matrix with 1 in row i and column j and zero elsewhere. An element of $\mathbb{C}{\mathbb{P}}^{n-1}$ is written in homogenous coordinates as $\left[(v_1\cdots v_n)\right]$, where we suppose $\sum |v_i{|}^2=1$. We sum over repeated indices unless otherwise indicated.

2. Preliminaries

2.1. Calculi and Connections

Definition 1. 

Given a first order calculus $({\Omega }_A^1,\mathrm{d})$ on an algebra A, the maximal prolongation calculus ${\Omega }_A$ has relations $\sum \mathrm{d}{c}_i\wedge \mathrm{d}{a}_i=0$ for every relation $\sum c_i\mathrm{d}{a}_i=0$ on ${\Omega }_A^1$, where $c_i,a_i\in A$.

Definition 2. 

The universal first order calculus ${\Omega }_{\mathrm{uni}}^1\left(A\right)$ on a unital algebra A is defined by

$${\Omega }_{\mathrm{uni}}^1\left(A\right)=ker·:A\otimes A\to A,$$

where · is the algebra product and ${\mathrm{d}}_{\mathrm{uni}}a=1\otimes a-a\otimes 1$.

The maximal prolongation of the universal calculus has ${\Omega }_{\mathrm{uni}}^n\left(A\right)\subset A^{\otimes n+1}$, which is the intersection of all the kernels of the multiplication maps between neighbouring factors, i.e.,

$${\Omega }_{\mathrm{uni}}^2\left(A\right)=ker(·\otimes \mathrm{id}:A\otimes A\otimes A\to A\otimes A)\cap ker(\mathrm{id}\otimes ·:A\otimes A\otimes A\to A\otimes A).$$

We now assume that the unital algebras A and B have calculi ${\Omega }_A^n$ and ${\Omega }_B^n$, respectively.

Definition 3. 

A right connection ${\nabla }_E:E\to E{\otimes }_B{\Omega }_B^1$ on a right B-module E is a linear map obeying the right Leibniz rule for $e\in E$ and $b\in B$

$${\nabla }_E\left(eb\right)=e\otimes \mathrm{d}b+{\nabla }_E\left(e\right).b.$$

(1)

Definition 4. 

Given the right connection $(E,{\nabla }_E)$ in Definition 3, we define for $n\ge 1$

$${\nabla }_E^{\left[n\right]}:E\underset{B}{\otimes }{\Omega }_B^n\to E\underset{B}{\otimes }{\Omega }_B^{n+1}$$

by ${\nabla }_E^{\left[1\right]}={\nabla }_E$ and for $n\ge 2$

$${\nabla }_E^{\left[n\right]}(e\otimes \xi )={\nabla }_{E}e\wedge \xi +e\otimes \mathrm{d}\xi .$$

The curvature of E is the right bimodule map

$$R_E={\nabla }_E^{\left[1\right]}{\nabla }_E:E\to E\underset{B}{\otimes }{\Omega }_B^2$$

and then for $e\otimes \xi \in E{\otimes }_B{\Omega }_B^n$

$${\nabla }_E^{[n+1]}{\nabla }_E^{\left[n\right]}(e\otimes \xi )=R_E\left(e\right)\wedge \xi .$$

The idea of a bimodule connection was introduced in [6,7,8] and used in [9,10]. It was used to construct connections on tensor products in [11] (see Proposition 1).

Definition 5. 

If E is an A-B bimodule, then $({\nabla }_E,{\sigma }_E)$ is a right bimodule connection where ${\nabla }_E$ is a right connection and there is a bimodule map

$${\sigma }_E:{\Omega }_A^1\underset{A}{\otimes }E\to E\underset{B}{\otimes }{\Omega }_B^1$$

so that

$${\nabla }_E\left(ae\right)={\sigma }_E(\mathrm{d}a\otimes e)+a.{\nabla }_{E}e.$$

2.2. Hilbert Bimodules

Note that, unlike most of the literature on Hilbert $C^{*}$-modules, we explicitly use conjugate bundles and modules. This is required to make the usual tensor products and connections work with inner products. Suppose that A and B are *-algebras. For a left A-module $E,\overline{E}$ is the conjugate vector space with right A-action $\overline{e}.a=\overline{a^{*}e}$, and for a right A module F, $\overline{F}$ is the conjugate vector space with left A-action $a.\overline{f}=\overline{f.a^{*}}$. For our A-B module E, $\overline{E}$ is a B-A bimodule with $b\overline{e}=\overline{e{b}^{*}}$ and $\overline{e}a=\overline{a^{*}e}$.

Definition 6. 

A differential calculus $({\Omega }_A,\mathrm{d})$ on a *-algebra A is a *-differential calculus if there are antilinear operators $*:{\Omega }_A^n\to {\Omega }_A^n$ so that ${(\xi \wedge \eta )}^{*}={(-1)}^{\left|\xi \right|\left|\eta \right|}{\eta }^{*}\wedge {\xi }^{*}$ where $\left|\eta \right|$ is the degree of η, i.e., $\eta \in {\Omega }_A^{\left|\eta \right|}$ and ${\left(\mathrm{d}\xi \right)}^{*}=\mathrm{d}\left({\xi }^{*}\right)$.

We now suppose that A and B have *-calculi. Then, for our right bimodule connection $({\nabla }_E,{\sigma }_E)$, we have a corresponding left bimodule connection $({\nabla }_{\overline{E}},{\sigma }_{\overline{E}})$ on $\overline{E}$ given by ${\nabla }_{\overline{E}}\overline{e}={\xi }^{*}\otimes \overline{f}$ where ${\nabla }_{E}e=f\otimes \xi$ (sum implicit) and ${\sigma }_{\overline{E}}(\overline{e}\otimes \eta )=k^{*}\otimes \overline{g}$ where ${\sigma }_E({\eta }^{*}\otimes e)=g\otimes k$.

We give a definition of inner product on an A-B bimodule E, where A and B are *-algebras. This is taken from the definition of Hilbert bimodules in [2], omitting norms and completion as we will need smooth function algebras. Of course, the modules with inner product we will talk about have completions which really are Hilbert bimodules.

Definition 7. 

$AB$-valued inner product on an A-B bimodule E is a B-bimodule map $⟨,⟩:\overline{E}{\otimes }_{A}E\to B$ obeying ${⟨\overline{e^{\prime }},e⟩}^{*}=⟨\overline{e},e^{\prime }⟩$ for all $e^{\prime },e\in E$ (the Hermitian condition) and $⟨\overline{e},e⟩\ge 0$ and $⟨\overline{e},e⟩=0$ only where $e=0$.

Given an inner product $⟨,⟩:\overline{E}{\otimes }_{A}E\to B$ the right connection ${\nabla }_E$ preserves the inner product if

$$(\mathrm{id}\otimes ⟨,⟩)({\nabla }_{\overline{E}}\otimes \mathrm{id})+(⟨,⟩\otimes \mathrm{id})(\mathrm{id}\otimes {\nabla }_E)=\mathrm{d}⟨,⟩.$$

(2)

2.3. Line Bundles and Calculus in $\mathbb{C}{\mathbb{P}}^{n-1}$

On $\mathbb{C}{\mathbb{P}}^{n-1}$ we have homogenous coordinates $v_i\in \mathbb{C}$ for $1\le i\le n$. We take $\underline{v}=(v_1,\cdots ,v_n)$ to lie on the sphere $S^{2n-1}$ in ${\mathbb{C}}^n$, i.e., ${\sum }_i{v}_i{\overline{v}}_i=1$. There is an action of the unit norm complex numbers $U_1$ on $S^{2n-1}$ by

$$\begin{array}{c}\hfill z▹(v_1,\cdots ,v_n)=(z{v}_1,\cdots ,z{v}_n).\end{array}$$

We define $\mathbb{C}{\mathbb{P}}^{n-1}$ as $S^{2n-1}$ quotiented by this circle action, identifying points $z▹\underline{v}\cong \underline{v}$ for all $z\in U_1$. We use notation $\left[\underline{v}\right]\in \mathbb{C}{\mathbb{P}}^{n-1}$ for the equivalence classes. We consider subsets of continuous functions on $S^{2n-1}$, defining for integer m

$$\begin{array}{c}\hfill C_m\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)=\{f\in C\left(S^{2n-1}\right):f(z▹\underline{v})=z^{m}f\left(\underline{v}\right)\mathrm{for}\mathrm{all}z\in U_1,\underline{v}\in S^{2n-1}\}\end{array}$$

and similarly $C_m^{\infty }\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ to be smooth functions. Then, $C_0^{\infty }\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ is the usual smooth functions on $\mathbb{C}{\mathbb{P}}^{n-1}$. There is an alternative view given by grading monomials in $v_i$ and ${\overline{v}}_i$ by $\left|\right|v_i\left|\right|=1$ and $\left|\right|{\overline{v}}_i\left|\right|=-1$. Then, a monomial of grade m is in $C_m\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$. A grade zero monomial such as $v_1{\overline{v}}_2{\overline{v}}_3{v}_4$ is invariant for the circle action and so gives a function on $\mathbb{C}{\mathbb{P}}^{n-1}$.

An element of the tautological bundle $\tau$ at $\left[\underline{v}\right]\in \mathbb{C}{\mathbb{P}}^{n-1}$ is given by $\alpha \underline{v}\in {\mathbb{C}}^n$ for $\alpha \in \mathbb{C}$ and the inner product on $\tau$ is given by

$$⟨\overline{\alpha \underline{v}},\beta \underline{v}⟩=\overline{\alpha }\beta \in \mathbb{C},$$

(3)

noting the use of the conjugate bundle to give bilinearity and be consistent with the earlier Hilbert $C^{*}$-bimodule inner product. A section of the tautological bundle is a function $r:\mathbb{C}{\mathbb{P}}^{n-1}\to {\mathrm{Row}}^n\left(\mathbb{C}\right)$ so that $r\left(\left[\underline{v}\right]\right)$ is a multiple of $\underline{v}$. We have a $1-1$ correspondence between continuous sections of $\tau$ and $C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$. If $f\in C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$, then $(f{v}_1,\cdots ,f{v}_n)$ is a section, and if $(r_1,\cdots ,r_n)$ is a section, then $r_i{\overline{v}}^i$ is in $C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$.

Recalling that ${\sum }_i{v}_i{\overline{v}}_i=1$ and applying $\mathrm{d}$ gives ${\sum }_i\left(\mathrm{d}{v}_i{\overline{v}}_i+v_i\mathrm{d}{\overline{v}}_i\right)=0$, and as we require a complex calculus on $\mathbb{C}{\mathbb{P}}^{n-1}$, we obtain both ${\sum }_i\mathrm{d}{v}_i{\overline{v}}_i=0$ and ${\sum }_i{v}_i\mathrm{d}{\overline{v}}_i=0$ as relations on ${\Omega }^1\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$. Applying $\mathrm{d}$ again gives ${\sum }_i\mathrm{d}{v}_i\wedge \mathrm{d}{\overline{v}}_i=0$ in ${\Omega }^2\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$.

2.4. Categories of Modules and Connections

For an algebra A, we take ${\mathcal{M}}_A$ to be the category of right A-modules and right module maps. If A has a differential calculus, we take ${\mathcal{E}}_A$ to be the category with objects $(E,{\nabla }_E)$, where E is a right A-module and ${\nabla }_E$ is a right connection on E. A morphism T from $(E,{\nabla }_E)$ to be $(F,{\nabla }_F)$ consists of a right module map $T:E\to F$, which commutes with the connections, i.e.,

$${\nabla }_{F}T=(T\otimes \mathrm{id}){\nabla }_E:E\to F\underset{A}{\otimes }{\Omega }_A^1.$$

Proposition 1. 

For a right A-B bimodule connection $({\nabla }_W,{\sigma }_W)$, there is a functor ${\otimes }_{A}W:{\mathcal{E}}_A\to {\mathcal{E}}_B$ sending $({\nabla }_F,F)$ to $({\nabla }_{F\otimes W},F{\otimes }_{A}W)$, where ${\nabla }_{F\otimes W}$ is

$${\nabla }_{F\otimes W}(f\otimes e)=(\mathrm{id}\otimes {\sigma }_W)({\nabla }_F\left(f\right)\otimes e)+f\otimes {\nabla }_W\left(e\right).$$

2.5. Holomorphic Bundles

Let B be a *-algebra with a *-differential calculus. We use the noncommutative complex calculi from [12,13]. Suppose we have a direct sum decomposition ${\Omega }_B^n={\oplus }_{p+q=n}{\Omega }_B^{p,q}$ as bimodules, and that ${\Omega }_B^{p,q}\wedge {\Omega }_B^{s,t}\subset {\Omega }_B^{p+s,q+t}$; $\mathrm{d}{\Omega }_B^{p,q}\subset {\Omega }_B^{p+1,q}\oplus {\Omega }_B^{p,q+1}$; and ${\left({\Omega }^{p,q}\right)}^{*}={\Omega }^{q,p}$. Using the projection operations for the direct sum ${\pi }^{p,q}:{\Omega }_B^{p+q}\to {\Omega }_B^{p,q}$, we can define

$$\begin{array}{c}\partial ={\pi }^{p+1,q}\mathrm{d}:{\Omega }_B^{p,q}\to {\Omega }_B^{p+1,q},\\ \overline{\partial }={\pi }^{p,q+1}\mathrm{d}:{\Omega }_B^{p,q}\to {\Omega }_B^{p,q+1},\end{array}$$

which gives a holomorphic calculus. Given a right connection ${\nabla }_G:G\to G{\otimes }_B{\Omega }_B^1$, then we define ${\overline{\partial }}_G=(\mathrm{id}\otimes {\pi }^{0,1}){\nabla }_G:G\to G{\otimes }_B{\Omega }_B^{0,1}$. The holomorphic curvature of G is defined to be the curvature of the ${\overline{\partial }}_G$ connection, i.e.,

$$(\mathrm{id}\otimes \overline{\partial }+{\overline{\partial }}_G\wedge \mathrm{id})\overline{\partial }:G\to G\otimes {\Omega }_B^{0,2}.$$

Definition 8. 

Suppose that we have a right connection ${\overline{\partial }}_G:G\to G{\otimes }_B{\Omega }_B^{0,1}$ with holomorphic curvature zero. Then, $(G,{\overline{\partial }}_G)$ is called a holomorphic right module.

3. The KSGNS Construction of the State Evaluation Map

For a subset $X\subset S$ of the state spaces of a $C^{*}$-algebra A, the positive map $\delta :A\to C\left(X\right)$ is given by $\delta \left(a\right)\left(\varphi \right)=\varphi \left(a\right)$ for $a\in A$ and $\varphi \in X$. We use a standard construction of a completely positive map using a Hilbert $C^{*}$-bimodule, and this is part of the KSGNS construction [2]. We start with $A\otimes C\left(X\right)$ as an A-$C\left(X\right)$ bimodule and the semi-inner product $⟨,⟩:\overline{A\otimes C\left(X\right)}{\otimes }_A(A\otimes C\left(X\right))\to C\left(X\right)$ defined by

$$⟨\overline{a\otimes f},a^{\prime }\otimes f^{\prime }⟩=f^{*}\delta \left(a^{*}{a}^{\prime }\right)f^{\prime }.$$

(4)

Set N to be the space of zero length vectors, i.e., $\sum a_i\otimes f_i$ so that

$$⟨\overline{\sum a_i\otimes f_i},\sum a_j\otimes f_j⟩=0.$$

Now, we define $E=(A\otimes C(X\left)\right)/N$. This has completion a Hilbert A-$C\left(X\right)$$C^{*}$-bimodule, and given $1\otimes 1\in E$, we have

$$⟨\overline{1\otimes 1},a.1\otimes 1⟩=\delta \left(a\right).$$

3.1. The Matrix Algebra Case

The pure states on $M_n\left(\mathbb{C}\right)$ are parametrised by $\underline{v}\in {\mathrm{Row}}^n\left(\mathbb{C}\right)$ by

$${\varphi }_{\underline{v}}\left(a\right)=\underline{v}a{\underline{v}}^{*}\in \mathbb{C},$$

(5)

where $\underline{v}{\underline{v}}^{*}=1$ for normalisation [1]. Because scalar multiplication of $\underline{v}$ by a unit norm complex number leaves the state unaffected the space of pure states is the quotient $X=\mathbb{C}{\mathbb{P}}^{n-1}$ of unit vectors in ${\mathrm{Row}}^n\left(\mathbb{C}\right)$, i.e., $S^{2n-1}$ quotiented by the circle group $U_1$. We take the positive map $\delta :M_n\left(\mathbb{C}\right)\to C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ defined by $\delta \left(a\right)\left(\left[\underline{v}\right]\right)={\varphi }_{\underline{v}}\left(a\right)$ for $\underline{v}\in S^{2n-1}$.

There is a unitary symmetry of the matrix algebra by inner automorphisms $a\mapsto ua{u}^{*}$ for $a\in M_n\left(\mathbb{C}\right)$ and $u\in U_n$. There is also a $U_n$ action on the pure state space $X=\mathbb{C}{\mathbb{P}}^{n-1}$ given by $\underline{v}\mapsto \underline{v}{u}^{*}$ for $\underline{v}\in S^{2n-1}$. The map $\delta :M_n\left(\mathbb{C}\right)\to C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ intertwines these actions.

We carry out the KSGNS construction given at the beginning of this section for $A=M_n\left(\mathbb{C}\right)$. We write $M_n\left(\mathbb{C}\right)\otimes C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ as ${\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C(\mathbb{C}{\mathbb{P}}^{n-1},{\mathrm{Row}}^n\left(\mathbb{C}\right))$, which are isomorphic as ${\mathrm{Row}}^n\left(\mathbb{C}\right)$ is finite dimensional. For $c_i\otimes r_i\in {\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C(\mathbb{C}{\mathbb{P}}^{n-1},{\mathrm{Row}}^n\left(\mathbb{C}\right))$, the inner product in (4) is

$$⟨\overline{c_1\otimes r_1},c_2\otimes r_2⟩\left(\left[\underline{v}\right]\right)=\underline{v}{r}_1{\left(\left[\underline{v}\right]\right)}^{*}{c}_1^{*}{c}_2{r}_2\left(\underline{v}\right){\underline{v}}^{*}\in \mathbb{C}$$

(6)

for $\underline{v}\in S^{2n-1}$, a row vector representing an element $\left[\underline{v}\right]$ of $\mathbb{C}{\mathbb{P}}^{n-1}$.

Proposition 2. 

The quotient of${\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C(\mathbb{C}{\mathbb{P}}^{n-1},{\mathrm{Row}}^n\left(\mathbb{C}\right))$by the length zero vectors N is isomorphic to${\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes \Gamma \tau$, where$\Gamma \tau$ is the continuous sections of the tautological bundle τ.

Proof. 

For $\underline{v}\in S^{2n-1}$, we look at the conditions for $c_i\otimes r_i$ to be in N, which is ${\sum }_{ij}⟨\overline{c_i\otimes r_i},c_i\otimes r_i⟩=0$ using (6). Using the projection matrix $P_{ij}={\overline{v}}_i{v}_j$, we see that

$$\begin{array}{c}\hfill ⟨c_1\otimes r_1,c_2,\otimes r_2⟩=⟨\overline{c_1\otimes r_{1}P},c_2,\otimes r_{2}P⟩\end{array}$$

just using the fact $v_i{\overline{v}}_i=1$ (summing over i). Thus, the null space N includes all $c\otimes r(1-P)$, and the only possible non-null elements are $c\otimes rP$, which is $c\otimes s$ where s is a multiple of $\underline{v}$. A quick check shows that all these are not null (except 0).  □

The sections $\Gamma \tau$ of $\tau$ are identified with $C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$, and so we have ${\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ with inner product

$$\begin{array}{c}\hfill ⟨\overline{c_1\otimes f_1},c_2\otimes f_2⟩=c_1^{*}{c}_2{f}_1^{*}{f}_2\in C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)\end{array}$$

(7)

and this a Hilbert $M_n$-$C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$$C^{*}$-bimodule. Finally, we consider $1\otimes 1\in M_n\left(\mathbb{C}\right)\otimes C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ and find $e_{1\otimes 1}=[1\otimes 1]\in {\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ under our isomorphism from Proposition 2. Take $h_i$ to be the column vector with 1 in position i and zero elsewhere. Then, in ${\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C(\mathbb{C}{\mathbb{P}}^{n-1},{\mathrm{Row}}^n\left(\mathbb{C}\right))$$e_{1\otimes 1}=[1\otimes 1]$ corresponds to $h_i\otimes h_i^{*}$ summing over i. Using the isomorphism from Section 2.3 between $\Gamma \tau$ and $C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$, $e_{1\otimes 1}=[1\otimes 1]$ corresponds to $h_i\otimes {\overline{v}}_i\in {\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ summing over i. Under the isomorphism, we adapt (5) to give $\varphi :M_n\to C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$, for $a=\left(a_{ij}\right)\in M_n$

$$\begin{array}{c}\hfill \varphi \left(a\right)=\sum _{ij}⟨\overline{h_i\otimes {\overline{v}}_i}\otimes a{h}_j\otimes {\overline{v}}_j⟩=\sum _{ij}{v}_i{a}_{ij}{\overline{v}}_j,\end{array}$$

(8)

and this is the state evaluation map.

4. Connections on the Hilbert ${\mathit{C}}^{*}$-Bimodule

We now have a formula (8) for the state evaluation map using bimodules, and we would like to ask whether it is differentiable. To do this, we use a bimodule connection. The first thing to do is to take the smooth functions as a subset of our Hilbert $C^{*}$-bimodule ${\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ by setting $E={\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}^{\infty }\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$.

4.1. Inner Product Preserving Connections on $E={\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}^{\infty }\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$

We have generators of $C_{-1}^{\infty }\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$, the smooth sections of $\tau$, given by ${\overline{v}}_i$ and a projection matrix $Q_{ij}=v_i{\overline{v}}_j$ so that ${\overline{v}}_i{Q}_{ij}={\overline{v}}_j$. We specify a right connection

$$\begin{array}{c}\hfill {\nabla }_E:{\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)\to {\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)\underset{C^{\infty }\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)}{\otimes }{\Omega }^1\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)\end{array}$$

for some ${\Gamma }^{pq}{}_{ij}\in {\Omega }^1\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ and summing over repeated indices

$$\begin{array}{c}\hfill {\nabla }_E(h_i\otimes {\overline{v}}_j)=h_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ij}.\end{array}$$

(9)

As

$$\begin{array}{cc}\hfill h_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ij}& =h_p\otimes {\overline{v}}_s{Q}_{sq}\otimes {\Gamma }^{pq}{}_{ij}=h_p\otimes {\overline{v}}_s\otimes Q_{sq}{\Gamma }^{pq}{}_{ij},\hfill \end{array}$$

we can suppose without loss of generality that

$$\begin{array}{c}\hfill {\Gamma }^{pq}{}_{ij}=Q_{qs}{\Gamma }^{ps}{}_{ij}.\end{array}$$

(10)

Additionally, using ${\overline{v}}_j={\overline{v}}_q{Q}_{qj}$

$$\begin{array}{cc}\hfill \nabla (h_i\otimes {\overline{v}}_j{Q}_{jk})& =h_i\otimes {\overline{v}}_j\otimes \mathrm{d}{Q}_{jk}+h_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ij}{Q}_{jk}\hfill \\ \hfill & =\nabla (h_i\otimes {\overline{v}}_k)=h_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ik},\hfill \end{array}$$

so we have

$$\begin{array}{c}\hfill {\Gamma }^{pq}{}_{ij}({\delta }_{jk}-Q_{jk})={\delta }_{pi}{Q}_{qj}\mathrm{d}{Q}_{jk}.\end{array}$$

(11)

Thus, for a right connection (9) we require (10) and (11) to be satisfied.

Proposition 3. 

The connection (9) is a bimodule connection with

$${\sigma }_E:{\Omega }_{\mathrm{uni}}^1\left(M_n\left(\mathbb{C}\right)\right)\underset{M_n\left(\mathbb{C}\right)}{\otimes }E\to E\otimes {\Omega }^1\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$$

extending to a bimodule map

$${\widehat{\sigma }}_E:M_n\left(\mathbb{C}\right)\otimes M_n\left(\mathbb{C}\right)\underset{M_n\left(\mathbb{C}\right)}{\otimes }E\to E\otimes {\Omega }^1\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$$

by the formula, for $E_{ij}$ the standard matrix with 1 in row i column j and zero elsewhere

$${\widehat{\sigma }}_E(E_{ab}\otimes E_{st}\otimes h_i\otimes {\overline{v}}_j)={\delta }_{ti}{h}_a\otimes {\overline{v}}_q\otimes {\Gamma }^{bq}{}_{sj}.$$

Proof. 

The bimodule connection condition gives

$$\begin{array}{cc}\hfill {\sigma }_E(\mathrm{d}{E}_{st}\otimes h_i\otimes {\overline{v}}_j)& ={\nabla }_E(E_{st}{h}_i\otimes {\overline{v}}_j)-E_{st}{\nabla }_E(h_i\otimes {\overline{v}}_j)\hfill \\ \hfill & ={\delta }_{ti}{\nabla }_E(h_s\otimes {\overline{v}}_j)-E_{st}{\nabla }_E(h_i\otimes {\overline{v}}_j)\hfill \\ \hfill & ={\delta }_{ti}{h}_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{sj}-E_{st}{h}_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ij}\hfill \\ \hfill & =\left({\delta }_{ti}{h}_p{\delta }_{sr}-{\delta }_{tp}{h}_s{\delta }_{ri}\right)\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{rj}.\hfill \end{array}$$

(12)

Note that ${\widehat{\sigma }}_E$ is explicitly a left module map and is extended to a right $C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ module map by multiplication on the rightmost factor. Then, for the universal calculus, we obtain $\mathrm{d}{E}_{st}=I_n\otimes E_{st}-E_{st}\otimes I_n$, and summing over k

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_E(\mathrm{d}{E}_{st}\otimes h_i\otimes {\overline{v}}_j)& ={\widehat{\sigma }}_E(E_{pp}\otimes E_{st}\otimes h_i\otimes {\overline{v}}_j)-{\widehat{\sigma }}_E(E_{st}\otimes E_{pp}\otimes h_i\otimes {\overline{v}}_j)\hfill \\ \hfill & ={\delta }_{ti}{h}_p{\overline{v}}_q\otimes {\Gamma }^{pq}{}_{rj}{\delta }_{sr}-{\delta }_{tp}{\delta }_{ri}{h}_s\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{rj}\hfill \end{array}$$

which agrees with (12).  □

The curvature of the connection is given by

$$\begin{array}{cc}\hfill R_E(h_i\otimes {\overline{v}}_j)& =(\mathrm{id}\otimes \mathrm{d}+{\nabla }_E\wedge \mathrm{id}){\nabla }_E(h_i\otimes {\overline{v}}_j)\hfill \\ \hfill & =h_p\otimes {\overline{v}}_q\otimes \mathrm{d}{\Gamma }^{pq}{}_{ij}+h_s\otimes {\overline{v}}_t\otimes {\Gamma }^{st}{}_{pq}\wedge {\Gamma }^{pq}{}_{ij}\hfill \\ \hfill & =h_p\otimes {\overline{v}}_q\otimes \left(\mathrm{d}{\Gamma }^{pq}{}_{ij}+{\Gamma }^{pq}{}_{st}\wedge {\Gamma }^{st}{}_{ij}\right).\hfill \end{array}$$

We set $X^{pq}{}_{ij}=\mathrm{d}{\Gamma }^{pq}{}_{ij}+{\Gamma }^{pq}{}_{st}\wedge {\Gamma }^{st}{}_{ij}$ so

$$R_E(h_i\otimes {\overline{v}}_j)=h_p\otimes {\overline{v}}_q\otimes X^{pq}{}_{ij}.$$

(13)

Using (22) and where $E_{rt}$ is the matrix with 1 in row p column t and zero elsewhere

$$\begin{array}{cc}\hfill R_E(E_{rt}{h}_i\otimes {\overline{v}}_j)-E_{rt}{R}_E(h_i\otimes {\overline{v}}_j)& ={\delta }_{ti}{h}_p\otimes {\overline{v}}_q\otimes X^{pq}{}_{rj}-E_{rt}{h}_p\otimes {\overline{v}}_q\otimes X^{pq}{}_{ij}\hfill \\ \hfill & ={\delta }_{ti}{h}_p\otimes {\overline{v}}_q\otimes X^{pq}{}_{rj}-{\delta }_{tp}{h}_r\otimes {\overline{v}}_q\otimes X^{pq}{}_{ij}.\hfill \end{array}$$

(14)

We see that the curvature is not necessarily a left module map, though by general theory it must be a right module map.

We require two additional properties of our connection: that it preserves the inner product (7) and that it vanishes on $e_{1\otimes 1}$. The inner product from (7) gives

$$\begin{array}{c}\hfill ⟨\overline{h_s\otimes {\overline{v}}_t},h_i\otimes {\overline{v}}_j⟩={\delta }_{si}{v}_t{\overline{v}}_j\end{array}$$

(15)

and for the connection (9) to preserve the inner product, we require

$$\begin{array}{cc}\hfill {\delta }_{is}\mathrm{d}\left(v_t{\overline{v}}_j\right)& =⟨\overline{h_s\otimes {\overline{v}}_t},h_p\otimes {\overline{v}}_q⟩{\Gamma }^{pq}{}_{ij}+{\left({\Gamma }^{pq}{}_{st}\right)}^{*}⟨\overline{h_p\otimes {\overline{v}}_q},h_i\otimes {\overline{v}}_j⟩\hfill \\ \hfill & ={\delta }_{sp}{v}_t{\overline{v}}_q{\Gamma }^{pq}{}_{ij}+{\left({\Gamma }^{pq}{}_{st}\right)}^{*}{\delta }_{pi}{v}_q{\overline{v}}_j.\hfill \end{array}$$

(16)

We also need for ${\nabla }_E\left(e_{1\otimes 1}\right)=0$

$$\begin{array}{c}\hfill 0={\nabla }_E(h_i\otimes {\overline{v}}_i)=h_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ii}\end{array}$$

(17)

so ${\Gamma }^{pq}{}_{ii}=0$.

4.2. A Simple Example of the Connection

Here, we find a simple example of a connection satisfying the previous conditions in Section 4.1. From (10), we have ${\Gamma }^{pq}{}_{rs}=v_q{C}^p{}_{rs}$ where $C^p{}_{rs}={\overline{v}}_j{\Gamma }^{pj}{}_{rs}$. Now, (11) becomes

$$\begin{array}{c}\hfill v_q{C}^p{}_{ij}({\delta }_{jk}-Q_{jk})={\delta }_{pi}{v}_q{\overline{v}}_s\mathrm{d}\left(v_s{\overline{v}}_k\right)\end{array}$$

and as this is true for all q we deduce, using the relations for ${\Omega }^1\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$

$$\begin{array}{c}\hfill C^p{}_{ij}({\delta }_{jk}-Q_{jk})={\delta }_{pi}{\overline{v}}_s\left(\mathrm{d}{v}_s{\overline{v}}_k+v_s\mathrm{d}{\overline{v}}_k\right)={\delta }_{pi}\mathrm{d}{\overline{v}}_k.\end{array}$$

(18)

Additionally, (16) gives

$$\begin{array}{cc}\hfill {\delta }_{is}\mathrm{d}{Q}_{tj}& ={\delta }_{sp}{v}_t{\overline{v}}_q{v}_q{C}^p{}_{ij}+{\overline{v}}_q{\left(C^p{}_{st}\right)}^{*}{\delta }_{pi}{v}_q{\overline{v}}_j\hfill \\ \hfill & ={\delta }_{sp}{v}_t{C}^p{}_{ij}+{\delta }_{pi}{\overline{v}}_j{\left(C^p{}_{st}\right)}^{*}=v_t{C}^s{}_{ij}+{\overline{v}}_j{\left(C^i{}_{st}\right)}^{*}.\hfill \end{array}$$

(19)

Thus, we have for a right connection (18), for metric preserving we obtain (19), and for $\nabla \left(e_{1\otimes 1}\right)=0$ we obtain $C^p{}_{ii}=0$. The curvature is

$$\begin{array}{c}\hfill R_E(h_i\otimes {\overline{v}}_j)=h_p\otimes {\overline{v}}_q\otimes \left(\mathrm{d}\left(v_q{C}^p{}_{ij}\right)+v_q{v}_t{C}^p{}_{st}\wedge C^s{}_{ij}\right),\end{array}$$

and using ${\overline{v}}_q={\overline{v}}_m{v}_m{\overline{v}}_q$

$$\begin{array}{cc}\hfill R_E(h_i\otimes {\overline{v}}_j)& =h_p\otimes {\overline{v}}_m\otimes v_m{\overline{v}}_q\left(\mathrm{d}{v}_q\wedge C^p{}_{ij}+v_q\mathrm{d}{C}^p{}_{ij}+v_q{v}_t{C}^p{}_{st}\wedge C^s{}_{ij}\right)\hfill \\ \hfill & =h_p\otimes {\overline{v}}_m\otimes v_m\left(\mathrm{d}{C}^p{}_{ij}+v_t{C}^p{}_{st}\wedge C^s{}_{ij}\right).\hfill \end{array}$$

(20)

To simplify this further, from (18), we write

$$\begin{array}{c}\hfill C^p{}_{ik}=C^p{}_{ij}({\delta }_{jk}-Q_{jk})+C^p{}_{ij}{Q}_{jk}={\delta }_{pi}\mathrm{d}{\overline{v}}_k+C^p{}_{ij}{v}_j{\overline{v}}_k,\end{array}$$

we set $D_{pi}=C^p{}_{ij}{v}_j$, and then $C^p{}_{ik}={\delta }_{pi}\mathrm{d}{\overline{v}}_k+D_{pi}{\overline{v}}_k$. Now, (18) is automatically true and (19) becomes

$$\begin{array}{cc}\hfill {\delta }_{is}(\mathrm{d}{v}_t{\overline{v}}_j+v_t\mathrm{d}{\overline{v}}_j)& =v_t({\delta }_{si}\mathrm{d}{\overline{v}}_j+D_{si}{\overline{v}}_j)+{\overline{v}}_j{({\delta }_{is}\mathrm{d}{\overline{v}}_t+D_{is}{\overline{v}}_t)}^{*}\hfill \\ \hfill & ={\delta }_{is}(v_t\mathrm{d}{\overline{v}}_j+{\overline{v}}_j\mathrm{d}{v}_t)+v_t{\overline{v}}_j(D_{si}+{\left(D_{is}\right)}^{*}).\hfill \end{array}$$

We conclude that for matrix D, we have (19) if and only if $D^{*}+D=0$ as a matrix. Next, we require

$$\begin{array}{c}\hfill C^p{}_{ii}={\delta }_{pi}\mathrm{d}{\overline{v}}_i+D_{pi}{\overline{v}}_i=\mathrm{d}{\overline{v}}_p+D_{pi}{\overline{v}}_i=0.\end{array}$$

(21)

Finally, we put

$$\begin{array}{c}\hfill D_{pi}=-\mathrm{d}{\overline{v}}_p{v}_i+\mathrm{d}{v}_i{\overline{v}}_p+G_{pi}.\end{array}$$

Now, we have from (21)

$$\begin{array}{c}\hfill D_{pi}{\overline{v}}_i=-\mathrm{d}{\overline{v}}_p+G_{pi}{\overline{v}}_i,\end{array}$$

so we have the condition $G_{pi}{\overline{v}}_i=0$, and

$$\begin{array}{c}\hfill {\left(D_{ip}\right)}^{*}=-\mathrm{d}{v}_i{\overline{v}}_p+\mathrm{d}{\overline{v}}_p{v}_i+{\left(G_{ip}\right)}^{*}\end{array}$$

so $D^{*}+D=0$ if and only if $G^{*}=-G$. Now, we calculate the bracket in the formula for the curvature in (20). This is

$$\begin{array}{c}\hfill \mathrm{d}{C}^p{}_{ij}+C^p{}_{st}{v}_t\wedge C^s{}_{ij}={\overline{v}}_j\left(G_{ps}\wedge G_{si}-v_i{G}_{ps}\wedge \mathrm{d}{\overline{v}}_s+{\overline{v}}_p\mathrm{d}{v}_s\wedge G_{si}+\mathrm{d}{G}_{pi}-\mathrm{d}{v}_i\wedge \mathrm{d}{\overline{v}}_p\right).\end{array}$$

We can simplify the curvature while satisfying all of our conditions simply by putting $G=0$, to give

$$\begin{array}{c}\hfill R_E(h_i\otimes {\overline{v}}_j)=h_p\otimes {\overline{v}}_m\otimes v_m{\overline{v}}_j\mathrm{d}{\overline{v}}_p\wedge \mathrm{d}{v}_i=h_p\otimes {\overline{v}}_j\otimes \mathrm{d}{\overline{v}}_p\wedge \mathrm{d}{v}_i.\end{array}$$

(22)

For completeness we calculate

$$\begin{array}{cc}\hfill {\Gamma }^{pq}{}_{rs}=v_q{C}^p{}_{rs}& =v_q\left({\delta }_{pr}\mathrm{d}{\overline{v}}_s+D_{pr}{\overline{v}}_s\right)\hfill \\ \hfill & =v_q\left({\delta }_{pr}\mathrm{d}{\overline{v}}_s+{\overline{v}}_s(-\mathrm{d}{\overline{v}}_p{v}_r+\mathrm{d}{v}_r{\overline{v}}_p)\right)\hfill \\ \hfill & =v_q\left({\delta }_{pr}\mathrm{d}{\overline{v}}_s-{\overline{v}}_s{v}_r\mathrm{d}{\overline{v}}_p+{\overline{v}}_s{\overline{v}}_p\mathrm{d}{v}_r\right),\hfill \end{array}$$

(23)

and from (13)

$$X^{pq}{}_{ij}={\delta }_{qj}\mathrm{d}{\overline{v}}_p\wedge \mathrm{d}{v}_i.$$

(24)

5. Differentiating Positive Maps

We wish to extend the map $\varphi :A\to B$ defined by $\varphi \left(a\right)=⟨\overline{e},ae⟩$ in (8) to a map of differential forms $\varphi :{\Omega }_A^m\to {\Omega }_B^m$. A theory of how to do this is set down in [3], (using left instead of right connections), but it assumes conditions on the curvature that we do not have and results in a cochain map, so we need to be more careful and give a more general account of the theory, beginning with how ${\sigma }_E$ extends to a map of differential forms, with general algebras $A,B$, and bimodule W.

5.1. General Theory of Extendability and Curvature

We begin with a right handed version of Lemma 3.72 in [3]. For algebras $A,B$ with calculi, we suppose that $({\nabla }_W,{\sigma }_W)$ is a bimodule connection on an A-B bimodule W. The curvature $R_W$ of a right bimodule connection must be a right module map but not necessarily a bimodule map.

Lemma 1. 

Given an A-B bimodule W with a right bimodule connection ${\nabla }_W:W\to W{\otimes }_B{\Omega }_B^1$ and ${\sigma }_W:{\Omega }_A^1{\otimes }_{A}W\to W{\otimes }_B{\Omega }_B^1$, for the curvature, we have

$$\begin{array}{c}{R}_W\left(ae\right)-a{R}_W\left(e\right)=({\sigma }_W\wedge \mathrm{id})(\mathrm{d}a\otimes {\nabla }_W\left(e\right))+(\mathrm{id}\otimes \mathrm{d}+{\nabla }_W\wedge \mathrm{id}){\sigma }_W(\mathrm{d}a\otimes e)\\ c{R}_W\left(ae\right)-ca{R}_W\left(e\right)=({\sigma }_W\wedge \mathrm{id})(c\mathrm{d}a\otimes {\nabla }_{W}e)+(\mathrm{id}\otimes \mathrm{d}+{\nabla }_W\wedge \mathrm{id}){\sigma }_W(c\mathrm{d}a\otimes e)\\ -({\sigma }_W\wedge \mathrm{id})(\mathrm{id}\otimes {\sigma }_W)(\mathrm{d}c\otimes \mathrm{d}a\otimes e).\end{array}$$

Proof. 

By definition of $R_W$

$$\begin{array}{cc}\hfill R_W\left(ae\right)& =(\mathrm{id}\otimes \mathrm{d}+{\nabla }_E\wedge \mathrm{id}){\nabla }_W\left(ae\right)\hfill \\ \hfill & =(\mathrm{id}\otimes \mathrm{d}+{\nabla }_W\wedge \mathrm{id})\left({\sigma }_W(\mathrm{d}a\otimes e)+a.{\nabla }_{W}e\right)\hfill \\ \hfill & =(\mathrm{id}\otimes \mathrm{d}+{\nabla }_W\wedge \mathrm{id}){\sigma }_W(\mathrm{d}a\otimes e)+({\sigma }_W\wedge \mathrm{id})(\mathrm{d}a\otimes {\nabla }_{W}e)+a.R_W\left(e\right).\hfill \end{array}$$

Now, multiply the first equation in the statement by $c\in A$ to obtain

$$\begin{array}{c}\hfill c{R}_W\left(ae\right)-ca{R}_W\left(e\right)=(\sigma \wedge \mathrm{id})(c\mathrm{d}a\otimes {\nabla }_{W}e)+c(\mathrm{id}\otimes \mathrm{d}+{\nabla }_W\wedge \mathrm{id}){\sigma }_W(\mathrm{d}a\otimes e),\end{array}$$

and use the definition of ${\sigma }_W$ again to obtain the second equation.  □

The following definition is a right version of extendability from [3].

Definition 9. 

Given an A-B bimodule W with a right bimodule connection ${\nabla }_W:W\to W{\otimes }_B{\Omega }_B^1$ and ${\sigma }_W:{\Omega }_A^1{\otimes }_{A}W\to W{\otimes }_B{\Omega }_B^1$, we say that $({\nabla }_W,{\sigma }_W)$ is extendable if ${\sigma }_W$ extends to a map ${\sigma }_W:{\Omega }_A^n{\otimes }_{A}W\to W{\otimes }_B{\Omega }_B^n$ such that for all $\xi ,\eta \in {\Omega }_A$

$$\begin{array}{c}\hfill {\sigma }_W(\xi \wedge \eta \otimes e)=({\sigma }_W\wedge \mathrm{id})(\mathrm{id}\otimes \sigma )(\xi \otimes \eta \otimes e).\end{array}$$

(25)

Corollary 1. 

The ${\sigma }_W$ in Lemma 1 is extendable for the maximal prolongation calculus ${\Omega }_A^n$ if and only if, for all $c_i$, $a_i\in A$ with ${\sum }_i{c}_i\mathrm{d}{a}_i=0\in {\Omega }_A^1$

$$\begin{array}{c}\hfill \sum _i\left(c_i{a}_i{R}_W\left(e\right)-c_i{R}_W\left(a_{i}e\right)\right)=0.\end{array}$$

(26)

Proof. 

To define a map $\sigma :{\Omega }_A^2{\otimes }_{A}W\to W{\otimes }_B{\Omega }_B^2$ by (25) where $\xi$, $\eta \in {\Omega }_A^1$, we require the RHS of (25) to vanish for all $\xi \wedge \eta =0$ (summation implicit). This is easiest if we have as few relations $\xi \wedge \eta =0$ as possible; thus we consider the maximal prolongation. In more detail, if we have $\sum c_i\mathrm{d}{a}_i=0$ in ${\Omega }_A^1$ then $\sum \mathrm{d}{c}_i\otimes \mathrm{d}{a}_i$ is in the kernel of ∧ and we then have from Lemma 1

$$\begin{array}{c}\hfill \sum \left(c_i{a}_i{R}_W\left(e\right)-c_i{R}_W\left(a_{i}e\right)\right)=\sum _i({\sigma }_W\wedge \mathrm{id})(\mathrm{id}\otimes {\sigma }_W)(\mathrm{d}{c}_i\otimes \mathrm{d}{a}_i\otimes e).\end{array}$$

(27)

Thus, we need to show that for all $\sum c_i\mathrm{d}{a}_i=0$ we have the LHS of (27) vanishing.  □

Corollary 2. 

Either of the following conditions imply the condition (26) in Corollary 1:

(a) 

$R_W$ is a left module map,

(b) 

${\Omega }_A^1$ is the universal calculus.

Proof. 

(a) is obvious from Corollary 1. For (b), by definition of the first order universal calculus, we have

$$\begin{array}{c}\hfill \sum c_i\mathrm{d}{a}_i=c_i\otimes a_i-c_i{a}_i\otimes 1\in A\otimes A\end{array}$$

and if this vanishes, then so does the LHS of (27).  □

Now, we assume extendability for ${\sigma }_W$ and work out the consequences.

Proposition 4. 

Given the conditions of Lemma 1 and assuming that ${\sigma }_W$ is extendable, the map $S_W:{\Omega }_A^n{\otimes }_{A}W\to W{\otimes }_B{\Omega }_B^{n+1}$ defined by

$$\begin{array}{cc}\hfill S_W(\xi \otimes e)& =({\sigma }_W\wedge \mathrm{id})(\xi \otimes {\nabla }_{W}e)-(\mathrm{id}\otimes \mathrm{d}+{\nabla }_W\wedge \mathrm{id}){\sigma }_W(\xi \otimes e){(-1)}^{\left|\xi \right|}\hfill \\ \hfill & +{\sigma }_W(\mathrm{d}\xi \otimes e){(-1)}^{\left|\xi \right|}\hfill \end{array}$$

(28)

is a well defined bimodule map, and

$$\begin{array}{c}\hfill S_W(\xi \wedge \kappa \otimes e)=({\sigma }_W\wedge \mathrm{id})(\mathrm{id}\otimes S_W)(\xi \otimes \kappa \otimes e)+{(-1)}^{\left|\kappa \right|}(S_W\wedge \mathrm{id})(\mathrm{id}\otimes {\sigma }_W)(\xi \otimes \kappa \otimes e).\end{array}$$

(29)

For the derivative of $S_W$, we have

$$\begin{array}{cc}\hfill {\nabla }_R^{\left[\right|\xi |+1]}{S}_W(\xi \otimes e)-S_W(\mathrm{d}\xi \otimes e)& =-{(-1)}^{\left|\xi \right|}(S_W\wedge \mathrm{id})(\xi \otimes {\nabla }_{W}e)\hfill \\ \hfill & +{(-1)}^{\left|\xi \right|}\left(({\sigma }_W\wedge \mathrm{id})(\mathrm{id}\otimes R_W)-(R_W\wedge \mathrm{id}){\sigma }_W\right).\hfill \end{array}$$

(30)

Proof. 

To check that it is well defined, we use

$$\begin{array}{cc}\hfill S_W(\xi a\otimes e)-S_W(\xi \otimes ae)& =-({\sigma }_W\wedge \mathrm{id})(\xi \otimes {\sigma }_W(\mathrm{d}a\otimes e))\hfill \\ \hfill & +{\sigma }_W\left(\left(d\right(\xi a)-(\mathrm{d}\xi \left)a\right)\otimes e\right){(-1)}^{\left|\xi \right|}\hfill \\ \hfill & =-{\sigma }_W(\xi \wedge \mathrm{d}a\otimes e)+{\sigma }_W(\xi \wedge \mathrm{d}a\otimes e)=0\hfill \end{array}$$

by Definition 9. To check that it is a right module map we use, where ${\sigma }_W(\xi \otimes e)=f\otimes \eta$

$$\begin{array}{cc}\hfill S(\xi \otimes ea)-S(\xi \otimes e)a& =({\sigma }_W\wedge \mathrm{id})(\xi \otimes e\otimes \mathrm{d}a)-(\mathrm{id}\otimes \mathrm{d})\left({\sigma }_W(\xi \otimes e)a\right){(-1)}^{\left|\xi \right|}\hfill \\ \hfill & +\left((\mathrm{id}\otimes \mathrm{d}){\sigma }_W(\xi \otimes e)\right)a{(-1)}^{\left|\xi \right|}\hfill \\ \hfill & =f\otimes \eta \wedge \mathrm{d}a-f\otimes \mathrm{d}\left(\eta a\right){(-1)}^{\left|\xi \right|}+f\otimes \mathrm{d}\eta .a{(-1)}^{\left|\xi \right|}.\hfill \end{array}$$

To check that it is a left module map we use

$$\begin{array}{cc}\hfill {(-1)}^{\left|\xi \right|}\left(S(a\xi \otimes e)-aS(\xi \otimes e)\right)& =-({\nabla }_W\wedge \mathrm{id})(a.{\sigma }_W(\xi \otimes e))+a({\nabla }_W\wedge \mathrm{id})\left({\sigma }_W(\xi \otimes e)\right)\hfill \\ \hfill & +{\sigma }_W(\mathrm{d}\left(a\xi \right)\otimes e)-{\sigma }_W(a.\mathrm{d}\xi \otimes e)\hfill \\ \hfill & =-{\nabla }_W\left(af\right)\wedge \eta +a{\nabla }_W\left(f\right)\wedge \eta +{\sigma }_W(\mathrm{d}a\wedge \xi \otimes e)\hfill \\ \hfill & =-{\sigma }_W(\mathrm{d}a\otimes f)\wedge \eta +{\sigma }_W(\mathrm{d}a\wedge \xi \otimes e)=0.\hfill \end{array}$$

To verify the product rule for $S_E$, consider

$$\begin{array}{c}\hfill S_W(\xi \wedge \kappa \otimes e)-({\sigma }_W\wedge \mathrm{id})(\mathrm{id}\otimes S_W)(\xi \otimes \kappa \otimes e),\end{array}$$

and use the Leibniz rule for $\mathrm{d}$ and extendability. For the last formula (30), we use

$$\begin{array}{cc}\hfill S_W(\mathrm{d}a\otimes e)& =R_W\left(ae\right)-a{R}_W\left(e\right)\hfill \end{array}$$

(31)

and standard manipulations. Recall that $R_W$ is not necessarily a left module map, but use of (29) shows that (30) is well defined on ${\Omega }_A{\otimes }_{A}W$.  □

Now suppose that A and B are *-algebras with *-calculi. Given an inner product $⟨,⟩:\overline{W}{\otimes }_{A}W\to B$, which is preserved by ${\nabla }_W$, we extend $\varphi :A\to B$ defined by $\varphi \left(a\right)=⟨\overline{e},ae⟩$ where ${\nabla }_{W}e=0$ to $\varphi :{\Omega }_A^n\to {\Omega }_B^n$ by

$$\begin{array}{c}\hfill \varphi \left(\xi \right)=(⟨,⟩\otimes \mathrm{id})(\overline{e}\otimes {\sigma }_W(\xi \otimes e)).\end{array}$$

(32)

Under the more restrictive conditions where $R_W$ is a bimodule map [3] $\varphi$ would be a cochain map. However, more generally we find a correction term.

Proposition 5. 

Assume the conditions of 1 and that ${\sigma }_W$ is extendable. If ${\nabla }_{W}e=0$ and ${\nabla }_W$ preserves the inner product then

$$\begin{array}{c}\hfill \mathrm{d}\varphi \left(\xi \right)=\varphi \left(\mathrm{d}\xi \right)-{(-1)}^{\left|\xi \right|}(⟨,⟩\otimes \mathrm{id})(\overline{e}\otimes S_W(\xi \otimes e)).\end{array}$$

(33)

Proof. 

Apply (28) to the formula obtained by differentiating (32).  □

In Proposition 1, we see that under the condition of Lemma 1 there is a functor $\otimes W$ from ${\mathcal{E}}_A$ to ${\mathcal{E}}_B$, using the specified connection on the tensor product. We would like to calculate the curvature of this tensor product connection, but as we noted before the curvature of W is not necessarily a left module map, so we need more generality than in [3].

Proposition 6. 

If $F\in {\mathcal{E}}_A$ and $({\nabla }_W,{\sigma }_W)$ is an extendable right bimodule connection on $W\in {}_A{\mathcal{M}}_B$ then the curvature of the tensor product connection is

$$R_{F\otimes W}=\mathrm{id}\otimes R_W+(\mathrm{id}\otimes {\sigma }_W)(R_F\otimes \mathrm{id})+(\mathrm{id}\otimes S_W)({\nabla }_F\otimes \mathrm{id})).$$

(34)

Note: The first and last terms are not well defined on $F{\otimes }_{A}W$, only their sum is.

Proof. 

Standard manipulation.  □

5.2. Applications to the State Map on Matrices

We return to our specific case of matrices, projective space and bimodule E. As we are using the universal calculus for matrices, by Corollary 2 we know that ${\sigma }_E$ from Section 4.1 is extendable. It will be convenient to extend the domain of definition of ${\sigma }_E$ given in Proposition 3 from ${\Omega }_{\mathrm{uni}}^1\left(M_n\right)$ to ${\Omega }_{\mathrm{uni}}^{m-1}\left(M_n\right)$, etc.

Proposition 7. 

Regarding ${\Omega }_{\mathrm{uni}}^{m-1}\left(M_n\left(\mathbb{C}\right)\right)$ as a subset of $M_n{\left(\mathbb{C}\right)}^{\otimes m}$, we find the formula

$${\widehat{\sigma }}_E:M_n^{\otimes m}\underset{M_n\left(\mathbb{C}\right)}{\otimes }E\to E\otimes {\Omega }^{m-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$$

which restricts to the extension of

$${\sigma }_E:{\Omega }_{\mathrm{uni}}^{m-1}\left(M_n\left(\mathbb{C}\right)\right)\underset{M_n\left(\mathbb{C}\right)}{\otimes }E\to E\otimes {\Omega }^{m-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$$

from Section 4.1 given by

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_E\left(E_{a_1{b}_1}\otimes E_{a_2{b}_2}\otimes \cdots \otimes E_{a_m{b}_m}\otimes h_i\otimes {\overline{v}}_j\right)& ={\delta }_{b_{m}i}{h}_{a_1}\otimes {\overline{v}}_{q_1}\otimes {\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge {\Gamma }^{b_2{q}_2}{}_{a_3{q}_3}\wedge \cdots \hfill \\ & \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_{m}j}.\hfill \end{array}$$

Proof. 

By induction. From Proposition 3, the formula works for $m=2$. Assume that it works for m, and then for $m+1$, given $\xi \in {\Omega }_{\mathrm{uni}}^1\left(M_n\left(\mathbb{C}\right)\right)$ and $\eta =E_{a_i{b}_1}\otimes E_{a_2{b}_2}\otimes \cdots \otimes E_{a_m{b}_m}$$\in {\Omega }_{\mathrm{uni}}^{m-1}\left(M_n\left(\mathbb{C}\right)\right)$

$$\begin{array}{cc}\hfill {\sigma }_E(\xi \wedge \eta \otimes h_i\otimes {\overline{v}}_j)& =(\mathrm{id}\otimes \wedge ){\sigma }_E(\xi \wedge \eta \otimes h_i\otimes {\overline{v}}_j)\hfill \\ \hfill & =({\sigma }_E\wedge \mathrm{id})(\xi \otimes {\sigma }_E(\eta \otimes h_i\otimes {\overline{v}}_j))\hfill \\ \hfill & ={\delta }_{b_{m}i}{\sigma }_E(\xi \otimes h_{a_1}\otimes {\overline{v}}_{q_1})\wedge {\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge {\Gamma }^{b_2{q}_2}{}_{a_3{q}_3}\wedge \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_{m}j}.\hfill \end{array}$$

Now, put $\xi =E_{ab}\otimes E_{st}$ to obtain

$$\begin{array}{cc}\hfill {\sigma }_E(\xi \wedge \eta \otimes h_i\otimes {\overline{v}}_j)& ={\delta }_{b_{m}i}{\widehat{\sigma }}_E(E_{ab}\otimes E_{st}\otimes h_{a_1}\otimes {\overline{v}}_{q_1})\wedge {\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge {\Gamma }^{b_2{q}_2}{}_{a_3{q}_3}\wedge \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_{m}j}\hfill \\ \hfill & ={\delta }_{b_{m}i}{\delta }_{t{a}_1}{h}_a\otimes {\overline{v}}_{q_0}\otimes {\Gamma }^{b{q}_0}{}_{s{q}_1}\wedge {\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_{m}j}\hfill \end{array}$$

and this is exactly what the formula gives on applying ${\widehat{\sigma }}_E$ to $\xi \wedge \eta \otimes h_i\otimes {\overline{v}}_j$ given

$$\begin{array}{c}\hfill E_{ab}\otimes E_{st}\underset{M_n\left(\mathbb{C}\right)}{\otimes }\xi ={\delta }_{t{a}_1}{E}_{ab}\otimes E_{s{b}_1}\otimes E_{a_2{b}_2}\otimes \cdots \otimes E_{a_m{b}_m}.\end{array}$$

 □

We can now extend the state evaluation map $\varphi :M_n\left(\mathbb{C}\right)\to C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ from (5) and (8) to forms by using (32).

Corollary 3. 

The function $\varphi :{\Omega }_{\mathrm{uni}}^{m-1}\left(M_n\left(\mathbb{C}\right)\right)\to {\Omega }^{m-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ is given by

$$\begin{array}{c}\hfill \varphi (E_{a_1{b}_1}\otimes \cdots \otimes E_{a_m{b}_m})=v_{a_1}{\overline{v}}_{q_1}{\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_m{b}_m}\end{array}$$

summing over $q_1,\cdots ,q_{m-1}$.

Proof. 

Summing over $i,j$,

$$\begin{array}{cc}\hfill \varphi (E_{a_1{b}_1}\otimes \cdots \otimes E_{a_m{b}_m})& =(⟨,⟩\otimes \mathrm{id})(\mathrm{id}\otimes {\widehat{\sigma }}_E)\left(\overline{h_j\otimes {\overline{v}}_j}\otimes E_{a_1{b}_1}\otimes \cdots \otimes E_{a_m{b}_m}\otimes h_i\otimes {\overline{v}}_i\right)\hfill \\ \hfill & ={\delta }_{b_{m}i}⟨\overline{h_j\otimes {\overline{v}}_j},h_{a_1}\otimes {\overline{v}}_{q_1}⟩{\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge {\Gamma }^{b_2{q}_2}{}_{a_3{q}_3}\wedge \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_{m}i}\hfill \\ \hfill & ={\delta }_{b_{m}i}{\delta }_{j{a}_1}{v}_j{\overline{v}}_{q_1}{\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge {\Gamma }^{b_2{q}_2}{}_{a_3{q}_3}\wedge \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_{m}i}.\hfill \end{array}$$

 □

Proposition 8. 

Similarly to ${\widehat{\sigma }}_E$, we can calculate an extension ${\widehat{S}}_E$ of $S_E$ to $M_n\otimes M_n$ instead of just ${\Omega }_{\mathrm{uni}}^1\left(M_n\right)$, giving

$$\begin{array}{cc}\hfill {\widehat{S}}_E(E_{ab}\otimes E_{rt}\otimes h_i\otimes {\overline{v}}_j)& ={\delta }_{ti}{h}_a\otimes {\overline{v}}_q\otimes X^{bq}{}_{rj}\hfill \end{array}$$

and this extends to higher forms by

$$\begin{array}{cc}\hfill & {\widehat{S}}_E\left(E_{a_1{b}_1}\otimes E_{a_2{b}_2}\otimes \cdots \otimes E_{a_m{b}_m}\otimes h_i\otimes {\overline{v}}_j\right)={\delta }_{b_{m}i}{h}_{a_1}\otimes {\overline{v}}_{q_1}\otimes \hfill \\ \hfill & \left(\begin{array}{c}{\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge {\Gamma }^{b_2{q}_2}{}_{a_3{q}_3}\wedge \cdots \wedge X^{b_{m-1}{q}_{m-1}}{}_{a_{m}j}+\cdots \\ +{(-1)}^{m-3}{\Gamma }^{b_1{q}_1}{}_{a_2{q}_2}\wedge X^{b_2{q}_2}{}_{a_3{q}_3}\wedge \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_{m}j}\\ +{(-1)}^{m-2}{X}^{b_1{q}_1}{}_{a_2{q}_2}\wedge {\Gamma }^{b_2{q}_2}{}_{a_3{q}_3}\wedge \cdots \wedge {\Gamma }^{b_{m-1}{q}_{m-1}}{}_{a_{m}j}\end{array}\right),\hfill \end{array}$$

where the wedge products alternate in sign and contain exactly one X factor.

Proof. 

We use (14) and (31) to find the first equation, using

$$\begin{array}{c}\hfill E_{ab}{S}_E(\mathrm{d}{E}_{rt}\otimes h_i\otimes {\overline{v}}_j)={\widehat{S}}_E\left((E_{ab}\otimes E_{rt}-E_{at}\otimes 1{\delta }_{br})\otimes h_i\otimes {\overline{v}}_j\right).\end{array}$$

(35)

The rest is a proof by induction, similar to Proposition 7 using Proposition 4.  □

6. Matrix Modules and Sheaves on $\mathbb{C}{\mathbb{P}}^{n-1}$

6.1. Differentiating the State Evaluation Map

We would like the state evaluation map extended to forms in Corollary 3 to be a cochain map, i.e., $\mathrm{d}\varphi \left(\xi \right)=\varphi \left(\mathrm{d}\xi \right)$. However, Proposition 5 gives an additional term that we must evaluate.

Proposition 9. 

For the usual calculus on projective space, the state evaluation map (8) is not a cochain map to the standard $\mathrm{d}$ calculus on $\mathbb{C}{\mathbb{P}}^{n-1}$.

Proof. 

Using Proposition 8 and (24), we evaluate the last term in (33)

$$\begin{array}{cc}\hfill (⟨,⟩\otimes \mathrm{id})\left(\overline{e_{1\otimes 1}}\otimes S_E(E_{ab}\otimes E_{rt}\otimes e_{1\otimes 1})\right)& =(⟨,⟩\otimes \mathrm{id})\left(\overline{h_k\otimes {\overline{v}}_k}{S}_E\otimes (E_{ab}\otimes E_{rt}\otimes h_i\otimes {\overline{v}}_i)\right)\hfill \\ \hfill & =⟨\overline{h_k\otimes {\overline{v}}_k},h_a\otimes {\overline{v}}_q⟩{\delta }_{ti}{X}^{bq}{}_{ri}\hfill \\ \hfill & =v_a{\overline{v}}_q{\delta }_{qt}\mathrm{d}{\overline{v}}_b\wedge \mathrm{d}{v}_r=v_a{\overline{v}}_t\mathrm{d}{\overline{v}}_b\wedge \mathrm{d}{v}_r,\hfill \end{array}$$

which is nonzero. Now, if $b\ne r$, then $E_{ab}\otimes E_{rt}\in {\Omega }_{\mathrm{uni}}^1\left(M_n\right)$.  □

This may seen disappointing, but it is an opportunity to consider the holomorphic structure or projective space. From Definition 8 and using (22), we see that $E={\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ with the connection in Section 4.1 is a holomorphic bundle over $\mathbb{C}{\mathbb{P}}^{n-1}$.

Theorem 1. 

For the $\overline{\partial }$ calculus on $\mathbb{C}{\mathbb{P}}^{n-1}$ and the universal calculus on $M_n$ the state evaluation map (2) and its extension to forms in Corollary 3 is a cochain map.

Proof. 

Proposition 5 will give the result if the $S_E$ then gives zero in the $\overline{\partial }$ calculus. This can be seen from Proposition 8 and (24).  □

Using the $\overline{\partial }$ calculus on $\mathbb{C}{\mathbb{P}}^{n-1}$ raises the possibility that the bimodule $E={\mathrm{Col}}^n\left(\mathbb{C}\right)$$\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ could be use to give a functor from $M_n$ modules on $\mathbb{C}{\mathbb{P}}^{n-1}$. First, we need to consider $M_n$ modules with connection.

6.2. Connections on Right Modules over $M_n\left(\mathbb{C}\right)$

In this subsection and the next, we take $r_i\in {\mathrm{Row}}^n\left(\mathbb{C}\right)$ to be the row vector with 1 in position i and zero elsewhere.

Proposition 10. 

Take the right $M_n\left(\mathbb{C}\right)$ module $F=V\otimes {\mathrm{Row}}^n\left(\mathbb{C}\right)$ for a vector space V, with action given by the matrix multiplication

$$\begin{array}{c}\hfill (v\otimes r_i)◃E_{jk}=v\otimes r_k{\delta }_{ij}.\end{array}$$

Then, a general right connection ${\nabla }_F$ for the universal calculus on $M_n$ is

$$\begin{array}{c}\hfill {\nabla }_F(v\otimes r_i)\in V\otimes {\mathrm{Row}}^n\left(\mathbb{C}\right)\underset{M_n}{\otimes }{\Omega }_{\mathrm{uni}}^1\left(M_n\right)\subset V\otimes {\mathrm{Row}}^n\left(\mathbb{C}\right)\underset{M_n}{\otimes }{M}_n\otimes M_n\end{array}$$

and using the fact that every 1-form on $M_n$ can be written as a sum of $E_{sj}.\mathrm{d}{E}_{pi}$, we can write

$${\nabla }_F(v\otimes r_i)=\sum _{pj}{L}_{jp}\left(v\right)\otimes r_j\otimes \mathrm{d}{E}_{pi}$$

(36)

for linear $L_{jp}:V\to V$ with ${\sum }_j{L}_{jj}\left(v\right)=v$. The curvature of the connection is

$$\begin{array}{c}\hfill R_F(v\otimes r_i)=\sum _{abjp}{L}_{ab}\left(L_{jp}\left(v\right)\right)\otimes r_a\otimes \mathrm{d}{E}_{bj}\wedge \mathrm{d}{E}_{pi}.\end{array}$$

Proof. 

By using the ${\mathrm{Row}}^n\left(\mathbb{C}\right){\otimes }_{M_n}{M}_n\cong {\mathrm{Row}}^n\left(\mathbb{C}\right)$, we obtain

$$\begin{array}{c}\hfill (V\otimes {\mathrm{Row}}^n\left(\mathbb{C}\right)\underset{M_n}{\otimes }{\Omega }_{\mathrm{uni}}^1\left(M_n\right)\cong V\otimes K,\end{array}$$

where $K=ker·:{\mathrm{Row}}^n\left(\mathbb{C}\right)\otimes M_n\to {\mathrm{Row}}^n\left(\mathbb{C}\right)$. We write summing over $j,p,q$,

$$\begin{array}{c}\hfill {\nabla }_F(v\otimes r_i)=S_{ijpq}\left(v\right)\otimes r_j\otimes E_{pq}\end{array}$$

and for this to be in $V\otimes K$ we need $S_{ijpq}\left(v\right)\otimes {\delta }_{jp}{r}_q=0$, i.e., ${\sum }_j{S}_{ijjq}=0$ for all $i,q$. We will also write

$$\begin{array}{c}\hfill {\nabla }_F(v\otimes r_i)=S_{ijpq}\left(v\right)\otimes r_j\otimes \mathrm{d}{E}_{pq}.\end{array}$$

and these are the same under the isomorphism as

$$\begin{array}{c}\hfill S_{ijpq}\left(v\right)\otimes r_j(I_n\otimes E_{pq}-E_{pq}\otimes I)=S_{ijpq}\left(v\right)\otimes r_j\otimes E_{pq}-S_{ijjq}\left(v\right)\otimes r_q\otimes I.\end{array}$$

The condition to be a right connection is, for all $i,s,t$,

$$\begin{array}{c}\hfill {\nabla }_F(v\otimes r_i{E}_{st})=\nabla (v\otimes r_i)E_{st}+v\otimes r_i\otimes \mathrm{d}{E}_{st}\end{array}$$

which gives, summing over $j,p,q$

$$\begin{array}{c}\hfill {\delta }_{is}{S}_{tjpq}\left(v\right)\otimes r_j\otimes E_{pq}=S_{ijpq}\left(v\right)\otimes r_j\otimes E_{pq}{E}_{st}+v\otimes r_i\otimes E_{st}-{\delta }_{is}v\otimes r_t\otimes I.\end{array}$$

This has general solution

$$\begin{array}{c}\hfill S_{ijpq}\left(v\right)=-v{\delta }_{ij}{\delta }_{pq}+{\delta }_{iq}{L}_{jp}\left(v\right),\end{array}$$

where ${\sum }_j{L}_{jj}\left(v\right)=v$.  □

If we take ${}_{M_n}\mathcal{M}$ to be the category of left $M_n$ modules and module maps, then there is a functor ${}_{M_n}\mathcal{M}\to {\mathcal{E}}_{M_n}$ to the category of right $M_n$ modules with right connections for the universal calculus. This is given by $V\mapsto V\otimes {\mathrm{Row}}^n\left(\mathbb{C}\right)$, and this is given the connection in Proposition 10, where we define $L_{ij}\left(v\right)$ by the right action $E_{ij}▹v=L_{ij}\left(v\right)$. The condition ${\sum }_j{L}_{jj}\left(v\right)=v$ is simply $I_n▹v=v$. Note that this will not give the most general $L_{ij}$ for Proposition 10, but the restriction to certain $L_{ij}$ is what we need in the next part.

6.3. Induced Holomorphic Bundles on $\mathbb{C}{\mathbb{P}}^{n-1}$

From Proposition 1, we know that there is a functor $\otimes E$ from ${\mathcal{E}}_{M_n}$ to ${\mathcal{E}}_{C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)}$. At the end of the last section, we had a functor from ${}_{M_n}\mathcal{M}$ to ${\mathcal{E}}_{M_n}$, and of course these can be composed. However, we know that the state evaluation map $\varphi$ is not a cochain map for the ordinary calculus on $\mathbb{C}{\mathbb{P}}^{n-1}$ (using the choice of connection in Section 4.2), but it is for the $\overline{\partial }$ calculus. It is then natural to ask if we obtain a functor into holomorphic bundles on $\mathbb{C}{\mathbb{P}}^{n-1}$. We use ${\pi }^{i,j}$ for the projection from ${\Omega }^{i+j}$ to ${\Omega }^{i,j}$.

Given a connection for the calculus ${\Omega }^n\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$, we can obtain a $\overline{\partial }$ connection (see Section 2.5) simply by composing with ${\pi }^{0,1}$. Then, to ensure that $F{\otimes }_{M_n}E$ is a homomorphic bimodule, we require that the ${\Omega }^{0,2}$ part of its curvature $R_{F\otimes E}$ vanishes.

Proposition 11. 

The ${\Omega }^{0,2}$ component of the curvature of $F{\otimes }_{M_n}E$ is

$$\begin{array}{cc}\hfill & (\mathrm{id}\otimes {\pi }^{0,2})R_{F\otimes E}(v\otimes r_t\otimes h_i\otimes v_j)\hfill \\ \hfill & =\sum _{abs}{L}_{ca}{L}_{bs}\left(v\right)\otimes {\overline{v}}_j\otimes {\delta }_{ti}{v}_a{v}_s\otimes \mathrm{d}{\overline{v}}_g\wedge \mathrm{d}{\overline{v}}_b-\sum _a{L}_{ca}\left(v\right)\otimes {\overline{v}}_j\otimes v_a{v}_i\otimes \mathrm{d}{\overline{v}}_g\wedge \mathrm{d}{\overline{v}}_t\hfill \\ \hfill & +\sum _{ab}{L}_{cg}{L}_{ba}\left(v\right)\otimes {\overline{v}}_j\otimes v_a{v}_i\otimes \mathrm{d}{\overline{v}}_b\wedge \mathrm{d}{\overline{v}}_t,\hfill \end{array}$$

and in particular, if $L_{cg}{L}_{es}={\delta }_{ge}{L}_{cs}$ then $(\mathrm{id}\otimes {\pi }^{0,2})R_{F\otimes E}=0$.

Proof. 

From Proposition 6, $R_{F\otimes E}$ splits into three bits, and the $\mathrm{id}\otimes R_E$ term does not have a $\mathrm{d}{\overline{v}}_i\wedge \mathrm{d}{\overline{v}}_j$ part as computed in (22). By Proposition 8 and Equation (24), the last term in the formula for $R_{F\otimes E}$ in Proposition 6 does not have a ${\Omega }^{0,2}$ part either, so we are left with

$$(\mathrm{id}\otimes {\pi }^{0,2})R_{F\otimes E}=(\mathrm{id}\otimes {\pi }^{0,2})\left((\mathrm{id}\otimes {\sigma }_E)(R_F\otimes \mathrm{id})\right).$$

Using (12) twice, we obtain

$$\begin{array}{cc}\hfill & (\mathrm{id}\otimes {\pi }^{0,2})\sigma \left(\mathrm{d}{E}_{ab}\wedge \mathrm{d}{E}_{st}\otimes h_i\otimes {\overline{v}}_j\right)\hfill \\ \hfill & =\sum _{pqge}\left({\delta }_{ti}{\delta }_{sr}{\delta }_{bp}{\delta }_{ae}{h}_g-{\delta }_{ti}{\delta }_{sr}{\delta }_{bg}{\delta }_{ep}{h}_a-{\delta }_{tp}{\delta }_{ri}{\delta }_{bs}{\delta }_{ae}{h}_g+{\delta }_{tp}{\delta }_{ri}{\delta }_{bg}{\delta }_{es}{h}_a\right)\otimes {\overline{v}}_f\otimes {\pi }^{0,2}({\Gamma }^{gf}{}_{eq}\wedge {\Gamma }^{pq}{}_{rj})\hfill \\ \hfill & =\sum _{pgefr}\left({\delta }_{ti}{\delta }_{sr}{\delta }_{bp}{\delta }_{ae}{h}_g-{\delta }_{ti}{\delta }_{sr}{\delta }_{bg}{\delta }_{ep}{h}_a-{\delta }_{tp}{\delta }_{ri}{\delta }_{bs}{\delta }_{ae}{h}_g+{\delta }_{tp}{\delta }_{ri}{\delta }_{bg}{\delta }_{es}{h}_a\right)\hfill \\ \hfill & \otimes {\overline{v}}_f\otimes v_f{v}_e\mathrm{d}{\overline{v}}_g\wedge (-{\delta }_{pr}\mathrm{d}{\overline{v}}_j+{\overline{v}}_j{v}_r\mathrm{d}{\overline{v}}_p)\hfill \\ \hfill & =\sum _g{h}_g\otimes {\overline{v}}_j\otimes \left({\delta }_{ti}{v}_a{v}_s\mathrm{d}{\overline{v}}_g\wedge \mathrm{d}{\overline{v}}_b-{\delta }_{bs}{v}_a{v}_i\mathrm{d}{\overline{v}}_g\wedge \mathrm{d}{\overline{v}}_t+{\delta }_{ag}{v}_s{v}_i\mathrm{d}{\overline{v}}_b\wedge \mathrm{d}{\overline{v}}_t\right)\hfill \\ \hfill & =\sum _{gef}{h}_g\otimes {\overline{v}}_j\otimes \left({\delta }_{ti}{\delta }_{eg}{\delta }_{bf}{v}_a{v}_s-{\delta }_{bs}{\delta }_{eg}{\delta }_{tf}{v}_a{v}_i+{\delta }_{ag}{\delta }_{be}{\delta }_{tf}{v}_s{v}_i\right)\mathrm{d}{\overline{v}}_e\wedge \mathrm{d}{\overline{v}}_f\hfill \end{array}$$

(37)

taking only the $\mathrm{d}\overline{v}\wedge \mathrm{d}\overline{v}$ component.

We are left with, using (37)

$$\begin{array}{cc}\hfill (\mathrm{id}\otimes {\pi }^{0,2})R_{F\otimes E}& =(\mathrm{id}\otimes {\pi }^{0,2})\left((\mathrm{id}\otimes {\sigma }_E)(R_F\otimes \mathrm{id})\right)\hfill \\ \hfill & =(\mathrm{id}\otimes {\pi }^{0,2})(\mathrm{id}\otimes {\sigma }_E)\left(R_F(v\otimes r_t)\otimes h_i\otimes {\overline{v}}_j\right)\hfill \\ \hfill & =(\mathrm{id}\otimes {\pi }^{0,2})\left(L_{ca}{L}_{bs}\left(v\right)\otimes r_c\otimes {\sigma }_E(\mathrm{d}{E}_{ab}\wedge \mathrm{d}{E}_{st}\otimes h_i\otimes {\overline{v}}_j)\right)\hfill \\ \hfill & =\sum _{gefabsc}(L_{ca}{L}_{bs}\left(v\right)\otimes r_c\otimes h_g\otimes {\overline{v}}_j\otimes \hfill \\ \hfill & \left({\delta }_{ti}{\delta }_{eg}{\delta }_{bf}{v}_a{v}_s-{\delta }_{bs}{\delta }_{eg}{\delta }_{tf}{v}_a{v}_i+{\delta }_{ag}{\delta }_{be}{\delta }_{tf}{v}_s{v}_i\right)\mathrm{d}{\overline{v}}_e\wedge \mathrm{d}{\overline{v}}_f,\hfill \end{array}$$

(38)

and for this to vanish, we need for all $t,i,j,g,c$,

$$\begin{array}{cc}\hfill & \sum _{efabs}(L_{ca}{L}_{bs}\left(v\right)\otimes {\overline{v}}_j\otimes \left({\delta }_{ti}{\delta }_{eg}{\delta }_{bf}{v}_a{v}_s-{\delta }_{bs}{\delta }_{eg}{\delta }_{tf}{v}_a{v}_i+{\delta }_{ag}{\delta }_{be}{\delta }_{tf}{v}_s{v}_i\right)\mathrm{d}{\overline{v}}_e\wedge \mathrm{d}{\overline{v}}_f=0\hfill \\ \hfill & =\sum _{abs}{L}_{ca}{L}_{bs}\left(v\right)\otimes {\overline{v}}_j\otimes {\delta }_{ti}{v}_a{v}_s\otimes \mathrm{d}{\overline{v}}_g\wedge \mathrm{d}{\overline{v}}_b-\sum _a{L}_{ca}\left(v\right)\otimes {\overline{v}}_j\otimes v_a{v}_i\otimes \mathrm{d}{\overline{v}}_g\wedge \mathrm{d}{\overline{v}}_t\hfill \\ \hfill & +\sum _{ab}{L}_{cg}{L}_{ba}\left(v\right)\otimes {\overline{v}}_j\otimes v_a{v}_i\otimes \mathrm{d}{\overline{v}}_b\wedge \mathrm{d}{\overline{v}}_t.\hfill \end{array}$$

(39)

If $L_{cg}{L}_{es}={\delta }_{ge}{L}_{cs}$; then, the result of (38) is

$$\begin{array}{cc}\hfill & \sum _{efabs}{L}_{cs}\left(v\right)\otimes {\delta }_{ab}\left({\delta }_{ti}{\delta }_{eg}{\delta }_{bf}{v}_a{v}_s-{\delta }_{bs}{\delta }_{eg}{\delta }_{tf}{v}_a{v}_i+{\delta }_{ag}{\delta }_{be}{\delta }_{tf}{v}_s{v}_i\right)\mathrm{d}{\overline{v}}_e\wedge \mathrm{d}{\overline{v}}_f\hfill \\ \hfill & =\sum _{efas}{L}_{cs}\left(v\right)\otimes \left({\delta }_{ti}{\delta }_{eg}{\delta }_{af}{v}_a{v}_s-{\delta }_{as}{\delta }_{eg}{\delta }_{tf}{v}_a{v}_i+{\delta }_{ag}{\delta }_{ae}{\delta }_{tf}{v}_s{v}_i\right)\mathrm{d}{\overline{v}}_e\wedge \mathrm{d}{\overline{v}}_f\hfill \\ \hfill & =\sum _{fas}{L}_{cs}\left(v\right)\otimes v_s\left({\delta }_{ti}{\delta }_{af}{v}_a-{\delta }_{as}{\delta }_{tf}{v}_i+{\delta }_{ag}{\delta }_{tf}{v}_i\right)\mathrm{d}{\overline{v}}_g\wedge \mathrm{d}{\overline{v}}_f\hfill \\ \hfill & ={\delta }_{ti}\sum _{fs}{L}_{cs}\left(v\right)\otimes v_s{v}_f\mathrm{d}{\overline{v}}_g\wedge \mathrm{d}{\overline{v}}_f=0.\hfill \end{array}$$

 □

Note that the conditions ${\sum }_i{L}_{ii}\left(v\right)=v$, and that in Proposition 11 they correspond to $L_{ij}$ being the left action of the matrix unit $E_{ij}$ in a representation of $M_n\left(\mathbb{C}\right)$. Set $F=V\otimes {\mathrm{Row}}^n\left(\mathbb{C}\right)$ as in Proposition 10, then

$$\begin{array}{c}\hfill F\underset{M_n\left(\mathbb{C}\right)}{\otimes }E=V\otimes {\mathrm{Row}}^n\left(\mathbb{C}\right)\underset{M_n\left(\mathbb{C}\right)}{\otimes }{\mathrm{Col}}^n\left(\mathbb{C}\right)\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right).\end{array}$$

For $w\in V$, using (9), Proposition (10) and (12)

$$\begin{array}{cc}\hfill {\nabla }_{F\otimes E}(w\otimes r_a\otimes h_i\otimes {\overline{v}}_j)& =(\mathrm{id}\otimes {\sigma }_E)\left({\nabla }_F(w\otimes r_a)\otimes (h_i\otimes {\overline{v}}_j)+w\otimes r_a\otimes {\nabla }_E(h_i\otimes {\overline{v}}_j)\right)\hfill \\ \hfill & =L_{ps}\left(w\right)\otimes r_p\otimes {\sigma }_E(\mathrm{d}{E}_{sa}\otimes h_i\otimes {\overline{v}}_j)+w\otimes r_a\otimes h_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ij}\hfill \\ \hfill & =L_{ps}\left(w\right)\otimes r_p\otimes ({\delta }_{ai}{h}_t{\delta }_{sr}-{\delta }_{at}{h}_s{\delta }_{ri})\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ij}\hfill \\ & +w\otimes r_a\otimes h_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ij}\hfill \\ \hfill & ={\delta }_{ai}{L}_{pr}\left(w\right)\otimes r_p\otimes h_t{\overline{v}}_q\otimes {\Gamma }^{tq}{}_{rj}+w\otimes r_a\otimes h_p\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{ij}\hfill \\ \hfill & -L_{ps}\left(w\right)\otimes r_p\otimes h_s\otimes {\overline{v}}_q\otimes {\Gamma }^{aq}{}_{ij}\hfill \\ \hfill & =({\delta }_{ai}{L}_{pr}\left(w\right)\otimes r_p\otimes h_t+w\otimes r_a\otimes h_t{\delta }_{ri}\hfill \\ & -{\delta }_{ri}{\delta }_{ta}{L}_{ps}\left(w\right)\otimes r_p\otimes h_s)\otimes {\overline{v}}_q\otimes {\Gamma }^{tq}{}_{rj}.\hfill \end{array}$$

Note ${\mathrm{Row}}^n\left(\mathbb{C}\right){\otimes }_{M_n}{\mathrm{Col}}^n\left(\mathbb{C}\right)\cong \mathbb{C}$ by $r_a\otimes h_i\mapsto {\delta }_{ai}\in \mathbb{C}$. Look at the last two terms of the last line of (40) using this isomorphism

$$\begin{array}{c}\hfill \left(w{\delta }_{at}{\delta }_{ri}-{\delta }_{ri}{\delta }_{ta}{L}_{ps}\left(w\right){\delta }_{ps}\right)\otimes {\overline{v}}_q\otimes {\Gamma }^{tq}{}_{rj}=\left(w{\delta }_{at}-{\delta }_{ta}{\delta }_{ps}{L}_{ps}\left(w\right)\right)\otimes {\overline{v}}_q\otimes {\Gamma }^{tq}{}_{ij}=0\end{array}$$

by Proposition (10). Thus, we can use the isomorphism to give a connection on $F{\otimes }_{M_n}E\cong V\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ given by

$$\begin{array}{c}\hfill \nabla (w\otimes {\overline{v}}_j)=L_{pr}\left(w\right)\otimes {\overline{v}}_q\otimes {\Gamma }^{pq}{}_{rj}.\end{array}$$

Corollary 4. 

For the special case of the connection in (23), we find

$$\begin{array}{cc}\hfill \nabla (w\otimes {\overline{v}}_j)& =L_{pr}\left(w\right)\otimes {\overline{v}}_q\otimes v_q\left({\delta }_{pr}\mathrm{d}{\overline{v}}_j-{\overline{v}}_j{v}_r\mathrm{d}{\overline{v}}_p+{\overline{v}}_j{\overline{v}}_p\mathrm{d}{v}_r\right)\hfill \\ \hfill & =w\otimes {\overline{v}}_q\otimes v_q\mathrm{d}{\overline{v}}_j+L_{pr}\left(w\right)\otimes {\overline{v}}_q\otimes v_q{\overline{v}}_j({\overline{v}}_p\mathrm{d}{\overline{v}}_r-v_r\mathrm{d}{\overline{v}}_p)\hfill \\ \hfill & =w\otimes {\overline{v}}_q\otimes v_q\mathrm{d}{\overline{v}}_j+L_{pr}\left(w\right)\otimes {\overline{v}}_j({\overline{v}}_p\mathrm{d}{\overline{v}}_r-v_r\mathrm{d}{\overline{v}}_p),\hfill \end{array}$$

(40)

and this splits into a ∂ and a $\overline{\partial }$ connection

$$\begin{array}{cc}\hfill {\partial }_V(w\otimes {\overline{v}}_j)& =L_{pr}\left(w\right)\otimes {\overline{v}}_j\otimes {\overline{v}}_p\mathrm{d}{v}_r\hfill \\ \hfill {\overline{\partial }}_V(w\otimes {\overline{v}}_j)& =w\otimes {\overline{v}}_q\otimes v_q\mathrm{d}{\overline{v}}_j-L_{pr}\left(w\right)\otimes {\overline{v}}_j\otimes v_r\mathrm{d}{\overline{v}}_p.\hfill \end{array}$$

(41)

Proposition 12. 

The composition of the given functor $\otimes E:{\mathcal{E}}_{M_n}\to {\mathcal{E}}_{C\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)}$ and the functor in Section 6.2${}_{M_n}\mathcal{M}\to {\mathcal{E}}_{M_n}$ gives a functor from ${}_{M_n}\mathcal{M}$ to holomorphic bundles on $\mathbb{C}{\mathbb{P}}^{n-1}$. It is given by V mapping to $V\otimes C_{-1}\left(\mathbb{C}{\mathbb{P}}^{n-1}\right)$ with the ${\overline{\partial }}_V$ connections given in Corollary 4.

Proof. 

The category of holomorphic bundles is given morphisms being module maps commutating with $\overline{\partial }$ operators as in Section 2.4. Most of this has been proved in the discussion previously. We explicitly check that we have a functor, i.e., that a $M_n$ module map $\theta :V\to Y$ gives a commutating diagram

which happens because the $L_{pr}$ maps commute with $\theta$ in the formula (41).  □