Abstract
In this paper, we calculate the Gaussian curvatures of the dual spherical indicatrix curves formed on unit dual sphere by the Blaschke vectors and dual instantaneous Pfaff vectors of dual parallel equidistant ruled surfaces (DPERS) and we give the relationships between these curvatures. In addition to—in cases where the base curves of these DPERS are closed—computing the dual integral invariants of the indicatrix curves. Additionally, we show the relationships between them. Finally, we provide an example for each of these indicatrix curves.
1. Introduction
The main sources for curves and surfaces in Euclidean space are [1,2,3,4,5]. The concept of ruled surfaces, formed by the movement of a line on a curve, has an important place in differential geometry. There are many studies on ruled surfaces in Euclidean and non-Euclidean spaces [6,7,8,9,10]. The concept of parallel equidistant ruled surfaces was first introduced by Valeontis [11]. The resources [12,13,14,15,16,17,18,19] can be examined for studies on these surfaces. Although dual numbers are a set of numbers defined by William Kingdon Clifford (1845–1879) [20], their first applications in geometry began with Eduard Study [21]. Dual numbers can be seen as similar to complex numbers, but they are important in terms of kinematics, especially in unit dual sphere applications. E. Study revealed that there is a strong relationship between a dual point on a unit dual sphere and an oriented line in the space of lines, and thus this concept gained meaning. Since kinematically correct beams are a family of axes of rotation, it is possible to examine the ruled surface of a motion over the unit dual sphere. A dual spherical curve on a dual sphere corresponds exactly to a ruled surface in the space of lines. Basic concepts in this field can be accessed from the resources [22,23,24,25]. Furthermore, some studies on dual curves or surfaces include Refs. [26,27,28,29,30]. In addition to geometry, studies on dual numbers and vectors are carried out in fields such as mechanical engineering, robot kinematics, physics and astronomy. The concept of motors was introduced by Clifford, but he did not examine the modeling of points, lines and planes in terms of motors. The sentence of motors is isomorphic to the sentence of dual quaternions. However, due to the geometric meaning of vectors as rotating planes, screws can be easily formulated using motors from a purely geometrical point of view. As a result, algebraic modeling of points, lines, and planes with motor algebra is easier with dual quaternions. The use of dual matrices and dual quaternions in robotics has increased in recent years [31,32,33,34,35]. The concept of dual numbers is studied by geometers in Euclidean spaces as well as in non-Euclidean spaces such as Lorentz–Minkowski spaces [36,37,38,39,40].
In Ref. [41], we defined parallel equidistant ruled surfaces (DPERS) and compared some of their geometric properties. In addition, we have shown that one of these surfaces is symmetrical to the other. In this paper, we calculate the Gaussian curvatures of the ruled surfaces corresponding in space of lines to the dual spherical indicatrix curves formed on a unit dual sphere by the Blaschke vectors and dual instantaneous Pfaff vectors of DPERS and we give the relationships between these curvatures. Additionally, in cases where the base curves of these DPERS are closed, we compute the dual integral invariants of the indicatrix curves. We also show the relationships between them. Finally, we provide an example for each of these indicatrix curves. It is possible to combine the results of this study with the concepts of submanifold theory or studies in other spaces and obtain new results [42,43,44,45,46,47].
2. Preliminaries
The set is called dual vector space and the elements of this set are called dual vectors, where and are the real and dual components of the vector , respectively. The operations of addition, multiplication by scalars, inner product, norm and vector product on this set are explained in [23,41]. The set is called a unit dual unit sphere and the elements of this set are called dual unit vectors [23]. The dual angle between the unit dual vectors and can be calculated with any of the following two equalities:
where is the unit dual vector, is the distance vector between and , . Additionally, ω is the real angle between the real vectors and and is the shortest distance between the vectors and ,22,23].
Theorem 1
(E. Study Mapping [21]). A directed line in the space of lines corresponds exactly to a dual point on the dual unit sphere.
The dual spherical curve drawn by the unit dual vector is expressed in the space of lines by the ruled surface, see Figure 1,
where is the base curve of the ruled surface and s is the arc lenght parameter of the curve [22,23]. That is, a dual spherical curve can be viewed as a ruled surface. The orthonormal system of the ruled surface are called Blaschke frame and also the values
are called Blaschke invariants, where are the reel components and are dual components of these invariants [22]. Besides and are the curvature and the torsion of the curve .
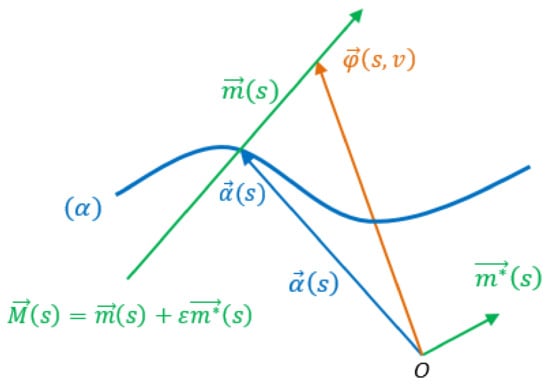
Figure 1.
The dual spherical expression of the ruled surface .
The Blaschke derivative formulas are as follows:
See [41] for the real and dual Equations (2) and (3). The dual pitch length, the dual pitch angle and the drall (parameter of distribution) of the closed ruled surface are, respectively [22],
where is the dual Steiner rotation vector and
The Gaussian curvature of the ruled surface is depicted by
where S is the shape operator, is the normal vector and is the base vectors [14]. If a ruled surface is isomorphic to the plane (the surface is developable), the drall (or Gaussian curvature) of this surface is zero everywhere.
The definition and properties of dual parallel equidistant ruled surfaces (DPERS) are also explained in [41]. In this section, the relations that will be used in the continuation of the study will be given. Let and be the Blaschke frames of the base curves of DPERS,
respectively, where is the base curve of the ruled surface and is the arc length parameter of the curve. There are the following relations between these vectors:
where and are the real and dual components of the vectors and , 41]. Additionally, are the perpendicular projection distances on the unit vectors , , of the vector , respectively [11]. The relationships between the Blaschke invariants , and , of DPERS are
respectively [41]. The arc length between the points corresponding to the striction curves of DPERS is [41]
The relationship between arc-length parameters of the base curves of DPERS is [41]
The relationship between the striction curves and of DPERS are
The relationships between the real and dual components of the dual instantaneous Pfaff vectors and of DPERS are [41]
The real and dual components of the dual Steiner vectors and of DPERS are [41]
The relationships between the real and dual components of the dual angles and between the vectors , and , of DPERS are
respectively [41].
3. The Integral Invariants of DPERS
In this section, we will compute the integral invariants of the closed ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed by the dual tangent, dual principal normal, dual binormal and intantaneous Pfaff vectors of the base curves of DPERS. While the next operations are performed, for shortness, the Equation (11) will be written as follows:
where
3.1. The Relationships between the Integral Invariants of the Closed Ruled Surfaces Formed by the Dual Tangent Vectors of DPERS
Let and be the dual tangent vectors of the base curves of DPERS and respectively. The parametric Equations of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed by these vectors on the unit dual sphere are written as follows (Figure 2):
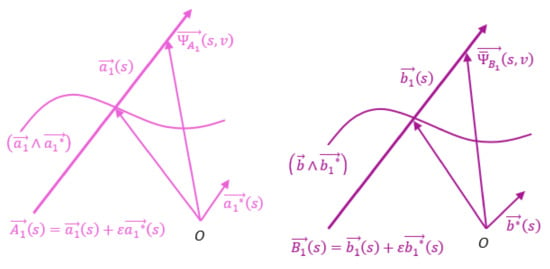
Figure 2.
The dual spherical expressions of ruled surfaces formed by dual tangent vectors of DPERS.
Theorem 2.
There are the following relationships between the dual pitch lengths, the dual pitch angles and the dralls of the closed ruled surfaces formed by the dual tangent vectors and of DPERS, respectively:
Proof.
From the Equations (4), (8) and (13), the pitch lengths of the ruled surfaces formed by and are found as
respectively. By using the Equations (10) and (15), the Equation is stated as follows more clearly:
Corollary 1.
The closed ruled surfaces formed by the dual tangent vectors and of DPERS are always isomorphic to the plane.
3.2. The Relationships between the Integral Invariants of the Closed Ruled Surfaces Formed by the Dual Principal Normal Vectors of DPERS
Let and be the dual principal normal vectors of the base curves of DPERS and respectively. The parametric Equations of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed by these vectors on the unit dual sphere are written as follows:
Theorem 3.
There are the following relationships between the dual pitch lengths, the dual pitch angles and the dralls of the closed ruled surfaces formed by the dual principal normal vectors and of DPERS, respectively:
Proof.
Corollary 2.
The closed ruled surfaces formed by the dual principal normal vectors and of DPERS are isomorphic to the plane if and only if
3.3. The Relationships between the Integral Invariants of the Closed Ruled Surfaces Formed by the Dual Binormal Vectors of DPERS
Let and be the dual binormal vectors of the base curves DPERS and respectively. The parametric Equations of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed by these vectors on the unit dual sphere are written as follows:
Theorem 4.
There are the following relationships between the dual pitch lengths, the dual pitch angle and the dralls of the closed ruled surfaces formed by the dual binormal vectors and of DPERS, respectively:
Proof.
Corollary 3.
The closed ruled surfaces formed by the dual binormal vectors and of DPERS are never isomorphic to the plane.
3.4. The Relationships between the Integral Invariants of the Closed Ruled Surfaces Formed by the Dual Instantaneous Pfaff Vectors of DPERS
The parametric Equations of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed by the unit dual vectors and in the direction of the dual instantaneous Pfaff vectors of DPERS on the dual unit sphere are written as follows:
Theorem 5.
There are the following relationships between the dual pitch lengths, the dual pitch angles and the dralls of the closed ruled surfaces formed by the dual instantaneous Pfaff vectors and of DPERS, respectively:
Proof.
From the Equations (4), (12) and (13), the pitch lengths of the ruled surfaces formed by the vectors and are obtained as
respectively. By using the Equations (10), (14) and (15), the Equation is stated as follows more clearly,
On the other hand, from the Equations (4), (12) and (13), the dual pitch angles of the ruled surfaces formed by and are obtained as follows:
Corollary 4.
The closed ruled surfaces formed by the dual instantaneous Pfaff vectors and of DPERS are always isomorphic to the plane.
4. The Gaussian Curvatures of DPERS
In this section, we will compute the Gaussian curvatures of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed by the dual tangent, dual principal normal, dual binormal and dual instantaneous Pfaff vectors of the base curves of DPERS.
4.1. The Relationship between the Gaussian Curvatures of the Ruled Surfaces Formed by the Dual Tangent Vectors of DPERS
Theorem 6.
There is the following relationship between the Gaussian curvatures of the ruled surfaces formed by the dual tangent vectors and of DPERS:
Proof.
If the ruled surface in the Equation (16) is derived according to the parameters s and v,
are obtained. If the vectors and in Equation (33) are performed the inner product operation,
is found. Since this inner product is non zero, the system is not an orthogonal system. So now, let us perform the Gram Schmitd ’s method on these vectors. Firstly, the following vectors are obtained:
Thus, if the vectors and in Equation (34) are rendered orthonormal,
are attained. Then, if the vectors and in Equation (35) are performed the vectoral product operation, the normal vector of the ruled surface is found as follows:
Let and be the shape operator and the Gaussian curvature of the ruled surface respectively. From the Equation (6),
is written. Here, from Equations (6) and (36),
Corollary 5.
The ruled surfaces formed by the dual tangent vectors and of DPERS are always isomorphic to the plane.
4.2. The Relationship between the Gaussian Curvatures of the Ruled Surfaces Formed by the Dual Principal Normal Vectors of DPERS
Theorem 7.
There is the following relationship between the Gaussian curvatures of the ruled surfaces formed by the dual principal normal vectors and of DPERS:
here and .
Proof.
If the ruled surface in the Equation (20) is derived according to the parameters s and v,
are obtained, here . If the vectors and in the Equation (41) are performed, the inner product operation,
is found. Since this inner product is non zero, the system is not an orthogonal system. So now, let us perform the Gram Schmitd ’s method on these vectors. Firstly, the following vectors are obtained:
Thus, if the vectors and in Equation (42) are rendered orthonormal,
are attained. Then, if the vectors and in Equation (43) are performed, the vectoral product operation, the normal vector of the ruled surface is found as follows:
Let and be the shape operator and the Gaussian curvature of the ruled surface respectively. From the Equation (6),
is written. From Equations (6) and (44),
where . If the Equations (43) and (46) are substituted in the Equation (45), the Gaussian curvature of the ruled surface is obtained as follows:
Likewise, the Gaussian curvature of the ruled surface is found as follows:
where 41]. If we take and the Equations (8) and (10) are substituted in Equation (48), we obtain
Thus, the proof is completed. □
Corollary 6.
The ruled surfaces formed by the dual principal normal vectors and of DPERS are isomorphic to the plane if and only if
4.3. The Relationship between the Gaussian Curvatures of the Ruled Surfaces Formed by the Dual Binormal Vectors of DPERS
Theorem 8.
There is the following relationship between the dual Gaussian curvatures of the ruled surfaces formed by the dual unit binormal vectorsandof DPERS:
whereand.
Proof.
If the ruled surface in the Equation (24) is derived according to the parameters s and v,
are obtained. If the vectors and in the Equation (51) are performed, the inner product operation,
is obtained. Since this inner product is non zero, the system is not an orthogonal system. So now, let us perform the Gram Schmitd ’s method on these vectors. Firstly, the following vectors are obtained:
Thus, if the vectors and in the Equation (52) are rendered orthonormal,
are attained. Then, if the vectors and in the Equation (53) are performed, the vectorial product operation, the normal vector of the ruled surface is found as follows:
Let and be the shape operator and the Gaussian curvature of the ruled surface respectively. From the Equation (6),
is written. From Equations (6) and (54), we get
where . If the Equations (53) and (56) are substituted in the Equation (55), the Gauss curvature of the ruled surface is obtained as follows:
Likewise, the Gaussian curvature of the ruled surface is found as follows:
Corollary 7.
The ruled surfaces formed by the dual binormal vectors and of DPERS are isomorphic to the plane if and only if
4.4. The Relationship between the Gaussian Curvatures of the Ruled Surfaces Formed by the Dual Instantaneous Pfaff Vectors of DPERS
Theorem 9.
There is the following relationship between the dual Gaussian curvatures of the ruled surfaces formed by the dual instantaneous Pfaff vectors and of DPERS:
Proof.
If the ruled surface in the Equation (28) is derived according to the parameters s and v,
are obtained. If the vectors and in the Equation (60) are performed, the inner product operation,
is found. Since this inner product is non zero, the system is not an orthogonal system. So now, let us perform the Gram Schmitd ’s method on these vectors. Firstly, the following vectors are obtained:
Thus, if the vectors and in the Equation (61) are rendered orthonormal,
are obtained. Here, after a series of long operations, we have
Then, if the vectors and in the Equation (62) are performed, the vectoral product operation, the normal vector of the ruled surface , is found as follows:
Let and be the shape operator and the Gaussian curvature of the ruled surface respectively. From the Equation (6),
is written. Here, from the Equations (6) and (64),
If the Equations (62) and (66) are substituted in the Equation (65), the Gaussian curvature of the ruled surface is obtained as follows:
Likewise, the Gaussian curvature of the ruled surface is found as follows:
Thus, the proof is completed. □
Corollary 8.
The ruled surfaces formed by the dual instantaneous Pfaff vectors and of DPERS are always isomorphic to the plane.
Example 1.
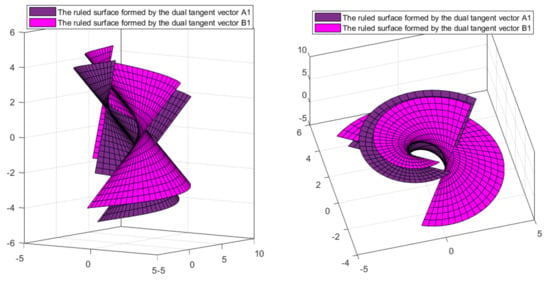
Let and be DPERS: ()
(i) The parametric expressions of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed on the unit dual sphere by the dual tangent vectors of these DPERS are (Figure 3)

Figure 3.
The ruled surfaces and formed by the dual tangent vectors and .
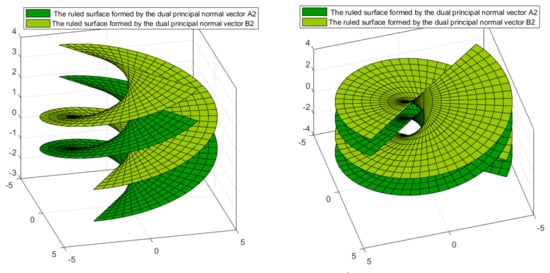
(ii) The parametric expressions of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed on the unit dual sphere by the dual principal normal vectors of these DPERS are (Figure 4)

Figure 4.
The ruled surfaces and formed by the dual principal normal vectors and .
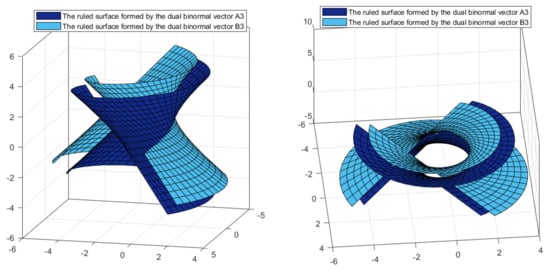
(iii) The parametric expressions of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed on the unit dual sphere by the dual binormal vectors of these DPERS are (Figure 5)

Figure 5.
The ruled surfaces and formed by the dual binormal vectors and .
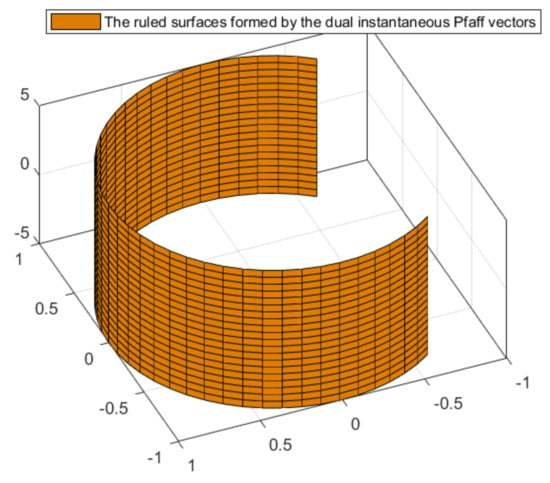
(iv) The parametric expressions of the ruled surfaces corresponding in the space of lines to the dual indicatrix curves formed on the unit dual sphere by the dual instantaneous Pfaff vectors of these DPERS are (Figure 6)

Figure 6.
The ruled surfaces and formed by the dual instantaneous Pfaff vectors and .
For the all graphs drawn in the above example, the parameter v is taken in the range −5:1/2:5, and the parameter t is in the range .
The dual spherical indicatrix curves corresponding on the unit dual sphere to these ruled surfaces can be shown imaginatively as in Figure 7.
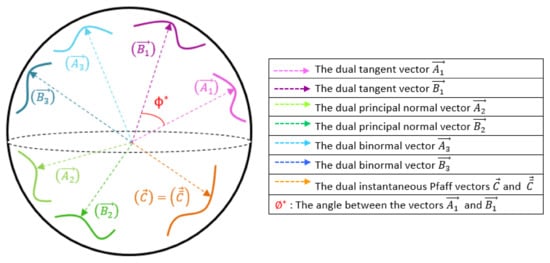
Figure 7.
The dual spherical indicatrix curves corresponding to the unit dual of the ruled surfaces sphere formed by the tangent, principal normal, binormal and instantaneous Pfaff vectors of DPERS (imaginary figure).
The ruled surfaces in the above example are not closed, but it is possible to find examples of closed ruled surfaces.
5. Discussion and Conclusions
In this study, the integral invariants and Gaussian curvatures of the ruled surfaces corresponding in the space of lines to the spherical indicator curves of the Blaschke vectors and the dual instantaneous Pfaff vectors on the unit dual sphere of the parallel equidistant ruled surfaces (DPERS), which were previously defined in [41] and some of their properties given, are investigated. As a result of this examination, considering the dralls (distribution parameters), it is concluded that the closed ruled surfaces formed by dual tangent and dual instantaneous Pfaff vectors of DPERS will always be isomorphic to plane (developable), the closed ruled surfaces formed by dual principal normal vectors of DPERS will always be isomorphic to plane under a certain condition (), and the closed ruled surfaces formed by dual binormal vectors of DPERS will never be isomorphic to plane. In addition, when Gaussian curvatures are examined, it is concluded that the ruled surfaces formed by dual tangent and instantaneous Pfaff vectors of DPERS will always be isomorphic to plane, while the closed ruled surfaces obtained by dual principal normal and dual binormal vectors will be isomorphic to plane under a certain condition (). This study can be combined with studies on submanifold theories, singularity theories, kinematics theories, etc. or it can be studied in non-Euclidean spaces also.
Author Contributions
Conceptualization, S.G.M., S.Ş. and L.G.; methodology, S.G.M., S.Ş. and L.G.; validation, S.G.M., S.Ş. and L.G.; formal analysis, S.G.M., S.Ş. and L.G.; investigation, S.G.M.; resources, S.G.M., S.Ş. and L.G.; writing—original draft preparation, S.G.M.; writing—review and editing, S.G.M., S.Ş. and L.G.; visualization, S.G.M., S.Ş. and L.G.; supervision, S.Ş. and L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We, the authors, gratefully and most sincerely thank the reviewers, who criticized and improved the quality of our article, for their generous comments, corrections and contributions, as well as the editor of the journal who took care of our article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hacisalioglu, H.H. Differential Geometry-II; Ankara University, Faculty of Science Publications: Ankara, Turkey, 1994; pp. 203–286. [Google Scholar]
- Ozdemir, M. Quaternions and Geometry; Altin Nokta Press: İzmir, Turkey, 2020; pp. 150–182. [Google Scholar]
- Sabuncuoglu, A. Differential Geometry; Nobel Press: Ankara, Turkey, 2006. [Google Scholar]
- Fenchel, W. On the Differential Geometry of Closed Space Curves. Bull. Am. Math. Soc. 1951, 57, 44–54. [Google Scholar] [CrossRef]
- Senatalar, M. Differential Geometry (Curves and Surfaces Theory); Istanbul State Engineering and Architecture Academy Publications: Istanbul, Turkey, 1978; pp. 153–170. [Google Scholar]
- Hagemann, M.; Klawitter, D.; Lordick, D. Force Driven Ruled Surfaces. J. Geom. Graph. 2013, 17, 193–204. [Google Scholar]
- Ali, A.T.; Abdel Aziz, H.S.; Sorour, A.H. Ruled surfaces generated by some special curves in Euclidean 3-Space. J. Egypt. Math. Soc. 2013, 21, 285–294. [Google Scholar] [CrossRef]
- Schaaf, A.; Ravani, B. Geometric Continuity of Ruled Surfaces. Comput. Aided Geom. Des. 1998, 15, 289–310. [Google Scholar] [CrossRef]
- Hacisalihoglu, H.H. On the pitch of a closed ruled surfaces. Mech. Mach. Theory 1972, 7, 291–305. [Google Scholar] [CrossRef]
- Senyurt, S.; Gur Mazlum, S.; Grilli, G. Gaussian curvatures of parallel ruled surfaces. Appl. Math. Sci. 2020, 14, 171–183. [Google Scholar] [CrossRef]
- Valeontis, I. Parallel P-Äquidistante Regelflachen Manuscripta. Mathematics 1986, 54, 391–404. [Google Scholar]
- Bektaş, M. On characterizations of general helices for ruled surfaces in the pseudo-Galilean space -(Part-I). J. Math. Kyoto Univ. 2004, 44, 523–528. [Google Scholar]
- Masal, M.; Kuruoglu, N. Some Characteristic Properties of the Parallel P-Equidistant Ruled Surfaces in The Euclidean Space. Pure Appl. Math. Sci. 1999, 50, 35–42. [Google Scholar]
- Masal, M.; Kuruoglu, N. Some Characteristic Properties of the Shape Operators of Parallel p-Equidistant Ruled Surfaces. Bull. Pure Appl. Sci. 2000, 19, 361–364. [Google Scholar]
- Masal, M.; Kuruoglu, N. Spacelike parallel pi-equidistant ruled surfaces in the Minkowski 3-space R13. Algebr. Groups Geom. 2005, 22, 13–24. [Google Scholar]
- Li, Y.; Şenyurt, S.; Özduran, A.; Canlı, D. The Characterizations of Parallel q-Equidistant Ruled Surfaces. Symmetry 2022, 14, 1879. [Google Scholar] [CrossRef]
- As, E.; Senyurt, S. Some Characteristic Properties of Parallel z-Equidistant Ruled Surfaces. Hindawi Publ. Corp. Math. Probl. Eng. 2013, 2013, 587289. [Google Scholar]
- Sarioglugil, A.; Senyurt, S.; Kuruoglu, N. On the Integral Invariants of the Closed Ruled Surfaces Generated by a Parallel p-Equidistant Dual Centroit Curve in the Line Space. Hadron. J. 2011, 34, 34–47. [Google Scholar]
- Senyurt, S. Integral Invariants of Parallel P-Equidistant Ruled Surfaces Which Are Generated by Instantaneous Pfaff Vector. Ordu Univ. Sci. Technol. J. 2012, 2, 13–22. [Google Scholar]
- Clifford, W.K. Preliminary sketch of biquaternions. Proc. Lond. Math. Soc. 1873, 1, 381–395. [Google Scholar] [CrossRef]
- Study, E. Geometrie der Dynamen; Verlag Teubner: Leipzig, Germany, 1903. [Google Scholar]
- Blaschke, W. Differential Geometry Courses; Istanbul University Publications: Istanbul, Turkey, 1949; pp. 332–345. [Google Scholar]
- Hacisalihoglu, H.H. The Motion Geometry and Quaternions Theory; Gazi University, Faculty of Science and Literature Publications: Ankara, Turkey, 1983; pp. 3–55. [Google Scholar]
- Hacisalihoglu, H.H. Acceleration Axes in Spatian Kinematics I. Commun. Fac. Sci. Univ. Ank. Ser. Math. Stat. 1971, 20, 1–15. [Google Scholar]
- Muller, H.R. Kinematics Courses; Ankara University Press: Ankara, Turkey, 1963; pp. 240–251. [Google Scholar]
- Bilici, M. On the Invariants of Ruled Surfaces Generated by the Dual Involute Frenet Trihedron. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2017, 66, 62–70. [Google Scholar]
- Oral, S.; Kazaz, M. Characterizations for Slant Ruled Surfaces in Dual Space. Iran. J. Sci. Technol. Trans. A Sci. 2017, 41, 191–197. [Google Scholar] [CrossRef]
- Güven, İ.A.; Kaya, S.; Hacisalihoğlu, H.H. On closed ruled surfaces concerned with dual Frenet and Bishop frames. J. Dyn. Syst. Geom. Theor. 2011, 9, 67–74. [Google Scholar] [CrossRef]
- Saracoglu, S.; Yayli, Y. Ruled Surfaces and Dual Spherical Curves. Acta Univ. Apulensis 2012, 20, 337–354. [Google Scholar]
- Gursoy, O. The dual angle of the closed ruled surfaces. Mech. Mach. Theory 1990, 25, 131–140. [Google Scholar] [CrossRef]
- Sahiner, B.; Kazaz, M.; Ugurlu, H.H. A Dual Method to Study Motion of a Robot End-Effector. J. Inform. Math. Sci. 2018, 10, 247–259. [Google Scholar] [CrossRef]
- Culmer, P.R.; Jackson, A.E.; Makower, S.; Richardson, R.; Cozens, J.A.; Levesley, M.C.; Bhakta, B.B. A control strategy for upper limb robotic rehabilitation with a dual robot system. IEEE/ASME Trans. Mechatron. 2009, 15, 575–585. [Google Scholar] [CrossRef]
- Gu, Y.L.; Luh, J. Dual-number transformation and its applications to robotics. IEEE J. Robot. Autom. 1987, 3, 615–623. [Google Scholar]
- Bayro-Corrochano, E.; Kähler, D. Motor algebra approach for computing the kinematics of robot manipulators. J. Robot. Syst. 2000, 17, 495–516. [Google Scholar] [CrossRef]
- Özgür, E.; Mezouar, Y. Kinematic modeling and control of a robot arm using unit dual quaternions. Robot. Auton. Syst. 2016, 77, 66–73. [Google Scholar] [CrossRef]
- Yayli, Y.; Çalişkan, A.; Uğurlu, H.H. The E. Study maps of circles on dual hyperbolic and Lorentzian unit spheres and . Math. Proc. R. Ir. Acad. 2002, 102A, 37–47. [Google Scholar] [CrossRef]
- Şenyurt, S.; Gür, S. Timelike–spacelike involute–evolute curve couple on dual Lorentzian space. J. Math. Comput. Sci. 2012, 2, 1808–1823. [Google Scholar]
- Bektas, Ö.; Senyurt, S. On Some Characterizations of Ruled Surface of a Closed Timelike Curve in Dual Lorentzian Space. Adv. Appl. Clifford Algebr. 2012, 22, 939–953. [Google Scholar] [CrossRef]
- Li, Y.L.; Alluhaibi, N.; Abdel-Baky, R.A. One-parameter Lorentzian dual spherical movements and invariants of the axodes. Symmetry 2022, 14, 1930. [Google Scholar] [CrossRef]
- Gür, S.; Şenyurt, S. Spacelike–timelike involute–evolute curve couple on dual Lorentzian space. J. Math. Comput. Sci. 2013, 3, 1054–1075. [Google Scholar]
- Gür Mazlum, S.; Şenyurt, S.; Grilli, L. The Dual Expression of Parallel Equidistant Ruled Surfaces in Euclidean 3-Space. Symmetry 2022, 14, 1062. [Google Scholar] [CrossRef]
- Li, Y.; Dey, S.; Pahan, S.; Ali, A. Geometry of conformal η-Ricci solitons and conformal η-Ricci almost solitons on Paracontact geometry. Open Math. 2022, 20, 1–20. [Google Scholar] [CrossRef]
- Li, Y.; Ali, A.; Mofarreh, F.; Alluhaibi, N. Homology groups in warped product submanifolds in hyperbolic spaces. J. Math. 2021, 2021, 8554738. [Google Scholar] [CrossRef]
- Yüzbaşı, Z.K.; Bektaş, M.; Yılmaz, M.Y. Compact Totally Real Minimal Submanifolds in a Bochner-Kaehler Manifold. Univers J. Math. Appl. 2018, 1, 254–257. [Google Scholar]
- Yılmaz, M.Y.; Bektaş, M. Curvature Inequalities between a Hessian Manifold with Constant Curvature and its Submanifolds. Math. Sci. Appl. -Notes 2017, 5, 27–33. [Google Scholar] [CrossRef]
- Li, Y.; Gür Mazlum, S.; Şenyurt, S. The Darboux Trihedrons of Timelike Surfaces in the Lorentzian 3-Space. Int. J. Geom. Methods Mod. Phys. 2023, 2350030, 1–35. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Sarkar, S.; Dey, S.; Bhattacharyya, A. Ricci Soliton and Certain Related Metrics on a Three-Dimensional Trans-Sasakian Manifold. Universe 2022, 8, 595. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).