Abstract
Designing a controller is typically an iterative process during which engineers must assess the performance of a design through time-consuming simulations; this becomes even more burdensome when using a population-based metaheuristic that evaluates every member of the population. Distributed algorithms can mitigate this issue, but these come with their own challenges. This is why, in this work, we propose a distributed and asynchronous bio-inspired algorithm to execute the simulations in parallel, using a multi-population multi-algorithmic approach. Following a cloud-native pattern, isolated populations interact asynchronously using a distributed message queue, which avoids idle cycles when waiting for other nodes to synchronize. The proposed algorithm can mix different metaheuristics, one for each population, first because it is possible and second because it can help keep total diversity high. To validate the speedup benefit of our proposal, we optimize the membership functions of a fuzzy controller for the trajectory tracking of a mobile autonomous robot using distributed versions of genetic algorithms, particle swarm optimization, and a mixed-metaheuristic configuration. We compare sequential versus distributed implementations and demonstrate the benefits of mixing the populations with distinct metaheuristics. We also propose a simple migration strategy that delivers satisfactory results. Moreover, we compare homogeneous and heterogenous configurations for the populations’ parameters. The results show that even when we use random heterogeneous parameter configuration in the distributed populations, we obtain an error similar to that in other work while significantly reducing the execution time.
1. Introduction
Modern control theory was created in the late 1960s with the development of model-based control (MBC) and optimal control techniques. MBC uses nonlinear difference (or differential) equations to describe the behavior of the dynamical system [1]. To apply MBC, a designer first needs to obtain a mathematical model of the plant and then design the controller using this model. In the early 70s, intelligent control [2] was developed as an alternative to traditional model-based control systems; in contrast with MBC, intelligent control uses human knowledge, operational research, and experimental evidence instead of a mathematical model to generate control actions. Fuzzy logic control has been one of the most successful intelligent control techniques from the earlier work of Mamdani [3], to more recent applications [4]. Another suitable method that is rapidly developing is data-driven control, which includes a broad family of techniques in which the mathematical model or the controller design is based entirely on datasets obtained directly from the process we need to control. Data-driven control includes methods such as reinforcement learning [5]; iterative learning control (ILC) [6]; and robust control tools such as Petersen’s Lemma [7], together with neural networks and genetic algorithms [8]. A critical advantage of fuzzy logic control is that it is implemented using a fuzzy inference system (FIS) that models the system’s knowledge base using fuzzy rules. Fuzzy rules have a human interpretation and can also be automatically or manually tuned; this is why we chose fuzzy controllers for this line of research. As in their model-based counterparts, designers of intelligent control systems also need to optimize the controllers’ parameters to handle the particularities of real-world problems. In the case of fuzzy controllers, several entities characterize the components of the fuzzy rule-based system. The core components are the fuzzy propositions constructing the fuzzy rules representing the knowledge of the system. Propositions are, in turn, constructed using fuzzy variables and fuzzy terms that are defined using MFs.
Optimizing the controllers’ parameters is challenging; on the one hand, we have a vast search space in the parameter’s domain. On the other, we need to execute one or more simulations to establish the performance of one configuration. These time-consuming problems make the manual tuning of parameters impractical [9]. Engineers often use metaheuristics not only to tune or adjust the parameters of fuzzy controllers but also to define the entire fuzzy controller structure. Metaheuristics often use techniques inspired by natural processes. For instance, the operators used by genetic algorithms (GAs) [10] are inspired by natural evolution. Using a chromosome to represent a candidate solution, the operators to generate a new population are a random crossover between individuals, a random mutation applied to the offspring, and a selection operator to decide which individuals will survive to the next generation. In this case, the crossover and selection operators impact how the search space is exploited, while the mutation operator influences the exploration of the search space near a promising solution. Evolutionary algorithms are not the only nature-inspired metaheuristic used in this area; other nature-inspired algorithms have been successfully employed in optimizing fuzzy inference systems for engineering and process control applications. These algorithms include both evolutionary algorithms (EAs) [11] and swarm intelligence (SI) [12]. Most researchers follow a fuzzy-evolutionary approach to optimize the parameters of fuzzy controllers [9,13].
In previous work [14], we established that tuning the MFs of fuzzy controllers using population-based metaheuristics demands the extensive use of computational resources. This demand stems from establishing the fitness of all candidate solutions, which requires running several simulations [15,16] for each candidate; this is a problem inherent to population-based algorithms. However, because evolutionary algorithms evaluate candidate solutions in isolation; they are a perfect match for their parallel execution. In the literature, we found only a few studies attempting to distribute fuzzy controllers’ optimization; however, these studies did not consider or take advantage of recent cloud-native technologies [17,18,19]. Cloud-native applications are designed as a composition of loosely coupled microservices, stateless processing nodes that react to events [20] produced by other microservices, scheduled or triggered by clients. Microservices typically run in isolated runtime environments called containers, which encapsulate not only the runtime environment, but also software libraries; binaries; configuration files; and in general, everything needed for the node to run autonomously. A containerized application is easily operated on automation platforms capable of taking containerized microservice-based applications from a local computer to be deployed in a cloud or a disposable infrastructure [21,22]. An important design principle is the use of an event-driven architecture in which microservices communicate asynchronously by emitting and reacting to events; this is often realized via message queues or external messaging services.
Our main contribution in this paper is a proposal of a distributed optimization method that speeds up the tuning of fuzzy control optimization problems with respect to sequential versions, without increasing the complexity for the user. This work proposes a multi-population, distributed optimization method considering current practices in constructing highly scalable, resilient, and replicable systems. Moreover, the architecture is capable of executing several bio-inspired algorithms simultaneously. In particular, we apply cloud-native principles and techniques [23] to implement a system capable of executing a multi-worker, multi-population, multi-algorithm optimization framework to speed up the time needed to execute the evolutionary fuzzy controller design algorithm. To demonstrate the applicability and speedup provided by the proposed method, we report an experimental case study of optimizing a fuzzy controller for trajectory tracking. This particular problem required a considerable execution time in our previous work, and we expect to reduce this time considerably by applying the proposed method by distributing the work. Furthermore, this work addresses the problem of setting the parameters for each population; this is an important factor in multi-populations algorithms because it has been found in other work to have an impact on the execution time and the optimization results [24,25]. In this work, we compare two strategies: the homogeneous setting using the same parameters in all populations and a heterogeneous strategy using distinct parameters for all populations.
In summary, we solve a fuzzy control problem by using a cloud-native distributed algorithm with few tunable parameters that has been enhanced with respect to the previous version by improving the selection procedures. In this paper, we try to prove that it effectively lowers costs by being able to find the solution in less time, and in which circumstances this solution can be better than sequential alternatives.
We organize the paper as follows: In Section 2, we present the state-of-the-art of distributed multi-population-based algorithms. In Section 3, we describe the method and the experimental setup in Section 4. The results of the experiments are presented in Section 5, and finally, in Section 6, we discuss the conclusions and future research directions.
2. State of the Art
Most of the lines of research we mentioned above emphasize parallelizing the evaluation of candidate solutions because this is the most resource-demanding part of the optimization algorithm. Alba and Tomassini [26] called this type of implementation global parallelization because, in this case, the population keeps the same panmictic-like properties found in a single global population, in which any individual can potentially mate with any other in the population. Only the fitness evaluation is carried out in parallel, following a standard primary/subordinate design. On the other hand, we have the multi-population or island models, in which the original population is partitioned into several demes or subpopulations that can run an isolated GA algorithm in parallel. Migration is an essential element of these parallel algorithms because it significantly affects how fast the solution is found. Migration describes how often and which individuals will be exchanged between populations. These earlier multi-population methods not only had the advantage of speeding the execution time but also, according to experimental results, added the benefit of preventing premature convergence to a local optimum by maintaining a higher diversity throughout the populations [27]. Furthermore, Starkweather et al. [24] concluded that distributed genetic algorithms are often superior to their single population counterparts, but this is only sometimes true; they compared different migration techniques and their relationship with performance.
Other population-based metaheuristics also have multi-population versions. For instance, there are many proposals on multi-swarm optimization methods [25] for the PSO algorithm; however, because the PSO algorithm is based on position, velocity, and distance between particles, researchers put more effort into the topology of communication between swarms. Using multiple populations also allows for establishing different configurations in each population, changing the parameters affecting exploration and exploitation to balance the emphasis between both strategies. This subject has also been explored extensively by researchers in this area. By having multiple populations, there is even the possibility of having entirely different metaheuristics in each population; recent work showed that this can also benefit the overall results [28,29]. Another critical factor in multi-population-based algorithms is the coordination between the nodes executing the algorithms in parallel. Researchers in PGAs have implemented both synchronous and asynchronous parallelization. An example of synchronous parallelization is the controller/worker model, in which the controller must wait for all workers to finish before continuing the execution. In contrast, asynchronous parallelization does not need to wait for other processed to continue working because work is not synchronized; this improves the scalability and reduces the execution time. In the literature, many studies compare the two methods, but in terms of speed of execution, asynchronous algorithms are the best option. Another advantage of asynchronous solutions is that they facilitate the communication of autonomous cooperating entities, as shown in work such as A-Teams [30], in which agents solve problems by modifying a shared memory without needing to know about each other or a coordination entity.
From early research on PGAs, many studies focused on the implementation details impacting the system’s performance. In this regard, current work emphasizes the exploitation of the most recent advances in computer technologies, for instance, the massive quantities of processing units found in modern GPUs [31]. However, arguably, the most significant paradigm shift has recently come from the emergence of the cloud platform. Parallel evolutionary algorithms leverage commercial, and even free, cloud services to deploy implementations [32]. A pioneering proposal was made by Veeramachaneni et al. [33] with a native cloud genetic programming framework called FlexGP. This system not only worked on the cloud (using Amazon Elastic Compute Cloud, a virtual machine service) but also tackled the different challenges in distributed computing in a novel way; in the same way as in our algorithm, every virtual machine used different algorithm parameters (and sampled the training data differently); however, they revealed in their paper the challenge of booting virtual machines on the cloud.
Cloud-native architectures soon evolved to use computing nodes for which the startup time and the overall cost were more lightweight and used isolated, “containerized”, operating system images; these were initially called by the same name as the company that proposed them, Docker, but are now an open standard supervised by the Open Computing Initiative. These container-based architectures are nowadays mainstream [34]; from the point of view of scientific computing, they enable replicability by not fully defining the infrastructure in which the experiment can run, thus creating “frozen” workflows that can be directly reused in new experiments on-premises, in paid infrastructure and even on your laptop. These methodologies and technologies eventually landed in the evolutionary computing field via the work published by Salza and Ferrucci [35]. Their main challenge was reducing overhead, which is achieved via the containerization of the fitness evaluation tasks; this speeds up the evolutionary algorithm by reducing node startup overhead and communication overhead, since the virtual network interfaces that the container possesses are much faster than whole virtual machines; latency is also expected to be lower.
All these attempts just adapt new infrastructure to old computation models; they could be implemented in a local setup if resources were available. However, cloud-native architectures go beyond that, offering new programming and communication paradigms; its full use yields a high-performance architecture that is, at the same time, cheaper since they use fewer resources. Our KafkEO [36] and EvoSwarm model [37] follow an event-driven architecture, and instead of having a central node to execute the genetic algorithm, delegating only the fitness evaluation to subordinate nodes as Salza and Ferrucci do, workers evolve subpopulations for several generations.
A more recent work by Ivanovic and Simic [38] centers on auto-scaling the number of microservices, considering the specifics of evolutionary algorithms. Increasing or reducing the number of workers as needed, for instance, increasing when the population needs to be evaluated or when a simulation will demand more resources. The aim is to reduce the overall computational cost. This work uses a primary/subordinate parallel execution with an event-driven architecture using the Kubernetes orchestration technology. A similar approach is followed by Dziurzanski et al. [34], also using Kubernetes and an auto-scaler but implementing an island model using a multi-objective genetic algorithm. Two real-world smart factory optimization scenarios are used as test cases, and the system is deployed on a Kubernetes cluster. This work follows a novel approach proposed by Arellano-Verdejo et al. [39], in which islands evolve, but there is no migration between them. When the entropy value of a pair of populations maximizes the diversity of the resulting island, these populations are merged into one, and the best-fitted individuals survive.
Instead of relying on message passing, some other proposed cloud native evolutionary algorithms use a pool-based approach [40]. In pool-based algorithms, isolated algorithms exchange candidate solutions through a shared pool, where they put and take solutions asynchronously. Examples of these algorithms are the SofEA [41], and EvoSpace [42] models. These implementations use the scalable storage services CouchDB and Redis, respectively. EvoSpace has a cloud-based implementation [43] and another version called evospace-js [44] using web technologies, the server (controller node) is implemented in node.js, and the workers run in Docker containers.
In this work, we propose an EvoSwarm-inspired algorithm applied to a simulation-based controller optimization problem that is both demanding in computational resources and more representative of a real-world problem. In the next section, we describe the proposed algorithm and implementation details. Table 1 gives a comparison of the key properties of the present work and related published work on cloud-native optimization methods.

Table 1.
Comparison of cloud-native population-based optimization. methods.
3. Materials and Methods
In the following subsections, we show the distribution model that is the core of this work. We first cover the main components of an event-driven architecture and then connect them with the multi-population-based algorithm. We also relate the abstract components with the particular design decisions of our implementation.
3.1. Populations and Workers
In this model, instead of having a single population, we have a set P of n populations. These populations () have a smaller number of candidate solutions than the single populations found in traditional sequential evolutionary algorithms; we sometimes refer to these elements as subpopulations because of the latter. Each population has a tuple , where is the current state j of the multiset X of n candidate solutions . At this level, we are only concerned with the population state before and after a metaheuristic algorithm evolved the population. We ignore the state changes in each iteration inside the algorithm and keep only the best individual of each iteration as a statistic. Statistics are stored in an ordered set . For instance, a GA starts with a population , and after the j execution of the algorithm, the population state would be . The set of parameters P includes the particular metaheuristic m that is to be executed on X and the parameters needed by that metaheuristic . The other configuration parameters are the population size n and the number of iterations (i.e., generations) to be executed . We define execution as running the metaheuristic for a specified number of iterations . A single population is executed several times during the lifetime of the algorithm, and this number is limited by the parameter (number of cycles). After each execution, there is a process of combination in which populations exchange candidate solutions with each other. We describe this process in detail below in Section 3.3. After this combination happens, populations can be executed again by their metaheuristic. This event-driven implementation decouples populations from the worker processes executing the metaheuristics. A population object is a static structure with the data described earlier . A schematic of an execution cycle is shown in Figure 1. In the middle, we have a set of workers (W) that continuously receive a blue( in state j) to execute a metaheuristic. After this, they send the evolved population blue( in a new state j) to the mixing process to continue the cycle. A worker is an agent running in a single process or thread. The worker pulls population messages from a queue and executes the specified metaheuristic. After each execution, it sends the resulting population to the mixer process.
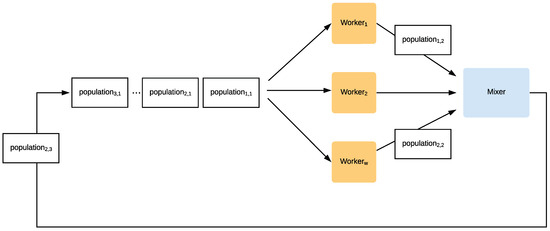
Figure 1.
The multi-population cycle consists of a set of populations P, each in a current state j, and a set (W) of w workers. Each population () is received by one of the workers. Then, after executing a metaheuristic, it sends the evolved population () to the mixer. In turn, the mixer swaps some candidate solutions between two populations, changing their state again and sending the resulting populations again to be processed by workers, closing the cycle.
Currently, populations are codified as JSON documents because the JSON format is easily interchangeable between software components. Most programming languages have standard libraries to parse the documents into native structures. Workers are deployed as Docker containers that include the python code and libraries to execute the algorithms and receive and send populations codified as JSON documents. We have been using the verbs receive and send, without specifying the details of how this communication happens. In the next section, we describe the communication strategy.
3.2. Message Queues
Message queues implement an asynchronous communication pattern between processes or threads. Communication is asynchronous because the sender and receiver do not need to interact with the queue simultaneously. Furthermore, the number of recipients or senders could grow without any changes to the configuration. Message queuing services are a central component in many cloud-based systems because they offer a scalable solution for inter-process communication. This work uses message queues as a scalable communication between architecture components. We use two queues:
- input queue. This queue receives populations that need to be sent to workers. When the algorithm starts, populations in their initial state are sent to this queue. Moreover, the mixing process sends combined populations to continue with the multi-population cycle. Workers constantly pull populations from this queue.
- output queue. Workers push the evolved populations to this queue. At the same time, the mixing process pulls populations from this queue to combine two or more populations.
Figure 2 shows the operation of a worker. Each worker is in an infinite loop pulling a message from the input queue; this is a blocking operation. After a population is pulled from the queue and has valid data, the metaheuristic algorithm specified is executed, starting from the current state of the population. After the execution is finished, the resulting population is pushed to the output queue, and the loop continues, pulling another population.
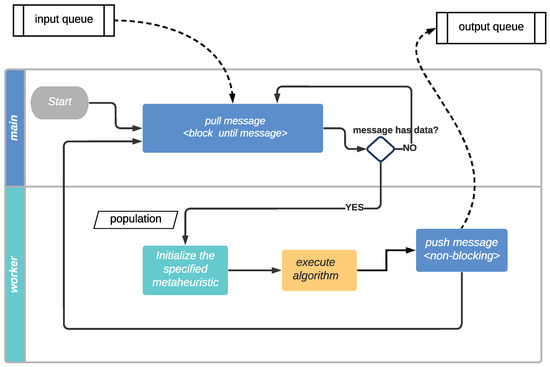
Figure 2.
The diagram shows the worker’s infinite loop operation and communication through the input and output queues. Inside each worker, there is a main method executing an infinite loop, constantly pulling messages from the input queue and blocking until a message is received. The message includes the population and the specified metaheuristic to execute. Workers are capable of executing all metaheuristics available. Once the message is received, the main method calls the worker object to execute the algorithm. After the algorithm runs, the worker pushes a message to the output queue; the message includes the resulting population.
3.3. Mixer
The components mentioned above can be included in a scalable method for running isolated algorithms. However, it needs to include a vital factor to become a multi-population model: the recombination or migration between populations to avoid premature convergence because smaller populations tend to converge faster than those more populated [45]. We propose a buffer-based mixer component for the recombination of populations. The buffer is a priority queue in which elements are ordered according to their fitness and keeps only the k-best individuals. The mixing algorithm waits until the buffer has at least k individuals before it starts mixing the populations. Before going into the recombination component details, we need first to discuss the communication topology that specifies how the populations communicate. Using a message queue for the temporal storage of populations establishes an order in which components receive data. Each population could have two contiguous populations in the queue, one in front and the other behind, as in a ring topology. Furthermore, since populations are in a queue, there is a temporal ordering, in which the last populations to arrive will be the last to be recombined. In this case, the simple strategy of recombining contiguous populations could slow the propagation of the best solutions along the ring. Depending on the problem, this could be a desirable property, as this increases the overall diversity, but also, the algorithm could take more time to reach a desirable solution. After running some preliminary experiments, we followed an elitist approach, which showed better results. We propose using a buffer with size k to keep the k-top individuals from all the populations received. Then, each population reaching the mixer has its k-worst solutions replaced with the k-top in the buffer. The mixing process has two additional responsibilities:
- Setup This is a one-time running task consisting of reading the algorithm’s configuration, creating the initial population structures, and pushing the messages to the input queue.
- Finishing the algorithm The mixer also keeps track of the number of populations that have been pulled from the output queue. It stops the algorithm if one of these two conditions is true: (1) the number of cycles has been reached, or (2) the error of the best controller found so far meets the desired criteria.
In Figure 3, the swimlanes highlight which component is responsible for executing elements of the algorithm defined in the past sections. The numbers in yellow squares allow us to describe the complete algorithm. The mixing process receives a configuration file, which includes the number of populations, metaheuristics, and their respective parameters (1). After generating the population messages, it pushes them to the input queue (2). Worker containers (3) pull the population messages as described in Section 3.1, execute a metaheuristic, and pushes the resulting population state to the output queue (4). The mixing process pulls populations from the output queue and follows the process described in Section 3.3. It stops the execution if conditions are met (5) or proceeds to swap the k-top individuals in the buffer with the worst k in the current population (6). Finally, it pushes the resulting population to the input queue to complete the loop.
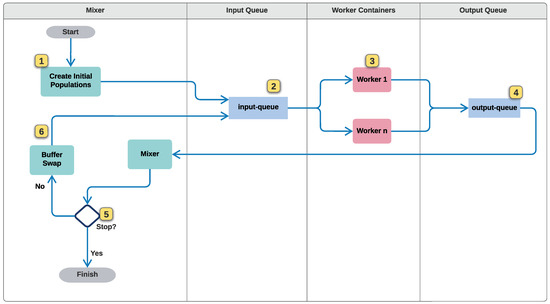
Figure 3.
The proposed architecture diagram shows each process in a swimlane, along with the message dataflow, message queues, and high-level responsibilities of each component. Numbers in yellow boxes indicate the order in which actions happen, and the details of each step is explained in the main text.
3.4. Controller Optimization and Simulations
The optimization of fuzzy controllers requires the components shown in Figure 4. First, it needs a parameterized fuzzy controller structure, as described in Section 1. In this work, we chose to optimize the parameters of some MFs of the controller. Designers can establish the granularity of each fuzzy variable. For instance, for measuring an error, we can use just three MFs—“HIGH-NEGATIVE”, “LOW”, and “HIGH-POSITIVE”—or increase the granularity by adding the fuzzy terms—“MEDIUM-NEGATIVE” and “MEDIUM-POSITIVE”—for a total of five MFs. Designers can decide to leave some fuzzy variables with fixed parameters, depending on the problem or the design strategy. In this implementation, the fuzzy-controller module is another parameter of the optimization process; this has the benefit of using other modules with more granularity or parameters. To simplify the optimization algorithm, we keep the domain of all parameters on the [0,1] domain and leave the parameterized controller’s designers the task of normalizing or adjusting the parameter’s values to their needs. Two more related components are needed to establish the fitness of the controller’s parameters. We need a dynamic model of the plant or robot to control and one or more control problem instances to simulate and observe the controller’s behavior. For instance, in this case, for a path-tracking controller, we need to test the control using a few paths for the mobile robot to follow. We then measure the average error of all simulations to establish the fitness of the candidate controller parameters. Again, designers can change the simulation model and the simulation problems for testing; these can increase the difficulty or use other variables for evaluating the performance.
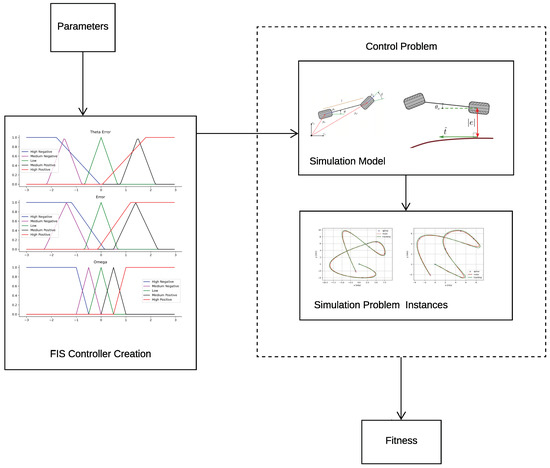
Figure 4.
The diagram shows the data flow of the higher-level components required to optimize the parameters of a fuzzy controller. The input is the collection of parameters representing a candidate solution, and the output is the fitness or quality measure of the candidate solution. It shows the FIS controller creation component, which generates a controller instance from the input parameters. The controller instance is then put to the test on a control problem. A control problem includes a simulation model that includes the kinematic model and the code needed to execute a simulation. The controller can be tested on several problem instances. For example, a path-tracking controller can be tested on different paths. We measure the error as the robot follows the path, and the final output is the average of these errors.
In the current implementation, each worker has the necessary python libraries for each component we just described. This component-based design has the flexibility required for other fuzzy control problems.
4. Experimental Setup
To validate the algorithm’s speed-up and optimization capabilities, we selected the computationally demanding task of tuning a path-tracking fuzzy controller for a bicycle-like mobile robot. Furthermore, in the literature, we have yet to find other researchers who applied cloud-native patterns for fuzzy systems’ optimization to solve similar problems. The following sections briefly explain the control problem and the fuzzy controller. The problem configuration is the same as our previous work [14], in which we compare several sequential optimization metaheuristics. We use the results of that work as the base of the comparison in this work.
4.1. Rear-Wheel Feedback and Kinematic Model
Figure 5 illustrates the kinematic model consisting of two wheels connected by a rigid link of length l [46,47]. The steering angle of the front wheel is , and the rear wheel position is at and . The heading is the angle between the link and the x axis. The unit tangent to the path at is shown in blue . We follow the model with nonholonomic restrictions described in [48]:
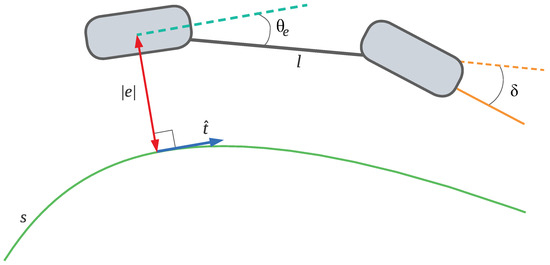
Figure 5.
Illustration of the feedback variables used for rear-wheel-based control. The transverse error e is the distance from the rear wheel to the nearest point in the path . When the error is positive, the wheel is to the right of the path. The wheel is to the left if the error has a negative sign. is the difference between the tangent at the nearest point in the path and the heading . The unit tangent to the path at is shown in blue . The controller outputs the heading rate , the variable we need to establish the steering angle (see Equation (2)).
The output of the controller is the angle between the limits of the vehicle and a desired velocity again limited by . The heading rate is related to the steering angle by
and we can simplify the heading dynamics to
The tracking error vector is the difference between the rear-wheel position and the reference point in the path
while the transverse error e is the cross product between the unit tangent vector and the tracking error vector d
with subscripts being the component indices of each vector. The heading error uses the angle between the robot’s heading vector and the tangent vector at :
4.2. Parametrizable Membership Functions
This section describes the fuzzy controller we want to optimize. The controller has two input variables and e, and a single output . All three variables have the same granularity using five fuzzy terms: high negative, medium negative, low, medium positive, and high positive. The sign of the error indicates if the angle is to the left or right of the path. The parameters of the MFs are shown in Table 2. As we can see, we have the same parameters with constant values, and others are defined with variables. We use ten parameters to define the MFs of the controller. We kept the MFs symmetrical around zero; thus, the middle point of the triangular function for low will be fixed at zero. Additionally, we kept the extreme values of the trapezoidal MFs constant. To limit the search space and to be able to compare against our previous results, we also kept the parameters of fixed. Using experimental knowledge from previous work, we defined different ranges for the possible values of the normalized parameters, which are shown in Table 3. The knowledge base of the fuzzy controller consists of 25 fuzzy rules and is presented in Table 4.

Table 2.
Ten parameter configuration for the fuzzy controller with a granularity of five symmetric MFs. Parameters for the output variable have constant values.

Table 3.
Ranges defined for each parameter for the 5MF controller.

Table 4.
Proposed fuzzy rules for the basic controller with three membership functions.
4.3. Multi-Population Algorithm Setup
We selected the GA and PSO algorithms for the multi-population-based optimization in this work. We based our decision on the results of our previous experiments and the differences in the techniques they use. GA is the canonical representative of an evolutionary algorithm, with favorable results in combinatorial and discrete optimization. It had the worst results from the metaheuristics selected in our previous experiment, so we are selecting this algorithm to represent the lower end of the results. It will be interesting to see if a multi-population version could improve the results. On the other hand, the PSO algorithm had the best results. We expected this because this algorithm is better suited for continuous optimization, as is the case for the current optimization problem. Furthermore, in previous work, using continuous optimization benchmarks, the combination of both metaheuristics performed better than any of them in isolation. In the following experiment, we test if this is the case for the current use case.
When using population-based metaheuristics, designers have the initial burden of establishing the algorithm’s parameters. As we discussed earlier, bio-inspired metaheuristics have parameters that control the balance between the exploration or exploitation of the search space [49]. If the algorithm over-exploits, then the risk of premature convergence increases. Moreover, if there is over-exploration, the search will be almost random, constantly jumping to a different area. A balance between the two strategies is needed to escape from local minima and to carry out a local search in a promising area. If we have multiple populations in our algorithm, we could change the parameters of some populations to favor exploration and others’ exploitation, keeping the two extremes in balance. A simple way to accomplish the exploration–exploitation balance is by using a heterogeneous strategy proposed by Gong et al. [50], which randomly sets the parameters of each population. Although simple, random parametrization obtained promising results in other multi-population-based algorithms. The other strategy found in the literature is using a single, well-balanced configuration for each metaheuristic algorithm and repeating the same configuration in all populations; we call this a homogeneous strategy. In this work, we compare the results of heterogeneous and homogeneous strategies for multi-population algorithms.
Table 5 shows the algorithms’ parameters for the sequential versions of the GA and PSO algorithms. For the GA, we used a tournament selection with three participants (). We applied a Gaussian mutation with and , with a probability of . We use a one-point crossover with a probability of . For the sequential PSO algorithm, we used a fully connected topology (on each subpopulation), with minimum and maximum speeds of and , respectively, and and . In the sequential case, both algorithms have a single population of 50 candidate solutions and run for 20 iterations. To compare against the multi-population versions, we need to keep the number of function evaluations equal. Hence, the comparison is fair, as both versions perform the same amount of processing. In the sequential version, the number of function evaluations is 1000. This number is obtained by multiplying the population size by the number of iterations. Table 6 shows the algorithms’ parameters for the distributed, multi-population versions of the GA and PSO algorithms. We used the same parameters as the sequential versions for the homogeneous parametrization. We used the same parameters for the heterogeneous versions as before, except for the following parameters affecting the exploration–exploitation balance in the GA and PSO algorithms. The mutation probability is selected for the GA from the range and the crossover probability from . For the PSO algorithm, we also selected the minimum speed between and the maximum from . Both and are in the range. For all the distributed versions, we set the number of populations (islands) to seven, each with a population size of nine. The population size is kept small because we estimate the total population size by multiplying the population size by the number of subpopulations; in this case, the total size is 63. Each worker will execute four iterations (generations) of the algorithm. All populations will complete four cycles; this means they will pass through the mixer module four times. As a result, the total number of function evaluations is 1008. About the same as the sequential, single-population versions.

Table 5.
Summary of the parameters for the sequential GA and PSO algorithms compared. The general parameters section indicates the parameters that are the same for both algorithms.

Table 6.
Summary of parameters for the multi-population versions of the GA and PSO algorithms. In the top section, we have the case in which all islands have the same parameters (homogeneous parametrization). In the next section, we have the heterogeneous parametrization, in this case, some parameters are randomly obtained from a range of values. Finally, the general multi-population parameters section indicates parameters that are the same for both algorithms.
We include in the comparison a combined version having four populations running a PSO algorithm and three populations running a GA. Algorithms in this combined version use the same parameters as above. This combination aims to test whether the combination of search strategies gives better results than the other versions. We executed these combinations using both parametrization strategies.
To compare the optimization algorithms, we tuned the parameters of the fuzzy system, detailed in Section 4.2. Each candidate solution has ten continuous parameters in the range. The control problem is to follow the three paths defined as cubic splines with parameters shown in Table 7, together with the parameters of the simulation. The fitness of each candidate solution is the average error of the three paths.

Table 7.
Simulation and spline parameters.
We ran 30 algorithm executions for each configuration on a workstation with AMD Ryzen 9 3900× 12-core CPU with 48 GB RAM running Ubuntu 21.04, and CPython 3.7.5. The distributed experiments run in containers deployed using a docker-compose script. The script defines a container for the Redis memory store, responsible for running the in-memory queues for the asynchronous interprocess communication. The script includes a worker definition, and at the start of the deployment, is scaled to seven worker containers, one for each of the seven populations. After each experiment, we destroyed all containers, so the next experiment would start with a clean state. The mixing process runs natively on the host machine. The code and data can be found in the GitHub repository https://github.com/mariosky/fuzzy-control (accessed on 17 January 2023). We compared the algorithms using the mean, median, and standard deviation of the RMSE of 30 algorithm executions. Moreover, we measured the execution time (in seconds) for each run of an algorithm configuration.
The speedup is an important performance metric because we aim to accelerate the program execution time. We base our speedup definition on the work of Touati et al. [51] as follows: Let be the base algorithm, and be the proposed alternative. Let X be the random variable representing the execution time of , and be a sample of n execution times. The proposed alternative can also be executed m times over the same optimization problem, and the execution time is similarly represented by Y and . With these two samples, we can define the observed speedup of the mean execution times as
In this work, the execution time samples consist of 30 observations (). The results are discussed in the next section.
5. Results
In this section, we present the results of the experiments, comparing a sequential and distributed implementation of the controller described in the previous sections, with the average RMSE of three paths to establish the fitness. First, we show the results regarding the RMSE obtained by the optimized controllers, and then, we center our attention on the time it took the experiments to complete.
5.1. RMSE
The RMSE results of several configurations are shown in Table 8. In the first two columns, we show the results of the sequential algorithms as published in our previous work [14]. We can see that the PSO algorithm obtained the best results overall, with a median RMSE of 0.00536160, the second-best result is the distributed heterogeneous version of the PSO-GA with a median of 0.00610783; this result is very close to the multi-algorithm version PSO with an RMSE of 0.00628949. After performing a statistical z-test between the distributed and sequential versions of the same algorithms, we did not find enough evidence to reject with . These results indicate that the results from the distributed and sequential versions are about the same, and the random parametrization of the multi-population version could be used, even having marginal benefits over the homogeneous version, without the need to find appropriate values for the parameters.

Table 8.
Results of the execution of 30 runs of the presented algorithms. The controller error is expressed as the RMSE obtained by the best controller found in each run. The table shows the results for the sequential (first two columns) and distributed versions of the multi-population-based algorithms: GA, PSO, and the combined version PSO-GA. The homogeneous versions are on the left-hand side and heterogeneous versions are on the right. The best result is shown in boldface; second best is underlined.
5.2. Execution Time Speedup
The complexity of the optimization process depends mainly on the cost of each simulation step. However, the cost depends on a multistep differential solver, the number of iterations of which changes depending on the initial conditions. Furthermore, there is also the added cost of obtaining the nearest point to the path in each step, as described in Section 4.1. On the other hand, the population-based algorithms implemented follow the same procedure: initialize the population with complexity, where n is the size of the population. Then, there is the step of creating or updating a new population; this is normally with m iterations and l parameters. Since this kind of metaheuristics does not have a deterministic number of steps to find a satisfactory solution, it is impossible to compute the computational complexity and, thus, compare algorithms on this basis. We will need to compare them experimentally. The observed execution times of sequential and multi-population configurations of the algorithms are shown in Table 9. The table shows execution times in seconds and the speedup against the sequential alternative in subscripts. In the case of the PSO-GA combined version, we used the execution time of the sequential PSO algorithm as the base. In the first two columns, we have the base times of the sequential GA and PSO versions. We notice that the GA completes the execution in less time than the PSO algorithm, but as the results in the previous section show, the RMSE results are worse. On the left side of Table 8, we present the execution times of both the homogeneous and heterogeneous alternatives. As expected, there is a speedup of around six times in the distributed PSO versions; this is not the case for the GA, reaching five times only on the heterogeneous distributed configuration. The PSO-GA heterogeneous variant gave the best speedup on average; this is an interesting result because it gives better results than the homogeneous PSO-GA configuration. Figure 6 shows the boxplot of the execution times: the noticeable differences between the GA (p = 0.000171) and PSO-GA (p = 0.000264), are confirmed with a z-test (n = 30, , independent samples); this was not the case for the PSO (p = 0.5104).

Table 9.
Results from 30 observations of the execution time for each of the presented algorithms. blueThe table shows execution times in seconds and the speedup against the sequential alternative in subscripts. The table shows the results for the sequential (first two columns) and distributed versions of the multi-population-based algorithms: GA, PSO, and the combined version PSO-GA. The homogeneous versions are on the left side and heterogeneous versions on the right.
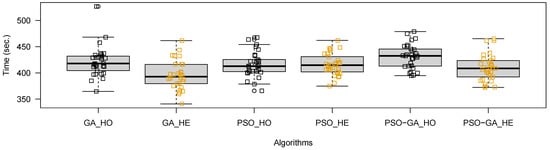
Figure 6.
Boxplot of the execution time in seconds for 30 runs of the distributed versions of the multi-population-based algorithms: GA, PSO, and the combined version PSO-GA. The homogeneous versions are on the left side (with black outlines and the _HO suffix) and the heterogeneous versions are on the right (with orange outlines and the suffix _HE).
These results confirm that a multi-population-based strategy offers a convenient speedup while keeping the results very similar to their sequential counterparts. Moreover, the combined algorithm offers better execution times, combining the continuous optimization capabilities of a PSO algorithm with the faster GA metaheuristic. Moreover, the randomized configuration parameters heterogeneous strategy gave better execution times when using the PSO-GA variant.
Finally, these experiments also exemplify the type of fuzzy controller optimizations we can perform and the speedup performance we can achieve with an implementation following an event-based architectural pattern. Another advantage of this pattern is that other researchers can replicate the experiments using a standard Docker deployment under the same software conditions. The containerized implementation could even be executed in a cloud environment from the same code base and Docker scripts, allowing the scalability options of more powerful virtual machines.
5.3. Discussion
From these experiments, we gather some insights into the problem and the algorithmic framework we have created to solve it. The sequential PSO algorithm is consistently beating all the other combinations from the algorithmic performance perspective, as seen in Table 8. However, the combined, heterogeneous, distributed PSO-GA offers the second-best performance, and also the lowest worst-case result. This means that if we are looking for a framework that in a single shot offers the best guarantee to succeed, the PSO-GA is probably the best, offering a worst-case result that is better than the median in many other cases (for instance, anyone that involves only a genetic algorithm).
Although the evolutionary algorithm is worse than the PSO in every setup, combining them is consistently better than any of them; combining the different exploitation/exploration capabilities of both seems to balance their shortcomings in that area. Looking at Table 9, however, reveals that this last combination obtains a very good median and average time to solution, with a 75% speedup over the sequential algorithm.
This leads us to conclude that the algorithm proposed in this paper is the best alternative if you want to obtain consistently good solutions in a very short amount of time, proving the value of the cloud-native design as well as the choices made in the population combination operators.
6. Conclusions
This paper presented a distributed, multi-population-based algorithm for fuzzy controller optimization. The implementation follows an event-based, cloud-native architectural pattern suitable for workstation or cloud platform deployment. We used industry-standard, open-source development tools and libraries, with Docker and docker-compose for container deployment and the Python language to develop a simulation and fuzzy controller environment. The code can be modified to add more control problems or metaheuristics. The algorithm is based on message queues for the asynchronous exchange of messages encoding populations of candidate solutions. The mixer component adds a buffer-based strategy for exchanging promising candidate solutions between populations. We propose the use of Docker containers as workers for the isolated execution of metaheuristics, similar to the island model. In this paper, we compared two multi-population versions using PSO, GA, and a combination of the two metaheuristics. As a case study, we used the proposed algorithm to optimize the parameters of the MFs of a fuzzy controller. The controller is applied to the autonomous path tracking using rear-wheel feedback. We optimized the controller using simulations to validate each candidate’s configuration; this was carried out by following three distinct paths and measuring the average RMSE.
We have performed an empirical evaluation of two multi-population configuration techniques. One configuration is based on a homogeneous configuration, using a set of parameters found experimentally. We also evaluated a heterogeneous configuration obtained by randomly initializing the parameters of each subpopulation. We found that the configuration strategy we chose significantly influences the execution time in some cases. We conclude that using the heterogeneous strategy on the combined PSO-GA improves the execution time. The results also show no statistical difference between the sequential and multi-population-based implementation of the algorithm, while there is a proportional speedup on the multi-population implementation. The distributed PSO version achieved better speedup than the distributed GA alternative, which could be explained because the GA has a lower execution time.
Having a multi-population algorithm opens many lines for further exploration. One possibility is to give each subpopulation different problem configurations, for instance, different simulation problems. Some populations could have paths with more difficulty or a shorter distance, while others have less complicated problems. Another option is using a multi-objective control problem, using other performance metrics, and having populations optimizing distinct objective functions. On the implementation side, a complete study of the speedup must include a different number of worker containers to see if the speedup scales with the number of workers/populations.
There are also different areas of application of this algorithm; in principle, metaheuristics such as the one proposed in this paper can be applied to any monomodal optimization problem where the fitness function can be formulated analytically. In this paper, we have proved that it can successfully be applied to fuzzy-based systems, since it can evolve them successfully and in a reasonable amount of time. This fact opens the possibility of applying it to relatively complicated problems to bring down the time required to obtain a solution by (roughly) an order of magnitude or, in a cloud environment, to reduce its cost; this will make this kind of system affordable to small and medium-sized enterprises who will be able to leverage it to add value to their portfolio. Since fuzzy controllers are used extensively on the Internet of Things [52], this could be an excellent area of application. This is left, however, as future work.
Author Contributions
Conceptualization, A.M., M.G.-V. and O.C.; methodology, A.M.; software, M.G.-V.; validation, O.C. and J.J.M.-G.; data curation, A.M.; writing—original draft preparation, A.M.; writing—review and editing, M.G.-V. and J.J.M.-G.; visualization, A.M.; supervision, O.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by projects TecNM-15340.22-P and DemocratAI PID2020-115570GB-C22.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data and code are available with an open source license from https://github.com/mariosky/fuzzy-control (accessed on 17 January 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Fu, K. Learning control systems and intelligent control systems: An intersection of artifical intelligence and automatic control. IEEE Trans. Autom. Control 1971, 16, 70–72. [Google Scholar]
- Mamdani, E.H. Application of fuzzy algorithms for control of simple dynamic plant. Proc. Inst. Electr. Eng. 1974, 121, 1585–1588. [Google Scholar] [CrossRef]
- Driankov, D.; Saffiotti, A. Fuzzy Logic Techniques for Autonomous Vehicle Navigation; Physica: Heidelberg, Germany, 2013; Volume 61. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Ahn, H.S.; Chen, Y.; Moore, K.L. Iterative learning control: Brief survey and categorization. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2007, 37, 1099–1121. [Google Scholar] [CrossRef]
- Bisoffi, A.; De Persis, C.; Tesi, P. Data-driven control via Petersen’s lemma. Automatica 2022, 145, 110537. [Google Scholar]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Salem, M.; Mora, A.M.; Guervós, J.J.M.; García-Sánchez, P. Evolving a TORCS Modular Fuzzy Driver Using Genetic Algorithms. In Proceedings of the Applications of Evolutionary Computation—21st International Conference, EvoApplications 2018, Parma, Italy, 4–6 April 2018; Sim, K., Kaufmann, P., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2018; Volume 10784, pp. 342–357. [Google Scholar] [CrossRef]
- Holland, J.H. Outline for a logical theory of adaptive systems. J. ACM (JACM) 1962, 9, 297–314. [Google Scholar] [CrossRef]
- Back, T. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Kennedy, J. Swarm intelligence. In Handbook of Nature-Inspired and Innovative Computing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 187–219. [Google Scholar]
- Castillo, O.; Melin, P. A review on the design and optimization of interval type-2 fuzzy controllers. Appl. Soft Comput. 2012, 12, 1267–1278. [Google Scholar] [CrossRef]
- Mancilla, A.; Castillo, O.; Valdez, M.G. Optimization of Fuzzy Logic Controllers with Distributed Bio-Inspired Algorithms. In Recent Advances of Hybrid Intelligent Systems Based on Soft Computing; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–11. [Google Scholar] [CrossRef]
- Mancilla, A.; Castillo, O.; Valdez, M.G. Evolutionary Approach to the Optimal Design of Fuzzy Controllers for Trajectory Tracking. In Proceedings of the Intelligent and Fuzzy Techniques for Emerging Conditions and Digital Transformation, Istanbul, Turkey, 24–26 August 2021; Kahraman, C., Cebi, S., Cevik Onar, S., Oztaysi, B., Tolga, A.C., Sari, I.U., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 461–468. [Google Scholar]
- Mancilla, A.; García-Valdez, M.; Castillo, O.; Merelo-Guervós, J.J. Optimal Fuzzy Controller Design for Autonomous Robot Path Tracking Using Population-Based Metaheuristics. Symmetry 2022, 14, 202. [Google Scholar] [CrossRef]
- Cortes-Rios, J.C.; Gómez-Ramírez, E.; Ortiz-de-la Vega, H.A.; Castillo, O.; Melin, P. Optimal design of interval type 2 fuzzy controllers based on a simple tuning algorithm. Appl. Soft Comput. 2014, 23, 270–285. [Google Scholar] [CrossRef]
- Oh, S.K.; Jang, H.J.; Pedrycz, W. The design of a fuzzy cascade controller for ball and beam system: A study in optimization with the use of parallel genetic algorithms. Eng. Appl. Artif. Intell. 2009, 22, 261–271. [Google Scholar]
- Ciurea, S. Determining the parameters of a Sugeno fuzzy controller using a parallel genetic algorithm. In Proceedings of the 2013 19th IEEE International Conference on Control Systems and Computer Science, Washington, DC, USA, 29–31 May 2013; pp. 36–43. [Google Scholar]
- Malawski, M.; Gajek, A.; Zima, A.; Balis, B.; Figiela, K. Serverless execution of scientific workflows: Experiments with HyperFlow, AWS Lambda and Google Cloud Functions. Future Gener. Comput. Syst. 2020, 110, 502–514. [Google Scholar] [CrossRef]
- Gilbert, J. Cloud Native Development Patterns and Best Practices: Practical Architectural Patterns for Building Modern, Distributed Cloud-Native Systems; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Kratzke, N.; Quint, P.C. Understanding cloud-native applications after 10 years of cloud computing-a systematic mapping study. J. Syst. Softw. 2017, 126, 1–16. [Google Scholar] [CrossRef]
- Scholl, B.; Swanson, T.; Jausovec, P. Cloud Native: Using Containers, Functions, and Data to Build Next-Generation Applications; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Starkweather, T.; Whitley, D.; Mathias, K. Optimization using distributed genetic algorithms. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Jerusalem, Israel, 9–14 October 1990; Springer: Berlin/Heidelberg, Germany, 1990; pp. 176–185. [Google Scholar]
- Ma, H.; Shen, S.; Yu, M.; Yang, Z.; Fei, M.; Zhou, H. Multi-population techniques in nature inspired optimization algorithms: A comprehensive survey. Swarm Evol. Comput. 2019, 44, 365–387. [Google Scholar]
- Alba, E.; Tomassini, M. Parallelism and evolutionary algorithms. IEEE Trans. Evol. Comput. 2002, 6, 443–462. [Google Scholar]
- Li, Y.; Zeng, X. Multi-population co-genetic algorithm with double chain-like agents structure for parallel global numerical optimization. Appl. Intell. 2010, 32, 292–310. [Google Scholar]
- García-Valdez, M.; Merelo, J.J. Event-Driven Multi-algorithm Optimization: Mixing Swarm and Evolutionary Strategies. In Proceedings of the International Conference on the Applications of Evolutionary Computation (Part of EvoStar), Virtual Event, 7–9 April 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 747–762. [Google Scholar]
- Mancilla, A.; Castillo, O.; Valdez, M.G. Mixing Population-Based Metaheuristics: An Approach Based on a Distributed-Queue for the Optimal Design of Fuzzy Controllers. In Proceedings of the International Conference on Intelligent and Fuzzy Systems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 839–846. [Google Scholar]
- Talukdar, S.; Baerentzen, L.; Gove, A.; De Souza, P. Asynchronous teams: Cooperation schemes for autonomous agents. J. Heuristics 1998, 4, 295–321. [Google Scholar]
- Singh, S.; Kaur, J.; Sinha, R.S. A comprehensive survey on various evolutionary algorithms on GPU. In Proceedings of the International Conference on Communication, Computing and Systems, Washington, DC, USA, 18–21 December 2014; pp. 83–88. [Google Scholar]
- Jankee, C.; Verel, S.; Derbel, B.; Fonlupt, C. A fitness cloud model for adaptive metaheuristic selection methods. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Edinburgh, UK, 17–21 September 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 80–90. [Google Scholar]
- Veeramachaneni, K.; Arnaldo, I.; Derby, O.; O’Reilly, U.M. FlexGP. J. Grid Comput. 2015, 13, 391–407. [Google Scholar]
- Dziurzanski, P.; Zhao, S.; Przewozniczek, M.; Komarnicki, M.; Indrusiak, L.S. Scalable distributed evolutionary algorithm orchestration using Docker containers. J. Comput. Sci. 2020, 40, 101069. [Google Scholar]
- Salza, P.; Ferrucci, F. Speed up genetic algorithms in the cloud using software containers. Future Gener. Comput. Syst. 2019, 92, 276–289. [Google Scholar] [CrossRef]
- Merelo Guervós, J.J.; García-Valdez, J.M. Introducing an event-based architecture for concurrent and distributed evolutionary algorithms. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Coimbra, Portugal, 8–12 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 399–410. [Google Scholar]
- Valdez, M.G.; Merelo-Guervós, J.J. A container-based cloud-native architecture for the reproducible execution of multi-population optimization algorithms. Future Gener. Comput. Syst. 2021, 116, 234–252. [Google Scholar]
- Ivanovic, M.; Simic, V. Efficient evolutionary optimization using predictive auto-scaling in containerized environment. Appl. Soft Comput. 2022, 129, 109610. [Google Scholar]
- Arellano-Verdejo, J.; Godoy-Calderon, S.; Alonso-Pecina, F.; Guzmán-Arenas, A.; Cruz-Chavez, M.A. A New Efficient Entropy Population-Merging Parallel Model for Evolutionary Algorithms. Int. J. Comput. Intell. Syst. 2017, 10, 1186–1197. [Google Scholar]
- Roy, G.; Lee, H.; Welch, J.L.; Zhao, Y.; Pandey, V.; Thurston, D. A distributed pool architecture for genetic algorithms. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 1177–1184. [Google Scholar]
- Merelo, J.J.; Fernandes, C.M.; Mora, A.M.; Esparcia, A.I. SofEA: A pool-based framework for evolutionary algorithms using couchdb. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, Lille, France, 10–14 July 2012; pp. 109–116. [Google Scholar]
- García-Valdez, M.; Trujillo, L.; Fernández de Vega, F.; Merelo Guervós, J.J.; Olague, G. EvoSpace: A distributed evolutionary platform based on the tuple space model. In Proceedings of the European Conference on the Applications of Evolutionary Computation, Vienna, Austria, 3–5 April 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 499–508. [Google Scholar]
- García-Valdez, M.; Trujillo, L.; Merelo, J.J.; Fernandez de Vega, F.; Olague, G. The EvoSpace model for pool-based evolutionary algorithms. J. Grid Comput. 2015, 13, 329–349. [Google Scholar]
- García-Valdez, M.; Merelo, J. evospace-js: Asynchronous pool-based execution of heterogeneous metaheuristics. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Berlin, Germany, 15–19 July 2017; pp. 1202–1208. [Google Scholar]
- Li, C.; Nguyen, T.T.; Yang, M.; Yang, S.; Zeng, S. Multi-population methods in unconstrained continuous dynamic environments: The challenges. Inf. Sci. 2015, 296, 95–118. [Google Scholar] [CrossRef]
- Pamucar, D.; Ćirović, G. Vehicle route selection with an adaptive neuro fuzzy inference system in uncertainty conditions. Decis. Mak. Appl. Manag. Eng. 2018, 1, 13–37. [Google Scholar] [CrossRef]
- De Luca, A.; Oriolo, G.; Samson, C. Feedback control of a nonholonomic car-like robot. In Robot Motion Planning and Control; Springer: Berlin/Heidelberg, Germany, 1998; pp. 171–253. [Google Scholar]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar]
- Yang, X.S.; Cui, Z.; Xiao, R.; Gandomi, A.H.; Karamanoglu, M. Swarm Intelligence and Bio-Inspired Computation: Theory and Applications; Newnes: Newton, MA, USA, 2013. [Google Scholar]
- Gong, Y.; Fukunaga, A. Distributed island-model genetic algorithms using heterogeneous parameter settings. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 820–827. [Google Scholar]
- Touati, S.A.A.; Worms, J.; Briais, S. The Speedup-Test: A statistical methodology for programme speedup analysis and computation. Concurr. Comput. Pract. Exp. 2013, 25, 1410–1426. [Google Scholar] [CrossRef]
- Kiraz, M.U.; Yilmaz, A. Comparison of ML algorithms to detect vulnerabilities of RPL-based IoT devices in intelligent and fuzzy systems. In Proceedings of the International Conference on Intelligent and Fuzzy Systems, Turkey, Bornova, 19–21 July 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 254–262. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).