Abstract
The development of automated systems for detecting defects in and damage to buildings is ongoing in the construction industry. Remaining aware of the surface conditions of buildings and making timely decisions regarding maintenance are crucial. In recent years, machine learning has emerged as a key technique in image classification methods. It can quickly handle large amounts of symmetry and asymmetry in images. In this study, three supervised machine learning models were trained and tested on images of efflorescence, and the performance of the models was compared. The results indicated that the support vector machine (SVM) model achieved the highest accuracy in classifying efflorescence (90.2%). The accuracy rates of the maximum likelihood (ML) and random forest (RF) models were 89.8% and 87.0%, respectively. This study examined the influence of different light sources and illumination intensity on classification models. The results indicated that light source conditions cause errors in image detection, and the machine learning field must prioritize resolving this problem.
1. Introduction
A humid environment that rains often can easily result in fault problems for buildings, such as efflorescence on wall surfaces, scaling on concrete, cracks, and corrosion on reinforcement. Such outer appearance defects on buildings are unsightly and affect the structural safety and the living quality of residents. The degradation of building surfaces is common. Therefore, the routine detection and quantification of surface defects is crucial for engineering personnel because these routine operations enable them to conduct maintenance work on time. Efflorescence is a type of defect that often occurs on building surfaces. In addition to being unsightly, efflorescence poses hazards toward structures, may jeopardize users’ health, and lowers their work efficiency. Efflorescence indicates the locations of pores, cracks, water seepage, and water leakage in structures. In summary, efflorescence is a key indicator of building degradation.
Efflorescence may result in an unsightly outer appearance but seldom affects the mechanical properties or durability of concrete. However, when efflorescence is left unattended for a long time or when no effective measures are adopted to eliminate efflorescence, it can corrode and spall concrete on the building’s surface. Efflorescence is often accompanied by other defects, such as cracking or spalling [1]. However, no test standards currently can be used to evaluate efflorescence in concrete masonry units or mortar [2]. Therefore, the ASTM [3] method is sometimes used for efflorescence sampling and testing. This method involves observing the efflorescence potential of concrete masonry units through visual inspection. No information has been presented on either the precision or bias of the efflorescence test method because the test result is nonquantitative. Therefore, this method cannot effectively confirm efflorescence and detect the area and quantity of efflorescence present.
Generally, building damage detection relies on human visual inspection to measure and evaluate defects. For example, Ada et al. [4] used visual inspection for RC damage after a fire (such as spalling, net-like cracks, and bared reinforcement). However, because manual inspection mainly involves human operations, it is time-consuming, unreliable, and costly [5]. Even for seasoned and trained personnel, performing manual visual inspections remains laborious and inefficient. Bianchini et al. [6] noted that technical personnel’s subjectivity is inevitably dependent on experience level, and this affects evaluation results. This is true even when carefully drafted and reliable manuals are used for evaluation. Therefore, the development of sensor-based automatized detection is imperative because it can lower dependence on manual measurement, reduce inspection time, and enhance inspection accuracy. Automatized digital image recognition is more efficient, consistent, accurate, and objective than human visual inspection.
Zhu and Brilakis [7] noted that overcoming the limitations of human building image inspections requires matching methods that rely on the visual features of materials and features contained in images for automatized information retrieval. Academics have proposed many visual-based methods that can detect damage. These methods mainly involve using image-processing techniques (IPTs) to compensate for the complexity of a task [8,9]. Within the past decade, advancement in the image-processing ability of digital cameras and computers has enabled researchers and industry personnel to process digital images effectively and extract useful information from these images. Cha et al. [10] pointed out that many IPTs are already used to detect civil infrastructure defects, extract defect features, and partially replace human on-site inspections (e.g., cracks on concrete surfaces and steel parts).
For image recognition and detection, some factors must be considered to effectively analyze the features and spectral properties of images. These factors include the material, quantity, scope, shape, texture, tone, and color of objects. Particularly, colors and textures are commonly used as classifying indicators because they can accurately describe the surface of objects in images [7]. However, certain damage features have colors similar to building surfaces. For example, most efflorescence appears to be white, whereas concrete is gray. Differentiating between the two can be difficult and results in a high misjudgment or misclassification probability. Enhancing the detection accuracy rate is a pressing problem that remains to be solved through classification techniques. Symmetry plays an important role in image processing and establishes supervised machine learning that incorporates symmetry into models, resulting in improved performance. Furthermore, since the proportion of data with different labels is often unbalanced, incorporating symmetry into machine learning models addresses this issue while promoting model accuracy.
Machine learning algorithms are commonly used in image recognition and classification, including in the detection of building damage. Damage classification involves the use of samples of training data to predict discrete class labels [11]. Support vector machine (SVM) and random forest (RF) can be used for classification tasks involving small training data sets. SVM can be used to overcome the problems of high dimensionality and insufficient training samples, whereas RF does not require extensive fine-tuning of hyperparameters and is able to learn complex classification functions. Other machine learning techniques commonly used for image classification are artificial neural networks [12], principal component analysis [13], and cluster analysis [14].
Although using images to recognize building damage has always been an active research domain and images are extensively used to evaluate quality in the operational and maintenance stages, research on the use of images to detect concrete efflorescence and comprehensive comparative research on selection of the most effective machine learning techniques is lacking. In this study, the researchers acquired images through digital camera–based remote sensing. Through this, the researchers could conduct low-cost and high-quality building damage detection experiments. In addition, the researchers conducted sample training and testing through different supervised machine learning methods and later analyzed the testing results to evaluate the performance of supervised machine learning methods for concrete efflorescence detection (classification).
2. Literature Review
In the past, some researchers generally used numerical analysis to simulate various damage conditions, such as: cracks [15,16], corrosion [17] and spalling [18]. Because machine learning and computer vision techniques have gradually developed over the past few years, machine vision–based surface defect inspection systems [19] and health monitoring [20] are increasingly common. Therefore, some researchers have used digital images and machine vision algorithms to measure the spalling defects of concrete facilities [21]. Brilakis et al. [22] pointed out that before calculating image features, required elements must be identified using appropriate material detection algorithms. In addition, recognition of patterns and target objects based on certain features (e.g., shape, texture, or color values) have matured as IPTs. Although IPTs have only recently been applied for civil engineering and building construction, selecting the best machine learning algorithm is necessary to develop any reliable image identification [23].
Machine learning applications in various research domains have greatly advanced in recent years. Research domains with significant achievements regarding the application of machine learning include human face recognition, autonomous cars, speech recognition, image identification, and machine translation. Machine learning involves computers autonomously learning certain tasks and performing measurement techniques to gradually improve techniques from experience. Among machine learning types, supervised machine learning involves learning or establishing a model from training data according to a predetermined direction or problem to be solved to infer new instances based on the model.
Supervised algorithms train themselves to detect patterns by using various manually annotated data or images. The training images typically depict the object of interest in several poses to cover all its possible outer appearances [24]. Classification is an image recognition task often used for conventional supervised machine learning. Good representative features are learned directly from labeled surface defect images through supervised learning. The discriminative feature representation of surface defects is the basis for detection systems, whereas classification precision is the main consideration for detection systems [25]. Finally, users can evaluate the quality of classification models (results) by using a confusion matrix and some evaluation indicators.
The classification approaches learn patterns of objects through supervised machine learning techniques from a set of distinctive features, a set of positive training examples, and a set of negative training examples [26]. Classification is the process of dividing data sets into categories or groups through adding labels. The purpose of classification is to examine all data characteristics and divide the data into several categories according to predefined categorization principles to allow a categorization model to automatically predict future data. Image classification mainly involves performing a spectral form of identification by using real data. Target categories that must be discriminated are first determined, and the training area for each category is selected. Finally, images are classified based on the spectral statistical values (including color and texture) of each sample area.
Supervised machine learning methods commonly used in classification models include the support vector machine (SVM), maximum likelihood (ML), decision tree (DT), and random forest (RF) methods. An example of unsupervised machine learning methods is cluster analysis. From algorithm differences, artificial neural network (ANN) can be divided into supervised ANNs (e.g., back-propagation neural network (BPNN) and probabilistic neural network (PNN)) and unsupervised ANNs (e.g., Kohonen neural network).
SVMs are nonparametric classifiers. Over the past few decades, SVMs have been the most commonly used method for image classification and recognition because SVMs exhibit favorable generalizability and do not require huge numbers of training samples. For the small scale training of data sets, SVMs are the most preferred classifiers [27]. Halfawy and Hengmeechai [26] reported that the application of SVMs has allowed researchers to recognize and classify sewer defects by using a small number of training data. In addition, SVMs exhibit high classification accuracy and are feasible for high dimensions [28]. Therefore, SVMs can learn high dimensional data with the help of Lagrange multipliers to achieve excellent generalization performance [29]. SVMs exhibit superior classification and recognition ability for complex structures and multiclass classifications to those of other types of classifiers. For example, Kim et al. [30] compared and analyzed three machine learning methods (i.e., SVMs, Gaussian mixture model, and ANN), and the results indicated that SVMs are advantageous for detecting the constitution of concrete structures in colored images. Chen et al. [31] combined SVMs and Fourier transformation (SVMRA) that proposed a novel effective method for recognizing nonuniformly illuminated images of rust. This new method was compared to two other expanded machine learning approaches (i.e., simplified k-means algorithm and neuro-fuzzy recognition approach), and the results indicated that SVMRA recognized rust on steel bridges most effectively.
ML is a supervised classification method based on the Bayes’ theorem. It involves assigning pixels to a category with the maximum likelihood by using a discriminant function. Thus, the training samples are used to derive the optimized probability model that is used for classification. When enough training samples are dispensed and the data set features are normally distributed, ML can produce accurate classification results [32]. In some instances, a single classifier cannot effectively handle classification and regression problems. To achieve effective results in such instances, several different learning methods must be combined. A combination of learning methods can be applied to enhance the robustness and accuracy of a model, which is known as ensemble learning. RF is classifiers comprising classification and regression trees (CART) and are an ensemble learning technique. The training process of RF is identical to that of CART. The main difference between the two methods is the randomly selected subset of candidate variables. In RF, a randomly selected subset of candidate variables provides the optimal choice of variables for each classification. Therefore, RF can operate with high efficiency in large data sets and measure feature importance in each category [33]. RF is applied as classifiers and is used extensively in various facility detection and building image classification operation [34,35,36].
ANNs do not need to assume that features are normally distributed because they can learn patterns in the data set by using neurons and networks to enhance a new model’s ability to classify accurately. Among ANN types, BPNNs are a highly complex classification technique that can construct models from nonlinear functions [37]. Yeh [38] adopted BPNNs to diagnose damage in prestressed concrete piles. Tam et al. [39] adopted a PNN developed by Specht to classify main reasons for damage in prestressed piles. Zhu and Brilakis [7] performed concrete region recognition by using an ANN-based classifier. A database of actual construction site images was used to test the overall validity of the concrete region detection method. The results indicated that an average precision and recall of 80% could be achieved. Kohonen networks were developed to measure the carbonation depth from the concrete images [40]. Mathavan et al. [41] proposed an unsupervised learning technique called the Kohonen map to detect cracks in 2D road images. Some researchers have applied ANNs to detect road surface cracks and defects [42,43]. However, noisy data reduce the accuracy of ANNs during image classification, and an extensive amount of time is needed for training [24].
Professionals in industry have effectively used deep learning to analyze numerical data and predict outcomes [44,45,46]. However, when the input data are image-based, conventional machine learning methods can detect targets after training on small image data sets. Deep learning models require intensive calculations and large image data sets to automatically learn from training data. In addition, the black box nature of deep learning algorithms, which is linked to the use of hidden layers, leads to a loss of interpretability. Researchers can understand the operation of different parts of parametric machine learning algorithms as well as the parameters of such algorithms, which, in principle, can be manually tuned if their effects are thoroughly understood [47]. Machine learning is still favored by researchers when dealing with image classification problems because machine learning algorithms have low computational complexity and high interpretability.
3. Research Methods and Materials
Supervised classification is a machine learning task that infers the relationship between “objects” and “labels” through inducing a training set, which is a collection of objects with known labels. In the future, such generalizations can be used to classify objects with unknown labels [48]. When supervised machine learning is used to classify images, the preconfiguration of an image’s pixel color/texture value is not necessary. Supervised machine learning classifies images from the statistical spectral values of training samples. Its main procedures include confirming materials to be detected, image capturing and processing, selecting classification approaches, selecting training samples (area), extracting features, and evaluating classification performance. Among various procedures, selecting an appropriate classification approach directly influences classification results.
3.1. Machine Learning Classifiers
The supervised classification requires the manual selection of a training area, and remaining areas not selected are classified using classification algorithms [49]. This type of supervised feature learning enables the model to learn about specific data features and manifest these features directly from image pixels [50].
3.1.1. Support Vector Machine (SVM)
SVMs are a machine learning method proposed by Vapnik [51] from statistical learning theory and a supervised classification algorithm. The main principle of SVMs is to mark hyperplanes in a sample space. The linear equation for marking hyperplanes is as displayed in Equation (1). In the equation, the training sample sets D = {xi, yi}; yi = {−1, + 1} and w = (w1, w2, …, wn) represent normal vectors, and they can determine the direction of hyperplanes. b represents the bias value and can determine the distance between the hyperplane and original point (0, 0). The distance between any point in the sample space and the hyperplane is r.
If these training data are linear and separable, two parallel hyperplanes separating the two types of data can be selected. The two hyperplanes are wT + b = 1 and wT + b = −1 (Figure 1). The area between hyperplanes is known as the margin, and the distance is 2/‖‖. To maximize the distance between hyperplanes, the ‖‖ must be minimized. The hyperplane in the middle of the maximum margin is the “Optimal hyperplane”. To ensure that the sample data points are all outside the margin area of the hyperplanes, a researcher must ensure that all training samples fulfill one of the conditions stated in Equation (1). To find the maximum margin hyperplane, parameters w and b fulfilling Equation (2) must be obtained, and the value of 2/‖‖ must be maximized.
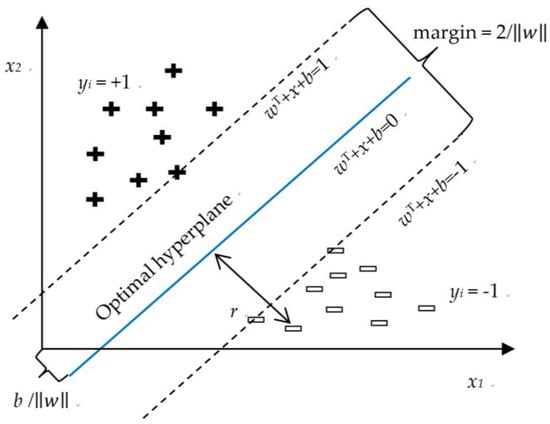
Figure 1.
SVM and hyperplane [51].
3.1.2. Maximum Likelihood (ML)
ML classification assumes that statistical data in all categories of each band are normally distributed, and the probability of a pixel belonging to a certain category is calculated and specified accordingly. Each pixel is assigned to the category with the highest probability (i.e., the maximum likelihood). If the highest probability is smaller than the assigned threshold value, the pixel remains unclassified or unknown. Therefore, ML classification can be achieved by calculating the discriminant function in Equation (3) for each pixel in an image [52].
In Equation (3), i represents the category, m represents the number of categories, ω is n dimension image data (n is the number of bands), P(ωi) is the probability that category ωi appears in the image, and all categories are assumed to be equal. |Σi| is the determinant of the covariance matrix of category ωi data. Σi−1 is the inverse matrix, and mi is the mean vector. These training pixels can provide the mean values and covariance of spectrum bands used for estimation. These data are then used to assign pixels to a category.
Classification involves identifying the category in which a sample x exhibits the largest likelihood function value. The sample can then be classified into the category. The largest value in the matrix is chosen, and x is assigned to the category. The rules of determining whether x should be classified as belonging to i or j categories are explained in Figure 2 (single dimension and using two categories as examples: i and j). (1) When x > x0, P(x|j) > (x|i), x is then classified into the j category. (2) When x < x0, P(x|j) < (x|i), x is then classified into the i category. (3) When x = x0, P(x|j) = (x|i), the probability of classifying x into either i or j categories is equal.
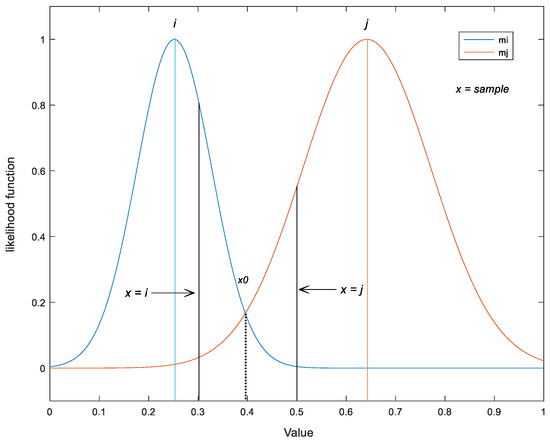
Figure 2.
Diagram of ML decision rule.
3.1.3. Random Forest (RF)
The RF algorithm is based on the CART concepts. During CART training, a variable is randomly selected, and a subset containing the kth variable is randomly selected from the variable set at the node of the tree. Subsequently, an optimal variable selected from this subset is used for splitting. Although the RF training process is identical to that of CART, when selecting the splitting variable in RF, the optimal variable is selected from the variable set (assuming there are dth variables) of the current node. If k = d with a conventional CART, when k = 1, a variable is randomly selected for splitting, which typically suggests that k = log2 d [53].
RFs create nonlinear decision boundaries through ensemble learning. This technique involves training many DTs on random subsets of training data. The forest is represented by the many created and trained DTs, and the final classification is the statistical mode of predictions collected by the trees [54]. Meyer et al. [55] noted that the subset of predicting variables is randomly selected at each split to distinguish the correlation between trees. The best predictor from a random subset is used at the respective split to partition data to obtain an optimal trade-off between insufficient data and overlearning.
3.2. Material and Image Processing
In this study, images and camera data mainly served as visual supplementary materials to help with defect recognition and evaluation. The maximum measurement distance of the portable camera sensing method was approximately 5 m. However, this method was useful for rapid space data collection, size estimation, and three-dimensional model construction [56]. The image sensor of the digital camera used in the current study could record image data (RGB) through manual operation by personnel or by being fixed to a camera stand. Because of characteristics such as being highly pixelated, compact, and easily portable, digital cameras are suitable for conducting sensing operations in locations where surfaces must be examined rapidly or where space is limited. Cameras can be used to sense various facilities within a small region. Therefore, digital cameras have already been extensively used to inspect the surface quality of buildings and civil infrastructures [57,58,59,60].
The surface complexity of the detected object, remote sensing environmental conditions, image resolution, and image-processing and classification methods all affect the detection results. In addition, if the optical axis of the optical camera is not perpendicular to the surface, the steep angle causes differences in the distance between the camera and surface to increase [61]. Therefore, when detecting concrete efflorescence by using a camera in the current study, building surfaces were recorded using orthographic projection. This reduced distance and area distortion caused by a tilted sensing angle. In addition, wall surfaces illuminated by natural light sources were selected. Finally, concrete surfaces perpendicular to the building floor were selected as sensing objects. All images were 3264 × 2448 pixels in size.
Image data consists of different classes and pixel values, and the distributions of classes and pixel values may vary. Pixel values can vary widely even within the same class. Therefore, scaling the input data to a certain range or normalizing the distribution of the data (to obtain a mean of 0 and a standard deviation of 1) is often necessary. In this study, image feature values were standardized through feature scaling to improve the efficiency and accuracy of machine learning models.
The supervised machine learning procedures in the current study were divided into two parts (Figure 3). (1) For the training model, supervised machine learning methods first needed image color values (RGB) as the base line, and the pixels were manually labeled for the efflorescence features in the image. The classifiers extracted training samples of damage features from these regions. (2) For the testing model, because different features in the research area exhibit spectral properties containing different colors, predicting variables (features) were calculated from the image. The actual efflorescence was labeled as the standard sample, and testing involved using the pixels of the original image. Finally, the performance of the three machine learning methods (i.e., SVM, ML, and RF) for detecting efflorescence was evaluated.

Figure 3.
The flowchart of damage detection in this study.
4. Model Evaluation Indicators
Hüthwohl and Brilakis [62] revealed that none of the metrics can reliably distinguish healthy and unhealthy concrete currently. Therefore, in addition to evaluating classification performance by using the most commonly used confusion matrix, this study evaluated classification performance by using other indicators from the confusion matrix. The classifier can be ensured to exhibit satisfactory generalizability and be able to evaluate the prediction accuracy of classifiers by examining confusion matrices [63]. A confusion matrix (Table 1) compared prediction data from the classification model against actual data. The columns represent predicted results, whereas the rows represent actual classification results. In summary, the confusion matrix can be used to evaluate the classification performance of the models. It is a method suitable for evaluating supervised classification methods.

Table 1.
Confusion matrix of classification model.
Assume that the classification model possesses two categories: A and B. When the classifier-predicted category is consistent with the actual category, the result is true (T). If the predicted and actual categories are inconsistent, the result is false (F). When a positive example is detected, the result is positive (P); by contrast, when a negative example is detected, the result is negative (N). Correct confusion matrix–based classification contains two scenarios (predictions). In the first scenario, the actual category is A, and the predicted category is also A. Such a result is a true positive (TP). In another scenario, the actual category is B, and the predicted category is also B. This is a true negative (TN). Two scenarios also involve misclassification errors (i.e., misjudgment). In the first scenario, the actual category is A, but the predicted category is B. This is a false negative (FN). The error when an element that should be classified into a certain category (A or B) but is actually not categorized into the correct category is an omission error (OE). The opposite of an OE is producer’s accuracy (PA). In the other scenario, the actual category is B but the predicted category is A. This is a false positive (FP). The error when an element should not be classified into a certain category (A or B) but is actually categorized into a category by mistake is a commission error (CE). The opposite of a CE is user’s accuracy (UA).
TP here refers to the quantity of correctly detected desired efflorescence pixels, whereas TN is the quantity of correctly detected non desired efflorescence pixels. FP is the quantity of incorrectly detected desired efflorescence pixels, and FN is the quantity of incorrectly detected non desired efflorescence pixels. In addition, the confusion matrix could calculate the accuracy, precision, recall, F1, Kappa, area under the curve (AUC), and Gini coefficient of the model. These values were then used to draw the receiver operating characteristic (ROC) and gain chart.
4.1. Accuracy
Accuracy refers to the ratio of instances in which the correct category was predicted. The formula for calculating accuracy is as presented in Table 2 (a). High accuracy indicates a low misjudgment ratio for categories. Although accuracy can be used to judge the overall correct classification rate, it is not ideal for gauging the results of unbalanced samples. When the ratio of a certain category is low and requires further attention, this can signify that the category exhibits a different level of importance. If judgment is only made from the accuracy, the results can be biased toward categories with high ratios. However, valuable information sometimes may be excavated from categories with low ratios.

Table 2.
Evaluation indicators for the detection model.
4.2. Precision and Recall
Although the accuracy can be used to measure the quality of classification models, it cannot serve all purposes in this respect. Thus, the precision and recall rate can be calculated and used as evaluation indicators. The formula for precision and recall are as listed in Table 2 (b) and (c). Precision is how many instances are predicted into the correct categories, and recall is the proportion of instances among certain categories that are correctly predicted.
4.3. F1
An inversely proportional relationship typically occurs between precision (P) and recall (R). High P values result in low R values. To obtain the maximum P and R values simultaneously, the F1 value is calculated from the harmonic mean of P and R. Therefore, P and R are considered simultaneously, and a balance between the two indicators is obtained and used to evaluate binary classification. Compared to conventional recognition accuracy indicators, F1 appears a reasonable indicator because the error costs of the positive and negative samples are assigned to others in the F1 approach [64]. Because numerators of P and R are TP, the average values of the F1 reciprocal must be used: 1/F1 = (1/P + 1/R)/2. The formula is presented in Table 2 (d).
4.4. ROC, AUC, and Gini Coefficient
Classifiers use the Receiver Operating Characteristic (ROC) for evaluation. The ROC curve is obtained from the confusion matrix. The X-axis represents FP ratio (1-Specificity), whereas the Y-axis represents TP ratio (Sensitivity) (Table 2 (e)). The ROC curve represents the relative relationship of two categories and depicts changes in the interaction conditions of sensitivity and specificity under this relative relationship. The ROC curve can be obtained through first plotting the operating point of each category on the X–Y plane. A curve should be drawn linking all operating points and should pass through both the minimum (0,0) and maximum points. ROC curve is often used to characterize the performance of imbalanced learning, as it is insensitive to class distribution [65].
For model performance analysis, an area under the curve (AUC) improves as it approaches 1. As the distance between the curve and reference line increases, the testing precision also increases, and the relevant formula is presented in Table 2 (f). The AUC is often an indicator for a measure of the prediction accuracy of classifiers. A value approaching 1.0 (i.e., the curve approaches the upper-left corner) indicates high prediction accuracy [26]. In addition, the AUC value can accurately evaluate the quality of models, even with unbalanced samples. The Gini coefficient is the ratio of the area between the ROC curve and the diagonal line and the area (0.5) of a triangle on the diagonal line. The Gini coefficient is also an indicator that evaluates classification performance. The Gini coefficient can be calculated from ROC and AUC values. The formula for calculating the Gini coefficient is presented in Table 2 (g). Generally, a Gini coefficient above 60% indicates a satisfactory classification model.
4.5. Kappa
Cohen [66] proposed the idea of Kappa to indicate the level of approximation between classification results and actual situations. It is extensively used to precisely estimate image classification. Kappa is used to verify the consistency of a method through repeated tests and measure the accuracy of two methods in classification results. Calculation of the Kappa coefficient is based on the overall statistical consistency of the confusion matrix, and categories not located in the diagonal lines of the confusion matrix are also considered. The formula for calculating the Kappa coefficient is presented in Table 2 (h). In the formula, P0 represents overall agreement probability (i.e., accuracy), and Pe represents agreement probability occurring by chance. The Kappa coefficient ranges between +1 (completely consistent) and −1 (completely inconsistent). A zero value indicates random classification [67]. Therefore, the Kappa value is regarded as an effective method for analyzing a single confusion matrix or comparing differences between various confusion matrices [68,69]. In addition, it can be used to explain the accuracy of CE and OE in classification [70].
4.6. Gain Chart
A gain chart is a commonly used classification model evaluation chart. It can be used to analyze the classification performance of models and can help the user find the optimal prediction model. Percentages on the horizontal axis are ordered from high to low and represent the percentage of the testing data set. The vertical axis represents the percentage of the actual predicted values (Table 2 (i)). A gain curve of the chart curving upward indicates a high model gain. If the gain curve distribution exhibits a 45° angle, this indicates a random model and that classification gains are nonexistent.
Machine learning models are based on constructive feedback; they obtain and process feedback in the form of various indicators and adjust accordingly until the desired accuracy is achieved. In addition to enabling users to distinguish the performance between models, other important functions of such indicators include facilitating interpretation of the results of the model and identifying the task or goal of interest. Therefore, different evaluation indicators are selected according to the distribution and features of data. When the distribution of classes is uneven, indicating data imbalance, precision, recall, F1, ROC, and AUC are generally used as evaluation indicators. The samples of efflorescence in the images used in the present study were similar to those of normal samples; therefore, the effect of data imbalance was negligible. Accuracy was identified as the most important indicator for evaluating the models.
5. Results and Discussion
In supervised classification, classification testing is mainly performed from training areas selected by users. Supervised classification exhibits more stable accuracy than unsupervised classification. However, detecting building damage involves classifying damage conditions from images by using machine learning classification. Thus, classification performance depends on whether users are professionally competent in image analysis and processes. In addition, training area selection may vary according to the surface complexity of detected objects and the intensity of light sources. Thus, even with a large amount of training samples, selecting specific data, research domains, applied characteristics, and presentation strategies are imperative [71].
5.1. Evaluation of Classification Models
SVMs can be used to solve many complex binary classification problems [72]. The concrete efflorescence detection in the current study was a binary classification task. A total of 500 random samples were selected for sample training and testing, and the accuracy, PA, UA, OE, and CE of the SVM were calculated and are presented in Table 3. Predicted quantity refers to the quantity of concrete efflorescence detected in the research area of the current study, whereas the actual (Truth) quantity refers to the amount of efflorescence plotted manually by hand. Accuracy refers to the ratio of instances in which the correct category was predicted. A high accuracy indicated a low misjudgment ratio for the category. For example, the quantity of efflorescence and normal (not efflorescence) correctly predicted by the SVM were 272 and 179, respectively. This was then divided by the total number of samples, n = 500. Thus, the accuracy rate was 90.2%. The accuracy of ML and RF was 89.8% and 87.0%, respectively (Table 4 and Table 5). Accuracy is an indicator that comprehensively considers TP, TN, FP, and FN measurements, which depend on the balanced quantity of positive and negative samples [62]. The ratio of efflorescence and normal in the current study in the random sample was 3:2. Both had a similar quantity ratio. Therefore, the classification accuracy of the supervised machine learning method could be evaluated by selecting the actual efflorescence area and the normal area.

Table 3.
Confusion matrix of SVM efflorescence classification.

Table 4.
Confusion matrix of ML efflorescence classification.

Table 5.
Confusion matrix of RF efflorescence classification.
Precision is the actual quantity of efflorescence divided by its total predicted quantity of efflorescence. For example, the actual quantity of efflorescence is 272. When this number is divided by the SVM-predicted quantity of efflorescence (i.e., 291), a precision rate of 93.4% is calculated. Recall is the predicted quantity of efflorescence divided by its actual quantity of efflorescence. For example, the predicted quantity of efflorescence is 272. When this number is divided by the actual quantity of efflorescence (i.e., 291), a recall rate of 90.1% is calculated (Table 3). As classifiers, SVMs and ML do not differ considerably in precision, recall, PA, and UA. All three supervised machine learning methods used in this study could accurately detect the presence of efflorescence. The researchers believed that this was caused by the different distribution of the spectral properties (RGB) of efflorescence and normal images. According to the results produced by the confusion matrices, the error rate (i.e., OE and CE) among different classifiers were nearly similar.
F1 is typically used to evaluate the classification performance of information retrieval [73]. Although accuracy can be used to evaluate the reliability of a classifier’s overall performance, the classification would be biased toward categories with high quantity ratios in cases of unbalanced categories. Introducing F1 enables the simultaneous consideration of false positives and false negatives. Large measured F1 values result in ideal identification performance. In the current study, the SVM exhibited its highest F1 value of 0.88, followed by RF (F1 = 0.874) and ML (F1 = 0.839).
The X-axis of the ROC curve represents the FP rate, whereas the Y-axis of the curve represents the TP rate. The FP rate is the probability of misjudgment when the data do not belong to a certain category, whereas the TP rate is the possibility of making a correct judgment when the data do belong to a certain category. Generally, large TP rates and small FP rates are desirable. If the curve passes through the left-upper corner point at (0, 1), it means the damage classification is perfect in accuracy [74]. The ROC curve was adopted in the current study to examine the true and false quantity of efflorescence based on the predicted and actual quantity of efflorescence. Therefore, the ROC curve could be used to measure changes in the TP rate under different FP rates. For the SVM, when the FP rate was 0.096, the TP rate was 0.901. For ML, when the FP rate was 0.101, the TP rate was 0.897. For RF, when the FP rate was 0.136, the TP rate was 0.874 (Figure 4).
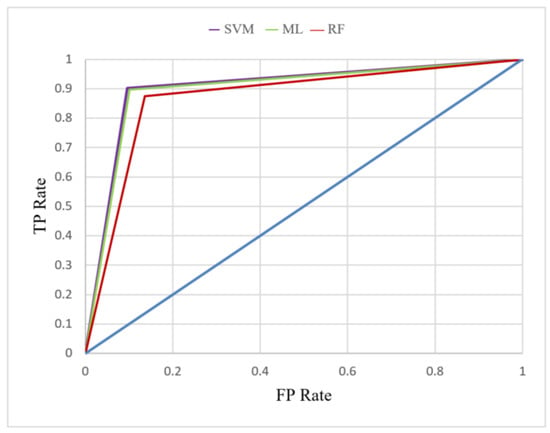
Figure 4.
ROC curve of the three machine learning algorithms.
In addition, the FP rate results vary according to the classification threshold value. Therefore, the size of the AUC can be used as an indicator to select the optimal classification model. The AUC can be used to verify the performance of the classification model. High AUC values result in satisfactory model performance. If a machine learning ROC curve is completely wrapped by another machine learning ROC curve, it confirms that the latter exhibits more satisfactory performance than the former (e.g., in Figure 4, the ROC curve of ML is wrapped by the ROC curve of the SVM). When two machine learning ROC curves intersect, judging which method exhibits more satisfactory performance becomes difficult. In such cases, the AUC value size must be compared. In this study, the SVM exhibited the highest AUC of 0.902, followed by those of ML (AUC = 0.898) and RF (AUC = 0.869) (Table 6). The size of the Gini coefficient is related to the AUC size (Gini = 2*AUC – 1). A large AUC results in a large Gini coefficient and favorable model performance. The Gini coefficient of the SVM and ML was 0.805 and 0.796, respectively, which indicates that the two methods exhibited similar classification model effectiveness. The Gini coefficient of the RF method was 0.738 (Table 6).

Table 6.
Classification performance of the supervised machine learning methods.
The Kappa coefficient typically ranges between 0 to 1, with 0.0–0.20 representing a slight consistency, 0.21–0.40 indicating a fair consistency, 0.41–0.60 indicating a moderate consistency, 0.61–0.80 indicating a substantial consistency, and 0.81–1.00 indicating nearly perfect consistency. The Kappa coefficient of the SVM, ML, and RF was 0.797, 0.789, and 0.731, respectively (Table 6). All three methods exhibited a substantial level of consistency. In addition, the researchers used the gain chart to evaluate the detection performance of the first 50% of test data. The concrete efflorescence detection results indicated that the SVM exhibited the highest performance, whereas RF exhibited the lowest performance. At 50% of the test set, the three types of supervised machine learning methods—SVM, ML, and RF—could predict 77.4%, 77.1%, and 75.1% of the actual values (Figure 5).
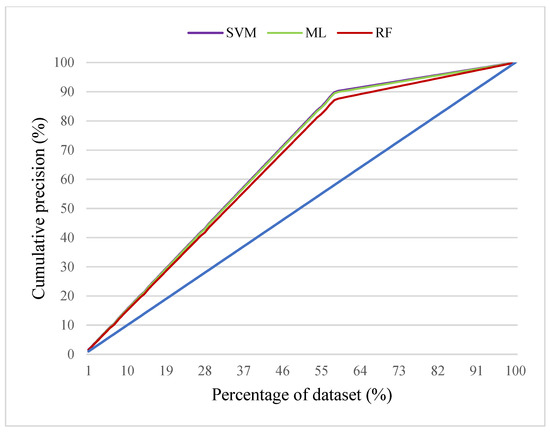
Figure 5.
Gain chart of three machine learning algorithms.
Evaluating the generalizability of machine learning methods requires effective and feasible experimental estimation methods. Evaluation standards for gauging models are also needed to measure performance. If the aim is to identify the most ideal classification results for specific research, a comparative study involving different classifiers is typically needed. Therefore, the researchers of the current study adopted the six evaluation indicators listed in Table 6 to evaluate the performance of the three supervised machine learning algorithms (i.e., SVM, ML, and RF) during classification. Overall, the SVM exhibited the highest concrete efflorescence detection (classification) performance, whereas ML. RF exhibited poorer overall performance. Both the SVM and ML are statistical learning classification methods. The SVM and ML detect the presence of concrete efflorescence more effectively than the rule-based classification approach of RF. Thus, they produce more ideal classification results than RF does. For example, data indicates that the SVM and ML performed more satisfactorily than RF across all evaluation indicators.
5.2. Efflorescence Detection Results
Step 1: The efflorescence in the image is manually labeled, and the features of the efflorescence regions are selected as training samples. Step 2: The characteristics of efflorescence differ from those of normal concrete; accordingly, each model calculates the feature values in each damage image and uses the values to detect efflorescence. Step 3: A total of 500 checkpoints are randomly generated from the image, and the efflorescence labels are used as the standard. Step 4: The model is evaluated on the basis of the classification results.
In this study, the researchers detected concrete efflorescence by using three supervised machine learning methods: the SVM, ML, and RF. Two classification categories were used in the current study: efflorescence areas (black) and normal areas (light gray). The efflorescence detection results of the SVM, ML, and RF, as displayed in Figure 6b–d, were compared to the original efflorescence image in Figure 6a. The three different classifiers produced nearly similar concrete efflorescence detection results. For the visual presentation, the three supervised classification methods did not exhibit prominent differences. Therefore, using the confusion matrix was necessary to verify the accuracy of supervised classification methods.

Figure 6.
Efflorescence detection results of various supervised machine learning methods.
The digital images obtained from the building surfaces contained valuable information. The digitized surface damage areas and quantity could be used to indicate the extent of building degradation. In the SVM efflorescence detection results, the scalar size of the spectrum of the digital image (Figure 7a) and vector of the spectrum (Figure 7b) were calculated, and the analysis indicated that the number of efflorescence scalar was 170 (the total quantity is 300), which constituted approximately 56.7% of the total scalar quantity. The number of the efflorescence vector was 102 (the total quantity was 192), which constituted approximately 53.1% of total vector quantity. The efflorescence ratio data could serve as a reference for facility managers to determine the scope of maintenance operations.
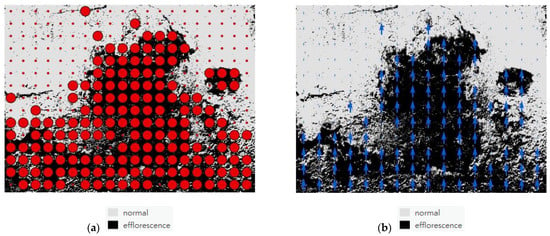
Figure 7.
Scalar and vector of the spectrum of SVM-based efflorescence detection. (a) The scalar of the spectrum and detection image and (b) The vector of the spectrum and the detection image.
Performance measurement reflects task requirements. When comparing the performance of classification models, using different evaluation indicators often results in different judgment outcomes. Therefore, the quality of models depends on the adopted machine learning algorithm, data, and purpose. Classification reliability is largely determined by the quality of training data, which is the image quality. Kakumanu et al. [75] noted that the color information of images may be influenced by environmental conditions, such as changes in illumination conditions, weather, background color, and characteristics of the camera used for computer vision. Therefore, in environments with different light sources and illumination intensity, the image information of building damage also differs, and these differences exert different levels of influence on machine learning detection results. During actual building damage detection operations, controlling environmental illumination conditions is difficult. Therefore, how different light source conditions and illumination intensity result in misjudgment must be understood.
Because the SVM detected concrete efflorescence more effectively than did ML and RF in this study, the researchers also compared the efflorescence detection performance of the SVM under different light sources and illumination intensity. Under illumination from artificial fluorescence light (Figure 8b) and nonuniform light (Figure 8c), the SVM may misjudge normal surfaces as those with efflorescence, and as illustrated by the red frame lines in Figure 8e,f. Various texture and color features were present on the concrete surface. Therefore, nonuniform light sources and illumination intensity typically result in many detection errors. When light intensity is compelling, it is difficult to distinguish efflorescence damage from the concrete surface with reflected light [76]. The SVM exhibited ideal efflorescence detection performance (Figure 8d) under the illumination of natural light (Figure 8a). Therefore, light source conditions may cause errors in image detection, and the machine learning field must prioritize resolving this problem.

Figure 8.
SVM detection results under different light source conditions: (a) natural light source, (b) fluorescence light source, (c) nonuniform light source, (d) SVM efflorescence detection under natural light source, (e) SVM efflorescence detection under fluorescence light source, and (f) SVM efflorescence detection under nonuniform light source.
Vetrivel et al. [71] stated that image-based classification methods exhibit differing performances according to the data type or classification scheme. For example, differences in factors such as the spectral band, supplementary data, and research area lead to different results for all classification methods. Apart from the classification method, the features of the image are crucial for influencing classification performance. In conclusion, classifying or detecting images depends on the following factors: training and testing data set, image type, image quality, and lighting conditions. Automatized surface damage detection is helpful for evaluating the overall quality of building condition information and helps enhance the effectiveness of building maintenance. However, such a method cannot resolve the entire problem and only represents one part of the complex inspection process. It mainly assists engineering personnel to effectively and rapidly detect surface defects on facilities. Constant and meticulous examination and adjustment still must be conducted to enhance the overall quality of examination data.
6. Conclusions
Developing automatized defect and damage detection has always been a direction pursued by the building industry. However, the greatest challenge now is enhancing the accuracy and effectiveness of detecting targeted objects by using high-quality sensor images and appropriate classification methods. Some researchers have attempted to develop advanced classification methods and techniques (e.g., machine learning or deep learning) for detection procedures such as image processing, training and testing, and evaluating performance. For example, Crespo et al. [77] used infrared images and unsupervised machine learning to detect efflorescence; the accuracy rates of the fuzzy k-means, k-means, and ISODATA algorithms ranged from 80.92% to 86.25%. Instead of unsupervised machine learning, this study used SVM-, ML-, and RF-based supervised machine learning algorithms, which can achieve higher performance because they can automatically extract abstract features of efflorescence from images with accuracy rates of 87% to 90.2%. Researchers have made remarkable progress in applying deep learning algorithms in image recognition. Bouzan et al. [78] used unmanned arial vehicle images and a convolutional neural network to detect efflorescence with a precision of 89%. The precision of machine learning models in the present study ranged from 90.7% to 93.4%. Because the images and devices used in the present study and the study by the above research differed considerably, the studies cannot be fairly compared; however, supervised machine learning still has certain advantages in detecting efflorescence.
The researchers of the current study constructed a concrete efflorescence detection model by using digital camera images and supervised machine learning methods, mainly to make use of high-resolution images and automatized and rapid machine learning detection methods to calculate the image data features of concrete efflorescence and subsequently use these features as the basis of classification. Subsequently, various evaluation indicators were used to verify the effectiveness of the classification models. The researchers adopted six types of evaluation indicators (i.e., accuracy, F1, AUC, Gini coefficient, Kappa, and gain chart) to comprehensively compare the classification performance of the three supervised machine learning methods. The results indicated that the SVM exhibited the highest concrete efflorescence detection performance, followed by ML. However, the two methods did not differ considerably in detection performance.
The current study also captured concrete efflorescence images under different conditions (e.g., natural and man-made light sources and nonuniform illumination). This experiment aimed to gain understanding on the influence of light source conditions and illumination intensity on classification results. This is beneficial for the development of robust classifiers. Improving computer vision techniques can reduce noise limitations, such as those caused by low light, low illumination intensity, nonuniform illumination, and shadow projection to ensure the extensive applicability of the techniques. Developing advanced image and machine learning techniques enables civil engineering personnel to automatically detect surface defects in target objects.
Images of damage collected in real-world environments often have heterogeneous stains and may overlap. Machine learning still has limitations in extracting features from such images. In addition, the color of efflorescence is similar to that of some types of concrete, and machine learning models can therefore easily confuse efflorescence with background materials. Machine learning models have difficulty taking full advantage of the multiple features extracted from efflorescence, resulting in a time-consuming and inaccurate training process for the model. Therefore, the use of machine learning to process and classify such images requires modification and feature extraction testing. Furthermore, supervised machine learning often requires manual labeling, which is resource-intensive and not conducive to automatic damage detection. The integration of pretrained machine learning models into drone-based or robotic systems to achieve real-time automated detection must be further explored in the future.
Author Contributions
C.-L.F. edited and wrote the manuscript; Y.-J.C. collected the data and analyzed the data; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article. The data presented in this study can be requested from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hüthwohl, P.; Brilakis, I.; Borrmann, A.; Sacks, R. Integrating RC bridge defect information into BIM models. J. Comput. Civ. Eng. 2018, 32. [Google Scholar] [CrossRef]
- ASTM C1400-11; Standard Guide for Reduction of Efflorescence Potential in New Masonry Walls. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM C67-02c; Standard Test Methods for Sampling and Testing Brick and Structural Clay Tile. ASTM International: West Conshohocken, PA, USA, 2002.
- Ada, M.; Sevim, B.; Yüzer, N.; Ayvaz, Y. Assessment of damages on a RC building after a big fire. Adv. Concr. Constr. 2018, 6, 177–197. [Google Scholar]
- Phares, B.M.; Washer, G.A.; Rolander, D.D.; Graybeal, B.A.; Moore, M. Routine highway bridge inspection condition documentation accuracy and reliability. J. Bridg. Eng. 2014, 9, 403–413. [Google Scholar] [CrossRef]
- Bianchini, A.; Bandini, P.; Smith, D.W. Interrater reliability of manual pavement distress evaluations. J. Transp. Eng. 2010, 136, 165–172. [Google Scholar] [CrossRef]
- Zhu, Z.; Brilakis, I. Parameter optimization for automated concrete detection in image data. Autom. Constr. 2010, 19, 944–953. [Google Scholar] [CrossRef]
- Cha, Y.J.; Chen, J.G.; Büyüköztürk, O. Output-only computer vision based damage detection using phase-based optical flow and unscented Kalman filters. Eng. Struct. 2017, 132, 300–313. [Google Scholar] [CrossRef]
- Chen, J.G.; Wadhwa, N.; Cha, Y.J.; Durand, F.; Freeman, W.T.; Buyukozturk, O. Modal identification of simple structures with high-speed video using motion magnification. J. Sound. Vib. 2015, 345, 58–71. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Büyüköztürk, O. Deep learning-based crack damage detection using convolutional neural networks. Comput. Civ. Infrastruct. Eng. 2017, 32, 361–378. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuen, K.V. Review of artificial intelligence-based bridge damage detection. Adv. Mech. Eng. 2022, 14, 16878132221122770. [Google Scholar] [CrossRef]
- Yoo, H.S.; Kim, Y.S. Development of a crack recognition algorithm from non-routed pavement images using artificial neural network and binary logistic regression. KSCE J. Civ. Eng. 2016, 20, 1151–1162. [Google Scholar] [CrossRef]
- Abdel-Qader, I.; Pashaie-Rad, S.; Abudayyeh, O.; Yehia, S. PCA-based algorithm for unsupervised bridge crack detection. Adv. Eng. Softw. 2006, 37, 771–778. [Google Scholar] [CrossRef]
- Lattanzi, D.; Miller, G.R. Robust automated concrete damage detection algorithms for field applications. J. Comput. Civ. Eng. 2014, 28, 253–262. [Google Scholar] [CrossRef]
- Choubey, R.K.; Kumar, S.; Rao, M.C. Effect of shear-span/depth ratio on cohesive crack and double-K fracture parameters of concrete. Adv. Concr. Constr. 2014, 2, 229–247. [Google Scholar] [CrossRef]
- Haeri, H.; Sarfarazi, V.; Zhu, Z.; Nejati, H.R. Numerical simulations of fracture shear test in anisotropy rocks with bedding layers. Adv. Concr. Constr. 2019, 7, 241–247. [Google Scholar]
- Ayinde, O.O.; Zuo, X.B.; Yin, G.J. Numerical analysis of concrete degradation due to chloride-induced. Adv. Concr. Constr. 2019, 7, 203–210. [Google Scholar]
- Zhang, B.; Cullen, M.; Kilpatrick, T. Spalling of heated high performance concrete due to thermal and hygric gradients. Adv. Concr. Constr. 2016, 4, 1–14. [Google Scholar] [CrossRef]
- Adhikari, R.S.; Moselhi, O.; Bagchi, A.; Rahmatian, A. Tracking of defects in reinforced concrete bridges using digital images. J. Comput. Civ. Eng. 2016, 30, 04016004. [Google Scholar] [CrossRef]
- Patange, A.D.; Jegadeeshwaran, R. A machine learning approach for vibration-based multipoint tool insert health prediction on vertical machining centre (VMC). Measurement 2021, 173, 108649. [Google Scholar] [CrossRef]
- German, S.; Brilakis, I.; Desroches, R. Rapid entropy-based detection and properties measurement of concrete spalling with machine vision for post-earthquake safety assessments. Adv. Eng. Inform. 2012, 26, 846–858. [Google Scholar] [CrossRef]
- Brilakis, I.; Fathi, H.; Rashidi, A. Progressive 3D reconstruction of infrastructure with videogrammetry. Autom. Constr. 2011, 20, 884–895. [Google Scholar] [CrossRef]
- Rashidi, A.; Sigari, M.H.; Maghiar, M.; Citrin, D. An analogy between various machine-learning technologys for detecting construction materials in digital images. KSCE J. Civ. Eng. 2016, 20, 1178–1188. [Google Scholar] [CrossRef]
- Radopoulou, S.C.; Brilakis, I. Automated detection of multiple pavement defects. J. Comput. Civ. Eng. 2017, 31. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, Y.; Zhang, D.; Xie, J.; Zhou, Y. Classification of surface defects on steel sheet using convolutional neural networks. Mater. Tehnol. 2017, 51, 123–131. [Google Scholar] [CrossRef]
- Halfawy, M.R.; Hengmeechai, J. Automated defect detection in sewer closed circuit television images using histograms of oriented gradients and support vector machine. Autom. Constr. 2014, 38, 1–13. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Pal, M.; Foody, G.M. Feature selection for classification of hyperspectral data by SVM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef]
- Ali, S.; Smith, K.A. On learning algorithm selection for classification. Appl. Soft Comput. J. 2006, 6, 119–138. [Google Scholar] [CrossRef]
- Kim, C.; Son, H.; Kim, C. Automated color model-based concrete detection in construction-site images by using machine learning algorithms. J. Comput. Civ. Eng. 2012, 26, 421–433. [Google Scholar]
- Chen, P.H.; Shen, H.K.; Lei, C.Y.; Chang, L.M. Support-vector-machine-based method for automated steel bridge rust assessment. Autom. Constr. 2012, 23, 9–19. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Batistella, M.; Moran, E. Comparison of land-cover classification methods in the Brazilian Amazon basin. Photogramm. Eng. Remote Sens. 2004, 6, 723–731. [Google Scholar] [CrossRef]
- Guo, L.; Chehata, N.; Mallet, C.; Boukir, S. Relevance of airborne lidar and multispectral image data for urban scene classification using Random Forests. ISPRS J. Photogramm. Remote Sens. 2011, 66, 56–66. [Google Scholar] [CrossRef]
- Alipour, M.; Harris, D.K.; Barnes, L.E.; Ozbulut, O.E.; Carroll, J. Load-capacity rating of bridge populations through machine learning: Application of decision trees and random forests. J. Bridg. Eng. 2017, 22, 04017076. [Google Scholar] [CrossRef]
- Assouline, D.; Mohajeri, N.; Scartezzini, J.L. Building rooftop classification using random forests for large-scale PV deployment. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications VIII, Warsaw, Poland, 5 October 2017; pp. 47–58. [Google Scholar]
- Harvey, R.R.; McBean, E.A. Predicting the structural condition of individual sanitary sewer pipes with random forests. Can. J. Civ. Eng. 2014, 41, 294–303. [Google Scholar] [CrossRef]
- Kim, C.; Son, H.; Hwang, N.; Kim, C.; Kim, C. Rapid and automated determination of rusted surface areas of a steel bridge for robotic maintenance systems. Autom. Constr. 2014, 42, 13–24. [Google Scholar]
- Yeh, I.C. Quantity estimating of building with logarithm-neuron networks. J. Const. Eng. Manag. 1998, 124, 374–380. [Google Scholar] [CrossRef]
- Tam, C.M.; Tong, K.L.; Lau, T.C.; Chan, K.K. Diagnosis of prestressed concrete pile defects using probabilistic neural networks. Eng. Struct. 2004, 26, 1155–1162. [Google Scholar] [CrossRef]
- Ruiz, C.C.; Caballero, J.L.; Martinez, J.H.; Aperador, W.A. Algorithms to measure carbonation depth in concrete structures sprayed with a phenolphthalein solution. Adv. Concr. Constr. 2020, 9, 257–265. [Google Scholar]
- Mathavan, S.; Rahman, M.; Kamal, K. Use of a self-organizing map for crack detection in highly textured pavement images. J. Infrastruct. Syst. 2015, 21, 04014052. [Google Scholar] [CrossRef]
- Ngwangwa, H.M.; Heyns, P.S.; Labuschagne, F.J.J.; Kululanga, G.K. Reconstruction of road defects and road roughness classification using vehicle responses with artificial neural networks simulation. J. Terramech. 2010, 47, 97–111. [Google Scholar] [CrossRef]
- Wu, L.; Mokhtari, S.; Nazef, A.; Nam, B.; Yun, H.B. Improvement of crack-detection accuracy using a novel crack defragmentation technology in image-based road assessment. J. Comput. Civ. Eng. 2019, 30, 04014118. [Google Scholar] [CrossRef]
- Bajaj, N.S.; Patange, A.D.; Jegadeeshwaran, R.; Kulkarni, K.A.; Ghatpande, R.S.; Kapadnis, A.M. A bayesian optimized discriminant analysis model for condition monitoring of face milling cutter using vibration datasets. J. Nondest. Eval. Diagn. Progn. Eng. Syst. 2022, 5, 021002. [Google Scholar] [CrossRef]
- Jatakar, K.H.; Mulgund, G.; Patange, A.D.; Deshmukh, B.B.; Rambhada, K.S. Multi-Point face milling tool condition monitoring through vibration spectrogram and LSTM-Autoencoder. Int. J. Perform. Eng. 2022, 18, 570–579. [Google Scholar] [CrossRef]
- Patil, S.S.; Pardeshi, S.S.; Pradhan, N.; Patange, A.D. Cutting tool condition monitoring using a deep learning-based artificial neural network. Int. J. Perform. Eng. 2022, 18, 37–46. [Google Scholar]
- Koch, C.; Georgieva, K.; Kasireddy, V.; Akinci, B.; Fieguth, P. A review on computer vision based defect detection and condition assessment of concrete and asphalt civil infrastructure. Adv. Eng. Inform. 2015, 29, 196–210. [Google Scholar] [CrossRef]
- Meijer, D.; Scholten, L.; Clemens, F.; Knobbe, A. A defect classification methodology for sewer image sets with convolutional neural networks. Autom. Constr. 2019, 104, 281–298. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Hoboken, NJ, USA, 2008. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Richards, J. Remote Sensing Digital Image Analysis; Springer: Berlin, Germany, 1999. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Castagno, J.; Atkins, E. Roof shape classification from LiDAR and satellite image data fusion using supervised learning. Sensors 2018, 18, 3960. [Google Scholar] [CrossRef]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Xiao, Y.; Feng, C.; Taguchi, Y.; Kamat, V.R. User-guided dimensional analysis of indoor building environments from single frames of RGB-D sensors. J. Comput. Civ. Eng. 2017, 31, 04017006. [Google Scholar] [CrossRef]
- Dawood, T.; Zhu, Z.; Zayed, T. Machine vision-based model for spalling detection and quantification in subway networks. Autom. Constr. 2017, 81, 149–160. [Google Scholar] [CrossRef]
- German, S.; Jeon, J.S.; Zhu, Z.; Bearman, C.; Brilakis, I.; DesRoches, R.; Lowes, L. Machine vision-enhanced postearthquake inspection. J. Comput. Civ. Eng. 2013, 27, 622–634. [Google Scholar] [CrossRef]
- Halfawy, M.R.; Hengmeechai, J. Integrated vision-based system for automated defect detection in sewer closed circuit television inspection videos. J. Comput. Civ. Eng. 2015, 29, 04014024. [Google Scholar] [CrossRef]
- Koch, C.; Jog, G.M.; Brilakis, I. Automated pothole distress assessment using asphalt pavement video data. J. Comput. Civ. Eng. 2013, 27, 370–378. [Google Scholar] [CrossRef]
- Hüthwohl, P.; Lu, R.; Brilakis, I. Multi-classifier for reinforced concrete bridge defects. Autom. Constr. 2019, 105, 102824. [Google Scholar] [CrossRef]
- Hüthwohl, P.; Brilakis, I. Detecting healthy concrete surfaces. Adv. Eng. Inform. 2018, 37, 150–162. [Google Scholar] [CrossRef]
- Kohavi, R.; Provost, F. Glossary of terms. Mach. Learn. 1998, 30, 271–274. [Google Scholar]
- Van Rijsbergen, C.J. Information Retrieval; Butterworths: London, UK, 1979. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Ben-David, A. Comparison of classification accuracy using Cohen’s weighted Kappa. Expert. Syst. Appl. 2008, 34, 825–832. [Google Scholar] [CrossRef]
- Foody, G.M. Thematic map comparison: Evaluating the statistical significance of differences in classification accuracy. Photogramm. Eng. Remote Sens. 2004, 5, 627–633. [Google Scholar] [CrossRef]
- Smits, P.C.; Dellepiane, S.G.; Schowengerdt, R.A. Quality assessment of image classification algorithms for land-cover mapping: A review and a proposal for a cost-based approach. Int. J. Remote Sens. 1999, 20, 1461–1486. [Google Scholar] [CrossRef]
- Fung, T.; Ledrew, E. The determination of optimal threshold levels for change detection using various accuracy indices. Photogramm. Eng. Remote Sens. 1988, 54, 1449–1454. [Google Scholar]
- Vetrivel, A.; Gerke, M.; Kerle, N.; Vosselman, G. Identification of structurally damaged areas in airborne oblique images using a Visual-Bag-of-Words approach. Remote Sens. 2016, 8, 231. [Google Scholar] [CrossRef]
- Kim, D.; Kim, D.H.; Chang, S.; Lee, J.J.; Lee, D.H. Stability number prediction for breakwater armor blocks using support vector regression. KSCE J. Civ. Eng. 2011, 15, 225–230. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness & correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Gui, G.; Pan, H.; Lin, Z.; Li, Y.; Yuan, Z. Data-driven support vector machine with optimization techniques for structural health monitoring and damage detection. KSCE J. Civ. Eng. 2017, 21, 523–534. [Google Scholar] [CrossRef]
- Kakumanu, P.; Makrogiannis, S.; Bourbakis, N. A survey of skin-color modeling and detection methods. Pattern Recognit. 2007, 40, 1106–1122. [Google Scholar] [CrossRef]
- Li, S.; Zhao, X.; Zhou, G. Automatic pixel-level multiple damage detection of concrete structure using fully convolutional network. Comput. Civ. Infrastruct. Eng. 2019, 34, 616–634. [Google Scholar] [CrossRef]
- Crespo, C.; Armesto, J.; González-Aguilera, D.; Arias, P. Damage detection on historical buildings using unsupervised classification techniques. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 184–188. [Google Scholar]
- Bouzan, G.B.; Fazzioni, P.F.; Faisca, R.G.; Soares, C.A. Building facade inspection: A system based on automated data acquisition, machine learning, and deep learning image classification methods. ARPN J. Eng. Appl. Sci. 2021, 16, 1516. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).