Application of Aboodh Homotopy Perturbation Transform Method for Fractional-Order Convection–Reaction–Diffusion Equation within Caputo and Atangana–Baleanu Operators
Abstract
1. Introduction
2. Basic Definitions
3. General Implementations of the AHPTM
4. Numerical Examples
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rashid, S.; Kubra, K.T.; Sultana, S.; Agarwal, P.; Osman, M.S. An approximate analytical view of physical and biological models in the setting of Caputo operator via Elzaki transform decomposition method. J. Comput. Appl. Math. 2022, 413, 114378. [Google Scholar] [CrossRef]
- Shi, L.; Tayebi, S.; Arqub, O.A.; Osman, M.S.; Agarwal, P.; Mahamoud, W.; Abdel-Aty, M.; Alhodaly, M. The novel cubic B-spline method for fractional Painleve and Bagley-Trovik equations in the Caputo, Caputo-Fabrizio, and conformable fractional sense. Alex. Eng. J. 2023, 65, 413–426. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Khalid, A.; Inc, M.; Rehan, A.; Nisar, K.S.; Osman, M.S. Cubic spline solutions of the ninth order linear and non-linear boundary value problems. Alex. Eng. J. 2022, 61, 11635–11649. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional calculus. In Fractals and Fractional Calculus in Continuum Mechanics; Springer: Vienna, Austria, 1997; pp. 223–276. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Ross, B. A brief history and exposition of the fundamental theory of fractional calculus. In Fractional Calculus and Its Applications; Springer: Berlin/Heidelberg, Germany, 1975; pp. 1–36. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Geophysics 1967, 31, 827–839. [Google Scholar]
- Caputo, M. Elasticita e dissipazione. Ann. Di Mat. Pura Ed Appl. 1969, 91, 191–213. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar]
- Wang, Q.A.; Zhang, Y. Fractional Schrodinger equation and its applications. Phys. Rep. 2017, 690, 1–83. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. Caputo-Fabrizio derivative applied to groundwater flow within confined aquifer. J. Eng. Mech. 2017, 143, D4016005. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Nieto, J.J. Analysis of an El nino-southern oscillation model with a new fractional derivative. Chaos Solitons Fractals 2017, 99, 109–115. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani Rubayyi, T. Numerical approximation of the space-time Caputo-Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 2016, 156. [Google Scholar] [CrossRef]
- Atangana, A. Non-validity of index law in fractional calculus: A fractional differential operator with Markovian and non-Markovian properties. Phys. A 2018, 505, 688–706. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and nonsingular kernel theory and application to heat transfer model. Therm. Sci. 2016, 18, 763–769. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastva, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematical Studies; Elsevier Publications: Amsterdam, The Netherlands, 2006; p. 204. [Google Scholar]
- Gomez-Aguilar, J.F.; Escobar-Jimenez, R.F.; Lopez-Lopez, M.G.; Alvarado-Martinez, V.M. Atangana-Baleanu fractional derivative applied to electromagnetic waves in dielectric media. J. Electromagn. Waves Appl. 2016, 30, 1937–1952. [Google Scholar] [CrossRef]
- Alkatahni, B.S.T. Chua’s circuit model with Atangana-Baleanu derivative with fractional order. Chaos Solitons Fractals 2016, 89, 547–551. [Google Scholar]
- Owolabi, K.M. Modelling and simulation of a dynamical system with the Atangana-Baleanu fractional derivative. Eur. Phys. J. Plus 2018, 133, 15. [Google Scholar]
- Sultana, M.; Arshad, U.; Ali, A.H.; Bazighifan, O.; Al-Moneef, A.A.; Nonlaopon, K. New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations. Symmetry 2022, 14, 1653. [Google Scholar] [CrossRef]
- Awuya, M.A.; Subasi, D. Aboodh transform iterative method for solving fractional partial differential equation with Mittag-Leffler Kernel. Symmetry 2021, 13, 2055. [Google Scholar]
- Shah, R.; Khan, H.; Baleanu, D. Fractional Whitham-Broer-Kaup equations within modified analytical approaches. Axioms 2019, 8, 125. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Khan, A. A comparative analysis of fractional-order kaup-kupershmidt equation within different operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Morton, K.W. Numerical Solution of Convection-Diffusion Problems; Chapman and Hall: London, UK, 1996. [Google Scholar]
- Makungu, M.; Haario, H.; Mahera, W.C. A generalised 1-dimensional particle transport method for convection diffusion reaction. Afrika Matematika 2012, 23, 21–39. [Google Scholar]
- Wang, Y.M. A modified accelerated monotone iterative method for finite difference reaction-diffusion-convection equations. J. Comput. Appl. Math. 2011, 235, 3646–3660. [Google Scholar]
- Harten, A.; Enquist, B.; Osher, S.; Chakravarthy, S. Uniformly high order essentially non-oscillatory schemes III. J. Comput. Phys. 1987, 71, 231–303. [Google Scholar] [CrossRef]
- Liu, X.D.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar]
- John, V.; Novo, J. On (essentially) non-oscillatory discretizations of evolutionary convection-diffusion equations. J. Comput. Phys. 2012, 231, 1570–1586. [Google Scholar] [CrossRef]
- Kailash, P.C. On the use of nonstandard finite difference methods. J. Differ. Equ. Appl. 2005, 11, 735–758. [Google Scholar]
- Kojouharov, H.V.; Chen, B.M. Nonstandard Methods for the Convective-Dispersive Transport Equation with Nonlinear Reactions; John Wiley and Sons: Hoboken, NJ, USA, 1999; pp. 617–624. [Google Scholar]
- Kaya, A. Finite difference approximations of multidimensional unsteady convection-diffusion-reaction equations. J. Comput. Phys. 2015, 285, 331–349. [Google Scholar]
- Kaya, A. A finite difference scheme for multidimensional convection-diffusionreaction equations. Comput. Meth. Appl. Mech. Eng. 2014, 278, 347–360. [Google Scholar]
- Brooks, A.N.; Hughes, T.J.R. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Meth. Appl. Mech. Eng. 1982, 32, 199–259. [Google Scholar] [CrossRef]
- Bause, M. Stabilized finite element methods with shock-capturing for nonlinear convection-diffusion-reaction models. In Numerical Mathematics and Advanced Applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 125–134. [Google Scholar]
- Yucel, H.; Stoll, M.; Benner, P. Discontinuous Galerkin finite element methods with shock-capturing for nonlinear convection dominated models. Comput. Chem. Eng. 2013, 58, 278–287. [Google Scholar]
- Uzunca, M.; Karasozen, B.; Manguoglu, M. Adaptive discontinuous Galerkin methods for non-linear diffusion-convection-reaction equations. Comput. Chem. Eng. 2014, 68, 24–37. [Google Scholar]
- Wang, Y.M.; Ren, L. Efficient compact finite difference methods for a class of time-fractional convection-reaction-diffusion equations with variable coefficients. Int. J. Comput. Math. 2019, 96, 264–297. [Google Scholar]

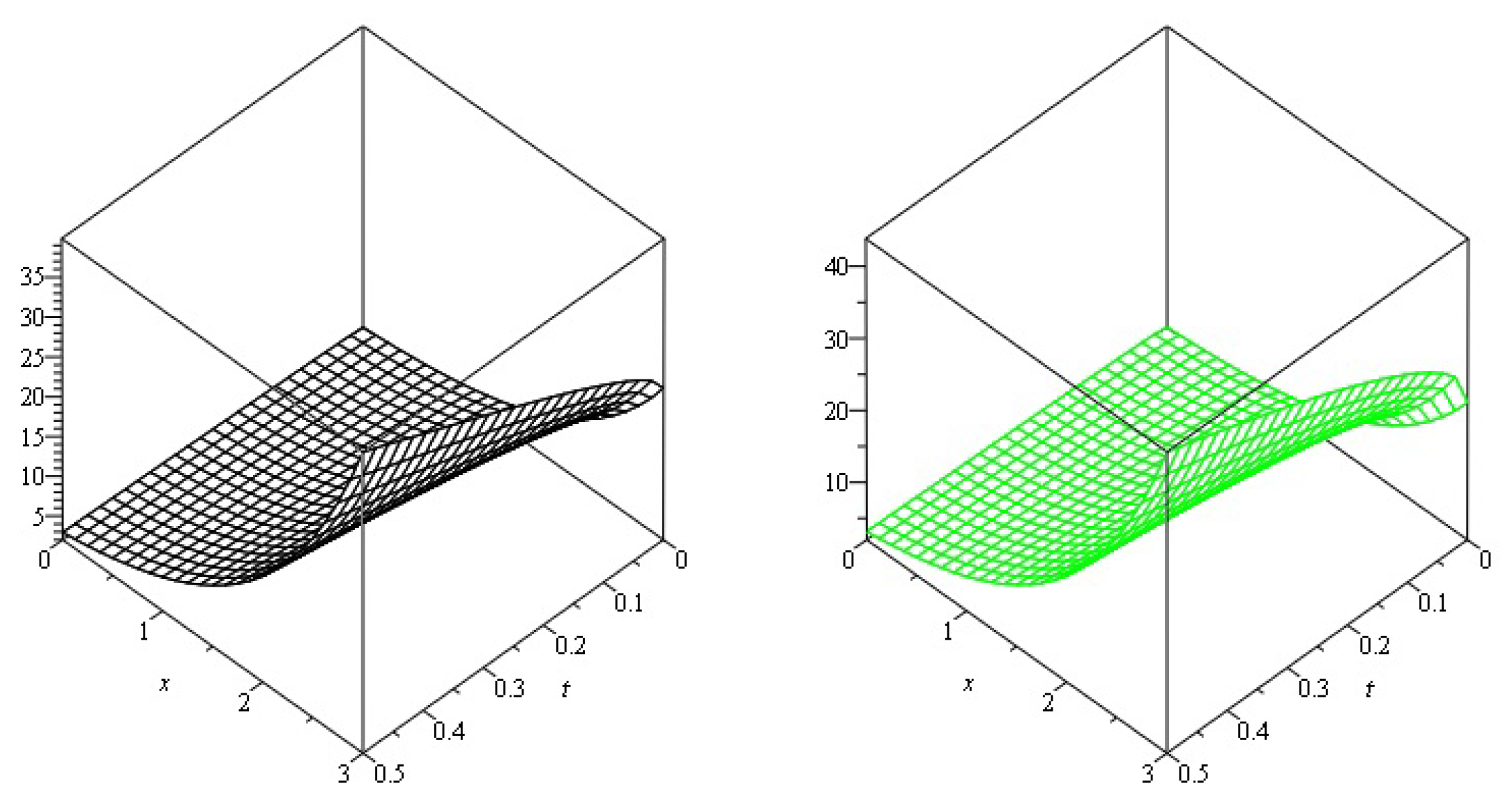
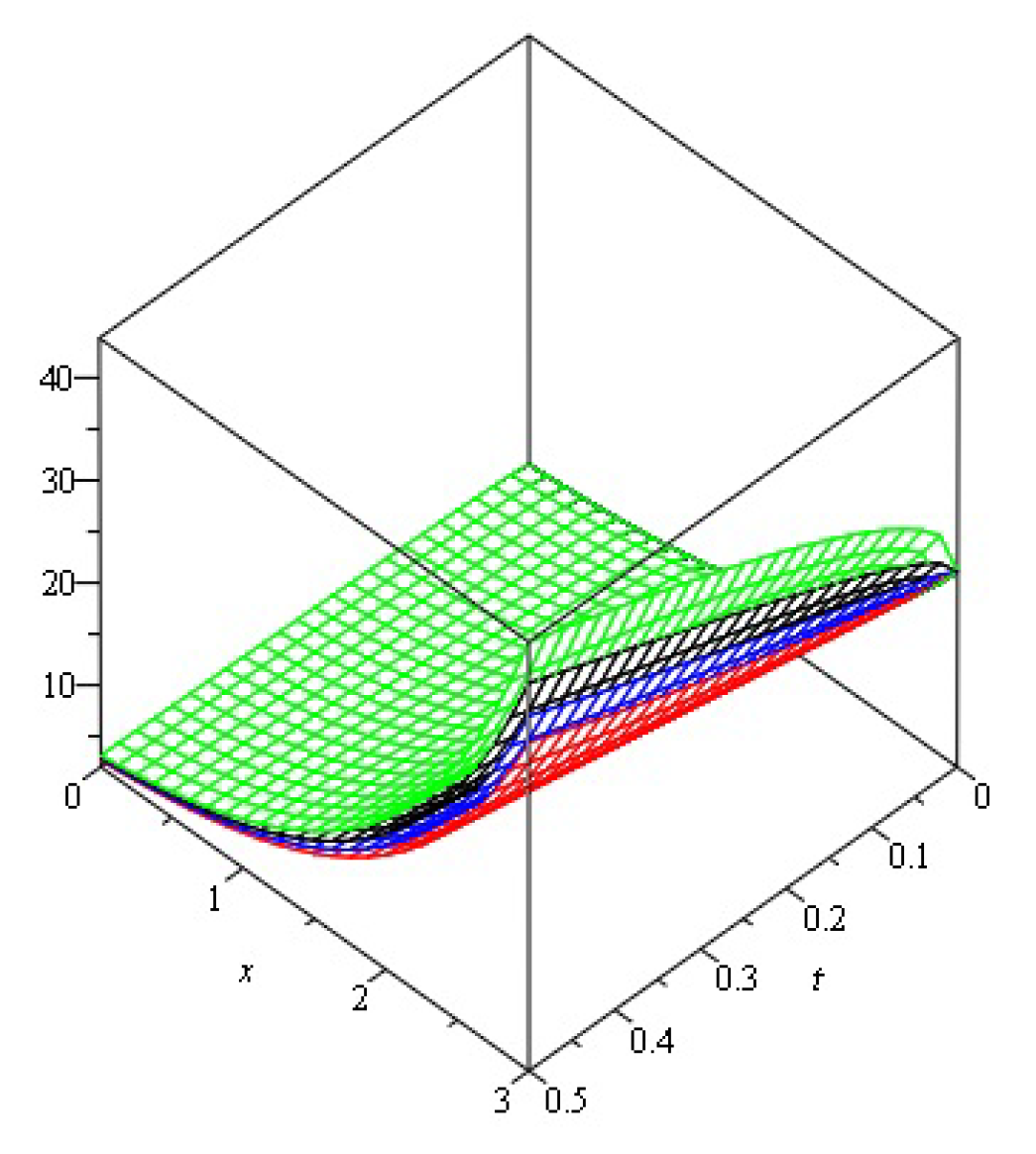

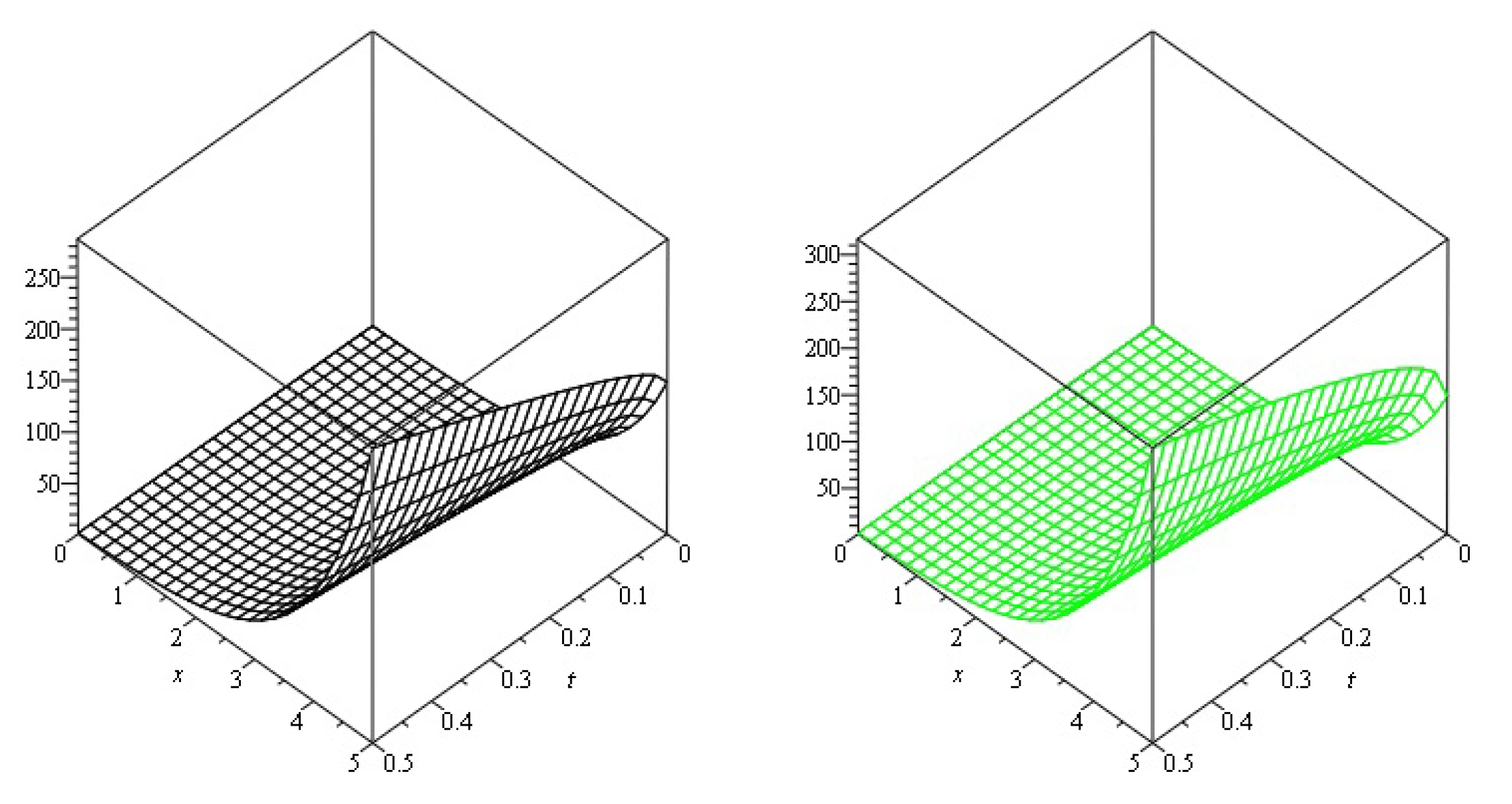
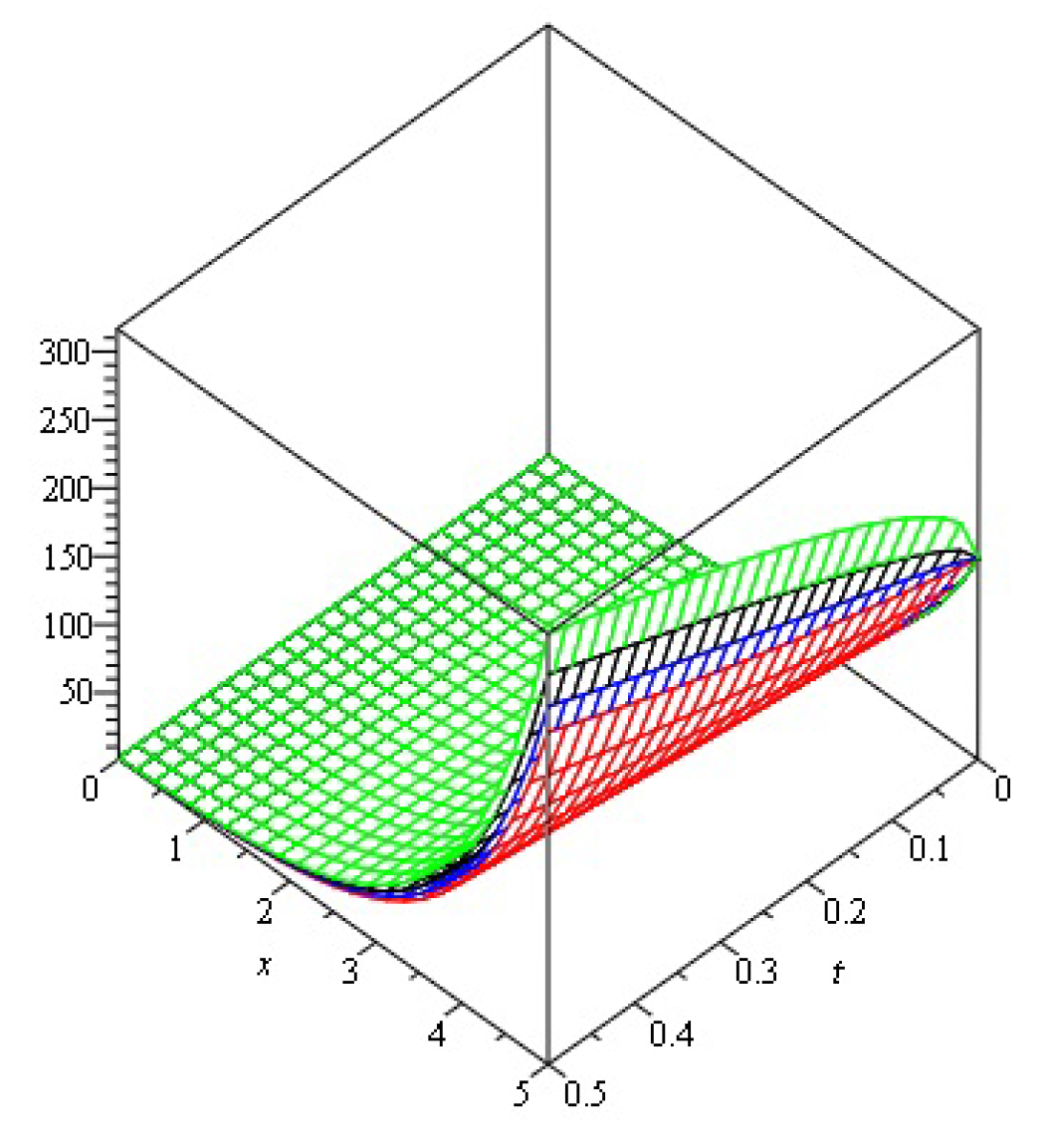
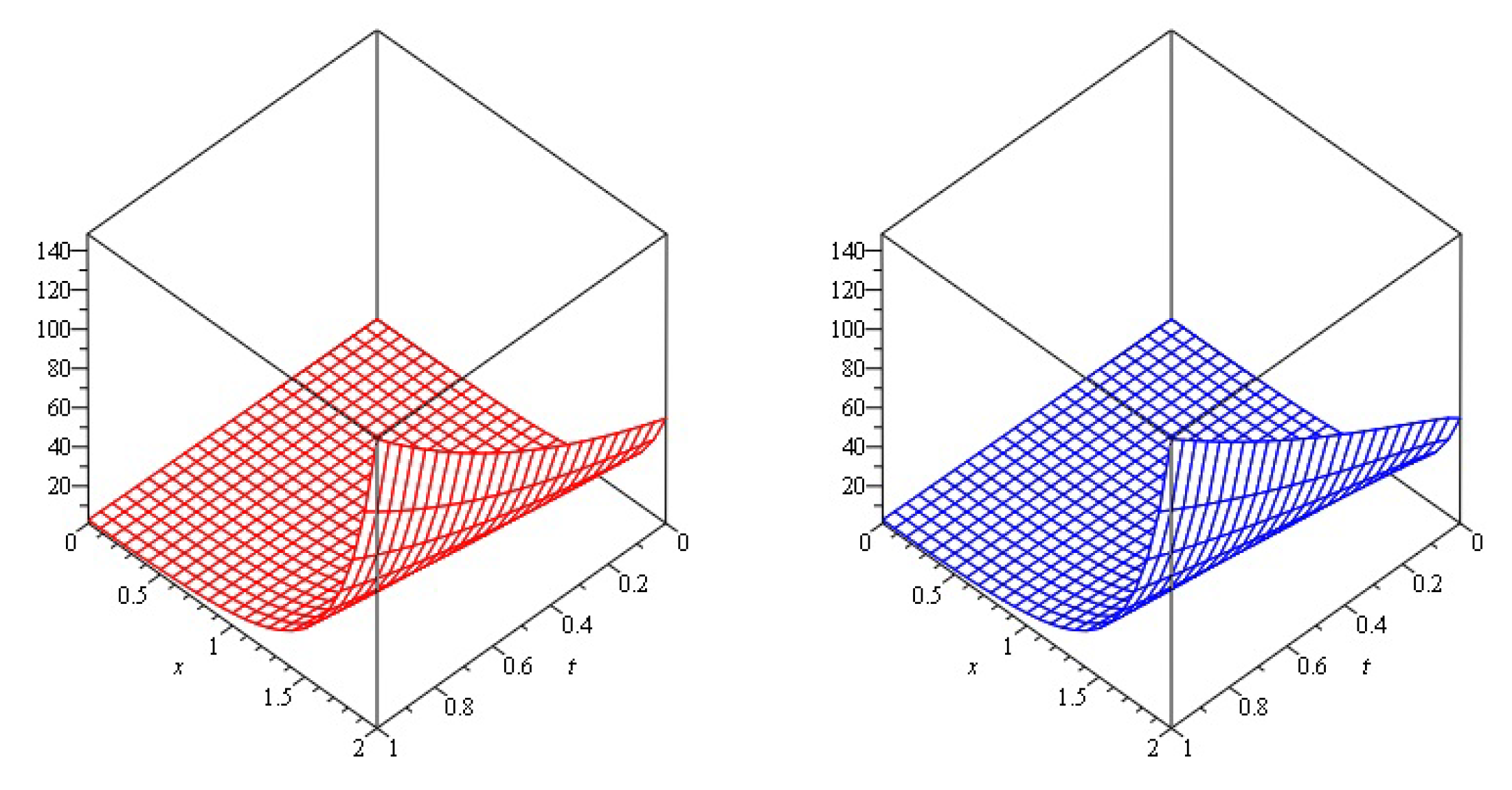
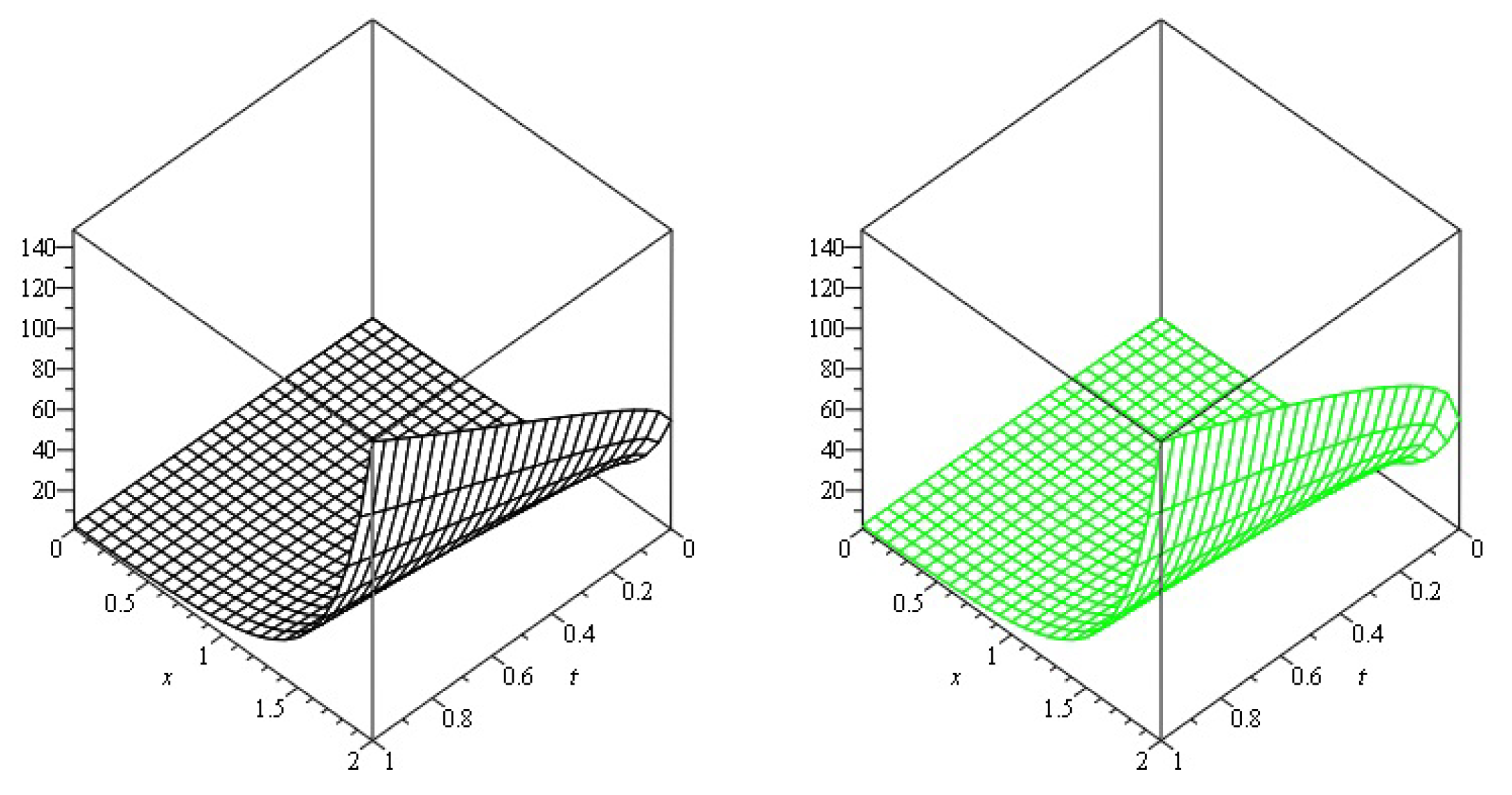

| 0.2 | 6.675299 | 4.333865 | 2.332431 | 9.89 | 9.89 | |
| 0.4 | 7.386577 | 4.894717 | 2.942858 | 1.001 | 1.001 | |
| 0.1 | 0.6 | 8.387471 | 5.465313 | 2.733155 | 9.89 | 9.89 |
| 0.8 | 9.767755 | 6.542168 | 3.336582 | 1 | 1 | |
| 1 | 1.1345997 | 7.347663 | 3.179329 | 9.88 | 9.88 | |
| 0.2 | 6.556379 | 4.334919 | 2.333458 | 2 | 2 | |
| 0.4 | 7.747667 | 4.895777 | 2.383888 | 2 | 2 | |
| 0.2 | 0.6 | 8.648573 | 5.536381 | 2.734189 | 1.888 | 1.888 |
| 0.8 | 9.76887 | 6.543245 | 3.337621 | 1.888 | 1.888 | |
| 1 | 1.2257131 | 7.348753 | 3.810374 | 2 | 2 | |
| 0.2 | 6.557455 | 4.33597 | 2.332285 | 3 | 3 | |
| 0.4 | 7.748751 | 4.896834 | 2.944917 | 3 | 3 | |
| 0.3 | 0.6 | 8.649669 | 5.467446 | 2.285223 | 2.888 | 2.888 |
| 0.8 | 9.76998 | 6.54432 | 3.33866 | 3 | 3 | |
| 1 | 1.2258258 | 7.349839 | 3.271419 | 3 | 3 | |
| 0.2 | 6.55853 | 4.337018 | 2.335509 | 4 | 4 | |
| 0.4 | 7.749836 | 4.897889 | 2.945945 | 4 | 4 | |
| 0.4 | 0.6 | 8.740765 | 5.468508 | 2.286254 | 3.888 | 3.888 |
| 0.8 | 9.86109 | 6.545391 | 3.339695 | 3.888 | 3.888 | |
| 1 | 1.2259384 | 7.33092 | 3.272459 | 3.888 | 3.888 | |
| 0.2 | 6.559601 | 4.338068 | 2.336532 | 5 | 5 | |
| 0.4 | 7.840915 | 4.898944 | 2.946969 | 5 | 5 | |
| 0.5 | 0.6 | 8.741856 | 5.46957 | 2.287282 | 5 | 5 |
| 0.8 | 9.862193 | 6.546462 | 3.320728 | 5 | 5 | |
| 1 | 1.2260503 | 7.332002 | 3.273497 | 4.888 | 4.888 |
| 0.2 | 3.557405 | 2.334925 | 1.333455 | 7 | 7 | |
| 0.4 | 4.74938 | 2.896239 | 1.382111 | 8 | 8 | |
| 0.1 | 0.6 | 5.741127 | 3.467401 | 1.723689 | 9 | 9 |
| 0.8 | 6.862448 | 4.544945 | 2.116459 | 1.1 | 1.1 | |
| 1 | 8.611962 | 5.331282 | 2.620625 | 1.3 | 1.3 | |
| 0.2 | 3.760071 | 2.335691 | 1.335325 | 2.3 | 2.3 | |
| 0.4 | 3.760071 | 2.897396 | 1.384174 | 2.8 | 2.8 | |
| 0.2 | 0.6 | 5.325102 | 13.560033 | 1.732986 | 3.6 | 3.6 |
| 0.8 | 6.575305 | 4.658161 | 2.338044 | 4.4 | 4.4 | |
| 1 | 8.355893 | 5.33521 | 2.63356 | 5.4 | 5.4 | |
| 0.2 | 3.762527 | 2.338313 | 1.334119 | 5.3 | 5.3 | |
| 0.4 | 4.855635 | 2.880377 | 1.835143 | 6.8 | 6.8 | |
| 0.3 | 0.6 | 5.748766 | 3.562453 | 1.726171 | 8.3 | 8.3 |
| 0.8 | 6.98178 | 4.641116 | 2.12049 | 1.01 | 1.01 | |
| 1 | 8.17336 | 5.44882 | 2.264327 | 1.33 | 1.33 | |
| 0.2 | 3.764844 | 2.339838 | 1.334858 | 9.7 | 9.7 | |
| 0.4 | 4.848465 | 2.88224 | 1.946045 | 1.28 | 1.28 | |
| 0.4 | 0.6 | 5.842223 | 3.564729 | 1.287273 | 1.35 | 1.35 |
| 0.8 | 6.966002 | 4.643896 | 2.321836 | 1.68 | 1.68 | |
| 1 | 8.718515 | 5.542215 | 2.275971 | 2.36 | 2.36 | |
| 0.2 | 3.767056 | 2.451291 | 1.225554 | 1.35 | 1.35 | |
| 0.4 | 4.941167 | 2.994014 | 1.496896 | 1.75 | 1.75 | |
| 0.5 | 0.6 | 5.845522 | 3.656895 | 1.828311 | 2.38 | 2.38 |
| 0.8 | 6.600033 | 4.466542 | 2.233105 | 2.87 | 2.87 | |
| 1 | 8.813439 | 5.545447 | 2.727521 | 3.3 | 3.3 |
| 0.2 | 3.215157 | 2.038429 | 1.014708 | 5 | 5 | |
| 0.4 | 3.253605 | 2.439059 | 1.147522 | 6 | 6 | |
| 0.1 | 0.6 | 4.293741 | 2.689147 | 1.423565 | 7 | 7 |
| 0.8 | 5.964407 | 3.976254 | 1.889115 | 1 | 1 | |
| 1 | 8.611962 | 5.331282 | 2.719625 | 1.3 | 1.3 | |
| 0.2 | 3.172428 | 2.072932 | 1.034449 | 2.1 | 2.1 | |
| 0.4 | 3.562165 | 2.240754 | 1.715358 | 2.4 | 2.4 | |
| 0.2 | 0.6 | 4.315869 | 2.681219 | 1.345586 | 2.8 | 2.8 |
| 0.8 | 5.968546 | 3.978995 | 1.989466 | 3.8 | 3.8 | |
| 1 | 8.176893 | 5.33521 | 2.27256 | 5.5 | 5.5 | |
| 0.2 | 3.139521 | 2.076315 | 1.034126 | 4.6 | 4.6 | |
| 0.4 | 3.258525 | 2.532313 | 1.167121 | 5.2 | 5.2 | |
| 0.3 | 0.6 | 4.299751 | 2.943122 | 1.463517 | 6.3 | 6.3 |
| 0.8 | 5.692359 | 3.791513 | 1.901598 | 8.5 | 8.5 | |
| 1 | 8.71336 | 5.33882 | 2.742327 | 1.33 | 1.33 | |
| 0.2 | 3.113495 | 2.078614 | 1.034755 | 8.3 | 8.3 | |
| 0.4 | 3.503752 | 2.335779 | 1.167831 | 9.3 | 9.3 | |
| 0.4 | 0.6 | 4.32147 | 2.847912 | 1.473385 | 1.41 | 1.41 |
| 0.8 | 5.750957 | 3.830882 | 1.910846 | 1.25 | 1.25 | |
| 1 | 8.175715 | 5.425215 | 2.752971 | 2.81 | 2.81 | |
| 0.2 | 3.12238 | 2.087752 | 1.03348 | 1.31 | 1.31 | |
| 0.4 | 3.523877 | 2.351574 | 1.1665 | 1.74 | 1.74 | |
| 0.5 | 0.6 | 4.351066 | 2.875517 | 1.483202 | 1.87 | 1.87 |
| 0.8 | 5.790391 | 3.860136 | 1.920927 | 2.29 | 2.29 | |
| 1 | 8.138439 | 5.433447 | 2.727521 | 3.3 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasmin, H. Application of Aboodh Homotopy Perturbation Transform Method for Fractional-Order Convection–Reaction–Diffusion Equation within Caputo and Atangana–Baleanu Operators. Symmetry 2023, 15, 453. https://doi.org/10.3390/sym15020453
Yasmin H. Application of Aboodh Homotopy Perturbation Transform Method for Fractional-Order Convection–Reaction–Diffusion Equation within Caputo and Atangana–Baleanu Operators. Symmetry. 2023; 15(2):453. https://doi.org/10.3390/sym15020453
Chicago/Turabian StyleYasmin, Humaira. 2023. "Application of Aboodh Homotopy Perturbation Transform Method for Fractional-Order Convection–Reaction–Diffusion Equation within Caputo and Atangana–Baleanu Operators" Symmetry 15, no. 2: 453. https://doi.org/10.3390/sym15020453
APA StyleYasmin, H. (2023). Application of Aboodh Homotopy Perturbation Transform Method for Fractional-Order Convection–Reaction–Diffusion Equation within Caputo and Atangana–Baleanu Operators. Symmetry, 15(2), 453. https://doi.org/10.3390/sym15020453









