Containment Control Problem of Linear Multiagent Systems with External Disturbance and DoS Attacks

Abstract

This work investigates the containment control for linear multiagent systems. We assume that the systems are subject to periodic energy-limited denial-of-service (DoS) attacks, which prevent agent-to-agent data transmission. It is assumed that the DoS attacks occur periodically based on the time sequence method. It is also assumed that some devices can be used to predict the duration of DoS attacks and uniform lower bound of communication areas. To achieve containment control, state and disturbance estimators are proposed for each following agent to estimate the relative state information. Under suitable conditions, the containment control problem can be solved with the designed controllers and observers. Finally, we provide a simulation result to confirm the theoretical analysis.

1. Introduction

In recent years, the challenge of coordinated control for multiagent systems has attracted significant research attention due to its several potential applications in spacecraft formation flying, sensor networks, cooperative surveillance, etc. As one of the many cooperation issues, consensus has received wide attention in the past decades. Current research on consensus can be roughly divided into two types, i.e., consensus without a leader [1,2] and consensus with one or multiple leaders. For a single leader case, the followers eventually converge to the state of the leader, a phenomenon called consensus tracking or leader-following consensus problem [3,4,5]. However, for multiple leaders, the followers eventually converge to a convex hull spanned by the leaders, called the containment control problem [6,7,8]. In [6], based on the output of adjacent agents, a distributed dynamic output feedback controller was developed to address the challenge of distributed containment control and provided a necessary and sufficient condition, which was only related to the spectral properties of the topology matrix. The problem of containment control laws was solved for both continuous-time and discrete-time cases in [7]. Considering the unknown leaders, two distributed control protocols based on state feedback and dynamic output feedback were locally designed, and the challenge of adaptive containment control for MASs was solved in [8].

Due to external disturbances, the consensus disturbance rejection problem has attracted substantial attention. In [9], two distributed protocols were designed for a Lipschitz multiagent system, i.e., one was to attain global consensus without external disturbances, whereas the other was to reach consensus with a guaranteed $H\infty$ performance. Considering the input delays and disturbances of the system, a controller based on a predictor and disturbance observer was designed for each follower [10]. Consensus could be achieved and all signals in the closed-loop dynamics were eventually and uniformly bounded with the designed distributed protocol. Wang analyzed the consensus disturbance rejection problem for multiple-input multiple-output (MIMO) linear MASs in [5], and consensus was achieved and the external disturbance was suppressed with suitable control parameters and a large average dwell time.

System security is an intriguing and important issue. Network security issues have been broadly studied over the past decade [11,12]. When a multiagent system is attacked, data exchange among agents is interrupted or destroyed, resulting in the instability of the entire system [13,14,15,16]. Generally, two types of attacks exist in a multiagent system, i.e., one is to attack the dynamic behavior (or closed-loop dynamics) of the agents, whereas the other is to attack the communication among the agents. Any attack will seriously influence the consensus properties of the whole system. The second case includes denial-of-service (DoS) attacks as in [13,14,15]. Considering channel interference by an energy-constrained attacker, optimal DoS attack schedules were constructed in [13] to maximize the expected average estimation error. To minimize unnecessary network traffic, Zha et al. proposed a distributed event-triggered secure consensus control for multiagent systems (MASs) subject to DoS attacks [14]. A secure consensus comprising two different measurements was proposed in [15]. The formation control problem for nonlinear multiagent systems (MASs) under DoS attacks was emphatically studied in [16], and the distributed hybrid event-triggering strategies (HETSs) could be applied to preserve formation control.

With this background, we explore the challenge of containment control for the multiagent system with external disturbances and DoS attacks. The contributions of this paper are summarized as follows: (1) The containment control problem of linear MASs with an external perturbation is considered, unlike [5], which only analyzed consensus tracking problems for linear MASs with deterministic disturbances. (2) Three observers are designed to solve the containment control problem, unlike [5,17], which assessed the consensus challenge in a secure network environment. This paper suggests that data exchange among agents is interrupted due to DoS attacks. Data interruption among agents affects the connectivity of the entire network. Therefore, the convergence of the system cannot be guaranteed. Therefore, we provide a summary based on [5] to expand its scope of application.

The subsequent sections are organized as follows. Section 2 introduces the relevant graph theory and the preliminary work. In Section 3, a containment control protocol based on three different observers, with or without attacks is proposed. Simulation examples are provided for the efficacy of the protocol in Section 4. Section 5 presents the conclusions and our future work.

2. Preliminaries and Problem Statement

Notations and Preliminary Results

The notations used in this paper are standard. R and C represent the real number set and complex number set, respectively. $R^{m\times n}$ is the set of $m\times n$ real matrices. I represents an identity matrix with a compatible dimension. ${}^T\left(o{r}^H\right)$ denotes transpose (conjugate transpose). $diag\left(g_1,g_2,\dots ,g_n\right)$ represents a diagonal matrix with diagonal elements $g_i(i=1,2,\dots ,n)$. Provided that the matrix A has n real eigenvalues, the largest and smallest eigenvalues are denoted by ${\lambda }_{max}\left(A\right)$ and ${\lambda }_{min}\left(A\right)$, respectively. For symmetric matrices A and B, $A>(\ge )B$ means that $A-B$ is positive (semi-)definite. The $n\times m$-dimensional zero matrix is denoted by $0_{n\times m}$. $\parallel •\parallel$ denotes the Euclidean norm, and ⊗ denotes the Kronecker product.

For the multiagent systems, a weighted graph $\mathcal{G}=\{\mathcal{V},\epsilon ,\mathcal{A}\}$ can be used to represent the interaction relationships among $N+M$ agents, where $\mathcal{V}=\{1,2,\cdots ,N+M\}$ is a node set, $\epsilon \subset \mathcal{V}\times \mathcal{V}$ represents an edge set, and an adjacency matrix is $\mathcal{A}=\left[a_{ij}\right]\in R^{(N+M)\times (N+M)}$. We assume that agents 1 to N and agents $N+1$ to $N+M$ are followers and leaders, respectively, and each follower has at least one neighbor, but the leaders have no neighbors. Of note, $(i,j)\in \epsilon$ indicates that agent j can obtain the information from agent i. The elements in $\mathcal{A}$ are non-negative, i.e., $a_{ij}>0$ if and only if $(i,j)\in \epsilon$ and $a_{ij}=0$ otherwise. At the same time, self-loops do not exist, i.e., $a_{ii}=0,\forall i\in \mathcal{V}$. A directed path from agent i to agent j is a sequence of edges of the form $(v_i,v_p),(v_p,v_q),\dots ,(v_r,v_j)$. Here, $\mathcal{D}=diag(d_1,d_2,\cdots ,d_{N+M})$ denotes a degree matrix, where $d_i={\displaystyle \sum _{j=1}^{N+M}}{a}_{ij}$. Then, the Laplacian matrix of graph $\mathcal{G}$ is defined as

$$L=\left[\begin{array}{cc}{L}_1& L_2\\ {\mathbf{0}}_{M\times N}& {\mathbf{0}}_{M\times M}\end{array}\right]$$

where $L_1\in {\mathbf{R}}^{N\times N}$ and $L_2\in {\mathbf{R}}^{N\times M}$.

Assumption 1.

For each follower, there is at least one leader that gives a directed path to the follower.

Lemma 1

([18]). If Assumption 1 holds, then all the eigenvalues of $L_1$ have positive real parts, each entry of $-L_1^{-1}{L}_2$ is nonnegative, and the sum of elements in each row of $-L_1^{-1}{L}_2$ is equal to one. Moreover, there exists a diagonal matrix $\varphi =diag({\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_N)$ with ${\varphi }_i>0,i=1,2,\cdots ,N$ such that $\varphi L_1+L_1^T\varphi >0_N$, where $L_1^T\varphi ={\mathbf{1}}_N$.

Obviously, there is $\varphi (L_1+{\varphi }^{-1}{L}_1^T\varphi )>0$ from the above Lemma 1 that is $\Omega =L_1+{\varphi }^{-1}{L}_1^T\varphi >0$. Then, there exists an orthogonal matrix $\overline{U}$, such that ${\overline{U}}^T\Omega \overline{U}=diag({\rho }_1,{\rho }_2,\cdots ,{\rho }_N)$. Therefore, we can let ${\rho }_0=min\{{\rho }_1,{\rho }_2,\cdots ,{\rho }_N\}$, and clearly, ${\rho }_0>0$.

Definition 1

([18]). A set $C\subseteq {\mathcal{R}}^N$ is convex if $(1-\lambda )x+\lambda y\in C$, for any $x,y\in C$, and any $\lambda \in [0,1]$. For a finite set of points $X=\{x_1,\dots ,x_q\}$, it the convex hull is defined as $Co\left(X\right)=\left\{{\displaystyle \sum _{i=1}^q}{a}_i{x}_i\right|x_i\in X,a_i\in {\mathcal{R}}^N,a_i\ge 0,{\displaystyle \sum _{i=1}^q}{a}_i=1\}$.

Herein, we consider multiagent systems comprising N followers and M leaders. Let $\mathcal{F}=\{1,2,\cdots ,N\}$ be the set of followers and $\mathcal{L}=\{N+1,N+2,\cdots ,N+M\}$ be the set of leaders. Here, all followers are assumed homogeneous, and their dynamics are given by

$$\begin{array}{c}{\dot{x}}_i\left(t\right)=A{x}_i+B{u}_i\left(t\right)+D{d}_i\left(t\right),\hfill \\ y_i\left(t\right)=C{x}_i\left(t\right),i\in \mathcal{F}.\hfill \end{array}$$

(1)

and the dynamics of the leaders are described by

$$\begin{array}{c}{\dot{x}}_i\left(t\right)=A{x}_i\left(t\right),\hfill \\ y_i\left(t\right)=C{x}_i\left(t\right),i\in \mathcal{L}\hfill \end{array}$$

(2)

where $x_i\left(t\right)\in {\mathbf{R}}^n$ is the agent i’s state, $u_i\left(t\right)\in {\mathbf{R}}^p$ is the agent i’s control input and $y_i\left(t\right)\in {\mathbf{R}}^q$ is the agent i’s measured output. A, B, C, and D are system matrices with appropriate dimensions. $d_i\left(t\right)\in {\mathbf{R}}^r$ is the external disturbance, generated by a linear exogenous system with the form

$${\dot{d}}_i\left(t\right)=S{d}_i\left(t\right),i\in \mathcal{F}.$$

(3)

where S is a constant matrix.

Then, we address the containment control problem of multiagent systems (1) and (2), which are defined as follows.

Definition 2.

For multiagent systems (1) and (2), containment control is achieved if the state of all followers asymptotically converges to the convex hull composed by the leaders as time goes infinity. That is, ${lim}_{t\to \infty }\parallel x_i-Co\left(x_j\right)\parallel =0$ holds for all $i\in \mathcal{F}$, $j\in \mathcal{L}.$

We always assumed that the state of the agent was difficult to obtain and the output of the agent could be obtained directly. To achieve the control objective, the relative output information was used based on the design of the observers and controller. With the developed control laws, the final state of the followers should converge asymptotically to the convex combination formed by the leaders, and the external disturbances should be suppressed. To complete further research, the following results and assumptions are given first, which are used later.

Lemma 2

([19]). Let S be a symmetric matrix partitioned into the block form $S=\left(\begin{array}{cc}{S}_{11}& S_{12}\\ S_{21}& S_{22}\end{array}\right)$, where $S_{11}$ and $S_{22}$ are symmetric and square, respectively. Then, $S<0$ if and only if

$$S_{11}<0,S_{22}-S_{21}{S}_{11}^{-1}{S}_{12}<0$$

or equivalently

$$S_{22}<0,S_{11}-S_{12}{S}_{22}^{-1}{S}_{21}<0$$

Lemma 3

([20]). Suppose that $\Omega \in R^{n\times n}$ is a Hermitian matrix, such that ${\lambda }_{min}(\Omega )I\le \Omega \le {\lambda }_{max}(\Omega )I$, where ${\lambda }_{max}(\Omega ),{\lambda }_{min}(\Omega )$ is, respectively, the maximum and minimum eigenvalue of Ω.

Lemma 4

([21]). Given a symmetric positive definite matrix P, the following inequality holds

$$2x^{T}y\le x^{T}Px+y^T{P}^{-1}y,$$

(4)

where $x,y\in R^n$ and P is a positive matrix.

Assumption 2.

The exosystem matrix S has different eigenvalues and only an imaginary part, meanwhile $(S,D)$ is observable.

Assumption 3.

The system matrix D for the disturbance in (1) satisfies the matching condition that there is a matrix $E\in {\mathbf{R}}^{p\times r}$ such that $D=BE$.

Assumption 4

([5]). The matrix triplet $(A,B,C)$ meets

(i)

rank($CB$) = rank(B) = p,

(ii)

rank $(\Omega )=n+p$, where $\Omega =\left[\begin{array}{cc}sI-A& B\\ C& \mathbf{0}\end{array}\right],\forall s\in \mathbb{C},Re\left(s\right)\ge 0.$

Let ${\xi }_i\left(t\right)={\displaystyle \sum _{j\in \mathcal{F}\bigcup \mathcal{L}}}{a}_{ij}\left(t\right)(x_i\left(t\right)-x_j\left(t\right))$ be a relative state vector, $i\in \mathcal{F}$, where the weight $a_{ij}\left(t\right)$ is chosen as follows in our problem:

$$a_{ij}\left(t\right)=\left\{\begin{array}{cc}{\alpha }_{ij}\hfill & \mathrm{if}\mathrm{agent}i\mathrm{is}\mathrm{connected}\mathrm{to}\mathrm{agent}j\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(5)

where ${\alpha }_{ij}>0$ $(i\in \mathcal{F},j\in \mathcal{F}\bigcup \mathcal{L})$ is the connection weight constant between agent i and agent j. For the considered multiagent system, it was assumed that the interconnection topology switched in a finite possible directed graph. The set of all possible topology graphs was denoted as $\tilde{M}=\{{\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_M\}$, with index set $\mathcal{P}=\{1,2,\dots ,M\}$. The switching signal $\sigma :[0,\infty )⟶\mathcal{P}$ was used to represent the index of the topology digraph, i.e., at each time t, the underlying graph was ${\mathcal{G}}_{\sigma \left(t\right)}$. Define

$$\overline{\lambda }=max\left({\lambda }_{max}\left(L_{1i}^T{L}_{1i}\right)\right|i\in \mathcal{P})$$

Then, we introduced the error vector for the followers

$$\xi \left(t\right)=(L_{1\sigma \left(t\right)}\otimes I_n)x_{\mathcal{F}}+(L_{2\sigma \left(t\right)}\otimes I_n)x_{\mathcal{L}}.$$

(6)

in which

$$\begin{array}{cc}& \xi \left(t\right)={({\xi }_1^T,{\xi }_2^T,\cdots ,{\xi }_N^T)}^T,\hfill \\ & x_{\mathcal{L}}={(x_{N+1}^T\left(t\right),x_{N+2}^T\left(t\right),\cdots ,x_{N+M}^T\left(t\right))}^T,\hfill \\ & x_{\mathcal{F}}={(x_1^T\left(t\right),x_2^T\left(t\right),\cdots ,x_N^T\left(t\right))}^T.\hfill \end{array}$$

It can be seen from Lemma 1 that the containment can be realized if $\xi \left(t\right)\to 0$, i.e., $x_{\mathcal{F}}\to (L_{1\sigma \left(t\right)}^{-1}{L}_{2\sigma \left(t\right)}\otimes I_n)x_{\mathcal{L}}$, as $t\to \infty$.

3. Main Results

Since we could not obtain the state of agent i directly, we could only use the output $y_i$ to design control protocols. In order to achieve the control objective, an observer (7) was adopted to estimate the relative state ${\xi }_i\left(t\right)$ by agent i

$$\begin{array}{cc}\hfill & {\widehat{\xi }}_i\left(t\right)={\omega }_i\left(t\right)-H(\sum _{j\in \mathcal{F}\bigcup \mathcal{L}}{a}_{ij}\left(t\right)(y_i\left(t\right)-y_j\left(t\right)))\hfill \\ \hfill & \begin{array}{cc}\hfill {\dot{\omega }}_i\left(t\right)& =(GA-FC){\omega }_i\left(t\right)+(F(I+CH)-GAH)\hfill \\ \hfill & (\sum _{j\in \mathcal{F}\bigcup \mathcal{L}}{a}_{ij}\left(t\right)(y_i\left(t\right)-y_j\left(t\right))),\hfill \end{array}\hfill \end{array}$$

(7)

where ${\omega }_i\left(t\right)\in {\mathbf{R}}^n$ is the internal state, $H=-B{\left[{\left(CB\right)}^T\left(CB\right)\right]}^{-1}{\left(CB\right)}^T$, $G=I+HC$, and $F\in {\mathbf{R}}^{n\times q}$ was chosen such that $GA-FC$ was stable.

Remark 1.

The first condition of Assumption 4 can ensure the existence of H and we can conclude that $GB=0$ and $GD=0$. At the same time, the second condition of Assumption 4 can guarantee that the matrix pair $(GA,C)$ is detectable, and that F exists. Therefore, there is a $W>0_n$ such that

$${\left(GA\right)}^{T}W+W\left(GA\right)-2C^{T}C<0_{n\times n}.$$

(8)

Then, we can design $F=-W^{-1}{C}^T$. Moreover, $(A,B)$ is controllable from the second condition of Assumption 4.

In this part, the following observer was constructed to recover $x_i$

$$\begin{array}{c}{\dot{\widehat{x}}}_i=A{\widehat{x}}_i+B{u}_i+D{\widehat{d}}_i-{\tau }_0({\tau }_i+1)RC({\delta }_i-{\widehat{\xi }}_i)\hfill \\ {\dot{\tau }}_i={({\delta }_i-{\widehat{\xi }}_i)}^T\Gamma ({\delta }_i-{\widehat{\xi }}_i)\hfill \end{array}$$

(9)

where ${\delta }_i\left(t\right)={\displaystyle \sum _{j\in \mathcal{F}\cup \mathcal{L}}}{a}_{ij}\left(t\right)({\widehat{x}}_i\left(t\right)-{\widehat{x}}_j\left(t\right))$, $\Gamma =P_1$, and ${\tau }_0$ is a positive constant.

From (7) and (9), the disturbance observer was designed as

$$\begin{array}{c}{\dot{z}}_i\left(t\right)=S{z}_i\left(t\right)+(SQ-QA){\widehat{\xi }}_i\left(t\right)-QBK{\delta }_i\left(t\right),\hfill \\ {\widehat{d}}_i\left(t\right)=z_i\left(t\right)+Q{\widehat{\xi }}_i\left(t\right),\hfill \end{array}$$

(10)

where ${\widehat{d}}_i\left(t\right)$ is the state of the disturbance observer and $z_i\left(t\right)$ is the internal state of the disturbance observer, and the gain matrices Q and K are given later.

Then, the distributed dynamic adaptive feedback control was given with the form

$$u_i=K{\widehat{x}}_i-E{\widehat{d}}_i$$

(11)

The design objective of this paper was to construct suitable gain matrices $K,R$, and Q to achieve containment control with the proposed protocols.

3.1. Containment Control of MASs with Directed Communication Graph without Attacks

In this part, we give one theorem for solving the containment control problem of MASs (1) and (2) under a directed communication topology.

Theorem 1.

Consider the multiagent system (1) and (2) with exogenous disturbance systems (3). Suppose that Assumptions 1–4 are satisfied. Gain matrices $K,R$ and Q can be chosen as $K=-{\alpha }_1{B}^T{P}_1$, $R=P_1^{-1}{C}^T$, $Q={\alpha }_2{P}_2^{-1}{D}^T$, where $P_1>0$ and $P_2>0$ satisfy (12)–(14)

$$A^T{P}_1+P_{1}A-P_{1}B{B}^T{P}_1+I_n\le -I_n$$

(12)

$$A^T{P}_1+P_{1}A-C^{T}C+I_n\le 0$$

(13)

$$S^T{P}_2+P_{2}S-D^{T}D+I_n<0$$

(14)

with ${\alpha }_1=\frac{1}{2}$, ${\alpha }_2>0$. and the following conditions hold:

$$\begin{array}{c}{\gamma }_1\ge \frac{{\tau }_0^2\overline{\lambda }{\lambda }_{max}\left(C^{T}C\right)}{\frac{{\tau }_0{\rho }_0}{2}-\frac{1}{1+\tilde{\tau }}}\hfill \\ {\alpha }_2\ge 1+{\gamma }_2+\frac{4{\gamma }_1\overline{\lambda }}{{\tau }_0{\rho }_0{\lambda }_{min}\left(C{P}_1^{-1}{P}_1^{-1}{C}^T\right)}\hfill \end{array}$$

(15)

in which ${\gamma }_1$ and ${\gamma }_2$ are positive constant and $\tilde{\tau }=max({\tau }_1,{\tau }_2,\dots ,{\tau }_N)$. Then, the containment control of MASs (1) and (2) can be achieved via the control protocol (11).

Proof. 

For convenience, let $\widehat{d}\left(t\right)={[{\widehat{d}}_1^T\left(t\right),{\widehat{d}}_2^T\left(t\right),\cdots ,{\widehat{d}}_N^T\left(t\right)]}^T$, $d\left(t\right)=[d_1^T\left(t\right),d_2^T\left(t\right),\cdots ,$ $d_N^T{\left(t\right)]}^T$, $\widehat{\xi }\left(t\right)={[{\widehat{\xi }}_1^T\left(t\right),{\widehat{\xi }}_2^T\left(t\right),\cdots ,{\widehat{\xi }}_N^T\left(t\right)]}^T$, and $\delta \left(t\right)={[{\delta }_1^T\left(t\right),{\delta }_2^T\left(t\right),\cdots ,{\delta }_N^T\left(t\right)]}^T$. Then, we can obtain the following closed-loop error dynamics

$$\dot{\xi }\left(t\right)=(I_N\otimes A)\xi \left(t\right)+(I_N\otimes BK)\delta \left(t\right)-(L_{1\sigma \left(t\right)}\otimes D)\tilde{d}\left(t\right),$$

(16)

where $\tilde{d}\left(t\right)=\widehat{d}\left(t\right)-d\left(t\right)$, and ${\widehat{x}}_{\mathcal{F}}\left(t\right)={[{\widehat{x}}_1^T\left(t\right),{\widehat{x}}_2^T\left(t\right),\cdots ,{\widehat{x}}_N^T\left(t\right)]}^T$.

By (7) and (11), we can get

$$\begin{array}{cc}\hfill \dot{\widehat{\xi }}\left(t\right)& =(I_N\otimes A)\widehat{\xi }\left(t\right)+(I_N\otimes (GA-FC-A))(\widehat{\xi }\left(t\right)-\xi \left(t\right))\hfill \\ \hfill & +(I_N\otimes BK)\delta \left(t\right)-(L_{1\sigma \left(t\right)}\otimes D)\tilde{d}\left(t\right).\hfill \end{array}$$

(17)

$$\dot{\delta }\left(t\right)=(I_N\otimes \left(A+BK\right))\delta \left(t\right)-{\tau }_0(L_{1\sigma \left(t\right)}(\tau +I_N)\otimes RC)\eta .$$

(18)

where $\eta \left(t\right)=\delta \left(t\right)-\widehat{\xi }\left(t\right)$.

Let $\tilde{\xi }\left(t\right)=\widehat{\xi }\left(t\right)-\xi \left(t\right)$, according to the above formula, we get

$$\dot{\tilde{\xi }}\left(t\right)=(I_N\otimes (GA-FC))\tilde{\xi }.$$

(19)

$$\begin{array}{cc}\hfill \dot{\eta }& =(I_N\otimes A-{\tau }_0{L}_{1\sigma \left(t\right)}(\tau +I_N)\otimes RC)\eta +(L_{1\sigma \left(t\right)}\otimes D)\tilde{d}-(I_N\otimes (GA-FC-A))\tilde{\xi }.\hfill \end{array}$$

(20)

where $\tau =diag({\tau }_1,{\tau }_2,\cdots ,{\tau }_N)$.

Combining (10) and (3), we have

$$\begin{array}{cc}\hfill \dot{\tilde{d}}\left(t\right)& =(I_N\otimes S-L_{1\sigma \left(t\right)}\otimes QD)\tilde{d}\left(t\right)+(I_N\otimes Q(GA-FC-A))\tilde{\xi }.\hfill \end{array}$$

(21)

It is easy to see that if ${lim}_{t\to \infty }\delta =0$, ${lim}_{t\to \infty }\tilde{d}=0$, ${lim}_{t\to \infty }\tilde{\xi }=0$, and ${lim}_{t\to \infty }\tilde{\eta }=0$, then ${lim}_{t\to \infty }\xi =0$, which means that the containment control is achieved. Thus, the containment control problem of MASs (1) and (2) is transformed into the stability problem of error systems (18)–(21).

Let $\sigma \left(t\right)=p$, and for any $\tau \in [t_j,t_{j+1}),j=0,1,\dots$, consider the following multiple Lyapunov function (22) for error systems (18)–(21)

$$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)+V_3\left(t\right)+V_4\left(t\right).$$

(22)

in which

$$\begin{array}{cc}& V_1\left(t\right)={\delta }^T\left(t\right)(\varphi \otimes P_1)\delta \left(t\right)\hfill \\ & V_2\left(t\right)={\tilde{d}}^T\left(t\right)(\varphi \otimes P_2)\tilde{d}\left(t\right)\hfill \\ & V_3\left(t\right)={\tilde{\xi }}^T\left(t\right)(\varphi \otimes P_3)\tilde{\xi }\left(t\right)\hfill \\ & V_4\left(t\right)=\frac{{\gamma }_1}{2}\sum _{i=1}^N{\Phi }_i({\tau }_i+2){\tau }_i\hfill \end{array}$$

where $P_3$ satisfies the LMI

$${(GA-FC)}^T{P}_3+P_3(GA-FC)+(\beta +1)I_n<0$$

(23)

and $\beta =\frac{4{\gamma }_1{\lambda }_{max}\left({(GA-FC-A)}^T(GA-FC-A)\right)\overline{\lambda }}{{\tau }_0{\rho }_0{\lambda }_{min}\left(C{P}_1^{-1}{P}_1^{-1}{C}^T\right)}+\frac{1}{{\gamma }_2}{\lambda }_{max}\left({(GA-FC-A)}^T(GA-FC-A)\right)$.

Then, taking the derivative of $V_1,V_2,V_3,V_4$ and using Lemma 4, we can get

$$\begin{array}{cc}\hfill {\dot{V}}_1& ={\delta }^T(\varphi \otimes (P_1(A+BK)+{(A+BK)}^T{P}_1))\delta -2{\delta }^T(\varphi \otimes P_1)({\tau }_0{L}_{1p}(\tau +I_N)\otimes RC)\eta \hfill \\ \hfill & \le {\delta }^T(\varphi \otimes (P_{1}A+A^T{P}_1-2{\alpha }_1{P}_{1}B{B}^T{P}_1))\delta +{\delta }^T(\varphi \otimes I_n)\delta \hfill \\ & +{\tau }_0^2\overline{\lambda }{\lambda }_{max}\left(C^{T}C\right){\eta }^T(\varphi {(I_N+\tau )}^2\otimes C^{T}C)\eta \hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\dot{V}}_2& ={\tilde{d}}^T(\varphi \otimes (P_{2}S+S^T{P}_2)-{\alpha }_2(\varphi L_{1p}+L_{1p}^T\varphi )\otimes D^{T}D)\tilde{d}+2{\tilde{d}}^T(\varphi \otimes D^T(GA-FC-A))\tilde{\xi }\hfill \\ \hfill & \le {\tilde{d}}^T(\varphi \otimes (P_{2}S+S^T{P}_2-{\alpha }_2(\varphi L_{1p}+L_{1p}^T\varphi )D^{T}D))\tilde{d}+{\gamma }_2{\tilde{d}}^T(\varphi \otimes D^{T}D)\tilde{d}\hfill \\ \hfill & +\frac{{\lambda }_{max}\left({(GA-FC-A)}^T(GA-FC-A)\right)}{{\gamma }_2}{\tilde{\xi }}^T(\varphi \otimes I_n)\tilde{\xi }.\hfill \end{array}$$

(25)

$${\dot{V}}_3={\tilde{\xi }}^T(\varphi \otimes ({(GA-FC)}^T{P}_3+P_3(GA-FC)))\tilde{\xi }.$$

(26)

$$\begin{array}{cc}\hfill {\dot{V}}_4& ={\gamma }_1\sum _{i=1}^N{\Phi }_i(1+{\tau }_i)\dot{{\tau }_i}\hfill \\ \hfill & =2{\gamma }_1{\eta }^T(\varphi (I_N+\tau )\otimes P_1)\dot{\eta }\hfill \\ \hfill & ={\gamma }_1{\eta }^T(\varphi (I_N+\tau )\otimes (A^T{P}_1+P_{1}A)-{\tau }_0(I_N+\tau )(\varphi L_{1p}+L_{1p}^T\varphi )(I_N+\tau )\otimes C^{T}C)\eta \hfill \\ \hfill & +2{\gamma }_1{\eta }^T(\varphi (I_N+\tau )L_{1p}\otimes P_{1}D)\tilde{d}-2{\gamma }_1{\eta }^T(\varphi (I_N+\tau )L_{1p}\otimes P_1(GA-FC-A))\tilde{\xi }\hfill \end{array}$$

(27)

According to Lemma 4, the following equalities hold

$$\begin{array}{cc}\hfill 2{\gamma }_1{\eta }^T(\varphi (I_N+\tau )L_{1p}\otimes P_{1}D)\tilde{d}\le & \frac{{\gamma }_1{\tau }_0{\rho }_0}{4}{\eta }^T(\varphi {(I_N+\tau )}^2\otimes C^{T}C)\eta \hfill \\ \hfill & +\frac{4{\gamma }_1\overline{\lambda }}{{\tau }_0{\rho }_0{\lambda }_{min}\left(C{P}_1^{-1}{P}_1^{-1}{C}^T\right)}{\tilde{d}}^T(\varphi \otimes D^{T}D)\tilde{d}\hfill \end{array}$$

(28)

$$\begin{array}{c}\hfill -2{\gamma }_1{\eta }^T[\varphi (I_N+\tau )L_1\otimes P_1(GA-FC-A)]\tilde{\xi }\le \frac{{\gamma }_1{\tau }_0{\rho }_0}{4}{\eta }^T(\varphi {(I_N+\tau )}^2\otimes C^{T}C)\eta \\ \hfill +\frac{4{\gamma }_1\overline{\lambda }{\lambda }_{max}{(GA-FC-A)}^T(GA-FC-A)}{{\tau }_0{\rho }_0{\lambda }_{min}\left(C{P}_1^{-1}{P}_1^{-1}{C}^T\right)}{\tilde{\xi }}^T(\varphi \otimes I_n)\tilde{\xi }\end{array}$$

(29)

According ${\alpha }_1=\frac{1}{2}$ and conditions (42), we can obtain

$$\begin{array}{cc}\hfill \dot{V}& \le {\delta }^T(\varphi \otimes (P_{1}A+A^T{P}_1-P_{1}B{B}^T{P}_1+I_n)\delta +{\eta }^T({\gamma }_1\varphi (I_N+\tau )\otimes (P_{1}A+A^T{P}_1-C^{T}C))\eta \hfill \\ \hfill & +{\tilde{d}}^T(\varphi \otimes (P_{2}S+S^T{P}_2-D^{T}D))\tilde{d}+{\tilde{\xi }}^T(\varphi \otimes ({(GA-FC)}^T{P}_3+P_3(GA-FC)+\beta I_n))\tilde{\xi }\hfill \\ \hfill & \le -\frac{1}{{\lambda }_{max}\left(P_1\right)}{\delta }^T(\varphi \otimes P_1){\delta }^T-\frac{1}{{\lambda }_{max}\left(P_2\right)}{\tilde{d}}^T(\varphi \otimes P_2)\tilde{d}\hfill \\ \hfill & -\frac{1}{{\lambda }_{max}\left(P_3\right)}{\tilde{\xi }}^T(\varphi \otimes P_3)\tilde{\xi }-{\eta }^T(\frac{{\gamma }_1}{2}\varphi (2\ast I_N+2\tau )\otimes I_n)\eta \hfill \\ \hfill & \le -\frac{1}{{\lambda }_{max}\left(P_1\right)}{V}_1-\frac{1}{{\lambda }_{max}\left(P_2\right)}{V}_2-\frac{1}{{\lambda }_{max}\left(P_3\right)}{V}_3-{\eta }^T(\frac{{\gamma }_1}{2}\varphi (2\ast I_N+\tau )\otimes I_n)\eta \hfill \\ \hfill & \le -\frac{1}{{\lambda }_{max}\left(P_1\right)}{V}_1-\frac{1}{{\lambda }_{max}\left(P_2\right)}{V}_2-\frac{1}{{\lambda }_{max}\left(P_3\right)}{V}_3-V_4\hfill \\ \hfill & \le -l_{1}V\hfill \end{array}$$

(30)

where $l_1=min(\frac{1}{{\lambda }_{max}\left(P_1\right)},\frac{1}{{\lambda }_{max}\left(P_2\right)},\frac{1}{{\lambda }_{max}\left(P_3\right)},1)$. Obviously, based on LMIs (12)–(14) and (23), we have $\dot{V}<0$. Therefore, through Lyapunov’s theory, we can get $\underset{t\to \infty }{lim}V\left(t\right)=0$, so $\delta \left(t\right)\to 0$, $\eta \left(t\right)\to 0$, $\tilde{d}\left(t\right)\to 0$, and $\tilde{\xi }\left(t\right)\to 0$. Then, according to the definition of $\delta \left(t\right)$, the MASs (1) and (2) with external disturbance systems (3) achieve containment control with the control protocol (11). This completes the proof. □

Remark 2.

If there is no external perturbation, that is $d_i\left(t\right)=0,\forall i\in \mathcal{F}$, the considered systems (1) and (2) can still achieve containment control with the designed control protocol (11) which is based on observers (9) and (10). Thus, the control protocol designed in this paper applies to more general systems because it is based on the relative output.

Remark 3.

Unlike article [5], which only discussed the case of a single leader, this paper primarily considered the problem of containment control for multiple leaders. Obviously, when $M=1$, the considered system in this paper becomes the system in [5], and the system can achieve the consensus if the conditions of Theorem 1 are satisfied. Moreover, article [17] only considered the consensus problem based on output feedback in the undirected communication topology. In this regard, this paper discussed the containment control problem based on adaptive observers in the directed communication topology, which means matrix $L_1$ associated with $\mathcal{G}$ is not the symmetric matrix, so it is more difficult to obtain the conditions for consensus.

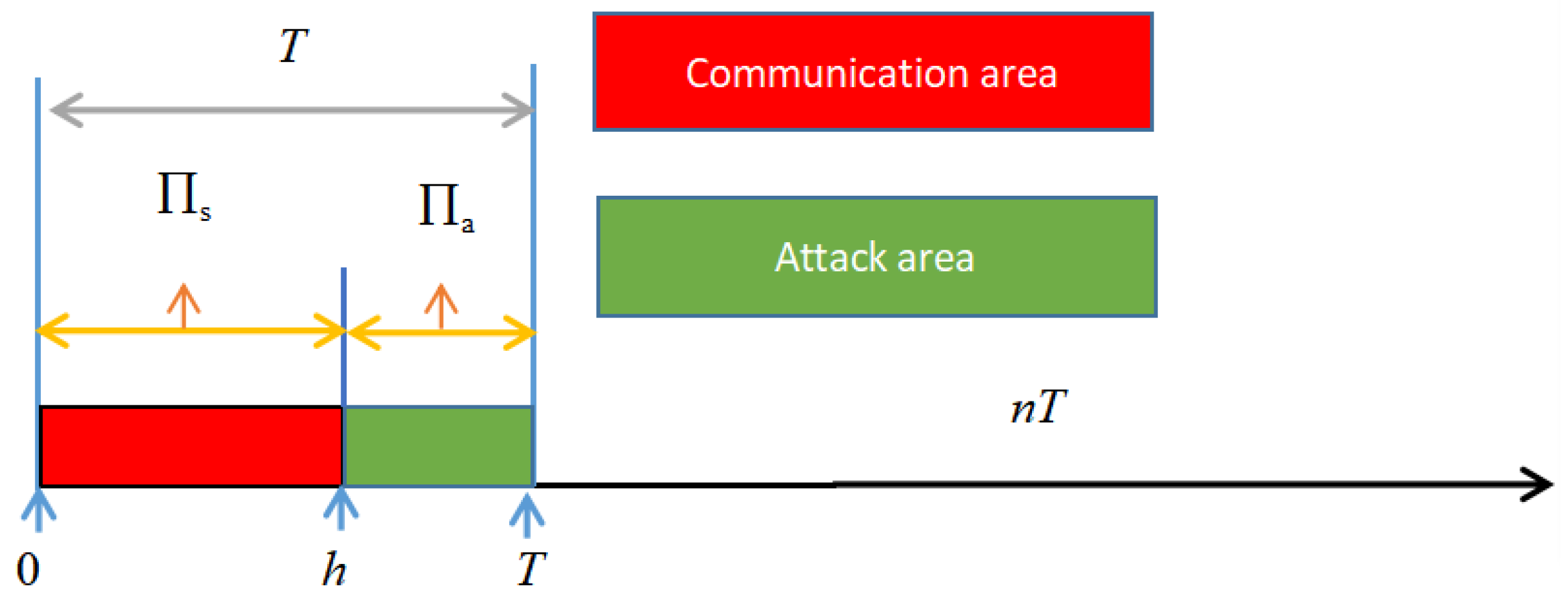
3.2. Containment Control of MASs with DoS Attacks

In this part, the secure containment control problem is considered for systems (1) and (2) under denial-of-service (DoS) attacks. We make the following assumptions to make it easier to deal with the problem.

Assumption 5.

The attackers have limited energy. They can only attack the network a limited number of times instead of unlimited times, and the duration for each attack is upper-bounded.

Assumption 6.

When the attack occurs, all communication among agents is interrupted.

Remark 4.

It is reasonable to assume that the energy of the attackers is limited in Assumption 5 since it represents several practical scenarios. For instance, many digital devices used as attack tools work with batteries, and their attack times are limited due to limited battery energy. The challenge of energy-constrained attacks has been recently discussed, see [13] for more details. Assumption 6, which can also be found in [22], is often a reality in practice.

Based on Assumptions 5 and 6, we can divide the first-period $n=1$, $[0,T]$ into two areas as shown in Figure 1, where the red area represents the communication area ${\Pi }_s$ $({\Pi }_s=[0,h])$ without the DoS attacks, the green area ${\Pi }_{\alpha }$ $({\Pi }_{\alpha }=[h,T))$ indicates the area where data transmission between agents is interrupted because of the DoS attacks.

Assumption 7.

For every attack period $\left[\right(n-1)T,nT],n=1,\dots$, the period T has been identified.

Since, for $t\in \left[\right(n-1)T+h,nT]$, the data exchange among agents is interrupted by cyberattacks, and the agents cannot communicate with their neighbors, the adaptive observer (9) can be modified as

$$\begin{array}{c}\hfill {\dot{\widehat{x}}}_i=\left\{\begin{array}{cc}A{\widehat{x}}_i+B{u}_i+D{\widehat{d}}_i-{\tau }_0({\tau }_i+1)RC({\delta }_i-{\widehat{\xi }}_i)\hfill & t\in \left[\right(n-1)T,(n-1)T+h)\hfill \\ A{\widehat{x}}_i+B{u}_i+D{\widehat{d}}_i\hfill & t\in \left[\right(n-1)T+h,nT)\hfill \end{array}\right.\end{array}$$

(31)

where ${\dot{\tau }}_i={({\delta }_i-{\widehat{\xi }}_i)}^T\Gamma ({\delta }_i-{\widehat{\xi }}_i)$, and thecontroller is still designed as $u_i=K{\widehat{x}}_i-E{\widehat{d}}_i$

The disturbance observers (10) and (7) are modified as

$$\begin{array}{c}\hfill {\dot{\widehat{d}}}_i\left(t\right)=\left\{\begin{array}{cc}{\dot{z}}_i\left(t\right)+Q{\dot{\widehat{\xi }}}_i\left(t\right)\hfill & t\in \left[\right(n-1)T,(n-1)T+h)\hfill \\ S{\widehat{d}}_i\left(t\right)\hfill & t\in \left[\right(n-1)T+h,nT)\hfill \end{array}\right.\end{array}$$

(32)

where ${\dot{z}}_i\left(t\right)=S{z}_i\left(t\right)+(SQ-QA){\widehat{\xi }}_i\left(t\right)-QBK{\delta }_i\left(t\right)$,

$$\dot{\delta }\left(t\right)=(I_N\otimes \left(A+BK\right))\delta \left(t\right)$$

(33)

$$\begin{array}{c}\hfill {\dot{\widehat{\xi }}}_i\left(t\right)=\left\{\begin{array}{cc}{\dot{\omega }}_i\left(t\right)-H({\displaystyle \sum _{j\in \mathcal{F}\bigcup \mathcal{L}}}{a}_{ij}\left(t\right)({\dot{y}}_i\left(t\right)-{\dot{y}}_j\left(t\right)))\hfill & t\in \left[\right(n-1)T,(n-1)T+h)\hfill \\ (I_N\otimes A)\widehat{\xi }\left(t\right)\hfill & t\in \left[\right(n-1)T+h,nT)\hfill \end{array}\right.\end{array}$$

(34)

where ${\dot{\omega }}_i\left(t\right)=(GA-FC){\omega }_i\left(t\right)+(F(I+CH)-GAH)({\displaystyle \sum _{j\in \mathcal{F}\bigcup \mathcal{L}}}{a}_{ij}\left(t\right)(y_i\left(t\right)-y_j\left(t\right)))$

Taking the same step as Section 3.1, we get

$$\begin{array}{c}\hfill \dot{\tilde{d}}\left(t\right)=\left\{\begin{array}{cc}(I_N\otimes S-L_{1\sigma \left(t\right)}\otimes QD)\tilde{d}\left(t\right)+(I_N\otimes Q(GA-FC-A))\tilde{\xi }\hfill & t\in \left[\right(n-1)T,(n-1)T+h)\hfill \\ (I_N\otimes S)\tilde{d}\left(t\right)\hfill & t\in \left[\right(n-1)T+h,nT)\hfill \end{array}\right.\end{array}$$

(35)

$$\begin{array}{c}\hfill \dot{\delta }\left(t\right)=\left\{\begin{array}{cc}(I_N\otimes \left(A+BK\right))\delta \left(t\right)-{\tau }_0(L_{1\sigma \left(t\right)}(\tau +I_N)\otimes RC)\eta \hfill & t\in \left[\right(n-1)T,(n-1)T+h)\hfill \\ (I_N\otimes \left(A+BK\right))\delta \left(t\right)\hfill & t\in \left[\right(n-1)T+h,nT)\hfill \end{array}\right.\end{array}$$

(36)

$$\begin{array}{c}\hfill \dot{\eta }\left(t\right)=\left\{\begin{array}{c}(I_N\otimes A-{\tau }_0{L}_{1\sigma \left(t\right)}(\tau +I_N)\otimes RC)\eta +(L_{1\sigma \left(t\right)}\otimes D)\tilde{d}\hfill \\ -(I_N\otimes (GA-FC-A))\tilde{\xi }\hfill & t\in \left[\right(n-1)T,(n-1)T+h)\hfill \\ (I_N\otimes A)\eta +(I_N\otimes BK)\delta \hfill & t\in \left[\right(n-1)T+h,nT)\hfill \end{array}\right.\end{array}$$

(37)

$$\begin{array}{c}\hfill \dot{\tilde{\xi }}\left(t\right)=\left\{\begin{array}{cc}(I_N\otimes (GA-FC))\tilde{\xi }\hfill & t\in \left[\right(n-1)T,(n-1)T+h)\hfill \\ (I_N\otimes A)\tilde{\xi }+(I_N\otimes BK)\delta \hfill & t\in \left[\right(n-1)T+h,nT)\hfill \end{array}\right.\end{array}$$

(38)

Then, we can establish the following result.

Theorem 2.

Provided that Assumptions 1–7 hold, consider there must exist $0<\varpi <1$, such that if $h>\varpi T$, the MASs (1) and (2) with exogenous disturbance systems (3) can reach consensus by employing the observer (34), the adaptive state estimator (31), and the disturbance observer (32) based on control protocol (11) with $K=-{\alpha }_1{B}^T{P}_1$, $R=P_1^{-1}{C}^T$, $Q={\alpha }_2{P}_2^{-1}{D}^T$, in which ${\alpha }_1=\frac{1}{2}$ and ${\alpha }_2$ are positive constants, and $P_1>0$, $P_2>0$ are obtained by solving LMIs (39)–(41):

$$A^T{P}_1+P_{1}A-P_{1}B{B}^T{P}_1+I_n\le -I_n$$

(39)

$$A^T{P}_1+P_{1}A-C^{T}C+I_n\le 0$$

(40)

$$S^T{P}_2+P_{2}S-D^{T}D+I_n<0$$

(41)

Then, the following conditions hold:

$$\begin{array}{c}{\gamma }_1\ge \frac{{\tau }_0^2\overline{\lambda }{\lambda }_{max}\left(C^{T}C\right)}{\frac{{\tau }_0{\rho }_0}{2}-\frac{1}{1+\tilde{\tau }}}\hfill \\ {\alpha }_2\ge 1+{\gamma }_2+\frac{4{\gamma }_1\overline{\lambda }}{{\tau }_0{\rho }_0{\lambda }_{min}\left(C{P}_1^{-1}{P}_1^{-1}{C}^T\right)}\hfill \end{array}$$

(42)

in which ${\gamma }_1$ and ${\gamma }_2$ are positive constants and $\tilde{\tau }=max({\tau }_1,{\tau }_2,\dots ,{\tau }_N)$.

Proof. 

Use the same Lyapunov function as for (22), in the communication area, for $t\in \left[\right(n-1)T,(n-1)T+h]$, from (30), we can obtain $\dot{V}\le -l_{1}V$

Now, considering $t\in \left[\right(n-1)T+h,nT]$, we take the derivative of $V_1,V_2,V_3,V_4$

$$\begin{array}{cc}\hfill {\dot{V}}_1& ={\delta }^T(\varphi \otimes (P_1(A+BK)+{(A+BK)}^T{P}_1))\delta \hfill \\ \hfill & \le {\delta }^T(\varphi \otimes (P_{1}A+A^T{P}_1-2{\alpha }_1{P}_{1}B{B}^T{P}_1))\delta \hfill \\ \hfill & \le -\frac{1}{{\lambda }_{max}\left(P_1\right)}{\delta }^T(\varphi \otimes P_1)\delta \hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {\dot{V}}_2& ={\tilde{d}}^T(\varphi \otimes (P_{2}S+S^T{P}_2)\tilde{d}\le \frac{{\lambda }_{max}\left(D^{T}D\right)}{{\lambda }_{min}\left(P_2\right)}{\tilde{d}}^T(\varphi \otimes P_2)\tilde{d}\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {\dot{V}}_3& ={\tilde{\xi }}^T(\varphi \otimes (A^T{P}_3+P_{3}A))\tilde{\xi }+2{\tilde{\xi }}^T(\varphi \otimes P_{3}BK)\delta \hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill 2{\tilde{\xi }}^T(\varphi \otimes P_{3}BK))\delta \le & {\tilde{\xi }}^T(\varphi \otimes {\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)))\tilde{\xi }+{\delta }^T(\varphi \otimes {\lambda }_{max}^2\left(P_3\right))\delta \hfill \\ \hfill \le & {\tilde{\xi }}^T(\varphi \otimes {\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)))\tilde{\xi }+\frac{{\lambda }_{max}^2\left(P_3\right)}{{\lambda }_{min}\left(P_1\right)}{\delta }^T(\varphi \otimes P_1)\delta \hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\dot{V}}_4& ={\gamma }_1\sum _{i=1}^N{\Phi }_i(1+{\tau }_i)\dot{{\tau }_i}\hfill \\ \hfill & =2{\gamma }_1{\eta }^T(\varphi (I_N+\tau )\otimes P_1)\dot{\eta }\hfill \\ \hfill & ={\gamma }_1{\eta }^T(\varphi (I_N+\tau )\otimes (A^T{P}_1+P_{1}A)\eta -2{\gamma }_1{\eta }^T(\varphi (I_N+\tau )\otimes P_{1}BK)\delta \hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & -2{\gamma }_1{\eta }^T(\varphi (I_N+\tau )\otimes P_{1}BK)\delta \le {\gamma }_1{\delta }^T(\varphi (I_N+\tau )\otimes I_n)\delta \hfill \\ & +{\gamma }_1{\eta }^T(\varphi (I_N+\tau )\otimes \left({\lambda }_{max}^2\left(P_1\right){\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)I_n\right))\eta \hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill {\dot{V}}_4& \le {\gamma }_1{\eta }^T(\varphi (I_N+\tau )\otimes (A^T{P}_1+P_{1}A+{\lambda }_{max}^2\left(P_1\right){\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)I_n)\eta +\frac{{\gamma }_1(1+{\tau }_0)}{{\lambda }_{min}\left(P_1\right)}{\delta }^T(\varphi \otimes P_1)\delta \hfill \\ \hfill & \le \frac{{\gamma }_1}{2}{\eta }^T(\varphi (2\ast I_N+2\tau )\otimes \left(({\lambda }_{max}^2\left(P_1\right)+1)\left({\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)\right)I_n\right)\eta +\frac{{\gamma }_1(1+{\tau }_0)}{{\lambda }_{min}\left(P_1\right)}{\delta }^T(\varphi \otimes P_1)\delta \hfill \\ \hfill & \le \frac{{\gamma }_1}{2}{\eta }^T(\varphi (4\ast I_N+2\tau )\otimes \left(({\lambda }_{max}^2\left(P_1\right)+1)\left({\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)\right)I_n\right)\eta +\frac{{\gamma }_1(1+{\tau }_0)}{{\lambda }_{min}\left(P_1\right)}{\delta }^T(\varphi \otimes P_1)\delta \hfill \\ \hfill & \le \frac{2({\lambda }_{max}^2\left(P_1\right)+1)({\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)}{{\lambda }_{min}\left(P_1\right)}{V}_4+\frac{{\gamma }_1(1+{\tau }_0)}{{\lambda }_{min}\left(P_1\right)}{\delta }^T(\varphi \otimes P_1)\delta \hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill \dot{V}& \le l_2{\delta }^T(\varphi \otimes P_1)\delta +l_2{\tilde{d}}^T(\varphi \otimes P_2)\tilde{d}+l_2{\tilde{\xi }}^T(\varphi \otimes P_3))\tilde{\xi }+l_2{V}_4=l_{2}V>0\hfill \end{array}$$

(50)

where $l_2=max(\frac{-1}{{\lambda }_{max}\left(P_1\right)}+\frac{{\lambda }_{max}^2\left(P_3\right)+{\gamma }_1+{\gamma }_1{\tau }_0}{{\lambda }_{min}\left(P_1\right)},\frac{{\lambda }_{max}\left(D^{T}D\right)}{{\lambda }_{min}\left(P_2\right)},\frac{{\lambda }_{max}(A^T{P}_3+P_{3}A+{\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)I_n)}{{\lambda }_{min}\left(P_3\right)},\frac{2({\lambda }_{max}^2\left(P_1\right)+1)({\lambda }_{max}\left({\left(BK\right)}^{T}BK\right)}{{\lambda }_{min}\left(P_1\right)})$

(1)

For $0\le t<h$, $V\left(t\right)\le V\left(0\right)exp(-l_{1}t)$ and $V\left(h\right)\le V\left(0\right)exp(-l_{1}h)$.

(2)

For $h\le t<T$, $V\left(t\right)\le V\left(h\right)exp\left(l_2(t-h)\right)\le V\left(0\right)exp(-l_{1}h+l_2(t-h))$ and $V\left(T\right)\le V\left(0\right)exp(-l_{1}h+l_2(T-h))$.

(3)

For $T\le t<T+h$, $V\left(t\right)\le V\left(T\right)exp(-l_1(t-T))\le V\left(0\right)exp(-l_{1}h-l_1(t-T)+l_2(T-h))$ and $V(T+h)\le V\left(0\right)exp(-2l_{1}h+l_2(T-h))$.

(4)

For $T+h\le t<2T$, $V\left(t\right)\le V(T+h)exp\left(l_2(t-T-h)\right)\le V\left(0\right)exp(-2l_{1}h+l_2(T-h)+l_2(t-T-h))$ and $V\left(2T\right)\le V\left(0\right)exp(-2l_{1}h+2l_2(T-h))$

By induction, we have

(5)

For $kT\le t<kT+h$, i.e., $\frac{t-h}{T}<k\le \frac{t}{T}$

$$\begin{array}{cc}\hfill V\left(t\right)& \le V\left(kT\right)exp(-l_1(t-kT))\hfill \\ \hfill & \le V\left(0\right)exp[-k{l}_{1}h+k{l}_2(T-h)-l_1(t-kT)]\hfill \\ \hfill & \le V\left(0\right)exp[-k{l}_{1}h+k{l}_2(T-h)]\hfill \\ \hfill & \le V\left(0\right)exp[-\frac{h{l}_1-(T-h)l_2}{T}(t-h)]\times exp\left(\frac{T-h}{T}{l}_{2}h\right)\hfill \\ \hfill & \le V\left(0\right)exp[-\frac{h{l}_1-(T-h)l_2}{T}(t-h)]\times exp\left[l_2(T-h)\right]\hfill \end{array}$$

(51)

(6)

For $kT+h\le t<kT+T$, i.e., $\frac{t-T}{T}<k\le \frac{t-h}{T}$

$$\begin{array}{cc}\hfill V\left(t\right)& \le V(kT+h)exp\left(l_2(t-kT-h)\right)\hfill \\ \hfill & \le V\left(0\right)exp[-(k+1)l_{1}h+(k+1)l_2(T-h)]\hfill \\ \hfill & \le V\left(0\right)exp[-\frac{h{l}_1-(T-h)l_2}{T}(t-h)]\times exp\left[l_2(T-h)\right]\hfill \end{array}$$

(52)

Therefore, for any $t>0$

$$\begin{array}{c}\hfill V\left(t\right)\le V\left(0\right)exp[-\frac{h{l}_1-(T-h)l_2}{T}(t-h)]\times exp\left[l_2(T-h)\right]\end{array}$$

(53)

If $h>\frac{l_2}{l_1+l_2}T$, then by defining $\varsigma \triangleq \frac{h{l}_1-(T-h)l_2}{T}>0$, we have

$$\parallel \delta \left(t\right)\parallel \le \sqrt{\frac{exp\left[l_2(T-h)\right]}{{\lambda }_{min}\left(P_1\right)}}\parallel \delta \left(0\right)\parallel exp[-\varsigma (t-h)]$$

which indicates the multiagent system can achieve containment control at the convergence rate of $\varsigma$. The proof is completed. □

Remark 5.

We can use the parameter ς to estimate the exponential convergence rate of the controlled system. The parameter ς is ostensibly determined by Tand h but actually depends on the controller K. Obtaining a small ϖ in the application is interesting. Setting $\overline{\varpi }$ as the upper limit of ϖ, as long as the effective estimation of ϖ is satisfied $1>\overline{\varpi }\ge \varpi$, i.e., if $h>\overline{\varpi }T$, then the multiagent system can achieve containment control by the proposed control law.

Remark 6.

For simplicity, this paper assumed that T and $T-h$ were fixed in each period. However, if the attack time is variable for each period i, the conclusion is also valid. For example, $T_i$ and $T_i-h_i$ are represented as the control period and attack period, respectively. According to our proof process, it is not difficult to see that the control law proposed can also solve the containment control problem under a DoS attack if $T_i$ is uniformly bounded and $h_i>\overline{\varpi }{T}_i$. Additionally, the attack can be partitioned into multiple agents, which can discontinuously locate in every period only if the total attack time is inferior to $(1-\varpi )T_i$. In addition, a larger attack width $T-h$ results in a larger control gain.

Remark 7.

Clearly, when $h=T$, the problem of containment control with DoS attacks becomes the problem of secure containment control. Moreover, the containment control can be achieved if the conditions of Theorem 2 are satisfied. Unlike the problem in [17,18], here, we considered the system with DoS attacks. When the system is attacked, the connectivity of the network is affected, which may result in the instability of the entire system. Thus, it is more challenging to consider the containment control problem with DoS attacks.

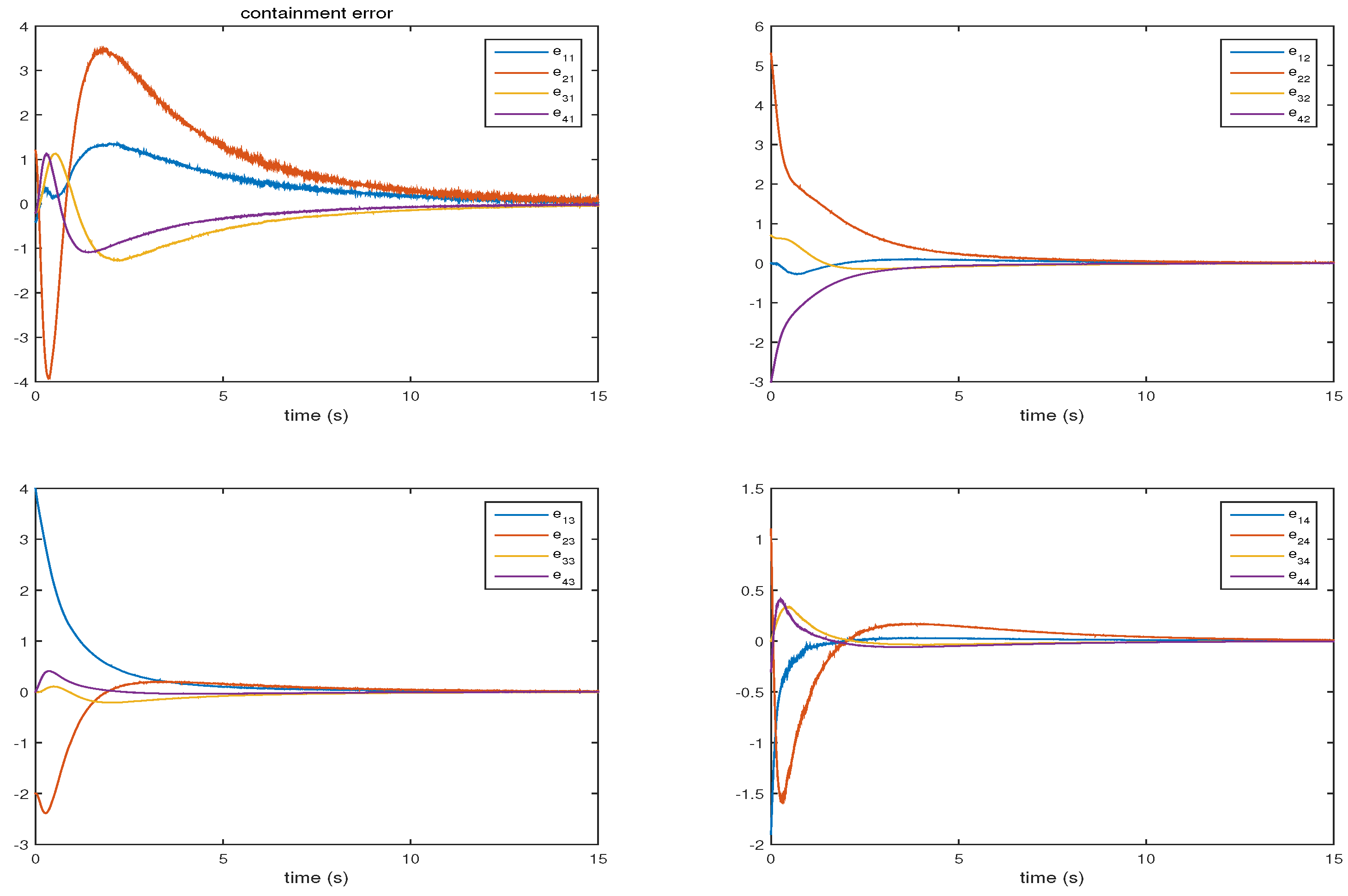
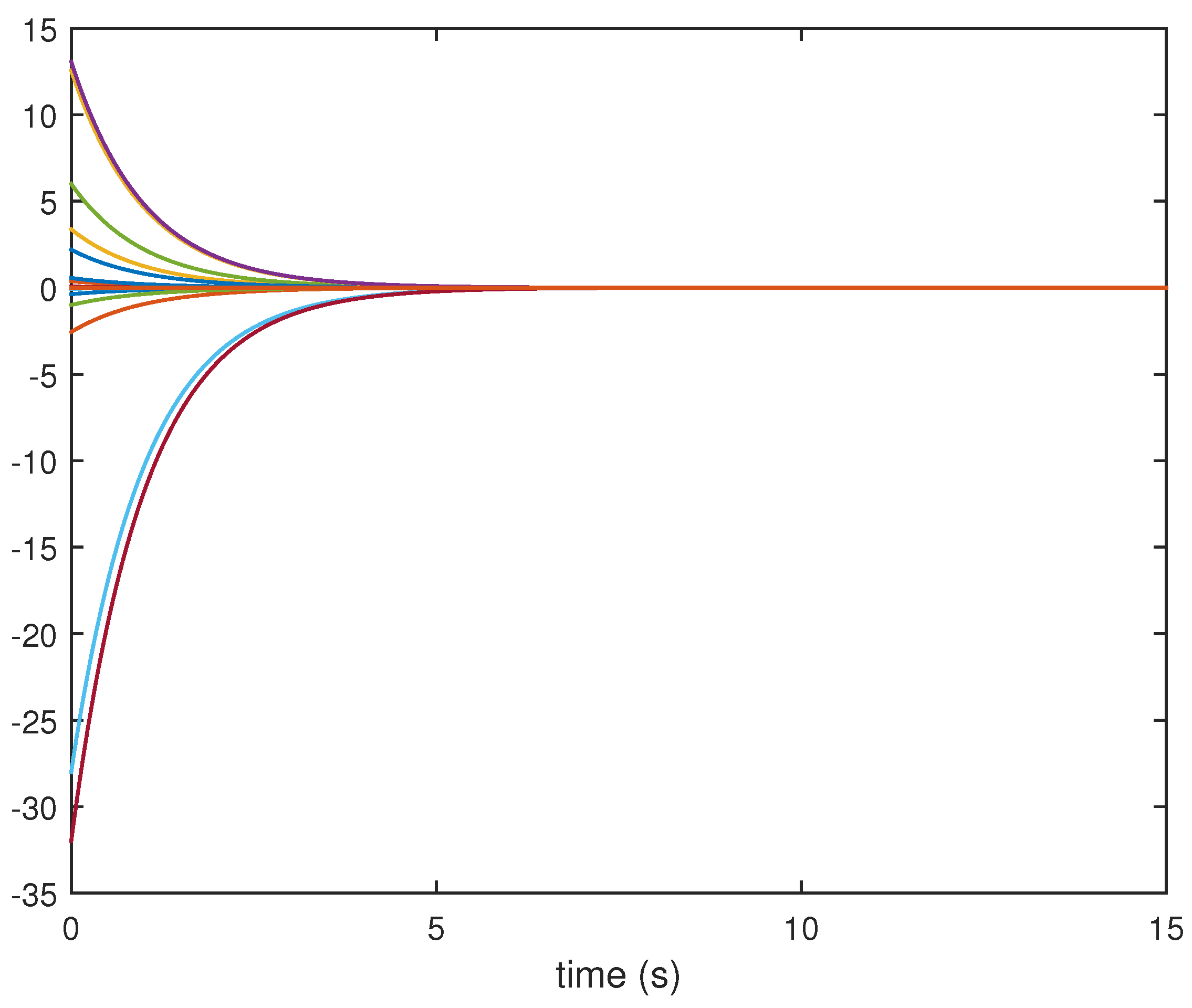
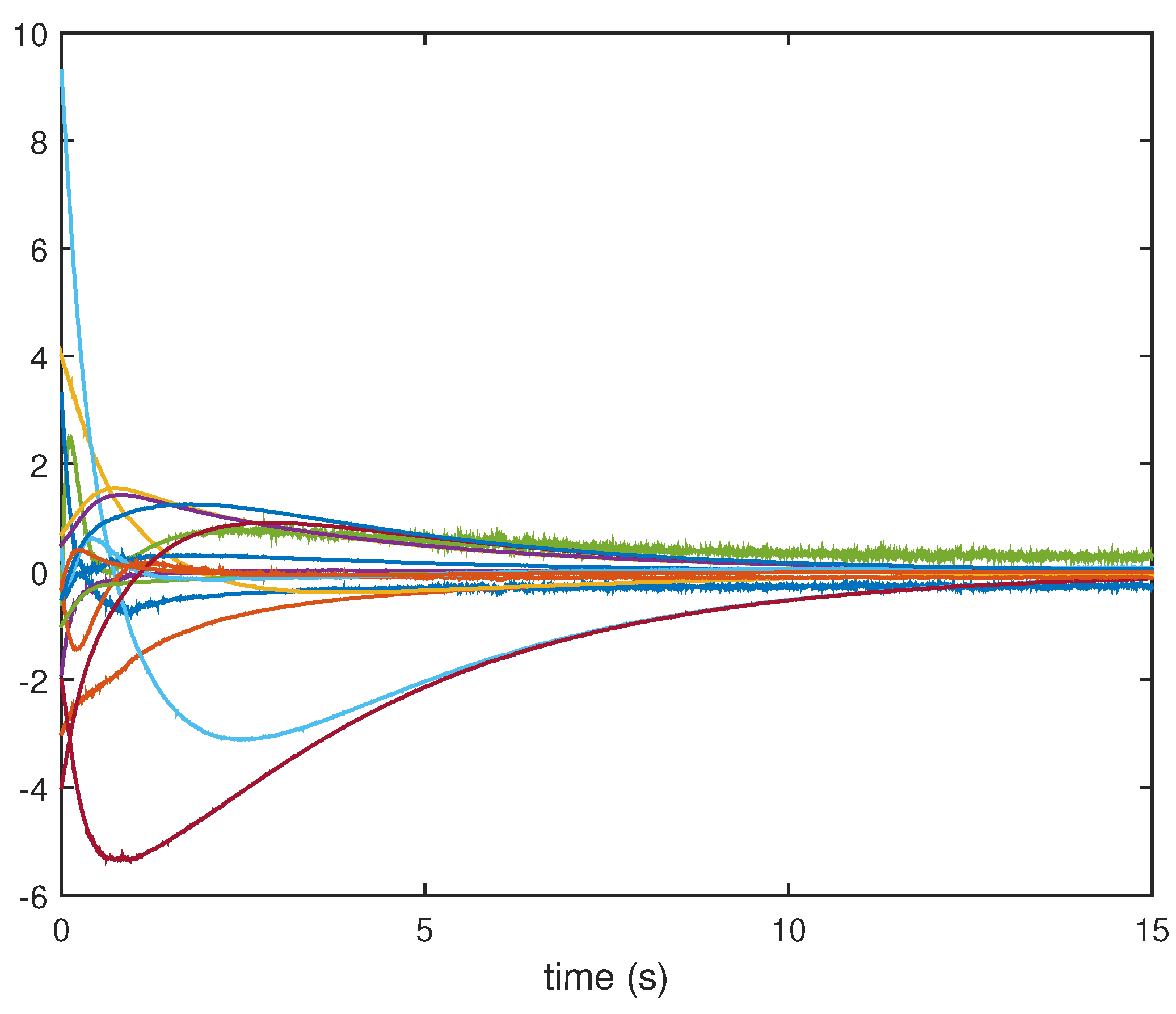
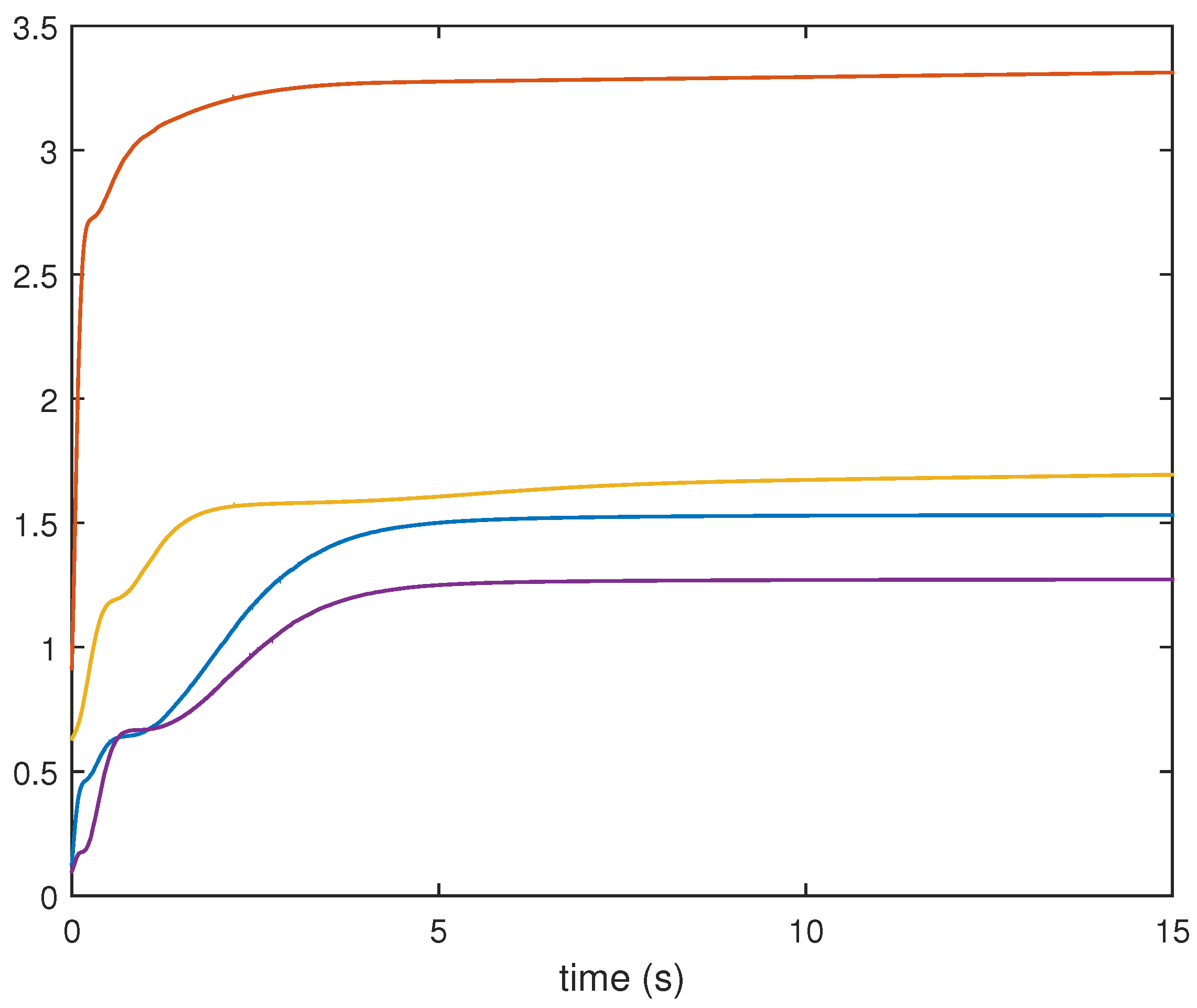
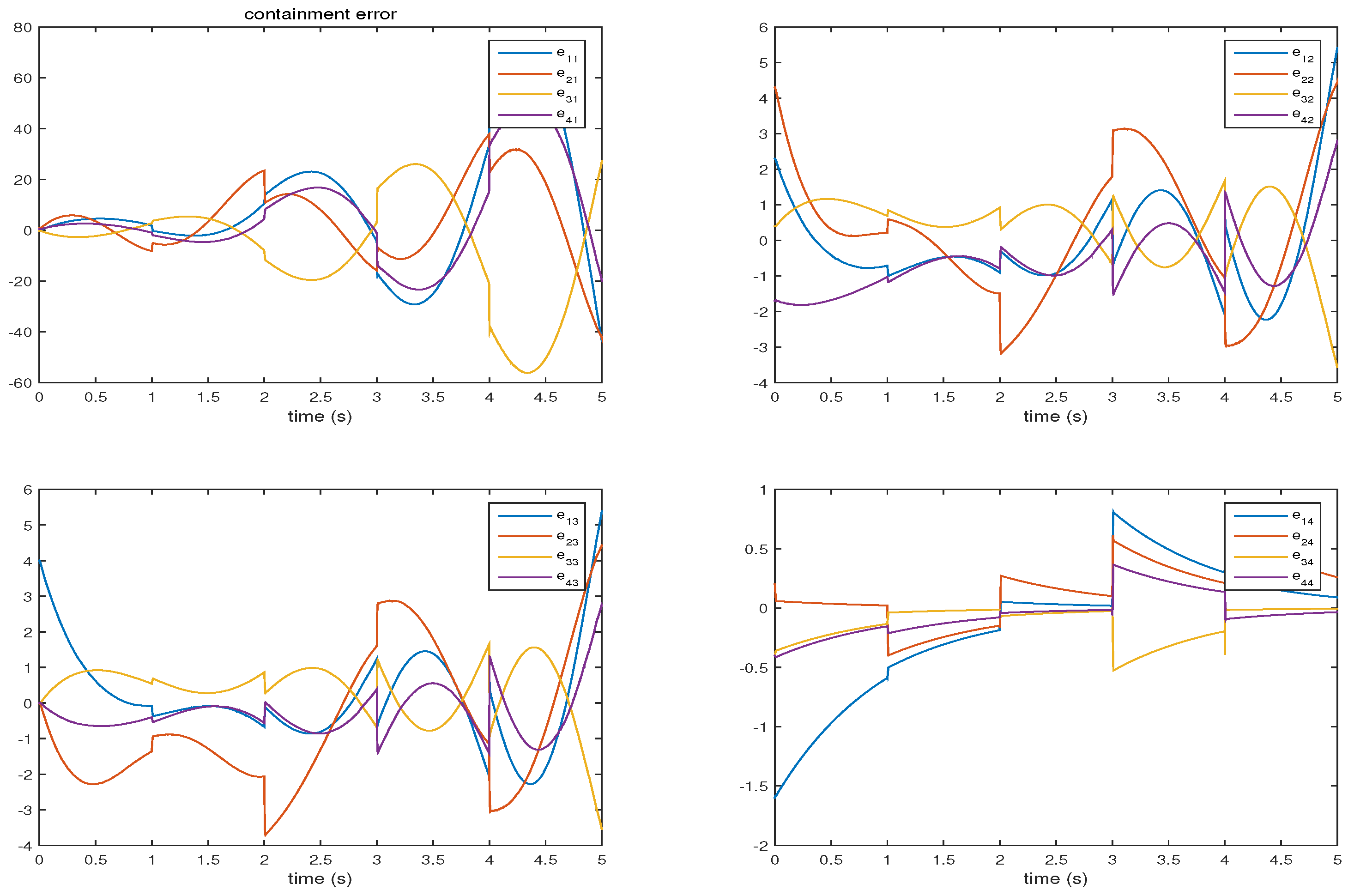
4. Numerical Example

We give two examples to show the practical validity of Theorems 1 and 2. In this section, the system matrices of linear multiagent systems (1) and (2) are

$$A=\left(\begin{array}{cccc}0& 0& 0& 0.1\\ 0& -1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& -1\end{array}\right),B=\left(\begin{array}{cc}2& 0\\ 0& 1\\ 0& 1\\ 0& 0\end{array}\right),C=\left(\begin{array}{cccc}1& 0.1& 0.1& 0\\ 0.1& 0.1& 0& 1\end{array}\right),S=\left(\begin{array}{cc}1& 1\\ 0& -1\end{array}\right),E=\left(\begin{array}{cc}2& 0\\ 0& 1\end{array}\right)$$

Then, we can get

$$H=\left(\begin{array}{cc}-1.2500& 2.500\\ 1.2500& -12.500\\ 1.2500& -12.5000\\ 0& 0\end{array}\right),G=\left(\begin{array}{cccc}0& 0.1250& -0.1250& 0\\ 0& -0.1250& 0.1250& 0\\ 0& -1.1250& 1.1250& 0\\ 0& 0& 0& 1.000\end{array}\right)$$

From (8), we get

$$F=\left(\begin{array}{cc}0.2281& 0.0197\\ 0.0227& 0.0271\\ 0.0210& 0.0266\\ 0& 0\end{array}\right)$$

Example 1.

Assuming the considered system consists of four followers and two leaders, and the interaction topology is directed and switched, then the Laplacian matrix of ${\mathcal{G}}_i(i=1,2)$ is as follows

$$L_i=\left(\begin{array}{cc}{L}_{1i}& L_{2i}\\ 0& 0\end{array}\right)$$

where

$$L_{11}=\left(\begin{array}{cccc}2& -1& 0& 0\\ -1& 3& -1& 0\\ 0& 0& 1& -1\\ 0& -1& 0& 1\end{array}\right),L_{12}=\left(\begin{array}{cccc}2& 0& -1& 0\\ 0& 2& -1& 0\\ 0& 0& 2& -1\\ 0& 0& -1& 2\end{array}\right),L_{21}=\left(\begin{array}{cc}-1& 0\\ 0& -1\\ 0& 0\\ 0& 0\end{array}\right),L_{22}=\left(\begin{array}{cc}0& -1\\ -1& 0\\ 0& -1\\ -1& 0\end{array}\right)$$

Take the parameter ${\alpha }_2=3$. Solving LMIs (12)–(14), we have

$$P_1=\left(\begin{array}{cccc}0.8089& -0.0211& -0.0200& 0.0542\\ -0.0211& 0.9110& -0.1836& -0.0187\\ -0.0200& -0.1836& 0.9128& -0.0005\\ 0.0542& -0.0187& -0.0005& 0.9159\end{array}\right),P_2=\left(\begin{array}{cc}3.3512& 1.5060\\ 1.5060& 5.5300\end{array}\right)$$

Moreover, we can obtain

$$K=\left(\begin{array}{cccc}-0.8089& 0.0211& 0.0200& -0.0542\\ 0.0205& -0.3637& -0.3646& 0.0096\end{array}\right),R=\left(\begin{array}{cc}1.2497& 0.1277\\ 0.1718& 0.1180\\ 0.1715& 0.0265\\ -0.0704& -0.0051\end{array}\right)$$

$$Q=\left(\begin{array}{cccc}2.4850& -0.1692& -0.1692& 0\\ -0.6768& 0.3765& 0.3765& 0\end{array}\right)$$

The initial value was taken randomly. It can be intuitively seen from Figure 2 that MASs (1) and (2) could achieve containment control with the perturbation observer-based control law (11), conforming with the result obtained from Theorem 1. Figure 3 and Figure 4 show the relative state error $\tilde{\xi }\left(t\right)$ and $\eta \left(t\right)$ converge to zero, and Figure 5 shows the evolution of the adaptive parameters from which it can be seen that the adaptive parameters converge to finite steady-state values.

Then, we considered the containment control under DoS attacks. Here, we took $h=0.8T$, from Figure 6 we can see the relative state error converges to zero which means containment control was achieved, and from Figure 7 we can see the adaptive parameters converge to finite steady-state values. However, Figure 8 shows that containment control could not be achieved if the duration of the DoS attack was too big.

5. Conclusions

This paper explored the challenge of containment control for linear multiagent systems with and without attacks in the presence of certain perturbations. Using the relative output information among adjacent agents, we proposed a control law based on a relative state observer, state estimator, and disturbance estimator to address the containment control problem. However, mechanisms for identifying attacks and isolating them remain unavailable. Future research should discuss how to identify attackers and isolate attacks.