Abstract
The Schrödinger–Newton model is a nonlinear system obtained by coupling the linear Schrödinger equation of canonical quantum mechanics with the Poisson equation of Newtonian mechanics. In this paper, we investigate the effects of dark energy on the time-dependent Schrödinger–Newton equations by including a new source term with energy density proportional to the cosmological constant , in addition to the particle-mass source term. The resulting Schrödinger–Newton– (S-N-) system cannot be solved exactly, in closed form, and one must resort to either numerical or semianalytical (i.e., series) solution methods. We apply the Adomian Decomposition Method, a very powerful method for solving a large class of nonlinear ordinary and partial differential equations, to obtain accurate series solutions of the S-N- system, for the first time. The dark energy dominated regime is also investigated in detail. We then compare our results to existing numerical solutions and analytical estimates and show that they are consistent with previous findings. Finally, we outline the advantages of using the Adomian Decomposition Method, which allows accurate solutions of the S-N- system to be obtained quickly, even with minimal computational resources. The extensive use of the Adomian Decomposition Method in the field of quantum mechanics and quantum field theory may open new mathematical, and physical, perspectives on obtaining semi-analytical solutions for some complex problems of quantum theory.
Keywords:
time-dependent Schrödinger–Newton equations; dark energy; Adomian Decomposition Method; series solutions PACS:
04.50.Kd; 04.20.Cv; 04.20.Fy
1. Introduction
Since the first attempts to create a quantum theory of the gravitational field in the 1930s [1,2], the search for a complete theory of quantum gravity has been one of the major fields of research in theoretical physics. In the pioneering work [1], Bronstein investigated the quantum mechanical measurement of the component of the Christoffel symbols. This led to a fundamental limit on the temporal uncertainty intrinsic to any quantum measurement, , where V and are the volume and the density of a self-gravitating massive body, respectively. The time uncertainty can then be related to the spatial uncertainty via . By introducing the standard mass–density–volume relation, , one also obtains the mass–time–density uncertainty relation, .
This was one of the first generalized uncertainty relations (GURs) and, since then, many others have been proposed in the literature. (See [3,4] for reviews.) Of these, the most widely studied are the generalized uncertainty principle (GUP) and the extended uncertainty principle (EUP). The former aims to incorporate the effects of canonical gravitational attraction between quantum mechanical particles [5,6], while the latter accounts for the repulsive effects of dark energy in the form of a cosmological constant, [7,8,9]. The extended generalized uncertainty principle (EGUP) accounts for both [10,11,12].
Over the years, many theoretical models and diverse approaches to the problem of quantum gravity have been developed. These include postulating the existence of the graviton, the hypothetical spin-2 boson that mediates quantum gravitational interactions, string theory, loop quantum gravity and noncommutative geometry, to mention just a few of the directions investigated. (For detailed presentations of the different approaches, see [13,14,15,16]. For recent reviews of the present status of quantum gravity research, see [17,18,19,20].) However, recently, important progress in experimental techniques has enabled researchers to cool, control and measure physical systems in the weak gravity and quantum mechanical regimes, with far greater accuracy than ever before. For the first time, it may be possible to directly observe quantum gravity effects at scales accessible in terrestrial and near-Earth-orbit laboratories, in near-future experiments [21,22].
Nonetheless, the conceptual and technical challenges to the construction of complete theory are manifold. From a quantum field theory perspective, even the Newtonian theory of gravity is problematic. Comparing Newton’s law of gravity, , where G is the gravitational constant and m the mass of the particle, with Coulomb’s law of electrostatics, , where is Coulomb’s constant and q the charge of the particle, it follows that the gravitational constant has mass dimension . Hence, the theory of Newtonian quantum gravity is nonrenormalizable. This result follows from the calculation of the graviton–graviton scattering at energy E, in which the divergent series appears [23]. The nonrenormalizability of such naive quantum gravity theories therefore suggests that new physics should emerge at the Planck scale, , where ℏ is Planck’s constant, c is the speed of light and denotes the mass of the proton.
Because of these challenges, much research interest has been devoted to the study of semi-classical models. In these models, matter fields are quantized while gravity remains classical or is perturbatively quantized at next-to-leading order in the expansion of the metric. Such an approach to quantum gravity was proposed in [24], which is based on the decomposition of the quantum metric into a classical and a fluctuating part, . Further assuming that , where is a classical tensor, one arrives at an effective gravitational Lagrangian of the form , where . The gravitational field equations obtained from this Lagrangian lead to theories that require geometry–matter coupling at the classical level. The coupling is of the kind that also appears in the type modified gravity theories [25,26] and the cosmological implications of effective field theories with fluctuating metric components were investigated in [27].
However, because gravity is in many ways different from the other fundamental forces and due to the intrinsic difficulties in its quantization, some researchers have suggested that the gravitational field may be essentially classical and that it should not and cannot be quantized [28,29]. However, even gravity is not quantum; ordinary matter is. Hence, in order to describe the gravitational dynamics of quantum fields, one must still combine classical gravity with quantized matter. In this scenario quantized matter is coupled to the classical gravitational field by replacing the classical energy momentum tensor, , with the expectation value of the energy–momentum operator, , in Einstein’s field equations. The expectation value is constructed by averaging with respect to an appropriately chosen quantum state, , yielding the semi-classical field equations [30],
Equation (1) can be also obtained from the variational principle [31], where is the standard Hilbert–Einstein action of general relativity, while the quantum part of the action, , is introduced in the form
By varying the quantum action (2) with respect to , we obtain the normalization condition and the following Schrödinger equation for ,
in addition to the semi-classical Einstein equations. Note that the Bianchi identities still impose the conservation of the effective energy–momentum tensor, .
The difficulty of building a successful quantum theory of general relativity, as well as the intrinsic problems of treating quantum field theories in curved spacetimes, have also led to the hypothesis that a satisfactory description of quantum gravity could be achieved by unifying quantum mechanics with Newtonian gravity [32]. This corresponds to the weak field limit of Equation (1), which reduce to the semi-classical Poisson equation
Equation (4) is the basis of the Schrödinger–Newton approach [21]. The Schrödinger–Newton model is a nonlinear system obtained by coupling the linear Schrödinger equation of canonical quantum mechanics with the Poisson equation of Newtonian mechanics. In this model, the equation of motion of a self-gravitating massive particle can be formulated as
where V is the canonical quantum potential and is the gravitational self-interaction potential, obtained by solving (4).
For a system of N non-relativistic free particles, and the mass–density operator may be written as , where . Equations (4) and (5) then combine to form
This is the standard Schrödinger–Newton equation, whose static and time-dependent solutions have been intensively investigated in [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. The average value of the self-interaction potential can be obtained as and it turns out that the particle behavior is essentially quantum if the condition , where R is average radius of the wave function, is satisfied [32].
Due to its extreme nonlinearity, the time-dependent Schrödinger–Newton system has mostly been investigated numerically. An exception is the variational approach, which was considered in [42], where the system of Equations (4) and (5) was investigated in the hydrodynamical representation of quantum mechanics. In this formalism, the wave function is represented as and the canonical Schrödinger equation reduces to the equations of classical fluid mechanics, in the presence of the quantum potential. The quantum fluid flows with a velocity and the equations of motion can be obtained from the Lagrangian
By adopting a spherical Gaussian profile for the density, , one can then obtain the gravitational potential and the Lagrangian of the system reduces to , where C is an arbitrary constant. The corresponding equation of motion for R is . Using this formalism, one can obtain the energy eigenvalues, linear frequencies and nonlinear late-time behavior of the S-N wave packet [42].
More recently, the Schrödinger–Newton system was generalized by considering the effects of dark energy in the form of a cosmological constant [54]. This is consistent with the standard CDM model of cosmology, in which it is assumed that the late-time acceleration of the Universe is driven by a constant vacuum energy density, [55]. (For alternative models of dark energy as modified gravity, see [56] and references therein.) The physically interesting regime in which dark energy dominates both gravitational self-attraction and canonical quantum diffusion was investigated numerically and using analytical estimates. It turns out that this takes place for objects with arbitrary mass that are sufficiently delocalized. An estimate of the minimum delocalization width required, of the order of 67 m, was determined and this prediction was verified by the numerical results.
However, the exact delocalization radius required for dark energy domination can be much higher for very massive particles. In general, the wave function of a free particle in the S-N- system was found to split into a core region that collapses due to gravitational self-attraction and an outer region that undergoes accelerated diffusion due to the presence of dark energy [54]. While the former behaviour is present in the standard S-N model [57], the latter is unique to the S-N- system. The order of magnitude of the critical radius separating collapse from expansion was found to match analytical estimates of the classical turnaround radius for a massive compact object in the presence of a cosmological constant [58].
The goal of this paper is to further investigate the mathematical and physical properties of the time-dependent S-N- system introduced in [54]. In order to obtain a better understanding of the dynamics of the model, we adopt a semi-analytical approach and construct series solutions using the Adomian Decomposition Method (ADM) [59,60,61,62]. This is a powerful method that can be used to obtain accurate series solutions of a large class of nonlinear differential equations and systems of equations, with applications in diverse fields of science and engineering [63,64,65,66,67,68,69,70,71,72,73,74,75]. Here, we apply it to the S-N- model for the first time.
An essential advantage of this method is that it can be used to obtain analytical approximations to the full numerical solutions, without any need for perturbation theory, closure approximations, linearization or discretization methods. For many highly nonlinear models, including the S-N and S-N- systems of equations, the use of these methods leads to complicated and time-consuming numerical computations. On the other hand, to obtain even approximate closed-form analytical solutions of a nonlinear problem requires introducing restrictive and simplifying assumptions. The key advantage of the ADM is that it can be used to find the solution of a given equation or system of equations in the form of a rapidly converging power series. Successive terms in the series are obtained via a recursive relation, with the help of a special class of functions known as Adomian polynomials [59,60,61,62]. In most cases the series converges fast, so that the application of this method saves a lot of computational time.
Although the ADM has been used extensively in many areas of engineering and physics, it has been used very little in the study of gravitation and quantum mechanics. (For some applications of the method in these fields, see [65,69,71].) In order to apply the method, we must first reformulate the time-dependent S-N- system as a system of two integral equations. We then obtain the series solutions of the system by expanding the nonlinear terms using the Adomian polynomials [59,60,61,62]. To eliminate the unwanted oscillatory behavior of the solution, we represent the Adomian series in terms of their Padé approximants.
After obtaining the recursive relation for the full S-N- system, we test the efficiency of the ADM for a free Gaussian wave packet, in the limit , . In this case, the canonical Schrödinger equation can be solved exactly and we show that the ADM recovers the exact solution in just a few simple steps. Next, series solutions are obtained for both the wave function and the gravitational potential, in the presence of gravitational self-interaction and dark energy. The associated probability density is computed with the help of the Padé approximants and we pay special attention to the dark energy dominated regime.
This paper is organized as follows. In Section 2, we present the basic structure and mathematical formalism of the Adomian Decomposition Method. The S-N- system is reformulated as a system of integral equations in Section 3 and the recurrence relations for the series solution of the system are obtained. The method is tested for the case of the canonical Schrödinger equation describing the free propagation of a Gaussian wave packet and it is shown that the exact solution of this system can be re-obtained in a few simple steps. We obtain the semi-analytical solution of the time-dependent S-N- system, for Gaussian initial conditions, in Section 4. The dark energy dominated regime is also considered in detail and a numerical analysis of the evolution of the probability density is presented. Our results are compared with previous analytical and numerical studies in Section 5 and our discussion and final conclusions are presented in Section 6.
2. The Adomian Decomposition Method
Let us consider a partial differential equation written in the general form
where , is the linear remainder operator that may contain partial derivatives with respect to x, is a nonlinear operator, which we assume is analytic and g is a non-homogeneous term that is independent of u. Equation (8) must be solved with the initial condition . We assume that is invertible, so that we can apply to both sides, obtaining
The ADM posits the existence of a series solution in which is given by
while the nonlinear term is decomposed as
where are the Adomian polynomials. These are generated according to the rule
Substituting the series expansions (10) and (11) into Equation (8), we find
Hence, we can obtain the following recurrence relation, giving the series solution of Equation (8) as
Therefore, we obtain the approximate solution of Equation (8) as
where
For a given nonlinearity , the Adomian polynomials are obtained as
and so on. The greater the number of terms, the higher the accuracy of the truncated series solution.
3. The Adomian Decomposition Method for the Time-Dependent Schrödinger–Newton- System
In the present section, we apply the Adomian Decomposition Method to obtain a semi-analytical solution for the time-dependent Schrödinger–Newton- system.
3.1. The S-N- System
For a single particle of mass m, the time-dependent S-N- system is given by the following two equations,
where the last term in the above Poisson equation was chosen so that the dark energy density is given by its standard form . For spherically symmetric systems, Equations (21) and (22) take the form
which must be solved with the boundary conditions and , respectively.
For simplicity, we assume that the initial state of the wave function is a spherically symmetric Gaussian,
satisfying the normalization condition and with initial width . The Gaussian initial state represents one of the few quantum states for which the time evolution for the free particle can be calculated, with the use of the Schrödinger equation, in a closed analytic form. It is thus very useful for comparing the exact and the semi-analytical solutions of the quantum evolution equations. A more general form of the Gaussian wave function is also possible, with , where is a constant. Adding such a new term linear in r is equivalent to a shift of the maximum of the Gaussian function and hence in the following we assume . The time evolution of the initial Gaussian wave function is obtained by solving the Schrödinger equation, which gives the expression of the wave function at arbitrary times. We do not consider stationary states and thus we do not impose any condition on the time or energy dependence of the wave function. Hence, in the present approach, no explicit dependence on the energy of the particle appears.
The gravitational potential , corresponding to the time-independent Gaussian wave packet, then satisfies the Poisson equation
whose general solution is
where is the error function and and are arbitrary integration constants. In order to avoid a singularity at the origin, we take . The initial distribution of the gravitational potential is then finite everywhere and satisfies the condition . By imposing the condition , we obtain . Hence, the initial distribution of the gravitational potential takes the form
3.2. The Adomian Decomposition Method for the S-N- System
Introducing the operators and , Equations (23) and (24) can be rewritten as
These equations can be solved formally to give
By taking into account the fact that and , we then obtain
where and are arbitrary integration functions. Using the Cauchy formula for repeated integration, , Equation (34) can be rewritten as
In order to make the gravitational potential finite at the origin , we chose , giving
We now determine the series solution of the reformulated system of Equations (33) and (36), by assuming expansions of the form
and
In addition, we decompose the terms and in terms of the Adomian polynomials as
Substituting the above decompositions into Equations (33) and (36), we obtain
In order to satisfy the boundary condition we take . Hence, we obtain the following recursive series solution for the time-dependent S-N- system,
Hence, the general solution of the S-N- system is obtained as
For the particle wave function, we obtain
The first three Adomian polynomials in each series are obtained as
and
respectively.
3.3. Testing the Adomian Decomposition Method
To test the efficiency of the ADM, we consider the evolution of a Gaussian wave packet in the absence of the gravitational interaction and dark energy, by setting . In this case, the evolution of the wave function is given by the canonical Schrödinger equation
and must be solved subject to the initial condition (25). The general solution of Equation (54), satisfying the required initial condition, is given by
The associated probability distribution is obtained as
In order to simplify the mathematical formalism, we introduce a new set of dimensionless variables , defined as
where denotes the proton mass and
respectively. Moreover, we rescale the wave function so that
The rescaled wave function satisfies the dimensionless Schrödinger equation
whose general solution, satisfying the initial condition (25), is given by
This may be expanded as a power series, with respect to the dimensionless time , as
To solve Equation (60) using the ADM, we apply the operator to both sides, giving
We then decompose into an infinite sum of components, so that , where the components will be determined recurrently. By substituting the series expansion into Equation (63), we obtain
Thus, we obtain the recursive relations
The first few iterations are given by
and
and so on. Clearly, the Adomian series solution exactly reproduces the series expansion of the exact solution (62) and, in the limit of an infinite number of iterations, fully recovers it. Hence, we have shown that the ADM gives the exact series representation of the solution of the spherically symmetric, three-dimensional Schrödinger equation describing the time-evolution of a free Gaussian wave packet.
The probability distribution is obtained as . Here, we approximate the series representation of by its Padé approximant , which is given by
Generally, for a power series of the form the Padé approximant of the order in the vicinity of the point is the rational function having the property that it takes the closest values to the given series near . Here, by , we have denoted the set of rational functions of the form , where P and Q are polynomials in z of degree and , respectively [76].
The comparison between the exact probability density of the Gaussian quantum wave packet,
and its approximation, given by Equation (70), is represented in Figure 1. As one can see from this figure, Equation (70) gives an excellent description of the time-evolution of the wave packet for and a good approximation for outside this range.
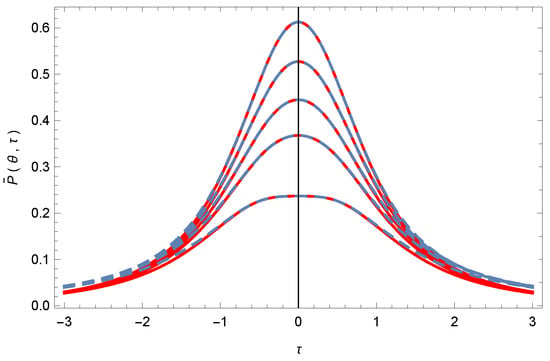
Figure 1.
Comparison of the Padé approximants of the ADM series solutions and exact solutions of the Schrödinger equation describing the probability density of the free evolution of a Gaussian wave packet, , for (lower curve), , , and (upper curve), respectively. The exact solutions are represented by solid curves, while the Padé approximants of the Adomian series are plotted as dashed curves.
4. Series Solution of the Time-Dependent Schrödinger–Newton- System
Using the mathematical formalism developed in the previous Section, we now construct explicit series solutions of the S-N- system. In addition, we perform a detailed numerical study. Our main goal is to highlight the effects of self-gravity and dark energy on the time-evolution of a quantum wave packet.
4.1. Semi-Analytical Solutions
In terms of the dimensionless variables and rescaled wave function , defined in Equations (57) and (59), the time-dependent S-N- equations take the form
where we have defined the dimensionless parameters
and introduced the rescaled gravitational potential as
The solution of Equations (72) and (73) can be represented as
so that the recurrence relation for the Adomian series is
where and are the Adomian polynomials corresponding to and , respectively.
By adopting the initial distribution of the wave function, the expression (25), which in the present dimensionless variables, becomes , and by assuming for the gravitational potential a distribution at given by
where we have denoted , we obtain the zeroth order terms as
and
Hence, we obtain the first order Adomian approximations of the wave function and of the gravitational potential for the S-N- system as
As one can see, immediately, satisfies the condition . The Adomian polynomial can be obtained immediately from Equation (49) and is given by
Thus, we obtain
The Adomian polynomial identically vanishes, since is a real function, while is a purely imaginary function, so that . Therefore, there is no contribution to the gravitational potential at this order of the approximation, . The second Adomian polynomial, defined according to , is obtained as
giving
and
For the Adomian polynomial , we obtain the simple expression
and, thus,
The next terms in the series solution of the S-N- equations can be computed easily using the same procedure. The series expansion simplifies significantly in the absence of the dark energy, . In this case, the effects of self-gravitational interaction on the quantum dynamics are described by the following approximations to the wave function:
The Padé Approximants
We again represent the probability density by its Padé approximant . In the first order of approximation, we obtain
and at the second order of approximation,
To the third order, the probability density can be approximated as
Higher order approximations of the probability density of a Gaussian wave packet, evolving under self-gravity in the presence of dark energy, can also be calculated easily with the aid of computer algebra systems. The gravitational self-potential can be approximated as
or, in terms of the Padé approximants of the power series,
4.2. The Dark Energy Dominated Regime
We now consider the limiting case in which the dark energy density dominates the matter density, . The Poisson equation then takes the simple form
and can be immediately integrated to give
where we have assumed that the background gravitational potential is independent of time. Hence, for the dark energy dominated phase, the Schrödinger equation takes the form
and can be formally solved to give
By decomposing the wave function as , we obtain the following recurrence relations for the determination of the components :
and the first few approximations of the quantum wave packet in the dark energy dominated regime are obtained as
The probability density of the Gaussian wave packet can be obtained, with the help of the Padé approximants, to different orders of approximation, as
and
and so on. The analytical expressions for the probability density can also be obtained easily to any desired order of approximation.
4.3. Numerical Analysis
In the final part of this section, we consider the numerical results obtained from the Adomian series solutions of the S-N- system. Our main goal is to highlight the effects of the self-gravitational potential and the dark energy density on the evolution of the probability density associated with the Gaussian quantum wave packet. In Figure 2, we present the three-dimensional evolution of the rescaled gravitational potential in the absence of dark energy, i.e., with and with . For convenience, we take as its initial value.
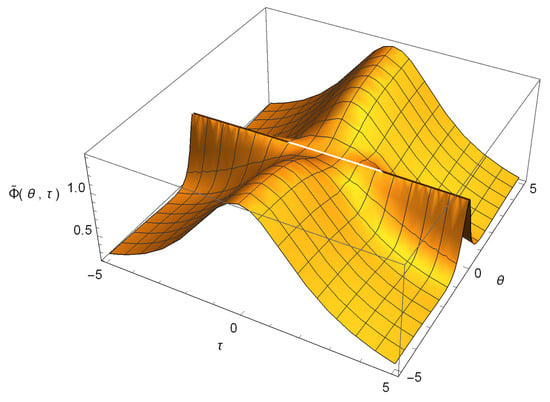
Figure 2.
Variation of the rescaled self-gravitational potential in the absence of dark energy (), for . The initial value of the potential is chosen as .
In this case, the gravitational potential can be approximated by
and the full solution satisfies the condition . Mathematically, a singularity develops in for values of satisfying . However, to at least the third order in the approximation, this equation does not have any real roots, except at .
The variation of the self-gravity potential in the presence of dark energy is represented in Figure 3, for two different values of ; and . In the large limit its behavior can be approximated as
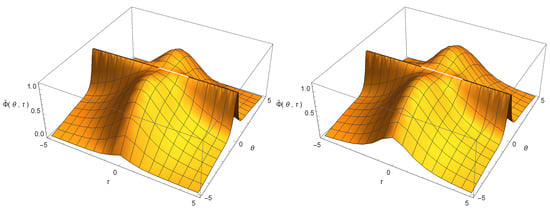
Figure 3.
Variation of the gravitational potential for (left panel) and for (right panel), for . For the initial value of the potential, we adopted the value .
Thus, we see that the presence of a positive cosmological constant does have a significant effect on the distribution of the gravitational potential. To at least the considered order of approximation, the condition still holds. On the other hand, as expected, . In both cases, the has a sharp maximum at the origin of the coordinate system, .
The time variation of the probability density of the Gaussian wave packet is represented, for fixed values of the radial coordinate , in Figure 4. There are two significant effects induced by the presence of the dark energy. As one can see from the left-hand panel, for (relatively) small values of the dimensionless radial coordinate , the probability density in the presence of almost coincides with the function describing the evolution with , for and has the same maximum value. In the absence of , the probability density tends to zero at a finite value of . However, dark energy significantly modifies the tail of the Gaussian distribution, which extends in time and induces much higher values of the probability density, as compared to the case. From the right-hand panel we see that, for larger values of , the dark energy has two different effects on the probability density. The first is a significant increase in the amplitude of the probability density, with the maximum increased by a factor of at least two. This indicates the increased probability of finding the wave packet at larger distances from the center, the effect being a direct consequence of the presence of repulsive dark energy. Secondly, at large distances, the probability density tends to zero. However, the decrease is much slower for and is directly correlated with the increase in the amplitude of the wave. Another interesting effect is related to the change in the shape of the wave function, which evolves from a single-peaked into a double-peaked symmetric function.
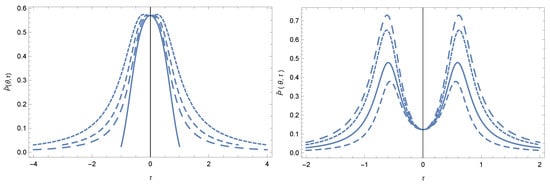
Figure 4.
Variation of the probability density at fixed values of . In the left-hand panel , while , , (solid curve), , , (dotted curve), , , (dotted curve) and , and (long dashed curve). In the right-hand panel , while , , (solid curve), , , (dotted curve), , , (dotted curve) and , and (long dashed curve). For the sake of presentation, the probability density was multiplied by a factor of .
The three-dimensional evolution of the wave packet in the presence of the self-gravitational field and the dark energy density is depicted in Figure 5. The same effects, as previously mentioned, are also apparent when considering the three-dimensional evolution of the wave packet. For large values of and , , but the dynamics of the transition to the asymptotic limit are strongly influenced by the presence of dark energy, whose effect becomes significant at late times and for large values of the radial coordinate.
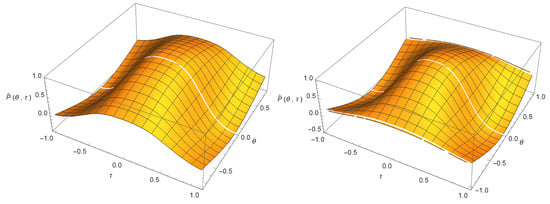
Figure 5.
Three-dimensional variation of the probability density for , and (left panel) and for , and (right panel), respectively.
The behavior of the probability density in the dark energy dominated regime is presented in Figure 6, for two distinct physical situations, corresponding to a fixed value of (left panel) and to a fixed value of (right panel). Even though, in this regime, there is a qualitative similarity with the case, significant differences also appear. The double-peaked shape of the Gaussian distribution is extended in time for fixed and the shape of the Gaussian tail is strongly modified, indicating an increase in the probability of finding the particle at higher values of . Moreover, the maximum value of the probability as a function of , at a given time, increases dramatically with increasing . However, at least at the considered order of approximation and for the adopted values of in the large limit, the probability distribution of the initially Gaussian wave packet still tends to zero. Nonetheless, much larger values of , in the range , would greatly modify the dynamics of the wave packet at infinity.
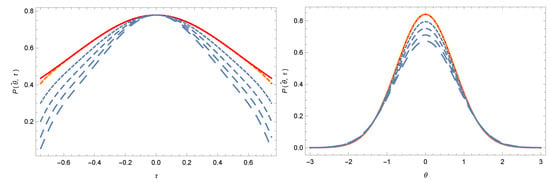
Figure 6.
Variation of the probability density in the dark energy dominated regime, for a fixed value of the radial coordinate, (left-hand panel), and for a fixed time, (right-hand panel). In each case, we plot the probability density for a range of parameter values, namely, , , which corresponds to the free evolution of the Gaussian wave packet (solid curve), , (dotted curve), , (short dashed curve), , (dashed curve) and , (long dashed curve).
5. Physical Implications
A particle obeying the S-N- equation of motion experiences three tendencies in its dynamics. Both canonical quantum diffusion and dark energy induced acceleration cause its wave function to spread, whereas Newtonian self-gravity, represented by the non-linear term, acts to localize the wave packet.
5.1. The Peak Radial Probability
In [54], it was argued that the relative strengths of these three tendencies can be estimated, at least approximately, by considering the motion of the peak radial probability density, . This is the position of the spherical shell at which the radial probability density reaches its maximum, that is, the radius at which the particle is most likely to be found at a given time t. It is determined by solving the equation
or, alternatively,
which is equivalent to setting or , respectively.
Qualitative Estimations
The contributions to the total acceleration experienced by due to canonical quantum diffusion, self-gravity and dark energy are then estimated as
and
The subscript SE refers to the canonical Schrödinger equation, SN refers to the standard Schrödinger–Newton contribution and denotes the additional term induced by the dark energy density.
In order to determine the regimes in which the different tendencies dominate the dynamics, we consider equality between the absolute magnitudes of the accelerations (120)–(122) in a pair-wise manner, i.e.,
or, equivalently,
plus
giving
and
yielding
where is the reduced Compton wavelength of the particle, is its Schwarzschild radius, cm is the Planck length and cm is the de Sitter radius. Note that the latter is comparable to the present day radius of the Universe [77] and that we have neglected numerical factors of order unity in all three equations.
The critical value of in Equation (127) is the classical turn-around radius for a spherical compact object in the Schwarzschild–de Sitter spacetime [58],
but the critical values given in Equations (123) and (125) include genuine quantum effects. The absolute magnitudes of all three contributions are equal when
or, equivalently,
where g and g are the Planck mass and the de Sitter mass, respectively. The approximate value of the peak radial probability is
and a more careful estimate, accounting accurately for numerical factors, gives m, as shown in [54].
For a Gaussian distribution, the initial peak radial probability is comparable to the initial width of the wave function, and the two are equivalent up to a multiplicative constant of order one for a large class of physically reasonable wave functions [54]. Therefore, Equation (132) also gives the order of magnitude value of the minimum initial width required, in order for the acceleration due to dark energy to dominate both canonical quantum diffusion and self-gravitation.
This is a very clear and somewhat surprising prediction: in the S-N- system, the spreading of any spherically symmetric wave packet with an initial width m will be dominated by the accelerated expansion of the Universe, due to dark energy, regardless of its initial mass. For particles with masses g, Equation (125) implies that the dark energy term always dominates over canonical quantum diffusion, whenever the initial width of the wave packet exceeds this critical value. For heavier particles, we expect the outer shells of the wave packet to undergo accelerated expansion due to dark energy while the inner core region contracts under self-gravity. By Equation (127), the critical radius marking the division between collapsing and expanding shells should be of the order of the classical turn-around radius (129).
5.2. Peak Probability in the ADM Approach
We now consider the behavior of the physical quantities introduced above by using the series solution of the S-N- system, obtained using the ADM. We first estimate for the free Gaussian wave packet, as given by Equation (71), which can be obtained as
By approximating the probability distribution of the wave function in the presence of the dark energy as given by Equation (114), we obtain for the expression
or, equivalently,
Figure 7 shows the evolution of , obtained from the Adomian series solution, for a Gaussian wave packet with (describing the effect of the background gravitational field) and for different values of the dimensionless dark energy parameter, . The presence of the gravitational field and of the dark energy significantly modifies the behavior of . However, in the absence of self-gravity, the peak probability density of the Gaussian wave packet satisfies in the presence of an extremely high dark energy density, corresponding to very large values of , the presence of the self-gravitational interaction significantly alters the behaviour of , at least at the first order of approximation, which may now tend to zero for finite values of . This represents the regime in which the total collapse of the wave function occurs under the action of self-gravitational attraction, which successfully counteracts both dark energy repulsion and canonical quantum diffusion. In the range , the time evolution of closely follows, on a qualitative level, the dynamics of , even though some small quantitative differences appear.
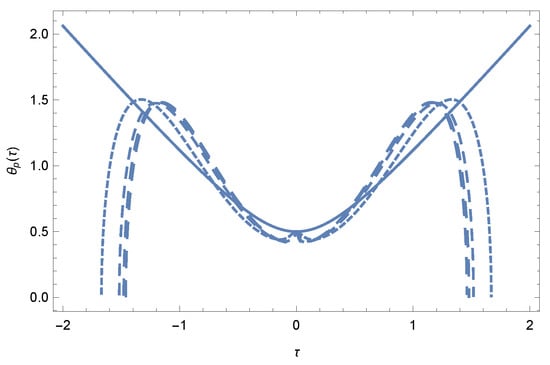
Figure 7.
Variation of as a function of the dimensionless time , for and for different values of : (dotted curve), (short dashed curve), (dashed curve) and (respectively). The time evolution of for the free Gaussian wave packet is represented by the solid curve.
In Figure 8, the dimensionless radial probability density is plotted for fixed and for various values of . This clearly shows the formation of a collapsing inner core and an outer shell undergoing accelerated expansion. The critical value of that demarcates between the two regions corresponds, to within an order of magnitude, to the classical turn-around radius of the particle mass.

Figure 8.
Variation, with respect to , of the radial probability density , for a fixed (left-hand panel) and for (right-hand panel), for , and , corresponding to the free Gaussian wave packet (solid curve) and for , and for different values of : (dotted curve), , (short dashed curve), , (dashed curve) and , (long dashed curve), respectively.
Finally, before concluding this section, we note that, since the Compton wavelength of the proton is of order m, lab-based experiments for which the dark energy dominated regime (131) and (132) is accessible require macromolecules with approximately 108 amu. This is two orders of magnitude below the estimated mass required for tests of the standard Schrödinger–Newton equation using opto-mechanical traps [78], which corresponds to the generic estimate for the onset of the semi-classical gravity regime with [30]. In other words, in terms of the mass parameter, current experiments are sufficiently precise to allow the effects of on the quantum dynamics of a macromolecule to be observed and measured. The associated length scale is 1–10 m, though, unfortunately, the associated time-scales may astronomical [54]. However, for macromolecules with ∼ amu, the canonical quantum contribution to the peak acceleration is of the same order as the dark energy contribution for m. This raises the intriguing possibility that dark energy effects may be observable in near-future experiments on local quantum systems, though, to date, the preceding order-of-magnitude estimates seem to have been overlooked in the quantum gravity literature. Crucially, the present work shows that we may go beyond such crude estimates, to obtain detailed analytical predictions of the S-N- model under realistic experimental conditions. As a proof-of-concept, our work also shows that we may fruitfully apply the ADM to any number of competing semi-classical gravity models [79,80,81]. This may be useful for a range of experimental tests, including tests of gravitationally induced wave function collapse [82,83,84].
6. Discussion and Final Remarks
In the present paper, we investigated the semi-analytical series solutions of the time-dependent Schrödinger–Newton– (S-N-) system, which describes quantum matter in the presence of a nonlinear self-gravitational interaction and a background dark energy density. For the latter, we adopted the simple form of a positive cosmological constant, which enters into the mathematical formalism through the modified Poisson equation. In order to solve the coupled system of S-N- equations, we used a powerful mathematical method called the Adomian Decomposition Method (ADM), which provides a fast and efficient way of obtaining series solutions of strongly nonlinear differential equations. The starting point of this method is the transformation of the given system of differential equations into an equivalent system of integral equations. Then, by positing the existence of series solutions of the integral system, one can obtain sets of recurrence relations for each unknown term in the power series expansion.
Usually, the ADM series converges fast, allowing detailed studies of the solutions of highly nonlinear differential equations using purely analytical methods. The main advantage of the method outlined in this paper is that it is based on a rigorous mathematical procedure, namely, the series expansions of the wave function and of the nonlinear self-gravity term, while at the same time providing results that are mathematically simple and physically intuitive. This allows an in-depth investigation of the role dark energy may play in the microscopic dynamics of a quantum particle.
In the cosmological context, the dark energy density can be inferred from the critical density of the Universe, given by g/cm, where is the present day value of the Hubble constant and km s Mpc. Since the cosmological data indicate a dark energy density of the order of , it follows that g/cm. On the other hand, the cosmological dark energy can be obtained from physical considerations, once it is interpreted as a vacuum energy, as , where and , where is the Planck length and is the de Sitter length [85,86,87]. This is consistent with the existence of the GUP and EUP [88] and with the recent tentative observational evidence for the granular nature of dark energy on scales of order mm [89,90,91,92,93].
In quantum physics, a quantum fluctuation (also called vacuum fluctuation), is the random variation of the energy at a point in space, due to the creation of virtual particle–antiparticle pairs. These pairs are continuously created in the space, according to the energy–time uncertainty principle, . In our present approach, we describe the effects of these processes on the quantum dynamics of the particle via a constant term. Even though, on a cosmological scale, the vacuum energy may have a very low (but extremely important) numerical value, quantum fluctuations may still have a significant impact on the local particle dynamics, at a microscopic level, over sufficiently long time-scales [54]. However, as a future extension of our current work, it would be interesting to reanalyze the problem using an alternative dark energy ansatz, which captures the oscillating or `granular’ nature of the dark energy density proposed in recent models [85,86,87,88,89,90,91,92,93].
With or without a dark energy term, the importance of the self-gravitational interaction essentially depends on the mass of the particle. For a particle with a mass of the order of g, where is the proton mass, the dimensionless coefficient given by Equation (74) is of order unity, . In this regime, the self-gravitational interaction has a significant effect on the evolution of the quantum wave packet. In the absence of dark energy, , it follows from Equation (75) that this phase corresponds to the standard gravity-dominated regime of the Schrödinger–Newton system.
Up to now, only very crude and approximate analytical methods could be used to investigate the dynamics of the Schrödinger–Newton– system. Although useful for developing our physical intuition and providing order-of-magnitude estimates, these are no substitute for accurate quantitative solutions. Conversely, obtaining accurate numerical solutions is resource intensive, requiring long periods of time to develop and run the relevant codes, which are also computationally demanding [54]. Moreover, the Adomian Decomposition Method presents some limitations in its application. Theoretically, the main problem of the method is related to the convergence of the Adomian series and to the fulfillment of the conditions required for the convergence. Practically, the limitations may be due to the slow convergence of the power series, requiring the computation of a very large number of terms, which may also become time consuming.
By contrast, the same results can be obtained using Adomian decomposition in a fraction of the time, with the help of a relatively simple Mathematica or Maple worksheet. Indeed, in [54], it was stated that “we must deal with a complicated integro-differential equation, with little hope for analytical exploration”. We have now shown that this is not the case and that the S-N- system may be investigated analytically, to any degree of desired accuracy, using the right series solution techniques. Thus, our results may open a new avenue of research in the field of quantum mechanics in the presence of gravitational fields. Moreover, the obtained results may shed some light on the important problem of the dark energy and its presence and influence, at atomic scales. The existence of some nontrivial physical effects due to the interaction between dark energy and elementary particles at the elementary particle level can also provide some possibilities for experimental investigation of the properties of the cosmological constant in a laboratory environment, thus linking large scale cosmological and astrophysical observations with microphysics.
By applying the Adomian Decomposition Method to PDEs, it should even be possible to obtain non-spherically symmetric solutions of the S-N- equations. To the best of the author’s knowledge, this has not yet been attempted in the existing literature, even numerically. Moreover, the investigation of other quantum mechanical systems, even in the presence of strong interactions, may become possible by using some adaptations or extensions of the Adomian Decomposition Method. The inclusion of the modified or semi-classical gravity effects may also be studied by using the same analytical approach.
The preliminary results presented here indicate that the Adomian Decomposition Method can be used to obtain accurate solutions to a wide variety of semi-classical gravity models, subject to a wide range of initial conditions. Ultimately, this should help us to test the predictions of these models in greater detail, under realistic experimental conditions [78].
Author Contributions
Conceptualization, T.H. and M.K.M.; Methodology, T.H. and M.K.M.; Software, T.H.; Validation, T.H. and M.K.M.; Formal analysis, T.H., M.J.L. and M.K.M.; Investigation, T.H. and M.J.L.; Resources, T.H., M.J.L. and M.K.M.; Data curation, T.H., M.J.L. and M.K.M.; Writing—original draft, T.H. and M.J.L.; Writing—review & editing, T.H., M.J.L. and M.K.M.; Visualization, T.H.; Supervision, T.H. and M.K.M.; Project administration, T.H., M.J.L. and M.K.M.; Funding acquisition, T.H. and M.J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Romanian Ministry of Education and Research, grant number PN-III-P4-ID-PCE-2020-2255 and the Natural Science Foundation of Guangdong Province, grant number 008120251030.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank the three anonymous reviewers for comments and suggestions that helped us to improve our manuscript. The work of TH is supported by a grant of the Romanian Ministry of Education and Research, CNCS-UEFISCDI, project number PN-III-P4-ID-PCE-2020-2255 (PNCDI III). ML thanks the Frankfurt Institute for Advanced Studies, for hospitality during the preparation of the first draft of this manuscript, the Department of Physics and Materials Science, Faculty of Science, Chiang Mai University, for providing research facilities and the Natural Science Foundation of Guangdong Province, which supported this work through grant no. 008120251030. We thank László Jenkovski, for inviting us to submit to the special is BGL-2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bronstein, M. Über den spontanen Zerfall der Photonen. Phys. Z. Sowjetunion 1936, 9, 140, Republished as Bronstein, M. Quantum theory of weak gravitational fields. Gen. Relativ. Gravit. 2012, 44, 267. [Google Scholar]
- Bronstein, M.P. Quantization of gravitational waves. Zh. Eksp. Teor. Fiz. 1936, 6, 195. [Google Scholar]
- Tawfik, A.N.; Diab, A.M. Review on Generalized Uncertainty Principle. Rept. Prog. Phys. 2015, 78, 126001. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Rel. 2013, 16, 2. [Google Scholar] [CrossRef]
- Adler, R.J.; Santiago, D.I. On gravity and the uncertainty principle. Mod. Phys. Lett. A 1999, 14, 1371. [Google Scholar] [CrossRef]
- Scardigli, F. Generalized uncertainty principle in quantum gravity from micro-black hole Gedanken experiment. Phys. Lett. B 1999, 452, 39. [Google Scholar] [CrossRef]
- Bolen, B.; Cavaglia, M. (Anti-)de Sitter black hole thermodynamics and the generalized uncertainty principle. Gen. Rel. Grav. 2005, 37, 1255. [Google Scholar] [CrossRef]
- Park, M. The Generalized Uncertainty Principle in (A)dS Space and the Modification of Hawking Temperature from the Minimal Length. Phys. Lett. B 2008, 659, 698. [Google Scholar] [CrossRef]
- Bambi, C.; Urban, F.R. Natural Extension of the Generalized Uncertainty Principle. Class. Quant. Grav. 2008, 25, 095006. [Google Scholar] [CrossRef]
- Lake, M.J.; Miller, M.; Ganardi, R.F.; Liu, Z.; Liang, S.D.; Paterek, T. Generalized uncertainty relations from superpositions of geometries. Class. Quant. Grav. 2019, 36, 155012. [Google Scholar] [CrossRef]
- Lake, M.J.; Miller, M.; Liang, S.-D. Generalized uncertainty relations for angular momentum and spin in quantum geometry. Universe 2020, 6, 56. [Google Scholar] [CrossRef]
- Lake, M.J. A New Approach to Generalized Uncertainty Relations. arXiv 2021, arXiv:2008.13183v1. [Google Scholar]
- Rovelli, C. Quantum Gravity, Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Mukhanov, V.; Winitzki, S. Introduction to Quantum Effects in Gravity; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Rovelli, C.; Vidatto, F. Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Becker, K.; Becker, M.; Schwarz, J.H. String Theory and M-Theory: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Modesto, L.; Rachwal, L. Nonlocal quantum gravity: A review. Int. J. Mod. Phys. 2017, 26, 1730020. [Google Scholar] [CrossRef]
- Gubitosi, G.; Ripken, C.; Saueressig, F. Scales and hierachies in asymptotically safe quantum gravity: A review. Found. Phys. 2019, 49, 972. [Google Scholar] [CrossRef]
- Loll, R. Quantum gravity from causal dynamical triangulations: A review. Class. Quantum Gravity 2020, 37, 013002. [Google Scholar] [CrossRef]
- Steinhaus, S. Coarse graining spin foam quantum gravity—A review. Front. Phys. 2020, 8, 295. [Google Scholar] [CrossRef]
- Carney, D.; Stamp, P.C.E.; Taylor, J.M. Tabletop experiments for quantum gravity: A user’s manual. Class. Quantum Gravity 2019, 36, 034001. [Google Scholar] [CrossRef]
- Kaltenbaek, R.; Aspelmeyer, M.; Vedral, V. Macroscopic quantum resonators (MAQRO): 2015 update. EPJ Quantum Technol. 2016, 3, 5. [Google Scholar] [CrossRef]
- Zee, A. Quantum Field Theory in a Nutshell; Princeton University Press: Princeton, NJ, USA; Oxford, UK, 2003. [Google Scholar]
- Dzhunushaliev, V.; Folomeev, V.; Kleihaus, B.; Kunz, J. Modified gravity from the quantum part of the metric. Eur. Phys. J. 2014, 74, 2743. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. 2011, 84, 024020. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N. Extensions of f(R) Gravity Curvature-Matter Couplings and Hybrid Metric-Palatini Theory; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Liu, X.; Harko, T.; Liang, S.-D. Cosmological implications of modified gravity induced by quantum metric fluctuations. Eur. Phys. J. 2016, 76, 420. [Google Scholar] [CrossRef]
- Møller, C. Les théories relativistes de la gravitation. Colloq. Int. CNRS 1962, 91, 1. [Google Scholar]
- Rosenfeld, L. On quantization of fields. Nucl. Phys. 1963, 40, 353. [Google Scholar] [CrossRef]
- Carlip, S. Is quantum gravity necessary? Class. Quant. Grav. 2008, 25, 154010. [Google Scholar] [CrossRef]
- Kibble, T.W.B.; Randjbar-Daemi, S. Non-linear coupling of quantum theory and classical gravity. J. Phys. A Math. Gen. 1980, 13, 141. [Google Scholar] [CrossRef]
- Diósi, L.; Lukács, B. In favor of a Newtonian quantum gravity. Ann. Phys. 1987, 499, 488. [Google Scholar] [CrossRef]
- Penrose, R. Quantum computation, entanglement and state reduction. Phil. Trans. R. Soc. Lond. 1998, A356, 1927. [Google Scholar] [CrossRef]
- Moroz, I.M.; Penrose, R.; Tod, K.P. Spherically-symmetric solutions of the Schrödinger-Newton equations. Class. Quantum Grav. 1998, 15, 2733. [Google Scholar] [CrossRef]
- Tod, K.P.; Moroz, I.M. An analytical approach to the Schrödinger-Newton equations. Nonlinearity 1999, 12, 201. [Google Scholar] [CrossRef]
- Lan, D. A quantum potential approach for the gravitational Schrödinger equation and its reduction into the Lane-Emden equation. Mod. Phys. Lett. 1999, 14, 2667. [Google Scholar] [CrossRef]
- Kumar, D.; Soni, V. Single particle Schrödinger equation with gravitational self-interaction. Phys. Lett. 2000, 271, 157. [Google Scholar] [CrossRef]
- Tod, K.P. The ground state energy of the Schrödinger–Newton equation. Phys. Lett. 2001, 280, 173. [Google Scholar] [CrossRef]
- Harrison, R.; Moroz, I.; Tod, K.P. A numerical study of the Schrödinger—Newton equations. Nonlinearity 2003, 16, 101. [Google Scholar] [CrossRef]
- Wei, J.; Winter, M. Strongly interacting bumps for the Schrödinger—Newton equations. J. Math. Phys. 2009, 50, 012905. [Google Scholar] [CrossRef]
- Giulini, D.; Grossardt, A. Gravitationally induced inhibitions of dispersion according to the Schrödinger—Newton equation. Class. Quantum Grav. 2011, 28, 195026. [Google Scholar] [CrossRef]
- Manfredi, G.; Hervieux, P.-A.; Haas, F. Variational approach to the time-dependent Schrödinger–Newton equations. Class. Quantum Grav. 2013, 30, 075006. [Google Scholar] [CrossRef]
- Duval, C.; Lazzarini, S. On the Schrödinger–Newton equation and its symmetries: A geometric view. Class. Quantum Gravity 2015, 32, 175006. [Google Scholar] [CrossRef]
- Diósi, L. Gravity-related wave function collapse: Is superfluid He exceptional? Found. Phys. 2014, 44, 483. [Google Scholar] [CrossRef]
- Grossardt, A.; Hiesmayr, B.C. Newtonian self-gravitation in the neutral meson system. Phys. Rev. 2015, 91, 064056. [Google Scholar] [CrossRef]
- Bera, S.; Mohan, R.; Singh, T.P. Stochastic modification of the Schrödinger-Newton equation. Phys. Rev. 2015, 92, 025054. [Google Scholar] [CrossRef]
- Bera, S.; Donadi, S.; Lochan, K.; Singh, T.P. A comparison between models of gravity induced decoherence. Found. Phys. 2015, 45, 1537. [Google Scholar] [CrossRef]
- Prosperi, G.M. Introduction of a Classical Level in Quantum Theory: Continuous Monitoring. Found. Phys. 2016, 46, 1426. [Google Scholar] [CrossRef]
- Bera, S.; Giri, P.; Singh, T.P. Spacetime Fluctuations and a Stochastic Schrödinger–Newton Equation. Found. Phys. 2017, 47, 897. [Google Scholar] [CrossRef]
- Tilloy, A.; Diósi, L. Principle of least decoherence for Newtonian semiclassical gravity. Phys. Rev. 2017, 96, 104045. [Google Scholar] [CrossRef]
- Howl, R.; Penrose, R.; Fuentes, I. Exploring the unification of quantum theory and general relativity with a Bose–Einstein condensate. New J. Phys. 2019, 21, 043047. [Google Scholar] [CrossRef]
- Diósi, L. Planck length challenges non-relativistic quantum mechanics of large masses. J. Phys. Conf. Ser. 2019, 1275, 011001. [Google Scholar] [CrossRef]
- Lotte, B.K.; Mishra, S. Effect of post-Newtonian-like self-energy, quantum gravity and exchange correlations on Schwarzschild black hole: Application of uncertainty principle. Mod. Phys. Lett. 2020, 35, 2050081. [Google Scholar] [CrossRef]
- Kelvin; Onggadinata, K.; Lake, M.J.; Paterek, T. Dark energy effects in the Schrödinger-Newton approach. Phys. Rev. 2020, 101, 063028. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy, Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Harko, T.; Lobo, F.S.N. Beyond Einstein’s General Relativity: Hybrid metric-Palatini gravity and curvature-matter couplings. Int. J. Mod. Phys. 2020, 29, 2030008. [Google Scholar] [CrossRef]
- Brizuela, D.; Duran-Cabac, A. Relativistic effects on the Schrödinger—Newton equation. Phys. Rev. D 2022, 106, 124038. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Dialektopoulos, K.F.; Romano, A.E.; Skordis, C.; Tomaras, T.N. The maximum sizes of large scale structures in alternative theories of gravity. J. Cosmol. Astropart. Phys. 2017, 2017, 018. [Google Scholar] [CrossRef]
- Adomian, G. Convergent series solution of nonlinear equations. J. Comput. Appl. Math. 1984, 11, 2. [Google Scholar] [CrossRef]
- Adomian, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Adomian, G.; Rach, R. Modified adomian polynomials. Math. Comput. Model. 1996, 24, 39. [Google Scholar] [CrossRef]
- Warwaz, A.-M. The modified decomposition method and Padé approximants for solving the Thomas–Fermi equation. Appl. Math. Comput. 1999, 105, 11. [Google Scholar]
- Warwaz, A.-M. A reliable modification of Adomian decomposition method. Appl. Math. Comput. 1999, 102, 77. [Google Scholar]
- Azreg-Ainou, M. Developed Adomian method for quadratic Kaluza–Klein relativity. Class. Quant. Grav. 2010, 27, 015012. [Google Scholar] [CrossRef]
- Wazwaz, A.-M.; Rach, R.; Duan, J.-S. A study on the systems of the Volterra integral forms of the Lane–Emden equations by the Adomian decomposition method. Math. Meth. Appl. Sci. 2014, 37, 10. [Google Scholar] [CrossRef]
- Ghasemi, H.; Ghovatmand, M.; Zarrinkamar, S.; Hassanabadi, H. Interaction of nanoparticles for the peristaltic flow in an asymmetric channel with the induced magnetic field. Eur. Phys. J. Plus 2014, 129, 32. [Google Scholar] [CrossRef]
- Rach, R.; Wazwaz, A.-M.; Duan, J.-S. The Volterra integral form of the Lane–Emden equation: New derivations and solution by the Adomian decomposition method. J. Appl. Math. Comput. 2015, 47, 365. [Google Scholar] [CrossRef]
- Battista, E.; Di Grezia, E.; Esposito, G. Bicharacteristics and Fourier integral operators in Kasner spacetime. Int. J. Geom. Methods Modern Phys. 2015, 12, 1550060. [Google Scholar]
- Duan, J.-S.; Rach, R.; Wazwaz, A.-M. Higher order numeric solutions of the Lane–Emden-type equations derived from the multi-stage modified Adomian decomposition method. Int. J. Comput. Math. 2017, 94, 197. [Google Scholar] [CrossRef]
- Mak, M.K.; Leung, C.S.; Harko, T. Computation of the general relativistic perihelion precession and of light deflection via the Laplace-Adomian Decomposition Method. Adv. High Energy Phys. 2018, 7093592. [Google Scholar] [CrossRef]
- Mak, M.K.; Leung, C.S.; Harko, T. Solving the nonlinear biharmonic equation by the Laplace-Adomian and Adomian Decomposition Methods. Surv. Math. Its Appl. 2018, 13, 183. [Google Scholar]
- Harko, T.; Mak, M.K.; Leung, C.S. Vortex solutions in atomic Bose-Einstein condensates via the Adomian decomposition method. Rom. Rep. Phys. 2020, 72, 116. [Google Scholar]
- Harko, T.; Mak, M.K. Series solution of the Susceptible-Infected-Recovered (SIR) epidemic model with vital dynamics via the Adomian and Laplace-Adomian Decomposition Methods. arXiv 2020, arXiv:2009.00434. [Google Scholar]
- Alam, M.N.; Tunç, C. Constructions of the optical solitons and other solitons to the conformable fractional Zakharov–Kuznetsov equation with power law nonlinearity. J. Taibah Univ. Sci. 2020, 14, 94. [Google Scholar] [CrossRef]
- Baker, G.A., Jr.; Graves-Morris, P. Padé Approximants; Cambridge University Press: Cambridge, UK; New York, NY, USA; Melbourn, Australia, 1996. [Google Scholar]
- Hobson, M.P.; Efstathiou, G.P.; Lasenby, A.N. General Relativity: An Introduction for Physicists; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Grossardt, A.; Bateman, J.; Ulbricht, H.; Bassi, A. Opto-mechanical test of the Schrödinger–Newton equation. Phys. Rev. 2016, 93, 096003. [Google Scholar]
- Karolyhazy, F. Gravitation and quantum mechanics of macroscopic objects. Nuovo Cim. 1966, 42, 390. [Google Scholar] [CrossRef]
- Diosi, L. Gravitation and quantum-mechanical localization of macro-objects. Phys. Lett. 1984, 105, 199. [Google Scholar] [CrossRef]
- Penrose, R. On Gravity’s Role in Quantum State Reduction. Gen. Rel. Grav. 1996, 28, 581. [Google Scholar] [CrossRef]
- Minar, J.; Sekatski, P.; Sangouard, N. Bounding quantum gravity inspired decoherence using atom interferometry. Phys. Rev. 2016, 94, 062111. [Google Scholar] [CrossRef]
- Bose, S.; Jacobs, K.; Knight, P.L. A scheme to probe the decoherence of a macroscopic object. Phys. Rev. 1999, 59, 3204. [Google Scholar] [CrossRef]
- van Meter, J. Test Schrödinger-Newton ‘collapse’ of the wave function. Class. Quant. Grav. 2011, 28, 215013. [Google Scholar] [CrossRef]
- Burikham, P.; Cheamsawat, K.; Harko, T.; Lake, M.J. The minimum mass of a spherically symmetric object in D-dimensions and its implications for the mass hierarchy problem. Eur. Phys. J. C 2015, 75, 442. [Google Scholar] [CrossRef]
- Lake, M.J. Is there a connection between “dark” and “light” physics? J. Phys. Conf. Ser. 2017, 883, 012001. [Google Scholar] [CrossRef]
- Lake, M.J. Minimum length uncertainty relations in the presence of dark energy. Galaxies 2019, 7, 11. [Google Scholar] [CrossRef]
- Lake, M.J. Why space must be quantised on a different scale to matter. arXiv 2020, arXiv:2005.12724v2. [Google Scholar]
- Hashiba, J. Dark Energy from Eternal Pair-production of Fermions. arXiv 2018, arXiv:1808.06517. [Google Scholar]
- Lake, M.J.; Jain, S.; Paterek, T. A simple model of a zero-energy expanding Universe. 2023; manuscript in preparation. [Google Scholar]
- Perivolaropoulos, L. Submillimeter spatial oscillations of Newton’s constant: Theoretical models and laboratory tests. Phys. Rev. D 2017, 95, 084050. [Google Scholar] [CrossRef]
- Antoniou, I.; Perivolaropoulos, L. Constraints on spatially oscillating sub-mm forces from the Stanford Optically Levitated Microsphere Experiment data. Phys. Rev. D 2017, 96, 104002. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Kazantzidis, L. Hints of Modified Gravity in Cosmos and in the Lab? Int. J. Mod. Phys. D 2019, 28, 1942001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).