Waiting for a Mathematical Theory of Living Systems from a Critical Review to Research Perspectives

Abstract

This paper presents a survey of advanced concepts and research perspectives, of a philosophical-mathematical approach to describe the dynamics of systems of many interacting living entities. The first part introduces the general conceptual framework. Then, a critical analysis of the existing literature is developed and referred to a multiscale view of a mathematics of living organisms. This paper attempts to understand how far the present state-of-the-art is far from the achievement of such challenging objective. The overall study leads to identify research perspectives and possible hints to deal with them.

1. Motivations and Plan of the Paper

The development of mathematical and physical tools to describe the dynamics of living organisms is one of the challenging scientific objectives of this century. This search requires new inventions rather than the use of known methods to be straightforwardly applied. The impact is not limited to science only as we live in a complex and fragile planet. Understanding what life is, leads to understand the planet and avoid, as far as we can, the collapse of the environment where we live.

Our paper attempts to provide a preliminary answer to the following key question:

What is life and how science can contribute to a mathematical theory of living systems?

We do not naively claim that the present state of the art can provide an exhaustive answer to this question. Indeed, we are aware that our contribution is still far away from a universal value, but we still try to reduce the gap between the present knowledge and what should be known. It is a challenging quest which, according to a not immediate perspective, will lead to a new mathematical theory combined with new interpretations of the physics of living systems.

The content of our paper is mainly focused on concepts, while formalized topics are presented only when they are necessary. The contents of the next sections are as follows.

Section 2 firstly, develops a philosophical–mathematical excursus on a pioneering literature, as well as on scientific contributions that define the conceptual difficulties to address the aforementioned objective. Then, a critical study of the complexity features of living organisms is proposed and, out of this preliminary study a possible strategy towards the derivation of mathematical models of living organisms is designed.

Section 3 firstly, shows how the so called kinetic theory of active particles is consistent with the said strategy and how it can be applied to well defined case studies. Then, it reports on three fields of applications. Specifically, social dynamics, the in-host immune competition, and the dynamics of human crowds. It provides a brief survey on one of the key steps in the development of a mathematical theory of life, i.e., the interpretation of multiscale problems in the spirit of the sixth Hilbert problem [1]. This means derivation of models at each scale based on the same principles and moving across scales by mathematical tools.

Section 4 contributes to an answer to the aforementioned key question and looks ahead to research perspectives. The section indicates that the key direction to be studied is the mathematical description of the individual based interactions and provides some perspective reasonings on the use of tools by artificial intelligence to address this problem.

2. From a Philosophical-Mathematical Excursus towards a Mathematics of Life

This section reports about some selected contributions to the interpretation and mathematical description of living organisms. Then, we move to a quest towards a mathematical theory.

2.1. A Philosophical–Mathematical Excursus

A strategic contribution to promote research activity on the main topic of this paper was delivered, in the year 2011, by the American Mathematical Society, the American Statistical Association, the Mathematical Association of America, and the Society for Industrial and Applied Mathematics announced the Mathematics. Indeed, the theme of the Mathematics Awareness Month was defined as follows: Unraveling Complex Systems. The following statement defines the key objective:

We are surrounded by complex systems. Familiar examples include power grids, transportation systems, financial markets, the Internet, and structures underlying everything from the environment to the cells in our bodies. Mathematical models can guide us in understanding these systems […].

Examples of complex systems in our society were presented, soon after, in [2], where the following examples were reported: vehicular traffic, crowds, multicellular systems, networks, financial markets, etc. These studies were anticipated by scientific books specifically devoted to this topic, see [3,4], and soon after [5], with main focus on the dynamics of large systems of very many interacting living entities. Each book presents a conceptually different approach inspired by mathematical tools of statistical physics. Analogous methods were also developed to model the competition between the immune system and cancer cells [6].

Before moving to the recent literature, let us examine some selected studies that appeared in the last century, with particular attention to the literature inspired by methods of statistical physics. We start from Erwin Schrodinger’s contributions based on the intuition that the collective dynamics of living systems is generated by individual based interactions [7]. In particular, a key interpretation is that living systems keep far from equilibrium as they continuously extract energy far from equilibrium. Further, a multiscale vision appears in his work by arguing that all scales, from genes to tissues, are involved in the dynamics.

Living matter, while not eluding the “laws of physics” as established up to date, is likely to involve “other laws of physic” hitherto unknown, which however, once they have been revealed, will form just as integral a part of science as the former.

He anticipates that this statement will be open to misconception and tries to clarify it. The main principle involved with “order-from-disorder” is the second law of thermodynamics, according to which entropy only increases in a closed system (such as the universe). Schrodinger explains that living matter evades the decay to thermodynamical equilibrium by homeostatically maintaining negative entropy in an open system.

The first contribution to model the dynamics of a well defined living system is due to Ilia Prigogine [8] who proposed, with Herman, a mathematical description of vehicular traffic by methods somehow related to the Boltzmann equation. Specifically, the dependent variable is the one-particle distribution function over the micro-state of vehicles defined by position and velocity. Prigogine’s approach considers the overall heterogeneity of slow and fat vehicles similarly to the dynamics of diluted gases. An important step forward is proposed in [9], where heterogeneity is modeled as an inner characteristics of each individual entity viewed as a vehicle-driver subsystem.

An interesting contribution was proposed in [10] concerning the social dynamics of certain species of insects, where interactions split the society into dominant and dominated. This paper has the merit of having inspired several subsequent contributions devoted to the modeling of social dynamics. Indeed, the derivation of a Fokker–Plank-like model transfers the information from the dynamics of interactions into the description of the collective dynamics. This paper was followed by new ideas in a totally different field, i.e., the modeling the competition between immune and cancer cells, where interactions include also birth and death dynamics [11]. This pioneering paper generated an intense research line reported in the book [6].

This brief excursus does not cover exhaustively the literature in the field. So far, the interested reader can discover additional titles in the bibliography of these books, as well as in surveys on the so-called behavioral dynamics [12]. An additional interesting source of concepts and ideas is the review [13] inspired by methods of the kinetic theory and non equilibrium dynamics. In addition, living systems are evolutionary. Therefore, the rules of the aforementioned dynamics and interactions evolve in time as Ernst Mayr teaches to us [14].

Out of the brief excursus above, we can conclude that, in the case of living organisms, the main difficulty to transfer the phenomenological reality into a mathematical framework is that we do not have sufficient knowledge to quantitatively identify the cause–effect link. Indeed, we do not have a physical theory of living systems, as observed in [7] and confirmed by various authors [15,16]. This conclusion is consistent with the statement by the Nobel laureate Lee Hartwell [17]

Although living systems obey the laws of physics and chemistry, the notion of function or purpose differentiates biology from other natural sciences. Organisms exist to reproduce, whereas, outside religious belief, rocks and stars have no purpose. Selection for function has produced the living cell, with a unique set of properties that distinguish it from inanimate systems of interacting molecules.

2.2. On a Strategy towards a Mathematics of Living Systems

As we have seen, a mathematical approach should tackle the difficulty of the lack of quantitative methods to describe causality dynamics. An additional difficulty to be tackled is that living systems are complex. Hence, modeling of individual dynamics does not straightforwardly lead to a mathematical description of collective emerging behaviors. Namely, it is very difficult to understand and model these systems based on the sole description of the dynamics and interactions of a few individual entities.

A first step toward a strategy in the quest for mathematical tools has been proposed in [3] and subsequently updated, mainly motivated by applications. We will not repeat well known concepts. The reader is referred, mainly to Section 3, to the open access article [18]. The strategy is based on the hypothesis that living, hence complex systems, present common features.

• Expression of functions: Living entities, which may be defined micro-systems to account that their representation is at the lower scale with respect to that of the global system. An alternative definition is active particles, shortly a-particles, see [18]. These have the ability to express a function called activity. These entities are able to develop specific strategies and organization abilities that depend on the state of the surrounding entities and environment.
• Heterogeneity: The ability to express the activity is not the same for all micro-systems as the expression of heterogeneous behaviors is a common feature of a great part of living systems.
• Nonlinearity of interactions: Interactions are nonlinearly additive, nonlocal, as they may involve entities that are not immediate neighbors and, in some cases, asymmetric. Active particles are sensitive not only to a selection of other individual entities, but to the overall system as a whole.
• Learning ability: Living systems receive inputs from the environments and have the ability to learn from past experience. Accordingly, the rules of interaction and activity they develop evolves in time.
• Functional subsystems: Active particles can aggregate into groups, called functional subsystems, shortly FSs, where they pursue the same objectives, share the same activity and interaction rules.
• Output of interactions: Interactions modify the activity and generate proliferative and destructive events.
• Darwinian mutations and selection: All living systems are evolutionary, as interactions can generate, by birth of aggregations, new entities that are increasingly fitted to the environment, that, in turn, generate new entities again more fitted to the environment.

The applications reviewed and critically analyzed in the next section aims at showing how specific models preserve the aforementioned complexity features. Therefore, models derived according to such strategy go beyond population dynamics that studies how the size and age composition of groups of individuals change over time.

The derivation can follow different approaches. For instance, the so-called kinetic theory of active particles [18], behavioral swarms [19], developed after the celebrated paper by Cucker and Smale [20], and Boltzmann and Fokker Plank methods [5]. Our paper mainly focuses on the first method which is inspired to methods of statistical physics, but some differences appear. These are put in evidence in the following sequential steps which describe the modeling approach:

• The overall system of a-particles is subdivided into functional subsystems accounting for the activity variables rather than physical properties of the matter of the system.
• The state of each FS is described by the one particle distribution function over the micro-state of the a-particles belonging to it: $f_i=f_i(t,\mathit{x},\mathit{v},\mathbf{u})$ with $f_i\ge 0$ for all $t,\mathit{x},\mathit{v},\mathbf{u}$, where t is time, $\mathit{x}$ and $\mathit{v}$ model the localization and velocity of the a-particle, and $\mathbf{u}$ is the activity shared by all a-particles of the FS.
• Interactions can produce onset or disappearance of new micro-systems, as well as transition across FSs. Their modeling is developed by theoretical tools of collective learning [21,22] and stochastic games theory [18].
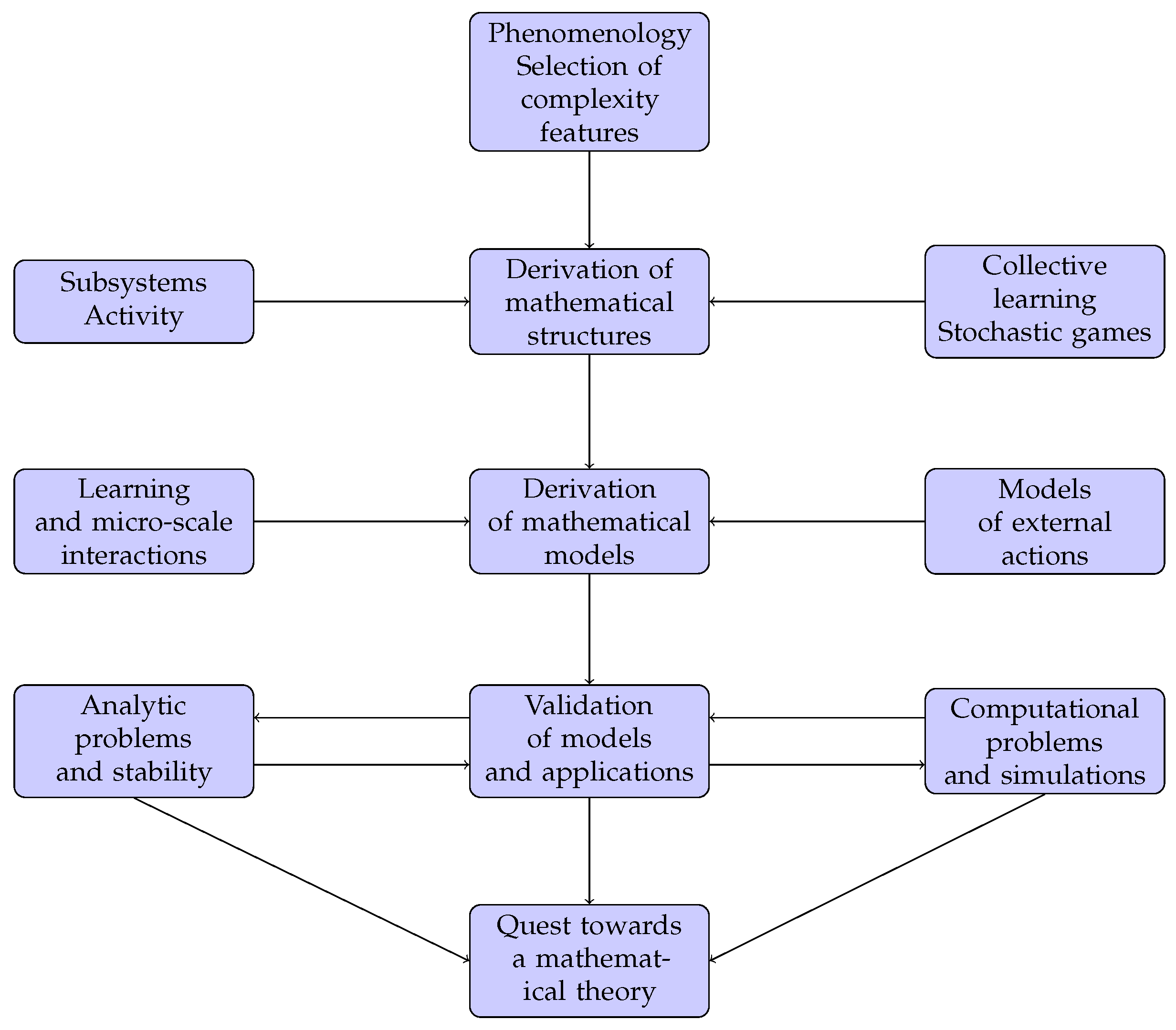
• Derivation of a general mathematical structure with the aim of offering the conceptual framework toward the derivation of specific models. This structure is required to express the dynamics of the complexity features of living systems.
• Derivation of specific models corresponding to well-defined classes of systems by implementing the said structure with suitable models of individual-based, micro-scale, interactions.

The following remarks provide a further insight of Figure 1.

• The phenomenological interpretation of living systems can take advantage of specific measurement devices, but it is always somehow conditioned by individual sensitivity within the framework of the sensitive world by Immanuel Kant [23,24] or even within the framework of the artificial world by Herbert Simon [25].
• Generally, the derivation of models is developed by a hierarchy in which each micro-system firstly learn from the other micro-systems and subsequently, modifies the mechanical state.
• The application of models generates challenging analytic and computational problems which require new inventions to tackle them in real applications by the critical analysis developed in the next section after a review of specific classes of models.

Once the main features of the approach have been defined, the interested reader is referred to the actual mathematical formalization [18]. However, the review of applications presented in the next section will provide formal indications on the mathematical structures used in specific applications.

The application of models to the study of real systems generates both analytically and computationally challenging mathematical problems. The whole path is shown in Figure 1, where each block indicates a well defined action of the modeling approach from the phenomenological interpretation of real system to the derivation of models followed by their applications. Even so, we still await a mathematical theory of living systems.

3. From Active Particles Methods to Selected Applications

The key step of the modeling strategy presented in Section 2 is the derivation of the mathematical structures charged to provide the conceptual framework for model derivation. Firstly, in the the case of space homogeneity and, subsequently, on the role that this specific dynamic can have on different types of space-dependent dynamics. These topics are treated in the next two subsections, while the third subsection presents some reasonings about research perspectives. The presentation is purposely selective rather than exhaustive. Indeed, we select some key papers to examine how the quest toward a mathematics for living systems has evolved within the general framework presented in the previous section.

3.1. Mathematical Models in Space Homogeneity

As mentioned, the kinetic theory of active particles was initially developed in the case of spatial homogeneity somehow inspired by the modeling of the social dynamics of certain insect populations. The first contribution to this theory focused on the modeling of the competition between cancer cells and the immune system [11]. This topic rapidly captured the attention of applied mathematicians who produced various contributions documented in the book [6]. In parallel, but with some delay, these methods were also applied to modeling social dynamics covering topics such as opinion formation [26,27,28] and collective learning [22].

The general mathematical structure which provides the framework for the derivation of these models is obtained by a balance of particles within the elementary volume of the micro-states. The structure is as follows:

$${\partial }_t{f}_i(t,\mathbf{u})=\left({\mathcal{C}}_i-{\mathcal{L}}_i\right)\left[\mathbf{f}\right](t,\mathbf{u})+\left({\mathcal{P}}_i-{\mathcal{D}}_i\right)\left[\mathbf{f}\right](t,\mathbf{u})={\mathcal{A}}_i\left[\mathbf{f}\right](t,\mathbf{u})+{\mathcal{B}}_i\left[\mathbf{f}\right](t,\mathbf{u}),$$

(1)

where ${\mathcal{A}}_i={\mathcal{C}}_i-{\mathcal{L}}_i$ and ${\mathcal{B}}_i={\mathcal{P}}_i-{\mathcal{D}}_i$ correspond, respectively, to the net rate generated by number conservative and proliferative/destructive dynamics. Both of them have the structure of a gain minus a loss term.

Let us consider frameworks that do not include dynamics across FSs. Technical calculations. reported in [18], Section 3, yield:

$$\begin{array}{c}{\mathcal{A}}_i=\sum _{k=1}^n{\int }_{D_{\mathbf{u}}\times D_{\mathbf{u}}}{\eta }_{ik}({\mathbf{u}}_{*},{\mathbf{u}}^{*}){\mathcal{C}}_{ik}\left[\mathbf{f}\right]\left({\mathbf{u}}_{*}\to \mathbf{u}|{\mathbf{u}}_{*},{\mathbf{u}}^{*}\right)f_i(t,{\mathbf{u}}_{*})f_k(t,{\mathbf{u}}^{*})d{\mathbf{u}}_{*}d{\mathbf{u}}^{*}\hfill \\ -f_i(t,\mathbf{u})\sum _{k=1}^n{\int }_{D_{\mathbf{u}}}{\eta }_{ik}(\mathbf{u},{\mathbf{u}}^{*})f_k(t,{\mathbf{u}}^{*})d{\mathbf{u}}^{*},\hfill \end{array}$$

(2)

and

$$\begin{array}{c}{\mathcal{B}}_i=\sum _{k=1}^n{\int }_{D_{\mathbf{u}}\times D_{\mathbf{u}}}{\mu }_{ik}({\mathbf{u}}_{*},{\mathbf{u}}^{*}){\mathcal{P}}_{ik}\left[\mathbf{f}\right]\left({\mathbf{u}}_{*}\to \mathbf{u}|{\mathbf{u}}_{*},{\mathbf{u}}^{*}\right)f_i(t,{\mathbf{u}}_{*})f_k(t,{\mathbf{u}}^{*})d{\mathbf{u}}_{*}d{\mathbf{u}}^{*}\hfill \\ -f_i(t,\mathbf{u})\sum _{k=1}^n{\int }_{D_{\mathbf{u}}}{\mu }_{ik}(\mathbf{u},{\mathbf{u}}^{*}){\mathcal{D}}_{ik}\left[\mathbf{f}\right](\mathbf{u},{\mathbf{u}}^{*})f_k(t,{\mathbf{u}}^{*})d{\mathbf{u}}^{*},\hfill \end{array}$$

(3)

where $\mathbf{f}$ denotes the set of all $f_i$, $D_{\mathbf{u}}$ is the domain of the activity variable, while interactions are modeled by the following terms:

• Interaction rate for conservative dynamics:${\eta }_{ik}({\mathbf{u}}_{*},{\mathbf{u}}^{*})$, which models the frequency of the interactions between a candidate i-micro-system with state ${\mathbf{u}}_{*}$ and a field k-micro-system with state ${\mathbf{u}}^{*}$, where the label i denotes the FS.
• Interaction rate for non-conservative dynamics:${\mu }_{ik}({\mathbf{u}}_{*},{\mathbf{u}}^{*})$, is analogous to ${\eta }_{ik}$, but corresponding to proliferative and destructive interactions.
• Transition probability density:${\mathcal{C}}_{ik}\left[\mathbf{f}\right]({\mathbf{u}}_{*}\to \mathbf{u}|{\mathbf{u}}_{*},{\mathbf{u}}^{*})$, which denotes the probability density that a candidate i-micro-system, with state ${\mathbf{u}}_{*}$, ends up into the state of the test micro-system of the same FS after an interaction with a field k-micro-system.
• Proliferative term:${\mathcal{P}}_{ik}\left[\mathbf{f}\right]({\mathbf{u}}_{*}\to \mathbf{u}|{\mathbf{u}}_{*},{\mathbf{u}}^{*})$, which models the proliferative events for a candidate h-particle, with state ${\mathbf{u}}_{*}$, into the same FS after interaction with a field k-particle with state ${\mathbf{u}}^{*}$.
• Destructive term:${\mathcal{D}}_{ik}\left[\mathbf{f}\right](\mathbf{u},{\mathbf{u}}^{*})$, which models the rate of destruction for a test i-particle in its own functional subsystem after an interaction with a field k-particle with state ${\mathbf{u}}^{*}$.

Test, candidate, and field micro-system denote, within a statistical framework, respectively, the micro-system charged to describe the overall state by a one particle distribution function, the micro-system which, by interaction with the field micro-system in its domain of interaction $D_{\mathbf{u}}$ takes, at time t, the state $\mathit{x},\mathit{v},\mathbf{u}$ of the test micro-system.

The pioneering paper [11] based the modeling approach to the structure delivered by Equations (1)–(3) specialized to three FSs corresponding tumor, immune and epithelial cells. A scalar variable was used for the activity corresponding to progression of the tumor cells, activation of the immune system from innate immunity to adaptative immunity. The model considered the ability of tumor to escape the learning ability of immune cells. Simulations have shown interesting emerging behaviors such as the bifurcation role of the parameters modeling activation of the immune system. Indeed, values over and down the said critical value denoted, respectively, the regression and prevalence of the tumor over the immune system.

This model has generated many interesting studies and developments. We have selected those that have generated significant improvements in the mathematical structure and, consequently, in the modeling approach.

This model has generated several interesting studies and developments. We have selected those which have produced significant improvements of the mathematical structure and, consequently, of the modeling approach.

• Modeling pseudo-Darwinian mutations to escape the control of the immune system has been developed in [29]. This paper has transferred into a mathematical framework the biological theory of cancer progression by mutations introduced by Hanahan and Weinberg [30,31].
• Modeling the competition between a virus and the immune system, accounting for the progression of the virus and the activation of the immune system has been proposed in [32].
• Somehow inspired to the above literature is the study developed in [33] to model the in-host dynamics in the upper respiratory tracts, where the virus proliferates, although contrasted by the immune system attempting to reduce the invasion ability of the virus. Further developments have been presented in [34] to consider the role of mutations and onset of new variants.

It is worth mentioning that the study of social systems in general has been, as mentioned, one of the first fields of application of the kinetic theory of active particles. The authors who have developed the aforementioned applications quickly recognized that this type of dynamics interacts with almost all other types of dynamics, in particular with the dynamics of biological systems. See the reviews [35,36], where in the latter the key open problem proposed in the last chapter of [37] have been tackled by constructive approach. In particular, it has been observed that almost all research activity was focused on consensus dynamics, while in reality interactions could also include the dynamics of dissent, see [37]. This observation has led to models where the interaction dynamic also depend on $\mathbf{f}$, see [38,39].

3.2. Mathematical Models with Space Dynamics

The kinetic theory of active particles has been firstly applied to modeling vehicular traffic on roads and subsequently human crowd dynamics. The mathematical structure used to derive models with space dynamics can be obtained by calculations analogous to those for the spatially homogeneous case. The result, in absence of dynamics across FSs, see [18], is as follows:

$$\begin{array}{ccc}& & ({\partial }_t+\mathit{v}·{\nabla }_{\mathit{x}})f_i(t,\mathit{x},\mathit{v},\mathbf{u})\hfill \\ & & =\sum _{k=1}^n{\int }_{D_G}{\eta }_{ik}({\mathit{w}}_{*},{\mathit{w}}^{*}){\mathcal{C}}_{ik}\left[\mathbf{f}\right]({\mathit{v}}_{*}\to \mathit{v},{\mathbf{u}}_{*}\to \mathbf{u}|{\mathit{w}}_{*},{\mathit{w}}^{*})\hfill \\ & & \times f_i(t,\mathit{x},{\mathit{v}}_{*},{\mathbf{u}}_{*})f_k(t,{\mathit{x}}^{*},{\mathit{v}}^{*},{\mathbf{u}}^{*})d{\mathit{x}}^{*}d{\mathit{v}}_{*}d{\mathit{v}}^{*}d{\mathbf{u}}_{*}d{\mathbf{u}}^{*}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & -f_i(t,\mathit{x},\mathit{v},\mathbf{u})\sum _{k=1}^n{\int }_{D_L}{\eta }_{ik}(\mathit{w},{\mathit{w}}^{*})f_k(t,{\mathit{x}}^{*},{\mathit{v}}^{*},{\mathbf{u}}^{*})d{\mathit{x}}^{*}d{\mathit{v}}^{*}d{\mathbf{u}}^{*},\hfill \end{array}$$

(5)

where $D_G=\Omega \times D_{\mathit{v}}\times D_{\mathit{v}}\times D_{\mathbf{u}}\times D_{\mathbf{u}}$, and $D_L=\Omega \times D_{\mathit{v}}\times D_{\mathbf{u}}$, define the interaction domains, while $\mathit{w}$, ${\mathit{w}}_{*}$ and ${\mathit{w}}^{*}$ denote, in a compacted form, the microscopic states $(\mathit{x},\mathit{v},\mathbf{u})$, $(\mathit{x},{\mathit{v}}_{*},{\mathbf{u}}_{*})$ and $({\mathit{x}}^{*},{\mathit{v}}^{*},{\mathbf{u}}^{*})$, respectively, and $\Omega$ is the (sensitivity) domain within which a particle, say candidate or test, feels the presence of the other particles.

Detailed calculations, see [40], indicate how $\Omega$ can be computed when the sensibility area ${\Omega }_s$ is given by an arc of circle, with radius R around the velocity direction. Then, if the visibility arc, symmetric or non-symmetric, is known, R is referred to the critical number of a-particles necessary to provide sufficient information. The meaning of the interaction terms $\eta$ and $\mathcal{C}$ is analogous to those described in Section 3.1.

Consider, similarly to Section 3.1, some selected applications which have brought to improvements of the mathematical structures. In detail, let us first consider the modeling of vehicular flow developed also thanks to the pioneering contributions [8,9]. The following articles [41,42,43,44] can be identified among various others. In detail, the concept that the interaction dynamics depend not only on the state on the vehicles, e.g., fast and slow vehicles but also on the local density was introduced in [41,42]. The role of drivers behavior was considered in [43].

These papers focus on a one lane flow and adopt a grid with discrete speeds. In [42] a fixed grid was used under the assumption that the probability of transition to an higher or to a lower velocity would depend on the local density. In particular, low density supports the speed increase, while high density supports the opposite dynamics. The same result was obtained in [41] which used a density dependent grid shrinking with the local density. This approach has the advantage of bringing the number of vehicles within each speed segment to the same order- in most cases almost the same number.

An interesting development consists in using a grid, not only for the speed, but also for the space, see [44,45]. Then, the model takes the structure of a system of ordinary differential equations, rather than that of a system of hyperbolic differential equations.

With reference to the study of human crowds, it should considered that the overall dynamic depends on the physical-emotional state of pedestrians and that such state is a dynamical variable that evolves in time and space as a result of interactions. Furthermore, this individual state is the key feature to be considered in the situations where safety problems should be considered [46,47,48]. Indeed, the recent literature in the field of crowd dynamics focuses on this type of problems. In particular, on how the stress modifies the trajectories of walkers from the rational ones, which improve safety, to unsafe conditions, where individuals are attracted toward overcrowded areas, see [49,50]. A literature focusing on this aspect of the modeling approach can be identified in various papers. In detail the following topics have been studied: self organization in corridors by which pedestrians moving in opposite directions in corridors organize their flows in the shape of fingers, see [49]; contrast of antagonist group, see [50]; a first step toward a multiscale vision by showing that the dynamics at each scale can be described by the same parameters [51]. In addition, we mention simulations developed in complex geometries, see [52], by methods specific of kinetic type equations [53].

We trust that the kinetic approach is more appropriate to explain the behavior of living entities, see the critical study in, see [54]. However, this aspect should also be considered at the lower and higher scale. This specific topic is treated in [55], where the activity is considered as dynamical variable which affects the collective dynamics at all scales, i.e., micro-, meso- and macro-scale. This result is also useful, as the cost of computing for kinetic theory equations is high compared with those of the equations at the low and higher scale. Further perspectives to be considered are the application of modeling tools developed for crowds to other types of collective motions, see [56] and correlation of crowd motions to probability of contagion [57,58].

3.3. A Forward Look to Perspectives in Modeling

The key block of the modeling approach, represented in Figure 1, refers to the selection of the mathematical structure and the modeling of interactions. The models we have reviewed have used “ad hoc” specialization of the more general structure. Therefore, a forward look to modeling perspectives should first consider further developments of the said structure according to the specific case study under consideration. Then, modeling should focus on interactions.

• Vector activity variable and related hierarchy of the development of the dynamics. Indeed, more that one variable might be necessary to characterize micro-systems. The difficulty in identifying the correlations between them suggests to understand whether the decision-making process, as often happens in living systems, follows a sequence linked to the components of the activity.
• Correlation of the role of the activity to the dynamics of the mechanical variables. This means selecting the velocity directions and then, adapting the speed to the local flow conditions. This selection is activity-driven. As an example, increasing stress conditions increases the tendency towards the main (overcrowded) stream rather than the seeking less crowded areas.
• Including mutations and selection also in the study of social systems. This type of dynamics is typical of biological systems. However, a dynamic across functional subsystems can be observed also in social systems. For instance in opinion dynamics micro-systems can move from a group of interest to another one.
• Exploring new mathematical structures. The reasoning on the possible developments of the mathematical structures reviewed in this section is definitely a strategic objective. However, a global vision should also consider other frameworks such as those mentioned in Section 2.2, i.e., behavioral swarms [19] and Boltzmann and Fokker-Plank methods [5] and even possible interactions between different frameworks.
• Exploring multi scale methods. The Hilbert’s sixth problem concerns the search of a unified mathematical approach to physical theories. A conceivable preliminary step would be the derivation of models at all scales by the same principles and, subsequently, the passage to mathematical (hence rigorous) methods from the low to the higher scale. This passage is depicted in Figure 2.

Concerning the fifth item, some encouraging results concerning both the derivation of models from the same principles at all scales, see the application of crowd dynamics [55], and the derivation of macroscopic equations from the underlying micro-scale description. This problem, has been intensively studied in the case of classical particles, see [59]. The study in the case of living a-particles needs to address the problem of the lack of general solutions for the equilibrium configurations and of a general kinetic model. This problem has been studied in [60,61] acting on a kinetic model obtained by adding to the spatially homogeneous case a kinetic jump-velocity perturbation, invented by [62] and used by various authors, for instance see [63,64,65,66]. Thus, writing the model in dimensionless form allows to extract a small parameter and find a power expansion of macroscopic models. The approach refers to diffusion limits [60,61], where various applications have been treated, see also the pioneering papers [67], for a general bibliography see also [68].

Highly complex is the modeling of the interactions, although a qualitative study of the causality dynamics can be developed. However, an important remark is that models refer each specific cause-effect relation to a parameter and that specific studies are, in some cases, developed to understand this matter. This is the case of models of crowd dynamics reviewed in Section 3.2. This matter will be further discussed in the next section. Indeed, refining the mathematical interpretation of interactions can provide an essential contribution to a mathematical theory of life.

4. On a Forward Look to a Mathematical Theory of Living Systems

Let us now consider the key question posed in Section 1 with the aim of understanding how far we still stand from a mathematical theory. The various applications reviewed in Section 3 support the idea that the mathematical approach can be rich enough to model various systems also in other fields such as social sciences and applied sciences in general, up to the ability to predict rare events, occasionally called black swan [69]. An example is the study of well-fare dynamics inducing radicalization against governments, as reviewed in the survey paper [36].

An additional encouraging sign is given by the contributions to the Hilbert problem, where un a few case studies mathematical models at the macro-scale have been derived from the underlying description at the micro scale [60,61].

However, the search for a mathematics of living systems is still a goal which requires a huge additional work. This problem, in fact, has not an immediate connections with the theories of mathematical physics as in the case of living organisms, we currently have not a realistic possibility to discover a physical theory that governs the huge number of variables involved in the dynamics. We do not have, at present, a realistic chance to discover a physical theory governing the enormous number of variables involved in the dynamics. On the other hand, one may see the mathematical structure as a mathematical theory, albeit not yet as a mathematical theory for living systems.

Although we are very far from this challenging objective (to claim otherwise would be naive), we may look ahead to a theory for specific classes of living systems. According to the fact that the theory presented in Section 2 has the merit of having reproduced some specific features of living systems and mathematical models with the ability of reproducing emerging behaviors and reveal new ones to be properly studied.

Therefore, one may use the definition mathematical theory to address the general framework presented in Section 2 and mathematical models for those which are derived referring to such structure, while we consider heuristic models those which are derived by phenomenological, ad hoc, assumptions.

Bearing all above in the mind, we trust that the kinetic theory of active particles is the framework to be used to describe the dynamics of the class of systems under consideration. However, we need inventions to model interactions to implement the structures offered by the theory of stochastic games. Accordingly, we focus on some perspectives of artificial intelligence and the approach to the databases. In order to lead to the calibration of the model by observed empirical data. This objective can be referred to a specific example by referring to the models of crowd dynamics proposed in [55]. We focus on the role of the activity on the decision making by which walkers design their walking strategy. As mentioned, individuals first select a walking direction and then, adapt the speed to the local density conditions. The interpretation proposed in [55] is based on theoretical tools of a stochastic game theory, but the support of empirical data is limited to observation of collective motion, but not to individual behaviors.

Although, we express appreciation for the experimental activity of scientists focused on the study of individual behaviors, see [70,71], and engineers that design devices for visual records, see [72]; still organizing a database of databases for calibration of models is not a easy task.

In general, it is possible to access databases including data specifically referring to the real systems object of a modeling approach. Thus, the predicted dynamics might be obtained by an interpretation of the data available for both system and dynamics. The first example consists in the identification of the parameters and of their temporal dynamics. So that the mathematical structure generates a model, while simulations deliver the collective behavior to be compared with the observed ones. A technical difficulty to face is that complex systems are often sensitive to small variation of parameters, hence data specific for a certain case study cannot be straightforwardly transferred to the case study under consideration.

The synthesis of all above reasonings, is also the closure of our paper.

After selecting of a specific class of case studies, databases can be organized to collect data on a selected number of interactions which are specific to the case studies. The selection should correspond to the causality action characterizing each interaction. Therefore, selecting in the database the dynamics close, with a suitable metric, to those treated by a model would lead to the calibration of the model.