Density of States for the Unitary Fermi Gas and the Schwarzschild Black Hole

Abstract

The density of states of a quantum system can be calculated from its definition, but, in some cases, this approach is quite cumbersome. Alternatively, the density of states can be deduced from the microcanonical entropy or from the canonical partition function. After discussing the relationship among these procedures, we suggest a simple numerical method, which is equivalent in the thermodynamic limit to perform a Legendre transformation, to obtain the density of states from the Helmholtz free energy. We apply this method to determine the many-body density of states of the unitary Fermi gas, a very dilute system of identical fermions interacting with a divergent scattering length. The unitary Fermi gas is highly symmetric due to the absence of any internal scale except for the average distance between two particles and, for this reason, its equation of state is called universal. In the last part of the paper, by using the same thermodynamical techniques, we review some properties of the density of states of a Schwarzschild black hole, which shares the problem of finding the density of states directly from its definition with the unitary Fermi gas.

1. Introduction

The density of states appears in many contexts of statistical mechanics [1] and quantum physics [2]. The density of states, which tells you how many quantum states exist in a given range of energy (or momentum), is extremely useful for the experimental and theoretical determination of several physical quantities [1,2]. In some cases, one deals with the single-particle density of states, namely the density of states of a single quantum particle in the presence of an external potential. The determination of this single-particle density of states is often quite simple. Instead, the calculation of the many-body density of states, i.e., the density of states of the system composed by many interacting quantum particles, is usually a difficult task. Indeed, although the density of states of a quantum system can be, in principle, derived from its definition, and this approach is not always straightforward, in particular for many-body problems. As an alternative, the density of states can be deduced from the microcanonical entropy or the canonical partition function. As is well known, in the appropriate thermodynamic limit, microcanonical observables can be related to the corresponding canonical ones by means of a Legendre transformation [1].

In this paper, we suggest a straightforward technique for deriving the density of states from the Helmholtz free energy. This procedure is nothing else than a Legendre transformation of the entropy from the canonical ensemble to the microcanonical ensemble. We apply this method to calculate the many-body density of states of the unitary Fermi gas, characterized by an interaction potential with a divergent s-wave scattering length [3]. When the s-wave scattering length becomes very large, the attractive Fermi gas of fermionic pairs with opposite spins is made of weakly bound dimers. Strictly speaking, the unitary Fermi gas is made of dimers with zero binding energy [3]. This system is very peculiar due to the absence of any intrinsic parameter, except for the number density. As a consequence, its equation of state is called universal [3]. In addition, for the unitary Fermi gas, the conformal invariance plays an important role, as discussed by Son and Wingate [4]. We show that a direct microcanonical evaluation of the many-body density of states of the unitary Fermi gas gives rise to a formula that seems intractable. Then, we exhibit an elegant derivation of the many-body density of states of the unitary Fermi gas starting from the canonical ensemble and applying a Legendre transformation. We believe that this canonical approach could be applied to other many-body systems; for instance, atomic nuclei, Bose–Einstein condensates, and superconductors.

Taking into account that the density of states is also currently a very hot topic in the physics of black holes for the condensed matter theoreticians [5], for the sake of entertainment, in the last part of the paper we review the density of states and other thermodynamical quantities of the Schwarzschild black hole. Additionally, for this astrophysical system, we derive the density of states starting from the canonical ensemble and applying a Legendre transformation. In this case, however, the procedure is quite simple.

2. General Properties of the Density of States

Let us consider a quantum system with microscopic Hamiltonian $\widehat{H}$ and macroscopic internal energy between E and $E+\Delta$, with $\Delta \ll E$ [1]. Following the Boltzmann’s idea [6], in the microcanonical ensemble, the entropy $S\left(E\right)$ of the system can be written as

$$S\left(E\right)=k_{B}ln\left(W\left(E\right)\right)$$

(1)

where $k_B$ is the Boltzmann constant and $W\left(E\right)$ is the number of accessible microstates between E and $E+\Delta$, that we call the adimensional density of states, given by [1]

$$W\left(E\right)=N(E+\Delta )-N\left(E\right)$$

(2)

where

$$N\left(E\right)=\mathrm{Tr}[\Theta (E-\widehat{H})]$$

(3)

is the number of states up to the energy E, with $\Theta \left(x\right)$ the Heaviside step function [1]. If $\Delta$ is sufficiently small, one has

$$W\left(E\right)\simeq D\left(E\right)\Delta$$

(4)

where

$$D\left(E\right)=\mathrm{Tr}\left[\delta (E-\widehat{H})\right]$$

(5)

is the density of states, with $\mathrm{Tr}$ being the trace on the Hilbert space of quantum states and $\delta \left(x\right)$ the Dirac delta function [1]. In the thermodynamic limit, one often writes

$$S\left(E\right)\simeq k_{B}ln\left(D\left(E\right)E_s\right)$$

(6)

with $E_s$ being a characteristic energy scale of the system (for instance, $E_s={\hslash }^2{n}^{2/3}/m$ for N identical particles of mass m in a volume V and number density $n=N/V$), because the intensive quantity $ln(\Delta /E_s)$ becomes negligible with respect to the extensive quantity $ln\left(D\left(E\right)E_s\right)$ [1].

Knowing the Hamiltonian $\widehat{H}$, one can calculate $D\left(E\right)$ by using Equation (5). Alternatively, knowing the microcanical entropy $S\left(E\right)$, one easily derives the adimensional density of states $W\left(E\right)$ from the entropy $S\left(E\right)$ as

$$W\left(E\right)=e^{S\left(E\right)/k_B}$$

(7)

The third principle of thermodynamics [1] states that $S\left(E_{gs}\right)=0$ with $E_{gs}$ being the ground-state energy of the system. Consequently, from Equation (7), we obtain $W\left(E_{gs}\right)=1$.

In the canonical ensemble, the Helmholtz free energy $F\left(T\right)$ of the system at temperature T is given by [1]

$$F\left(T\right)=-k_{B}Tln\left(\mathcal{Z}\right(T\left)\right)$$

(8)

where $\mathcal{Z}\left(T\right)$ is the partition function, defined as

$$\mathcal{Z}\left(T\right)=\mathrm{Tr}\left[e^{-\widehat{H}/\left(k_{B}T\right)}\right]$$

(9)

It is not difficult to show that the partition function $\mathcal{Z}\left(T\right)$ is directly related to the density of states $D\left(E\right)$. In fact,

$$\mathrm{Tr}\left[e^{-\widehat{H}/\left(k_{B}T\right)}\right]=\mathrm{Tr}[\int dE\delta (E-\widehat{H})e^{-E/\left(k_{B}T\right)}]=\int dE\mathrm{Tr}\left[\delta (E-\widehat{H})\right]e^{-E/\left(k_{B}T\right)}$$

(10)

and consequently

$$\mathcal{Z}\left(T\right)=\int dED\left(E\right)e^{-E/\left(k_{B}T\right)}.$$

(11)

Inverting this formula, one obtains the density of states $D\left(E\right)$ as a function of the partition function $\mathcal{Z}\left(T\right)$, and then also $D\left(E\right)$ as a function of the Helmholtz free energy $F\left(T\right)$. However, this procedure is quite cumbersome because it involves the calculation of an anti-Laplace transformation.

In this paper, we suggest a much simpler procedure to obtain the adimensional density of states $W\left(E\right)$ from the Helmholtz free energy $F\left(T\right)$. In the canonical ensemble, the entropy S as a function of the temperature T, namely $S\left(T\right)$, is given by

$$S\left(T\right)=-{\left(\frac{\partial F\left(T\right)}{\partial T}\right)}_{N,V}$$

(12)

that is the partial derivative of the Helmholtz free energy $F\left(T\right)$ with respect to the temperature T at fixed number N of particles and volume V. Moreover, the internal energy $E\left(T\right)$ reads

$$E\left(T\right)=F\left(T\right)+TS\left(T\right)$$

(13)

Both $S\left(T\right)$ and $E\left(T\right)$ depend on the temperature T. This means that T can be considered as a dummy variable to obtain, or analytically or numerically, the parametric curve S vs. E, i.e., $S=S\left(E\right)$, which could be a multivalued function. In this way, we are actually performing, in the thermodynamic limit, a Legendre transformation of the entropy from the canonical ensemble to the microcanonical ensemble. Having this result, one can then use Equation (7) to find the adimensional density of states $W\left(E\right)$.

3. Unitary Fermi Gas

In 2004, the crossover from the Bardeen–Cooper–Schrieffer (BCS) state of weakly-correlated pairs of fermions to the Bose–Einstein condensation (BEC) of diatomic molecules was observed with ultracold gases of two-component fermionic ${}^{40}$K or ${}^6$Li atoms [7,8,9]. This BCS–BEC crossover is obtained by using a Fano–Feshbach resonance to change the strength of the effective inter-atomic attraction and, consequently, the 3D s-wave scattering length a [3,10].

Given a gas of N atomic fermions in a volume V with two equally-populated spin components, i.e., $N_{\uparrow }=N_{\downarrow }=N/2$, the system is dilute if the characteristic range $r_e$ of the inter-atomic potential is much smaller than the average interparticle separation $d=n^{-1/3}$ with $n=N/V$ the total number density, namely

$$r_e\ll d$$

(14)

The system is strongly interacting if the scattering length a of the inter-atomic potential greatly exceeds the average interparticle separation $d=n^{-1/3}$, i.e.,

$$d\ll \left|a\right|$$

(15)

The unitarity regime [10] is characterized by both these conditions:

$$r_e\ll d\ll \left|a\right|$$

(16)

Under these conditions, the dilute but strongly interacting Fermi gas is called unitary Fermi gas.

Ideally, the unitarity limit corresponds to

$$r_e=0\mathrm{and}a=\pm \infty$$

(17)

In a uniform configuration and at zero temperature, the only length characterizing the Fermi gas in the unitarity limit is the average interparticle distance $d=n^{-1/3}$.

In this case, simply for dimensional reasons, the ground-state energy must be [3]

$$E_{gs}=\xi \frac{3}{5}\frac{{\hslash }^2}{2m}{\left(3{\pi }^2\right)}^{2/3}{n}^{2/3}N=\xi \frac{3}{5}{ϵ}_{F}N$$

(18)

with ${ϵ}_F={\hslash }^2{\left(3{\pi }^2\right)}^{2/3}{n}^{2/3}/\left(2m\right)$ Fermi energy of the ideal gas and $\xi$ a universal unknown parameter: the Bertsch parameter. Monte Carlo calculations and experimental data with dilute and ultracold atoms suggest that, at zero temperature, the unitary Fermi gas is a superfuid with $\xi \simeq 0.4$ [3].

We model [11,12,13] the many-body quantum Hamiltonian $\widehat{H}$ of the uniform unitary Fermi gas with the simple effective Hamiltonian

$$\widehat{H}=E_{gs}+\sum _{\sigma =\uparrow ,\downarrow }\sum _{\mathbf{k}}{ϵ}_{\mathrm{sp}}\left(k\right){\widehat{c}}_{\mathbf{k}\sigma }^{†}{\widehat{c}}_{\mathbf{k}\sigma }+\sum _{\mathbf{q}}{ϵ}_{\mathrm{col}}\left(q\right){\widehat{b}}_{\mathbf{q}}^{†}{\widehat{b}}_{\mathbf{q}}$$

(19)

where ${\widehat{c}}_{\mathbf{k}\sigma }^{†}$ is the creation operator and ${\widehat{c}}_{\mathbf{k}\sigma }$ the annihilation operator of fermionic single-particle excitations characterized by energy ${ϵ}_{\mathrm{sp}}\left(k\right)$, spin $\sigma$, and wavevector $\mathbf{k}$. Similarly, ${\widehat{b}}_{\mathbf{q}}^{†}$ is the creation operator and ${\widehat{b}}_{\mathbf{q}}$ the annihilation operator of bosonic collective excitations with energy ${ϵ}_{\mathrm{col}}\left(q\right)$ and wavevector $\mathbf{q}$.

The energy of the BCS-like excitations can be written as

$${ϵ}_{\mathrm{sp}}\left(k\right)=\sqrt{{\left(\frac{{\hslash }^2{k}^2}{2m}-\zeta {ϵ}_F\right)}^2+{\Delta }_0^2}$$

(20)

where $\zeta$ = 0.9 takes into account many-body effects on the Fermi surface [14]. Instead, ${\Delta }_0=\gamma {ϵ}_F$ is the energy gap with $\gamma =0.45$ [15].

The energy of collective elementary excitations is instead assumed to be given by

$${ϵ}_{\mathrm{col}}\left(q\right)=\sqrt{\frac{{\hslash }^2{q}^2}{2m}\left(2m{c}_B^2+\lambda \frac{{\hslash }^2{q}^2}{2m}\right)},$$

(21)

where $c_B=\sqrt{\xi /3}{v}_F$ with $v_F=\sqrt{2{ϵ}_F/m}$. In Ref. [12], we used the value $\lambda =0.25$, which is consistent with a macroscopic time-dependent nonlinear Schrödinger equation approach without the inclusion of spurious terms [16]. In a recent paper [13], we used instead $\lambda =0.08$, which is the value obtained [17] from the beyond-mean-field GPF theory [18] at unitarity.

3.1. Attempt of Direct Evaluation of the Many-Body Density of States

We try to write the density of states $D\left(E\right)$ of the unitary Fermi gas by using Equation (5) with Equation (19). We immediately find

$$D\left(E\right)=\sum _{\left\{n_{\mathbf{k}\sigma }\right\}}\sum _{\left\{n_{\mathbf{q}}\right\}}\delta \left(E-E_{gs}-\sum _{\sigma =\uparrow ,\downarrow }\sum _{\mathbf{k}}{ϵ}_{\mathrm{sp}}\left(k\right)n_{\mathbf{k}\sigma }-\sum _{\mathbf{q}}{ϵ}_{\mathrm{col}}\left(q\right)n_{\mathbf{q}}\right),$$

(22)

where $n_{\mathbf{k}\sigma }$ and $n_{\mathbf{q}}$ are the occupation numbers of single-particle and collective excitations, respectively. It is important to remark that Equation (22) is the many-body density of states of the system and not the much more familiar single-particle density of states.

Taking into account the Fourier representation of the Dirac delta function $\delta \left(x\right)$, we have

$$\begin{array}{ccc}\hfill D\left(E\right)& =& \sum _{\left\{n_{\mathbf{k}\sigma }\right\}}\sum _{\left\{n_{\mathbf{q}}\right\}}\frac{1}{2\pi }\int d\xi e^{i\xi \left(E-E_{gs}-{\sum }_{\sigma =\uparrow ,\downarrow }{\sum }_{\mathbf{k}}{ϵ}_{\mathrm{sp}}\left(k\right)n_{\mathbf{k}\sigma }-{\sum }_{\mathbf{q}}{ϵ}_{\mathrm{col}}\left(q\right)n_{\mathbf{q}}\right)}\hfill \\ & =& \frac{1}{2\pi }\int d\xi e^{i\xi (E-E_{gs})}\sum _{\left\{n_{\mathbf{k}\sigma }\right\}}{e}^{-i\xi {\sum }_{\sigma =\uparrow ,\downarrow }{\sum }_{\mathbf{k}}{ϵ}_{\mathrm{sp}}\left(k\right)n_{\mathbf{k}\sigma }}\sum _{\left\{n_{\mathbf{q}}\right\}}{e}^{-i\xi {\sum }_{\mathbf{q}}{ϵ}_{\mathrm{col}}\left(q\right)n_{\mathbf{q}}}\hfill \\ & =& \frac{1}{2\pi }\int d\xi e^{i\xi (E-E_{gs})}\prod _{\sigma =\uparrow ,\downarrow }\prod _{\mathbf{k}}\sum _{n_{\mathbf{k}\sigma }=0,1}{e}^{-i\xi {ϵ}_{\mathrm{sp}}\left(k\right)n_{\mathbf{k}\sigma }}\prod _{\mathbf{q}}\sum _{n_{\mathbf{q}}=0}^{+\infty }{e}^{-i\xi {ϵ}_{\mathrm{col}}\left(q\right)n_{\mathbf{q}}}\hfill \\ & =& \frac{1}{2\pi }\int d\xi e^{i\xi (E-E_{gs})}\prod _{\sigma =\uparrow ,\downarrow }\prod _{\mathbf{k}}(1+e^{-i\xi {ϵ}_{\mathrm{sp}}\left(k\right)})\prod _{\mathbf{q}}\frac{1}{1-e^{-i\xi {ϵ}_{\mathrm{col}}\left(q\right)}}.\hfill \end{array}$$

(23)

Unfortunately, Equation (23) does not help very much to obtain a tractable expression of the density of states. For this reason, in the next section, we analyze the same system in the canonical ensemble, where we will find a similar, but more manageable, formula for the partition function. The reason is that, working in the canonical ensemble, the statistical independence of non-interacting macroscopic subsystems is ensured by the canonical density operator $e^{-\widehat{H}/\left(k_{B}T\right)}$, which is an exponential operator [1].

3.2. Canonical Ensemble

As previously discussed, in the canonical ensemble, the Helmholtz free energy $F\left(T\right)$ of the system is obtained from the partition function $\mathcal{Z}\left(T\right)$ adopting Equations (8) and (9) [1]. In particular, by using Equations (9) and (19), we find

$$\begin{array}{ccc}\hfill \mathcal{Z}\left(T\right)& =& \sum _{\left\{n_{\mathbf{k}\sigma }\right\}}\sum _{\left\{n_{\mathbf{q}}\right\}}{e}^{-\left(E_{gs}+{\sum }_{\sigma =\uparrow ,\downarrow }{\sum }_{\mathbf{k}}{ϵ}_{\mathrm{sp}}\left(k\right)n_{\mathbf{k}\sigma }+{\sum }_{\mathbf{q}}{ϵ}_{\mathrm{col}}\left(q\right)n_{\mathbf{q}}\right)/\left(k_{B}T\right)}\hfill \\ & =& e^{-E_{gs}/\left(k_{B}T\right)}\sum _{\left\{n_{\mathbf{k}\sigma }\right\}}{e}^{-\left({\sum }_{\sigma =\uparrow ,\downarrow }{\sum }_{\mathbf{k}}{ϵ}_{\mathrm{sp}}\left(k\right)n_{\mathbf{k}\sigma }\right)/\left(k_{B}T\right)}\sum _{\left\{n_{\mathbf{q}}\right\}}{e}^{-\left({\sum }_{\mathbf{q}}{ϵ}_{\mathrm{col}}\left(q\right)n_{\mathbf{q}}\right)/\left(k_{B}T\right)}\hfill \\ & =& e^{-E_{gs}/\left(k_{B}T\right)}\prod _{\sigma =\uparrow ,\downarrow }\prod _{\mathbf{k}}\sum _{n_{\mathbf{k}\sigma }=0,1}{e}^{-({ϵ}_{\mathrm{sp}}\left(k\right)/\left(k_{B}T\right))n_{\mathbf{k}\sigma }}\prod _{\mathbf{q}}\sum _{n_{\mathbf{q}}=0}^{+\infty }{e}^{-({ϵ}_{\mathrm{col}}\left(q\right)/\left(k_{B}T\right))n_{\mathbf{q}}}\hfill \end{array}$$

(24)

Thus, we can write

$$\mathcal{Z}\left(T\right)={\mathcal{Z}}_{\mathrm{gs}}\left(T\right){\mathcal{Z}}_{\mathrm{sp}}\left(T\right){\mathcal{Z}}_{\mathrm{col}}\left(T\right)$$

(25)

where

$$\begin{array}{ccc}\hfill {\mathcal{Z}}_{\mathrm{gs}}\left(T\right)& =& e^{-E_{\mathrm{gs}}/\left(k_{B}T\right)}\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill {\mathcal{Z}}_{\mathrm{sp}}\left(T\right)& =& \prod _{\sigma =\uparrow ,\downarrow }\prod _{\mathbf{k}}(1+e^{-{ϵ}_{\mathrm{sp}}\left(k\right)/\left(k_{B}T\right)})\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill {\mathcal{Z}}_{col}\left(T\right)& =& \prod _{\mathbf{q}}\frac{1}{1-e^{-{ϵ}_{\mathrm{col}}\left(q\right)/\left(k_{B}T\right)}}\hfill \end{array}$$

(28)

With the help of Equation (8), the corresponding Helmholtz free energy reads

$$F\left(T\right)=F_{\mathrm{gs}}+F_{\mathrm{sp}}\left(T\right)+F_{\mathrm{col}}\left(T\right)$$

(29)

where $F_{\mathrm{gs}}=E_{\mathrm{gs}}$,

$$F_{\mathrm{sp}}\left(T\right)=-2k_{B}T\sum _{\mathbf{k}}ln[1+e^{-{ϵ}_{\mathrm{sp}}\left(k\right)/\left(k_{B}T\right)}]$$

(30)

and

$$F_{\mathrm{col}}\left(T\right)=-k_{B}T\sum _{\mathbf{q}}ln[1-e^{-{ϵ}_{\mathrm{col}}\left(q\right)/\left(k_{B}T\right)}]$$

(31)

Quite remarkably, the total free energy $F\left(T\right)$ can be written [12] in a compact form as

$$F\left(T\right)=N{ϵ}_F\Phi \left(\frac{T}{T_F}\right)$$

(32)

where, $\Phi \left(x\right)$ depends on the scaled temperature $x\equiv T/T_F$ only, with $T_F={ϵ}_F/k_B$ the Fermi temperature. In particular, we have

$$\begin{array}{ccc}\hfill \Phi \left(x\right)& =& \frac{3}{5}\xi -3x{\int }_0^{+\infty }ln\left[1+e^{-{\widetilde{ϵ}}_{\mathrm{sp}}\left(u\right)/x}\right]u^2\mathrm{d}u\hfill \\ & +& \frac{3}{2}x{\int }_0^{+\infty }ln\left[1-e^{-{\widetilde{ϵ}}_{\mathrm{col}}\left(u\right)/x}\right]u^2\mathrm{d}u\hfill \end{array}$$

(33)

Here the integrals replace the summations. For example, ${\sum }_{\mathbf{k}}\to V\int d^3\mathbf{k}/{\left(2\pi \right)}^3$. Moreover, we set ${\widetilde{ϵ}}_{\mathrm{col}}\left(u\right)=\sqrt{u^2(4\xi /3+\lambda u^2)}$ and ${\widetilde{ϵ}}_{\mathrm{sp}}\left(u\right)=\sqrt{{(u^2-\zeta )}^2+{\gamma }^2}$.

We can now calculate the entropy $S\left(T\right)$ and the internal energy $E\left(T\right)$ by using Equations (12) and (13). In particular, taking into account Equation (33), we find for the entropy

$$S\left(T\right)=-N{k}_B{\Phi }^{\prime }\left(\frac{T}{T_F}\right)$$

(34)

where ${\Phi }^{\prime }\left(x\right)=d\Phi \left(x\right)/dx$. Furthermore, for the internal energy E we obtain the expression

$$E\left(T\right)=N{ϵ}_F\left[\Phi \left(\frac{T}{T_F}\right)-\frac{T}{T_F}{\Phi }^{\prime }\left(\frac{T}{T_F}\right)\right]$$

(35)

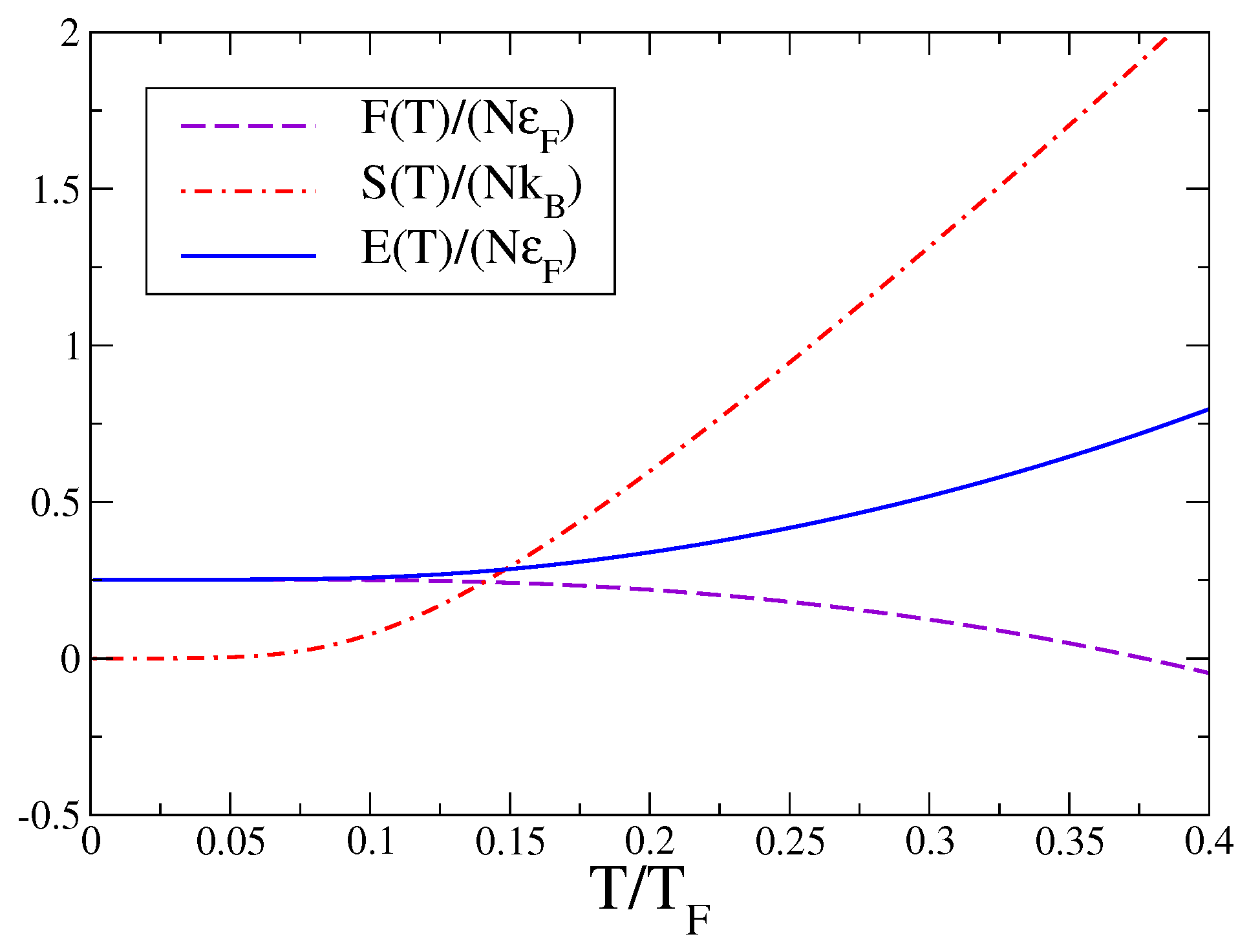
In Figure 1, we plot the free energy $F\left(T\right)$, the entropy $S\left(T\right)$, and the internal energy $E\left(T\right)$ of the unitary Fermi gas by using Equations (32), (34), and (35). We choose the following values for the parameters of our model: $\xi =0.42$, $\lambda =0.25$, $\zeta =0.9$, and $\gamma =0.45$. The figure shows that, by increasing the temperature T, the Helmholtz free energy $F\left(T\right)$ monotonically decreases, while both the internal energy $E\left(T\right)$ and the entropy $S\left(T\right)$ are monotonic growing functions.

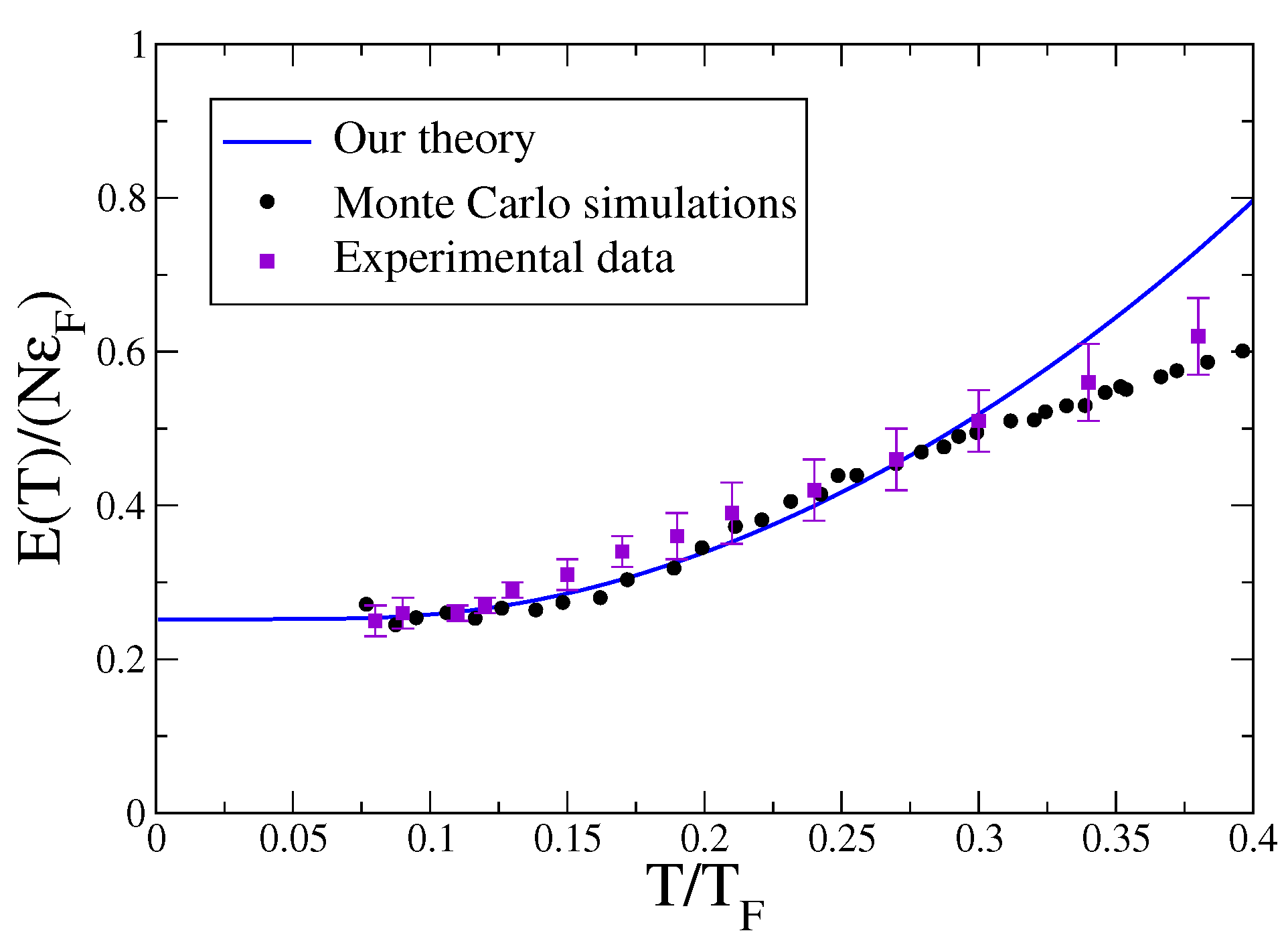
It is important to stress that our model for the low-temperature thermodyamics of the unitary Fermi gas seems to be in quite good agreement with both Monte Carlo simulations [19] and experimental data [20]. In particular, in Figure 2, we compare our internal energy $E\left(T\right)$ (solid line) with Monte Carlo calculations (filled circles) and experimental results (filled squares). Indeed, the agreement among these different datasets is impressive. We stress that Equation (19) is a low-temperature Hamiltonian because we are not taking into account the fact that, in general, the elementary excitations ${ϵ}_{sp}\left(k\right)$ and ${ϵ}_{col}\left(q\right)$ depend on the temperature T.

3.3. Numerical Calculation of the Many-Body Density of States

As previously discussed, having $S\left(T\right)$ and $E\left(T\right)$, we can immediately obtain the curve $S=S\left(E\right)$ by using T as a dummy variable. This is a Legendre transformation from $S\left(T\right)$ to $S\left(E\right)$. In Figure 3, we plot this curve (dashed line) and also the curve (solid line) of the adimensional many-body density of states $W\left(E\right)$, which is obtained from Equation (7).

Figure 3 shows that, by increasing the internal energy E, there is a monotonic growth of both entropy $S\left(E\right)$ and adimensional density of states $W\left(E\right)$. This is a consequence of the monotonic behavior as a function of T of both S and E. Clearly, $S\left(E_{gs}\right)=0$, $W\left(E_{gs}\right)=1$, and $W\left(E\right)$ is an exponential function of the internal energy E.

We remark that the entropy (34) and the internal energy (35) are additive, i.e.,

$$\begin{array}{ccc}\hfill S\left(T\right)& =& S_{gs}+S_{sp}\left(T\right)+S_{col}\left(T\right)\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill E\left(T\right)& =& E_{gs}+E_{sp}\left(T\right)+E_{col}\left(T\right)\hfill \end{array}$$

(37)

with $S_{sg}=0$ and $E_{gs}=(3/5)N{ϵ}_F\xi$. Moreover, the adimensional density of the states $W\left(E\right)$ satisfies, in the thermodynamic limit, the equation

$$W\left(E\right)=W_{gs}\left(E_{gs}\right)W_{sp}\left(E_{sp}\right)W_{col}\left(E_{col}\right),$$

(38)

where $W_{gs}\left(E_{gs}\right)=e^{S_{gs}\left(E_{gs}\right)/k_B}=1$, $W_{sp}\left(E_{sp}\right)=e^{S_{sp}\left(E_{sp}\right)/k_B}$, and $W_{col}\left(E_{col}\right)=e^{S_{col}\left(E_{col}\right)/k_B}$.

In Figure 4, we plot the entropy and the adimensional density of states of both collective and single-particle elementary excitations.

4. Schwarzschild Black Hole

In this section, we derive the adimensional density of states of a Schwarzschild black hole [5,21] from the microcanonical entropy and also from the canonical Helmholtz free energy. These are known results, but they are, however, highly non-trivial. We remark that the derivation of the density of states of a black hole directly from its definition is quite controversial because a fully consistent quantum Hamiltonian $\widehat{H}$ of the black hole is not yet available [21].

For a Schwarzschild black hole of mass M, which does not rotate and has no electric charge, the Bekenstein–Hawking entropy [22,23] is given by

$$S\left(M\right)=\frac{4\pi k_B}{\hslash }\frac{G{M}^2}{c}$$

(39)

where G is the gravitational constant, ℏ is the reduced Planck constant and c is the speed of light in a vacuum. Assuming that the internal energy E of the system is [24]

$$E=M{c}^2$$

(40)

we immediately obtain the microcanonical entropy

$$S\left(E\right)=\frac{4\pi k_{B}G}{\hslash c^5}{E}^2$$

(41)

and also, by using Equation (7), the adimensional density of states

$$W\left(E\right)=e^{\frac{4\pi G}{\hslash c^5}{E}^2}$$

(42)

From Equation (40), we have $E_{gs}=0$ and, as expected, from Equation (42) it follows $W\left(E_{gs}\right)=W\left(0\right)=1$.

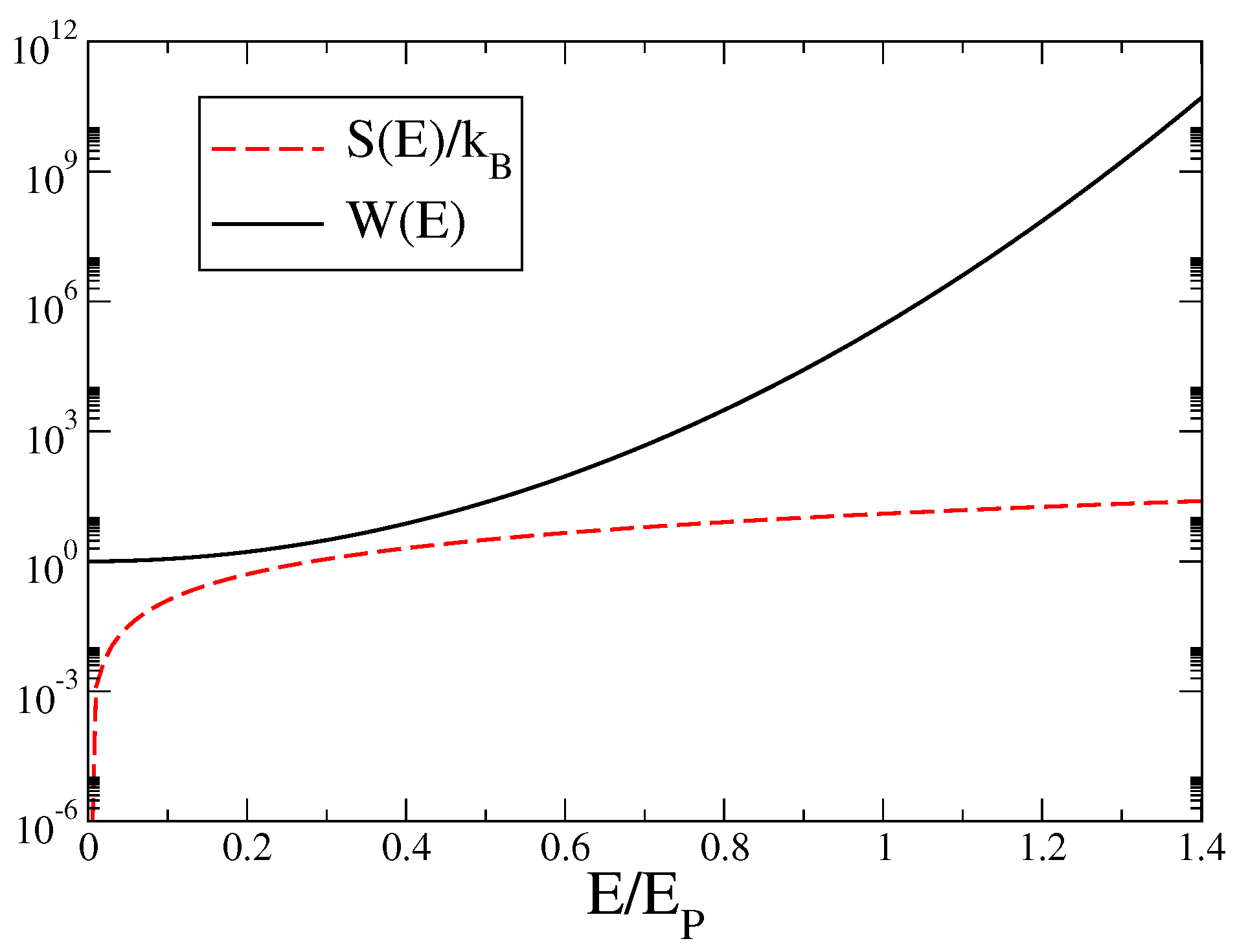
In Figure 5, we plot the curves of the scaled entropy $S\left(E\right)/k_B$ (dashed line) and of the adimensional density of states $W\left(E\right)$, obtained with Equations (41) and (42). The vertical axis is in a log scale to contain the huge increase of $W\left(E\right)$ with E.

Notice that, in the microcanonical ensemble, the temperature T of the system is defined as

$$\frac{1}{T}=\frac{\partial S\left(E\right)}{\partial E}$$

(43)

For the Schwarzschild black hole, using Equation (41), we find

$$\frac{1}{T}=\frac{8\pi k_{B}G}{\hslash c^5}E$$

(44)

or, equivalently, using also Equation (40), we obtain

$$T=\frac{\hslash c^3}{8M\pi k_{B}G}$$

(45)

that is the so-called Hawking temperature [25].

Let us now consider the Schwarzschild black hole within the framework of the canonical ensemble. Because the quantum Hamiltonian $\widehat{H}$ of a black hole is somehow unknown, Gibbons and Hawking in their approach [26] did not use Equation (9). Instead, they derived the canonical partition function $Z\left(T\right)$ of the Schwarzschild black hole from the path integral formula

$$\mathcal{Z}\left(T\right)=\int \mathcal{D}\left[g_{\mu \nu }\left(x\right)\right]e^{-\frac{1}{\hslash }\int d^3\mathbf{x}{\int }_0^{\hslash /\left(k_{B}T\right)}d\tau \sqrt{g}\mathcal{L}\left(g_{\mu \nu }\left(x\right)\right)}$$

(46)

where $g_{\mu }\left(x\right)$ is the metric tensor, $x=(c\tau ,\mathbf{x})$ is the space-time coordinate with $\tau$ being the imaginary time, g is the determinant of the metric tensor, and $\mathcal{L}\left(g_{\mu \nu }\left(x\right)\right)$ is the Euclidean Lagrangian density of the Einstein–Hilbert action [27,28]. Taking into account the Schwarzschild solution of the metric tensor [29] generated by a spherical object of mass M and using a semiclassical approximation of Equation (46) with the inclusion of appropriate boundary terms, Gibbons and Hawking [26] basically found

$$\mathcal{Z}\left(T\right)=e^{-c^5\hslash /\left(16\pi G{k}_B^2{T}^2\right)}$$

(47)

It is important to observe that Equation (47) was obtained by Gibbons and Hawking by also using Equation (45), which is a crucial constraint derived by imposing the regularity of the Euclidean Schwarzschild metric at the Schwarzschild radius $r_s=2GM/c^2$.

From Equations (8) and (47), we then obtain the Helmholtz free energy

$$F\left(T\right)=\frac{c^5\hslash }{16\pi G{k}_{B}T}$$

(48)

We now calculate the entropy $S\left(T\right)$ and the internal energy $E\left(T\right)$ by using Equations (12) and (13). We find

$$S\left(T\right)=\frac{c^5\hslash }{16\pi G{k}_B{T}^2}$$

(49)

and

$$E\left(T\right)=\frac{c^5\hslash }{8\pi G{k}_{B}T}$$

(50)

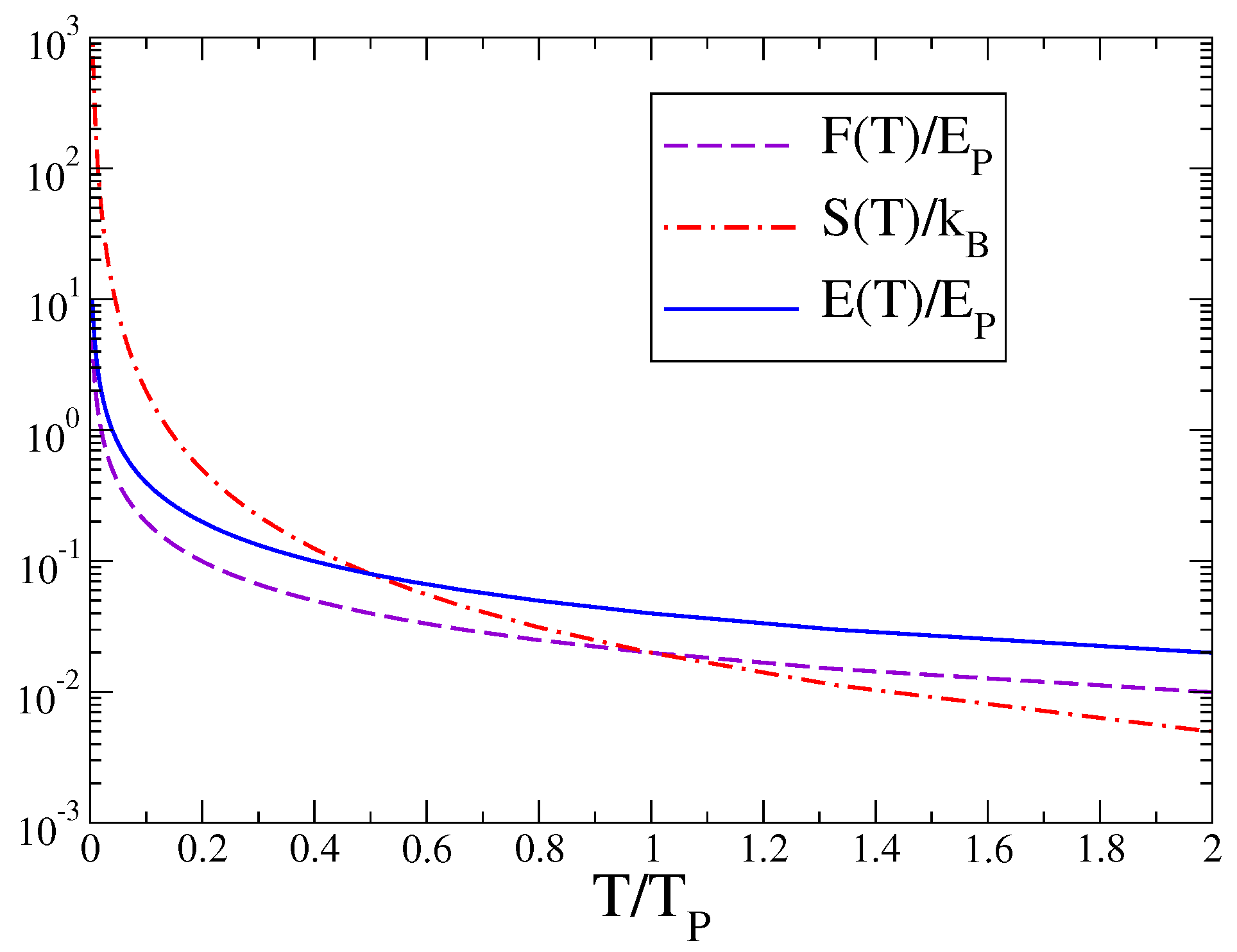
For the sake of completeness, in Figure 6, we report the free energy $F\left(T\right)$, the entropy $S\left(T\right)$, and the internal energy $E\left(T\right)$, obtained with Equations (48)–(50). The figure shows the very unusual behavior of these quantities by increasing the temperature T: they are all monotonically decreasing.

As previously discussed, both the canonical entropy $S\left(T\right)$ and the canonical internal energy $E\left(T\right)$ are functions of the absolute temperature T, which can be considered as a dummy variable to obtain the parametric curve S vs. E. In this case, we can directly find the inverse of Equation (50), which is exactly Equation (44). Inserting this formula into Equation (49), i.e., performing analytically a Legendre transformation, we obtain the microcanonical entropy $S\left(E\right)$ of Equation (41) and finally the adimensional density of states $W\left(E\right)$ given, again, by Equation (42).

5. Conclusions

In conclusion, we stress again that the knowledge of the number of quantum states in a given range of energy is a crucial quantity in many context of physics. Although the density of states can be determined from its microcanonical definition, this method is not always simple. As an alternative, the density of states can be inferred from the microcanonical entropy or the canonical partition. After discussing how these processes relate to one another, we have offered a straightforward technique, based on the Legendre transformation, for deriving the density of states from the Helmholtz free energy. As an enlightening example, the unitary Fermi gas, an extremely dilute system of identical fermions interacting with divergent scattering length, has been studied to determine the many-body density of states. In Section 3.1, we have found that the computation of the density of states from its definition is an hard task, while in Section 3.3, we have obtained it quite easily working in the canonical ensemble. Finally, we have used the same thermodynamical framework to review the adimensional density of states of a Schwarzschild black hole with the Gibbson-Hawking formalism. Also in this case, a calculation of the density of states from its definition is highly demanding. However, for the Schwarzschild black hole, one quite easily obtains the density of state from the microcanonical entropy (as discussed in several textbooks) or from the canonical free energy.