A New Class of Graph Grammars and Modelling of Certain Biological Structures

Abstract

Graph grammars can be used to model the development of diverse graph families. Since their creation in the late 1960s, graph grammars have found usage in a variety of fields, such as the design of sophisticated computer systems and electronic circuits, as well as visual languages, computer animation, and even the modelling of intricate molecular structures Replacement of edges and nodes are the two primary approaches of graph rewriting. In this paper we introduce a new type of node replacement graph grammar known as nc-eNCE graph grammar. With this new class of graph grammars we generated certain graph classes and we showed that these class of graph grammars are more powerful than the existing edge and node controlled embedding graph grammars. In addition, these graph grammars were used to model several common protein secondary structures such as parallel and anti-parallel $\beta$-sheet structures in different configurations. The use of these graph grammars in modelling other bio-chemical structures and their interactions remains to be explored.

1. Introduction

Graphs offer a logical and relevant approach in representing a collection of items as nodes and their interactions as edges. Numerous fields of study and practical applications have benefited from the broad influence of graph theory. Problems in combinatorial optimization [1], which include selecting the best option from a limited number of options, have been studied using graph theory. Various applications, including routing in communication networks [2], transportation systems, and geographic information systems, use shortest path algorithms in graphs. Graph coloring has several applications in scheduling, register allocation, and resource allocation, among others. Graph theory is also used in the study of network reliability, which is a measure of the ability of a communication network to function correctly even in the presence of failures or disruptions. Network reliability can be modeled as a graph, and graph-theoretic techniques can be used to analyze the robustness of the network and identify potential points of failure.

In biology, graphs can be used to represent the relationships between different biological entities, such as genes, proteins, and metabolic pathways [3]. One of the major applications of graph theory in biology is the study of protein-protein interaction networks [4], which are networks of proteins that interact with each other in the cell. These networks can be represented as graphs, with the vertices representing the proteins and the edges representing the interactions between the proteins. Graph-theoretic techniques have been used to study the topology and structure of protein-protein interaction networks and to identify key proteins that play important roles in the network.

Another application of graph theory in biology is the study of metabolic networks, which are networks of chemical reactions that take place in the cell. These networks can also be represented as graphs, with the vertices representing the chemical compounds and the edges representing the reactions between the compounds. Graph-theoretic techniques have been used to study the structure and function of metabolic networks and to identify key pathways that are involved in the metabolism of the cell. In addition, graph theory has been used to study the structure and function of other types of biological networks, such as gene regulatory networks [5], neural networks, and social networks.

Generation of families of graphs [6,7,8] has been studied extensively. Graph grammars which were introduced in sixties have evoked the interest of researchers due to the possibilities of their application in disciplines that range from program design to modelling of biochemical interactions. They are used to formalise the idea of a set of graphs that can be specified recursively. The technique of transformation of a graph is known as graph rewriting. This involves starting with a graph G (which is called host graph) from which a subgraph S is removed and then embedding a graph E with the remaining portion of G, say, R. Graph rewriting is usually performed by the recursive replacement of either a node or an edge. We develop non-confluent edge and node label controlled embedding to generate new graphs. This class of graph grammars have an enhanced generative capacity compared to normal node-replacement graph grammars.

A protein, on the other hand, is a complex organic compound made up of amino acids linked by chemical bonds [9,10]. An alphabetic string of 20 letters can be used to represent the linear amino acid sequence that makes up a protein’s fundamental structure. Secondary structures in proteins are created by the local orientation of amino acids along the chain. These structures are stabilised by hydrogen interactions among the amino-keto groups in the peptide bond. Protein secondary structures are divided into four categories: $\alpha$-helix, $\beta$-sheet, turns, and coils.

There are many areas of application of different formalisms of graph grammars. Recently, Guo et al. [11] have studied graph grammars for molecular generation. Here we study non-confluent eNCE graph grammars for modelling biological structures. Section 2 covers the essential definitions involving graph grammars. Section 3 introduces the notion of Non-confluent eNCE ($nceNCE$) graph grammars and some variants of this class of graph grammars. Section 4 addresses the application of constructs discussed earlier in the simulation and structural analysis of some standard biological structures. We then demonstrate how parallel and anti-parallel $\beta$-sheet structures are generated using our new grammar.

2. Graph Grammars

In general, a graph grammar [7,12] has a set of rules with the format $p(M,D,E)$ which are used to recursively transform a host graph H (initially H is the start graph $G_S)$. Here M (known as mother graph) is a subgraph of $G_S$ which is to be replaced by another graph D (known as daughter graph). New edges are to be established with designated nodes of D due to the loss of edges incident to the vertices in M using an appropriate embedding mechanism E. As a result a new family of graphs is generated.

Graph grammars have been applied to the modelling of numerous biological structures. They have been used to forecast protein folding patterns as well as model the structure and dynamics of proteins. The structure and operation of genetic networks, including the control of gene expression, have been modelled using graph grammars. The structure and operation of metabolic pathways, including the movement of metabolites through a cell, have been modelled using graph grammars. The structure and operation of cell signalling pathways, which are crucial in cell communication, have been modelled using graph grammars.

A bipartite graph can also be used to represent a graph grammar. The edges in the bipartite graph represent the production rules of the grammar, connecting a nonterminal symbol on the left of a rule to the terminal symbols on the right that it can be expanded into. In this representation, a graph can be generated by starting with a single nonterminal symbol and repeatedly expanding it according to the production rules until only terminal symbols remain. This process is called graph rewriting, and the resulting graph is called a derived graph.

Embedding styles may be categorized into two types, namely, connecting and gluing. In a graph grammar based on gluing [8,13,14,15], certain nodes of $H^{\prime }$ ($H^{\prime }=H-M$) and D are fused. In addition, some edges in H (which were initially incident on M) and D are fused.

In the connecting approach [6], new edges are introduced between the daughter graph D and some specific nodes of $H^{\prime }$ (which were initially adjacent with nodes in M).

Node Replacement Graph Grammars

When M is a single node and the connection instructions are independently defined for each production rule, the graph grammar is termed as a node replacement graph grammar [16].

A graph grammar is said to be a node label controlled ($NLC$) [17,18] graph grammar if the nodes that participate in the embedding process are specified using labels. When a production rule is applied, a node labelled by the non-terminal A is removed and instead a graph D is embedded. This embedding is done using any valid connection instruction with the format ($\alpha ,\beta$). As a result of the application of this connection instruction, undirected edges labelled $\beta$ are established between some node of D and any neighbor of A in H which had an edge labelled $\alpha$ incident on it and some node of D. Formally we have the definition:

Definition 1

([17]). A construct $nG=(\Sigma ,\Gamma ,P,C,G_S)$ is known as an $NLC$ graph grammar where

• Σ is an alphabet used to label nodes,
• Γ is a collection of terminal symbols in Σ,
• A production rule in P, $p:A\to D$ acts on the mother node labelled A,
• C is a collection of embedding instructions in $\Sigma \times \Sigma$,
• $G_S$ is the initial graph.

We say $G\stackrel{p}{\Rightarrow }{G}^{\prime }$ or $G\Rightarrow G^{\prime }$ if an application of p to the graph G yields $G^{\prime }$. Furthermore we can write $G\stackrel{*}{\Rightarrow }H$ if

$$G\Rightarrow G_1\Rightarrow G_2\Rightarrow \cdots \Rightarrow G_n=H$$

This grammar [19] generates the language

$$L\left(nG\right)=\{G\in G_{\Gamma }|G_S\stackrel{*}{\Rightarrow }G\}$$

and all nodes of graphs in $G_{\Gamma }$ are labelled using Γ.

In a neighbourhood controlled embedding ($NCE$) [6] we have: ${}_{c}G=(\Sigma ,\Gamma ,P,S)$, each production rule p: $A\to (D,C)$ has an independent connection instruction C unlike the construct in Definition 1. Here $C\subseteq \Sigma \times N_D$ and $N_D$ is a collection of nodes in D.

Another extension of the $NLC$ embedding [17] is the $eNCE$ or edge and node controlled embedding [6] which uses both edge and node labels to specify the new edges added during the embedding process. Formally, we have the definition:

Definition 2

([20]). A construct ${}_{e}G=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S)$ is known as $eNCE$ graph grammar where

• Σ and Γ are sets of symbols used to label nodes and edges respectively,
• Δ and Ω are the collections of terminal symbols in Σ and Γ respectively,
• A production rule in P, $p:A\to (D,C)$ acting on the mother node M with label A has a collection C of connection instructions $(a,p\mid q,B)$ associated with it. Here B is a node in D and x with label a is one of the neighbors of M. The edge p which connected x and M is removed and an edge q is established between x and B.
• $G_S$ is the initial graph.

The graph grammar ${}_{e}G$ generates the language [19]

$$L{(}_{e}G)=\{G\in G_{\Delta }|G_S\stackrel{*}{\Rightarrow }G\}$$

where all the nodes of graphs in $G_{\Delta }$ are labelled using Δ. Here $G_S\stackrel{*}{\Rightarrow }G$ is defined as in Definition 1.

3. Non-Confluent Edge and Node Controlled Embedding $(\mathit{nc}$-$\mathit{eNCE})$ Graph Grammar

In order to introduce a measure of determinism in the intrinsically non-deterministic concept of a graph grammar, we restrict the sequence of production rules used and thereby obtain a new class of graph grammar. Formally we have the definition:

Definition 3

([21]). A construct $ncG=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$ is known as an $nc\text{-}eNCE$ graph grammar where

• Σ and Γ are sets of symbols used to label nodes and edges respectively,
• Δ and Ω are the collections of terminal symbols in Σ and Γ respectively,
• A production rule in P, $p:A\to (D,C)$ acting on the mother node M with label A has a collection C of connection instructions $(a,p\mid q,B)$ associated with it. Here x with label a is a neighbor of M and B is a node in D. The edge p which connected x and M is removed and a new edge q is established between x and B.
• $G_S$ is the initial graph,
• The regular control, $R\left(P\right)$, regulates the sequence of application of the production rules.

The graph grammars $ncG$ generates the language

$$L\left(ncG\right)=\{G\in G_{\Delta }|G_S\stackrel{R\left(P\right)}{\Rightarrow }G\}$$

Here, all the nodes of graphs in $G_{\Delta }$ are labelled using $\Delta$ and $G_S\stackrel{*}{\Rightarrow }G$ is defined as in Definition 1. The ordered application of productions in the sequence $p_1,p_2,\cdots ,p_n$ ($p_1{p}_2\cdots p_n\in L\left(R\left(P\right)\right)$ leads to the generation of graphs specified by the language of the grammar.

3.1. nc-$eNCE$ Graph Grammar with Deletion $(dnc$-$eNCE)$

In order to improve its generative capability, we introduce here another version of the $nc$-$eNCE$ graph grammar. In this version there are some special productions used to simply delete a node and establish edges between its neighbors. Formally, we have the definition:

Definition 4.

A construct $dncG=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$ is known as a $dnc$-$eNCE$ graph grammar ($nc$-$eNCE$ graph grammar with deletion) where,

• Σ is an alphabet used to label nodes,
• $\Delta \subset \Sigma$ is a collection of terminal symbols,
• Γ is an edge labelling alphabet,
• Ω is the edge labels of the final graph, [22].
• P contains in addition to productions defined in Definition 2, the rules $A\to \epsilon$ where, M labelled A is the node to be deleted. The connection instruction for this rule has the format $\left(\right(a,x),z,(y,b\left)\right)$. In this rule the edges labelled x, y connecting M to a and b respectively are removed, and a new edge with label z is established between the two nodes.
• $G_S$ is the initial graph.
• The regular control $R\left(P\right)$ regulates the sequence of application production rules.

The graph grammar $dncG$ generates the language

$$L\left(dncG\right)=\{G\in G_{\Delta }|G_S\stackrel{R\left(P\right)}{\Rightarrow }G\}$$

where all the nodes of graphs in $G_{\Delta }$ is labelled using $\Delta$. The following example shows the generation of a parse tree with yield $\left\{w{w}^{r}w{w}^r\right|w\in {(a+b)}^{*}\}$ using a $dnc$-$eNCE$ graph grammar $nc{G}_T$.

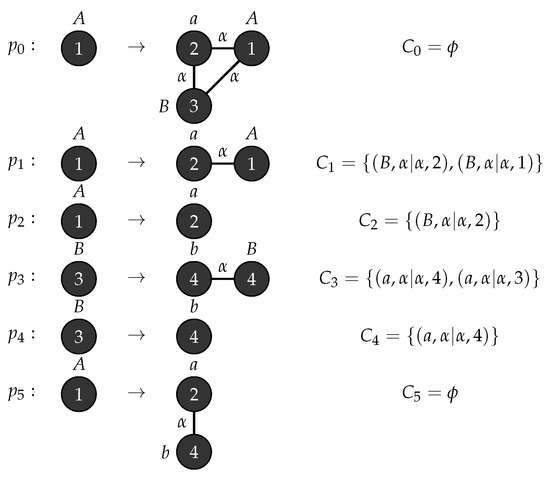
Example 1.

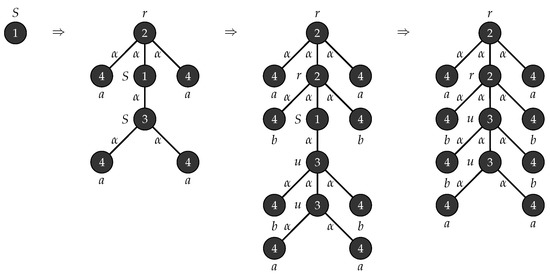
Consider $dncG=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$ with $\Sigma =\{S,r,u,a,b\}$, $\Delta =\{r,u,a,b\}$, $\Gamma =\left\{\alpha \right\}$, $\Omega =\left\{\alpha \right\}$, $P=\{p_1,p_2,p_3\}$, $G_S$ consists of a single mode labelled S and $R\left(P\right)={(p_1+p_2)}^{*}{p}_3$. Figure 1 depicts the production rules that generates parse trees with the yield $w{w}^{r}w{w}^r,w\in {(a+b)}^{*}$ and Figure 2 demonstrates the application of these rules when $w=ab$.

Figure 1. Production rules for tree strings $w{w}^{r}w{w}^r,w\in {(a+b)}^{*}$.

Figure 2. Derivation of trees with yield $w{w}^{r}w{w}^r,w\in {(a+b)}^{*}$.

3.2. Non-Confluent $eNCE$ Graph Grammar with $\psi$ Labelled Edges $(\psi nc$-$eNCE)$

Another version of the $nc$-$eNCE$ graph grammar introduces special edges labelled $\psi$. Formally, we have the following definition.

Definition 5.

A construct $\psi ncG=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,$ $R\left(P\right))$ is known as a non-confluent $eNCE$ graph grammar with ψ labelled edges or simply $\psi nc$-$eNCE$ graph grammar where

• Σ is an alphabet used to label nodes,
• $\Delta \subset \Sigma$ is a collection of terminal symbols,
• $\Gamma \cup \psi$ is the edge labelling alphabet,
• Ω is the collection of edge labels of the final graph,
• P contains rules similar to those in Definition 2. In addition we introduce a special edge label ψ which acts as follows: While concatenating two graphs together or embedding a daughter graph in a mother graph, this edge can be introduced between two nodes with terminal labels. The connection instruction associated with this edge has the format $(x,\psi ,y)$. This label can be bypassed or ignored while specifying the graph language.
• $G_S$ is the initial graph.
• The regular control $R\left(P\right)$ regulates the sequence of application of the production rules.

The graph grammar $\psi ncG$ generates the language $L\left(\psi ncG\right)=\{G\in G_{\Delta }|G_S\stackrel{R\left(P\right)}{\Rightarrow }G\}$ where all the nodes of graphs in $G_{\Delta }$ is labelled using $\Delta$. Edges with label $\psi$ can be used with $nc$-$eNCE$ graph grammars as well as $dnc$-$eNCE$ graph grammars for connecting two or more graphs without loss of generality.

Example 2.

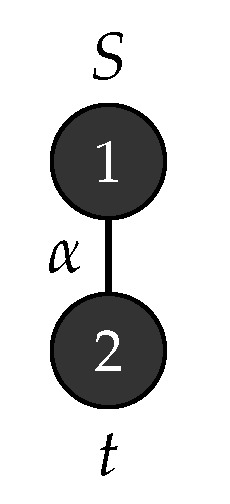
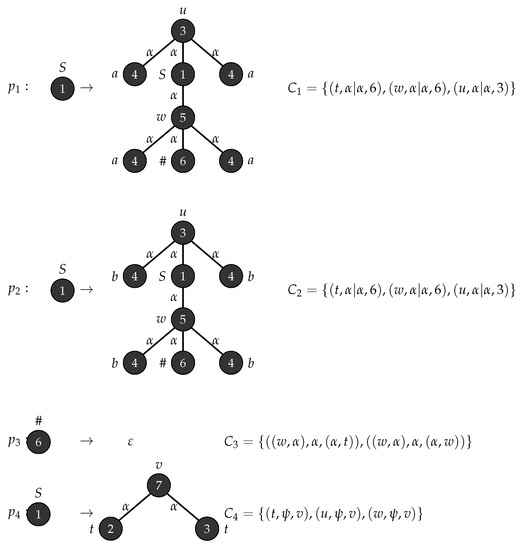
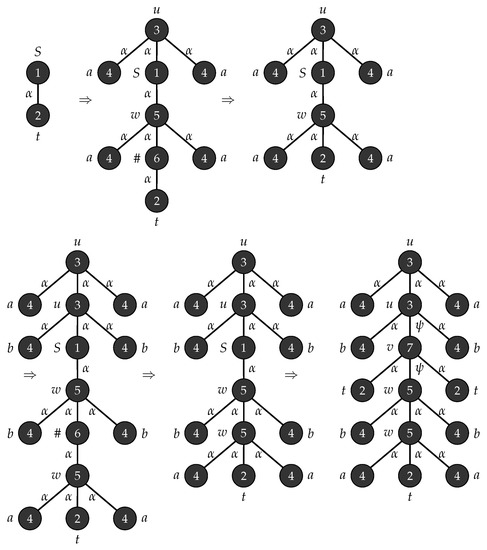
Consider the graph grammar $\psi ncG=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$, with $\Sigma =\{S,t,\#,u,v,w\}$, $\Delta =\{t,u,v,w,a,b\}$, $\Gamma =\left\{\alpha \right\}$, $\Omega =\left\{\alpha \right\}$, $P=\{p_1,p_2,p_3,p_4\}$, $G_S$ is the graph shown in Figure 3 and $R\left(P\right)={\left((p_1+p_2)p_3\right)}^{*}{p}_4$. Figure 4 depicts the production rules that generates a parse tree with the yield $wt{w}^{r}twt{w}^r,w\in {(a+b)}^{*}$. Figure 5 shows the application of these rules when $w=ab$.

Figure 3. Start graph $G_S$.

Figure 4. Production rules for tree string $wt{w}^{r}twt{w}^r,w\in {(a+b)}^{*}$.

Figure 5. Derivation of the tree string $abtbatabtba$.

The graph grammar in Example 2 can generate parse trees with yield of the form $\left\{wt{w}^{r}twt{w}^r\right|w\in {(a+b)}^{*}\}$. Figure 5 shows the derivation of tree yielding the string $abtbatabtba$ which is obtained when $w=ab$.

4. Generation of Certain Graph Classes

The class of $nc\text{-}eNCE$ graph grammars are capable of generating several graph classes. Some of these graph classes are dealt with in the following results.

4.1. Wheel Graphs

Definition 6

([23]). A wheel graph $W_n$ is a graph that consists of a central node, called the hub, and several spoke nodes that are connected to the hub. The spoke nodes are connected to the hub by edges, and to each other by a rim or cycle of edges. The number of spoke nodes in a wheel graph is referred to as its order. A wheel graph with n spoke nodes is also known as a wheel graph of order n.

Lemma 1.

The class of wheel graphs can be generated by a $nc$-$eNCE$ graph grammar.

Proof. 

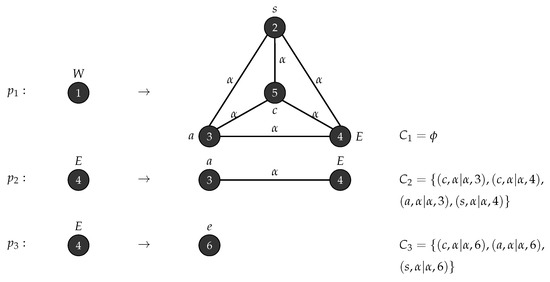
Consider $nc{G}_W=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$, $\Sigma =\{W,E,a,c,s,e\}$, $\Delta =\{a,c,s,e\}$, $\Gamma =\left\{\alpha \right\}$, $\Omega =\left\{\alpha \right\}$, $P=\{p_1,p_2,p_3\}$, $G_S$ consists of a single node labelled W and R(P)= $p_1{p}_2^{*}{p}_3$. The productions in P are depicted in Figure 6. □

Figure 6. Production rules for Wheel graph.

Figure 7 shows the generation of the Wheel graph $W_6$ using the grammar $nc{G}_W$.

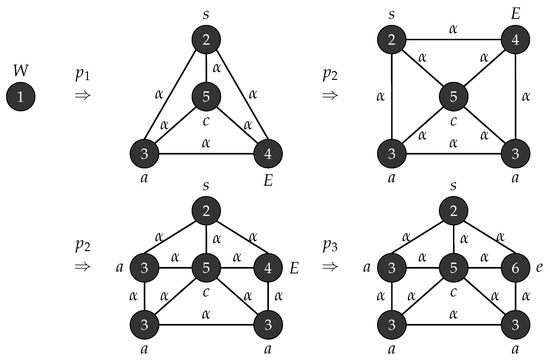
Figure 7. Generation of the Wheel graph $W_6$.

4.2. Complete Bipartite Graphs

Definition 7

([23]). A bipartite graph is a graph in which the vertex set can be decomposed into 2 disjoint sets such that no two vertices within the same set are adjacent. A complete bipartite graph is a bipartite graph such that every vertex in the first set is connected to each vertex of the second set.

Lemma 2.

The class of complete bipartite graphs can be generated by a $nc$-$eNCE$ graph grammar.

Proof. 

Let $ncCB=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,S=A,R(P\left)\right)$ be an $nc$-$eNCE$ graph grammar with, $\Sigma =\{A,a,b\}$, $\Delta =\{a,b\}$, $\Gamma =\{\alpha ,\beta \}$, $\Omega =\left\{\alpha \right\}$, $P=\{p_0,p_1,p_2,p_3,p_4,p_5\}$ and $R\left(P\right)=\left(p_0{p}_1^{*}{p}_2{p}_3^{*}{p}_4\right)+p_5$. Figure 8 shows the production rules and the associated connection instructions for generating complete bipartite graphs. □

Figure 8. Production rules for Complete bipartite graph.

4.3. Binary Tree

Definition 8

([23]). A rooted tree is a connected acyclic graph which has a special vertex called the root. A binary tree is a rooted tree in which each vertex has at most two children.

Lemma 3.

The class of binary trees can be generated by a $nc$-$eNCE$ graph grammar.

Proof. 

Let $ncBT=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,S=A,R(P\left)\right)$ be an $nc$-$eNCE$ graph grammar with, $\Sigma =\{A,a\}$, $\Delta =\left\{a\right\}$, $\Gamma =\left\{\alpha \right\}$, $\Omega =\left\{\alpha \right\}$, $P=\{p_1,p_2,p_3\}$ and $R\left(P\right)={(p_1+p_2)}^{*}{p}_3^{+}$. Figure 9 shows the production rules and the associated connection instructions for generating binary trees. □

Figure 9. Production rules for Binary Tree.

Other classic graph classes which can be generated using $nc$-$eNCE$ graph grammars include complete graphs, caterpillar graphs and star graphs. In fact $nc$-$eNCE$ graph grammars provide finite tools for the generation of such classic graph classes.

5. Generative Power of $\mathit{nc}$-$\mathit{eNCE}$ Graph Grammars

Theorem 1.

Let $eNCEGG$ be the class of all the Edge and Node Controlled Embedding Graph Grammars and $nc$-$eNCEGG$ be the class of all the Non-Confluential Edge and Node Controlled Embedding Graph Grammars. Then $L\left(eNCEGG\right)\subset L(nc$-$eNCEGG)$.

Proof. 

Let ${}_{e}G=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S)\in eNCEGG$ with $P=\{p_1,p_2,p_3,\cdots ,p_m\}$ and let $A=\{W\in P^{*}|G_S\stackrel{W}{\Rightarrow }G\in L{(}_{e}G)\}$. Then we can construct an $nc\text{-}eNCEGG$, $ncG=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$ where all the components except $R\left(P\right)$ can be obtained from ${}_{e}G$ and $R\left(P\right)$ is a regular expression corresponding to set A. □

Theorem 2.

$L(nc$-$eNCEGG)-L(eNCEGG)\ne \varphi$

Proof. 

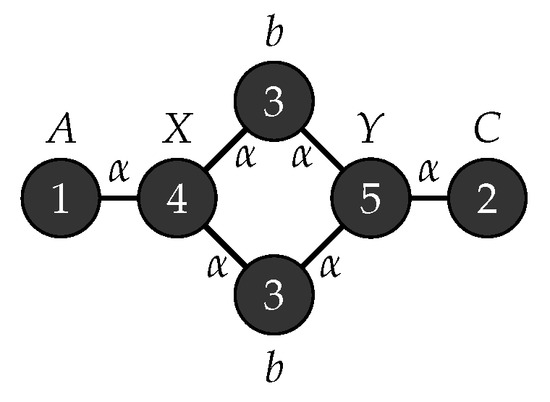
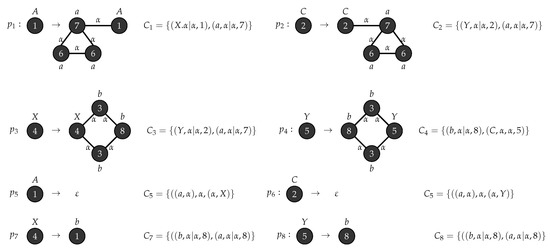
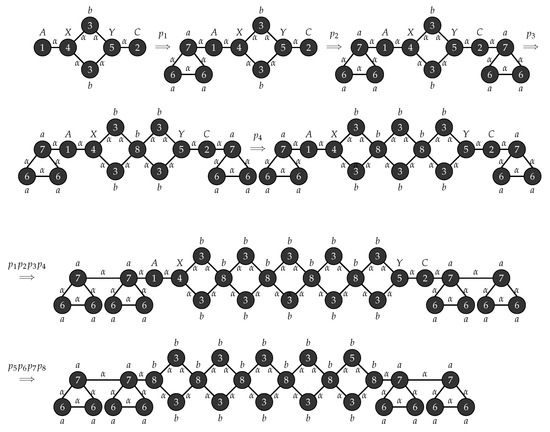
Consider a graph language consisting of graphs of the form shown in Figure 10. This graph can be interpreted as follows: Each graph contains a series of n hanging triangles T followed by a series of $(2n+1)$ rhombuses R glued together and followed again by a series of n hanging triangles T. This graph language can now be represented using the string language $L=\{T^n{R}^{2n+1}{T}^n,n\ge 0\}$. It is known that the language L is not context free. Based on this feature of non-contextfreeness it can be shown that any graph language of this form cannot be generated using an edge and node controlled embedding graph grammar. The $eNCEGG$ production rules can be applied in any order and a single node replacement happens when we apply a rule. Hence any grammar of this type will generate certain graphs which are not in the required form. We now show that this graph language can be generated using a non-confluential edge and node controlled embedding graph grammars as follows. Consider an $nc$-$eNCEGG$ $nc{G}_{diff}=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$, $\Sigma =\{A,C,X,Y,a,b\}$, $\Delta =\{a,b\}$, $\Gamma =\left\{\alpha \right\}$, $\Omega =\left\{\alpha \right\}$, $P=\{p_1,p_2,p_3,p_4,p_5,p_6,p_7,p_8\}$, $G_S$ is the graph in Figure 11 and $R\left(P\right)={\left(p_1{p}_2{p}_3{p}_4\right)}^{*}\left(p_5{p}_6{p}_7{p}_8\right)$. Figure 12 shows the production rules and the associated connection instructions for generating the pattern of the form $T^n{R}^{2n+1}{T}^n,n\ge 0$. Figure 13 shows the derivation of the pattern of the form $T^n{R}^{2n+1}{T}^n,n=2$. □

Figure 10. $L=\{T^n{R}^{2n+1}{T}^n,n\ge 0\}$.

Figure 11. Start graph $G_S$.

Figure 12. Production rules for $nc{G}_{diff}$.

Figure 13. Sample derivation for grammar in Example for $n=2$.

6. Modelling of Biological Structures

Graphs and graph grammars play a pivotal role in the field of bioinformatics, especially in studies related to structural analysis of DNA and proteins. In particular the secondary structure prediction of proteins is a topic of active research [9,10,24]. In this section, we show how $nc$-$eNCE$ graph grammars can be used to model some biological structures with their associated characteristics.

In Example 2, an informal description of this concept is shown using a $\psi nc$-$eNCE$ graph grammar to generate a tree with its yield given by a string that can be read from leftmost leaf node label to the right most leaf node label. The structure shown in Figure 5 is a linguistic description of anti-parallel $\beta$-sheet structure of protein. The symbols $a,b$ and t in the graph shown in Figure 5 can be replaced with the corresponding amino-acid sequences so that the original $\beta$-sheet sequence can be obtained. Since the generated structure is a tree, it can be parsed using a computational device. This model can also be used to learn and predict the occurrence of a beta sheet structure when a sequence is given. The following examples shows the generation of some popular $\beta$-sheet structures.

6.1. Modelling of Parallel $\beta$-Sheet Structures

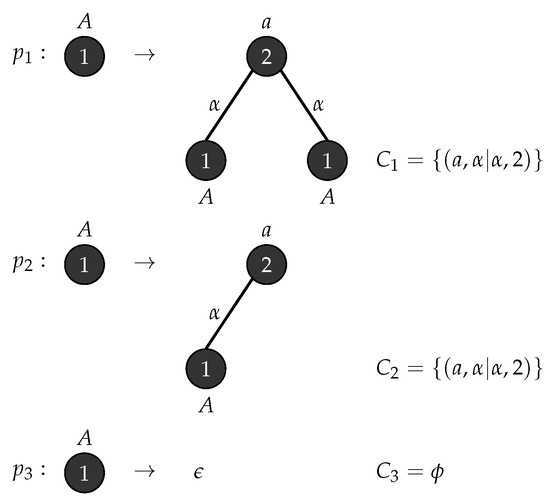
Consider an $dnc$-$eNCE$ graph grammar $p\beta ncG=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$ with $\Sigma =\{S,t,\#,u_1,u_2,l_1,l_2,v,a,b\}$, $\Delta =\{u_1,u_2,l_1,l_2,a,b,v\}$, $\Gamma =\left\{\alpha \right\}$, $\Omega =\left\{\alpha \right\}$, $P=\{p_1,p_2,p_3,p_4,p_5\}$, $G_S$ is the graph in Figure 14 and $R\left(P\right)={\left((p_1+p_2)p_3{p}_4\right)}^{*}{p}_5$. Figure 15 depicts the production rules that generate parse trees with yield $w{l}_{1}w{l}_{2}w,w\in {(a+b)}^{*}$. Figure 16 show the application of these rules when $w=ab$.

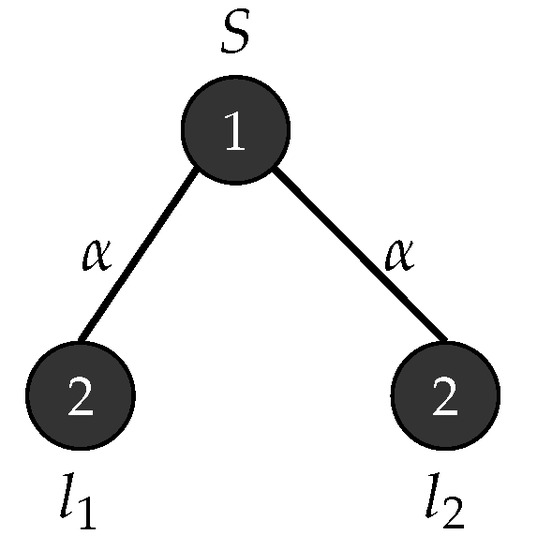
Figure 14. Start graph $G_S$.

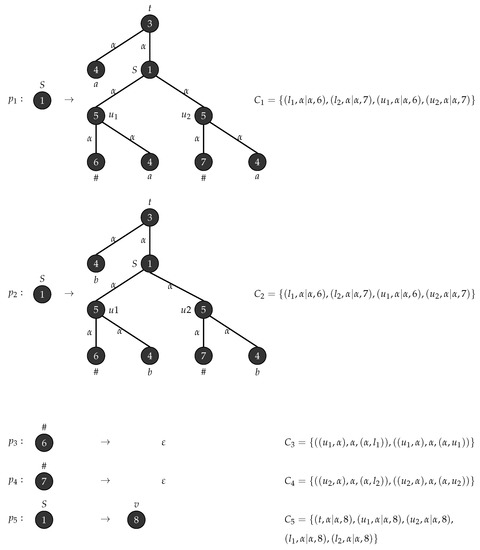
Figure 15. Production rules for tree strings $w{l}_{1}w{l}_{2}w,w\in {(a+b)}^{*}$.

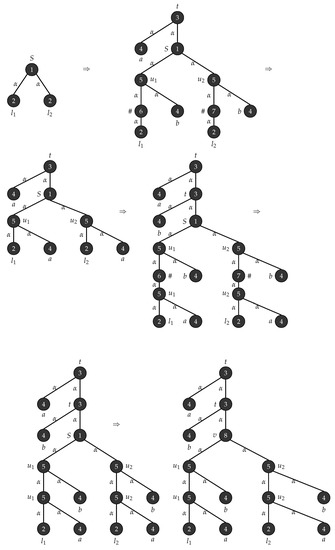
Figure 16. Derivation for tree strings $w{l}_{1}w{l}_{2}w,w\in {(a+b)}^{*}$.

6.2. Modelling of Anti-Parallel $\beta$-Sheet Structures with a Semi-Greek Key Conformation

Consider $g\beta ncG=(\Sigma ,\Delta ,\Gamma ,\Omega ,P,G_S,R\left(P\right))$ with $\Sigma =\{S,l_1,l_2,t,u,\#,v,a,b\}$, $\Delta =\{l_1,l_2,t,u,v,a,$ $b\}$, $\Gamma =\left\{\alpha \right\}$, $\Omega =\left\{\alpha \right\}$, $P=\{p_1,p_2,p_3,p_4\}$, $G_S$ is the graph in Figure 17 and $R\left(P\right)={\left((p_1+p_2)p_3\right)}^{*}{p}_4$. Figure 18 depicts the production rules that generate parse trees with the yield $w{l}_1{w}^r{l}_2{w}^r,W\in {(a+b)}^{*}$. Figure 19 shows the application of these rules when $w=ab$.

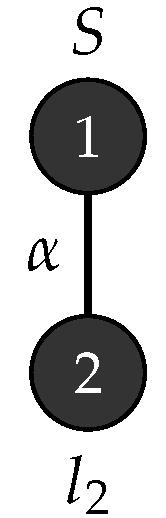
Figure 17. Start graph $G_S$.

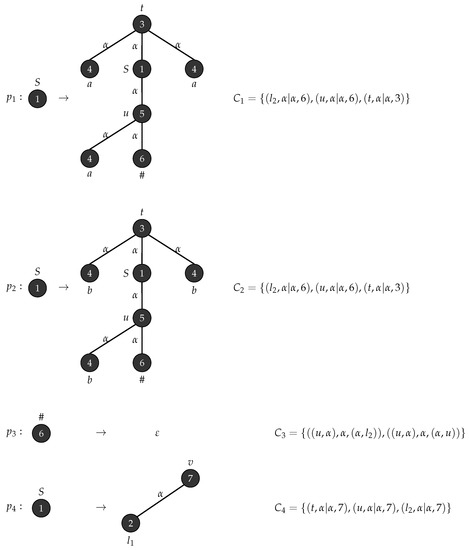
Figure 18. Production rules for tree strings $w{l}_1{w}^r{l}_2{w}^r,w\in {(a+b)}^{*}$.

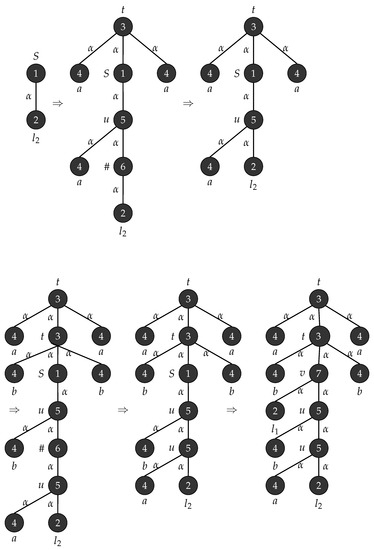
Figure 19. Derivation of tree strings $w{l}_1{w}^r{l}_2{w}^r,w\in {(a+b)}^{*}$.

As stated in the introduction, we investigate the modelling and prediction of the $\beta$-sheet regions. Figure 5, Figure 16 and Figure 19 depict this feature, as does Figure 20, which shows a schematic illustration of various common $\beta$-sheet configurations. The $\beta$-sheet strands are shown by solid arrow marks, while the turns between the strands are represented by light line segments. Another illustration can be found to the right of this schemata, which depicts the beta sheets with amino acids (stereotyped as a and b) held together by the hydrogen bond (shown with dotted lines). This leads us to believe that there is a strong link between amino acids in those positions. Our new grammar, together with its variants, can handle these beta sheet topologies. Parsing becomes easier when the development of graphs using our grammar is limited by the regular control of graph production rules. It is also worth noting that there will be sequences in between the $\beta$-sheet sections that can be handled by the $nc$-$eNCE$ graph grammar.

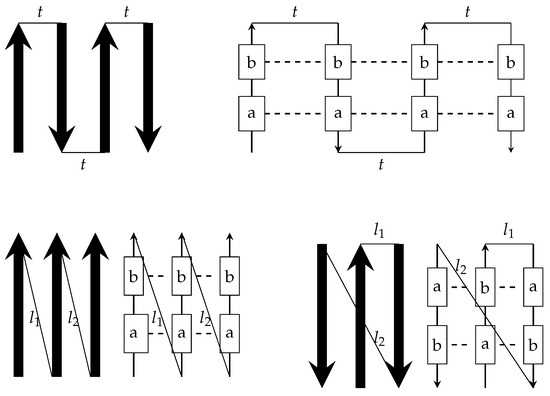
Figure 20. Schematic illustration of different $\beta$ sheet configurations.

7. Conclusions

We have established a new type of edge and node driven embedding graph grammar called $nc$-$eNCE$ graph grammars along with some variants. We have shown how some of the classic symmetric graph classes can be easily generated by our new graph grammar. The generative power of $nc$-$eNCE$ graph grammars have been demonstrated. We have shown how these grammars can be used to represent and analyse biological structures such as $\beta$-sheets in proteins. It will be interesting to see how these grammars are used for identifying biochemical structures especially those of higher order proteins and their symmetry in terms of the sequences of amino acids present. It will also be of high interest if we can apply these graph grammar constructs and explore their symmetry in building unpredictable linear games.