A Preconditioner for Galerkin–Legendre Spectral All-at-Once System from Time-Space Fractional Diffusion Equation
Abstract
:1. Introduction
2. GL1-GLS Discretization and the All-at-Once System
2.1. The Time-Stepping Discretization
2.2. The Galerkin–Legendre Spectral All-at-Once System
3. The Block L-Diagonal Preconditioner
3.1. Derivation of the General Block L-Diagonal Preconditioner
3.2. Theoretical Analyses of the Block L-Diagonal Preconditioner
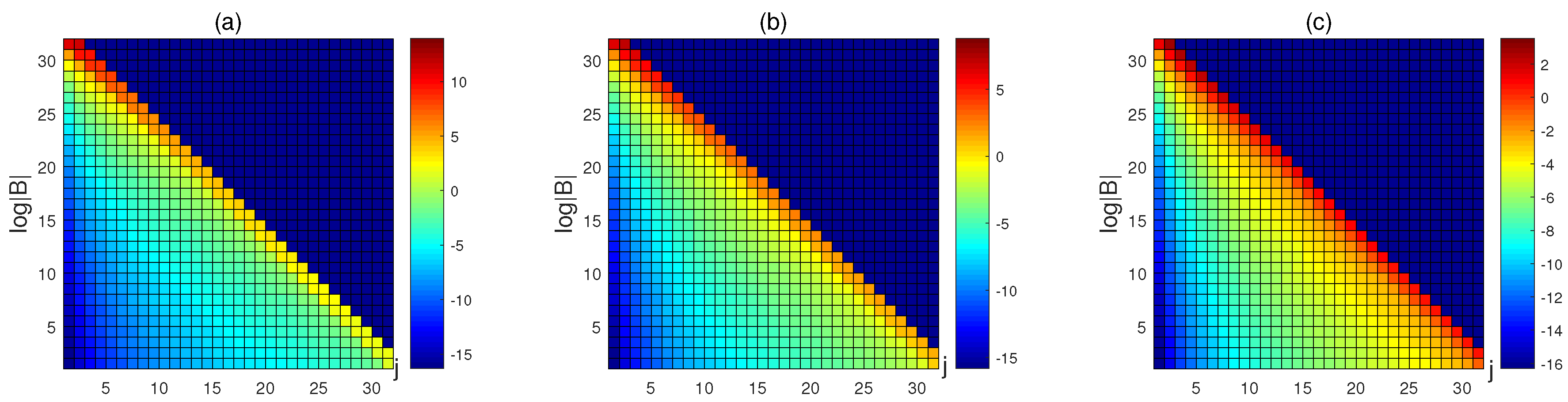
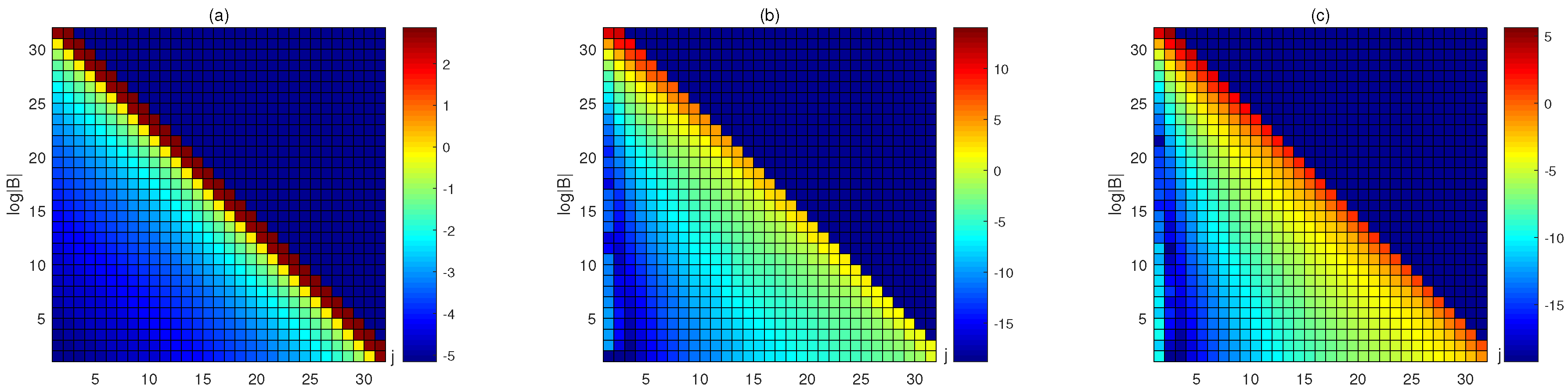
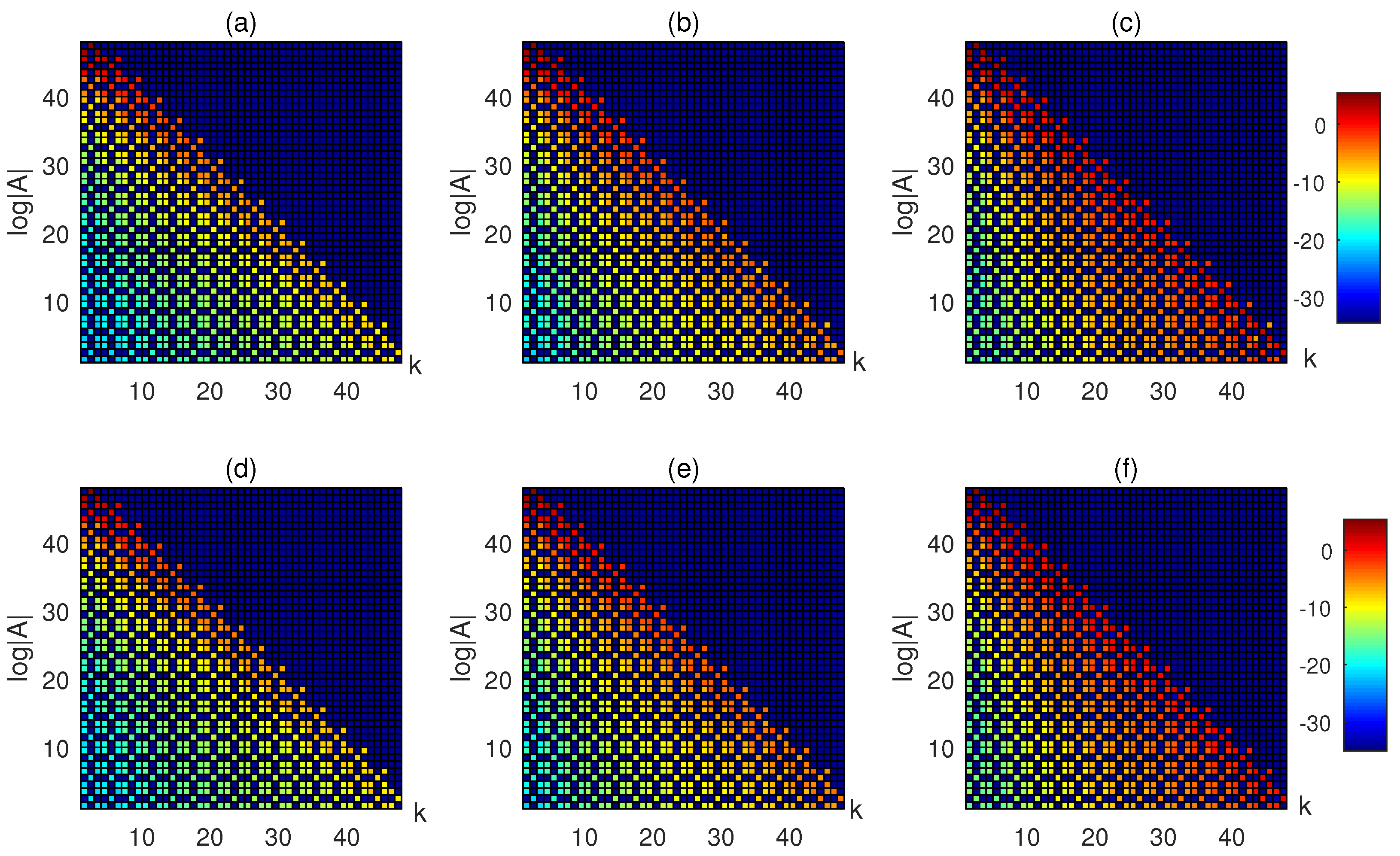
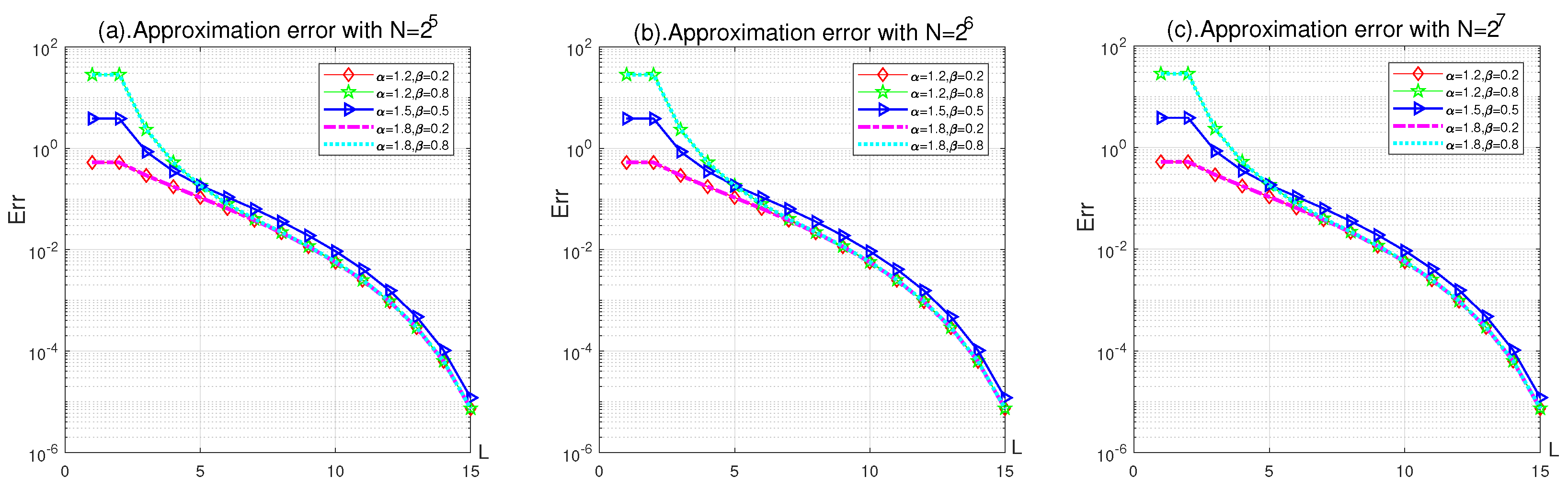
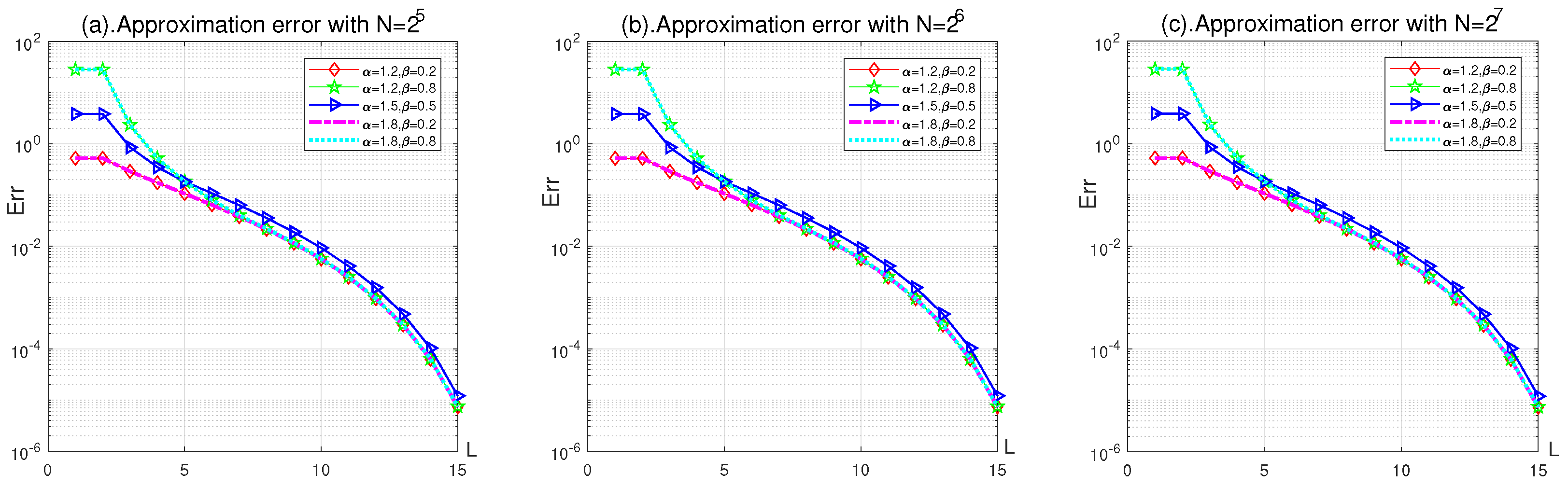
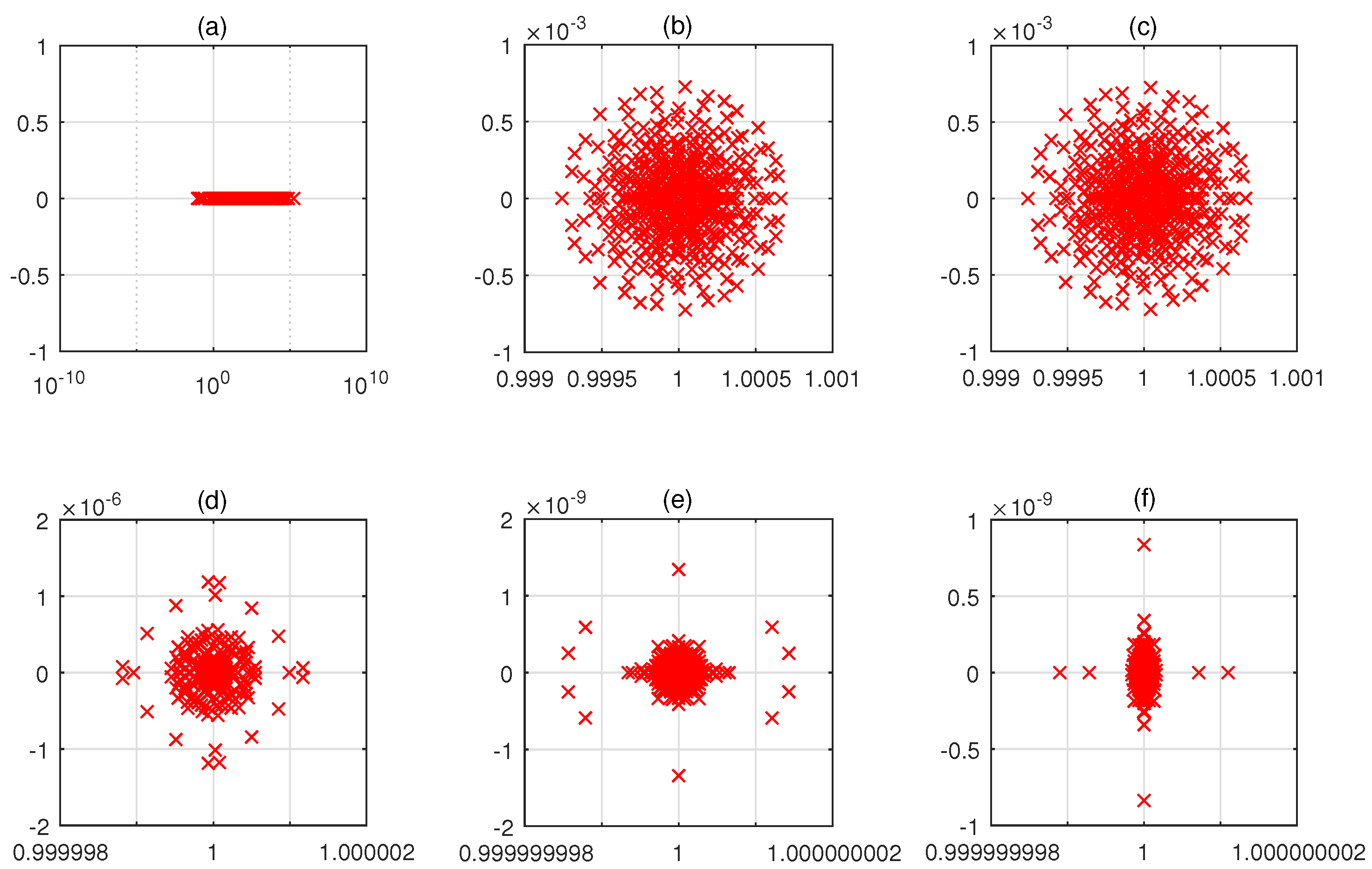
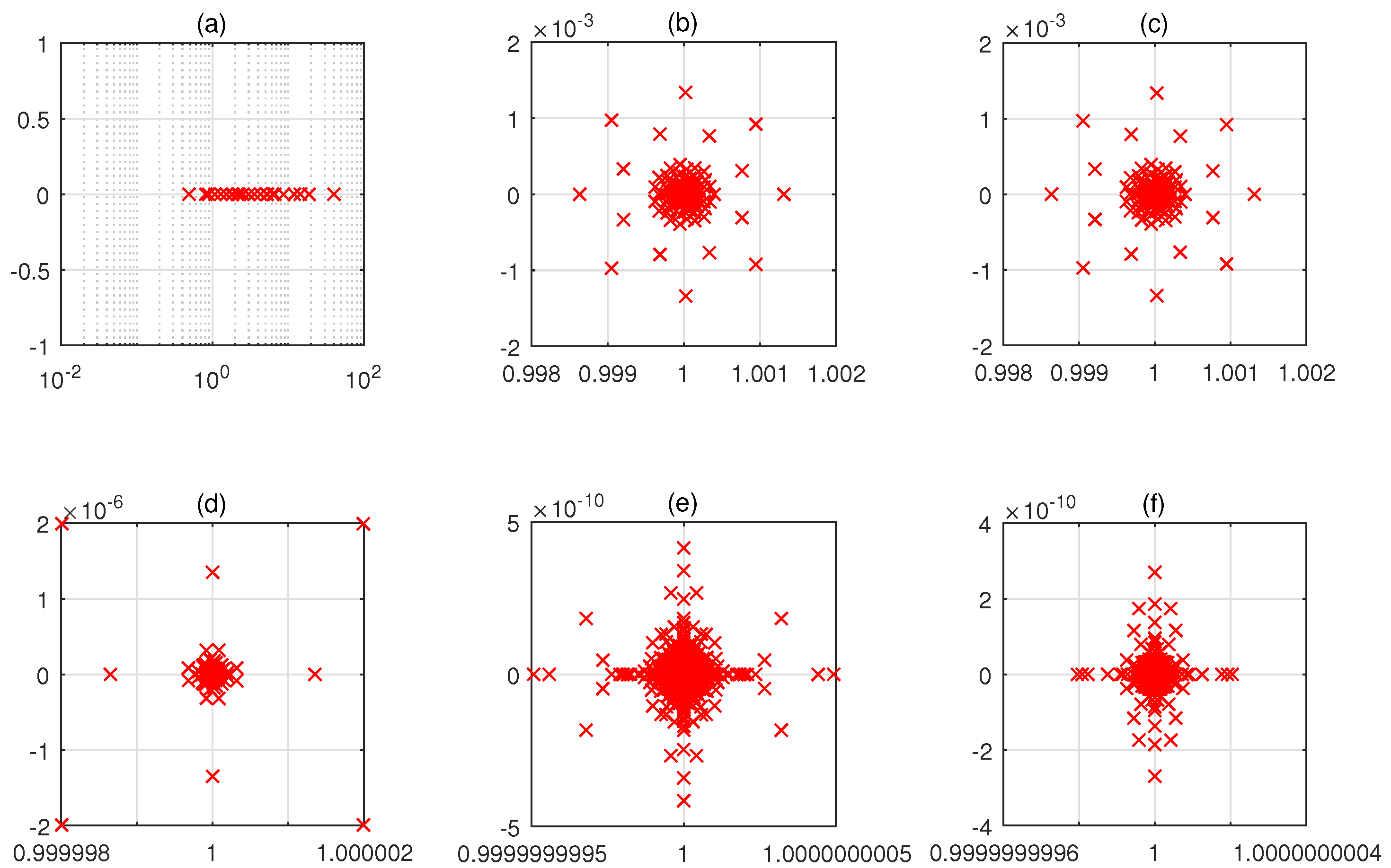
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Collins, R.E. Quantum mechanics as a classical diffusion process. Found Phys. Lett. 1992, 5, 63–69. [Google Scholar] [CrossRef]
- Fan, C.; Liu, K.X.; Chen, Y.G.; Xue, Y.C.; Zhao, J.; Khudoley, A. A new modelling method of material removal profile for electrorheological polishing with a mini annular integrated electrode. J. Mater. Process. Technol. 2022, 305, 117589. [Google Scholar] [CrossRef]
- Zhao, J.; Ge, J.Y.; Khudoley, A.; Chen, H.Y. Numerical and experimental investigation on the material removal profile during polishing of inner surfaces using an abrasive rotating jet. Tribol. Int. 2024, 191, 109125. [Google Scholar] [CrossRef]
- Bouchaud, J.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Li, C.P.; Chen, Y.Q. Fractional differential models for anomalous diffusion. Phys. A 2010, 389, 2719–2724. [Google Scholar] [CrossRef]
- Chaves, A.S. A fractional diffusion equation to describe Lévy flights. Phys. Lett. A 1998, 239, 13–16. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional-order governing equation of Lévy Motion. Water Resour. Res. 2000, 36, 1413–1423. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent II. Geophys. J. R. Astr. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- West, B.J.; Bologna, M.; Grigolini, P. Physics of Fractal Operators; Springer: New York, NY, USA, 2003. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science and Business Media: New York, NY, USA, 2010. [Google Scholar]
- Gorenflo, R.; Mainardi, F.; Moretti, D.; Pagnini, G.; Paradisi, P. Discrete random walk models for space-time fractional diffusion. Chem. Phys. 2002, 284, 52–541. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Benson, D.A.; Scheffler, H.P.; Baeumer, B. Stochastic solution of space-time fractional diffusion equations. Phys. Rev. E 2002, 65, 041103. [Google Scholar] [CrossRef] [PubMed]
- Saichev, A.I.; Zaslavsky, G.M. Fractional kinetic equations: Solutions and applications. Chaos Interdiscip. J. Nonlinear Sci. 1997, 7, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Phys. A 2000, 284, 376–384. [Google Scholar] [CrossRef]
- Obembe, A.; Hossain, M.; Abu-Khamsin, S. Variable-order derivative time fractional diffusion model for heterogeneous porous media. J. Petrol. Sci. Eng. 2017, 152, 391–405. [Google Scholar] [CrossRef]
- Liang, Y.J.; Chen, W.; Xu, W.; Sun, H.G. Distributed order Hausdorff derivative diffusion model to characterize non-Fickian diffusion in porous media. Commun. Nonlinear Sci. 2019, 70, 384–393. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, Y.Q.; Chen, W. Random-order fractional differential equation models. Signal Process. 2011, 91, 525–530. [Google Scholar] [CrossRef]
- Kumar, S.; Alam, K.; Chauhan, A. Fractional derivative based nonlinear diffusion model for image denoising. SeMA 2022, 79, 355–364. [Google Scholar] [CrossRef]
- Zhang, H.; Lv, Y. Galerkin method for a backward problem of time-space fractional symmetric diffusion equation. Symmetry 2023, 15, 1057. [Google Scholar] [CrossRef]
- Guo, B.Y.; Wang, Z.Q. Legendre-Gauss collocation methods for ordinary differential equations. Adv. Comput. Math. 2009, 30, 249–280. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods, Algorithms, Analysis, and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Sheng, C.T.; Shen, J. A space-time Petrov-Galerkin spectral method for time fractional diffusion equation. Numer. Math. Theory Methods Appl. 2018, 11, 854–876. [Google Scholar] [CrossRef]
- Li, X.J.; Xu, X.J. A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Fakhar-Izadi, F.; Shabgard, N. Time-space spectral Galerkin method for time-fractional fourth-order partial differential equations. J. Appl. Math. Comput. 2022, 68, 4253–4272. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Ye, X.; Xu, C. Spectral optimization methods for the time fractional diffusion inverse problem. Numer. Math. Theory Methods Appl. 2013, 6, 499–519. [Google Scholar]
- Zaky, M.A.; Hendy, A.S.; Macias-Diaz, J.E. Semi-implicit Galerkin-legendre spectral schemes for nonlinear time-space fractional diffusion-reaction equations with smooth and nonsmooth solutions. J. Sci. Comput. 2000, 82, 1–27. [Google Scholar] [CrossRef]
- Zaky, M.A.; Hendy, A.S. Convergence analysis of an L1-continuous Galerkin method for nonlinear time-space fractional Schrodinger equation. Int. J. Comput. Math. 2021, 98, 1420–1437. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Discontinuous spectral element methods for time-and space-fractional advection equations. SIAM J. Sci. Comput. 2014, 36, B684–B707. [Google Scholar] [CrossRef]
- Hu, C.; Lv, S.J.; Chen, W.P. Spectral methods for the time fractional diffusion-wave equation in a semi-infinite channel. Comput. Math. Appl. 2016, 9, 1818–1830. [Google Scholar]
- Huang, Y.; Skandari, M.H.N.; Mohammadizadeh, F.; Tehrani, H.A.; Georgiev, S.G.; Tohidi, E.; Shateyi, S. Space-time spectral collocation method for solving Burgers equations with the convergence analysis. Symmetry 2019, 11, 1439. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, M. Finite difference schemes for time-space fractional diffusion equations in one-and two-dimensions. Commun. Appl. Math. Comput. 2023, 5, 1674–1696. [Google Scholar] [CrossRef]
- Dong, J.P.; Xu, M.Y. Space-time fractional Schrödinger equation with time-independent potentials. J. Math. Anal. Appl. 2008, 344, 1005–1017. [Google Scholar] [CrossRef]
- Shen, J.; Sun, Z.; Du, R. Fast finite difference schemes for time-fractional diffusion equations with a weak singularity at initial time. East Asian J. Appl. Math. 2018, 8, 834–858. [Google Scholar] [CrossRef]
- Duo, S.W.; Ju, L.L.; Zhang, Y.Z. A fast algorithm for solving the space-time fractional diffusion equation. Comput. Math. Appl. 2018, 75, 1929–1941. [Google Scholar] [CrossRef]
- Zhou, J.F.; Gu, X.M.; Zhao, Y.L.; Li, H. A fast compact difference scheme with unequal time-steps for the tempered time-fractional Black-Scholes model. Int. J. Comput. Math. 2023. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhu, P.Y.; Luo, W.H. A fast second-order implicit scheme for non-linear time-space fractional diffusion equation with time delay and drift term. Appl. Math. Comput. 2018, 336, 231–248. [Google Scholar] [CrossRef]
- Li, M.; Wei, Y.F.; Niu, B.Q.; Zhao, Y.L. Fast L2-1σ Galerkin FEMs for generalized nonlinear coupled Schrödinger equations with Caputo derivatives. Appl. Math. Comput. 2022, 416, 126734. [Google Scholar]
- McDonald, E.; Pestana, J.; Wathen, A. Preconditioning and iterative solution of all-at-once systems for evolutionary partial differential equations. SIAM J. Sci. Comput. 2018, 40, A1012–A1033. [Google Scholar] [CrossRef]
- Goddard, A.; Wathen, A. A note on parallel preconditioning for all-at-once evolutionary PDEs. Electron. Trans. Numer. Anal. 2019, 51, 135–150. [Google Scholar] [CrossRef]
- Lin, X.L.; Ng, M.K.; Zhi, Y. A parallel-in-time two-sided preconditioning for all-at-once system from a non-local evolutionary equation with weakly singular kernel. J. Comput. Phys. 2021, 434, 110221. [Google Scholar] [CrossRef]
- Wu, S.L.; Zhou, T.; Zhou, Z. A uniform spectral analysis for a preconditioned all-at-once system from first-order and second-order evolutionary problems. SIAM J. Matrix Anal. Appl. 2022, 43, 1331–1353. [Google Scholar] [CrossRef]
- Stynes, M. A survey of the L1 scheme in the discretisation of time-fractional problems. Numer. Math. Theory Meth. Appl. 2022, 15, 1173–1192. [Google Scholar] [CrossRef]
- Gao, G.H.; Sun, Z.Z.; Zhang, H.W. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 2014, 259, 33–50. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Huang, Y.C.; Lei, S.L. A fast numerical method for block lower triangular Toeplitz with dense Toeplitz blocks system with applications to time-space fractional diffusion equations. Numer. Algorithm 2017, 76, 605–616. [Google Scholar] [CrossRef]
- Jia, J.; Wang, H.; Zheng, X. A fast algorithm for time-fractional diffusion equation with space-time-dependent variable order. Numer. Algorithm 2023, 94, 1705–1730. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Bertaccini, D.; Durastante, F. Limited memory block preconditioners for fast solution of fractional partial differential equations. J. Sci. Comput. 2018, 77, 950–970. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, T.; Lv, W. Block preconditioning strategies for time-space fractional diffusion equations. Appl. Math. Comput. 2018, 337, 41–53. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Gu, X.M.; Li, M.; Jian, H.Y. Preconditioners for all-at-once system from the fractional mobile/immobile advection-diffusion model. J. Appl. Math. Comput. 2021, 65, 669–691. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhu, P.Y.; Gu, X.M.; Zhao, X.L.; Cao, J. A limited-memory block bi-diagonal Toeplitz preconditioner for block lower triangular Toeplitz system from time-space fractional diffusion equation. J. Comput. Appl. Math. 2019, 362, 99–115. [Google Scholar] [CrossRef]
- Gu, X.M.; Zhao, Y.L.; Zhao, X.L.; Carpentieri, B.; Huang, Y.Y. A Note on parallel preconditioning for the all-at-once solution of Riesz fractional diffusion equations. Numer. Math. Theory Meth. Appl. 2021, 14, 893–919. [Google Scholar]
- Zhao, Y.L.; Gu, X.M.; Hu, L. A bilateral preconditioning for an L2-type all-at-once system from time-space non-local evolution equations with a weakly singular kernel. Comput. Math. Appl. 2023, 148, 200–210. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Gu, X.M.; Ostermann, A. A preconditioning technique for an all-at-once system from Volterra subdiffusion equations with graded time steps. J. Sci. Comput. 2021, 88, 11. [Google Scholar] [CrossRef]





| TS | PGMRES (L = 0) | PGMRES (L = 1) | PGMRES (L = 2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (, ) | N | Time | Its | Time | Cond | Its | Time | Cond | Its | Time |
| (1.2, 0.2) | 0.0467 | 118 | 0.0260 | 12 | 0.0624 | 12 | 0.0684 | |||
| 0.1326 | 129 | 1.1481 | 12 | 0.1872 | 12 | 0.2004 | ||||
| 1.2871 | 147 | 11.4620 | 12 | 2.0208 | 12 | 2.0796 | ||||
| (1.2, 0.8) | 0.0457 | † | — | 46 | 0.2397 | 46 | 0.2623 | |||
| 0.1328 | † | — | 59 | 0.9206 | 59 | 0.9852 | ||||
| 1.2962 | † | — | 50 | 8.4211 | 50 | 8.6656 | ||||
| (1.5, 0.5) | 0.0471 | 242 | 0.4841 | 44 | 0.2289 | 44 | 0.2508 | |||
| 0.1504 | 284 | 2.5277 | 44 | 0.6865 | 44 | 0.7349 | ||||
| 1.2913 | 334 | 18.7640 | 44 | 7.4096 | 44 | 7.6252 | ||||
| (1.8, 0.2) | 0.0500 | 250 | 0.5007 | 26 | 0.1301 | 26 | 0.1483 | |||
| 0.1355 | 337 | 2.9993 | 24 | 0.3745 | 24 | 0.4018 | ||||
| 1.2899 | 452 | 21.9922 | 23 | 3.8733 | 23 | 3.9859 | ||||
| (1.8, 0.8) | 0.0496 | † | — | 41 | 0.2132 | 41 | 0.2338 | |||
| 0.1311 | † | — | 41 | 0.6397 | 41 | 0.6847 | ||||
| 1.2867 | † | — | 40 | 6.7361 | 40 | 6.9324 | ||||
| PGMRES (= 5) | PGMRES (= 8) | PGMRES (= 10) | ||||||||
| (, ) | ||||||||||
| (1.2, 0.2) | 7 | 0.0441 | 2.2266 | 4 | 0.0364 | 1.3307 | 4 | 0.0484 | ||
| 7 | 0.1253 | 4 | 0.1024 | 3 | 0.1113 | |||||
| 7 | 1.2747 | 4 | 0.9460 | 3 | 1.0827 | |||||
| (1.2, 0.8) | 7 | 0.0441 | 5 | 0.0459 | 5 | 0.0484 | ||||
| 7 | 0.1253 | 5 | 0.1281 | 4 | 0.1485 | |||||
| 7 | 1.2745 | 6 | 1.4013 | 4 | 1.4410 | |||||
| (1.5,0.5) | 7 | 0.0440 | 4 | 0.0365 | 4 | 0.0483 | ||||
| 7 | 0.1252 | 4 | 0.1026 | 4 | 0.1486 | |||||
| 7 | 1.2746 | 4 | 0.9461 | 4 | 1.4410 | |||||
| (1.8, 0.2) | 7 | 0.0442 | 4 | 0.0365 | 4 | 0.0485 | ||||
| 7 | 0.1255 | 4 | 0.1025 | 4 | 0.1486 | |||||
| 7 | 1.2745 | 4 | 0.9461 | 4 | 1.4411 | |||||
| (1.8, 0.8) | 6 | 0.0378 | 4 | 0.0366 | 4 | 0.0485 | ||||
| 6 | 0.1074 | 4 | 0.1026 | 4 | 0.1485 | |||||
| 6 | 1.0990 | 4 | 0.9462 | 3 | 1.0873 | |||||
| TS | PGMRES (L = 0) | PGMRES (L = 1) | PGMRES (L = 2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (, ) | M | Time | Its | Time | Cond | Its | Time | Cond | Its | Time |
| (1.2, 0.2) | 0.0061 | 111 | 0.0777 | 7 | 0.0063 | 7 | 0.0091 | |||
| 0.0321 | 219 | 0.4380 | 11 | 0.0572 | 11 | 0.0637 | ||||
| 0.1826 | 393 | 3.5370 | 16 | 0.2512 | 16 | 0.2703 | ||||
| (1.2, 0.8) | 0.0073 | 325 | 0.2279 | 6 | 0.0054 | 6 | 0.0079 | |||
| 0.0327 | 720 | 1.9477 | 9 | 0.0466 | 9 | 0.0516 | ||||
| 0.1831 | † | — | 66 | 1.0363 | 66 | 1.1201 | ||||
| (1.5, 0.5) | 0.0075 | 216 | 0.1520 | 6 | 0.0057 | 6 | 0.0078 | |||
| 0.0349 | 417 | 0.8970 | 11 | 0.0573 | 11 | 0.0639 | ||||
| 0.1858 | 958 | 9.4513 | 19 | 0.2984 | 19 | 0.3231 | ||||
| (1.8, 0.2) | 0.0056 | 123 | 0.0867 | 5 | 0.0047 | 5 | 0.0056 | |||
| 0.0323 | 243 | 0.4986 | 11 | 0.0573 | 11 | 0.0636 | ||||
| 0.1722 | † | — | 66 | 1.0371 | 66 | 1.1206 | ||||
| (1.8, 0.8) | 0.0070 | 260 | 0.1822 | 5 | 0.0045 | 5 | 0.0059 | |||
| 0.0328 | 542 | 1.3312 | 9 | 0.0467 | 9 | 0.0519 | ||||
| 0.1744 | † | — | 14 | 0.2199 | 14 | 0.2376 | ||||
| PGMRES (= 3) | PGMRES (= 5) | PGMRES (= 8) | ||||||||
| (, ) | ||||||||||
| (1.2, 0.2) | 6.8387 | 5 | 0.0071 | 1.1243 | 2 | 0.0037 | 1.0000 | 1 | 0.0059 | |
| 8 | 0.0480 | 5 | 0.0322 | 2 | 0.0330 | |||||
| 12 | 0.2112 | 9 | 0.1647 | 7 | 0.1813 | |||||
| (1.2, 0.8) | 5 | 0.0073 | 3 | 0.0059 | 1 | 0.0061 | ||||
| 7 | 0.0423 | 5 | 0.0325 | 3 | 0.0376 | |||||
| 22 | 0.3876 | 9 | 0.1649 | 6 | 0.1659 | |||||
| (1.5, 0.5) | 4 | 0.0057 | 3 | 0.0056 | 1 | 0.0063 | ||||
| 7 | 0.0425 | 5 | 0.0325 | 3 | 0.0379 | |||||
| 13 | 0.2289 | 9 | 0.1646 | 6 | 0.1657 | |||||
| (1.8, 0.2) | 4 | 0.0059 | 2 | 0.0039 | 1 | 0.0060 | ||||
| 8 | 0.0483 | 5 | 0.0322 | 3 | 0.0377 | |||||
| 33 | 0.5809 | 9 | 0.1647 | 7 | 0.1816 | |||||
| (1.8, 0.8) | 4 | 0.0059 | 3 | 0.0057 | 1 | 0.0063 | ||||
| 6 | 0.0362 | 5 | 0.0323 | 3 | 0.0377 | |||||
| 11 | 0.1941 | 7 | 0.1281 | 6 | 0.1555 | |||||
| PGMRES (L = 0) | PGMRES (L = 1) | PGMRES (L = 2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (, ) | N | Time | Its | Time | Cond | Its | Time | Cond | Its | Time |
| (1.2, 0.2) | 0.0451 | † | — | 29 | 0.1508 | 29 | 0.1656 | |||
| 0.1136 | † | — | 20 | 0.3121 | 20 | 0.3341 | ||||
| 1.1024 | † | — | 30 | 5.0520 | 30 | 5.1990 | ||||
| (1.2, 0.8) | 0.0390 | † | — | 13 | 0.0679 | 13 | 0.0741 | |||
| 0.1137 | † | — | 13 | 0.2029 | 13 | 0.2173 | ||||
| 1.1023 | 929 | 25.6340 | 13 | 2.1893 | 13 | 2.2529 | ||||
| (1.5, 0.5) | 0.0392 | 329 | 0.6583 | 13 | 0.0677 | 13 | 0.0743 | |||
| 0.0960 | 386 | 3.4356 | 12 | 0.1875 | 12 | 0.2004 | ||||
| 0.9211 | 451 | 21.8463 | 12 | 2.0209 | 12 | 2.0799 | ||||
| (1.8, 0.2) | 0.0263 | 172 | 0.3441 | 9 | 0.0468 | 9 | 0.0513 | |||
| 0.0601 | 222 | 1.9758 | 8 | 0.1249 | 8 | 0.1336 | ||||
| 0.5567 | 295 | 17.0707 | 8 | 1.3473 | 8 | 1.3865 | ||||
| (1.8, 0.8) | 0.0340 | † | — | 11 | 0.0574 | 11 | 0.0627 | |||
| 0.0778 | 591 | 5.2599 | 11 | 0.1717 | 11 | 0.1838 | ||||
| 0.9292 | † | — | 11 | 1.8526 | 11 | 1.9663 | ||||
| PGMRES (= 5) | PGMRES (= 8) | PGMRES (= 10) | ||||||||
| (, ) | ||||||||||
| (1.2, 0.2) | 7 | 0.0442 | 4 | 0.0367 | 3 | 0.0363 | ||||
| 6 | 0.1074 | 3 | 0.0769 | 3 | 0.1113 | |||||
| 6 | 1.0927 | 3 | 0.7006 | 3 | 1.0801 | |||||
| (1.2, 0.8) | 6 | 0.0379 | 5 | 0.0455 | 4 | 0.0485 | ||||
| 6 | 0.1076 | 4 | 0.1024 | 4 | 0.1486 | |||||
| 6 | 1.0927 | 2 | 0.4716 | 3 | 1.0804 | |||||
| (1.5, 0.5) | 6 | 0.0381 | 4 | 0.0367 | 3 | 0.0365 | ||||
| 5 | 0.0896 | 4 | 0.1024 | 3 | 0.1113 | |||||
| 5 | 0.9105 | 4 | 0.9342 | 2 | 0.7203 | |||||
| (1.8, 0.2) | 4 | 0.0253 | 3 | 0.0274 | 3 | 0.0365 | ||||
| 3 | 0.0538 | 2 | 0.0521 | 2 | 0.0742 | |||||
| 3 | 0.5464 | 2 | 0.4717 | 2 | 0.7204 | |||||
| (1.8, 0.8) | 5 | 0.0317 | 4 | 0.0369 | 3 | 0.0363 | ||||
| 4 | 0.0716 | 3 | 0.0767 | 2 | 0.0742 | |||||
| 5 | 0.9102 | 2 | 0.4716 | 2 | 0.7206 | |||||
| PGMRES (L = 0) | PGMRES (L = 1) | PGMRES (L = 2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (, ) | M | Time | Its | Time | Cond | Its | Time | Cond | Its | Time |
| (1.2, 0.2) | 0.0073 | 167 | 0.1336 | 6 | 0.0061 | 6 | 0.0090 | |||
| 0.0318 | 301 | 0.9280 | 10 | 0.0559 | 10 | 0.0623 | ||||
| 0.1818 | 661 | 6.1404 | 18 | 0.2376 | 18 | 0.3130 | ||||
| (1.2, 1.8) | 0.0079 | 393 | 0.3157 | 6 | 0.0059 | 6 | 0.0089 | |||
| 0.0331 | 824 | 2.0452 | 7 | 0.0394 | 7 | 0.0434 | ||||
| 0.1809 | † | — | 12 | 0.1585 | 12 | 0.2083 | ||||
| (1.5, 0.5) | 0.0068 | 265 | 0.2123 | 6 | 0.0061 | 6 | 0.0091 | |||
| 0.0326 | 550 | 1.5621 | 10 | 0.0561 | 10 | 0.0623 | ||||
| 0.1792 | † | — | 16 | 0.2116 | 16 | 0.2776 | ||||
| (1.8, 0.2) | 0.007 | 132 | 0.1059 | 5 | 0.0050 | 1.7026 | 5 | 0.0075 | ||
| 0.0311 | 240 | 0.5966 | 8 | 0.0449 | 8 | 0.0498 | ||||
| 0.1801 | 448 | 4.1666 | 12 | 0.1587 | 12 | 0.2086 | ||||
| (1.8, 0.8) | 0.0074 | 292 | 0.2336 | 4 | 0.0041 | 3.0889 | 4 | 0.0060 | ||
| 0.0329 | 677 | 1.7383 | 7 | 0.0392 | 7 | 0.0437 | ||||
| 0.1797 | † | — | 11 | 0.1456 | 11 | 0.1916 | ||||
| PGMRES (= 3) | PGMRES (= 5) | PGMRES (= 8) | ||||||||
| (, ) | ||||||||||
| (1.2, 0.2) | 1.5404 | 4 | 0.0081 | 1.0063 | 3 | 0.0069 | 1.0000 | 1 | 0.0071 | |
| 8 | 0.0552 | 4 | 0.0300 | 3 | 0.0279 | |||||
| 12 | 0.2196 | 8 | 0.1536 | 6 | 0.1590 | |||||
| (1.2,1.8) | 4 | 0.0083 | 3 | 0.0067 | 1 | 0.0073 | ||||
| 6 | 0.0414 | 4 | 0.0304 | 2 | 0.0213 | |||||
| 9 | 0.1649 | 6 | 0.1152 | 5 | 0.1325 | |||||
| (1.5, 0.5) | 4 | 0.0081 | 2 | 0.0047 | 1 | 0.0069 | ||||
| 6 | 0.0417 | 4 | 0.0301 | 3 | 0.0281 | |||||
| 11 | 0.2013 | 8 | 0.1539 | 5 | 0.1327 | |||||
| (1.8, 0.2) | 4 | 0.0085 | 2 | 0.0051 | 1 | 0.0067 | ||||
| 5 | 0.0347 | 4 | 0.0299 | 2 | 0.0213 | |||||
| 9 | 0.1646 | 6 | 0.1150 | 3 | 0.0795 | |||||
| (1.8, 0.8) | 3 | 0.0064 | 2 | 0.0049 | 1 | 0.0071 | ||||
| 5 | 0.0349 | 3 | 0.0226 | 2 | 0.0216 | |||||
| 8 | 0.1464 | 5 | 0.0960 | 3 | 0.0795 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhang, S. A Preconditioner for Galerkin–Legendre Spectral All-at-Once System from Time-Space Fractional Diffusion Equation. Symmetry 2023, 15, 2144. https://doi.org/10.3390/sym15122144
Wang M, Zhang S. A Preconditioner for Galerkin–Legendre Spectral All-at-Once System from Time-Space Fractional Diffusion Equation. Symmetry. 2023; 15(12):2144. https://doi.org/10.3390/sym15122144
Chicago/Turabian StyleWang, Meijuan, and Shugong Zhang. 2023. "A Preconditioner for Galerkin–Legendre Spectral All-at-Once System from Time-Space Fractional Diffusion Equation" Symmetry 15, no. 12: 2144. https://doi.org/10.3390/sym15122144
APA StyleWang, M., & Zhang, S. (2023). A Preconditioner for Galerkin–Legendre Spectral All-at-Once System from Time-Space Fractional Diffusion Equation. Symmetry, 15(12), 2144. https://doi.org/10.3390/sym15122144






