Modular Conjectures for Direct Product of Finite Groups ^†

Abstract

The representation theory of a finite group, G, is an important area of research currently. This paper studied the modular representation of finite groups, which are direct products. There are three approaches to studying this representation: the ring approach, the character approach, and the module approach. Moreover, we learned some of the important conjectures in this representation, which link a representation of a finite group and its local subgroups, which are normalizer non-trivial p-subgroups. These conjectures are the McKay conjecture, Alperin’s weight conjecture, and the ordinary weight conjecture. The main aim of the proposed paper was to investigate these conjectures of direct products, the direct summands of which satisfy these conjectures for the associated tensor product of the p-block. We obtained the results by assuming the conjectures are true. Then, we used the properties of the direct products.

1. Introduction

The study of modular representation theory started in the mid of 20th Century. However, several fundamental questions remain unsolved in the ordinary representations, as well as in the modular representations of finite groups [1]. In 1963, R. Brauer [2] proposed a list of deep conjectures regarding modular and ordinary representations of finite groups, that were still unsolved. In this paper, we concentrated on conjectures that connect the representation theory of a finite group, $G,$ and its local subgroups. The term “local subgroups” refers to the normalizer of p-subgroups in G, where p is a prime number. We are concerned with the McKay conjecture, Alperin’s weight conjecture, and the ordinary weight conjecture.

Since the realization of the classification theorem of finite simple groups, it has been a natural approach to survey the main conjectures in modular representations theory to establish whether simple groups satisfy them. These conjectures have been confirmed for various simple groups. But, we still need to establish how to reduce them to the case of finite simple groups in efficient work. This motivated us to study the block theory and important conjectures and to deal with these conjectures in the context of the direct product. This is possibly the first step in an attempt at a reduction of work.

In this paper, we demonstrate that the tensor product satisfies these conjectures if every direct summand satisfies them. To realize this aim, we used cancellation methods and applied Robinson’s method with a simple observation for the products of the invariant numbers, which are associated with each block under consideration.

The paper is organized as follows. Section 2 sets out the preliminary and background concepts required for the introduction of the subject. Section 3 is devoted to the study of the core open conjectures of modular representation theory. Section 4 contains our main discovery, contributions, and main results. The main achievements of the paper can be summarized in the following points:

• We study the theorem regarding the tensor product of two blocks satisfying the McKay conjecture in $G=G_1\times G_2$ and present the proof for this theorem using a new method.
• We study the theorem regarding the tensor product of two blocks satisfying the Alperin’s weight conjecture in $G=G_1\times G_2$ and present the proof for this theorem using a new method.
• We introduce a new theorem regarding the tensor product of two blocks satisfying the ordinary weight conjecture in $G=G_1\times G_2$ and present the proof of this theorem.

Literature Review of the Conjectures

Let G be a finite group and p be a prime number dividing the order $\left|G\right|$ of G. The McKay conjecture (MC) [3] is one of the most-interesting open problems in the area of the representation theory of finite groups. This conjecture is given in its original form first in the case that G is a simple group, and the prime $p=2$ by J. McKay [4,5]. The most-straightforward general version of the conjecture asserts that the number of irreducible ordinary characters of G of a degree not divisible by p is the same if computed in a p-Sylow normalizer of G. This version was noticed by J. McKay [1,5] in 1972. In 1973, I. M. Isaacs [6] proved this conjecture for all odd-order groups and every prime. In 1976, J. L. Alperin [7] generalized the McKay conjecture to Brauer blocks, which is now known as the Alperin–McKay conjecture (AMC). In 1978, T. R. Wolf [8] provided a proof for all solvable groups. Subsequently, in 1980, the Alperin–McKay conjecture was proven for p-solvable groups by T. Okuyama and M. Wajima [9] and independently confirmed by E. C. Dade [10]. The McKay conjecture is known to hold true for symmetric groups, $S_n$, and alternating groups, $A_n$, which was proven by J. B. Olsson [11] and for the general linear groups and the covering groups of $S_n$ and $A_n$, which were proven by J. B. Olsson and G. O. Michler [12,13]. In 1998, R.A. Wilson [14] presented a proof of the McKay conjecture for all sporadic simple groups and for all primes. There are many ways to strengthen these conjectures, which have been suggested by I. M. Isaacs and G. Navarro in [15] and by G. Navarro [16], which involve Galois automorphisms. Further ways of strengthening were provided by A. Turull [17], which involve fields of character values and local Schur indices. These ways of strengthening were confirmed by A. Turull [18] for p-solvable groups.

Alperin’s weight conjecture (AWC) was stated by J. L. Alperin [1,19] in 1986, and it is one of the main problems in the representation theory of finite groups. Alperin’s weight conjecture asserts that, for any finite group, G, the number of irreducible Brauer characters of G equals the number of conjugacy classes of the weights of G. This conjecture has a block version, which asserts that, if G is a finite group, p is a prime number, and B is a p-block of G, then the number of irreducible Brauer characters of B equals the number of conjugacy classes of weights of B. In 1989, R. Knörr and G. R. Robinson in [1,20] reformulated this conjecture and found a significant relationship between the Alperin–McKay conjecture and Alperin’s weight conjecture in the case of certain defect groups. Alperin’s weight conjecture holds for many large families of finite groups: for p-solvable groups, which were confirmed by I. Isaacs and G. Navarro [21], for a general linear group, $\mathrm{G}{\mathrm{l}}_n\left(q\right)$, and symmetric groups, $S_n$, which was shown by J. L. Alperin and P. Fong in [22], as well as for the groups Lie type in defining characteristic, which was shown to hold by M. Cabanes in [23]. This conjecture was shown to hold by the work of R. Brauer, E. C. Dade, J. B. Olsson, and B. Sambale in the lecture notes in [24] for all blocks such that the defect group is cyclic or metacyclic.

The ordinary weight conjecture (OWC) is the third conjecture and focuses on estimating the number of irreducible ordinary characters in a p-block B, which has a defect, d. We shall give some historical background to the ordinary weight conjecture (OWC) by recasting what G. R. Robinson discovered in the paper [25]. The idea is to attempt to obtain block-theoretic information p-locally. The starting point was Alperin’s weight conjecture in the paper [19]. Then, in the paper [20], we see a clever reformulation of Alperin’s weight conjecture. However, in [26], E. C. Dade used the Clifford theory to produce more conjectures, which are known as Dade’s conjectures. G. R. Robinson developed the ordinary weight conjecture (OWC) in the paper [27]. The idea in [27] is that the local computations necessary for OWC the ordinary weight conjecture for a given block, B, can be achieved using p-local invariants in the normalizers of certain objects, known as Brauer subpairs. The ordinary weight conjecture holds in the following situations: p-solvable groups, nilpotent p-blocks, p-blocks with a cyclic defect group, dihedral, semi-dihedral, or (generalized) quaternion. The methods for providing the proof are different. However, the most-important technique involves using the sum of the chain complexes and cancellation methods, as demonstrated by G. R. Robinson [28,29].

2. Preliminaries

In this paper, we worked on a finite group, G, and a prime number, p, which divides the order of G. We assumed $(K,R,F)$ to be a p-modular system, where R is a complete discrete valuation ring, K is the field of fractions with characteristic zero, which has $\left|G\right|th$ roots of unity, and $F=R/\left(\pi \right)$ is the residue field with characteristic p such that $\left(\pi \right)$ is the Jacobson radical of R and the unique maximal ideal of R containing the prime number p. Let n be a natural number and $\mathrm{G}{\mathrm{L}}_n\left(K\right)$ be the general linear group of degree n. We write $\rho :G\to \mathrm{G}{\mathrm{L}}_n\left(K\right)$ to be a representation of the group G, which affords $\chi$, where $\chi$ is a character of G, which is defined by $\chi \left(g\right)=\mathrm{tr}\rho \left(g\right)$ for all $g\in G$ where $\mathrm{tr}\rho \left(g\right)$ is the trace of the matrix $\rho \left(g\right)$. We denote $\mathrm{Irr}\left(G\right)$ for the set of all irreducible ordinary characters of the finite group G and the number of these characters by $k\left(G\right).$ The values of the irreducible characters on the different conjugacy classes of G are given by the character table of G. The first row is usually indexed by the trivial character, i.e., $\chi \left(g\right)=1$ for all $g\in G$. The first column usually indexes the identity element of G and contains the degrees of the irreducible characters. We say that an element, g, in the finite group G is p-regular if $\mathrm{g}.\mathrm{c}.\mathrm{d}(p,\left|g\right|)=1$, where g.c.d represents the greatest common divisor. We write $G^{\circ }$ for the set of all p-regular elements. If we restrict the irreducible ordinary character to $G^{\circ }$, we obtain the Brauer character. The set of all irreducible Brauer characters of G is denoted by $\mathrm{IBr}\left(G\right)=\left\{{\vartheta }_1,\dots ,{\vartheta }_l\right\}$. The number of the set of all irreducible Brauer characters of G is the same as the number of p-regular classes, i.e., $\left|\mathrm{IBr}\left(G\right)\right|=|\mathrm{Cl}\left(G^{\circ }\right)|$. The Brauer character can be written as follows:

$${\mathrm{Res}}_{G^{\circ }}^G\left({\chi }_j\right)=d_{{\vartheta }_1{\chi }_j}{\vartheta }_1+\cdots +d_{{\vartheta }_l{\chi }_j}{\vartheta }_l,$$

where $d_{{\vartheta }_1{\chi }_j},\dots ,d_{{\vartheta }_l{\chi }_j}$ are positive integers, and every $d_{{\vartheta }_1{\chi }_j},\dots ,d_{{\vartheta }_l{\chi }_j}$ is called the decomposition number. The matrix D with the entries’ decomposition number was called the decomposition matrix in [30].

The Cartan matrix is a square matrix, which is defined by $C=D·D^t$, where D is the decomposition matrix and $D^t$ is the transpose of the matrix D. The group algebra $RG$ splits into two-sided ideals $B_i$ of $RG$, and each of them was called a p-block in [30].

We mean by a defect group of the p-block B a p-subgroup of the finite group G, which measures whether or not the p-block B has a simple algebra structure. In other words, B is only semisimple if such a defect group is the identity subgroup of G in [31]. For $x\in G$, we write the symbol $C_G\left(x\right)$ to denote the centralizer of x in G, and for the ordinary irreducible characters ${\chi }_m,{\chi }_n$ belonging to $\mathrm{Irr}\left(G\right),$ we can define the p-block by the character theory approach, which is the equivalence class of the following equivalence relation:

$${\chi }_m\sim {\chi }_n\iff \frac{[G:C_G\left(x\right)]{\chi }_m\left(x\right)}{{\chi }_m\left(1\right)}{\equiv }_p\frac{[G:C_G\left(x\right)]{\chi }_n\left(x\right)}{{\chi }_n\left(1\right)}:1⩽n,m⩽k\left(G\right),x\in G,$$

where ${\equiv }_p$ represents congruence modulo p in [32,33]. The block theory was devised by R. Brauer, which uses character theory. Then, G. A. Green introduced the module theory. We call this $B_{\circ }\left(G\right)$, which is the principal block, which contains the trivial character. We considered the inclusion $\mathrm{Irr}\left(G\right)\supseteq \mathrm{Irr}\left(B\right)=\left\{\chi \in \mathrm{Irr}\left(G\right);\chi \in B\right\}$. We write $k\left(B\right)$ to refer to the cardinality of $\mathrm{Irr}\left(B\right)$. We considered the inclusion $\mathrm{IBr}\left(G\right)\supseteq \mathrm{IBr}\left(B\right)=\left\{\vartheta \in \mathrm{IBr}\left(G\right);\vartheta \in B\right\}$. We write $l\left(B\right)$ to refer to the number of the elements in the set $\mathrm{IBr}\left(B\right)$ in [32].

Every irreducible ordinary character of the finite group G has a positive integer $d\left(\chi \right)$ which is called the defect number of $\chi$. We obtained $d\left(\chi \right)$ by the following:

$$p^{d\left(\chi \right)}\chi {\left(1\right)}_p={\left|G\right|}_p$$

where ${\left|G\right|}_p$ is the p-part of the order of G and $\chi {\left(1\right)}_p$ is the p-part of the degree of the irreducible character $\chi$. If $\chi {\left(1\right)}_p={\left|G\right|}_p$, we say that $\chi$ has defect zero [33,34].

The maximal defect numbers of irreducible characters in the block B are called defect numbers of the block B and are denoted by $d\left(B\right)$. We can define $h\left(\chi \right)$ as the height number of the irreducible character $\chi$ by the following relation:

$$d\left(B\right)=d\left(\chi \right)+h\left(\chi \right).$$

An irreducible character $\chi$ is said to be of height zero if $h\left(\chi \right)=0$. Then we have in this case $d\left(B\right)=h\left(\chi \right)$, we say that $\chi$ has full height. Then, the zero defect has full height, and the inverse is true.

We use the notations $\delta \left(B\right)$ and $\delta \left(C\right)$ to denote the defect group of the block B with order $p^{d\left(B\right)}$ and the defect group of a conjugacy class C, respectively [30].

Much of the research in representation theory currently is devoted to proving the Alperin weight conjecture. If P is a p-subgroup of G, a p-weight of G is a pair

$$(P,\psi ),$$

where $\psi \in \mathrm{Irr}(N_G\left(P\right)/P)$ is such that $\psi {\left(1\right)}_p={\left[N_G\left(P\right)/P\right]}_p$ (that is, $\psi$ has p-defect zero considered as a character of $N_G\left(P\right)/P$). If $(P,\psi )$ is a p-weight and $g\in G$, then ${(P,\psi )}^g=(P^g,{\psi }^g)$ is another p-weight. The Alperin weight conjecture states that the number of p-regular classes of G is the number of G-classes of p-weights in [32].

If B is a p-block of G, a p-weight $(P,\psi )$ belongs to B if the block $b\in Bl\left(N_G\left(P\right)\right)$ of $\psi$ induces B. The Alperin weight conjecture in the block form asserts that $l\left(B\right)$ is the number of G-classes of p-weights belonging to B. There are many fascinating consequences of this conjecture. As we see, Alperin’s conjecture tells us that important pieces of information on blocks can be computed locally [32]. On the other hand, a direct product of groups is a tool to obtain new groups from known groups. We refer to the group $G_1\times G_2$ as a direct product of $G_1$ and $G_2$ and $b_1\otimes b_2$ as a tensor product of $b_1$ and $b_2$. If Q is a Sylow p-subgroup of G, we use the symbol $N_G\left(Q\right)$ to denote the normalizer of Q in G.

Definition 1

([35,36]). Suppose that $G_1$ and $G_2$ are finite groups. The direct product of two groups is defined as the following:

$$G_1\times G_2=\left\{(g_1,g_2)|g_1\in G_1\mathrm{and}{g}_2\in G_2\right\}.$$

The product operation defined on $G_1\times G_2$ is as follows:

$$\begin{array}{c}\hfill (g_1,g_2)·(g_1^{‵},g_2^{‵})=(g_1{g}_1^{‵},g_2{g}_2^{‵}),\end{array}$$

(1)

where $g_1{g}_1^{‵}$ is the product in a group $G_1$ and $g_2{g}_2^{‵}$ is the product in group $G_2$.

Theorem 1.

$(G_1\times G_2,·)$, where · is defined in Definition 1, forms a group. This group is called the external direct product of two groups: $G_1$ and $G_2$.

Theorem 2.

If $H_1$ and $H_2$ are subgroups of $G_1$ and $G_2$ respectively, then $H_1\times H_2$ is a subgroup of $G_1\times G_2$.

Proof.

• Let $(h_1,h_2),(h_1^{‵},h_2^{‵})\in H_1\times H_2(\mathrm{i}.\mathrm{e}.,h_1,h_1^{‵}\in H_1\mathrm{and}{h}_2,h_2^{‵}\in H_2)$, where $H_1,H_2$ are subgroups of $G_1,G_2$, respectively. Then, $h_1{h}_1^{‵}\in H_1$ and $h_2{h}_2^{‵}\in H_2$. Therefore,

  $$(h_1,h_2)·(h_1^{‵},h_2^{‵})=(h_1{h}_1^{‵},h_2{h}_2^{‵})\in H_1\times H_2.$$

  Hence, the product · is closed on $H_1\times H_2$.
• Let $1_{G_1}$ and $1_{G_2}$ be the identity in $G_1$ and $G_2$, respectively. Then, $(1_{G_1},1_{G_2})$ is the identity element in $G_1\times G_2.$ Since $H_1$ and $H_2$ are subgroups of $G_1$ and $G_2$, then $1_{G_1}\in H_1$ and $1_{G_2}\in H_2$. Therefore, $(1_{G_1},1_{G_2})\in H_1\times H_2.$ So, $H_1\times H_2$ contains the identity element.
• If $(h_1,h_2)\in H_1\times H_2$, then there exists ${(h_1,h_2)}^{-1}=(h_1^{-1},h_2^{-1})$, which is the inverse in $H_1\times H_2$. Since $h_1^{-1}\in H_1$ and $h_2^{-1}\in H_2$, because $H_1,H_2$ are subgroups of $G_1,G_2,$ thus $H_1\times H_2$ is a subgroup of $G_1\times G_2$.

□

Note 1.

Not all subgroups of $G_1\times G_2$ are in the form $H_1\times H_2$ for subgroups $H_1⩽G_1$ and $H_2⩽G_2$. For example, ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$ with four elements, ${\mathbb{Z}}_2\times {\mathbb{Z}}_2=\left\{(0,0),(1,0),(0,1),(1,1)\right\}$ and $H=\left\{(0,0),(1,1)\right\}\subseteq {\mathbb{Z}}_2\times {\mathbb{Z}}_2$. H is a subgroup of ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$, but $\nexists H_1⩽{\mathbb{Z}}_2$ and $H_2⩽{\mathbb{Z}}_2$ such that $H=H_1\times H_2$, where ∄ means not existent.

Example 1.

The external direct product $S_3\times {\mathbb{Z}}_2$ is isomorphic to $D_{12}.$ First, note that $S_3$ is non-Abelian. Then, the direct product $S_3\times {\mathbb{Z}}_2$ is non-Abelian. Thus, $S_3\times {\mathbb{Z}}_2$ is neither isomorphic to ${\mathbb{Z}}_{12}$ nor ${\mathbb{Z}}_6\times {\mathbb{Z}}_2$. Also, since $S_3\times {\mathbb{Z}}_2$ has element $\left(\right(123),1)$ with order $l.c.m(3,2)=6$, therefore $A_4$ has no element of order six. Thus, $S_3\times {\mathbb{Z}}_2\ncong A_4$. Hence, $S_3\times {\mathbb{Z}}_2\cong D_{12}$.

There are many properties for a direct product of finite groups.

Lemma 1

([35,37]). Suppose that G is a finite group and G is the external direct product of two groups: $G_1$ and $G_2$. If H is the external direct product of two groups, $H_1$ and $H_2$, such that $H_1$ is a subgroup of $G_1$ and $H_2$ is a subgroup of $G_2,$ then $N_G\left(H\right)=N_{G_1}\left(H_1\right)\times N_{G_2}\left(H_2\right)$.

Proof.

Let $(g_1,g_2)\in N_G\left(H\right)$. Then, $(g_1,g_2)(h_1,h_2)=(h_1,h_2)(g_1,g_2)$ $\mathrm{for} \mathrm{all} (h_1,h_2)\in H$. This implies $(g_1{h}_1,g_2{h}_2)=(h_1{g}_1,h_2{g}_2)$$\Rightarrow g_1{h}_1=h_1{g}_1$ and $g_2{h}_2=h_2{g}_2\mathrm{for}\mathrm{all}{h}_1\in H_1,h_2\in H_2.$ Thus, $g_1\in N_{G_1}\left(H_1\right)$ and $g_2\in N_{G_2}\left(H_2\right).$ Hence, $N_G\left(H\right)\subseteq N_{G_1}\left(H_1\right)\times N_{G_2}\left(H_2\right).$ Let $(g_1,g_2)\in N_{G_1}\left(H_1\right)\times N_{G_2}\left(H_2\right).$ Then $g_1{h}_1=h_1{g}_1$ and $g_2{h}_2=h_2{g}_2$ for all $h_1\in H_1,$$h_2\in H_2$$\Rightarrow (g_1{h}_1,g_2{h}_2)=(h_1{g}_1,h_2{g}_2)$$\Rightarrow (g_1,g_2)(h_1,h_2)=(h_1,h_2)(g_1,g_2)$ for all $(h_1,h_2)$$\in H.$ Thus, $(g_1,g_2)\in N_G\left(H\right)$. Hence, $N_{G_1}\left(H_1\right)\times N_{G_2}\left(H_2\right)$$\subseteq N_G\left(H\right).$ Then, $N_G\left(H\right)=N_{G_1}\left(H_1\right)\times N_{G_2}\left(H_2\right).$ □

Lemma 2

([37]). Suppose that G is a finite group and G is the external direct product of two groups: $G_1$ and $G_2$. If C is a conjugacy class of G, then $C_1\in Cl\left(G_1\right)$ is the conjugacy class of $G_1$, and $C_2\in Cl\left(G_2\right)$ is the conjugacy class of $G_2$ such that

$$C=C_1\times C_2=\left\{\left(c_1,c_2\right)|c_1\in C_1,c_2\in C_2\right\}.$$

There are some properties of the direct product associated with the characters.

Theorem 3.

Suppose that H is a subgroup of the finite group G and χ is an irreducible character of $G,$ whereas φ is an irreducible character of H. Then, $\chi \times \phi$ is the irreducible character of $G\times H$, where $\chi \times \phi :\left(g,h\right)\mapsto \chi \left(g\right)\phi \left(h\right)$.

Proof.

We have

$$\begin{array}{cc}\hfill {⟨\chi \times \phi ,\chi \times \phi ⟩}_{G\times H}& =\frac{1}{\left|G\times H\right|}\sum _{(g,h)\in G\times H}\chi \left(g\right)\phi \left(h\right)·\overline{\chi \left(g\right)\phi \left(h\right)}\hfill \\ \hfill & =\frac{1}{\left|G\right|}\left(\sum _{g\in G}\chi \left(g\right)\overline{\chi \left(g\right)}\right)·\frac{1}{\left|H\right|}\left(\sum _{h\in H}\phi \left(h\right)\overline{\phi \left(h\right)}\right)\hfill \\ \hfill & ={⟨\chi ,\chi ⟩}_G·{⟨\phi ,\phi ⟩}_H\hfill \\ \hfill & =1·1=1,\left(\mathrm{because}\chi ,\phi \mathrm{are}\mathrm{irreducible}\mathrm{characters}\right),\hfill \end{array}$$

where ${⟨-,-⟩}_G$ represents the inner product of class functions of G. □

The following concerns the properties of the blocks. Before mentioning that property, there are some definitions and theorems related to it in Proposition 1.

Definition 2

([30]). Suppose that H is a subgroup of the finite group G and b is a block of $RH$. We say that $b^g$ is the G-conjugate block of b if $b^g=g^{-1}bg$ is the block of $R{H}^g$ for all $g\in G$.

Definition 3

([30,32]). Let H be a normal subgroup of G and $g\in G.$ If b is a block of the subgroup H of G, then the set $I_G\left(b\right)=\left\{g\in G;b^g=b\right\}$ is called the inertial group of b.

Note 2.

We note that $H⩽I_G\left(b\right)⩽G$.

Definition 4.

Suppose that G is a finite group and H is a normal subgroup of G. Let b be a block of H of G and $I_G\left(b\right)$ be the inertial group of b. If we set

$$f_b=\sum _{g\in I_G\left(b\right)\setminus G}{\left(e_b\right)}^g,$$

then $f_b$ is the central idempotent of $RG$, and there is a primitive idempotent decomposition $f_b={\displaystyle \sum _{i=1}^r}{e}_{B_i}(B_i\in Bl\left(G\right))$ in $Z\left(RG\right)$, where $Z\left(RG\right)$ is the center of the group algebra $RG$. Then, we say that $B_i$ covers b.

Theorem 4

(Passman). Let G be a finite group, H be a normal subgroup of G, and B be a block of $G.$ If b is a block of $H,$ then B covers $b\iff$${\omega }_B^{*}\left(\hat{C}\right)={\omega }_b^{*}\left(\hat{C}\right)$ for every conjugacy class $C\in Cl\left(G\right)$ contained in H, where ${\omega }_B^{*},{\omega }_b^{*}$ are irreducible F-linear representations of $Z\left(FG\right),Z\left(FH\right),$ respectively, and $\hat{C}$ is the class sum of the conjugacy class C.

Proof.

See ([30], Chapter 5, p. 338). □

Proposition 1

([37]). Suppose that G is a finite group, and G is the external direct product of two groups: $G_1$ and $G_2$. If $b_1$ is a block of $G_1$ with $f_1$ and $b_2$ is a block of $G_2$ with $f_2$, then $f_1{f}_2$ is the block idempotent of $G.$ Consequently, we obtain the block of G by the tensor product of blocks of $G_1$ and blocks of $G_2$.

$$Bl\left(G\right)=\left\{b_i\otimes b_j|b_i\in Bl\left(G_1\right),b_j\in Bl\left(G_2\right)\right\}.$$

Proof. 

The central idempotents of $Z\left(RG\right)$ are denoted by $f_1$ and $f_2$. Therefore, $Z\left(RG\right)$ is closed under the multiplication operation. Then, $f_1{f}_2$ is the central idempotent of $Z\left(RG\right)$. We want to show that $f_1{f}_2$ is primitive. Since $G_1$ and $G_2$ are normal subgroups of G and the commutator of $G_1$ and $G_2$ equals one, we have two inertial groups: $I_G\left(b_1\right)=\left\{g_1\in G_1;b_1^{g_1}=b_1\right\}$ and $I_G\left(b_2\right)=\left\{g_2\in G_2;b_2^{g_2}=b_2\right\}$. Both $I_G\left(b_1\right)$ and $I_G\left(b_2\right)$ are G. So, there exist two expressions of $f_1$ and $f_2$ as the sum of primitive idempotents $f_1=\sum f_{B_i}$ ($B_i$ are blocks of G) and $f_2=\sum f_{B_j}$ ($B_j$ are blocks of G); hence, $f_1{f}_2=\sum f_{B_k}$ ($B_k$ are blocks of G), where every $B_k$ covers both $b_1$ and $b_2$. Now, it is necessary to prove that $f_1{f}_2$ is primitive. We will prove that there exists a unique block of G that covers both $b_1$ and $b_2$. We assumed that B and $B^{\prime }$ are blocks of G such that B and $B^{\prime }$ cover both $b_1$ and $b_2$. If C is a conjugacy class of $G^{\circ }$, then, by Lemma 2, there exists a conjugacy class $C_1$ of $G_1^{\circ }$ and a conjugacy class $C_2$ of $G_2^{\circ }$ such that $C=C_1\times C_2$. By Theorem 4, we have:

$$\begin{array}{cc}\hfill {\omega }_B^{*}\left(\hat{C}\right)& ={\omega }_B^{*}\left(\widehat{C_1}\widehat{C_2}\right)\hfill \\ & ={\omega }_B^{*}\left(\widehat{C_1}\right){\omega }_B^{*}\left(\widehat{C_2}\right)\left(\mathrm{because}{\omega }_B^{*}\mathrm{is}\mathrm{an}\mathrm{algebra}\mathrm{homomorphism}\right)\hfill \\ & ={\omega }_{b_1}^{*}\left(\widehat{C_1}\right){\omega }_{b_2}^{*}\left(\widehat{C_2}\right)\left(\mathrm{by}\mathrm{Theorem}4\right)\hfill \\ & ={\omega }_{B^{\prime }}^{*}\left(\widehat{C_1}\right){\omega }_{B^{\prime }}^{*}\left(\widehat{C_2}\right)\left(\mathrm{by}\mathrm{Theorem}4\right)\hfill \\ & ={\omega }_{B^{\prime }}^{*}\left(\widehat{C_1}\widehat{C_2}\right)={\omega }_{B^{\prime }}^{*}\left(\hat{C}\right).\hfill \end{array}$$

Thus, $f_1{f}_2=f_B$, where B is a block of G. Consequently, there is an expression of one as the sum of primitive central idempotents $1={\displaystyle \sum _{b_i\in Bl\left(G_1\right)}}{\displaystyle \sum _{b_j\in Bl\left(G_2\right)}}{f}_{b_i}{f}_{b_j}.$ Because the map

$$\theta :RG\to R{G}_1{\otimes }_{R}R{G}_2$$

given by

$$\theta \left((x,y)\right)=x\otimes y,\forall x\in G_1,y\in G_2$$

is an isomorphism map, then $RG\cong R{G}_1{\otimes }_{R}R{G}_2$. The block of G is the tensor product of blocks of $G_1$ and blocks of $G_2$. □

Corollary 1

([37]). Suppose that G is a finite group and G is the external direct product of two groups: $G_1$ and $G_2$. If B is a block of G such that B is the tensor product of two blocks $b_1$ and $b_2$, where $b_1$ and $b_2$ are the blocks of $G_1$ and $G_2$, respectively, then $l\left(B\right)=l\left(b_1\right)l\left(b_2\right)$ and $k\left(B\right)=k\left(b_1\right)k\left(b_2\right)$.

The following property concerns the important matrix known as the Cartan matrix.

Proposition 2

([37]). Suppose that G is a finite group, and G is the external direct product of two groups: $G_1$ and $G_2$. If B is a block of G such that B is the tensor product of $b_1$ and $b_2$, where $b_1$ and $b_2$ are the blocks of $G_1$ and $G_2$, respectively, then the rows and columns of the Cartan matrix $C_B$ of B can be arranged to have the form $C_B=C_{b_1}\otimes C_{b_2}$, where ⊗ denotes the Kronecker product.

Proof. 

We assumed that $D_B$ is the decomposition matrix of block B. Since F and K are the splitting fields of G, we know that every irreducible character $\chi$ of the block B has the form $\chi ={\chi }_1{\chi }_2$, where ${\chi }_1$ is an irreducible character of a block $b_1$ and ${\chi }_2$ is an irreducible character of a block $b_2$. Also, every irreducible Brauer character $\vartheta$ of the block B has the form $\vartheta ={\vartheta }_1{\vartheta }_2$, where ${\vartheta }_1$ is an irreducible Brauer character of $b_1$ and ${\vartheta }_2$ is an irreducible Brauer character of $b_2.$ By the definition of the decomposition matrix, we can write $D_B$ as follows: $D_B=D_{b_1}\otimes D_{b_2}.$ From the definition of the Cartan matrix, we have $C_B=D_B{D}_B^t$. Hence, we can write $C_B$ as follows: $C_B=C_{b_1}\otimes C_{b_2}$. □

The following definition and Lemma 3 prove Proposition 3.

Definition 5

([37]). Suppose that G is a finite group and P is a p-subgroup of G. If P is the unique maximal normal p-subgroup of $N_G\left(P\right)$, then P is called the radical p-subgroup of G.

Lemma 3

([37]). Let $G=G_1\times G_2$ be the direct product of $G_1$ and $G_2$. If R is the radical p-subgroup of G, then $R_1=R\cap G_1$ and $R_2=R\cap G_2$ are radical p-subgroups of $G_1$ and $G_2,$ respectively. Moreover, $R=R_1\times R_2$.

Remark 1.

We write $Rad\left(G\right)/G$ for the set of representatives for the conjugacy classes of the radical p-subgroups of G.

Proposition 3

([37]). Suppose that G is a finite group, and G is the direct product of $G_1$ and $G_2$. If B is a block of G and B is the tensor product of $b_1$ and $b_2$, where $b_1$ is a block of $G_1$ and $b_2$ is a block of $G_2$, then $\delta \left(B\right){=}_G\delta \left(b_1\right)\times \delta \left(b_2\right)$.

Proof. 

From the theorem of Fong (see [30], Theorem 5.16, p. 345), we obtain $G_1\cap \delta \left(B\right){=}_{G_1}\delta \left(b_1\right)$ and $G_2\cap \delta \left(B\right){=}_{G_2}\delta \left(b_2\right)$. From Lemma 3, we obtain $\delta \left(B\right){=}_G\delta \left(b_1\right)\times \delta \left(b_2\right)$ because $\delta \left(B\right)$ is the radical p-subgroup. □

3. Methodology

Representation research is a tremendously active topic of study. In this work, our methodology and tactics are typical. Our strategy was to construct and research new issues using the body of prior publications in this sector. We concentrated on three conjectures: the McKay conjecture, Alperin’s weight conjecture, and the ordinary weight conjecture. Character theory is the main tool for studying group theory. We used the relationship between these to obtain our main results.

4. Conjectures We Are Looking For

In this section, we use $p^{d_i}$ to denote the highest power of p, dividing $\frac{\left|G\right|}{{\chi }_i\left(1\right)};i=1,\dots ,k\left(G\right),$ where ${\chi }_i\left(1\right)$ is the degree of the irreducible character of G and $d_i$ is named a p-defect. If Q is a Sylow p-subgroup of order $p^a$, then $d_i\in \left\{0,1,\dots ,a\right\}$ for $i=1,\dots ,k\left(G\right)$. We write $k_d\left(G\right)$ of the number of irreducible characters of p-defect d of a finite group G for $d=0,1,\dots ,a$.

4.1. McKay Conjecture

Initially, we discuss the simplest conjecture, which is expressed by the case $d=a$. This conjecture deals with the number of irreducible characters of the finite group G of degree prime to p. We begin by stating simple information about the first to notice this conjecture (J. McKay) [1,5] in 1972.

John K. S. McKay (born 18 November 1939 in Kent) is a dual British/Canadian resident and a mathematician at Concordia University. He is known for his discovery of monstrous moonshine, his collaborative construction of certain sporadic simple groups, the McKay conjecture in representation theory, and the McKay correspondence relating some finite groups to Lie groups. McKay received his Bachelor’s and Diploma’s degrees from the University of Manchester in 1961 and 1962, respectively, and his Ph.D. from the University of Edinburgh in 1971. He has been a Professor of Computer Science at Concordia University since 1974. In 2000, he was made a Fellow of the Royal Society of Canada, and in 2003, he was awarded the CRM-Fields-PIMS prize. The Université de Montréal and Concordia University jointly arranged a conference in April 2007 to honor John McKay’s four decades of service.

Now, we study the McKay conjecture in two cases: in the case of groups and in the case of blocks. The following conjecture is the McKay conjecture in the case of groups.

Conjecture 1

(McKay (1972) [33]). Suppose that G is a finite group of order $p^a·m$, where p is the prime number and $a,m\in \mathbb{N}$ and $g.c.d(p,m)=1$. If Q is a Sylow p-subgroup of G of order $p^a$ and ${\mathrm{Irr}}_{p^{\circ }}\left(G\right)$ is the collection of irreducible ordinary characters such that $p\nmid \chi \left(1\right),$ then

$$k_a\left(G\right)=k_a\left(N_G\left(Q\right)\right),$$

where $k_a\left(G\right)$ is the number of ${\mathrm{Irr}}_{p^{\circ }}\left(G\right)$.

The following is an example of the McKay conjecture.

Example 2.

Let $G=S_4$ be the symmetric group of degree four of order 24. The irreducible ordinary characters Table 1 of $S_4$ is as follows.

Table 1. Irreducible ordinary characters table of $S_4$.

$\left|{\mathit{g}}_{\mathit{i}}\right|$	1	6	3	6	8
${\mathit{g}}_{\mathit{i}}$	[(1)]	[(1 2)]	[(1 2) (3 4)]	[(1 2 3)]	[(1 2 3 4)]
${\chi }_1$	1	1	1	1	1
${\chi }_2$	1	−1	1	1	−1
${\chi }_3$	2	0	2	−1	0
${\chi }_4$	3	1	−1	0	−1
${\chi }_5$	3	−1	−1	0	1

If $p=2$ and $Q=D_8=⟨\left(12\right)\left(34\right),\left(1234\right)⟩$ is the Sylow 2 subgroup of $S_4$, we have $D_8⩽N_{S_4}\left(D_8\right)⩽S_4.$ The normalizer $N_{S_4}\left(D_8\right)$ of $D_8$ in $S_4$ is $D_8$ or $S_4$. But, $Q=D_8$ is not normal in $S_4$, and therefore, $N_{S_4}\left(D_8\right)\ne S_4$. Thus, $N_{S_4}\left(D_8\right)=D_8.$ The irreducible ordinary characters Table 2 of $D_8$ is as follows.

Table 2. Irreducible ordinary characters table of $D_8$.

$\left|{\mathit{y}}_{\mathit{i}}\right|$	1	2	1	2	2
${\mathit{y}}_{\mathit{i}}$	[(1)]	[(1 2)]	[(1 2) (3 4)]	[(1 4)(2 3)]	[(1 3 2 4)]
${\phi }_1$	1	1	1	1	1
${\phi }_2$	1	−1	1	−1	1
${\phi }_3$	1	1	1	−1	−1
${\phi }_4$	1	−1	1	1	−1
${\phi }_5$	2	0	−2	0	0

We have ${Res}_{D_8}^{S_4}\left({\chi }_1\right)={\phi }_1,{\mathit{Res}}_{D_8}^{S_4}\left({\chi }_2\right)={\phi }_4,{\mathit{Res}}_{D_8}^{S_4}\left({\chi }_4\right)={\phi }_3+{\phi }_5,{\mathit{Res}}_{D_8}^{S_4}\left({\chi }_5\right)={\phi }_2+{\phi }_5.$ ${\mathit{Irr}}_{2^{\circ }}\left(S_4\right)=\left\{\chi \in \mathit{Irr}\left(S_4\right);2\nmid \chi \left(1\right)\right\}=\left\{{\chi }_1,{\chi }_2,{\chi }_4,{\chi }_5\right\}$. ${\mathit{Irr}}_{2^{\circ }}\left(N\left(D_8\right)\right)=\left\{\phi \in \mathit{Irr}\left(N\left(D_8\right)\right)\right.$; $\left.2\nmid \phi \left(1\right)\right\}=\left\{\phi \in \mathit{Irr}\left(D_8\right);2\nmid \phi \left(1\right)\right\}=\left\{{\phi }_1,{\phi }_2,{\phi }_3,{\phi }_4\right\}$.

Proof. 

Define the function

$$\mathrm{Y}:{\mathrm{Irr}}_{2^{\circ }}\left(S_4\right)\to {\mathrm{Irr}}_{2^{\circ }}\left(N_{S_4}\left(D_8\right)\right),$$

$$\mathrm{Y}:\left\{{\chi }_1,{\chi }_2,{\chi }_4,{\chi }_5\right\}\to \left\{{\phi }_1,{\phi }_2,{\phi }_3,{\phi }_4\right\},$$

given by

$$\begin{array}{cc}\hfill \mathrm{Y}\left(\chi \right)& ={\mathrm{Res}}_{D_8}^{S_4}\left(\chi \right)\mathrm{such}\mathrm{that}2\nmid {\mathrm{Res}}_{D_8}^{S_4}\left(\chi \right)\left(1\right).\hfill \\ \hfill \mathrm{Y}\left({\chi }_1\right)& ={\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_1\right)\mathrm{such}\mathrm{that}2\nmid {\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_1\right)\left(1\right)={\phi }_1\left(1\right),\hfill \\ \hfill \mathrm{Y}\left({\chi }_2\right)& ={\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_2\right)\mathrm{such}\mathrm{that}2\nmid {\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_2\right)\left(1\right)={\phi }_4\left(1\right),\hfill \\ \hfill \mathrm{Y}\left({\chi }_4\right)& ={\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_4\right)\mathrm{such}\mathrm{that}2\nmid {\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_4\right)\left(1\right)={\phi }_3\left(1\right),\hfill \\ \hfill \mathrm{Y}\left({\chi }_5\right)& ={\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_5\right)\mathrm{such}\mathrm{that}2\nmid {\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_5\right)\left(1\right)={\phi }_2\left(1\right).\hfill \end{array}$$

See Figure 1 which depicts the relation map between ${\mathrm{Irr}}_{2^{\circ }}\left(S_4\right)\mathrm{and}{\mathrm{Irr}}_{2^{\circ }}\left(N_{S_4}\left(D_8\right)\right).$

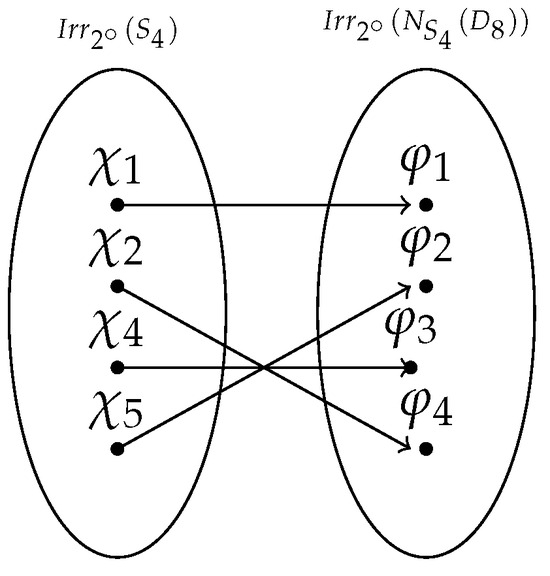
Figure 1. Relation-map between ${\mathrm{Irr}}_{2^{\circ }}\left(S_4\right)\mathrm{and}{\mathrm{Irr}}_{2^{\circ }}\left(N_{S_4}\left(D_8\right)\right)$.

• $\mathrm{Y}$ is injective because, if:

  $$\begin{array}{cc}\hfill \mathrm{Y}\left({\chi }_1\right)& =\mathrm{Y}\left({\chi }_2\right)\hfill \\ \hfill \Rightarrow {\phi }_1& ={\phi }_4\hfill \\ \hfill \Rightarrow {\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_1\right)& ={\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_2\right)\mathrm{such}\mathrm{that}2\nmid {\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_1\right)\left(1\right),2\nmid {\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_2\right)\left(1\right)\hfill \\ \hfill \Rightarrow {\mathrm{Ind}}_{D_8}^{S_4}\left({\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_1\right)\right)& ={\mathrm{Ind}}_{D_8}^{S_4}\left({\mathrm{Res}}_{D_8}^{S_4}\left({\chi }_2\right)\right)\hfill \\ \hfill \Rightarrow {\chi }_1& ={\chi }_2.\hfill \end{array}$$

  where ${\mathrm{Ind}}_{D_8}^{S_4}$ is the induction from $D_8$ to $S_4$ and ${\mathrm{Res}}_{D_8}^{S_4}$ is the restriction from $S_4$ to $D_8$.
• $\mathrm{Y}$ is surjective because $\forall \phi \in {\mathrm{Irr}}_{2^{\circ }}\left(N_{S_4}\left(D_8\right)\right),\exists \chi \in {\mathrm{Irr}}_{2^{\circ }}\left(S_4\right)$ such that $\mathrm{Y}\left(\chi \right)=\phi .$ Then, $\mathrm{Y}$ is a bijective function.

□

The following is the definition of the Brauer map.

Definition 6

([33]). Let P be a p-subgroup of G. We define the Brauer map as follows:

$${\mathit{Br}}_P:ZFG\to ZF{C}_G\left(P\right),$$

by given

$${\mathit{Br}}_P\left(\sum _{x\in G}{\alpha }_{x}x\right)=\sum _{x\in C_G\left(P\right)}{\alpha }_{x}x.$$

The following theorem tells us how to construct a p-block of the normalizer of the defect group of block B of G.

Theorem 5

(The first main theorem [30]). Suppose that G is a finite group, P is a p-subgroup of G, and $\mathit{Bl}\left(G\right|P)$ is the set of blocks of G with defect group P. There is a bijective map

$$\theta :\mathit{Bl}\left(G\right|P)\to \mathit{Bl}\left(N_G\left(P\right)\right|P),$$

such that ${\mathit{Br}}_P\left(e_B^{*}\right)=e_{\theta \left(B\right)}$ for all $B\in \mathit{Bl}\left(G\right).$ We use the notation ${\mathit{Br}}_P$ to denote the Brauer map.

Definition 7

([33]). Let $\delta \left(B\right)$ be a defect group of a p-block B of the finite group G. We say that b is the Brauer correspondent of B if b is the unique p-block of $N_G\left(\delta \left(B\right)\right)$ such that $b^G=B$.

The McKay conjecture was refined and extended to contain Brauer blocks by J. Alperin, known as the Alperin–McKay conjecture which tells us using locally data about the number of height zero irreducible ordinary characters in block B of $G.$

Conjecture 2

(Alperin (1976) [1]). Suppose that G is a finite group, p is a prime number, and $\delta \left(B\right)$ is a defect group of p-block B of $G.$ If ${\mathit{Irr}}_0\left(B\right)$ is the collection of height zero irreducible ordinary characters in $B,$ and b is the Brauer correspondent block of B in normalizer $N_G\left(\delta \left(B\right)\right)$ of $\delta \left(B\right)$, then

$$|{\mathit{Irr}}_0\left(B\right)|=|{\mathit{Irr}}_0\left(b\right)|.$$

where $|{\mathit{Irr}}_0\left(B\right)|$ is the cardinality of ${\mathit{Irr}}_0\left(B\right)$.

Note 3.

If the defect groups of blocks are Sylow p-subgroups, then the Alperin–McKay conjecture 2⇒ the McKay conjecture 1.

Example 3.

Let $G=S_4$ be the symmetric group of order 24, $p=2$, and $B=\left\{{\chi }_1,{\chi }_2,{\chi }_3,{\chi }_4,{\chi }_5\right\}$ be a block of $S_4$ with defect group $D_8$. If the normalizer of $D_8$ is $N_{S_4}\left(D_8\right)=D_8$ and $b=\left\{{\chi }_1,{\chi }_2,{\chi }_3,{\chi }_4,{\chi }_5\right\}$ is the Brauer correspondent block of B in $D_8$, we have $Ir{r}_0\left(B\right)=\left\{{\chi }_1,{\chi }_2,{\chi }_4,{\chi }_5\right\}$ with $J{\mathit{Irr}}_0\left(B\right)=4$, and ${\mathit{Irr}}_0\left(b\right)=\left\{{\chi }_1,{\chi }_2,{\chi }_3,{\chi }_4\right\}$ with $J{\mathit{Irr}}_0\left(b\right)=4$. Thus, $J{\mathit{Irr}}_0\left(B\right)=4=J{\mathit{Irr}}_0\left(b\right)$.

The McKay conjecture is known to hold for the following groups:

• p-solvable groups (for p prime number) [9,10].
• Alternating groups [11].
• Symmetric groups [11].
• Sporadic simple groups and some classes of finite groups of the Lie type [14].

Now, we investigate the McKay conjecture of direct product in which direct summands satisfy the McKay conjecture in the case of groups.

Proposition 4

([37]). Suppose that G is a finite group and G is the external direct product of two groups: $G_1$ and $G_2$. If $G_1$ and $G_2$ satisfy the McKay conjecture, then G satisfies the McKay conjecture.

Proof. 

The Sylow p-subgroup of G is denoted by Q. Then, there exist $Q_1$ as the Sylow p-subgroup of $G_1$ and $Q_2$ as the Sylow p-subgroup of $G_2$. Let $\left|Q\right|=p^a$, $\left|Q_1\right|=p^{a_1}$ and $\left|Q_2\right|=p^{a_2}$. Then, $lo{g}_p\left|Q\right|=a$, $lo{g}_p\left|Q_1\right|=a_1$, and $lo{g}_p\left|Q_2\right|=a_2$. Thus, $k_a\left(G\right)=k_{a_1}\left(G_1\right)k_{a_2}\left(G_2\right)$. From Lemma 1 and assuming $G_1$ and $G_2$ satisfy the McKay conjecture, we have

$$\begin{array}{ccc}\hfill k_a\left(G\right)=k_{a_1}\left(G_1\right)k_{a_2}\left(G_2\right)& =k_{a_1}\left(N_{G_1}\left(Q_1\right)\right)k_{a_2}\left(N_{G_2}\left(Q_2\right)\right)\hfill & \hfill \left(\mathrm{by}\mathrm{Conjecture}1\right)\\ \hfill & =k_a(N_{G_1}\left(Q_1\right)\times N_{G_2}\left(Q_2\right))\hfill & \\ \hfill & =k_a\left(N_G\left(Q\right)\right)\hfill & \hfill \left(\mathrm{by}\mathrm{Lemma}1\right),\end{array}$$

where $lo{g}_p\left|Q\right|$ is the logarithm of order Q to the base p. □

4.2. Alperin’s Weight Conjecture

In this subsection, we mention the second conjecture, which is expressed by the extreme case $d=0$. This conjecture focuses on the calculation of the number of irreducible Brauer characters of group G. We begin by stating simple information about J. Alperin [1,19], who in 1986 coined this conjecture.

In 1937, Jonathan Lazare Alperin was born. He is an American mathematician who specializes in the field of group theory, known as algebra. He is notable for his work on group theory, according to Mathematical Reviews.

Alperin attended school at Princeton University and wrote his Ph.D. dissertation in 1961 “On a Special Class of Regular p-Groups” under the direction of Graham Higman. He was awarded a Guggenheim Fellowship in 1974. He has been a visiting scholar at the center for Advanced Research many times (1969, 1979, and 1983). He became a Fellow of the Mathematical Society of America in 2012.

Alperin is a University of Chicago Professor. He has published over 60 papers, and his work has been cited over 500 times. He is also known for his conjecture (Alperin 1987), a subject of current research in modular representation theory, and for his work on the local control of fusion (Alperin 1967), part of local group theory. The Alperin–Brauer–Gorenstein theorem was proven in (Alperin 1970), giving the classification of finite simple groups with quasi-dihedral subgroups of Sylow 2.

The following conjecture is Alperin’s weight conjecture in the case of groups.

Conjecture 3

(Alperin (1986) [33]). Suppose that G is a finite group, p is a prime number. If P runs over all p-subgroup of G, then

$$\sum _P\frac{k_0(N_G\left(P\right)/P)}{\left[G:N_G\left(P\right)\right]}=l\left(G\right),$$

where $k_0\left(G\right)$ is the number of irreducible characters, whose degree is divisible by the order of a Sylow p-subgroup of G, and $l\left(G\right)$ is the number of irreducible Brauer characters of G. When P is replaced by the conjugate of $P,$ the summand $\frac{k_0(N_G\left(P\right)/P)}{\left[G:N_G\left(P\right)\right]}$ does not change. Because the number of the conjugate of P is $\left[G:N_G\left(P\right)\right]$, where $\left[G:N_G\left(P\right)\right]$ means the index of $N_G\left(P\right)$ in G, then Alperin’s weight conjecture can also be expressed as follows:

$$\sum _P{k}_0(N_G\left(P\right)/P)=l\left(G\right),$$

where P ranges over the set of representatives for the conjugacy classes of radical p-subgroups of G.

The following is an example of Alperin’s weight conjecture.

Example 4.

Let $G=A_4$ be the alternating group of order $12=2^2\times 3$, $p=2$. The group $A_4$ has three p-regular conjugacy class representatives: $\left[\left(1_{A_4}\right)\right]$, $\left[\left(132\right)\right]$, and $\left[\left(123\right)\right]$; then, $A_4$ has three irreducible Brauer characters; hence, $l\left(A_4\right)=3$. In Table 3 all the representatives P of p-subgroups of $A_4$, which conjugate P:

Table 3. All the representatives P of p-subgroups of $A_4$, which conjugate P.

P	${\mathit{N}}_{{\mathit{A}}_4}\left(\mathit{P}\right)/\mathit{P}$	${\mathit{\chi }}_{\mathit{i}}\left(1\right)$ of ${\mathit{N}}_{{\mathit{A}}_4}\left(\mathit{P}\right)/\mathit{P}$	Order of Sylow p	${\mathit{k}}_0({\mathit{N}}_{{\mathit{A}}_4}\left(\mathit{P}\right)/\mathit{P})$
$V_4$	$C_3$	1,1,1	1	3
$C_2$	$C_2$	1,1	2	0
$\left(1_{A_4}\right)$	$A_4$	1,1,1,3	4	0

Hence, ${\displaystyle \sum _P}{k}_0(N_{A_4}\left(P\right)/P)=3=l\left(A_4\right)$.

We mention Alperin’s weight conjecture in the case of blocks. However, before we mention this conjecture, it is important to provide some definitions.

Definition 8

([32]). Let P be a subgroup of G. We say that a pair $(P,\psi )$ is a p-weight of G if P is a radical p-subgroup of G and ψ is a defect zero considered an irreducible character of $N_G\left(P\right)/P$.

Definition 9

([32]). If the element $g\in G$ and the pair $(P,\psi )$ is a p-weight of G, then the pair ${(P,\psi )}^g=(P^g,{\psi }^g)$ is called the G-conjugacy class of $(P,\psi )$ and is denoted by $[P,\psi ]$.

Note 4.

If ψ belongs to the block b of $N_G\left(P\right)$, then $(P,\psi )$ belongs to the block $b^G$ of the finite group G.

Conjecture 4

(Alperin (1986) [1]). Suppose that G is a finite group and p is a prime number. If B is a p-block of G and $\left[P,\psi \right]$ is a G-conjugacy class of $(P,\psi )$, then

$$l\left(B\right)=|\left\{\left[P,\psi \right]|\left(P,\psi \right)a\mathrm{p-weight},\mathrm{which}\mathrm{belongs}\mathrm{to}B\right\}|.$$

R. Knörr and G. R. Robinson [1,20] reformulated of this conjecture. Now, we state this reformulation.

Theorem 6

(Knörr-Robinson (1989)). For a prime number, p, the following two statements are equivalent:

• Alperin’s weight Conjecture 4 holds for all p-blocks of all finite groups;
• For all p-blocks B of all finite groups, we have:

  $$\sum _{\sigma \in \mathcal{P}\left(G\right)/\sim }{(-1)}^{\left|\sigma \right|}l\left(B_{\sigma }\right)=0,$$

  where the sum runs over the chains in the set of chains of p-subgroups of G, which are denoted by $\mathcal{P}\left(G\right)$ up to G-conjugacy, $\sigma =1=P_0<P_1<\cdots <P_n$ is a chain in $\mathcal{P}$ of length $n=\left|\sigma \right|$, and $B_{\sigma }$ is the union of all blocks b of $N_G\left(\sigma \right)=\cap N\left(P_i\right),0⩽i⩽n$, with $b^G=B$.

Knörr and Robinson reported a significant relationship between the Alperin–McKay conjecture and Alperin’s weight conjecture in the case of abelian defect groups.

Theorem 7

(Knörr–Robinson (1989) [1]). The following two statements are equivalent for a prime number p:

• The Alperin–McKay conjecture 2 holds for each p-block with the abelian defect;
• Alperin’s weight conjecture 4 holds for each p-block with the abelian defect.

Alperin’s weight conjecture is known to hold for the following kinds of groups:

• For nilpotent p-blocks [20];
• p-solvable groups [21];
• Symmetric groups and general linear groups [22];
• Finite groups of the Lie type in natural characteristics [23].

To prove the following proposition, we need Lemma 3 and Remark 1.

Proposition 5

([37]). Suppose that G is a finite group and G is the external direct product of two groups: $G_1$ and $G_2$. If $G_1$ and $G_2$ satisfy Alperin’s weight conjecture, then G satisfies Alperin’s weight conjecture.

Proof. 

The number of irreducible Brauer characters is denoted by $l\left(G\right)$, i.e., $l\left(G\right)=\left|\mathrm{IBr}\left(G\right)\right|=|Cl\left(G^{\circ }\right)|$. From Lemmas 1–3, assumptions $G_1$ and $G_2$ satisfy Alperin’s weight conjecture, and we have

$$\begin{array}{cc}\hfill l\left(G\right)& =l\left(G_1\right)l\left(G_2\right)\hfill \\ & =\left(\sum _{R_1\in Rad\left(G_1\right)/G_1}{k}_0(N_{G_1}\left(R_1\right)/R_1)\right)\left(\sum _{R_2\in Rad\left(G_2\right)/G_2}{k}_0(N_{G_2}\left(R_2\right)/R_2)\right)\hfill \\ & =\sum _{R_1\in Rad\left(G_1\right)/G_1}\sum _{R_2\in Rad\left(G_2\right)/G_2}{k}_0(N_{G_1}\left(R_1\right)/R_1)k_0(N_{G_2}\left(R_2\right)/R_2)\hfill \\ & =\sum _{R\in Rad\left(G\right)/G}{k}_0(N_G\left(R\right)/R)(\mathrm{by}\mathrm{Lemmas}1–3)\hfill \end{array}$$

where $R=R_1\times R_2$. □

4.3. Ordinary Weight Conjecture

This subsection addresses the third conjecture, which focuses on the calculation of the number of ordinary irreducible characters in a p-block that have defect d. At the start of this section, we begin by stating simple information about G. R. Robinson, who coined this conjecture.

Professor Geoffrey Robinson, Emeritus Professor, contributed to more than 120 papers of a high standard. His research interests are primarily the representation theory of finite groups, especially modular representations, and he has worked at the following universities: Manchester, Chicago, Florida, Leicester, Birmingham, Aberdeen, Bristol, and Lancaster.

Definition 10

([34,38]). Let G be a finite group, p be a prime number, and P be a p-subgroup of G. If $b_P$ is the p-block of $C_G\left(P\right)$, then the pair $(P,b_P)$ is named a $(G,B)$-subpair.

Definition 11

([38]). The set $\mathcal{N}\left(B\right)=\left\{\sigma |\sigma =(V_1,b_1)<(V_2,b_2)<\cdots <(V_n,b_n)\right\}$, where every $(V_i,b_i)⊲(V_n,b_n),i=1,\dots ,n$.

Definition 12

([25]). Let σ be a chain. The number of p-subgroups in a chain σ is called the length of σ and denoted by $\left|\sigma \right|$.

Note 5.

We note that G acts on the normal chains of B-subpairs by conjugation. If σ belongs to such chains, then there is a stabilizer of σ, which is denoted by $G_{\sigma }$.

Next, we address the ordinary weight conjecture.

Conjecture 5

([25]). Suppose that G is a finite group, p is a prime number and B is a p-block of positive defect of G. For every non-negative integer d, we have

$$k_d\left(B\right)=\sum _{\sigma \in \mathcal{N}\left(B\right)/G}{(-1)}^{\left|\sigma \right|+1}\sum _{\mu \in {\mathit{Irr}}_d\left(V_{\sigma }\right)/G_{\sigma }}{f}_0\left(\frac{I_{G_{\sigma }}\left(\mu \right)}{V_{\sigma }},b^{\sigma }\right),$$

where $k_d\left(B\right)$ is the number of ordinary irreducible characters in B of defect d, and we denote $V_{\sigma }$ for the subgroup that we find in the first B-subpair of σ. The set ${\mathit{Irr}}_d\left(V_{\sigma }\right)$ is the set of ordinary irreducible characters, which have defect d of the subgroup $V_{\sigma }$. We write $b^{\sigma }$ for the block that appears in the last B-subpair in the chain σ, and $I_{G_{\sigma }}\left(\mu \right)$ refers to the inertial subgroup of μ, where μ is the ordinary irreducible character of the p-subgroup $V_{\sigma }$. We define $f_0\left(\frac{I_{G_{\sigma }}\left(\mu \right)}{V_{\sigma }},b^{\sigma }\right)$ as the number of p-blocks of defect zero in the section $\frac{I_{G_{\sigma }}\left(\mu \right)}{V_{\sigma }}$, which are not annihilated by $1_{b^{\sigma }}$ when considered as $I_{G_{\sigma }}\left(\mu \right)$-modules.

The ordinary weight conjecture holds in the following groups:

• Nilpotent p-blocks [20].
• p-solvable groups [21].
• p-blocks with the cyclic defect group, dihedral, semi-dihedral, or (generalized) quaternion [23].

5. Main Results

In this section, we determine whether the tensor product satisfies the McKay conjecture, Alperin’s weight conjecture, and the ordinary weight conjecture if every direct summand satisfies them or not.

Theorem 8.

Let G be a finite group, which is the external direct product of two groups: $G_1$ and $G_2$. Suppose that B is a block of G, which is the tensor product of two blocks, $B_1$ and $B_2$, where $B_1$ and $B_2$ are blocks of $G_1$ and $G_2$, respectively. If $B_1$ and $B_2$ satisfy the McKay conjecture, then B satisfies the McKay conjecture.

Proof. 

Let $B_1$ be the block of $G_1$ that satisfies the McKay conjecture. Then:

$$|{\mathrm{Irr}}_0\left(B_1\right)|=|{\mathrm{Irr}}_0\left(b_1\right)|.$$

(2)

Let $B_2$ be the block of $G_2$ that satisfies the McKay conjecture. Then:

$$|{\mathrm{Irr}}_0\left(B_2\right)|=|{\mathrm{Irr}}_0\left(b_2\right)|.$$

(3)

By multiplying both sides of Equation (2) with Equation (3), we have:

$$|{\mathrm{Irr}}_0\left(B_1\right)\left|\right|{\mathrm{Irr}}_0\left(B_2\right)|=|{\mathrm{Irr}}_0\left(b_1\right)\left|\right|{\mathrm{Irr}}_0\left(b_2\right)|.$$

By Proposition 1, we have:

$$|{\mathrm{Irr}}_0(B=B_1\otimes B_2)|=|{\mathrm{Irr}}_0(b=b_1\otimes b_2)|.$$

Thus $B=B_1\otimes B_2$ satisfies the McKay conjecture. □

Theorem 9.

Let G be a finite group, which is the external direct product of two groups: $G_1$ and $G_2$. Suppose that B is a block of G, which is the tensor product of two blocks, $B_1$ and $B_2$, where $B_1$ and $B_2$ are blocks of $G_1$ and $G_2$, respectively. If $B_1$ and $B_2$ satisfy Alperin’s weight conjecture, then B satisfies Alperin’s weight conjecture.

Proof. 

Let $B_1$ be the block of $G_1$ that satisfies Alperin’s weight conjecture. Then:

$$l\left(B_1\right)=\left|\left\{\left[P_1,{\psi }_1\right]|(P_1,{\psi }_1)\mathrm{a}\mathrm{p-weight}\mathrm{belonging}\mathrm{to}{B}_1\right\}\right|.$$

(4)

Let $B_2$ be the block of $G_2$ that satisfies Alperin’s weight conjecture. Then:

$$l\left(B_2\right)=\left|\left\{\left[P_2,{\psi }_2\right]|(P_2,{\psi }_2)\mathrm{a}\mathrm{p-weight}\mathrm{belonging}\mathrm{to}{B}_2\right\}\right|.$$

(5)

By multiplying both sides of Equation (4) with Equation (5), we have:

$$l(B=B_1\otimes B_2)=\left|\left\{\left[P_1\times P_2,{\psi }_1\otimes {\psi }_2\right]|(P_1\times P_2,{\psi }_1\otimes {\psi }_2)\mathrm{a}\mathrm{p-weight}\mathrm{belonging}\mathrm{to}B=B_1\otimes B_2\right\}\right|.$$

Thus, $B=B_1\otimes B_2$ is a block of $G=G_1\times G_2$ and satisfies Alperin’s weight conjecture. □

Theorem 10.

Let G be a finite group, which is the external direct product of two groups: $G_1$ and $G_2$. Suppose that B is a block of G, which is the tensor product of two blocks, $B_1$ and $B_2$, where $B_1$ and $B_2$ are blocks of $G_1$ and $G_2$, respectively. If $B_1$ and $B_2$ satisfy the ordinary weight conjecture, then B satisfies the ordinary weight conjecture.

Proof. 

Let $B_1$ be the block of $G_1$ that satisfies the ordinary weight conjecture. Then:

$$k_d\left(B_1\right)=\sum _{{\sigma }_1\in \mathcal{N}\left(B_1\right)/G_1}{(-1)}^{\left|{\sigma }_1\right|+1}\sum _{{\mu }_1\in {\mathrm{Irr}}_d\left(V_{{\sigma }_1}\right)/{G_1}_{{\sigma }_1}}{f}_0\left(\frac{I_{{G_1}_{{\sigma }_1}}\left({\mu }_1\right)}{V_{{\sigma }_1}},b_1^{{\sigma }_1}\right).$$

(6)

Let $B_2$ be the block of $G_2$ that satisfies the ordinary weight conjecture. Then:

$$k_d\left(B_2\right)=\sum _{{\sigma }_2\in \mathcal{N}\left(B_2\right)/G_2}{(-1)}^{\left|{\sigma }_2\right|+1}\sum _{{\mu }_2\in {\mathrm{Irr}}_d\left(V_{{\sigma }_2}\right)/{G_2}_{{\sigma }_2}}{f}_0\left(\frac{I_{{G_2}_{{\sigma }_2}}\left({\mu }_2\right)}{V_{{\sigma }_2}},b_2^{{\sigma }_2}\right).$$

(7)

By multiplying both sides of Equation (6) with (7), we have:

$$k_d\left(B\right)=\sum _{\sigma \in \mathcal{N}\left(B\right)/G}{(-1)}^{\left|\sigma \right|+1}\sum _{\mu \in {\mathrm{Irr}}_d\left(V_{\sigma }\right)/G_{\sigma }}{f}_0\left(\frac{I_{G_{\sigma }}\left(\mu \right)}{V_{\sigma }},b^{\sigma }\right),$$

(8)

where $B=B_1\otimes B_2,\sigma ={\sigma }_1\times {\sigma }_2$ and $b=b_1\otimes b_2.$ Thus $B=B_1\otimes B_2$ satisfies the ordinary weight conjecture. □

Our main results in this section appear fundamental in the sense that we dealt with the direct product, block theory, as well as conjectures in an environment of the tensor product. We emphasized the use of cancellation methods and applied the Robinson methods by a simple observation for the products of the invariant numbers associated with each block under consideration.

6. Discussion

Character theory is not purely a mathematical subject. Character theory can be used with efficiency in the calculations of the orbitals of atoms. In particular, symmetry and group theory have many applications in chemistry. For quantum chemistry, character theory is used frequently. Character tables have been used for molecular orbitals [39,40,41,42]. However, we believe that our research has applications of symmetry in supramolecular chemistry. See the references [42,43,44], which can link our approaches to supramolecular chemistry. The symmetry and structure are readable group theory for chemists; see [45]. Current improvements in all of these basic conjectures provide hope that the proof of some of them may be possible in the immediate future. More research on the following topics can be extended to this article in the future. We will prove these conjectures in general. We will also show these conjectures in the semidirect product, and we will study other conjectures like Brauer’s height zero conjecture and Brauer’s k(B)-conjecture and will solve them in general.

7. Conclusions

The representation theory of finite groups can be traced back to more than ten decades ago. Its principles were first put forth by Frobenius, Burnside, Schur, and later, Brauer. It is believed that Frobenius and Burnside were the first to realize recognize the significance of representation theory for investigating the configuration of finite groups. Even now, their traditional works astonish us with their profundity and creativity, and many specialists are still thinking deeply about the same primary issues. Much of the representation theory of finite groups these days is devoted to several conjectures, which state that certain invariants of finite group G can be computed locally. These conjectures connect two sets, which are otherwise seemingly unrelated. The conjecture is part of philosophy in which the properties of the representations of the whole group are determined from local information subgroups, which have the form $N_G\left(H\right)$, where H is a p-group. This paper focused on the McKay conjecture, Alperin’s weight conjecture, and the ordinary weight conjecture. This paper sought to determine whether or not the tensor product of two blocks satisfies these conjectures in the direct product group of two finite groups.

In order to understand our findings, it is necessary to study the concept of blocks because this concept was defined in the approach of ring theory and the approach of character theory. Then, consideration was given to certain concepts associated with it such as the defect number, defect group of block, defect group of the conjugacy class, and height number. Also, we explained the concepts of the direct product of finite groups and some properties related to the direct product of finite groups, as well as some properties related to the direct product of blocks and defect groups. Subsequently, we considered some of the fundamental problems in representation theory, especially the modular representation, and focused on the McKay conjecture, Alperin’s weight conjecture, and the ordinary weight conjecture. We studied some of the conjectures of the direct product as the McKay conjecture of the direct product in case groups and Alperin’s weight conjecture of the direct product in case groups. In addition, we discussed some of the results regarding conjectures of the direct product as the McKay conjecture of the direct product in case blocks, Alperin’s weight conjecture of the direct product in case blocks, and the ordinary weight conjecture of the direct product in case blocks. We deduced that the tensor product of two blocks that satisfy these conjectures is a block that satisfies these conjectures.