Designing Legged Wheels for Stair Climbing

Abstract

Mobile robotics has been used in recent years to provide various types of services in fields such as agriculture, surveillance, rehabilitation, space exploration, and logistics, among others. In many cases, mobile robots need to overcome complex obstacles where traditional wheels are not the best solution, and many researchers have proposed legged wheel hybrid designs. This paper presents a comprehensive study on the effect of the geometry of legged wheels on the performance of mobile robots in climbing stairs. The method used to develop this research is dynamic simulation, in which the parameters that affect the kinematics and dynamics of the robot are included. Subsequently, the results of how the robot manages to perform the test, the torque of the motors, and the contact force of the wheels are analyzed. The main hypothesis of this research is that the opening of the legs of the wheels is a geometric parameter that determines whether the structure will be able to climb the stairs. After 63 simulations, the proportional relationship between the diagonal of the stands and the opening of the wheel legs ranges between 1.11 and 1.53. This parameter showed a strong correlation with the torque of the motors and significant differences in terms of the simulations that succeeded in climbing the stairs and those that did not. These results were used to state a design method for flat, robotic structures using legged wheels. This method was validated by an additional simulation that was performed for a four-legged wheel. It can be concluded that the contribution of this work is a series of steps with which to design these mechanical structures to climb the stairs based on the proposed indicator.

1. Introduction

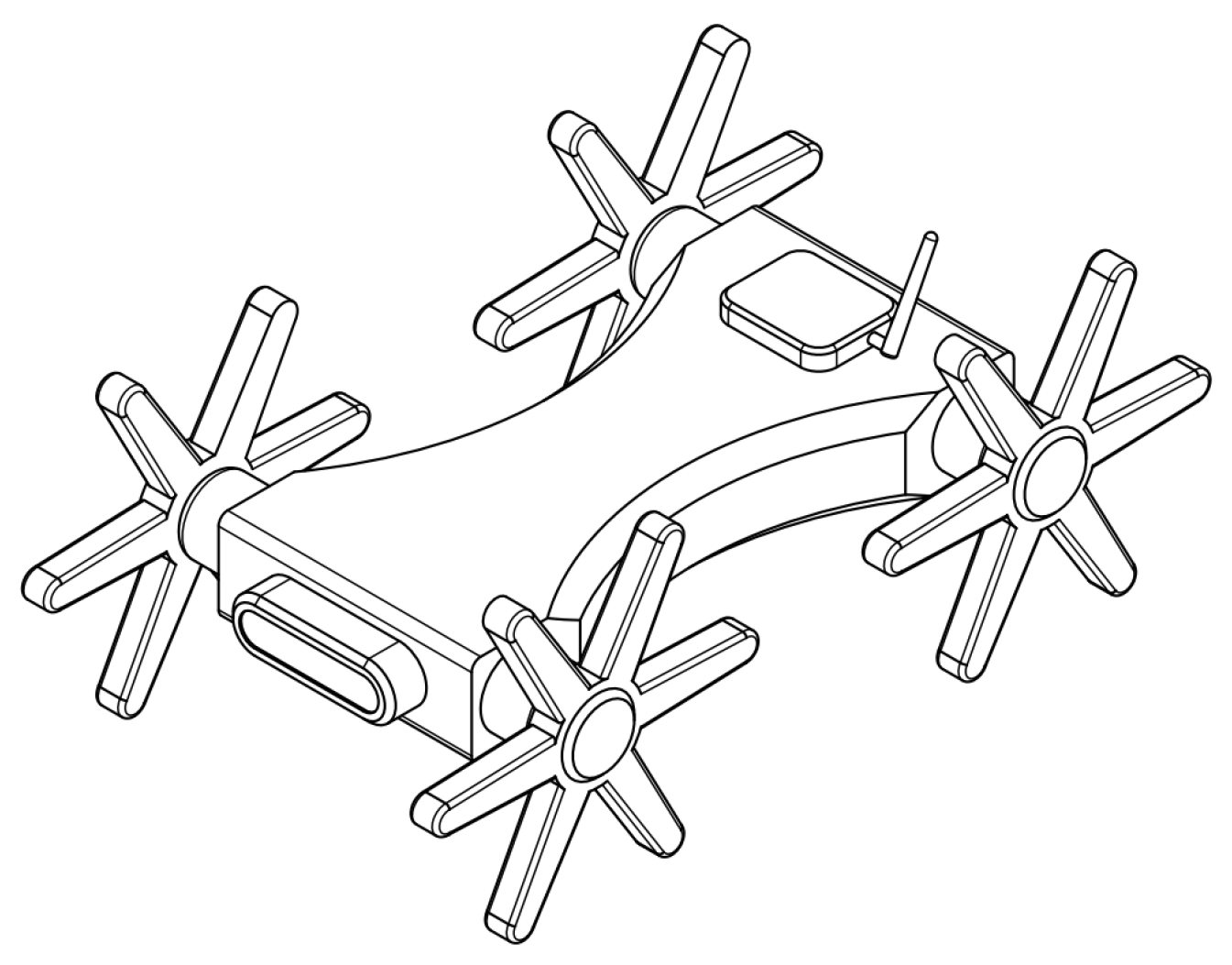
The locomotion system is a critical component of any robot as it enables it to travel to the location where it will carry out inspection or operation tasks. Consequently, numerous researchers have devoted their efforts to creating locomotion systems that enhance the mobility of robots in challenging terrains. In terrestrial settings, two of the most common locomotion methods available are based on wheels and legs, as shown in Figure 1.

Figure 1. Example of a robot with legged wheels.

When it comes to flat surfaces, a locomotion system with wheels is the most suitable option. The efficiency of this system is considerably superior to that of legged locomotion when traveling across even terrain [1]. On the contrary, legged locomotion systems are known for their superior maneuverability in unstructured environments.

In recent years, some researchers have proposed designs of hybrid locomotion systems based on wheels and legs [2]. In this work, the height of the stairs is related to the height of the robot, classified as low, medium, and high. These proposals can be classified as robots with wheels and legs, transformable wheels/legs, wheeled legs, and legged wheels.

Robots can use different strategies to climb obstacles using wheels and legs in alternation. Legs are employed when the wheels are not able to cross an obstacle. A different design concept corresponds to wheels that can be transformed into legs [3,4]. Tadakuma et al. [3] presented the design of a transformable wheel composed of a three -degrees-of-freedom serial mechanism. On the other hand, in [4], Lin and Shen introduced the design of a wheel that transforms into a C-shaped leg. Another approach to the design of the locomotion system involves attaching wheels to the ends of mechanical limbs. These limbs can be activated [5], under-actuated [6], or passive. By doing so, the position of the wheels around the robot’s center of mass can be altered, enabling the robot to overcome obstacles and maintain its stability.

Some researchers have implemented legged wheels in mobile robots. A legged wheel is a symmetrical body with multiple limbs that are rotated by an actuator; this concept was initially proposed in [7,8]. In [9], Eich et al. presented the Asguard mobile robot. The robot has four actuated-legged wheels with five limbs with a flexible tip. The robot has an additional rotational degree of freedom along the body axis, serving as an elastic spinal column. This robot is capable of climbing stairs, traversing very rough terrain, and moving quickly on flat ground.

On the other hand, some designs of legged wheels that can change their shape have been proposed [10]. In this document, we will refer to these devices as variable geometry legged wheels (VGLWs). In [11], Moreno et al. introduced the Heise wheels, a series of two-degrees-of-freedom mechanisms that are capable of transforming a circular wheel into a legged wheel. A linear actuator extends/flexes the limbs of the wheels, and this permits adjustments to the geometry of the wheel according to the terrain it is traversing. In the literature, different designs of VGLWs can be found. There are one- [10], two- [12,13,14,15,16,17], and three- [18] degrees-of-freedom VGLWs. Most of the designs employ electric actuators, but some proposals use pneumatic [19] and hydraulic actuation [20]. The designs of underactuated VGLWs are described in [21,22].

There is a wide variety of applications for mobile robots, including assistance in household activities, surveillance and security, healthcare and rehabilitation, agriculture, and space exploration. Legged wheels and VGLWs can be useful in overcoming steps or stairs in structured environments or traversing difficult, unstructured terrains or stairs. Different robots have been used for stair climbing, relating some parameters to the design. The HyTRo-I robot deploys retractable leg mechanisms to climb stairs when the height of the step is greater than the radius of the wheel [23]. The robot, named LZ-1, uses a wheel mechanism based on a mecanum wheel [24]. One of its most important design parameters is the consecutive angles between the legs; in this case, only the height, h, of the stair is related. On the other hand, the 4r+2P robot uses a crank mechanism to place a fixed part on the stairs and then raise its two wheels [25]. In order to perform this operation, they calculated the angle that indicates the position of the crank in relation to the wheels and related the height, h, and friction coefficient. The minimalist robot is based on the connection of three links, with two wheels at the beginning and end of the scientific chain to lift the stairs [26]. The design parameters that relate to the steps are the height of the step and the distance between the centers when placing the wheels at the corners of the steps. The track wheel robot has four active pulleys and four slave pulleys, with which it can form a three-link kinematic chain [27]. These links are synchronized to allow it to pass over the steps. The design parameter used is the height of the step. Finally, we observed the implementation of an anti-skid mechanism in a conventional wheel to climb the stairs [28]. The primary aim of this study is to formulate a design theory that relies on the geometric parameters of legged wheels to facilitate the efficient climbing of stairs by robots.

This paper presents a comprehensive study on the effect of the geometry of the legged wheels on the performance of a mobile robot in the stair climbing task. As main parameters, we consider the number of legs, the diameter of the wheels, and the distance between the wheels. In this paper, we have different sections, starting with the method section. This section explains the interaction and the steps to determine the parameters that influence the design of these structures. The results section presents the statistical analysis showing how many times the geometric configuration of the structure was able to overcome obstacles. The implementation section provides a case study aimed at validating the steps of the proposed design theory. Finally, the conclusion section summarizes the work carried out in this article and its relevance to the field of robotics.

2. Methods

Since it is necessary to determine the parameters that have the greatest impact on the design of these robotic structures, a series of dynamic simulations in solidworks is proposed. The main hypothesis to be tested is if the dimensionless quotient $c_{mor}$ of the wheel opening $O_N$ and the diagonal $l_d$ of the stair step has a direct relationship with the robot’s progress on the proposed task, as in (1), shown in Figure 2. The independent variables were $N_i$, the number of legs of the wheel; $c_w$, the distance (cm) between the center of the wheels; $w_r$, the radius of the wheel (cm), and $l_h$, the height (cm) of the steps, and the dependent variable was whether the robot could climb and descend stairs. For these simulations, $l_w$ is the width (cm) of the steps, w is the angular velocity (rpm), ${\mu }_k$ is the static friction coefficient, and ${\mu }_s$ is the dynamic friction coefficient, and these were taken as constants, where $O_N$ (cm) can be calculated by (2).

$$c_{mor}=O_N/l_d$$

(1)

$$O_N=2w_{r}sin(\theta /2)$$

(2)

Figure 2. Geometrical parameters of a legged wheel.

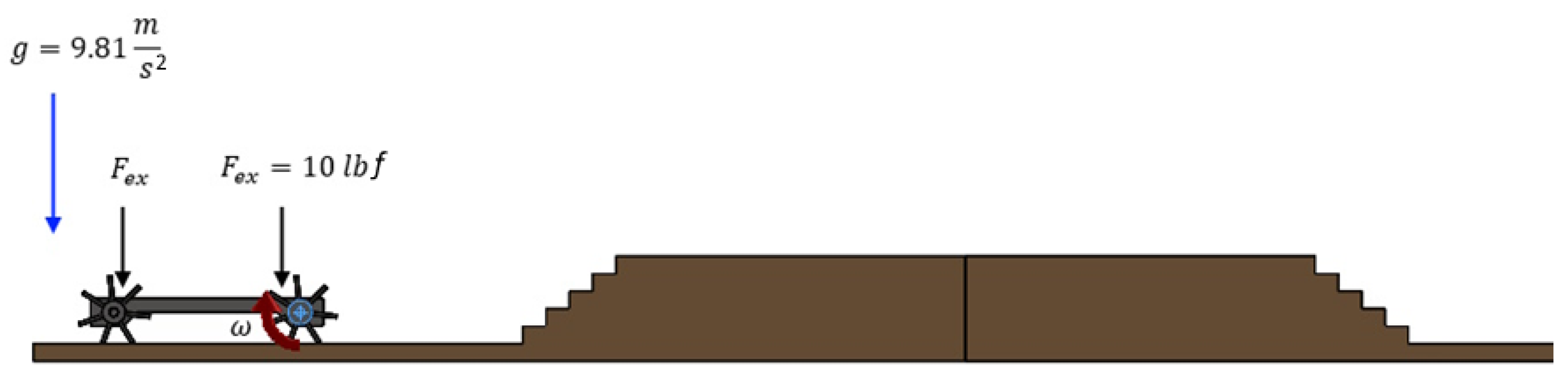
When performing the simulations, the robot is on the ground, so the effect of gravity allows it to have contact with the ground while the wheels rotate at a given speed. The robot moves towards the stairs, which it tries to climb using the extremities as support points. The robot structure is flat, so this structure also has contact with the stairs. Finally, the structures that manage to go up the stairs must go downstairs with the same dimensions as the climbing ones. The parameters of the simulations are shown in Table 1.

Table 1. Robot geometric parameter tests; $N_i$ is the number of legs.

${\mathit{N}}_{\mathit{i}}$	${\mathit{l}}_{\mathit{h}}$	${\mathit{c}}_{\mathit{w}}$	${\mathit{w}}_{\mathit{r}}$
3 a 10	2	32	15
3 a 10	2	32	18
3 a 10	2	32	21
3 a 10	2	42	21
3 a 10	2	42	18
3 a 10	5	42	15
3 a 10	5	42	21
3 a 10	5	32	21

2.1. Simulation

By using Table 1, 63 simulations were performed, in which the scenarios were varied to see the behavior of the robot when trying to climb the stairs. These 63 simulations are the combinations of varying the wheels from 3 to 10 legs, with eight different radii of wheels to climb two types of stairs with different dimensions. Figure 3 is an example of the simulations performed, applying gravity to the robot structure. The angular velocity of the robot motors was varied from $w_0$ = 15 rpm and ended the simulation with $w_f$ = 10 rpm. These angular velocities, according to different authors, show some variations, with [29] using 6.667 rpm, whereas [30,31] used 15 rpm, and [32] used 16.5 rpm. Two external forces, $F_{ex}$ (20 lbf) are applied to the ends of the structure due to the design of it, which is hollow in the center. Variations in the weight that such a structure can carry range from 1.6 lbf to 20 lbf [33].

Figure 3. Solidworks scenario and simulation parameters of a mobile robot.

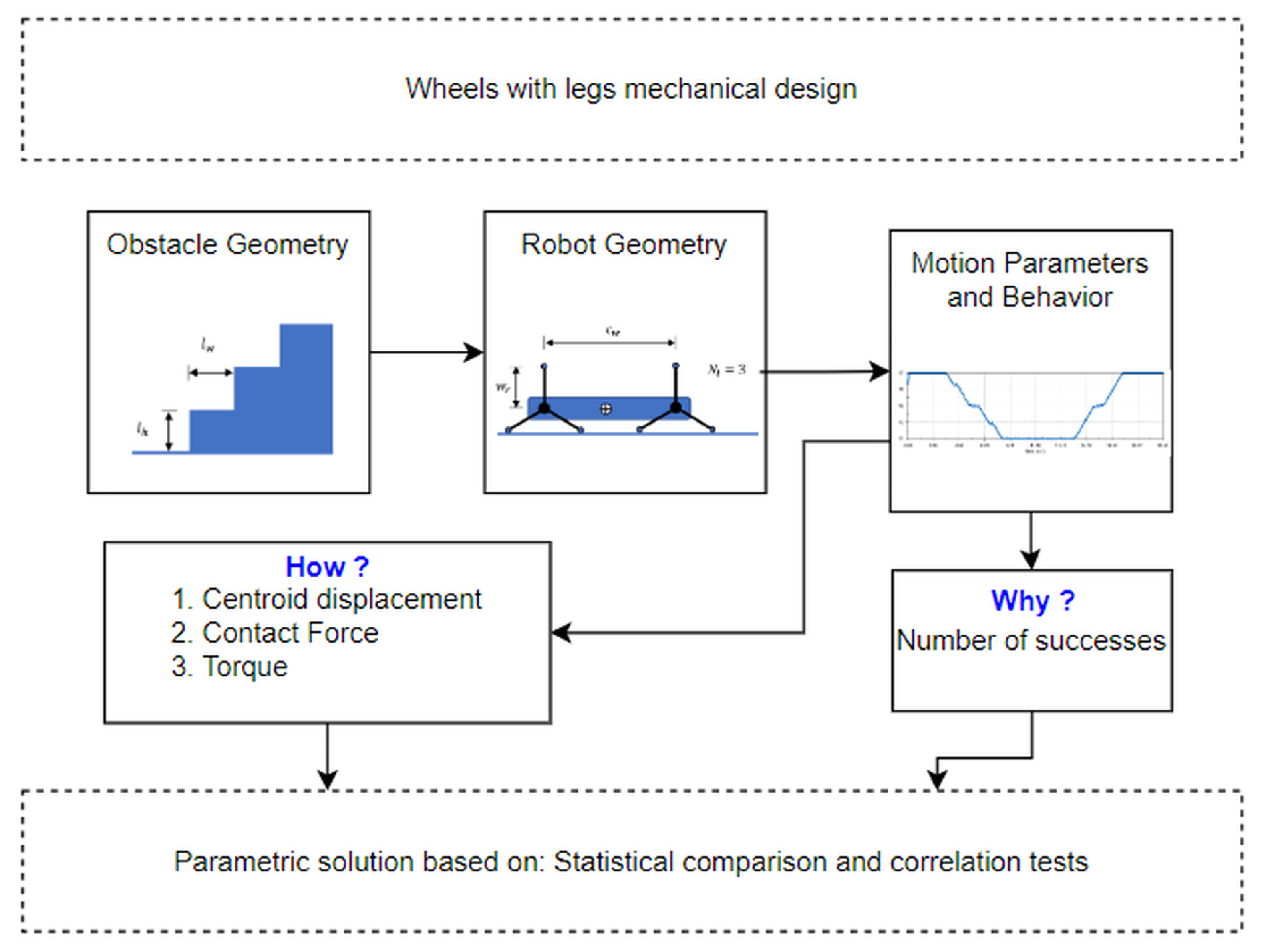
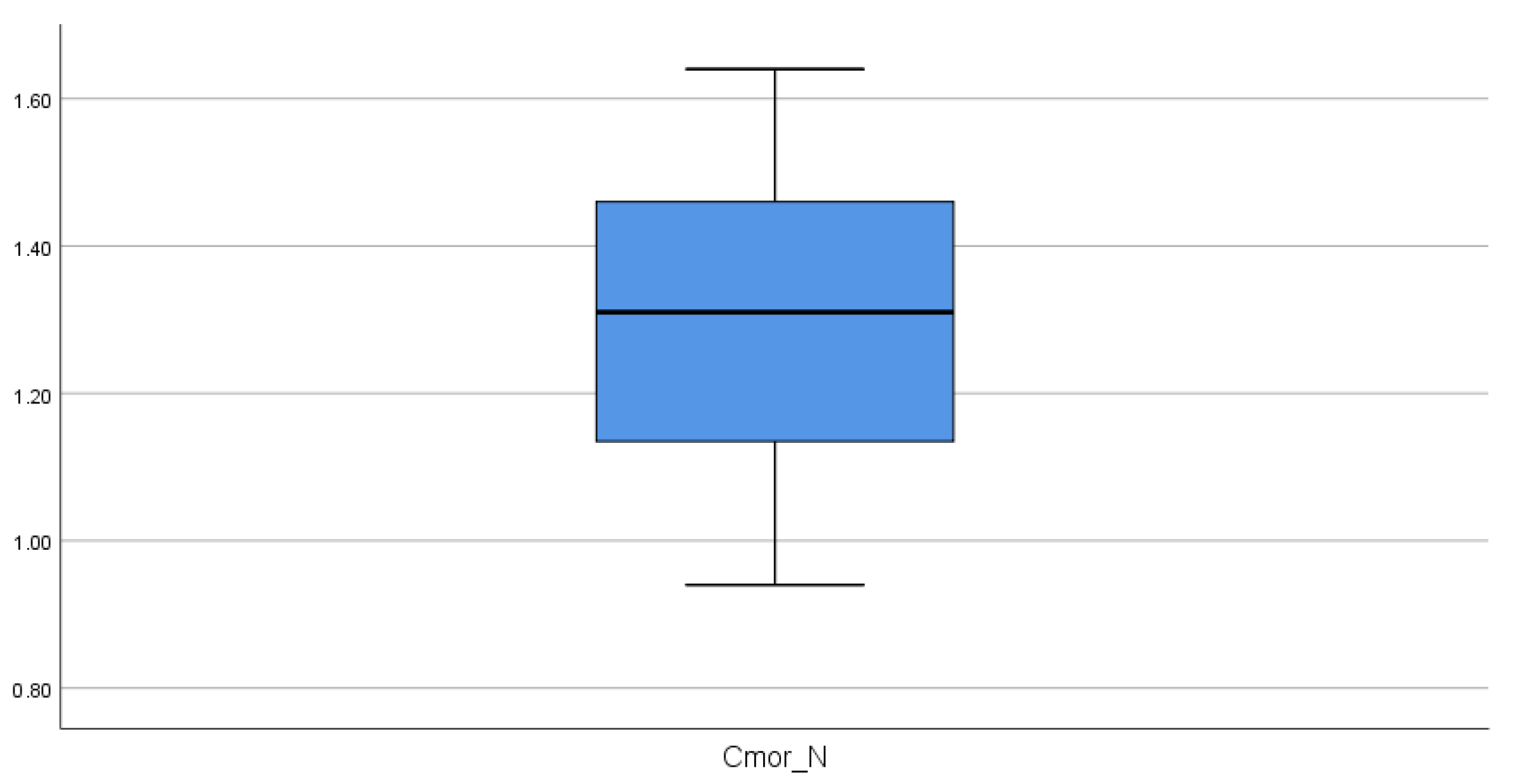
In order to verify if this ratio has normal behavior, a Shapiro–Wilk test was performed on all the calculated coefficients grouped by their $c_w$. Subsequently, the results of how the robot manages to perform the test, the torque of the motors, and the contact force were analyzed. For this, the successful coefficients were categorized to find the ranges in which the probability of success of the robot is higher. The complete method of this research can be seen in Figure 4. At the end of the statistical analysis, an additional simulation is carried out to calculate the dimensions of the wheel legs based on (2) for a stair with dimensions different from those already carried out.

Figure 4. Geometrical parameters of a mobile robot.

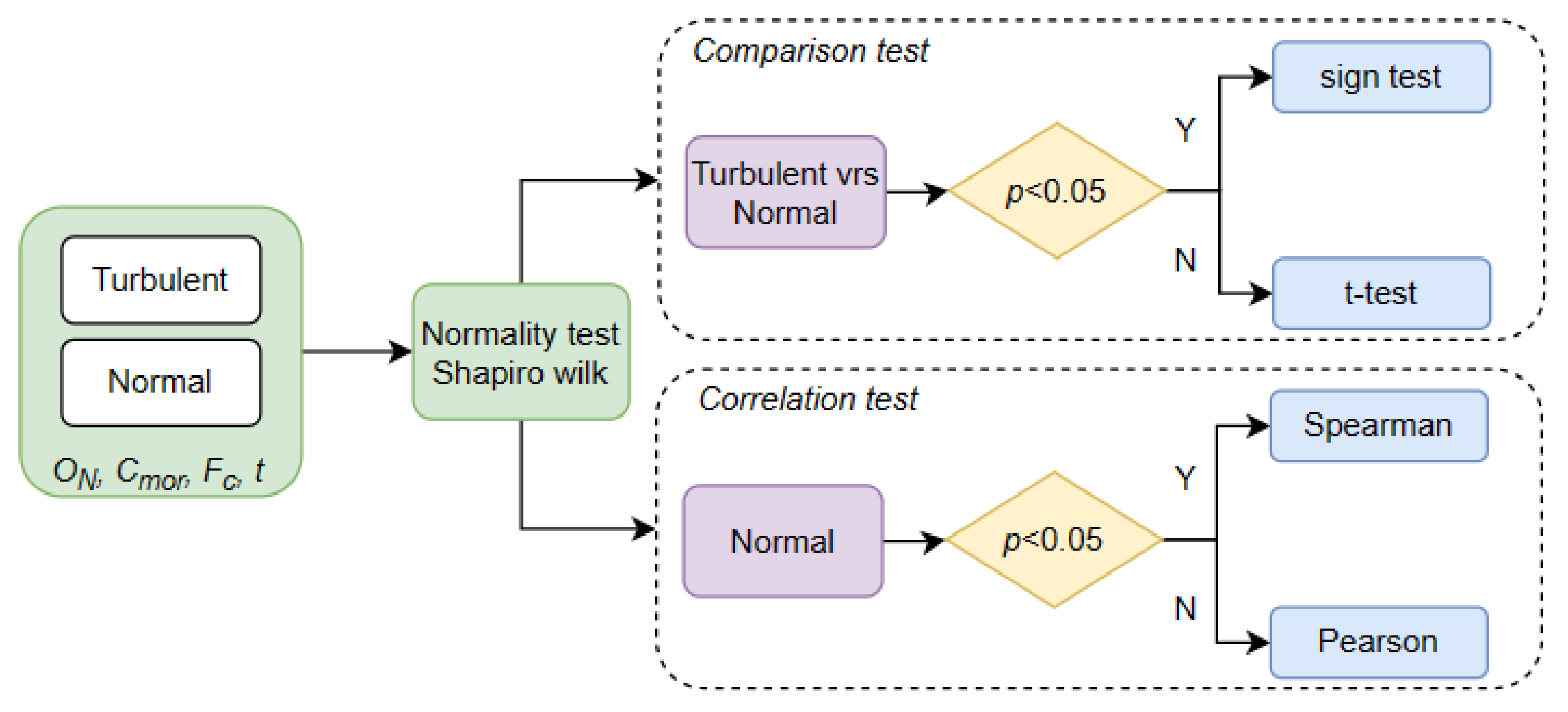
2.2. Why Did the Robot Succeed?

The first question of this research is, why do some wheel configurations manage to climb stairs and others do not? The ratio of the opening of the extremities and the diagonal of the stairs were calculated to check if this indicator is determinant in the design of these robotic structures. For this purpose, the configurations of wheels and structures that climb the stairs were separated from those that do not, performing statistical tests to demonstrate that they have significant differences. Subsequently, the confidence interval where the indicator has a higher probability of success is determined.

The two parameters to analyze are $c_{mor}$ and $c_w$, which demonstrate that these parameters affect the success of the robotic structure in solving the problem. The use of statistical tests was proposed, as shown in Figure 5.

Figure 5. Statistical comparison flow.

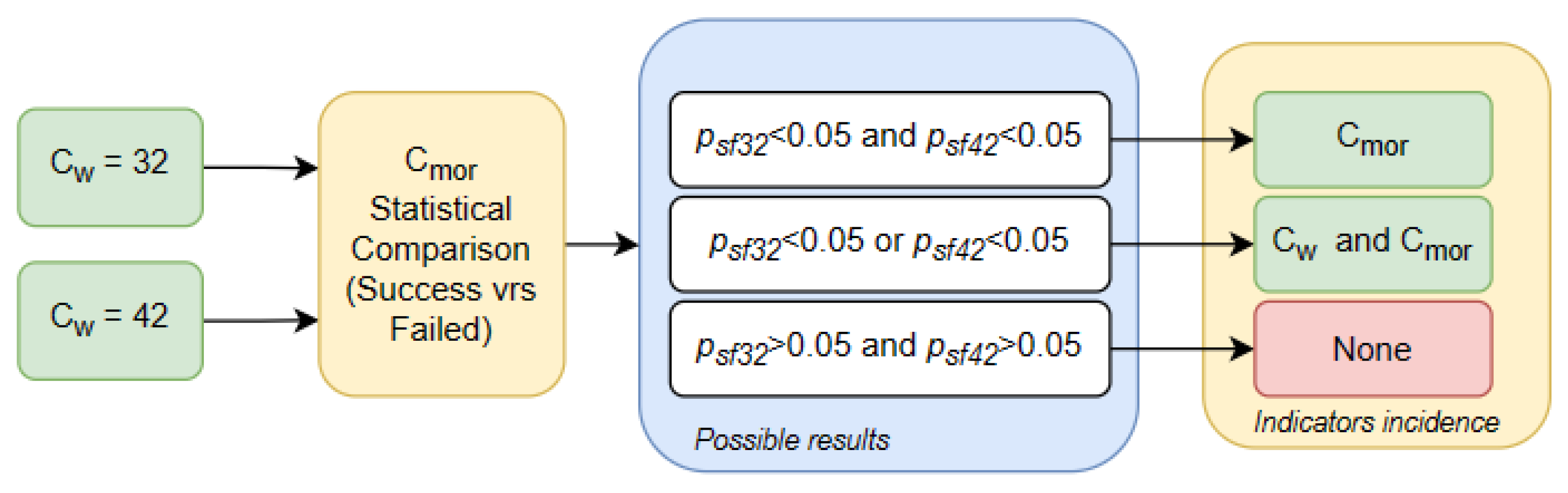
For the $c_{mor}$, the total number of tests was divided according to its $c_w$ and according to the success or failure in performing the test. Subsequently, a normality test was applied according to its $c_w$ to determine the type of statistical comparison test to be performed. If the statistical comparison test obtained a value $p<0.05$, it means that there was a significant difference between the value, $c_{mor}$, of the successes and failures. Figure 6 allowed us to determine the incidence of the indicators in the design of these structures.

Figure 6. Possible indicators incidence.

2.3. How Does the Robot Succeed?

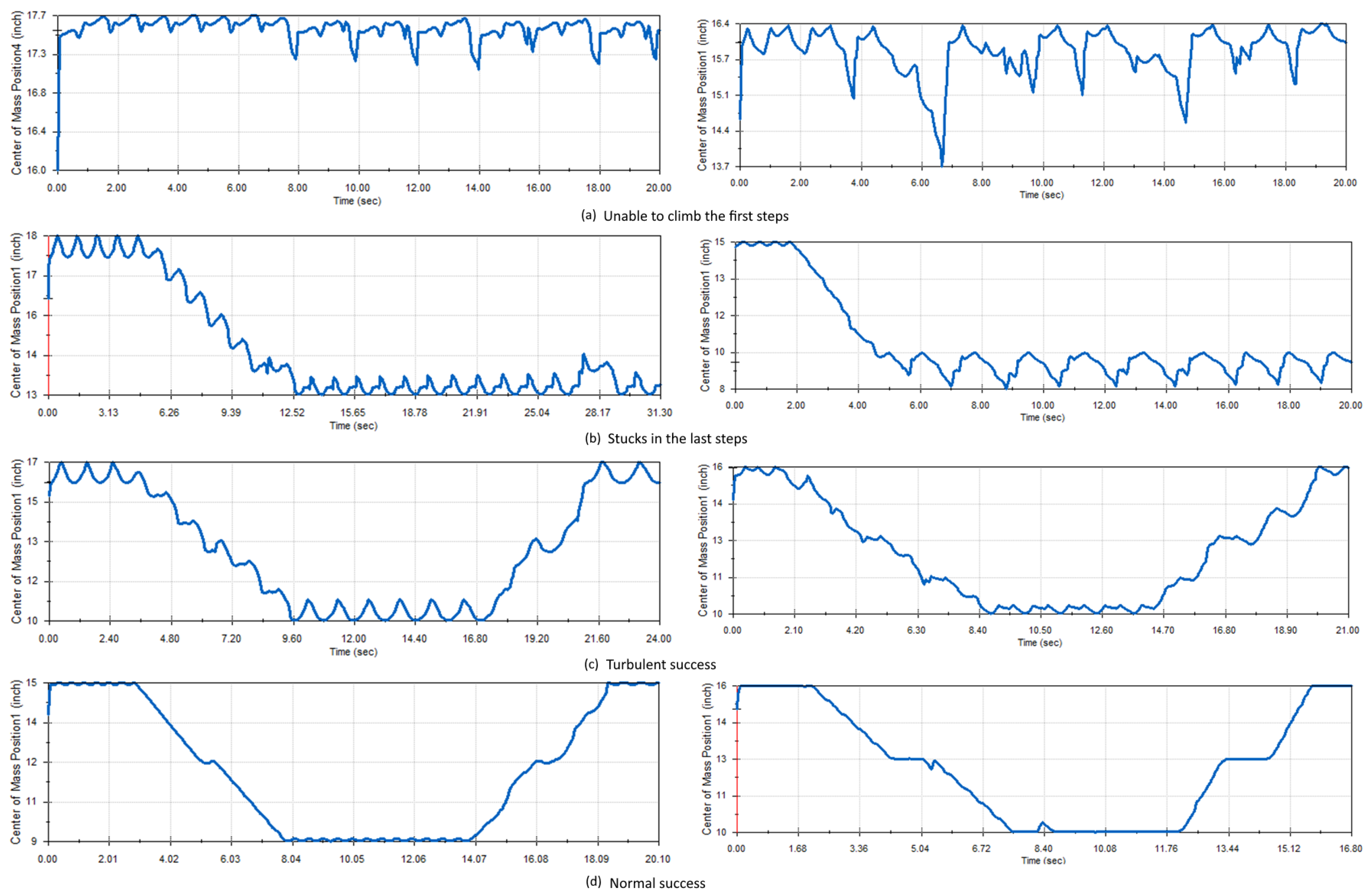
The second question of this research tries to help describe graphically and statistically how the robots climb. On many occasions, the robot can solve the problem of climbing the stairs, but it generates contact forces that can damage the structure, very high torques that can overload the motors, or constant vibrations that can reduce the life of the equipment. Therefore, the simulations will be graphically classified based on the behavior of the center of gravity of the structure. This will be classified into four groups: the first and second groups are the structures that did not manage to climb, the third group represents the structures that climb but without stabilizing their center of mass (turbulent), and the fourth group represents the structures that climb by stabilizing their center of mass (normal). 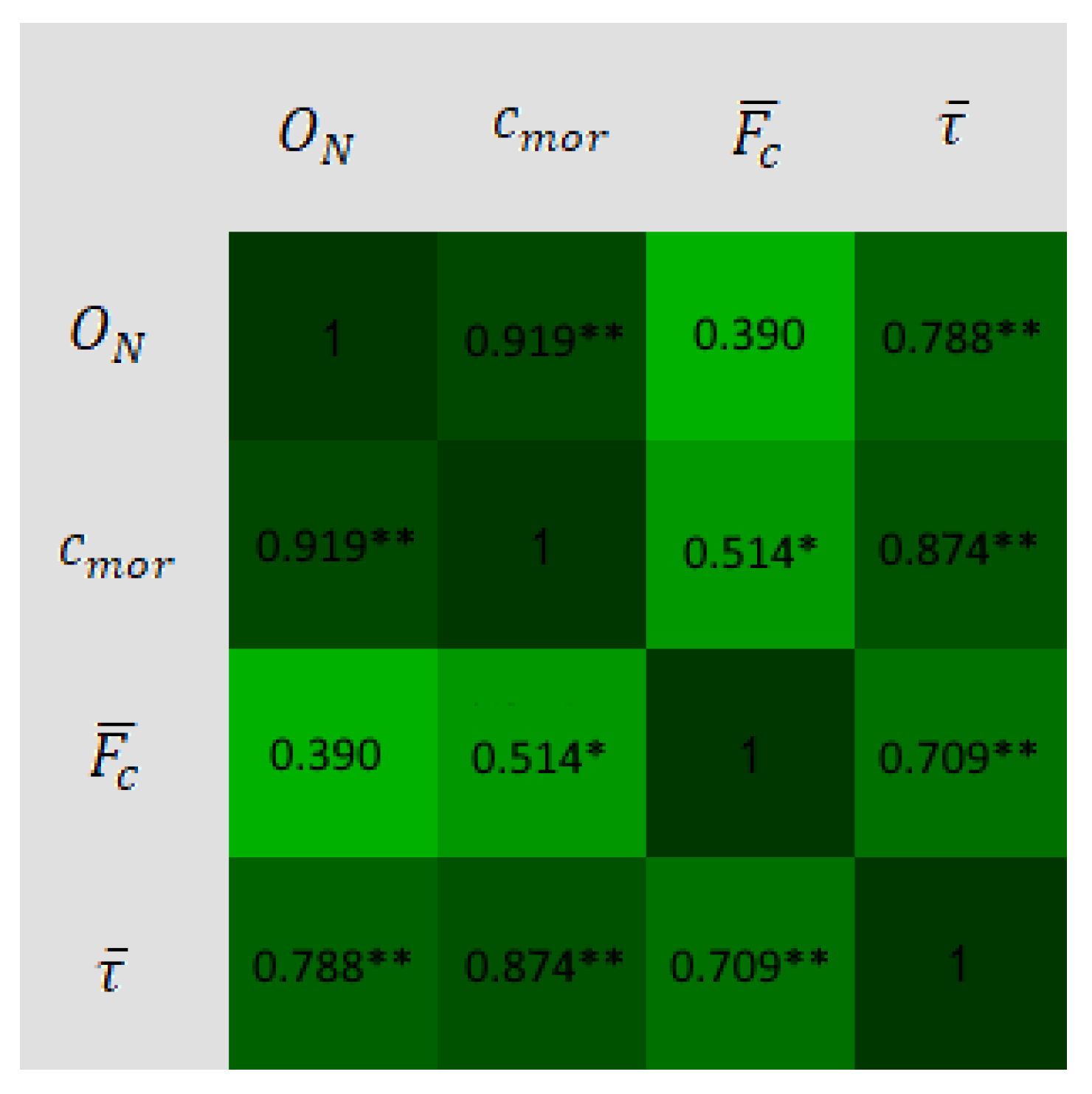Statistical tests were then performed to compare whether the indicators shown in Figure 7 had different behavior. Finally, a correlation test was performed to determine how much $c_{mor}$ affects the design.

Figure 7. Statistical comparison and correlation flow.

3. Results

3.1. Why Did the Robot Succeed?

The main hypothesis of the proposed problem is that the opening of the wheels directly influences the climbing of the stairs. For this purpose, we propose calculating the quotient of the opening of the extremities of the wheels between the diagonal of the stairs; this quotient is an indicator that has been named $c_{mor}$. For the 63 tests, the indicator $c_{mor}$ is calculated, and the tests are categorized between those that climb the stairs and those that do not, as shown in Table 2 and Table 3. In order to answer the question, the study is divided according to the length of the $c_w$ structure, and the normality test was applied to decide the statistical test time to be applied. In the case of the $c_w$ = 32 structure, a significance level of $p_{ns}$ (p value for success) = 0.918 and $p_{nf}$ (p value for failed) = 0.594 with 10 degrees of freedom was obtained for the tests that passed and those that failed, respectively. Therefore, a student’s t-test was applied to compare whether there were significant differences between the two sets of data. The result of the t-test gave a significance of $p_{sf}$ (p value t test comparison success vrs failed) = 0.008, which is $p<0.05$. So, it can be concluded that both samples have significant differences.

Table 2. Robot geometric parameter tests results for 32 mm.

n	${\mathit{N}}_{\mathit{i}}$	${\mathit{l}}_{\mathit{h}}$	${\mathit{C}}_{\mathit{w}}$	${\mathit{w}}_{\mathit{d}}$	${\mathit{l}}_{\mathit{d}}$	$\mathit{\theta }$	${\mathit{O}}_{\mathit{N}}$	${\mathit{C}}_{\mathit{mor}}$	State	${\mathit{F}}_{\mathit{c}}$ (lbf)	$\mathit{\tau }$ (lbf·inch)
1	3	2	32	15	5.00	60.00	15.00	3.00	No Success	–	–
2	4	2	32	15	5.00	45.00	11.48	2.30	No Success	–	–
3	5	2	32	15	5.00	36.00	9.27	1.85	Turbulent	18.01	6.15
4	6	2	32	15	5.00	30.00	7.76	1.55	Turbulent	16.55	5.38
5	7	2	32	15	5.00	25.71	6.68	1.34	Turbulent	16.30	5.00
6	8	2	32	15	5.00	22.50	5.85	1.17	Turbulent	17.88	5.26
7	9	2	32	15	5.00	20.00	5.21	1.04	Success	9.87	3.01
8	10	2	32	15	5.00	18.00	4.69	0.94	Success	16.16	5.54
9	9	2	32	18	5.00	20.00	6.25	1.25	Success	4.94	7.04
10	10	2	32	18	5.00	18.00	5.63	1.13	Success	3.23	5.13
11	8	2	32	18	5.00	22.50	7.02	1.40	Success	16.79	7.36
12	7	2	32	18	5.00	25.71	8.01	1.60	Success	4.71	8.34
13	6	2	32	18	5.00	30.00	9.32	1.86	Turbulent	14.96	8.92
14	5	2	32	18	5.00	36.00	11.12	2.22	Turbulent	13.82	9.62
15	4	2	32	18	5.00	45.00	13.78	2.76	Turbulent	18.06	11.15
16	3	2	32	18	5.00	60.00	18.00	3.60	No Success	–	–
17	10	2	32	21	5.00	18.00	6.57	1.31	Success	18.99	8.51
18	9	2	32	21	5.00	20.00	7.29	1.46	Success	18.35	9.06
19	8	2	32	21	5.00	22.50	8.19	1.64	Success	17.85	9.88
20	7	2	32	21	5.00	25.71	9.35	1.87	Turbulent	17.58	10.23
21	6	2	32	21	5.00	30.00	10.87	2.17	Turbulent	15.49	10.91
22	5	2	32	21	5.00	36.00	12.98	2.60	Turbulent	16.73	12.31
23	4	2	32	21	5.00	45.00	16.07	3.21	Turbulent	19.58	14.80
24	3	2	32	21	5.00	60.00	21.00	4.20	No Success	–	–
57	10	5	32	21	6.40	18.00	6.57	1.03	No Success	–	–
58	9	5	32	21	6.40	20.00	7.29	1.14	Turbulent	8.39	5.92
59	8	5	32	21	6.40	22.50	8.19	1.28	No Success	–	–
60	7	5	32	21	6.40	25.71	9.35	1.46	No Success	–	–
61	6	5	32	21	6.40	30.00	10.87	1.70	No Success	–	–
62	5	5	32	21	6.40	36.00	12.98	2.03	No Success	–	–
63	4	5	32	21	6.40	45.00	16.07	2.51	Turbulent	7.07	6.70

Table 3. Robot geometric parameter tests results for 42 mm.

n	${\mathit{N}}_{\mathit{i}}$	${\mathit{l}}_{\mathit{h}}$	${\mathit{C}}_{\mathit{w}}$	${\mathit{w}}_{\mathit{d}}$	${\mathit{l}}_{\mathit{d}}$	$\mathit{\theta }$	${\mathit{O}}_{\mathit{n}}$	${\mathit{C}}_{\mathit{mor}}$	State	${\mathit{F}}_{\mathit{c}}$ (lbf)	$\mathit{\tau }$ (lbf·inch)
25	3	2	42	21	5.00	60.00	21.00	4.20	No Success	–	–
26	4	2	42	21	5.00	45.00	16.07	3.21	Turbulent	27.12	18.63
27	5	2	42	21	5.00	36.00	12.98	2.60	Turbulent	14.05	13.55
28	6	2	42	21	5.00	30.00	10.87	2.17	Turbulent	20.08	12.80
29	7	2	42	21	5.00	25.71	9.35	1.87	Turbulent	18.23	10.81
30	8	2	42	21	5.00	22.50	8.19	1.64	Success	20.62	10.50
31	9	2	42	21	5.00	20.00	7.29	1.46	Success	22.75	10.25
32	10	2	42	21	5.00	18.00	6.57	1.31	Success	19.61	8.99
33	10	2	42	18	5.00	18.00	5.63	1.13	Success	18.10	7.24
34	9	2	42	18	5.00	20.00	6.25	1.25	Success	17.52	7.22
35	8	2	42	18	5.00	22.50	7.02	1.40	Success	13.87	8.58
36	7	2	42	18	5.00	25.71	8.01	1.60	Turbulent	18.40	9.13
37	6	2	42	18	5.00	30.00	9.32	1.86	Turbulent	17.45	10.07
38	5	2	42	18	5.00	36.00	11.12	2.22	Success	18.64	11.94
39	4	2	42	18	5.00	45.00	13.78	2.76	Turbulent	19.38	12.85
40	3	2	42	18	5.00	60.00	18.00	3.60	No Success	–	–
41	3	5	42	15	6.40	60.00	15.00	2.34	No Success	–	–
42	4	5	42	15	6.40	45.00	11.48	1.79	No Success	–	–
43	5	5	42	15	6.40	36.00	9.27	1.45	No Success	–	–
44	6	5	42	15	6.40	30.00	7.76	1.21	No Success	–	–
45	7	5	42	15	6.40	25.71	6.68	1.04	No Success	–	–
46	8	5	42	15	6.40	22.50	5.85	0.91	No Success	–	–
47	9	5	42	15	6.40	20.00	5.21	0.81	No Success	–	–
48	10	5	42	15	6.40	18.00	4.69	0.73	No Success	–	–
49	10	5	42	21	6.40	18.00	6.57	1.03	No Success	–	–
50	9	5	42	21	6.40	20.00	7.29	1.14	Success	–	–
51	8	5	42	21	6.40	22.50	8.19	1.28	No Success	–	–
52	7	5	42	21	6.40	25.71	9.35	1.46	No Success	–	–
53	6	5	42	21	6.40	30.00	10.87	1.70	No Success	–	–
54	5	5	42	21	6.40	36.00	12.98	2.03	No Success	–	–
55	4	5	42	21	6.40	45.00	16.07	2.51	No Success	–	–
56	3	5	42	21	6.40	60.00	21.00	3.28	No Success	–	–

For the second group of tests, where $c_w$ = 42 was used, the normality test was applied, obtaining a significance level of $p_{ns}$ = 0.118 and $p_{nf}$ = 0.033, meaning one of the datasets does not have normal behavior. Therefore, the non-parametric sign test was applied to make a comparison, which gives $p_{sf}=0.057$, with $p>0.05$. It can be concluded that both samples have no significant differences.

In this case, the structure with a higher $c_w$ had less success and no significant differences due to the kinematic stuck problem that occurs with planar structure; Figure 8 shows the stuck point.

Figure 8. Kinematic stuck problem. The blue line represents the distance between the contact point of the wheel leg and the stuck point. The red lines are the dimensions of the robot structures.

Suppose that the robotic structure is placed at the midpoint of the tier and is planned to exit at four tiers, $d_e$, as given by (3), where $e_X$ and $e_Y$ represents the number of steps (number of horizontal and vertical segments of a step) in relation to the stuck point.

$$d_e=\sqrt{{\left(e_X{l}_w\right)}^2+{\left(e_Y{l}_h\right)}^2}$$

(3)

Regarding ${\theta }_l$ as the angle of the leg measured around the point of contact with the step and with respect to a horizontal line, the internal angle $\varphi$ can be calculated by (4):

$$\varphi ={\theta }_1-ta{n}^{-1}[e_Y{l}_h/\left(e_X{l}_w\right)]$$

(4)

So, the exact point where getting stuck occurs can be calculated using (5).

$$c_{e1}=\sqrt{w_r^2+d_e^2-2w_r{d}_{e}cos\left(\varphi \right)}$$

(5)

The part of the structure remaining above the stuck point is given by (6).

$$c_{e2}=c_w-c_{e1}$$

(6)

So, the stuck height, $h_e$, is given by (7).

$$h_e=c_{e2}sin\left(\gamma \right)$$

(7)

where $\gamma ={\theta }_l+\beta -\pi$ and $\beta ={sin}^{-1}(d_{e}sin\varphi /c_{e1})$. For the structure to have an increase in the probability of success, it must have $w_r$> $h_e$; if these values are equal, the friction or the small contact surface could decrease the probability of success.

In order to avoid this problem, the wheels must be close to the stuck point, so Equation (8) is proposed to solve the problem. $\alpha$ can vary between 0 and 1, but $c_w$ must be greater than $w_r$ by two-fold.

$$c_w=c_{e1}+\alpha w_r$$

(8)

Based on these statistical comparison tests, it was shown that there is a difference between the opening of the limb $c_{mor}$; therefore, it can be said that this opening has an incidence on the design of these wheels. This indicator relates the grip space that the wheels have to the dimensions of the stairs. Therefore, as was established in the methodology, if one of the $p_{s}f$ was greater than 0.05, it could be concluded that both $c_{mor}$ and $c_w$ are important indicators in the design of this structures. In Table 2, the successful results were varied, as the dimensions of the stairs were smaller compared to the opening of the legs, which increased the probability of success. However, in Table 3, larger stairs dimensions and a larger center-to-center distance of the structure did not improve the robot’s ability to climb the harrows. This is due to the fact that the robot tends to get stuck on the steps when climbing.

3.2. How Did the Robot Succeed?

During the simulations, the behavior of the center of mass was plotted to analyze how it was affected by the opening of the wheels. These graphs were classified into four behaviors, which are described below. The first behavior is that the robotic structures became stuck at the beginning of the staircase. In these cases, the graphs that have this behavior show a series of almost symmetrical wave cycles, as the structure fails to climb and gets stuck in a cyclic manner, as shown in Figure 9. The second behavior is that the structures managed to climb the stairs but got stuck in the last steps. In these cases, the graph initially shows a downward diagonal motion and then generates wave cycles showing that the structure gets stuck at the top of the staircase. The third behavior is when the structure manages to perform the test but in a turbulent manner. In these cases, the graph shows a diagonal downward trend and then a diagonal upward trend. In the diagonal movement, slight wave cycles are observed, and even some hits to the robotic structure manage to be overcome. The fourth behavior occurs when the structure manages to perform the test with an almost perfect V-graph. In this case, some noise is included in the graph, but they are not cyclic.

Figure 9. Center of mass categorization (inverted centroid due to the position in the simulation).

In this case, the maximum torque and contact forces of each wheel are extracted, and the averaged results of the simulations are presented in Table 2 and Table 3. When the tests were categorized according to the behavior of their centroid, we proceeded to make a statistical comparison of the motors and the contact forces on the wheels. For this comparison, only the third and fourth categories were taken into account since the categories that do not solve the problem do not contribute to the study of how the robot solves the problem. For this purpose, the information for each test of these categories was downloaded, and a normality test was used to determine the statistical test to be implemented. Table 4 shows the normality test of the limb opening $O_N$, the indicated $c_{mor}$, contact force, and torque. The only parameter with a p-value < 0.05 is the contact force of the turbulent category; therefore, the statistical test for the comparison of contact forces was the nonparametric sign test. For the comparison of the other parameters, the t-test was applied.

Table 4. Shapiro–Wilk test.

Category	Parameter	Significance
Turbulent	$O_N$	0.508
Turbulent	$C_{mor}$	0.503
Turbulent	$F_c$	0.008
Turbulent	$\tau$	0.612
Normal	$O_N$	0.622
Normal	$C_{mor}$	0.683
Normal	$F_c$	0.039
Normal	$\tau$	0.636

Table 5 shows the results of the t-test, comparing the parameters by category. A significance value of $p<0.05$ was found between the samples. Therefore, it can be concluded that $O_N$, $C_{mor}$, and torque have significant differences. In the case of the force sign test, $F_c$, a significance value $p=0.607$ with $p>0.05$ shows that there are no significant differences between the contact forces.

Table 5. t-test.

Category	Parameter	Significance
$O_N$	5.017	0.000
$C_{mor}$	5.205	0.000
$\tau$	2.738	0.016

Finally, the parameters of the normal category were correlated to understand how the indicator $c_{mor}$ correlates with the other parameters. Figure 10 shows the correlation matrix of the Pearson coefficient. Because $O_N$ is used to calculate the $c_{mor}$ indicator, a correlation of 92% was obtained. This indicator has a correlation of 87.4% with the $\stackrel{-}{\tau }$ of the motors, which have significant differences for the stability of the center of mass of the structure, whereas it has a lower correlation with the $F_c$, but this is always higher than 50%.

Figure 10. Pearson correlation coefficient matrix results. * Correlation is significant at the 0.05 level. ** Correlation is significant at the 0.01 level.

Based on the results obtained, a design theory for flat robotic structures using legged wheels is proposed. This theory is based on a $c_{mor}$ indicator that relates the opening of the limbs to the diagonal of the obstacles. Geometric requirements were shown to be necessary to avoid the structure becoming stuck while climbing stairs. The indicator showed significant differences between those tests that succeeded in overcoming the obstacle and those that did not when the stuck point was avoided. This showed that the relationship of the opening of the extremities, $O_N$, and the diagonal, $d_e$, are elements that explain why some of these structures manage to overcome the obstacles if they avoid the stuck point. Many of the structures that managed to overcome the obstacle did so in a turbulent manner, and this was analyzed graphically. The structures for which the center of gravity was turbulent and those with higher stability showed significant differences in the torque of their motors, which differs from the contact force values. Therefore, to overcome the obstacle stably, the robotic structures must remain within the limits shown in Figure 11. Finally, the Pearson correlation test for the dataset that reaches the obstacle stably shows that the proposed indicator $c_{mor}$ has a strong relationship with torque and a moderate relationship with contact force.

Figure 11. Box-and-whisker plot of the $C_{mor}$ indicator. Mean: 1.32; standard deviation: 0.21; variance: 0.045; lower limit: 1.11; upper limit: 1.53.

4. Application

4.1. Study Case

In this paper, we propose how to calculate the dimensions of a wheel with legs. These dimensions are based on an indicator obtained from the 63 simulations performed. This indicator has been statistically tested to show that it has a direct effect on the efficiency of these robotic structures for climbing stairs. In order to realize the application of the use of this theory, a different type of stairs with dimensions that are not covered in the preliminary tests is proposed for climbing. Step 1: The geometric parameters are shown in columns $l_h$ and $l_w$ of Table 6. We calculated $l_d$ for each case using (9). The geometric parameters shown in Table 6 were calculated using a $C_{mor}$ of 1.3 and (10).

$$l_d=\sqrt{l_w^2+l_h^2}$$

(9)

$$O_N=c_{mor}{l}_d$$

(10)

Table 6. Implementation of geometric parameters.

${\mathit{l}}_{\mathit{h}}$	${\mathit{l}}_{\mathit{w}}$	${\mathit{l}}_{\mathit{d}}$	${\mathit{O}}_{\mathit{N}}$
12	18	21.63	28.12

Step 2: The calculation was performed for different extremities, as shown in Table 7, using Equations (2)–(5) and (8), with $\alpha =0.96$.

Table 7. Possible geometric solutions using ${\theta }_1$ as $\pi$.

N	${\mathit{w}}_{\mathit{r}}$	${\mathit{c}}_{\mathit{w}}$
3	16.2370	43.7746
4	19.8862	45.4306
5	23.9231	67.9617
6	28.1233	69.9735
7	32.4088	72.3779
8	36.7449	75.1905

Step 3: Evaluate the results obtained using dynamic simulation. Figure 12 shows the behavior of the centroid during the simulation.

Figure 12. Implementation results (inverted centroid due to the position in the simulation).

4.2. What Happens If the c_mor Is Reduced?

In order to address the question, three additional simulations were conducted using the same parameters as outlined in Section 4.1. The sole variation was in the $c_{mor}$ value, which was reduced to 1.1, 0.9, and 0.75, respectively, to observe the behavior of the robotic structure. As $c_{mor}$ decreases, the probability of success also decreases, as indicated in Table 8. With $c_{mor}$ values of 0.75 and 0.9, the generation of contact forces in the structure becomes apparent due to a small $w_r$. Conversely, when it falls within the range of 1.1 to 1.3, the task can be successfully executed. At a $c_{mor}$ of 1.1, both torque and contact forces were lower. On the other hand, a $c_{mor}$ of 1.3 allowed the task to be completed in a shorter timeframe. Therefore, depending on the application, the design can fall within the $c_{mor}$ range of 1.1 to 1.3.

Table 8. Geometric solutions for N = 4 ($F_{cw}$: contact force in the wheels; $F_{cs}$: contact force in the structure).

${\mathit{c}}_{\mathit{mor}}$	${\mathit{w}}_{\mathit{r}}$	${\mathit{c}}_{\mathit{w}}$	State	$\mathit{\tau }$ (lbf·inch)	${\mathit{F}}_{\mathit{cw}}$ (lbf)	${\mathit{F}}_{\mathit{cs}}$ (lbf)
0.75	11.4728	42.1621	Failed	–	–	–
0.90	13.7674	42.8665	Success	19.40	6.93	0.05
1.10	16.8268	44.0161	Success	17.29	6.29	0.00
1.30	19.8862	45.8609	Success	22.05	6.84	0.00

5. Discussion

Although numerous authors have previously presented diverse analyses and methodologies for the design of hybrid wheels, it should be noted that many of these works predefine the various geometric attributes of the wheels, notably the number of legs [7,9,12,22,32,34,35,36,37]. In contrast to these prior approaches, our research takes a problem-centric approach, establishing a fundamental link between the harrow’s dimensions and the wheel opening as its foundational premise. In order to identify the appropriate design parameters, we conducted a statistical analysis, varying the number of legs through simulations. To our knowledge, there is only one study that uses a similar approach: using statistics to determine wheel efficiency and the optimal number of legs by taking step height as a parameter [38]. In our work, the number of legs is determined in accordance with the step’s height and also considers the spacing between the wheel centers in the robot design. This aligns with what previous authors suggest, with a key distinction being that our method allows the designer to select the number of legs, as there is no single solution. The critical element in our approach is the introduced metric, $c_{mor}$, which relates the step’s height and width by considering its diagonal and the wheel’s opening. This method is shown in the application section, where the procedure for dimensioning the wheels and the distance between the centers is exemplified. Notably, a major difference from prior work, like [38], is that, as legs are added, the radius of the wheel decreases. In contrast, our proposed method exhibits an inverse relationship; as the number of legs increases, the radius of the wheel also increases. Therefore, the main contributions of this work are as follows:

• The proposed indicator $c_{mor}$ was determined to relate the harrow dimensions to the opening of the wheel legs. This adimentional parameter showed the highest efficiency for overcoming the stairs at a value of 1.3; it also showed a strong correlation with motor torque and a weak correlation with contact force.
• The development of a method for designing wheels with legs based on the center distance parameter $c_w$ and the indicator $c_{mor}$.

6. Conclusions

The development of this work showed several of the problems that robotic structures must overcome to climb sets of stairs. First, it was shown that the opening of the legs of the wheels is a geometric parameter that determines whether the structure will be able to climb the stairs. The second problem is when the robot becomes stuck, which occurs at the beginning of the step or at some point during the climb of the structure. In order to solve these problems, 63 simulations were performed whereby the wheel opening, $O_N$, the wheel radius, $w_r$, and the distance between the centers of the front and rear wheels, $c_w$, were varied. The statistical tests showed significant differences between the geometric parameters that succeeded and those that did not. Furthermore, strong correlations were obtained between $c_{mor}$ and motor torque, and at a lower level, with contact force. Therefore, it is concluded that the proposed indicator $c_{mor}$, and the center-to-center distance, $c_w$, are the geometric parameters with the greatest impact when constructing these structures. A design methodology based on the geometry of the wheel is proposed using $c_{mor}$ and the geometry of the structure $c_w$. This methodology was validated with an additional simulation that was performed with a four-legged wheel. In future work, we propose the fabrication of robots by applying this methodology, where the main limitation found is the dimensions of the wheels.