Impact of White Noise on the Exact Solutions of the Stochastic Riemann Wave Equation in Quantum Mechanics
Abstract
:1. Introduction
2. Wave Equation for the SRWE
3. Exact Stochastic Solutions of SRWE
3.1. Modified Extended tanh Function Method
3.2. Mapping Method
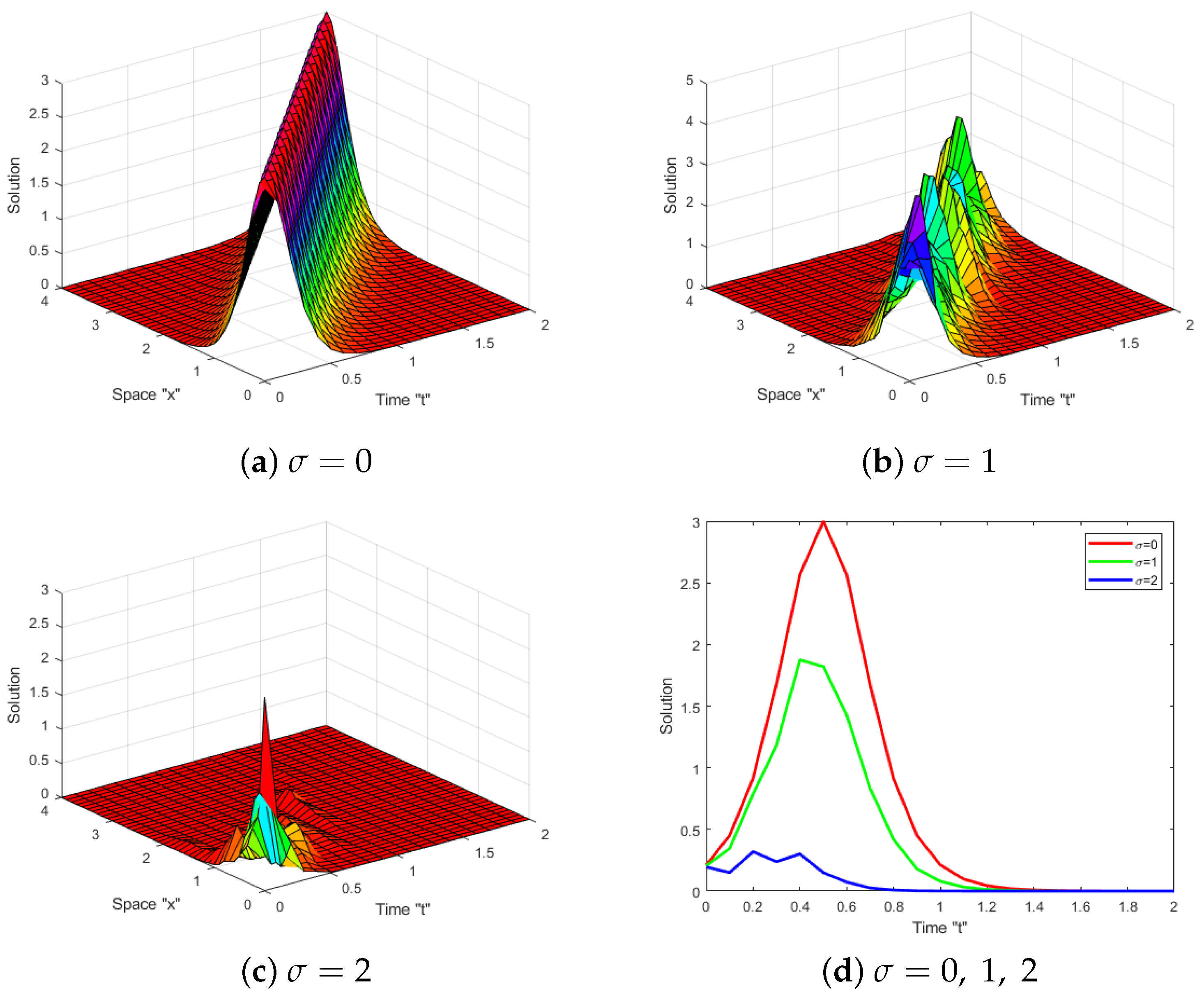
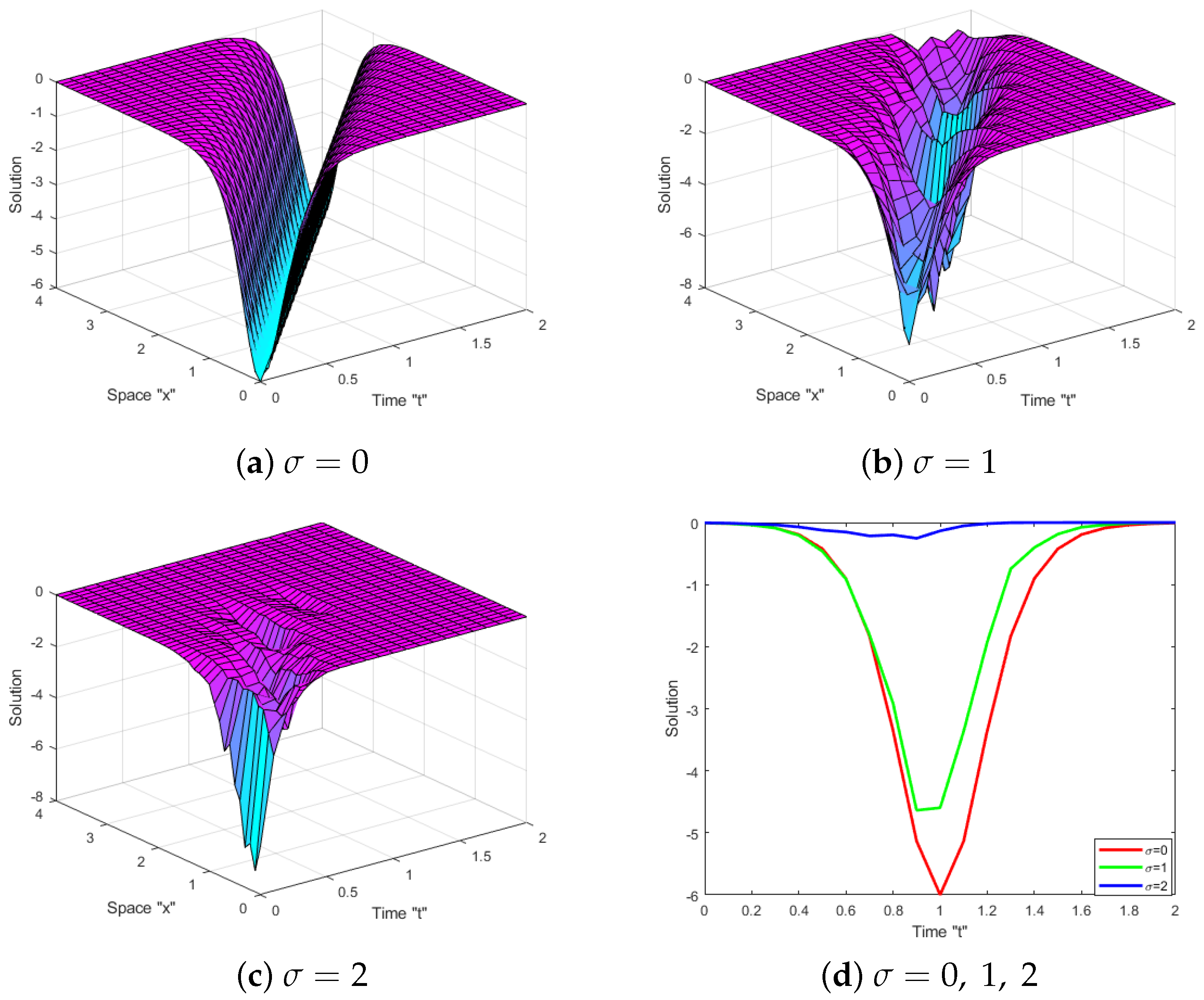
4. The Impact of White Noise
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arnold, L. Random Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Imkeller, P.; Monahan, A.H. Conceptual stochastic climate models. Stoch. Dynam. 2002, 2, 311–326. [Google Scholar] [CrossRef]
- Mouy, M.; Boulares, H.; Alshammari, S.; Alshammari, M.; Laskri, Y.; Mohammed, W.W. On Averaging Principle for Caputo-Hadamard Fractional Stochastic Differential Pantograph Equation. Fractal Fract. 2023, 7, 31. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C. Solitary solutions for the stochastic Fokas system found in monomode optical fibers. Symmetry 2023, 15, 1433. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A.; Alngar, M.E.M.; Biswas, A.; Moraru, L.; Khan, S.; Yıldırım, Y.; Alshehri, H.M.; Belic, M.R. Dispersive optical solitons with Schrödinger–Hirota model having multiplicative white noise via Itô Calculus. Phys. Lett. A 2022, 445, 128268. [Google Scholar] [CrossRef]
- Al-Askar, F.M. The solitary wave solutions of the stochastic Heisenberg ferromagnetic spin chain equation using two different analytical methods. Front. Phys. 2023, 11, 1267673. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. The Solitary Solutions for the Stochastic Jimbo–Miwa Equation Perturbed by White Noise. Symmetry 2023, 15, 1153. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M.; Shohib, R.M.A.; Gepreel, K.A.; Nofal, T.A. Optical solitons with (2+1)-dimensional nonlinear Schrödinger equation having spatio-temporal dispersion and multiplicative white noise via Itô calculus. Optik 2022, 261, 169204. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C. The soliton solutions for the (4+1)-dimensional stochastic Fokas equation. Math. Methods Appl. Sci. 2023, 46, 7589–7597. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Johnson, S.; Yildirim, A.; Kumar, S.; Biswas, A. Soliton solutions to coupled nonlinear wave equations in (2+1)-dimensions. Indian J. Phys. 2013, 87, 281–287. [Google Scholar] [CrossRef]
- Roy, R.; Barman, H.K.; Islam, M.N.; Akbar, M.A. Bright-dark wave envelopes of nonlinear regularized-long-wave and Riemann wave models in plasma physics. Results Phys. 2021, 30, 104832. [Google Scholar] [CrossRef]
- Barman, H.K.; Seadawy, A.R.; Akbar, M.A.; Baleanu, D. Competent closed form soliton solutions to the Riemann wave equation and the Novikov-Veselov equation. Results Phys. 2020, 17, 103131. [Google Scholar] [CrossRef]
- Barman, H.K.; Aktar, M.S.; Uddin, M.H.; Akbar, M.A.; Baleanu, D.; Osman, M. Physically significant wave solutions to the Riemann wave equations and the Landau-Ginsburg-Higgs equation. Results Phys. 2004, 22, 683–691. [Google Scholar] [CrossRef]
- Hao, H.-H.; Zhang, D.-J.; Zhang, J.-B.; Yao, Y.-Q. Rational and periodic solutions for a (2 + 1)-dimensional breaking soliton equation associated with ZS-AKNS hierarchy. Commun. Theor. Phys. 2010, 53, 430. [Google Scholar] [CrossRef]
- Duran, S. Breaking theory of solitary waves for the Riemann wave equation in fluid dynamics. Int. J. Mod. Phys. B 2021, 35, 2150130. [Google Scholar] [CrossRef]
- Attaullah; Shakeel, M.; Ahmad, B.; Shah, N.A.; Chung, J.D. Solitons solution of Riemann wave equation via modified exp function method. Symmetry 2022, 14, 2574. [Google Scholar] [CrossRef]
- Majid, S.Z.; Faridi, W.A.; Asjad, M.I.; Abd El-Rahman, M.; Eldin, S.M. Explicit soliton structure formation for the Riemann Wave equation and a sensitive demonstration. Fractal Fract. 2023, 7, 102. [Google Scholar] [CrossRef]
- Elwakil, S.A.; El-Labany, S.K.; Zahran, M.A.; Sabry, R. Modified extended tanh-function method and its applications to nonlinear equations. Appl. Math. Comput. 2005, 161, 403–412. [Google Scholar] [CrossRef]
- Peng, Y.Z. Exact solutions for some nonlinear partial differential equations. Phys. Lett. A 2013, 314, 401–418. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; Cesarano, C.; Rizk, D.; Aly, E.S.; El-Morshedy, M. Impact of White Noise on the Exact Solutions of the Stochastic Riemann Wave Equation in Quantum Mechanics. Symmetry 2023, 15, 2070. https://doi.org/10.3390/sym15112070
Mohammed WW, Cesarano C, Rizk D, Aly ES, El-Morshedy M. Impact of White Noise on the Exact Solutions of the Stochastic Riemann Wave Equation in Quantum Mechanics. Symmetry. 2023; 15(11):2070. https://doi.org/10.3390/sym15112070
Chicago/Turabian StyleMohammed, Wael W., Clemente Cesarano, Doaa Rizk, Elkhateeb S. Aly, and Mahmoud El-Morshedy. 2023. "Impact of White Noise on the Exact Solutions of the Stochastic Riemann Wave Equation in Quantum Mechanics" Symmetry 15, no. 11: 2070. https://doi.org/10.3390/sym15112070
APA StyleMohammed, W. W., Cesarano, C., Rizk, D., Aly, E. S., & El-Morshedy, M. (2023). Impact of White Noise on the Exact Solutions of the Stochastic Riemann Wave Equation in Quantum Mechanics. Symmetry, 15(11), 2070. https://doi.org/10.3390/sym15112070








