Angular-Momentum Modes in a Bosonic Condensate Trapped in the Inverse-Square Potential
Abstract
:1. Introduction and the Model
2. Analytical Considerations
2.1. The Framework for the Analysis of the Gross–Pitaevskii Equation
2.2. Identifying Vortex (Sectoral) States with Equal Magnetic and Orbital Quantum Numbers,
2.3. Identifying the States with
2.4. The Global Approximation for the States with
2.5. The Thomas–Fermi (TF) Approximation
3. Numerical Results
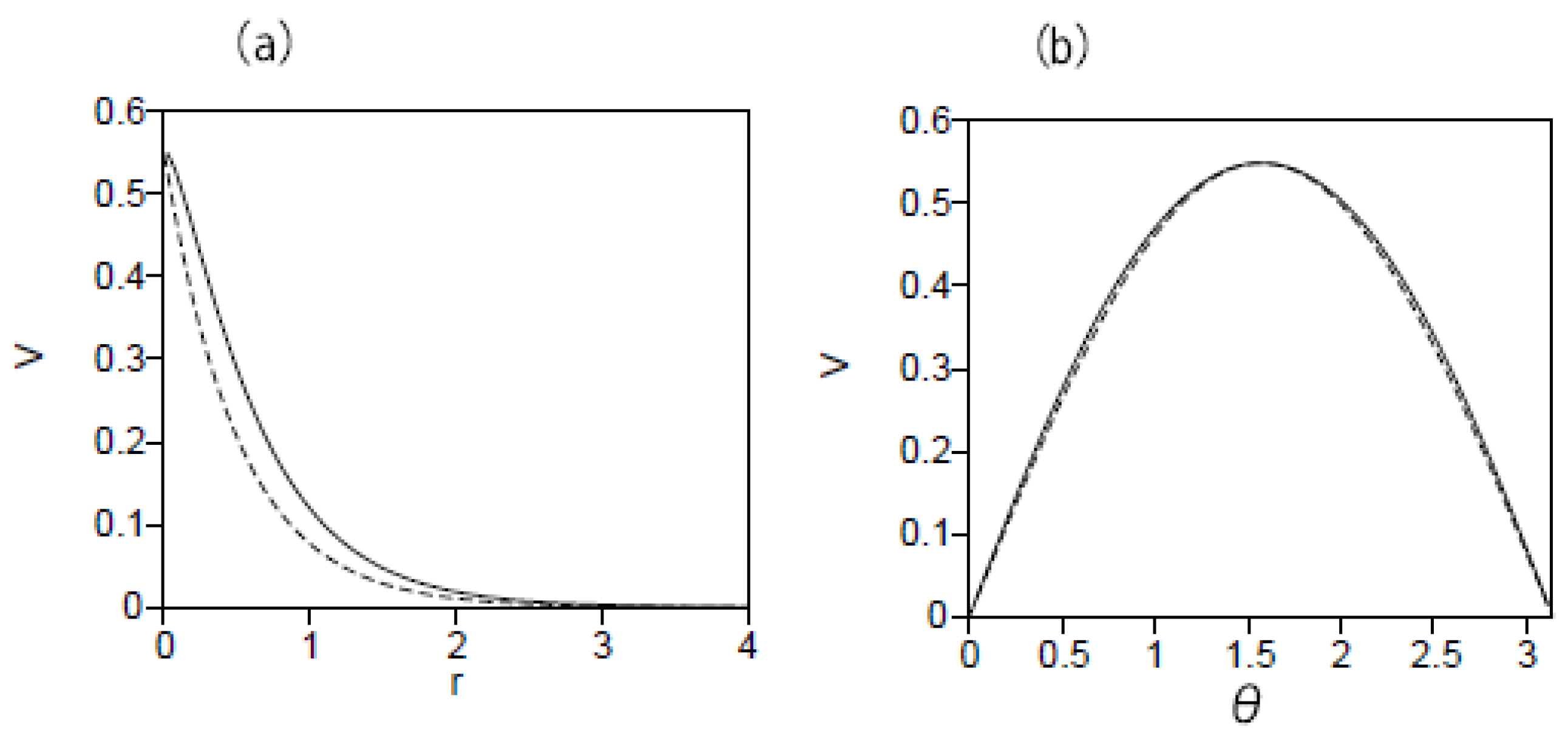
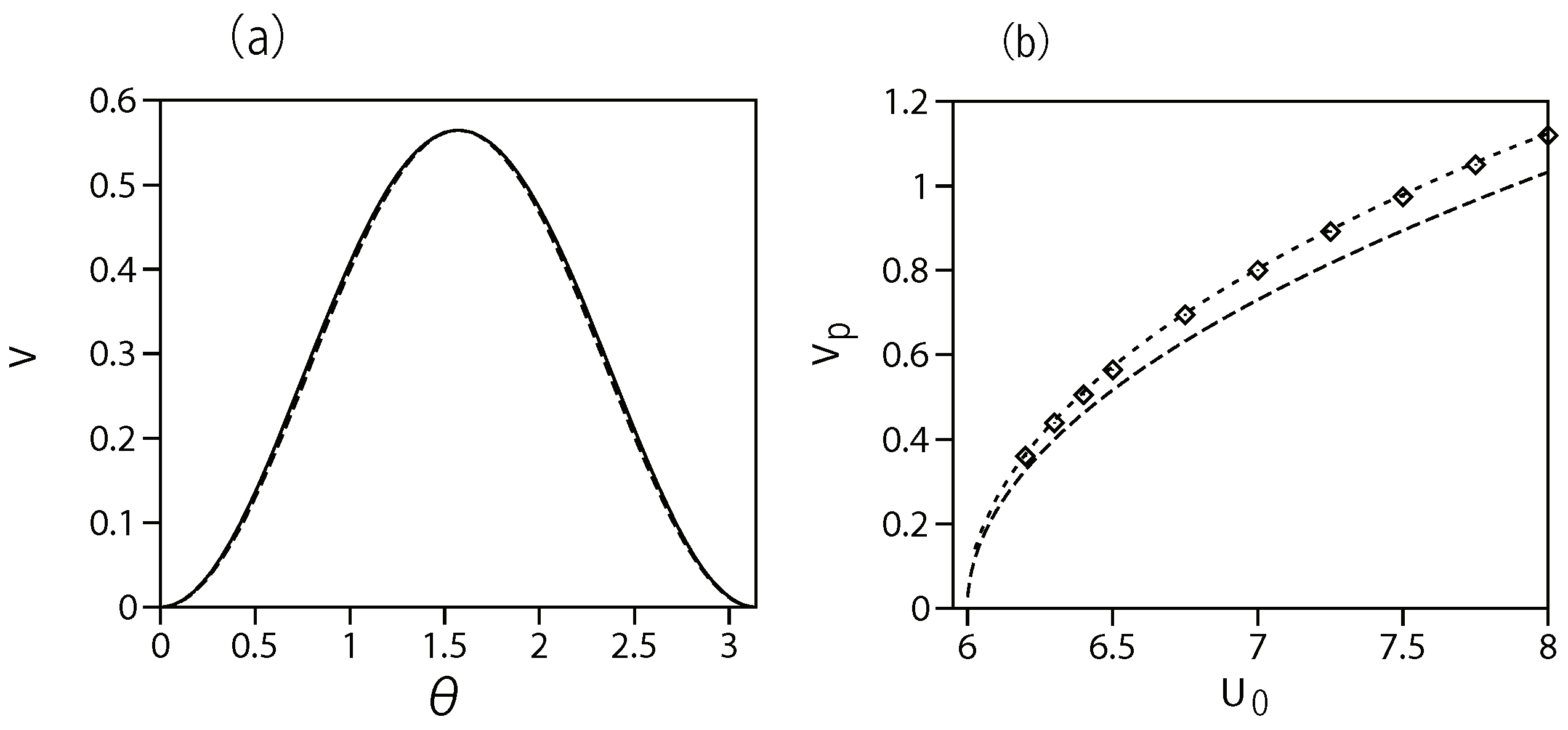
3.1. The Stationary Vortex (Sectoral) Modes with
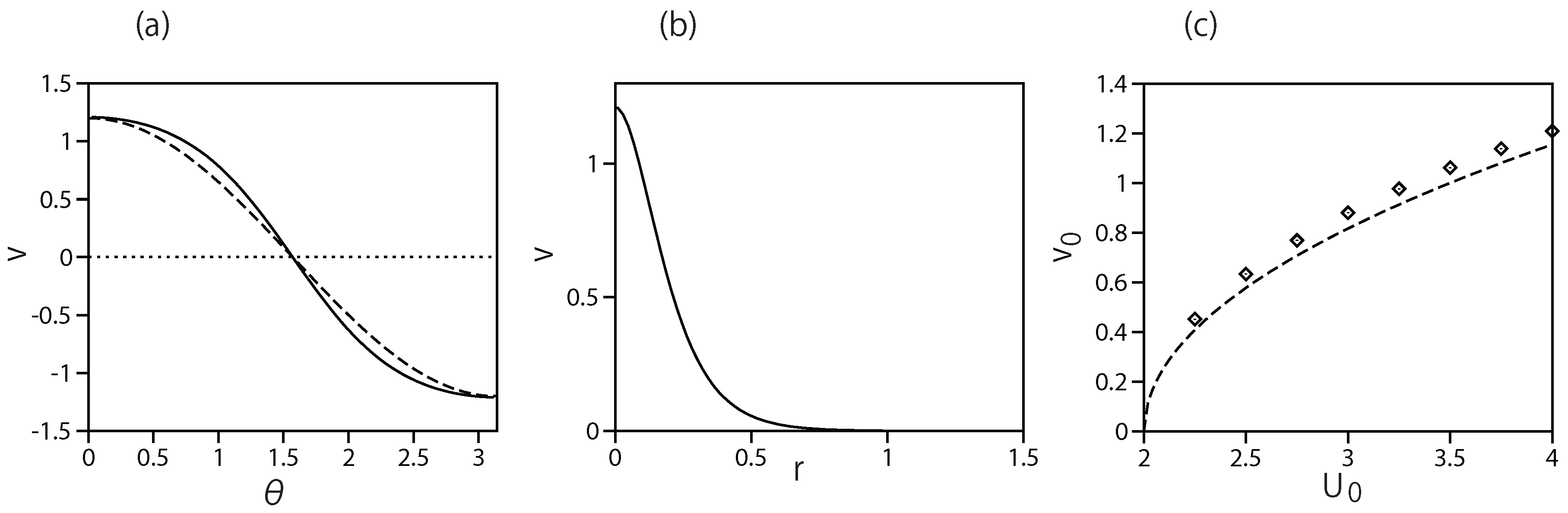
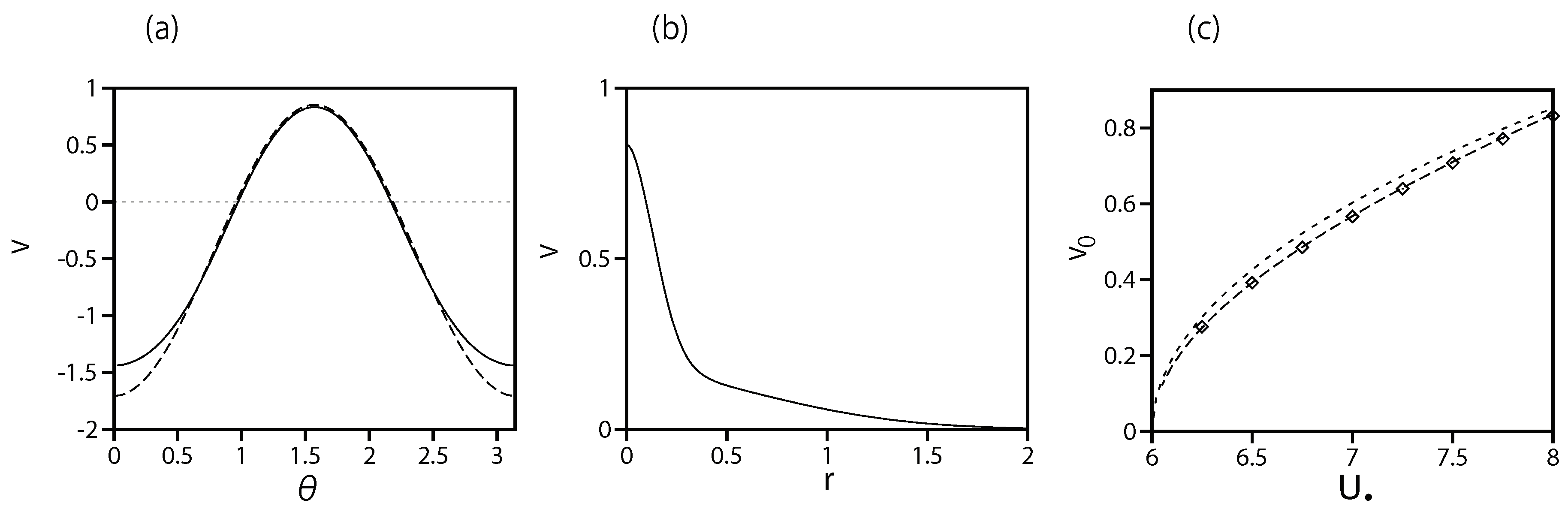
3.2. The Bound States with
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Nonrelativistic Theory; Nauka Publishers: Moscow, Russia, 1974. [Google Scholar]
- Tribelsky, M.I. Exact solutions to fall of particle to singular potential: Classical versus quantum cases. Proc. R. Soc. A 2023, 479, 20230366. [Google Scholar] [CrossRef]
- Gupta, K.S.; Rajeev, S.G. Renormalization in quantum mechanics. Phys. Rev. D 1993, 48, 5940–5945. [Google Scholar] [CrossRef] [PubMed]
- Camblong, H.E.; Epele, L.N.; Fanchiotti, H.; García Canal, C.A. Renormalization of the inverse square potential. Phys. Rev. Lett. 2000, 85, 1590. [Google Scholar] [CrossRef] [PubMed]
- Olshanii, M.; Perrin, H.; Lorent, V. Example of a quantum anomaly in the physics of ultracold gases. Phys. Rev. Lett. 2010, 105, 095302. [Google Scholar] [CrossRef]
- Ávila-Aoki, M.; Cisneros, C.; Martínez-y-Romero, R.P.; Núñez-Yepez, H.N.; Salas-Brito, A.L. Classical and quantum motion in an inverse square potential. Phys. Lett. A 2009, 373, 418–421. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum-mechanical collapse by repulsive interactions in a quantum gas. Phys. Rev. A 2000, 83, 013607. [Google Scholar] [CrossRef]
- Brazhnyi, V.A.; Konotop, V.V. Theory of nonlinear matter waves in optical lattices. Mod. Phys. Lett. B 2004, 18, 627–651. [Google Scholar] [CrossRef]
- Morsch, O.; Oberthaler, M. Dynamics of Bose-Einstein condensates in optical lattices. Rev. Mod. Phys. 2006, 78, 179–212. [Google Scholar] [CrossRef]
- Lewenstein, M.; Sanpera, A.; Ahufinger, V. Ultracold Atoms in Optical Lattices: Simulating Quantum Many-Body Systems; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Henderson, K.; Ryu, C.; MacCormick, C.; Boshier, M.G. Experimental demonstration of painting arbitrary and dynamic potentials for Bose-Einstein condensates. New J. Phys. 2009, 11, 043030. [Google Scholar] [CrossRef]
- Zou, Y.-Q.; Le Cerf, É.; Bakkali-Hassani, B.; Maury, C.; Chauveau, G.; Castilho, P.C.M.; Saint-Jalm, R.; Nascimbene, S.; Dalibard, J.; Beugnon, J. Optical control of the density and spin spatial profiles of a planar Bose gas. J. Phys. B 2021, 54, 08LT01. [Google Scholar] [CrossRef]
- Richaud, A.; Massignan, P.; Penna, V.; Fetter, A.L. Dynamics of a massive superfluid vortex in rk confining potentials. Phys. Rev. A 2022, 106, 063307. [Google Scholar] [CrossRef]
- Tabak, M.; Hammer, J.; Glinsky, M.E.; Kruer, W.L.; Wilks, S.C.; Woodworth, J.; Campbell, E.M.; Perry, M.D.; Mason, R.J. Ignition and high-gain with ultrapowerful lasers. Phys. Plasmas 1994, 1, 1626–1634. [Google Scholar] [CrossRef]
- Lindl, J.D.; Amendt, P.; Berger, R.L.; Glendinning, S.G.; Glenzer, S.H.; Haan, S.W.; Kauffman, R.L.; Landen, O.L.; Suter, L.J. The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 2004, 11, 339–491. [Google Scholar] [CrossRef]
- Grimm, R.; Weidemüller, M.; Ovchinnikov, Y.B. Optical dipole traps for neutral atoms, Advances In Atomic. Mol. Opt. Phys. 2000, 42, 95–170. [Google Scholar]
- Deiglmayr, J.; Grochola, A.; Repp, M.; Mörtlbauer, K.; Glück, C.; Lange, J.; Dulieu, O.; Wester, R.; Weidemüller, M. Formation of ultracold polar molecules in the rovibrational ground state. Phys. Rev. Lett. 2008, 101, 133004. [Google Scholar] [CrossRef] [PubMed]
- Ospelkaus, S.; Ni, K.-K.; Quéméner, G.; Neyenhuis, B.; Wang, D.; de Miranda, M.H.G.; Bohn, J.L.; Ye, J.; Jin, D.S. Controlling the hyperfine state of rovibronic ground-state polar molecules. Phys. Rev. Lett. 2010, 104, 030402. [Google Scholar] [CrossRef]
- Schmid, S.; Härter, A.; Denschlag, J.H. Dynamics of a cold trapped ion in a Bose-Einstein condensate. Phys. Rev. Lett. 2010, 105, 133202. [Google Scholar] [CrossRef] [PubMed]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation; Clarendon: Oxford, UK, 2003. [Google Scholar]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum collapse in binary bosonic gases. Phys. Rev. A 2013, 88, 043638. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Malomed, B.A. Quantum versus mean-field collapse in a many-body system. Phys. Rev. A 2015, 92, 043632. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Solitons in combined linear and nonlinear lattice potential. Phys. Rev. A 2010, 81, 013624. [Google Scholar] [CrossRef]
- Vakhitov, M.; Kolokolov, A. Stationary solutions of the wave equation in a medium with nonlinearity saturation, Radiophys. Quantum Electron. 1973, 16, 783–789. [Google Scholar]
- Bergé, L. Wave collapse in physics: Principles and applications to light and plasma waves. Phys. Rep. 1998, 303, 259–370. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum collapse in an anisotropic gas of dipolar bosons. Phys. Rev. A 2011, 84, 033616. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute low-dimensional liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright soliton to quantum droplet transition in a mixture of Bose-Einstein condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-bound quantum droplets of atomic mixtures in free space? Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wachtler, F.; Santos, L.; Ferlaino, F. Quantum-fluctuation-driven crossover from a dilute Bose-Einstein condensate to a macrodroplet in a dipolar quantum fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Bottcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef] [PubMed]
- Shamriz, E.; Chen, Z.; Malomed, B.A. Suppression of the quasi-two-dimensional quantum collapse in the attraction field by the Lee-Huang-Yang effect. Phys. Rev. A 2020, 101, 063628. [Google Scholar] [CrossRef]
- Antoine, X.; Bao, W.; Besse, C. Computational methods for the dynamics of the nonlinear Schrödinger/Gross–Pitaevskii equations. Comput. Phys. Commun. 2013, 184, 2621–2633. [Google Scholar] [CrossRef]
- Quiroga-Teixeiro, M.; Michinel, H. Stable azimuthal stationary state in quintic nonlinear optical media. J. Opt. Soc. Am. B 1997, 14, 2004–2009. [Google Scholar] [CrossRef]
- Pego, R.L.; Warchall, H.A. Spectrally stable encapsulated vortices for nonlinear Schrödinger equations. J. Nonlinear Sci. 2002, 12, 347–394. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakaguchi, H.; Malomed, B.A. Angular-Momentum Modes in a Bosonic Condensate Trapped in the Inverse-Square Potential. Symmetry 2023, 15, 2060. https://doi.org/10.3390/sym15112060
Sakaguchi H, Malomed BA. Angular-Momentum Modes in a Bosonic Condensate Trapped in the Inverse-Square Potential. Symmetry. 2023; 15(11):2060. https://doi.org/10.3390/sym15112060
Chicago/Turabian StyleSakaguchi, Hidetsugu, and Boris A. Malomed. 2023. "Angular-Momentum Modes in a Bosonic Condensate Trapped in the Inverse-Square Potential" Symmetry 15, no. 11: 2060. https://doi.org/10.3390/sym15112060
APA StyleSakaguchi, H., & Malomed, B. A. (2023). Angular-Momentum Modes in a Bosonic Condensate Trapped in the Inverse-Square Potential. Symmetry, 15(11), 2060. https://doi.org/10.3390/sym15112060





