The Chromatic Entropy of Linear Supertrees and Its Application

Abstract

Shannon entropy plays an important role in the field of information theory, and various graph entropies, including the chromatic entropy, have been proposed by researchers based on Shannon entropy with different graph variables. The applications of the graph entropies are found in numerous areas such as physical chemistry, medicine, and biology. The present research aims to study the chromatic entropy based on the vertex strong coloring of a linear $p$-uniform supertree. The maximal and minimal values of the $p$-uniform supertree are determined. Moreover, in order to investigate the generalization of dendrimers, a new class of $p$-uniform supertrees called hyper-dendrimers is proposed. In particular, the extremal values of chromatic entropy found in the research for supertrees are applied to explore the behavior of the hyper-dendrimers.

1. Introduction

In 1949, Shannon proposed the concept of entropy for the first time, now named Shannon entropy [1], which is defined as

$$I\left(p\right)=-{\sum }_{i=1}^n\left(p_i\log p_i\right),$$

where $p=(p_1,p_2,\dots ,p_n)$ is a probability distribution with ${ p}_i\in [0,1]$ and ${\sum }_{i=1}^n{p}_i=1$.

Shannon entropy is of great importance in the field of graph structure information theory. Based on Shannon entropy and some graph variables, many graph entropies were proposed; we refer to the reader to [2,3,4,5,6,7,8,9,10,11,12,13,14,15]. For graph entropy, there are lots of applications in chemistry, network, biology and so on; we refer to the reader to [16,17,18,19,20,21,22,23].

As a generalization of ordinary graphs, hypergraphs can express complex and high order relations such that it is often used to model complex systems. A hypergraph $H=\left(V\left(H\right),E\left(H\right)\right)$ with $n$ vertices and $m$ edges consist of a set of vertices, $V\left(H\right)=\left\{v_1,v_2,\dots ,v_n\right\}$, and a set of edges, $E\left(H\right)=\left\{e_1,e_2,\dots ,e_m\right\}$, where $e_i\ne \varnothing$, $e_i\subseteq E\left(H\right)$, $i=\mathrm{1,2},\dots ,m$. If $\left|e_i\right|=p$ for $\forall e_i\in E\left(H\right)$, then hypergraph $H$ is called $p$-uniform. For a $p$-uniform hypergraph $H$, the degree $d_v$ of a vertex $v\in V\left(H\right)$ is defined as $d_v=\left|\left\{e_j:v\in e_j\in E\left(H\right)\right\}\right|$, see [11]. If a vertex $v$ with $d_v=1$, then vertex $v$ is called a pendent vertex. Otherwise, it is called a non-pendent vertex. The distance, $d\left(u,v\right)$, between two vertices, $u$ and $v$, is the minimum length of a path connecting $u$ and $v.$ The radius, $r\left(v\right)$, of vertex $v$ in $H$ is defined by $r\left(v\right)=\mathrm{m}\mathrm{a}\mathrm{x}\left\{d(u,v)|u\in V\right\}$. A hyper-path $P$ with the length of $t$ in hypergraph $H$ is a vertex-hyperedge alternative sequence: $P=v_0{e}_1{v}_1{e}_2{v}_3{e}_3\cdots v_t{e}_t$, where $v_i,v_{i+1}\in e_{i+1}, i=0,1,\cdots ,i-1$. In particular, if there are exactly two vertices in each hyperedge, then the hypergraph $H$ is an ordinary graph and the hyper-path $P$ is a path. For more terminologies, we refer readers to reference [24].

$$P=v_o{e}_1{v}_1{e}_2{v}_2\cdots e_t{v}_t,$$

where $v_i,v_{i+1}\in e_{i+1},i=0,1,\cdots ,i-1$.

Definition of edge contracting.

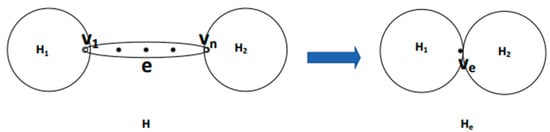
Let $H=(V, E)$ be a hypergraph with hyperedge $e=\{v_1,v_2,\dots ,v_n\}$ and exists $E_1\left(H\right)\subseteq E\left(H\right)$ such that the edges in $E_1\left(H\right)$ are incident with $v_1,v_2$…$v_n$. In $H$, by contracting the hyperedge $e$ into a vertex $v_e$ such that the vertex $v_e$ is incident with all the edges in $E_1\left(H\right)$, we get a new hypergraph, denoted by $H_e$. (See Figure 1).

Figure 1. The edge contracting $H$.

In particular, if $H=(V, E)$ is a $p$-uniform hypergraph, then by contracting for an edge $e$, we get a new hypergraph, $H_e=\left(V\right(H_e), E(H_e\left)\right)$, satisfying $\left|V\right(H_e\left)\right|=\left|V\right(H\left)\right|-(p-1)$ and $\left|E\right(H_e\left)\right|=\left|E\right(H\left)\right|-1$.

If there are at least two colors in each edge of hypergraph $H$, then $H$ is properly colored. If the same color appears in one edge no more than one time in $H$, then $H$ is strongly colored. The strong chromatic number $\chi \left(H\right)$ is the smallest number such that hypergraph $H$ has a strong coloring. If a partition $\left(V_1,V_2,\dots ,V_k\right)$ of $V \left(H\right)$ is its $k$-coloring, then it is called a chromatic decomposition of $H$. Define a non-decreasing chromatic decomposition by $c,$ whose sequence is denoted by${ \pi }_c\left(H\right)=(\left|V_1\right|,\left|V_2\right|,\dots ,\left|V_k\right|)$, where $\left|V_1\right|\le \left|V_2\right|\le \dots \left|V_k\right|$. A kind of graph entropy based on the strong coloring of hypergraphs is defined as follows.

Definition 1

([5]). Let $H=(V (H), E(H\left)\right)$ be a hypergraph with $n$ vertices and $m$ edges. Let $\hat{V}=(V_1,V_2,\dots ,V_k)$ be an arbitrary chromatic decomposition of $H$ and $\chi \left(H\right)=k$, then the graph entropy based on the vertex strong coloring $I_c\left(H\right)$ of $H$, called the chromatic entropy of hypergraph $H$, is given by

$$\begin{array}{cc}{I}_c(H)& =\underset{\hat{V}}{\min }\{-{\displaystyle \sum _{i=1}^k\frac{\left|V_i\right|}{n}\log }\frac{\left|V_i\right|}{n}\}\hfill \\ & =\log n-\underset{\hat{V}}{\max }\{\frac{1}{n}{\displaystyle \sum _{i=1}^k\left|V_i\right|\log }\left|V_i\right|\}.\hfill \end{array}$$

Assume $f(H)=\underset{\hat{V}}{\max }{\displaystyle \sum _{i=1}^k\left|V_i\right|}\log \left|V_i\right|$, then $I_c\left(H\right)=\mathrm{l}\mathrm{o}\mathrm{g}n-\frac{f\left(H\right)}{n}$.

Up until now, the research works on the chromatic entropy of a hypergraph are found in only one paper: we refer to the reader to [8]. In it, some tight upper and lower bounds of such graph entropy, as well as the corresponding extremal hypergraphs, are obtained.

In this research, the chromatic entropy based on the vertex strong coloring of a linear $p$-uniform supertree is investigated and the maximal and minimal values are given. Furthermore, a new kind of $p$-uniform supertrees, called hyper-dendrimers, are proposed. And we apply the results on the extremal values of chromatic entropy for linear $p$-uniform supertrees to the case of hyper-dendrimers.

The structure of this work is as follows. In Section 2, the extension of dendrimers in hypergraphs is presented. Some basic concepts and lemmas are given in Section 3. In Section 4, we show the main results of this work, which are about the extremal values of the chromatic entropy for supertrees. In Section 5, the results in Section 4 are applied to explore the behavior of hyper-dendrimers. A short conclusion of this paper is given in Section 6.

It is worth nothing that there are some basic information about graphs and mathematical notations that need to be explained. In the whole paper, all the hypergraphs are undirected and unweighted. Specially, $⌈\frac{n}{p}⌉$ stands for the ceiling of ($\frac{n}{p}$), and $\left[\frac{n}{p}\right]$ stands for the int of ($\frac{n}{p}$).

2. The Extension of Dendrimers in Hypergraphs

Indeed, dendrimers are nanoscale radially symmetric molecules with definite, uniform, and monodisperse structures, with typical symmetrical nuclei, inner shells, and outer shells. Due to the richness and diversity of dendrimers, they have good biological properties such that there are many applications in biomedical and pharmaceutical fields, as well as in chemistry [17,18,25,26].

In 1995, Elena and Skorobogatov [27] proposed a hypergraph model of non-classical molecular structures with multicentric delocalization bonds and presented a comparative analysis method of organometallic molecular structure model and hypergraph model indices. Using the characteristics of a hypergraph to represent the molecular structure of non-classical compounds opens a new research field, which not only generalizes the results of chemical application of graph theory, but also expands the application range of hypergraph theory [28,29].

Inspired by the above, we are interested in the structure of dendrimer in hypergraphs. Therefore, based on the concept of the dendrimer, the definition of hyper-dendrimer is given below.

Definition 2.

Let $D_{n, p}$ be a linear $p$-uniform supertree with $n$ vertices, and the size of $D_{n,p}$ is $\frac{n-1}{p-1}$, where $p\ne 0$, and $n\ne 0$. If the following conditions can be satisfied, then $D_{n,p}$ is called a homogeneous hyper-dendrimer.

(i) 

The degrees of all non-pendant vertices of $D_{n,p}$ are the same; and the degree of all non-pendant vertices of $D_{n,p}$ is at least 2.

(ii) 

There is a central vertex $u$ in $D_{n,p}$ satisfying that $D_{n,p}$ is symmetric with respect to vertex $u$. Otherwise, there is one central edge $e$ in $D_{n,p}$ such that it can be changed into a $p$-uniform supertree possessing a central vertex by contracting the edge $e$.

The set of these kinds of hyper-dendrimers is denoted by ${\mathbb{D}}_{n,p}$. Obviously, ${\mathbb{D}}_{n,p}\ne \varnothing$.

Two hyper-dendrimers with a central vertex, $u$, and a central edge, e, are given in Figure 2 and Figure 3, respectively. Obviously, as $p=2$, $D_{n,2}$ is a dendrimer. Two dendrimers with a central vertex $u$ and a central edge $e$ are shown in Figure 4 and Figure 5, respectively.

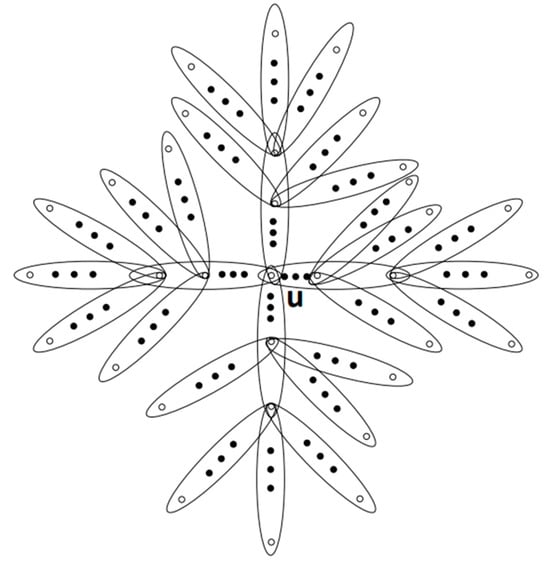
Figure 2. The hyper-dendrimer with a central vertex, $u$.

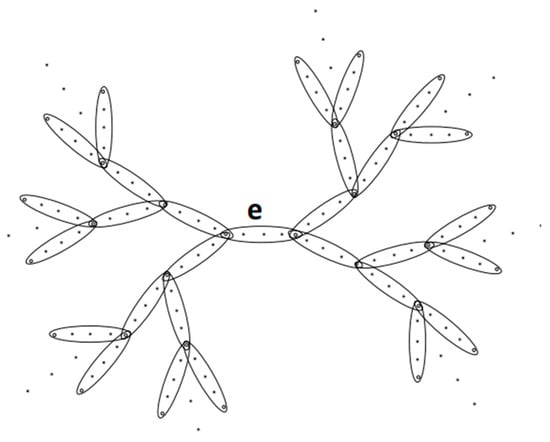
Figure 3. The hyper-dendrimer, $H_2^0$, with a central edge, $e$.

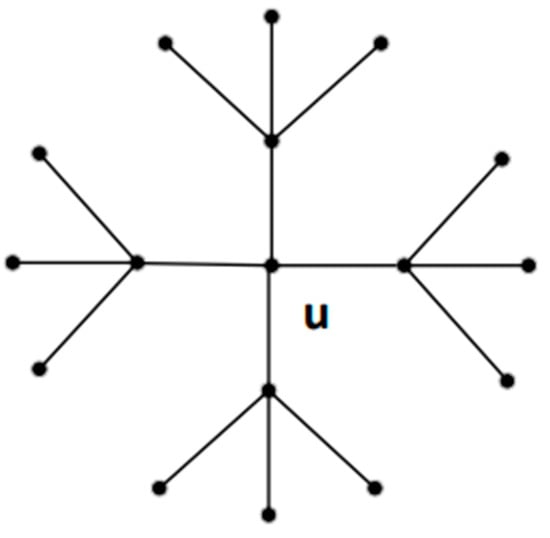
Figure 4. The dendrimer with a central vertex, $u$.

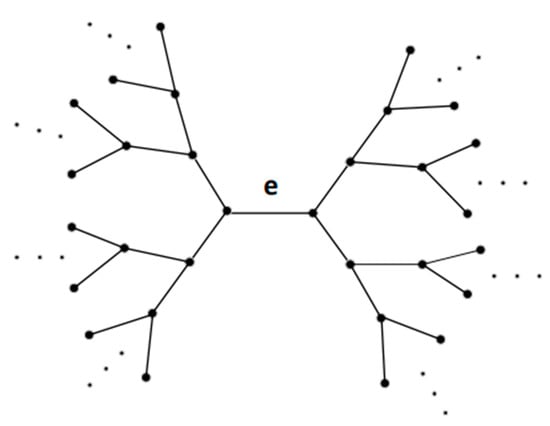
Figure 5. The dendrimer with a central edge, $e$.

3. Preliminaries

In this section, some basic concepts and lemmas are given.

Definition 3

([30]). A supertree is a hypergraph which is both connected and acyclic.

Definition 4

([31]). Let $G=\left(V, E\right)$ be a 2-uniform graph. For any$k \ge 3$, the $k$-th power of $G$, denoted by $G^k:=\left(V^k,E^k\right)$, is defined as the $k$-uniform hypergraph with the set of vertices $V^k=V\cup \left({\cup }_{e\in E}\right\{i_{e,1},\cdots ,i_{e,k-2}\left\}\right)$and the set of edges $E^k=\{e\cup \left\{i_{e,1},\cdots ,i_{e,k-2}\}|e\in E\right\}\}$, where $i_{e,1},\cdots ,i_{e,k-2}$ are new added vertices for $e$.

Definition 5

([31]). The $k$-th power of $S_n$, denoted by $S_n^k$, is called a hyper-star.

Definition 6

([24]). A hypergraph is linear if it is simple and $\left|e_i\cap e_j\right|\le 1$ for all $i,j\in I$ where $i\ne j$.

In the whole paper, the linear $p$-uniform supertree with $n$ vertices is denoted by $T_{n,p}$. By the Definition 3 and Definition 6 above, it is easy to see that the size of $T_{n,p}$ is $\frac{n-1}{p-1}$. Moreover, the set of all this kind of supertrees is denoted by ${\mathcal{T}}_{n,p}$.

Definition 7

([30]). (Moving edges operation) Let $r\ge 1$ and $H=\left(V\right(H),E(H\left)\right)$ be a hypergraph with $u\in V\left(H\right)$ and $e_1,e_2,\dots ,e_r\in E\left(H\right)$ such that $u\notin e_i$ for $i=\mathrm{1,2},\dots ,r.$ Suppose that $v_i\in e_i$and write $e_i^{\prime }=\left(e_i\backslash \left\{v_i\right\}\right)\cup \left\{u\right\}$, $i=\mathrm{1,2},\dots ,r.$ Let $H^{\prime }=\left(V\right(H), E(H^{\prime }\left)\right)$ be the hypergraph with $E\left(H^{\prime }\right)=\left(E\left(H\right)\backslash \{e_1,\dots ,e_r\}\right)\cup \{e_1^{\prime },\dots ,e_r^{\prime }\}$. Then we say that $H^{\prime }$is obtained from$H$ by moving edges $(e_1,\dots ,e_r)$ from $(v_1,\dots ,v_r)$ to$u$.

Lemma 1

([5]). Let $H=(V,E)$ be a $k$-uniform hypergraph $(k\ge 3)$ on $n$ vertices with $m$ edges and $l=1$ connected component. If $k\ge c\left(H\right)+2$, then $\chi \left(H\right)=k$.

Lemma 2

([5]). Suppose $f\left(X\right)={\sum }_{i=1}^n{x}_{i}log{x}_i$, where $X=\left\{x_1,\dots ,x_n\right\}\in \mathbb{x}$, and $\mathbb{x}=\left\{\{x_1,\dots ,x_n\}|x_1\ge \dots \ge x_n,{\sum }_{i=1}^n{x}_i=N_0, x_i\in Z^{+}(1\le i\le n,N_0\in Z^{+})\right\}$. For any $x_i$,$x_j\in X$, if $\left|x_i-x_j\right|=0$ or $\left|x_i-x_j\right|=1$, then $f\left(X\right)$ obtains the minimal value.

4. The Chromatic Entropy of Linear Supertrees

Now we show an operation of moving edges for a linear $p$-uniform supertree $T_{n,p}$ such that its chromatic entropy decreases. Denote the non-decreasing chromatic decomposition sequence of $T_{n,p}$ by${ \pi }_c\left(T_{n, p}\right)$. Suppose $u$ is the vertex with the maximum degree among $\mathrm{V}\left(T_{n, p}\right)$. There exists $e_1\in E\left(T_{n, p}\right)$ and $v_1\in e_1$ but$u\notin e_1$. Using the operation of moving edges in$T_{n,p}$ in Definition 7, we obtain a new supertree ${T^{\prime }}_{n,p}$ with ${T^{\prime }}_{n,p}=\left(V_{T_{n, p}},E_{{T^{\prime }}_{n, p}}\right)$, where

$$E_{{T^{\prime }}_{n, p}}=\left(E_{T_{n, p}}\backslash \left\{e_1\right\}\right)\cup \left\{e_1^{\prime }\right\}, e_1^{\prime }=\left(e_1\backslash \left\{v_1\right\}\right)\cup \left\{u\right\}.$$

Then we obtain a new non-decreasing chromatic sequence ${\pi }_{c^{\prime }}\left({T^{\prime }}_{n, p}\right)$ with a strong color $c^{\prime }$ of ${T^{\prime }}_{n,p}$. Thus, we have

Lemma 3.

For any $T_{n,p}\in {\mathcal{T}}_{n, p}$, $I_c\left(T_{n,p}\right)\ge I_{c^{\prime }}\left({T^{\prime }}_{n,p}\right)$ follows.

Proof. 

If $p=2$, then $T_{n,p}$ and ${T^{\prime }}_{n,p}$ are bipartite graphs. Then $\chi \left(T_{n, p}\right)=\chi \left({T^{\prime }}_{n, p}\right)=$ 2. As $p\ge 3$, by Lemma 1, $\chi \left(T_{n, p}\right)=\chi \left({T^{\prime }}_{n, p}\right)=p$.

Let${ \pi }_c\left(T_{n, p}\right)=(\left|V_1\right|,\dots ,\left|V_i\right|\dots ,\left|V_j\right|,\dots ,\left|V_p\right|)$. Now we discuss the following two cases based on the colors of vertices $u$ and$v_1$.

Case 1. The colors of vertices $u$ and$v_1$ are the same in $T_{n,p}$. Then it does not change the chromatic decomposition sequence of $T_{n,p}$ under the operation of moving edges, i.e., ${\pi }_c\left(T_{n,p}\right)={\pi }_{c^{\prime }}\left({T^{\prime }}_{n, p}\right)$. Therefore, we have ${ I}_{c^{\prime }}\left({T^{\prime }}_{n, p}\right)=I_c\left(T_{n, p}\right)$.

Case 2. The color of the vertex $v_1$ is different from that for vertex$u$ in $T_{n,p}$. Since vertex $u$ is with the maximum degree in $T_{n,p}$, without loss of generality, it is colored with color $i$ and the vertex $v_1$ is colored with color $j$. Since supertree $T_{n,p}$ is p-uniform, the other$(p-1)$ vertices of $e_1$ are colored with colors$1, 2,\dots , i,\dots , j-1, j+1,\dots , p$, respectively. By the operation of moving edges, a new edge $e_1^{\prime }$ can be obtained, which consists of the $(p-1)$ vertices of $e_1$ and vertex $u$. Therefore, we get a supertree ${T^{\prime }}_{n,p}$ with $E_{{T^{\prime }}_{n, p}}=\left(E_{T_{n, p}}\backslash \left\{e_1\right\}\right)\cup \left\{e_1^{\prime }\right\}$, where $e_1^{\prime }=\left(e_1\backslash \left\{v_1\right\}\right)\cup \left\{u\right\}$. Since $T_{n,p}$ is strong coloring, there is a vertex $v_2$ with color $i$ in $e_1$. Now we color $v_2$ with color $j$ in $e_1^{\prime }$. For the rest of vertices, their colors remain unchanged. Then we get a strong coloring $c^{\prime }$ of ${T^{\prime }}_{n,p}$. It is easy to find that the number of vertices with color $i$ decreases by 1, and that with color $j$ increases by 1. It arrives at ${\pi }_{c^{\prime }}\left({T^{\prime }}_{n, p}\right)=(\left|V_1\right|,\dots ,\left|V_i\right|-1,\dots ,\left|V_j\right|+1,\dots ,\left|V_p\right|)$.

Therefore,

$$\begin{array}{cc}f({\pi }_c(T_{n,p}))-f({\pi }_{c^{’}}(T_{n,p}^{’}))& =(\left|V_i\right|\log \left|V_i\right|+\left|V_j\right|\log \left|V_j\right|)-[(\left|V_i\right|-1)\log (\left|V_i\right|-1)\\ & +(\left|V_j\right|+1)\log (\left|V_j\right|+1)]\hfill \\ & =(\log {\xi }_1+\frac{1}{\ln 2})-(\log {\xi }_2+\frac{1}{\ln 2})\hfill \\ & <0\hfill \end{array}$$

where ${\mathsf{\xi }}_1\in (\left|V_i\right|-1,\left|V_i\right|)$,${\mathsf{\xi }}_2\in (\left|V_j\right|,\left|V_j\right|+1)$.

Then $f\left({\pi }_c\right(T_{n,p}\left)\right)<f\left({\pi }_{c^{\prime }}\right({T^{\prime }}_{n,p}\left)\right)$. By Definition 1, we have $I_c\left(T_{n,p}\right)>I_{c^{\prime }}\left({T^{\prime }}_{n,p}\right)$. □

By using Lemma 3 repeatedly, for any linear $p$-uniform supertree $T_{n,p}$, we obtain.

Theorem 1.

For any $T_{n,p}\in {\mathcal{T}}_{n, p}$, $I_c\left(T_{n, p}\right)\ge logn-\frac{m(p-1)logm}{n}$ follows, where $m=\frac{n-1}{p-1}$ and equality holds as $T_{n,p}\cong S_n^p$.

Proof. 

By Lemma 1, $\chi \left(S_n^p\right)=$ p. For hyper-star $S_n^p$, without loss of generality, we color the vertex possessing the maximum degree with color $1$, and color the other vertices in different edges with colors $2, 3, \cdots , p$, respectively. Then we get a strong coloring of $S_n^p$ with

$${\pi }_c\left(S_n^p\right)=\left(\left|V_1\right|=1,\left|V_2\right|=m,\left|V_3\right|=m,\cdots ,\left|V_p\right|=m\right).$$

Then $I_c\left(S_n^p\right)=\mathrm{l}\mathrm{o}\mathrm{g}n-\frac{m(p-1)\mathrm{l}\mathrm{o}\mathrm{g}m}{n}$. Using Lemma 3 repeatedly, we have $I_c\left(T_{n, p}\right)\ge I_c\left(S_n^p\right)$. □

Theorem 2.

For any $T_{n,p}\in {\mathcal{T}}_{n,p}$, it holds

$$I_c\left(T_{n, p}\right)\le \mathrm{l}\mathrm{o}\mathrm{g}n-\frac{1}{n}\left[a⌈\frac{n}{p}⌉\mathrm{l}\mathrm{o}\mathrm{g}a⌈\frac{n}{p}⌉+\left(p-a\right)\left[\frac{n}{p}\right]\mathrm{l}\mathrm{o}\mathrm{g}\left[\frac{n}{p}\right]\right],$$

where $a=n-p⌊\frac{n}{p}⌋$ and equality holds as $T_{n,p}\cong H$, where $H$ is the linear $p$-uniform supertree obtained by attaching pendant edges as many as possible to a hyper-path satisfying that its maximum degree is 2.

Proof. 

By Lemma 1, $\chi \left(H\right)=p$. Let $t$ be the number of all non-pendant edges of $H$. By the structure of $H$, there is only one hyper-path, $P$, which is composed of the $t$ non-pendant edges. That is,

$$P=v_o{e}_1{v}_1{e}_2{v}_2\cdots e_t{v}_t,$$

where $v_i,v_{i+1}\in e_{i+1},i=0,1,\cdots ,i-1$.

According to the strong coloring for a hypergraph, we color the vertices of $P$ in the order $e_1,e_2,\cdots ,e_t$ with $p$ colors $\left\{\mathrm{1,2},\cdots ,p\right\}$ in sequence. Then for each pendant edge, we color $p-1$ vertices of degree 1 with $p-1$ colors, respectively, which are different from that of the non-pendant vertex in the same pendant edge. Thus, we obtain a chromatic composition sequence of $H$ for strong coloring, which is given as follows.

$$\left|V_1\right|=\cdots =\left|V_a\right|=⌈\frac{n}{p}⌉,\left|V_{a+1}\right|=\cdots =\left|V_p\right|=⌊\frac{n}{p}⌋,$$

where $a=n-p⌊\frac{n}{p}⌋$. And it arrives

$$I_c\left(H\right)=\mathrm{l}\mathrm{o}\mathrm{g}n-\frac{1}{n}\left[a⌈\frac{n}{p}⌉\mathrm{l}\mathrm{o}\mathrm{g}a⌈\frac{n}{p}⌉+\left(p-a\right)\left[\frac{n}{p}\right]\mathrm{l}\mathrm{o}\mathrm{g}\left[\frac{n}{p}\right]\right].$$

Note that $\left|\left|V_i\right|-|V_j|\right|\le 1$, where $1\le i\le j\le p.$ By Lemma 2, the inequality follows. □

5. Applications on Chromatic Entropy for Hyper-Dendrimers

Considering the discussions above, the structure of hyper-star can also be considered as a hyper-dendrimer. From Theorem 1, the following corollary can be obtained directly.

Corollary 1.

For any $D_{n, p}\in {\mathbb{D}}_{n, p}$, $I_c\left(D_{n, p}\right)\ge logn-\frac{m(p-1)logm}{n}$ holds, where $m=\frac{n-1}{p-1}$ and equality holds as $D_{n,p}\cong S_n^p$.

In fact, for any hyper-dendrimer $D_{n,p}$, it can be obtained from the expending of a core molecule, which is a supertree with small orders. Inversely, we focus on the polymerization of a hyper-dendrimer, which can intuitively be presented in the dynamic process of reducing the chromatic entropy value by repeatedly using Lemma 3, where the polymerization means that the hyper-dendrimer with a complex structure scale was reduced by the operation of moving edges, but the number of vertices and edges remained unchanged. Two cases of polymerization for a hyper-dendrimer are shown as follows.

Case 1. Let $D_{n,p}\cong H_1^0$, whose central vertex is $u$. The hyper-dendrimer $H_1^0$ can be seen in Figure 6. Let the radius of vertex $u$ be $r$. In $H_1^0$, if the edge $e$ containing $p$ vertices whose distances from the central vertex $u$ are all $r$, by the operation of moving edges, the edge $e$ is moved to vertex $u$, i.e., the edge appeared in the red cycle. After similar operations for such kind of edges, we get hypergraph $H_1^1$. By Lemma 3, ${I_c(H}_1^1)<{I_c(H}_1^0)$. In $H_1^1$, if an edge containing $p$ vertices whose distances from the central vertex $u$ are all $r-1$, by the operation of moving edges, the edge is moved to vertex $u$, i.e., the edge appeared in the green cycle. After similar operations for such kind of edges, we get hypergraph $H_1^2$. By Lemma 3, ${I_c(H}_1^2)<{I_c(H}_1^1)$. We repeat these operations until $r=1$. Then it arrives at

$${I_c(S}_n^p)={{{I_c(H}_1^{r-1})<\cdots <{I_c(H}_1^2)<I}_c(H}_1^1)<{I_c(H}_1^0)$$

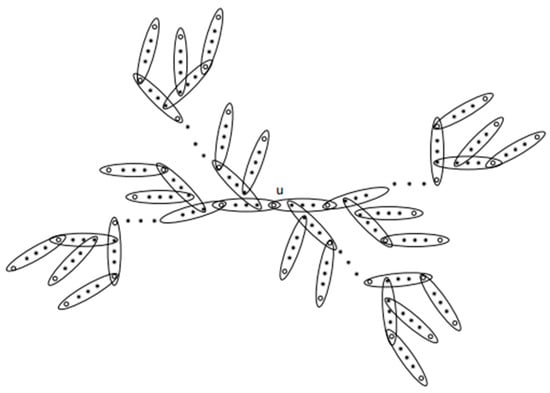
Figure 6. The hyper-dendrimer $H_1^0$.

The corresponding process can be seen in Figure 7.

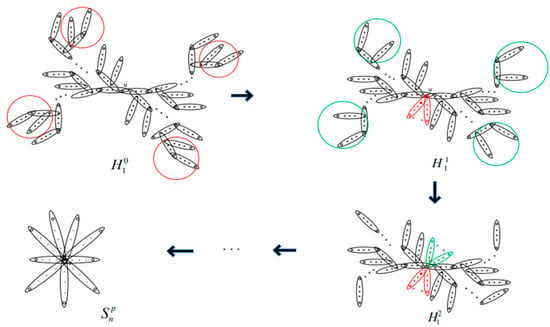
Figure 7. The process of moving edges in $H_1^0$ forwards a hyper-star.

Case 2. Let $D_{n,p}\cong H_2^0$, in which there is a central edge, $e$. The hyper-dendrimer $H_2^0$ can be found in Figure 3. Let $u\in e$ be a non-pendant vertex, whose radius is $r$. Through similar operations as Case 1, with the decreasing of the radius of $u$, a series of graphs $H_2^1$, $H_2^2$, $\cdots$, $H_2^{\mathrm{r}-1}$ can be obtained. Thus, by Lemma 3, we have

$${I_c(S}_n^p)={{{I_c(H}_2^{\mathrm{r}-1})<\cdots <{I_c(H}_2^2)<I}_c(H}_2^1)<{I_c(H}_2^0).$$

The corresponding process can be seen in Figure 8.

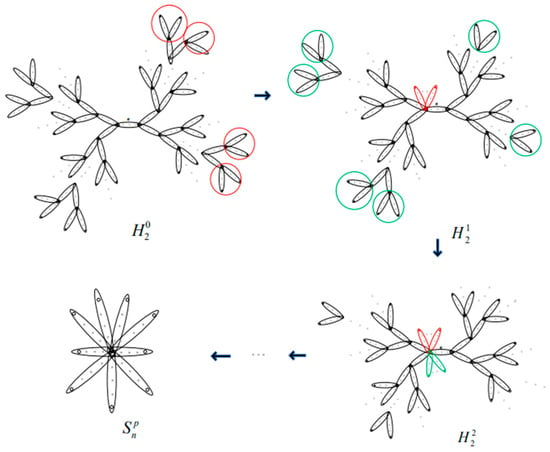
Figure 8. The process of moving edges in $H_2^0$ forwards a hyper-star.

Therefore, the hyper-star $S_n^p$ attains the minimal value among ${\mathbb{D}}_{n,p}$.

Though hyper-dendrimers are a class of special linear supertrees, they behave differently in the extremal graphs on their chromatic entropy due to the symmetry of a hyper-dendrimer.

Theorem 3.

For any $D_{n,p}\in {\mathbb{D}}_{n,p}$, it follows

$$I_c\left({\mathrm{D}}_{n, p}\right)\le \mathrm{l}\mathrm{o}\mathrm{g}n-\frac{1}{n}\left[a⌈\frac{n}{p}⌉\mathrm{l}\mathrm{o}\mathrm{g}a⌈\frac{n}{p}⌉+\left(p-a\right)\left[\frac{n}{p}\right]\mathrm{l}\mathrm{o}\mathrm{g}\left[\frac{n}{p}\right]\right],$$

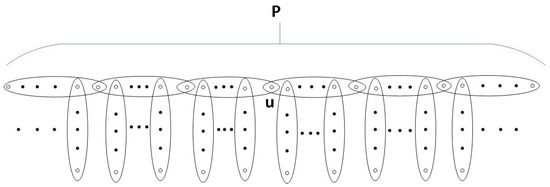
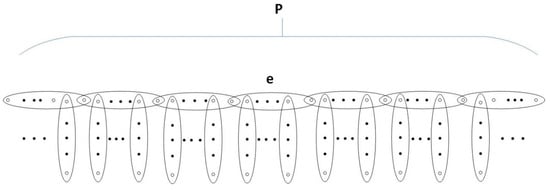
where $a=n-p\left[\frac{n}{p}\right]$ and equality holds as ${\mathrm{D}}_{n,p}\cong H_0$, where $H_0$ is the hyper-dendrimer obtained from attaching pendant edges as many as possible to a hyper-path, P, such that its maximum degree is 2. In particular, if the size of $H_0$ is even, then $H_0$ is a hyper-dendrimer with a central vertex $u$ (see Figure 9). Otherwise, $H_0$is a hyper-dendrimer with a central edge, $e$ (see Figure 10).

Figure 9. The hyper-dendrimer $H_0$ with a central vertex $u$.

Figure 10. The hyper-dendrimer $H_0$ with a central edge $e$.

Proof. 

With a similar coloring as $H$ in the proof of Theorem 2, by the structure of $H_0$ and Lemma 3, the result holds. □

Next, we give an example to show that there are different supertrees sharing the same maximal chromatic entropy.

Example 1.

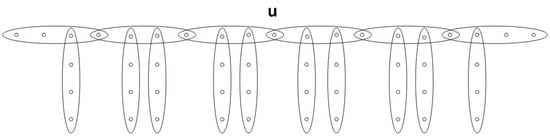
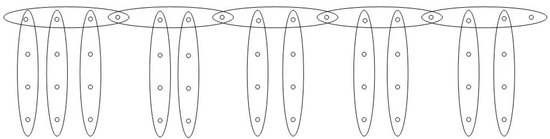
The hyper-dendrimer $D_{49,4}$ and the linear 4-uniform supertree $T_{49,4}$ are drawn in Figure 11 and Figure 12, respectively. We can check that $I_c\left(D_{49,4}\right)={I_c(T}_{49,4})=log49-\frac{1}{49}(36log12+13log13).$ However, the hyper-dendrimer $D_{49,4}$ is symmetrical respect to the central vertex $u$, which is different from $T_{49,4}$.

Figure 11. The hyper-dendrimer $D_{49,4}$.

Figure 12. The linear 4-uniform supertree $T_{49,4}$.

6. Conclusions

This work studies the extremal values as well as the corresponding extremal graphs of the chromatic entropy for linear $p$-uniform supertrees. Besides, new kinds of supertrees based on dendrimers are constructed, called hyper-dendrimer. Moreover, the dynamic process of chromatic entropy for hyper-dendrimers are shown by using the operation of moving edges. In the future, we will continue to consider the extremal values of chromatic entropy for some other special classes of hypergraphs, such as the unicyclic hypergraphs and bicyclic hypergraphs.