Abstract
Obtaining a suitable chemical composition for high-entropy alloys (HEAs) with superior mechanical properties and good biocompatibility is still a formidable challenge through conventional trial-and-error methods. Here, based on a large amount of experimental data, a machine learning technique may be used to establish the relationship between the composition and the mechanical properties of the biocompatible HEAs. Subsequently, first-principles calculations are performed to verify the accuracy of the prediction results from the machine learning model. The predicted Young’s modulus and yield strength of HEAs performed very well in the previous experiments. In addition, the effect on the mechanical properties of alloying an element is investigated in the selected Ti-Zr-Hf-Nb-Ta HEA with the high crystal symmetry. Finally, the Ti8-Zr20-Hf16-Nb35-Ta21 HEA predicted by the machine learning model exhibits a good combination of biocompatibility and mechanical performance, attributed to a significant electron flow and charge recombination. This work reveals the importance of these strategies, combined with machine learning and first-principles calculations, on the development of advanced biocompatible HEAs.
1. Introduction
The emergence of high-entropy alloys (HEAs) has disrupted the conventional approach to alloy design [1,2,3,4]. HEAs are typically composed of multiple alloying elements in nearly equal proportions and are fundamentally different from traditional alloys that rely on one or two primary elements [5,6,7,8]. Due to their unique mechanical properties, HEAs offer unparalleled advantages in a wide range of applications, such as aerospace, nuclear fusion, and medicine [9,10,11,12,13,14,15]. Recently, numerous novel HEAs and their corresponding models have been rapidly developed [16,17]. Compared with commercially available Ti6-Al4-V, the mechanical and biocompatibility properties, as well as processing routes of biomedical high-entropy alloys are discussed [16]. The microstructure, and the mechanical properties of body-centered cubic Hf-Mox-Nb-Ta-Ti-Zr alloys are investigated, and have been found to exhibit excellent room-temperature plasticity (>50%) and a high strength of 1015 MPa [17]. However, achieving the creation of HEAs with exceptional mechanical properties and favorable biocompatibility by adjusting the appropriate composition ratio remains a significant challenge.
Using a vacuum arc melting technique, the near equiatomic-concentration Nb-Ti-V-Ta-Alx alloys with single-phase BCC lattice are prepared under a high-purity argon atmosphere. These have high compressive yield strength and ductility, which can be attributed to solid solution strengthening [18]. Guided by CALPHAD modeling, the refractory medium-entropy alloy Mo-Nb-Ta-V has a Vickers microhardness of 4.95 GPa and a yield strength of 1.5 GPa due to a small negative departure from ideal mixing [19]. A single body-centered cubic refractory Hf25-Nb25-Ti25-Zr25 high entropy alloy has the fracture strength and plastic strain of 969 MPa and 14.9%, respectively, owing to the significant work-hardening effect from the movement and multiplication of dislocations [20]. Using Ab initio calculation and experiment, Ti20-Zr20-Hf20-Nb20-V20 alloy shows high strength and homogeneous deformation under compression at room temperature [21].
Machine learning methods have been extensively utilized in material design [1,3,22,23,24,25]. Without explicit physical formulas, machine learning has the capability to independently capture the relationship between input and output data based on a large data set. Moreover, it enables the accurate establishment of nonlinear and highly complex predictive models for the relevant parameters [2,3]. Based on high-throughput simulation combined with a machine learning approach, the relationship between the composition and mechanical properties is determined in the medium entropy alloys [4]. Subsequently, the “composition-hardness” model in the nickel-based superalloys is built using machine learning coupled with a high-throughput experiment. Then, the optimal composition for the high-hardness superalloys is obtained using the simulated annealing algorithm, and this composition is validated by Thermo-Calc software [1]. Using a machine learning-based alloy design system to facilitate the rational design of HEAs, the valance electron concentration plays an important role in the prediction of hardness [22]. A machine learning framework is used to predict the microhardness of high-entropy alloys, and ANN shows better performance for the new experimental data [23]. In addition, the first-principles calculation is a popular computational method by which to predict the material properties [2]. Based on the basic physical information, such as the electronic structure, Planck’s constant, and Boltzmann’s constant, the first-principles calculations provide a deep understanding of the mechanical properties of materials at the atomic and electronic scales [3,26,27,28,29,30].
In this work, a composition–property relationship for the biocompatibility of HEAs is built using machine learning combined with first-principles calculations. The flow chart representing this is presented in Figure 1. The different alloying elements are considered in HEAs. The contents of elements affect the mechanical properties, as well as the stability and safety, of the alloy in the organism. The mechanical properties of HEAs are mainly expressed in Young’s modulus and yield strength [1,2,3]. Sufficient strength and appropriate elasticity are critical for biomaterials. After data collection, machine learning and first-principles calculations, an accurate prediction model is established. The optimal proportion of HEA with a good combination of biocompatibility and mechanical performance is obtained.
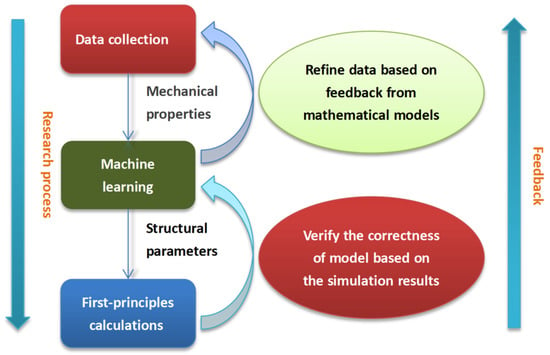
Figure 1.
Flow chart representing the process of obtaining the best-performing HEA using machine learning combined with first-principles calculation.
2. Computational Method
2.1. Machine Learning
In this work, a neural network method is employed, as shown in Figure 1. Because the neural network algorithms require a large amount of input and output data to find the empirical rules, we are able to collect a huge size of data from the previous literature [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], and then filter them under the following conditions. The insoluble metal elements, such as Ti, Al, and Zr, are mainly selected here. Ti is an excellent bioengineering material, due to the way that its density is similar to that of bone, and because it is non-toxic with high strength and good biocompatibility. Al has good plasticity and biocompatibility. During data collection, if any HEAs contain elements such as Fe, Ni, W, and Mg, these HEAs are removed in the data system. These elements are not the optimal biocompatible components. Ni has good mechanical properties, but shows a strong toxic effect. In addition, W could cause the blocked blood vessels to pass through [31,32,33,34,35,36,37]. Therefore, after continuous screening, the Ti-Nb-Ta-Hf-Zr alloy systems are selected as the input data for the machine learning method [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25].
In order to improve the training accuracy, the atomic ratios of the initial data are taken for the calculation. The physical quantity of the original material is calculated by the first-principle techniques as the intermediate quantity of the atomic ratio in the alternative material. The calculated physical quantities are the atomic radius, the mixing entropy, the mixing enthalpy, the electronegativity difference and the valence electron concentration. These unique physical properties of the metals establish a link between the element data and the mechanical properties in HEAs, which improve the correctness and accuracy for machine learning.
The atomic radius is generally expressed by the distance between two adjacent atoms. The calculation formula of atomic radius is expressed by [14,16].
where is the average atomic radius, ci represents the concentration of the element , and the atomic radius of the element .
The mixing entropy is used to characterize the disorder degree of the system state after the two or more different substances are mixed. The HEAs have a high mixing entropy effect in terms of their thermodynamics. The calculation formula of the mixing entropy is written as [14,16].
There is a linear relationship between the glass transition temperature of the bulk amorphous alloys and the absolute value of the alloy mixing enthalpy. The high absolute value of the mixing enthalpy leads to the high glass transition temperature. The formula of mixing enthalpy is expressed by [14,16].
The electronegativity characterizes the ability of an atom to attract the electrons in a compound. The formula of the electronegativity difference is written as [14,16].
The valence electron concentration is the average number of the valence electrons per atom in a substance [37]. The valence electron concentration is given by [14,16].
2.2. First-Principles Calculation
Density functional theory (DFT) is the most widely used theory among all of the first-principles calculation methods in physics and chemistry. Using electron density instead of wave function as the research variable makes it convenient to deal with the concept and practice of this theory. DFT simplifies the multi-body problem, which is caused by the interaction of electrons in an external electrostatic potential. This problem can manifest in the form of a non-interacting electron moving within the effective potential field, and deals with the resulting exchange correlation. Here, by using the DFT calculation, we can obtain the accurate mechanical properties of a particular composition of an HEA. The DFT calculation is also used to verify the accuracy of the machine learning model. The HEA model is built using the substitution of a random atom, as has been widely adopted in previous work. The commutative and correlation function has been modified by Perdew–Burke–Ernzerhof under the generalized gradient approximation. After the test, the truncation energy of the plane wave group is set to 500 eV, the density of K point is 5 × 5 × 5, the energy convergence standard is set to 0.01 meV, and the force convergence standard is 30 meV/A.
3. Results and Discussion
The yield strength and the elastic modulus of the existing HEAs are collected from previous experimental results [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36], and then the key physical parameters mentioned above are calculated [37]. Here, the calculated atomic radius, the mixing entropy, the mixing enthalpy, the electronegativity difference, and the valence electron concentration can used as the input set for the machine learning method. The Young’s modulus and yield strength of the HEAs are trained as the output sets. Here, 80% of the data set would be regarded as the training set, 10% would be regarded as the verification set, and 10% would be regarded as the test set.
Figure 2 shows the error distribution of the Young’s modulus in the HEAs obtained by machine learning. In addition, the data in the experimental test set are randomly sampled at each machine learning model. The prediction value with an error less than 10% is 86.4%, and the accurate prediction with almost zero error is 31.1%. The prediction error is within 10% for the sample with a Young’s modulus greater than 100 GPa. Overall, however, the results obtained by machine learning are relatively good [1,3]. Most of the data fall at a fairly accurate zero point. The data used for testing are mostly matched the results of the machine learning. This verifies that the model is valid for predicting the Young’s modulus of the HEA.
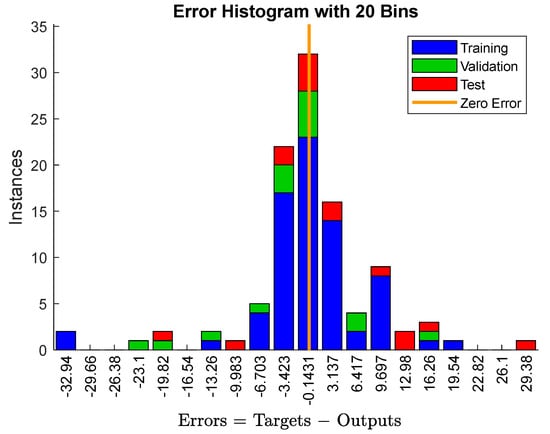
Figure 2.
The error analysis data of the Young’s modulus using the machine learning method. The abscissa represents the error interval, and the ordinate represents the amount of data in the error interval.
Figure 3 plots the differences of the Young’s modulus derived from the machine learning in the original data. According to the actual distribution of the scatter points, the scatter data in the graph are fitted linearly [1,3,37]. In order to ensure the randomness of the prediction, the samples in each data set are randomly selected. When the slope of the fitting curve is close to 1, the prediction accuracy is higher. The offsets of the data of the samples in other sections are basically smaller, and the average prediction accuracy has reached 96.6%. It can be seen that a sample with a large offset is generated in the range of the elastic modulus of 120–140 GPa. In addition, the overall prediction accuracy of the validation set has reached 95.2%. Even if abnormal data exist, the prediction model of the Young’s modulus still maintains a good forecast accuracy. Thus, the machine learning model used can effectively predict and evaluate the Young’s modulus in complex alloys.

Figure 3.
The verification and accuracy of Young’s modulus. The abscissa is the predicted target value, and the ordinate is the actual predicted output value.
Figure 4 shows that there are errors in the predicted yield strength in 86 of the 126 samples. The yield strength falls between −102.9 MPa and 107 MPa and has a relatively larger deviation. Here, the error value of the yield strength for the 14 samples is close to 0. The prediction rate of the sample with the low error is 68.3%, while the accurate prediction rate with the zero error is only 10.4%. According to Figure 4, the prediction accuracy of the yield strength is relatively high. In all of the data, the eighteen samples have a yield strength below 1 GPa, and two of the samples are even below 700 MPa. In addition, all of the sample classifications suggest that the absolute values with an error of 68.3% remain in a small range.
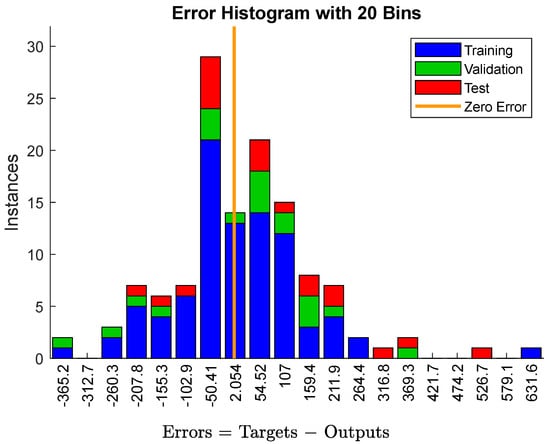
Figure 4.
The error analysis data of yield strength. The abscissa represents the error interval, and the ordinate represents the number of data in the error interval.
Figure 5 plots the data sets containing the yield strength in the original data. In the fitting legend of the training set, except for one sample with a larger deviation, the samples are distributed near the fitting line, and the comprehensive accuracy of prediction reaches 92.5%. It can be seen that the model generated by the training set is usually accurate. In the test set, the comprehensive accuracy for the predicted yield strength is 81.8%. Some samples deviate greatly from the fitting line. Thus, the actual predicted accuracy is relatively poor. It is speculated that the offset samples in the training set may affect the prediction result. Here, the machine learning model only predicts the yield strength of the HEA within a certain range. Although the overall accuracy reaches 90% in yield strength, the prediction result shows a larger deviation, and should be improved based on the physical model in future [37]. Recently, a machine learning-assisted physical model has been developed to predict the flow stress, dynamic recrystallization kinetic, and grain size evolution in a powder metallurgy superalloy [38]. In addition, a general machine learning method based on graph neural networks has been built for the prediction of the density of states purely from their atomic positions at six orders of magnitude [39] allowing it to effectively screen more complex functional properties. Hence, a machine-learning combined with a physical-model approach is urgently needed to be developed in order to determine the alloy system with the optimal performance.
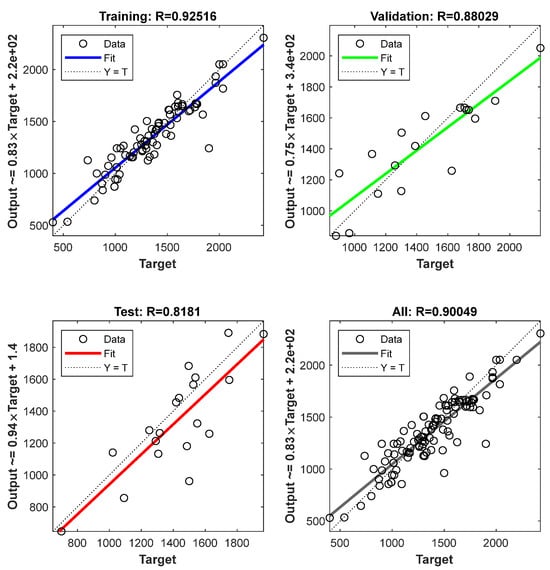
Figure 5.
The training and verification accuracy of the yield strength. The abscissa represents the predicted target value, and the ordinate represents the actual predicted output value.
In order to obtain the Ti-Nb-Ta-Hf-Zr HEA with excellent mechanical properties, the content of the single element is changed, and the contents of the other elements maintain a constant proportion. The influence of the element on the Young’s modulus and the yield strength of the Ti-Nb-Ta-Hf-Zr HEA are obtained using the trained machine learning model, as shown in Figure 6 and Figure 7. Then, the reasonable composition range would be determined from the trained machine learning model. Figure 6 shows the effect of element concentration on the Young’s modulus. Generally speaking, the contents of the Nb and Ta elements are high, and the elastic modulus of the corresponding alloy is high. The high content of the Zr element leads to the decrease of the elastic modulus. When the element content is less than 20%, the Ti and Hf elements have a smaller influence on the elastic modulus, and the Zr, Nb and Ta elements have a larger influence. When the element content is higher than 20% and lower than 40%, the contents of the Ti, Hf and Zr elements are higher, and the elastic modulus of the corresponding alloy is lower.

Figure 6.
Effect of the concentration on the Young’s modulus of the Ti-Nb-Ta-Hf-Zr HEA.
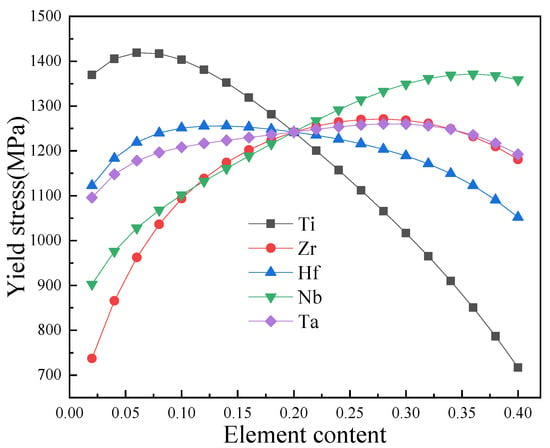
Figure 7.
Effect of the element concentration on the yield strength of the Ti-Nb-Ta-Hf-Zr HEA.
From Figure 7, we can see that the concentrations of the Hf and Ta elements have a smaller influence on the yield strength in the Ti-Nb-Ta-Hf-Zr HEA, while the concentrations of the Ti, Zr and Nb elements play a key role in yield strength. When the content of the Ti element is low, the yield strength is maintained at a high level, about 1400 MPa (Figure 7). Through a comprehensive comparison of Figure 6 and Figure 7, we can see that, after removing the mutation variables in the data, the optimal Ti content is 0–40%, the Nb content is 0–40%, the Ta content is 0–40%, the Hf content is 0–40%, and the Zr content is 0–40% for the high Young’s modulus and the yield strength in the Ti-Nb-Ta-Hf-Zr HEA. From Figure 6 and Figure 7, we see that 0.1% is set as the component gradient value, and that the intermediate physical quantities, including the mixing entropy, the mixing optimal, the electronegativity difference, the atomic radius, and the valence electron concentration, are calculated [3,37]. Using the machine learning model, Table 1 shows some of the excellent mechanical properties obtained, and the results can be verified by the first-principles calculations.

Table 1.
The predicted results of the Young’s modulus and yield strength.
Based on the results from the machine learning, the Ti8-Zr20-Hf16-Nb35-Ta21 HEA with the best combination of the Young’s modulus and the yield strength is determined. Subsequently, a random solid solution model of the alloy used for the first-principles calculation is established, as shown in Figure 8a. The charge–density difference is used to visualize the change of the charge after the interaction of the individual fragments or the change of the electron density during the formation of atoms into molecules. Here, the charge–density difference is calculated as follows:
where is the charge density of the whole system and and are the charge densities of the composed fragment.

Figure 8.
(a) A supercell structure of the Ti8-Zr20-Hf16-Nb35-Ta21 HEA. (b) The distribution of the charge–density difference. (c) The partial density of states for the Ti, Zr, Hf, Nb, and Ta elements in the s atomic orbitals, the p atomic orbitals, and the d atomic orbitals.
Figure 8b shows the charge–density difference of the Nb, Zr, Ta, Hf, and Ti elements in the Ti8-Zr20-Hf16-Nb35-Ta21 HEA. Here, the charge–density difference is more significant in the Ti and Zr atoms. The results demonstrate the significant electron flow and charge recombination among the Ti and Zr elements, leading to the formation of the covalent bonds to enhance the phase stability and the strength. In addition, the partial density of states for the Ti, Zr, Hf, Nb, and Ta elements in different atomic orbitals is given in Figure 8c. As is well known, the valence electron concentration plays a key role in the mechanical properties of the alloys [40]. The electronic density of states from the p atomic orbitals and the d atomic orbitals is mainly situated from −5.0 eV up to the Fermi energy level at 0 eV. Here, these partial bonding states occupied would be favorable to the stabilization of the bcc Ti8-Zr20-Hf16-Nb35-Ta21 HEA [41]. Recently, the element distribution characteristics and oxygen occupation properties in the Ti-Zr-Hf-Nb HEA were studied based on first principles, molecular dynamics and Monte Carlo calculations, with findings that indicate that the short-range order characteristic and oxygen occupation effects play a key role in the phase stability when regulating the mechanical properties [42]. A class of Co-Cr-Fe-Ni-based HEAs can be designed on demand by the synergistic doping of Cu and Mo elements based on the first-principles and multi-principal alloy design concepts, and the Co-Cr-Fe-Ni-Cu0.25-Mo0.75 HEA coating with good corrosion and slurry erosion performances can be determined [43]. Hence, via density functional theory, the design of HEAs is relatively easy to implement.
4. Conclusions
In summary, biocompatible non-isoatomic Ti-Nb-Ta-Hf-Zr HEA is screened using a combination of first-principles calculations and a machine learning method. The Young’s modulus and the yield strength are obtained by the machine learning algorithms based on the previous experimental data. A Ti8-Zr20-Hf16-Nb35-Ta21 HEA with excellent performance is selected by the machine learning, where its yield strength and Young’s modulus is 1.47 GPa and 102.9 GPa, respectively, due to the high crystal symmetry and unique charge–density difference. In addition, the detailed symmetry structure, Young’s modulus, and stability are calculated and verified using first-principles calculations. Therefore, the combination of first-principles calculations with a machine learning approach enables the efficient and targeted screening of a large number of the “compose–property” hyperspaces in the non-isoatomic HEAs.
Author Contributions
Conceptualization, S.P., J.L. and Q.F.; methodology, G.Z., Z.Z., R.F. and W.Z.; software, G.Z. and Z.Z.; validation, R.F. and W.Z.; formal analysis, G.Z., Z.Z., R.F. and W.Z.; investigation, G.Z., Z.Z., R.F., W.Z. and J.L.; resources, G.Z. and Z.Z.; data curation, R.F. and W.Z.; writing—original draft preparation, G.Z., Z.Z., R.F., W.Z., S.P., J.L. and Q.F.; writing—review and editing, G.Z., Z.Z., S.P., J.L., F.F. and Q.F.; visualization, G.Z., Z.Z., R.F., W.Z. and S.P.; supervision, S.P., J.L. and Q.F.; project administration, S.P., J.L., F.F. and Q.F.; funding acquisition, J.L. and Q.F. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to sincerely thank the National Natural Science Foundation of China (U2267252, 12372069, and 12172123), Natural Science Foundation of Hunan Province (2022JJ20001), and the Hunan Provincial Innovation Foundation for Postgraduate (CX20220378).
Data Availability Statement
All data used in this work are shown in the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Z.; Xie, B.B.; Fang, Q.; Liu, F.; Li, J.; Tan, L.; Huang, Z.; Zhao, L.; Jiang, L. Coupling high-throughput experiment and machine learning to optimize elemental composition in nickel-based superalloys. MRS Commun. 2021, 11, 411–417. [Google Scholar]
- Chen, Y.; Zhao, Q.K.; Wu, H.; Fang, Q.H.; Li, J. Effect of interstitial N atom on physical and mechanical properties of FeCoCrNiMn high-entropy alloys: A first-principles study. Phys. B 2021, 615, 413078. [Google Scholar]
- Li, J.; Xie, B.B.; Fang, Q.H.; Liu, B.; Liu, Y.; Liaw, P.K. High-throughput simulation combined machine learning search for optimum elemental composition in medium entropy alloy. J. Mater. Sci. Technol. 2021, 68, 70–75. [Google Scholar]
- González-Masís, J.; Cubero-Sesin, J.M.; Campos-Quirós, A.; Edalati, K. Synthesis of biocompaatible high-entropy alloy TiNbZrTaHf by high-pressure torsion. Mater. Sci. Eng. A 2021, 825, 141869. [Google Scholar]
- Hua, N.B.; Wang, W.J.; Wang, Q.T.; Ye, Y.X.; Lin, S.H.; Zhang, L.; Guo, Q.H.; Liaw, P.K. Mechanical, corrosion, and wear properties of biomedical Ti–Zr–Nb–Ta–Mo high entropy alloys. J. Alloys Compd. 2021, 861, 157997. [Google Scholar]
- Qiao, D.X.; Liang, H.; Wu, S.Y.; He, J.Y.; Cao, Z.Q.; Lu, Y.P.; Li, T.J. The mechanical and oxidation properties of novel B2-ordered Ti2ZrHf0.5VNb0.5Alx refractory high-entropy alloys. Mater. Charact. 2021, 178, 111287. [Google Scholar]
- Guo, N.N.; Wang, L.; Luo, L.S.; Li, X.Z.; Chen, R.R.; Su, Y.Q.; Guo, J.J.; Fu, H.Z. Microstructure and mechanical properties of in-situ MC-carbide particulates-reinforced refractory high-entropy Mo0.5NbHf0.5ZrTi matrix alloy composite. Intermetallics 2016, 69, 74–77. [Google Scholar]
- Maulik, O.; Kumar, D.; Kumar, S.; Dewangan, S.K.; Kumar, V. Structure and properties of light weight high entropy alloys: A brief review. Mater. Res. Exp. 2018, 5, 052001. [Google Scholar]
- Gurel, S.; Nazarahari, A.; Canadinc, D.; Cabuk, H.; Bal, B. Assessment of biocompatibility of novel TiTaHf-based high entropy alloys for utility in orthopedic implants. Mater. Chem. Phys. 2021, 266, 124573. [Google Scholar]
- Wang, S.P.; Xu, J. TiZrNbTaMo high-entropy alloy designed for orthopedic implants: As-cast microstructure and mechanical properties. Mater. Sci. Eng. C 2017, 73, 80–89. [Google Scholar]
- Ishimoto, T.; Ozasa, R.; Nakano, K.; Weinmann, M.; Schnitter, C.; Stenzel, M.; Matsugaki, A.; Nagase, T.; Matsuzaka, T.; Todai, M.; et al. Development of TiNbTaZrMo bio-high entropy alloy (BioHEA) super-solid solution by selective laser melting, and its improved mechanical property and biocompatibility. Scr. Mater. 2021, 194, 113658. [Google Scholar]
- Yang, W.; Liu, Y.; Pang, S.; Liaw, P.K.; Zhang, T. Bio-corrosion behavior and in vitro biocompatibility of equimolar Ti-Zr-Hf-Nb-Ta high-entropy alloy. Intermetallics 2020, 124, 106845. [Google Scholar]
- Wang, S.; Wu, D.; She, H.; Wu, M.X.; Shu, D.; Dong, A.; Lai, H.C.; Sun, B.; Wang, S.; Wu, D.; et al. Design of high-ductile medium entropy alloys for dental implants. Mater. Sci. Eng. C 2020, 3, 110959. [Google Scholar]
- Zhang, Y.; Yang, X.; Liaw, P.K. Alloy design and properties optimization of high entropy alloys. JOM 2012, 64, 830–838. [Google Scholar]
- Song, Q.T.; Xu, J. (TiZrNbTa)90Mo10 high-entropy alloy: Electrochemical behavior and passive film characterization under exposure to Ringer’s solution. Corros. Sci. 2020, 167, 108513. [Google Scholar]
- Castro, D.; Jaeger, P.; Baptista, A.C.; Oliveira, J.P. An overview of high-entropy alloys as biomaterials. Metals 2021, 11, 648. [Google Scholar] [CrossRef]
- Juan, C.C.; Tseng, K.K.; Hsu, W.L.; Tsai, M.H.; Tsai, C.W.; Lin, C.M.; Chen, S.K.; Lin, S.J.; Yeh, J.W. Solution strengthening of ductile refractory HfMoxNbTaTiZr high-entropy alloys. Mater. Lett. 2016, 175, 284–287. [Google Scholar]
- Yang, X.; Zhang, Y.; Liaw, P.K. Microstructure and compressive properties of NbTiVTaAlx high entropy alloys. Procedia Eng. 2012, 36, 292–298. [Google Scholar] [CrossRef]
- Yao, H.; Qiao, J.W.; Gao, M.C.; Hawk, J.A.; Ma, S.G.; Zhou, H. MoNbTaV medium-entropy alloy. Entropy 2016, 18, 189. [Google Scholar]
- Wu, Y.D.; Cai, Y.H.; Wang, T.; Si, J.J.; Zhu, J.; Wang, Y.D.; Hui, X.D. A refractory Hf25Nb25Ti25Zr25 high-entropy alloy with excellent structural stability and tensile properties. Mater. Lett. 2014, 130, 277–280. [Google Scholar]
- Fazakas, E.; Zadorozhnyy, V.; Varga, L.K.; Inoue, A.; Louzguine-Luzgin, D.V.; Tian, F.; Vitos, L. Experimental and theoretical study of Ti20Zr20Hf20Nb20X20 (X¼ V or Cr) refractory high-entropy alloys. Int. J. Refract. Met. Hard Mater. 2014, 47, 131–138. [Google Scholar] [CrossRef]
- Yang, C.; Ren, C.; Jia, Y.; Wang, G.; Li, M.; Lu, W. A machine learning-based alloy design system to facilitate the rational design of high entropy alloys with enhanced hardness. Acta Mater. 2022, 222, 117431. [Google Scholar] [CrossRef]
- Bundela, A.S.; Rahul, M.R. Machine learning-enabled framework for the prediction of mechanical properties in new high entropy alloys. J. Alloys Compd. 2022, 908, 164578. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, B.; Guo, W.; Fu, A.; Duan, H.; Li, W. Corrosion behavior and mechanism of FeCrNi medium entropy alloy prepared by powder metallurgy. J. Alloys Comp. 2021, 867, 159094. [Google Scholar] [CrossRef]
- Stepanov, N.D.; Shaysultanov, D.G.; Salishchev, G.A.; Tikhonovsky, M.A. Structure and mechanical properties of a light weight AlNbTiV high entropy alloy. Mater. Lett. 2015, 142, 153–155. [Google Scholar] [CrossRef]
- Senkov, O.N.; Woodward, C.; Miracle, D.B. Microstructure and properties of aluminum-containing refractory high entropy alloys. JOM 2014, 66, 2030–2042. [Google Scholar] [CrossRef]
- Lin, H.; Tong, M.; Wang, H.; Lu, N.; Fang, Q.H.; Li, J. Influence of chemical composition on mechanical properties and energy absorption of CoNiFeCr high entropy alloys: A first-principles study. Phys. B 2022, 640, 414029. [Google Scholar] [CrossRef]
- Chen, S.Y.; Yang, X.; Dahmen, K.A.; Liaw, P.K.; Zhang, Y. Microstructures and crackling noise of AlxNbTiMoV high entropy alloys. Entropy 2014, 16, 870–884. [Google Scholar] [CrossRef]
- Schuh, B.; Voelker, B.; Todt, J.; Schell, N.; Perriere, L.; Li, J.; Couzinie, J.P.; Hohenwarter, A. Thermodynamic instability of a nanocrystalline, single-phase TiZrNbHfTa alloy and its impact on the mechanical properties. Acta Mater. 2018, 142, 201–212. [Google Scholar] [CrossRef]
- Lin, C.M.; Juan, C.C.; Chang, C.H.; Tsai, C.W.; Yeh, J.W. Effect of Al addition on mechanical properties and microstructure of refractory AlxHfNbTaTiZr alloys. J. Alloys Compd. 2015, 624, 100–107. [Google Scholar] [CrossRef]
- Yao, H.W.; Qiao, J.W.; Gao, M.C.; Hawk, J.A.; Ma, S.G.; Zhou, H.F.; Zhang, Y. NbTaV-(Ti,W) refractory high-entropy alloys: Experiments and modeling. Mater. Sci. Eng. A 2016, 674, 203–211. [Google Scholar] [CrossRef]
- Wu, Y.D.; Cai, Y.H.; Chen, X.H.; Wang, T.; Si, J.J.; Wang, L.; Wang, Y.D.; Hui, X.D. Phase composition and solid solution strengthening effect in TiZrNbMoV high-entropy alloys. Mater. Des. 2015, 83, 651–660. [Google Scholar] [CrossRef]
- Ye, Y.F.; Wang, Q.; Lu, J.; Liu, C.T.; Yang, Y. High-entropy alloy: Challenges and prospects. Mater. Today 2016, 19, 349–362. [Google Scholar] [CrossRef]
- George, E.P.; Raabe, D.; Ritchie, R.O. High-entropy alloys. Nat. Rev. Mater. 2019, 4, 515–534. [Google Scholar] [CrossRef]
- Huang, H.; Wu, Y.; He, J.; Wang, H.; Liu, X.; An, K.; Wu, W.; Lu, Z. Phase-transformation ductilization of brittle high-entropy alloys via metastability engineering. Adv. Mater. 2017, 29, 1701678. [Google Scholar] [CrossRef]
- Shi, Z.; Fang, Q.H.; Liaw, P.K.; Li, J. Corrosion-resistant biomedical high entropy alloys: A review. Adv. Eng. Mater. 2023. [Google Scholar] [CrossRef]
- Li, J.; Xie, B.B.; Li, L.; Liu, B.; Liu, Y.; Shaysultanov, D.; Fang, Q.H.; Stepanov, N.; Liaw, P.K. Performance-oriented multistage design for multi-principal element alloys with low cost yet high efficiency. Mater. Horiz. 2022, 9, 1518–1525. [Google Scholar] [CrossRef]
- Hao, W.Q.; Tan, L.; Yang, X.G.; Shi, D.Q.; Wang, M.L.; Miao, G.L.; Fan, Y.S. A physics-informed machine learning approach for notch fatigue evaluation of alloys used in aerospace. Int. J. Fatigue 2023, 170, 107536. [Google Scholar] [CrossRef]
- Fung, V.; Ganesh, P.; Sumpter, B.G. Physically informed machine learning prediction of electronic density of states. Chem. Mater. 2022, 34, 4848–4855. [Google Scholar] [CrossRef]
- Zhao, S.J.; Egami, T.; Stocks, G.M.; Zhang, Y.W. Effect of d electrons on defect properties in equiatomic NiCoCr and NiCoFeCr concentrated solid solution alloys. Phys. Rev. Mater. 2018, 2, 013602. [Google Scholar] [CrossRef]
- Ravindran, P.; Asokamani, R. Correlation between electronic structure, mechanical properties and phase stability in intermetallic compounds. Bull. Mater. Sci. 1997, 20, 613. [Google Scholar] [CrossRef]
- Chen, A.; Pan, Y.; Dai, J.; Fu, W.; Song, X. Theoretical study on the element distribution characteristics and the effects of oxygen in TiZrHfNb high entropy alloys. Mater. Today Commun. 2023, 36, 106922. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Zhang, X.; Zhang, Y.; Chen, Y.; Zhu, L.; Zhou, M. Corrosion-erosion behavior and mechanism of CuMo co-doped CoCrFeNi high-entropy alloy coating prepared by directed energy deposition. Surf. Coat. Technol. 2022, 451, 129055. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).