Ulam–Hyers Stability of Linear Differential Equation with General Transform
Abstract
:1. Introduction
2. Preliminary Results
- ,
- ,
- .
3. Main Stability Results
4. Discussion on Additional Stability
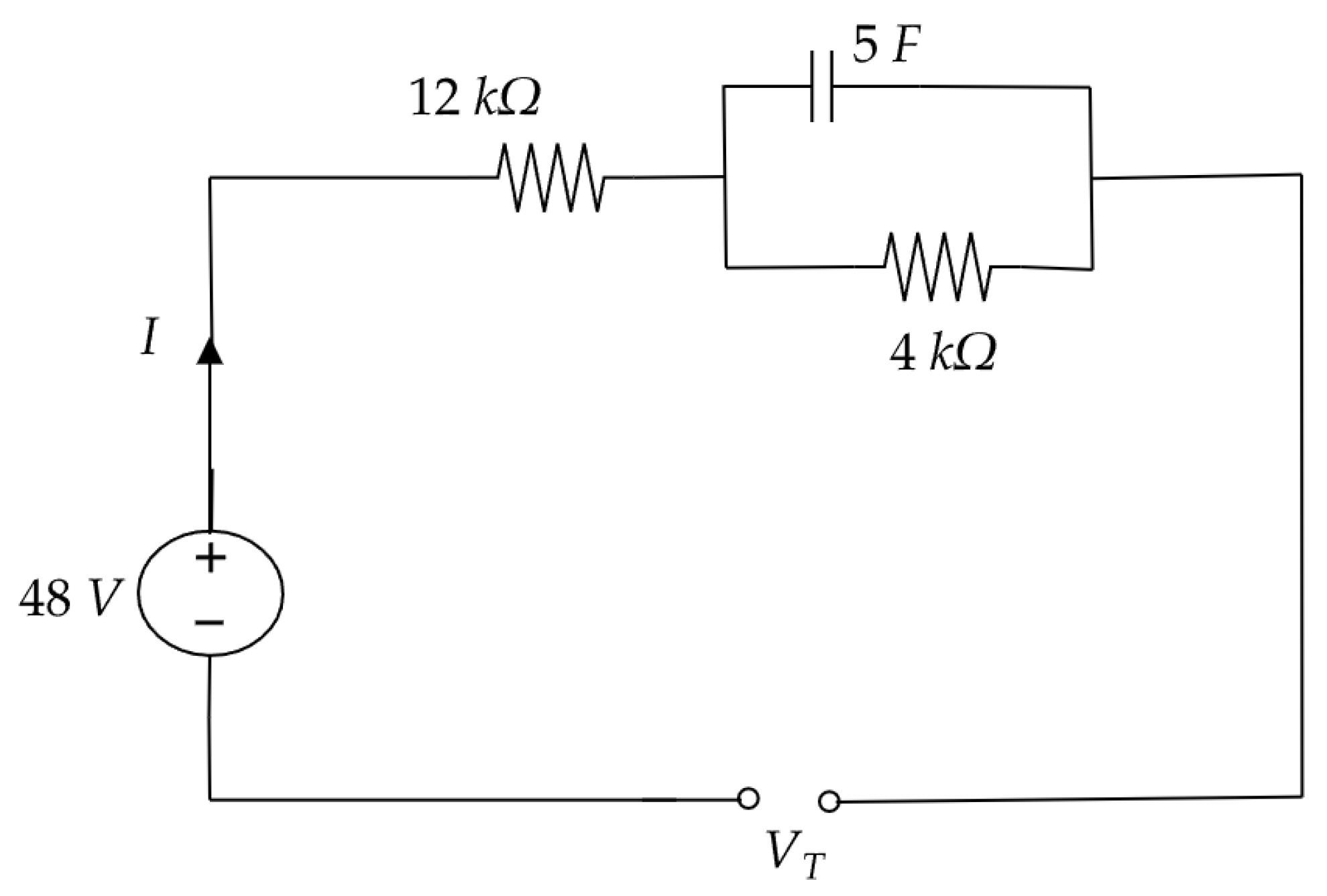
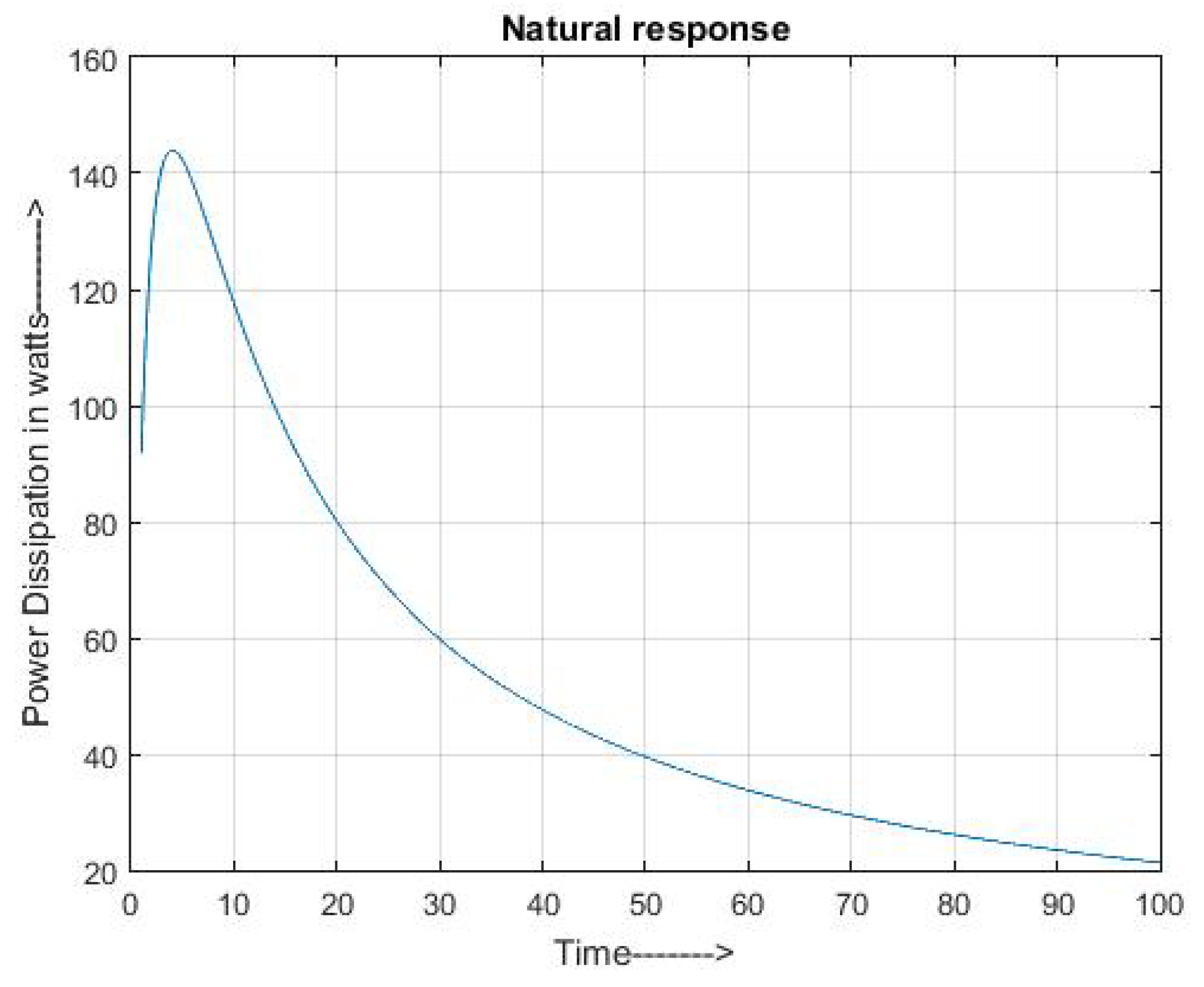
5. Examples
6. Applications of General Integral Transform
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ulam, S.M. Problems in Modern Mathematics; John Wiley and Sons: New York, NY, USA, 1964. [Google Scholar]
- Hyers, D.H. On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 1941, 27, 222–224. [Google Scholar] [CrossRef] [PubMed]
- Aoki, T. On the stability of the linear transformation in Banach spaces. J. Math. Soc. Jpn. 1950, 2, 64–66. [Google Scholar] [CrossRef]
- Rassias, T.M. On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 1978, 72, 297–300. [Google Scholar] [CrossRef]
- Selvam, A.; Sabarinathan, S.; Kumar, B.V.S.; Byeon, H.; Guedri, K.; Eldin, S.M.; Khan, M.I.; Govindan, V. Ulam-Hyers stability of tuberculosis and COVID-19 co-infection model under Atangana-Baleanu fractal-fractional operator. Sci. Rep. 2023, 13, 9012. [Google Scholar] [CrossRef]
- Sivashankar, M.; Sabarinathan, S.; Nisar, K.S.; Ravichandran, C.; Kumar, B.V.S. Some properties and stability of Helmholtz model involved with nonlinear fractional difference equations and its relevance with quadcopter. Chaos Solitons Fractals 2023, 168, 113161. [Google Scholar] [CrossRef]
- Yin, L.; Geng, Z.; Björneklett, A.; Söderlund, E.; Thiringer, T.; Brandell, D. An integrated flow electric thermal model for a cylindrical Li-I on battery module with a direct liquid cooling strategy. Energy Technol. 2022, 10, 2101131. [Google Scholar] [CrossRef]
- Pachaiyappan, D.; Murali, R.; Park, C.; Lee, J.R. Relation between electrical resistance and conductance using multifarious functional equations and applications to parallel circuit. J. Inequal. Appl. 2022, 2022, 60. [Google Scholar] [CrossRef]
- Khan, N.; Ahmad, Z.; Shah, J.; Murtaza, S.; Albalwi, M.D.; Ahmad, H.; Baili, J.; Yao, S.W. Dynamics of chaotic system based on circuit design with Ulam stability through fractal-fractional derivative with power law kernel. Sci. Rep. 2023, 13, 5043. [Google Scholar] [CrossRef] [PubMed]
- Kalvandi, V.; Eghbali, N.; Rassias, J.M. Mittag-Leffler-Hyers-Ulam stability of fractional differential equations of second order. J. Math. Ext. 2019, 13, 29–43. [Google Scholar]
- Selvam, A.; Sabarinathan, S.; Pinelas, S. The Aboodh transform techniques to Ulam type stability of linear delay differential equation. Int. J. Appl. Comput. Math. 2023, 9, 105. [Google Scholar] [CrossRef]
- Rezaei, H.; Jung, S.M.; Rassias, T.M. Laplace transform and Hyers-Ulam stability of linear differential equations. J. Math. Anal. Appl. 2013, 403, 244–251. [Google Scholar] [CrossRef]
- Selvam, A.; Sabarinathan, S.; Noeiaghdam, S.; Govindan, V. Fractional Fourier transform and Ulam stability of fractional differential equation with fractional Caputo-type derivative. J. Funct. Spaces 2022, 2022, 3777566. [Google Scholar] [CrossRef]
- Murali, R.; Selvan, A.P.; Park, C. Ulam stability of linear differential equations using Fourier transform. Aims Math. 2020, 5, 766–780. [Google Scholar]
- Sivashankar, M.; Sabarinathan, S.; Govindan, V.; Fernandez-Gamiz, U. Noeiaghdam, Stability analysis of COVID-19 outbreak using Caputo-Fabrizio fractional differential equation. Aims Math. 2023, 8, 2720–2735. [Google Scholar] [CrossRef]
- Murali, R.; Selvan, A.P.; Park, C.; Lee, J.R. Aboodh transform and the stability of second order linear differential equations. Adv. Differ. Equ. 2021, 2021, 296. [Google Scholar] [CrossRef]
- Aruldass, A.R.; Divyakumari, P.; Park, C. Hyers-Ulam stability of second-order differential equations using Mahgoub transform. Adv. Differ. Equ. 2021, 2021, 23. [Google Scholar] [CrossRef]
- Rassias, J.M.; Murali, R.; Selvan, A.P. Mittag-Leffler-Hyers-Ulam stability of linear differential equations using Fourier transforms. J. Comput. Anal. Appl. 2021, 29, 68–85. [Google Scholar]
- Jafari, H. A new general integral transform for solving integral equations. J. Adv. Res. 2021, 32, 133–138. [Google Scholar] [CrossRef] [PubMed]
- El-Mesady, A.I.; Hamed, Y.S.; Alsharif, A.M. Jafari transformation for solving a system of ordinary differential equations with medical application. Fractal Fract. 2021, 130, 130. [Google Scholar] [CrossRef]
- Jafari, H.; Manjarekar, S. A modification on the new general integral transform. Adv. Math. Model. Appl. 2022, 7, 253–263. [Google Scholar]
- Meddahi, M.; Jafari, H.; Yang, X.J. Towards new general double integral transform and its applications to differential equations. Math. Methods Appl. Sci. 2022, 45, 1916–1933. [Google Scholar] [CrossRef]
- Khirsariya, S.R.; Rao, S.B.; Chauhan, J.P. A novel hybrid technique to obtain the solution of generalized fractional-order differential equations. Math. Comput. Simul. 2023, 205, 272–290. [Google Scholar] [CrossRef]
- Meddahi, M.; Jafari, H.; Ncube, M.N. New general integral transform via Atangana-Baleanu derivatives. Adv. Differ. Equ. 2021, 385, 1–14. [Google Scholar] [CrossRef]
- Alqifiary, Q.H.; Jung, S.M. Laplace transform and generalized Hyers-Ulam stability of linear differential equations. Electron. J. Differ. Equ. 2014, 2014, 1–11. [Google Scholar]
- Găvruţa, P.; Jung, S.M.; Li, Y. Hyers-Ulam stability for second-order linear differential equations with boundary conditions. Electron. J. Differ. Equ. 2011, 2011, 1–5. [Google Scholar]
- Qarawani, M.N. Hyers-Ulam stability of a generalized second order nonlinear differential equation. Appl. Math. 2012, 3, 1857–1861. [Google Scholar] [CrossRef]
- Alqhtani, M.; Saad, K.M.; Shah, R.; Hamanah, W.M. Discovering novel soliton solutions for (3+1)-modified fractional Zakharov-Kuznetsov equation in electrical engineering through an analytical approach. Opt. Quantum Electron. 2023, 55, 1149. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Yasmin, H.; Shah, R.; Ullah, R.; Khan, A. Fractional-order modeling: Analysis of foam drainage and Fisher’s equations. Open Phys. 2023, 21, 20230115. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Probing families of optical soliton solutions in fractional perturbed Radhakrishnan-Kundu-Lakshmanan model with improved versions of extended direct algebraic method. Fractal Fract. 2023, 7, 512. [Google Scholar] [CrossRef]
- Aggarwal, S.; Chaudhary, R. A comparative study of Mohand and Laplace transforms. J. Emerg. Technol. Innov. Res. 2019, 6, 230–240. [Google Scholar]

| Function | New Integral Transforms |
|---|---|
| 1 | |
| s | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinelas, S.; Selvam, A.; Sabarinathan, S. Ulam–Hyers Stability of Linear Differential Equation with General Transform. Symmetry 2023, 15, 2023. https://doi.org/10.3390/sym15112023
Pinelas S, Selvam A, Sabarinathan S. Ulam–Hyers Stability of Linear Differential Equation with General Transform. Symmetry. 2023; 15(11):2023. https://doi.org/10.3390/sym15112023
Chicago/Turabian StylePinelas, Sandra, Arunachalam Selvam, and Sriramulu Sabarinathan. 2023. "Ulam–Hyers Stability of Linear Differential Equation with General Transform" Symmetry 15, no. 11: 2023. https://doi.org/10.3390/sym15112023
APA StylePinelas, S., Selvam, A., & Sabarinathan, S. (2023). Ulam–Hyers Stability of Linear Differential Equation with General Transform. Symmetry, 15(11), 2023. https://doi.org/10.3390/sym15112023







