Distributed Rotational Inertia Load Excitation Model and Its Impact on High-Speed Jointed Rotor Dynamic Response
Abstract
:1. Introduction
2. Distributed Rotational Excitation Model for High-Speed Rotor System
2.1. Configuration of a Typical High-Speed Jointed Rotor
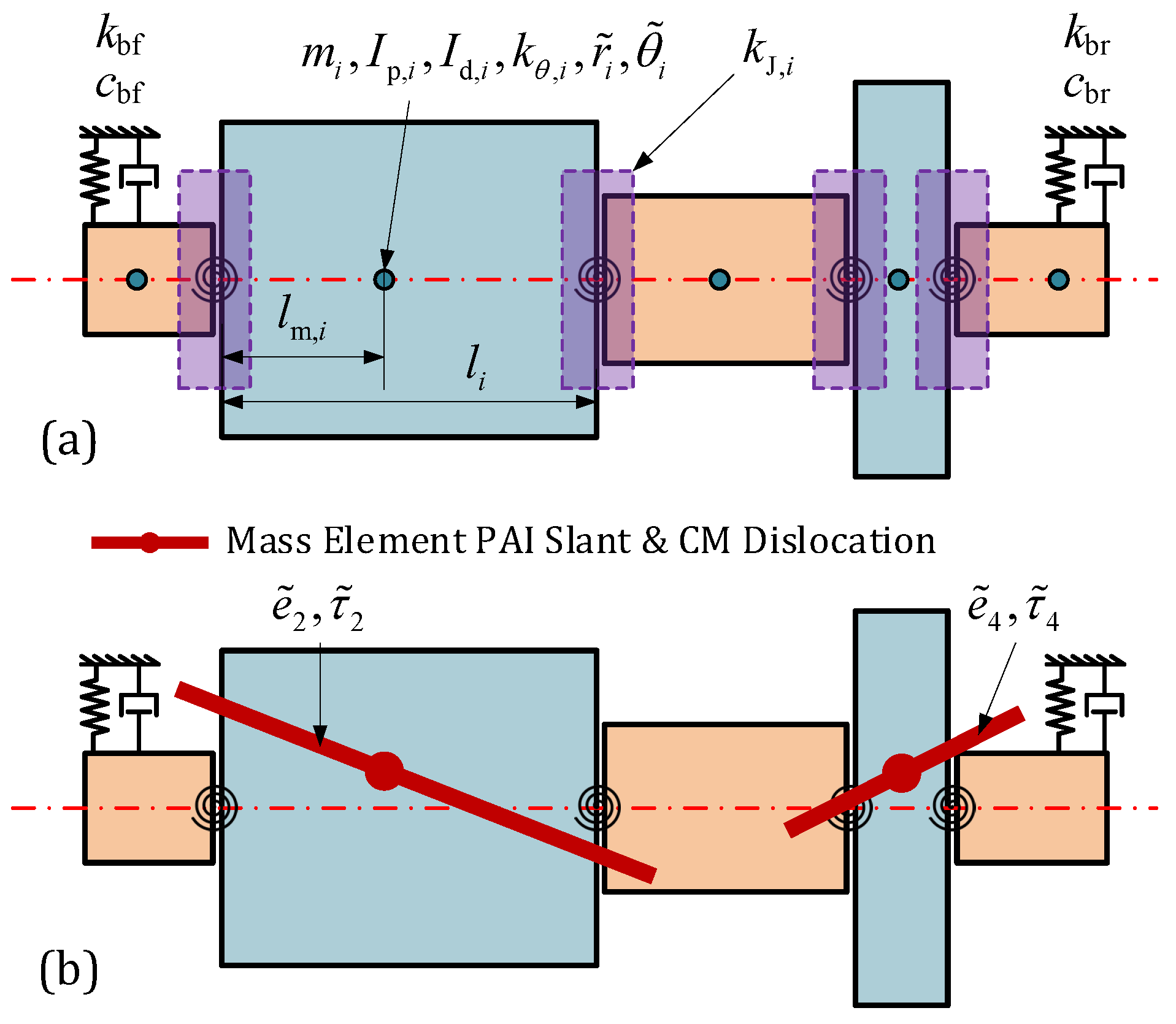
2.2. Description of the Rotational Inertia Load Distributed in the Rotor
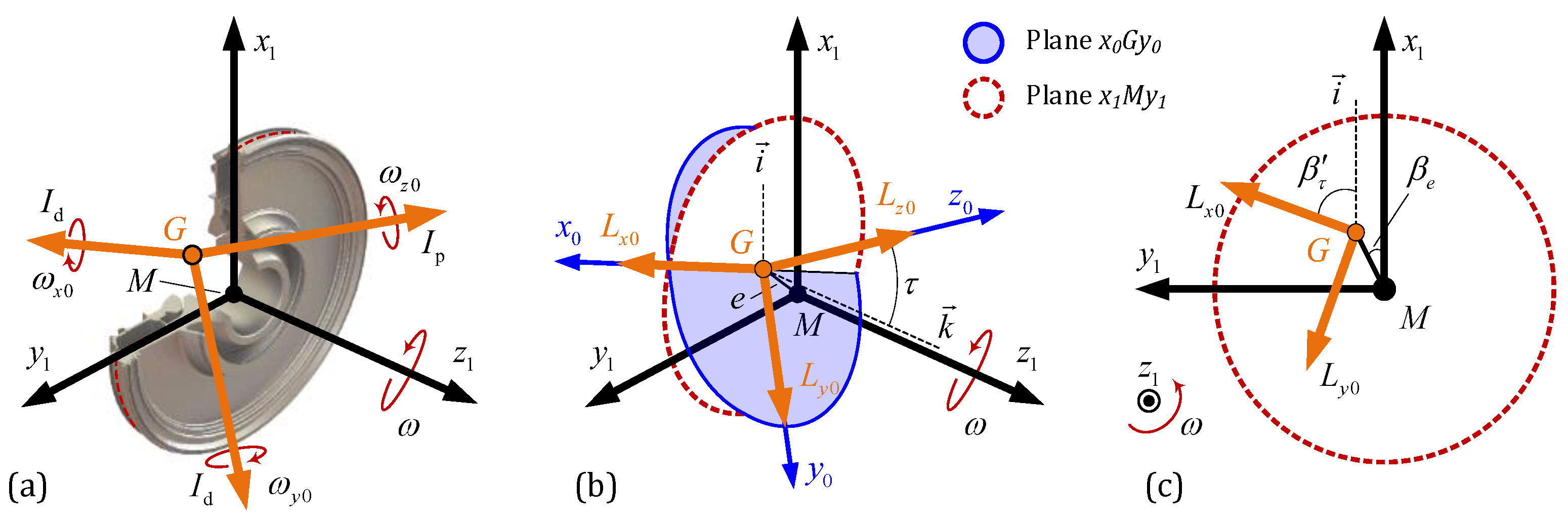
2.2.1. Description Method Based on PAI Slant and CM Offset
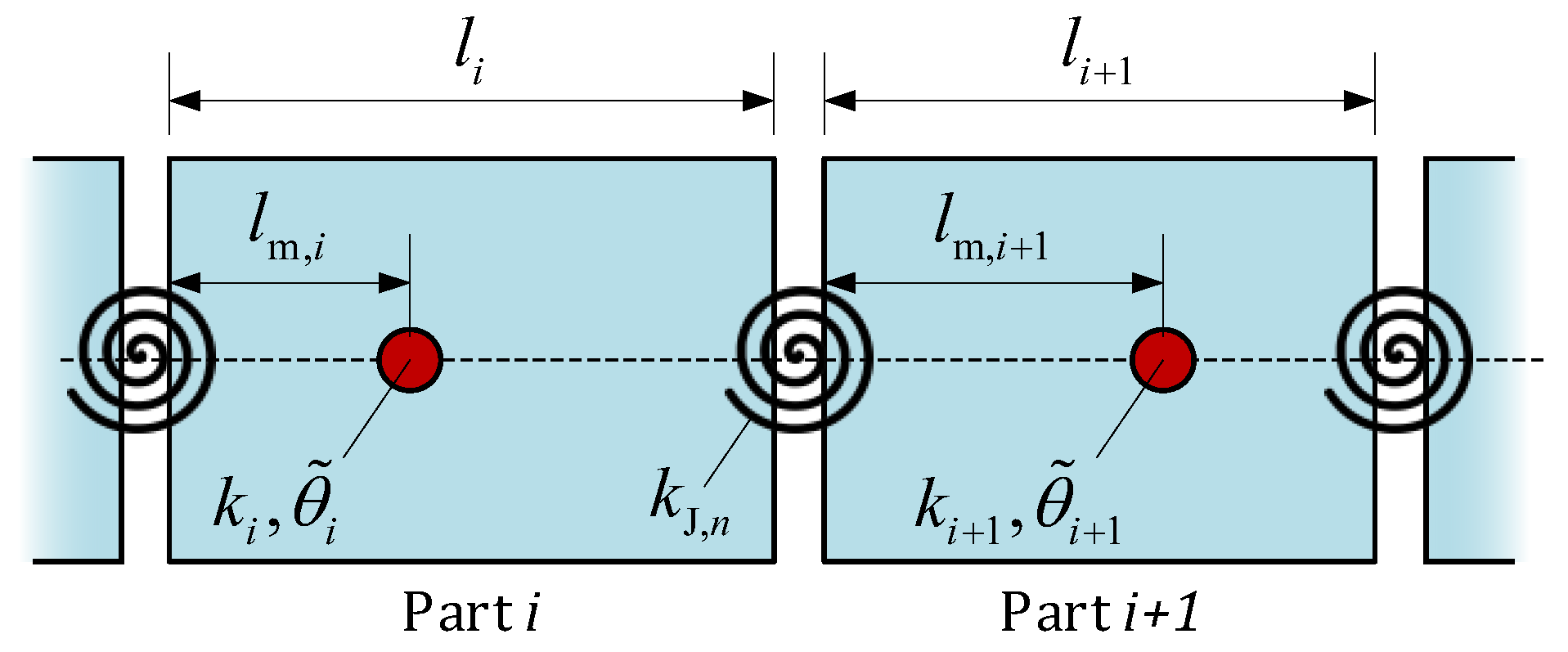
2.2.2. Axial Distribution of the Rotational Inertia Load of a Rotor
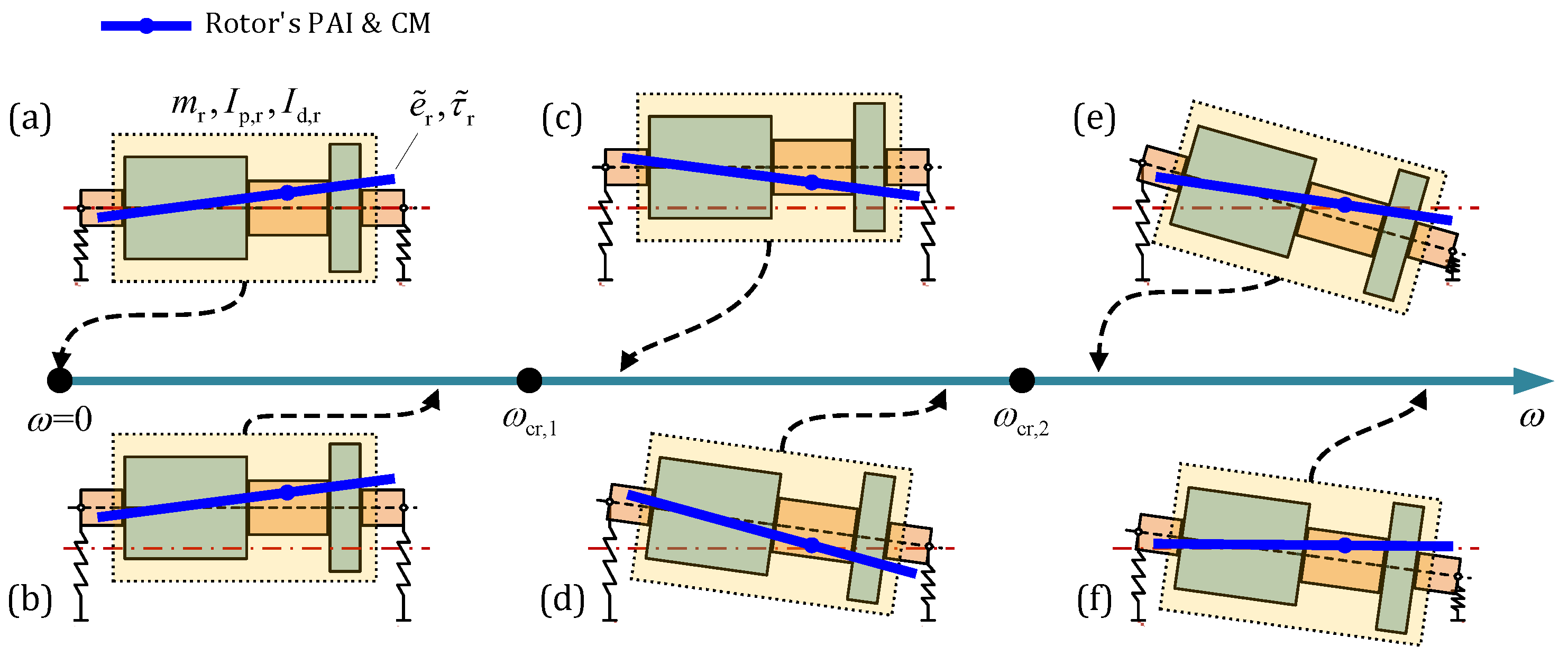
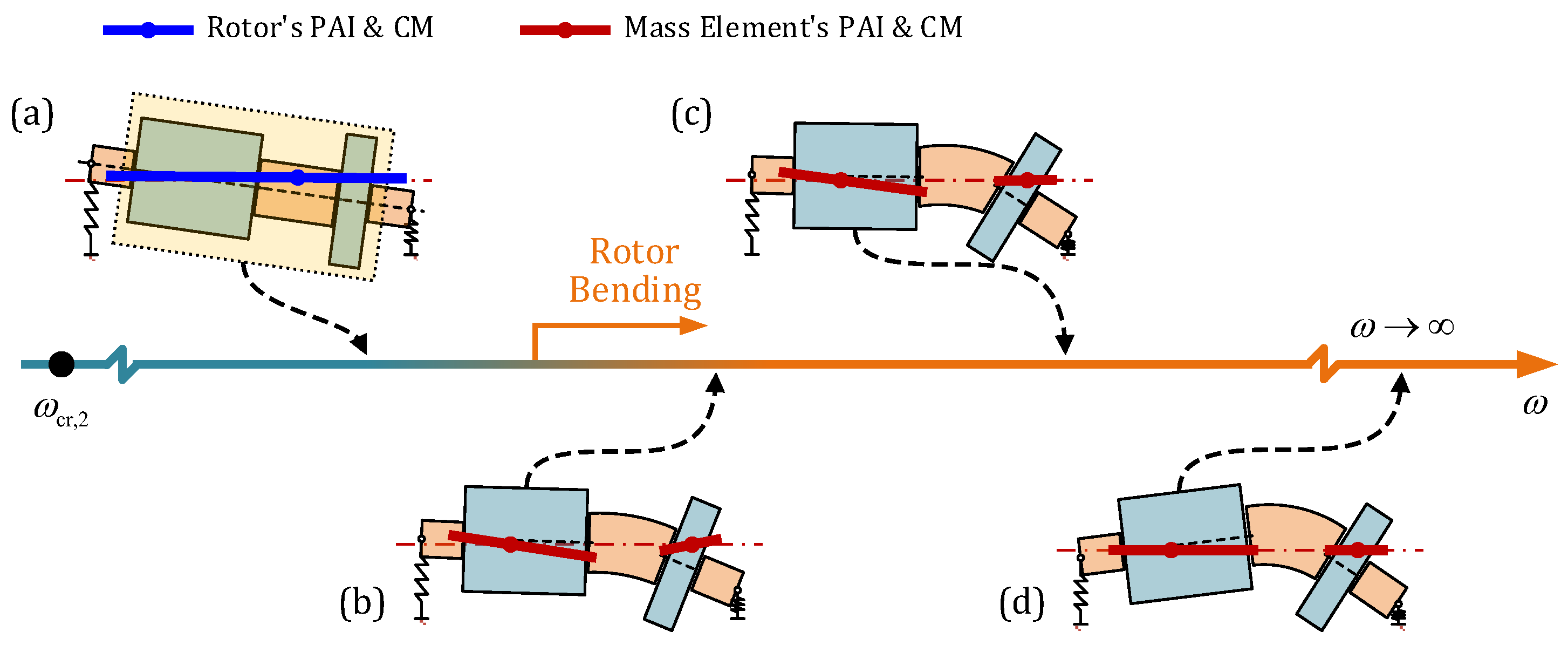
2.3. Influence of the Motion State of the Rotor
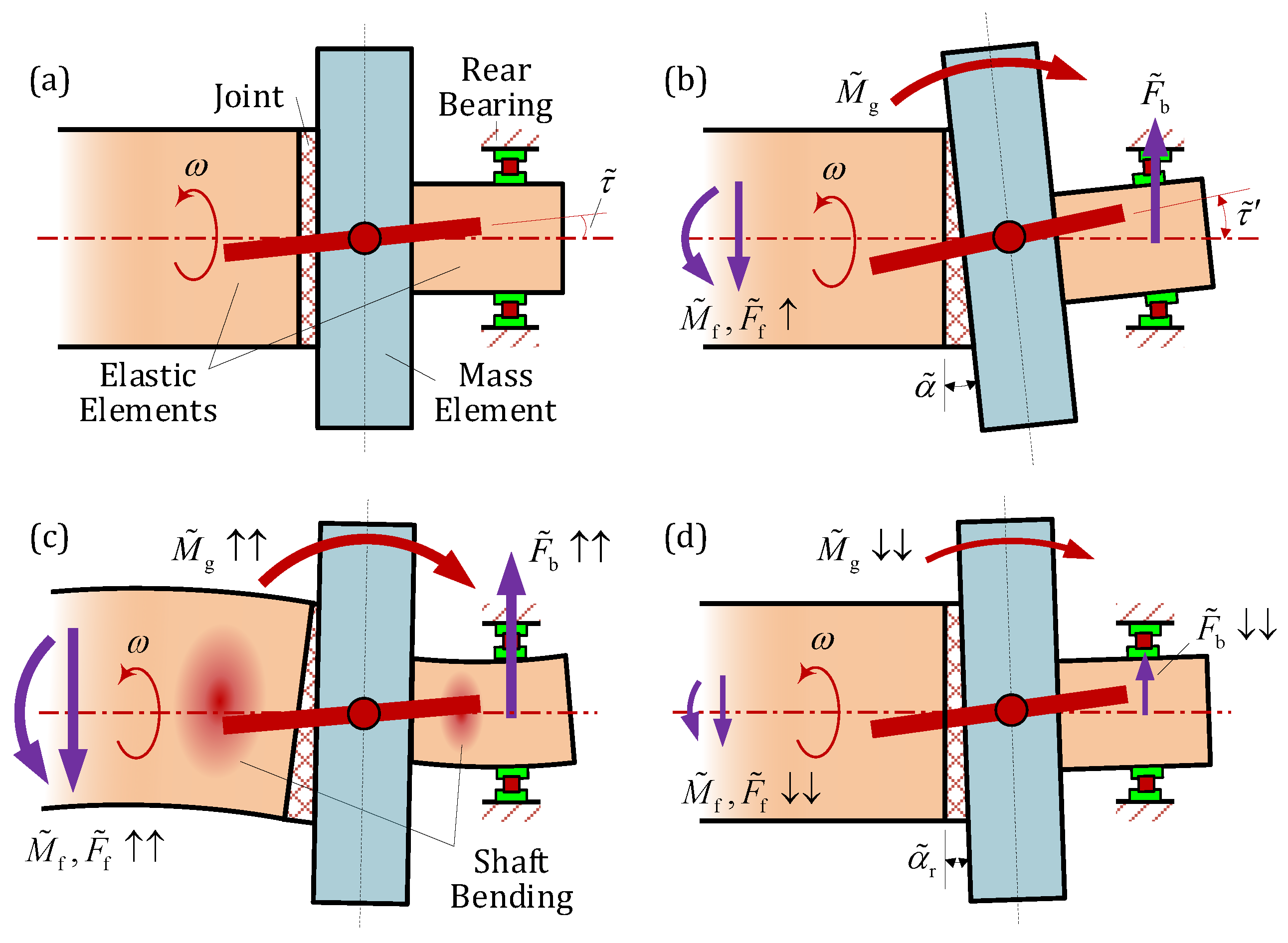
2.4. Influence of the Mechanical Characteristic of the Joints
2.4.1. Bending Stiffness Loss of the Joints
2.4.2. Sudden Angular Deformation
3. Dynamic Model for High-Speed Jointed Rotor System
3.1. Parameters of Rotor System
3.2. Rotor Motion Differential Equations Based on Lagrange’s Method
3.3. Mechanical Characteristics of Joints in the Dynamic Rotor Model
3.3.1. Bending Stiffness Loss of the Joints
3.3.2. Sudden Angular Deformation of the Joint
4. Simulation of High-Speed Jointed Rotor System
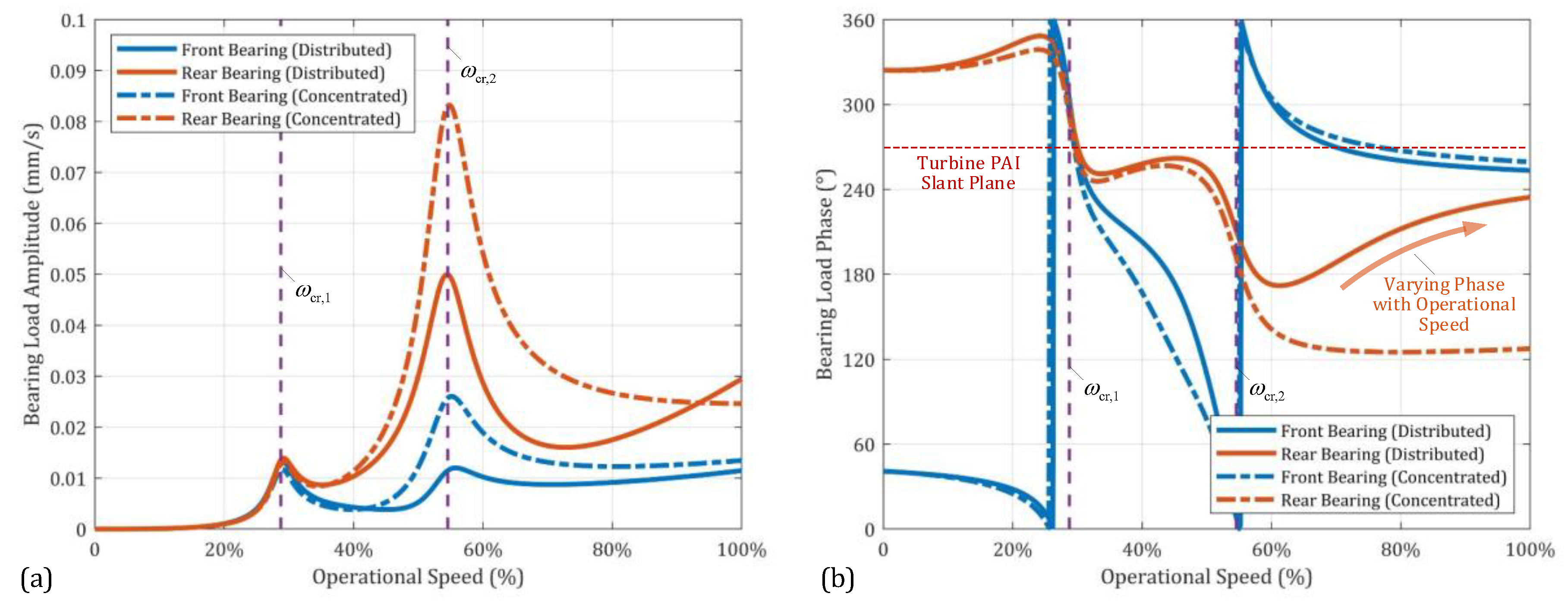
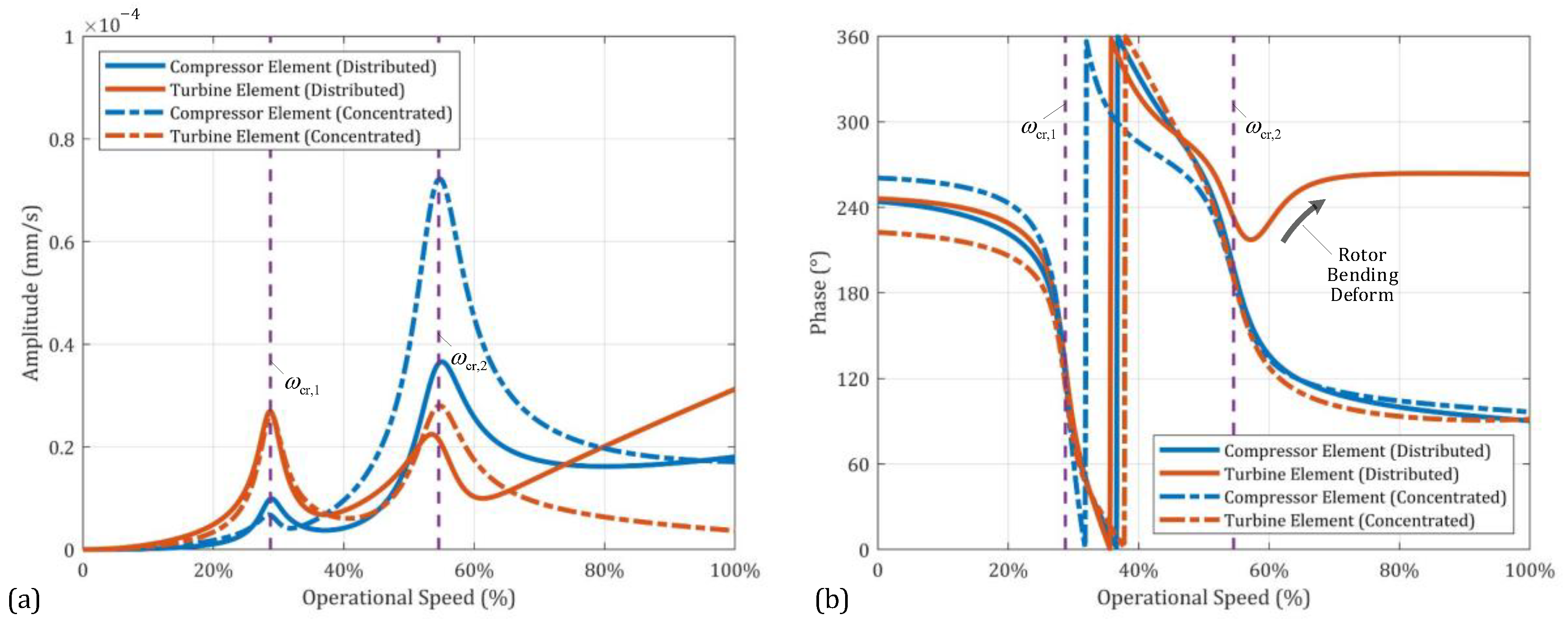
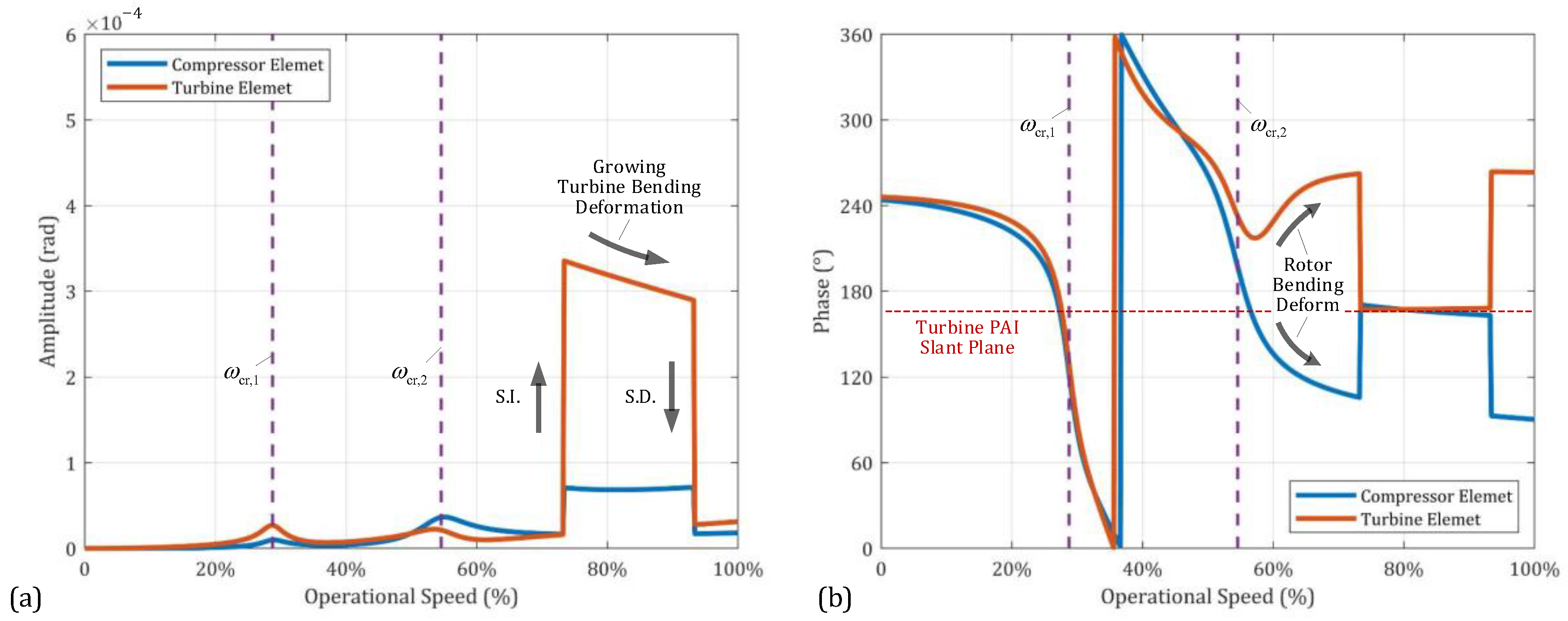
4.1. Rotor Dynamic Response with Different Excitation Model
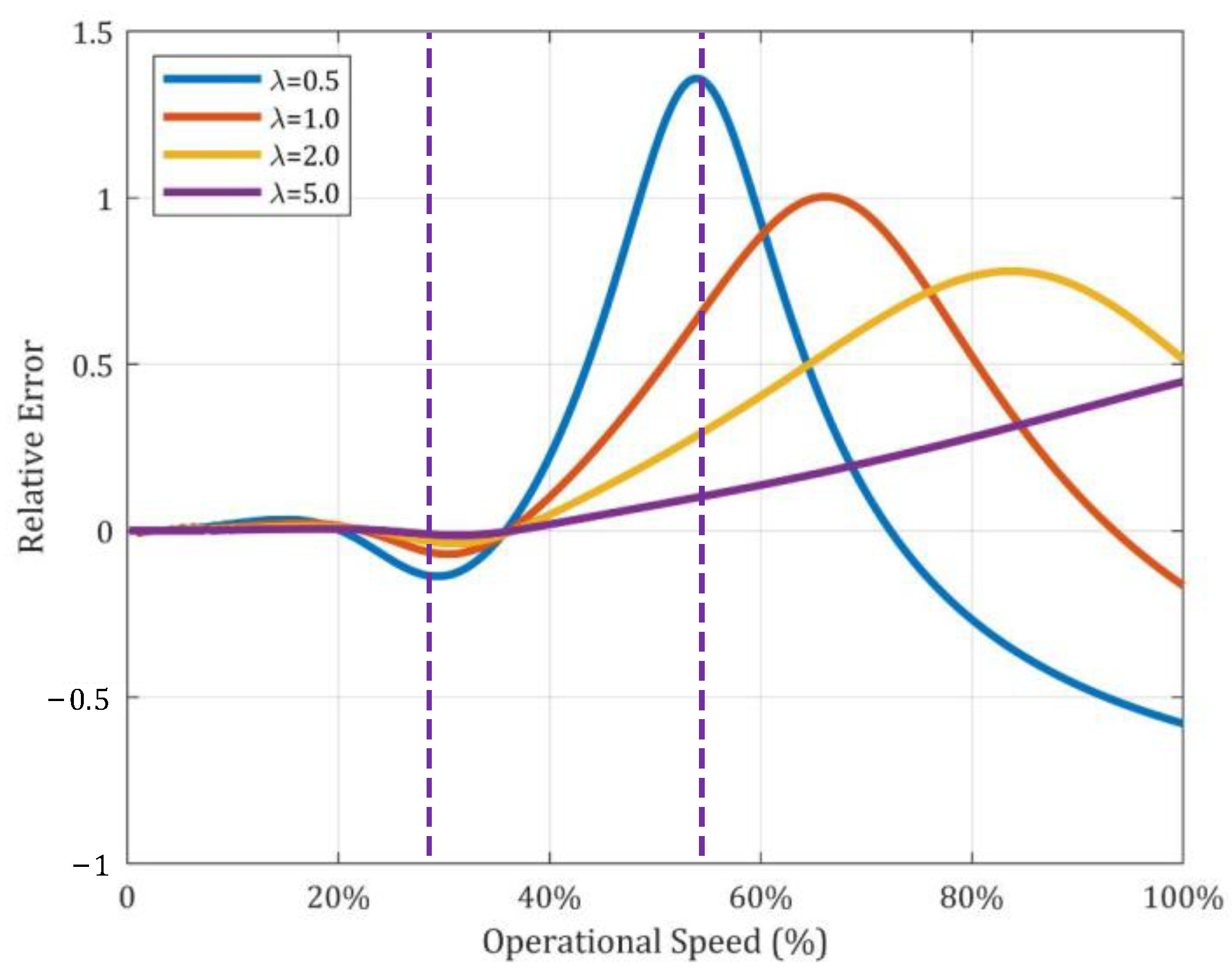
4.2. Impact of Joint Bending Stiffness on Rotor Dynamics
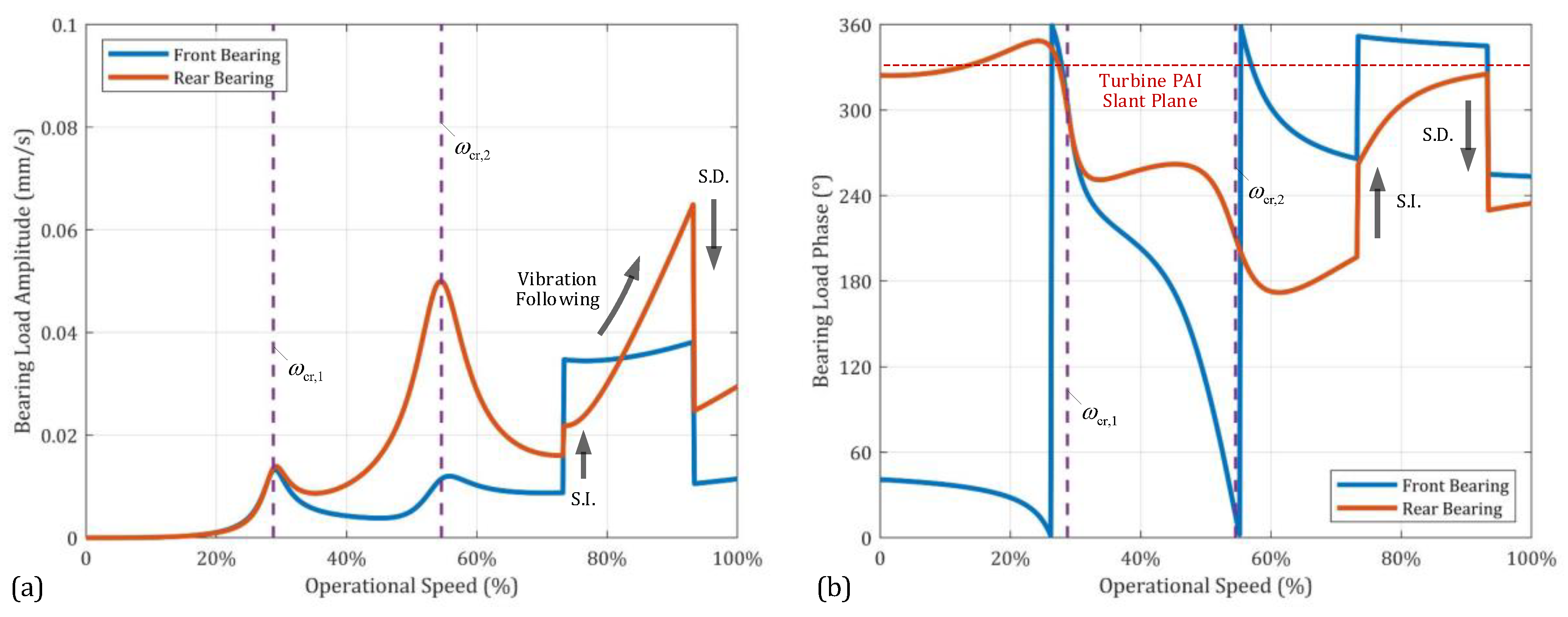
4.3. Impact of Joints’ Angular Deformation on Rotor Dynamics
5. Dynamic Experiment of High-Speed Jointed Rotor System
5.1. Experimental Facility and Test Method
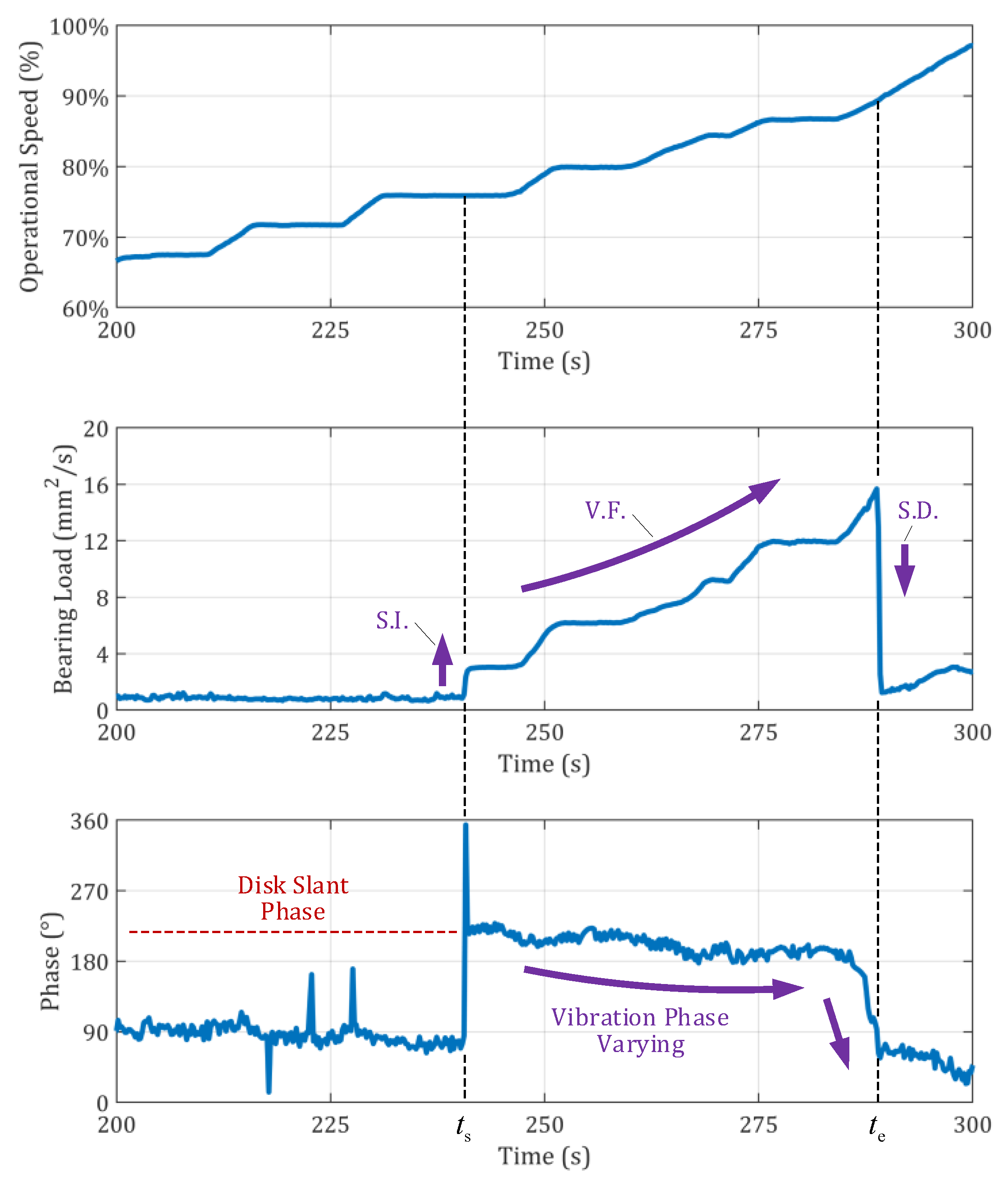
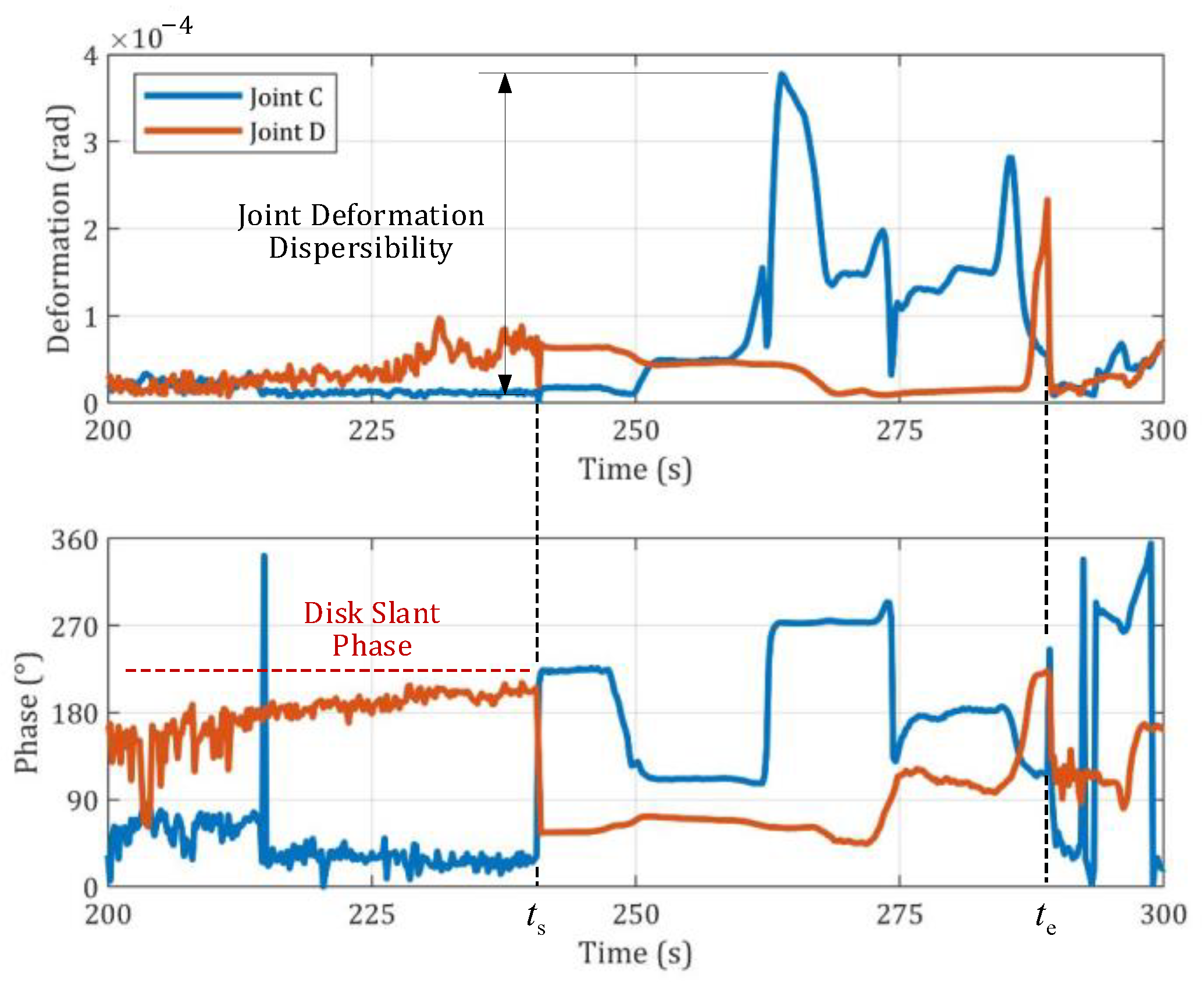
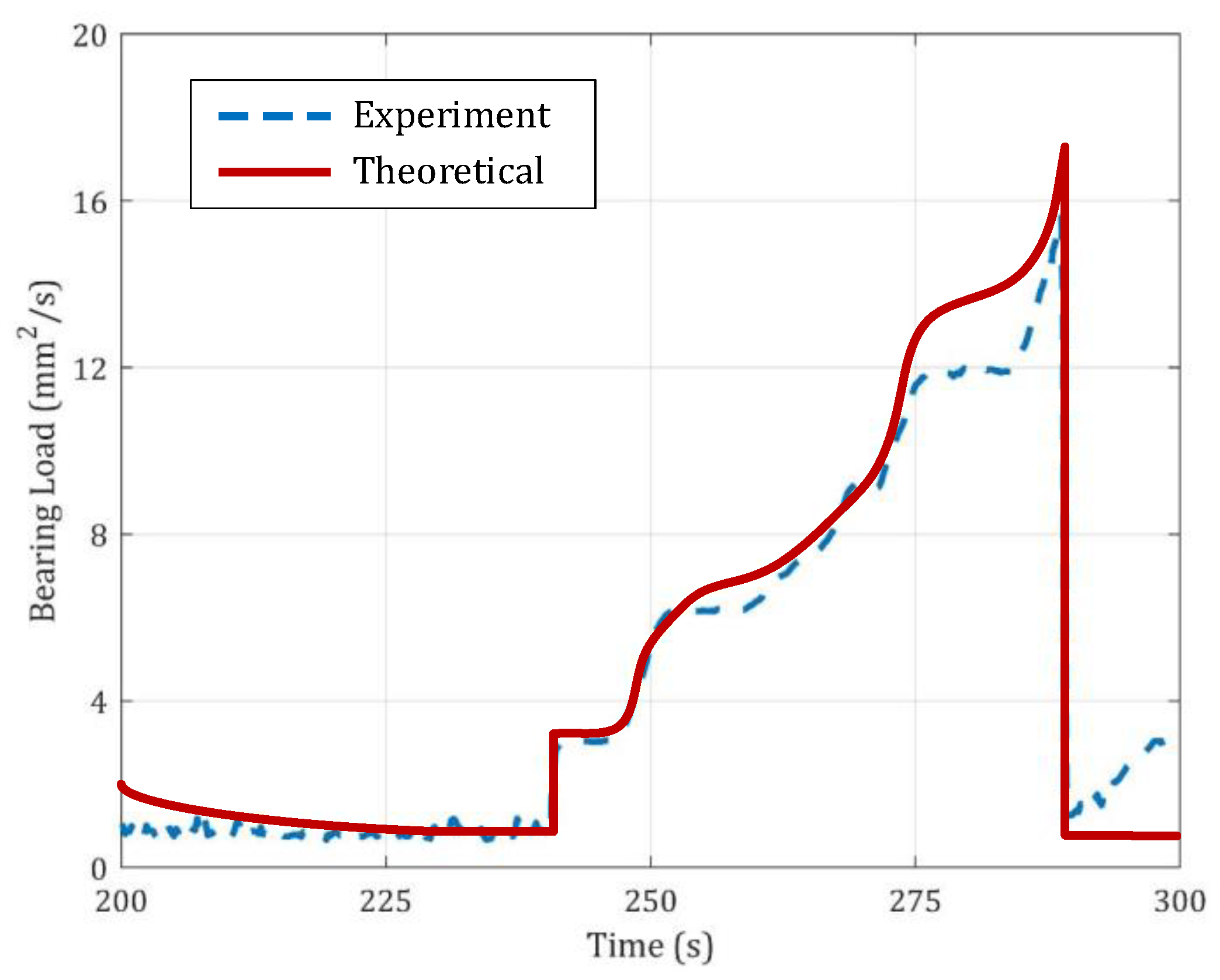
5.2. Rotor Dynamic Response and Joint Angular Deformation
6. Conclusions
- In the low-speed range, rotor bending deformation can be neglected, and the rotor can be approximated as a rigid body. The rotor’s CM offset and PAI slant dominate the whole rotor’s dynamic response. However, as the operational speed exceeds the first/second critical speeds, the influence of rotational inertia forces/moments caused by the whole rotor diminishes with increasing speed.
- In the high-speed range, local mass asymmetry, particularly in the thin-disk turbine element, becomes more evident. The rotational inertia moment generated by the turbine element rapidly increases with the operational speed, even in the supercritical state, becoming the primary excitation source for rotor dynamic response. Excessive PAI slant of the turbine element can lead to a continuous increase and potential over-scale of the rotor’s dynamic response.
- Bending stiffness loss in the joints between mass elements weakens the rotor’s integrity, intensifying the effect of the locally generated rotational inertia load and exacerbating the phenomenon of vibration following and dynamic response amplitude at high operational speeds.
- Under complex load environments, sudden angular deformation of the joints due to interfacial slip induces a sudden increase in angular displacement of surrounding mass elements, especially for the turbine element. The additional PAI slant of the turbine element causes a sudden increase in rotor dynamic response and vibration following. When the rotational inertia moment is significant enough to cause joint interface slip again, the angular deformation of the joints abruptly decreases, and the PAI of the turbine element returns to its original angular position, leading to a sudden drop in rotor dynamic response.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jeffcott, H.H. The lateral vibration of loaded shafts in the neighbourhood of a whirling speed—The effect of want of balance. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1919, 37, 304–314. [Google Scholar] [CrossRef]
- Rao, J.S. History of Rotating Machinery Dynamics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Smith, D.M. The motion of a rotor carried by a flexible shaft in flexible bearings. Proc. Roy. Soc. 1933, 142, 92–118. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; McGraw-Hill Book Company: New York, NY, USA, 1940. [Google Scholar]
- Timoshenko, S.P. Vibration Problems in Engineering; D. Van Nostrand Company Inc.: New York, NY, USA, 1955. [Google Scholar]
- Carnegie, W. Rotary inertia and gyroscopic effects in overhung shaft systems. Bull. Mech. Eng. Educ. 1964, 3, 191. [Google Scholar]
- Kikuchi, K. Analysis of unbalance vibration of rotating shaft system with many bearings and disks. Bull. JSME 1970, 13, 864–872. [Google Scholar] [CrossRef]
- Cruz, W.; Arzola, N.; Araque, O. Modeling and experimental validation of the vibration in an unbalance multi-stage rotor. J. Mech. Eng. Sci. 2019, 13, 5703–5716. [Google Scholar] [CrossRef]
- Datz, J.; Karimi, M.; Marburg, S. Effect of Uncertainty in the Balancing Weights on the Vibration Response of a High-Speed Rotor. J. Vib. Acoust. 2021, 143, 061002. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Chen, Y.S.; Li, H.L.; Hou, L. Reversible model-simplifying method for aero-engine rotor systems. J. Aerosp. Power 2016, 31, 57–64. [Google Scholar]
- Nicholas, J.C.; Gunter, E.J.; Allaire, P.E. Effect of residual shaft bow on unbalance response and balancing of a single mass flexible rotor—Part I: Unbalance response. J. Eng. Power. 1976, 98, 171–181. [Google Scholar] [CrossRef]
- Nicholas, J.C.; Gunter, E.J.; Allaire, P.E. Effect of Residual Shaft Bow on Unbalance Response and Balancing of a Single Mass Flexible Rotor—Part II: Balancing. J. Eng. Power. 1976, 98, 182–187. [Google Scholar] [CrossRef]
- Yanhong, M.A.; Haizhou, L.I.U.; Wangqun, D.E.N.G.; Hai, Y.A.N.G.; Jie, H.O.N.G. Vibration response analysis of rotor system with initial thermal deformation. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 227–233. [Google Scholar]
- Hong, J.; Yan, Q.; Sun, B.; Ma, Y. Vibration Failure Analysis of Multi-Disk High-Speed Rotor Based on Rotary Inertia Load Model. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Rotterdam, The Netherlands, 13–17 June 2022; Volume 86076. [Google Scholar]
- Ishida, Y.; Toshio, Y. Linear and Nonlinear Rotordynamics: A Modern Treatment with Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Liu, Y.; Liu, H.; Wang, N. Effects of typical machining errors on the nonlinear dynamic characteristics of rod-fastened rotor bearing system. J. Vib. Acoust. 2017, 139, 011004. [Google Scholar] [CrossRef]
- Han, Z.; Wang, D.; Wang, Y.; Hong, J.; Cheng, R. Dynamic effects of the initial skewness of the inertial principal axis on the rotor with bolted joint. Mech. Syst. Signal Process. 2023, 200, 110564. [Google Scholar] [CrossRef]
- Qin, Z.Y.; Han, Q.K.; Chu, F.L. Analytical model of bolted disk-drum joints and its application to dynamic analysis of jointed rotor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 228, 55808444. [Google Scholar] [CrossRef]
- Luan, Y.; Guan, Z.Q.; Cheng, G.D.; Liu, S. A simplified nonlinear dynamic model for the analysis of pipe structures with bolted flange joints. J. Sound Vib. 2012, 331, 325–344. [Google Scholar] [CrossRef]
- Zhuo, M.; Yang, L.H.; Yu, L. Contact Stiffness Calculation and Effects on Rotordynamic of Rod Fastened Rotor. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, Phoenix, AR, USA, 11–17 November 2016. [Google Scholar]
- Hong, J.; Chen, X.; Wang, Y.; Ma, Y. Optimization of dynamics of non-continuous rotor based on model of rotor stiffness. Mech. Syst. Signal Process. 2019, 131, 166–182. [Google Scholar] [CrossRef]
- Ma, Y.; Ni, Y.; Chen, X. Bending stiffness loss of rod-rabbet joints and its effect on vibration response of rotor systems. Acta Aeronaut. Astronaut. Sin. 2021, 42, 223861. [Google Scholar]
- Chen, X.; Ma, Y.; Hong, J. Vibration suppression of additional unbalance caused by the non-continuous characteristics of a typical aero-engine rotor. In International Conference on Rotor Dynamics; Springer: New York, NY, USA, 2018; pp. 34–48. [Google Scholar]
- Liu, S.; Ma, Y.; Zhang, D.; Hong, J. Studies on dynamic characteristics of the joint in the aero-engine rotor system. Mech. Syst. Signal Process. 2012, 29, 120–136. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Fan, B.W. Nonlinear dynamic properties of disk-bolt rotor with interfacial cutting faults on assembly surfaces. J. Vib. Control 2018, 24, 4369–4382. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Fan, B. Numerical analysis on the static–dynamic coupling influences of parallelism flaw in disc-rod rotor ball bearing system. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2018, 232, 103–112. [Google Scholar] [CrossRef]
- Barragan, J.M. Engine Vibration Monitoring and Diagnosis Based on On-Board Captured Data; MTU Aero Engines Gmbh Munich: Munich, Germany, 2003. [Google Scholar]
- Zhao, B.; Sun, Q.; Zhao, R.; Yang, Y.; Sun, K.; Mu, X. Mass-eccentricity nonlinear evolution mechanism of combined rotor in fretting slip process. Tribol. Int. 2023, 179, 108195. [Google Scholar] [CrossRef]
- Zhao, B.; Sun, Q.; Yang, Y.; Sun, K.; Liu, Z. Study on interface non-uniform slip of combined rotor considering real preload distribution. Tribol. Int. 2022, 169, 107482. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, D.; Zhu, X.; Hong, J. Study on the stiffness loss and the dynamic influence on rotor system of the bolted flange joint. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Dusseldorf, Germany, 16–20 June 2014; Volume 45769. [Google Scholar]
- Nizametdinov, F.R.; Romashin, Y.S.; Berne, A.L.; Leontyev, M.K. Investigation of bending stiffness of gas turbine engine rotor flanged connection. J. Mech. 2020, 36, 729–736. [Google Scholar] [CrossRef]
- Hong, J.; Xu, X.; Su, Z.; Ma, Y. Joint stiffness loss and vibration characteristics of high-speed rotor. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 18–25. [Google Scholar]
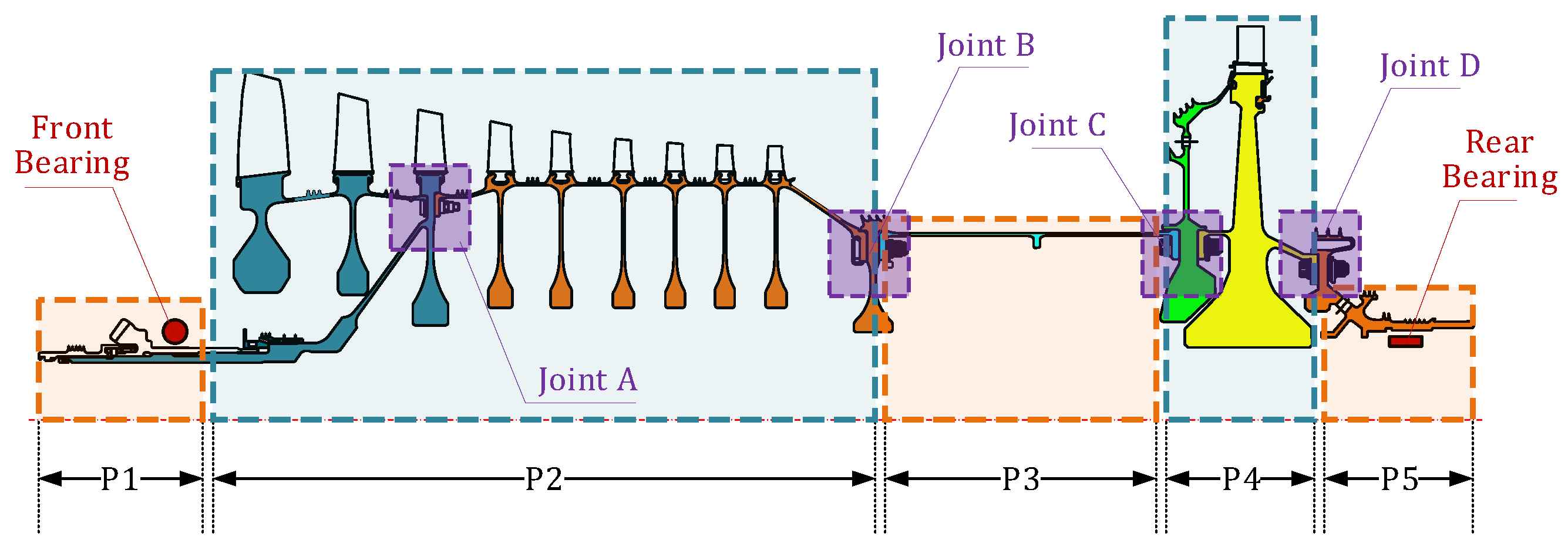
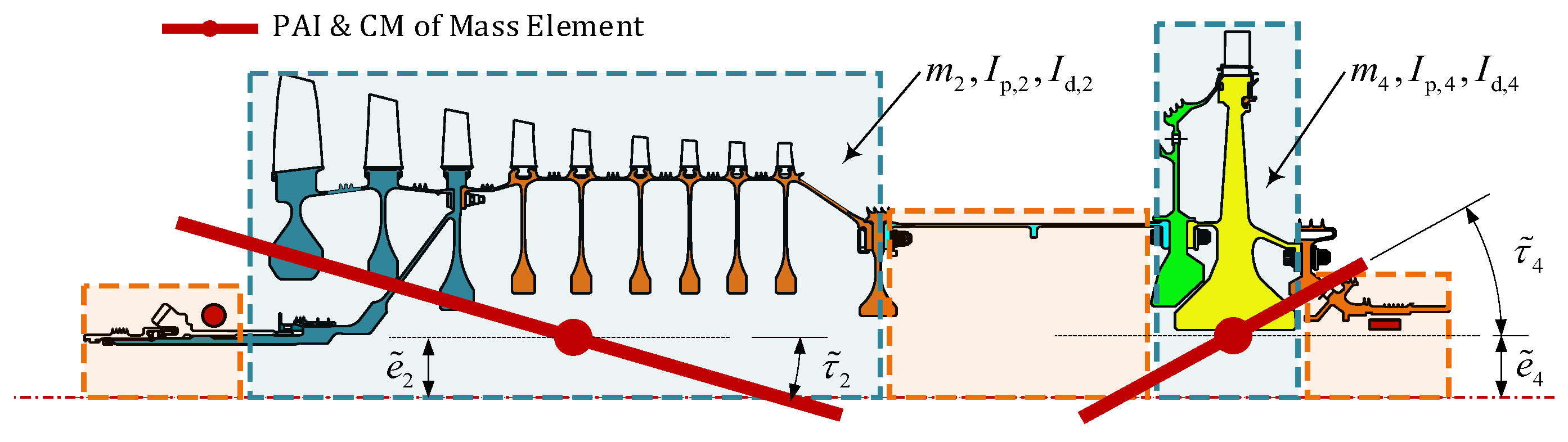




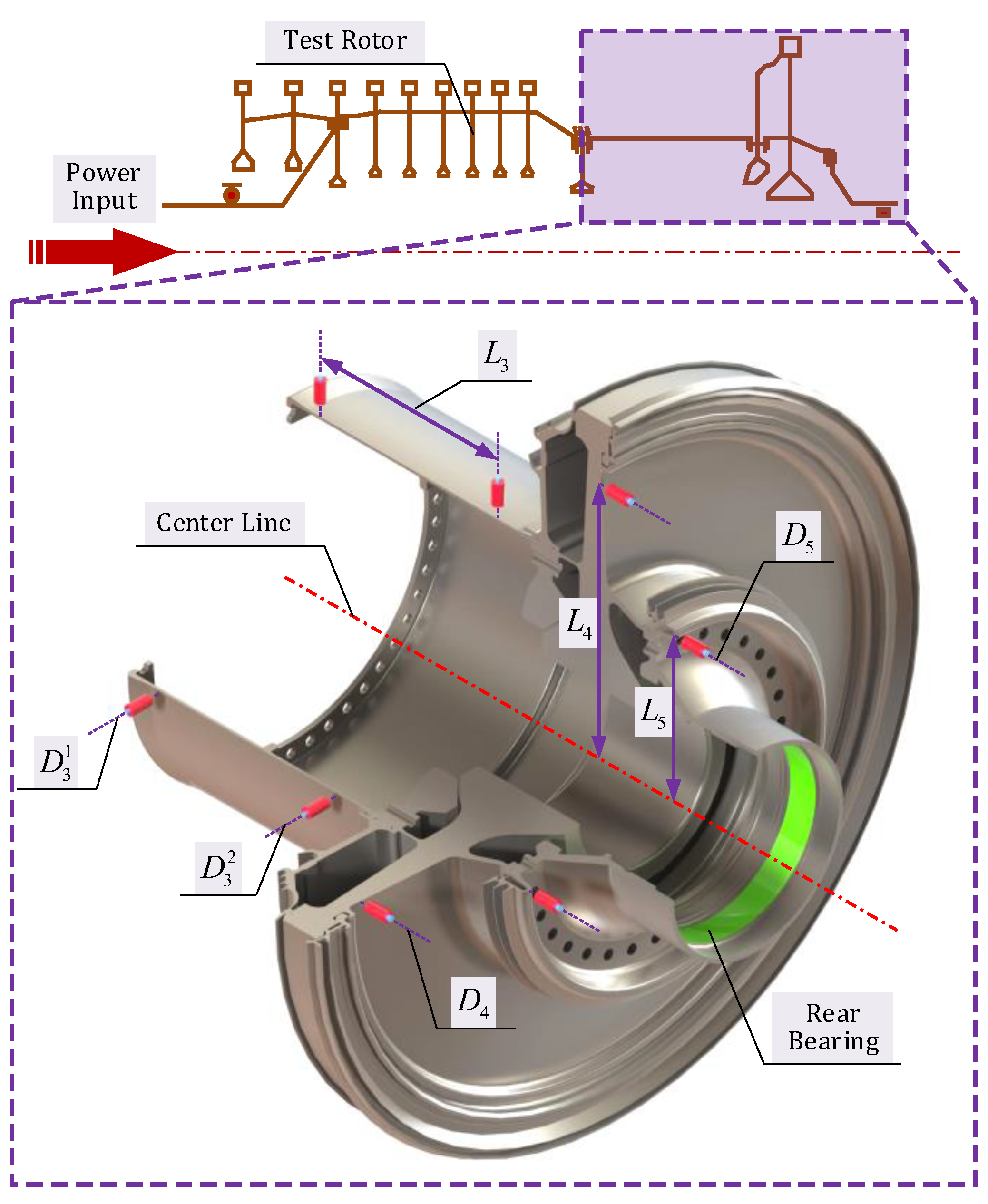
| Element ID | P1 | P2 | P3 | P4 | P5 | Rotor |
|---|---|---|---|---|---|---|
| (kg) | 10 | 100 | 10 | 100 | 10 | 230 |
| () | 7.0 × 104 | 3.5 × 106 | 1.5 × 105 | 5.5 × 106 | 1.5 × 105 | 9.4 × 106 |
| () | 7.8 × 105 | 4.7 × 106 | 1.2 × 105 | 2.8 × 106 | 8.3 × 104 | 2.8 × 107 |
| 0.09 | 0.74 | 1.26 | 1.94 | 1.80 | 0.33 | |
| () | 7.3 × 109 | 10.0 × 1010 | 2.6 × 109 | 10.0 × 1010 | 0.4 × 109 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Hong, J.; Chen, X. Distributed Rotational Inertia Load Excitation Model and Its Impact on High-Speed Jointed Rotor Dynamic Response. Symmetry 2023, 15, 2009. https://doi.org/10.3390/sym15112009
Wu F, Hong J, Chen X. Distributed Rotational Inertia Load Excitation Model and Its Impact on High-Speed Jointed Rotor Dynamic Response. Symmetry. 2023; 15(11):2009. https://doi.org/10.3390/sym15112009
Chicago/Turabian StyleWu, Fayong, Jie Hong, and Xueqi Chen. 2023. "Distributed Rotational Inertia Load Excitation Model and Its Impact on High-Speed Jointed Rotor Dynamic Response" Symmetry 15, no. 11: 2009. https://doi.org/10.3390/sym15112009
APA StyleWu, F., Hong, J., & Chen, X. (2023). Distributed Rotational Inertia Load Excitation Model and Its Impact on High-Speed Jointed Rotor Dynamic Response. Symmetry, 15(11), 2009. https://doi.org/10.3390/sym15112009







