Applications of First-Order Differential Subordination for Subfamilies of Analytic Functions Related to Symmetric Image Domains

Abstract

This paper presents a geometric approach to the problems in differential subordination theory. The necessary conditions for a function to be in various subfamilies of the class of starlike functions and the class of Carathéodory functions are studied, respectively. Further, several consequences of the findings are derived.

1. Introduction

Let $\mathbb{C}$ be the complex plane and $\mathbb{E}=\{z:z\in \mathbb{C}$ and $\left|z\right|<1\}$ be the open unit disk. Let $\mathcal{A}$ represent the collection of all analytic functions, u, defined on $\mathbb{E}$ and fulfill the criteria $u\left(0\right)=0$ and $u^{\prime }\left(0\right)-1=0$. Thus, each function, u, in class $\mathcal{A}$ has the following Taylor series expansion:

$$u\left(z\right)=z+\underset{n=2}{\sum ^{\infty }}{a}_n{z}^n,z\in \mathbb{E}.$$

(1)

The various subclasses of $\mathcal{A}$ have been studied intensively, for instance, Ref. [1]. Further, let $\mathcal{S}$ denote a subfamily of $\mathcal{A}$, whose members are univalent in unit disk $\mathbb{E}$. Let ${\mathcal{S}}^{\ast }\left(\alpha \right)$ and $\mathcal{C}\left(\alpha \right)$ be the subfamilies of $\mathcal{A}$ for $0\le \alpha <1$, where ${\mathcal{S}}^{\ast }\left(\alpha \right)$ represents starlike functions of order $\alpha$, and $\mathcal{C}\left(\alpha \right)$ represents convex functions of order $\alpha$. Analytically, these families are represented by

$${\mathcal{S}}^{\ast }\left(\alpha \right)=\left\{u\in \mathcal{A}:\mathrm{Re}\left(\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)>\alpha \right\},$$

and

$$\mathcal{C}\left(\alpha \right)=\left\{u\in \mathcal{A}:\mathrm{Re}\left(\frac{{\left(z{u}^{\prime }\left(z\right)\right)}^{\prime }}{u\left(z\right)}\right)>\alpha \right\}.$$

In particular, if $\alpha =0$, then we can observe that ${\mathcal{S}}^{\ast }\left(0\right)={\mathcal{S}}^{\ast }$ and $\mathcal{C}\left(0\right)=\mathcal{C}$ are well-known families of starlike functions and convex functions, respectively.

Moreover, for two functions, $u_1,u_2\in \mathcal{A}$, the expression $u_1\prec u_2$ denotes that the function $u_1$ is subordinate to the function $u_2$ if there exists an analytic function, $\mu$, with the following properties:

$$\left|\mu \left(z\right)\right|\le \left|z\right|\mathrm{and}\mu \left(0\right)=0$$

such that

$$u_1\left(z\right)=u_2\left(\mu \left(z\right)\right)\forall z\in \mathbb{E}.$$

In addition, if $u_2\in \mathcal{S}$, then the aforementioned conditions can be expressed as follows:

$$u_1\prec u_2\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{u}_1\left(0\right)=u_2\left(0\right)\mathrm{and}{u}_1\left(\mathbb{E}\right)\subset u_2\left(\mathbb{E}\right).$$

In 1992, Ma and Minda defined [2]

$${\mathcal{S}}^{\ast }\left(\varphi \right)=\left\{u\in \mathcal{A}:\frac{z{u}^{{}^{\prime }}\left(z\right)}{u\left(z\right)}\prec \varphi \left(z\right)\right\}$$

(2)

with $\mathrm{Re}\left(\varphi \right)>0$ in $\mathbb{E}$. Additionally, the function $\varphi$ maps $\mathbb{E}$ onto a star-shaped region, and the image domain is symmetric about the real axis and starlike with respect to $\varphi \left(0\right)=1$, with ${\varphi }^{{}^{\prime }}\left(0\right)>0$. The set ${\mathcal{S}}^{\ast }\left(\varphi \right)$ generalizes several subfamilies of the function class $\mathcal{A}$. Here are seven examples.

1. The class ${\mathcal{S}}^{\ast }[L,M]$ of Janowski starlike functions (see [3,4]) can be viewed by

$${\mathcal{S}}^{\ast }[L,M]={\mathcal{S}}^{\ast }\left(\frac{1+Lz}{1+Mz}\right),$$

where $-1\le M<L\le 1$ and $\varphi \left(z\right)=\frac{1+Lz}{1+Mz}$.

2. For $\varphi \left(z\right)=\sqrt{1+z},$ the family ${\mathcal{S}}_{\mathcal{L}}^{\ast }={\mathcal{S}}^{\ast }\left(\sqrt{1+z}\right)$ was established by Sokól et al. [5].

$3.$ For $\varphi \left(z\right)=1+sin\left(z\right),$ the class ${\mathcal{S}}_{sin}^{\ast }={\mathcal{S}}^{\ast }\left(1+sin\left(z\right)\right)$ was introduced and studied by Cho et al. [6].

$4.$ Considering the function $\varphi \left(z\right)=1+z-\frac{1}{3}{z}^3,$ we get the family ${\mathcal{S}}_{nep}^{\ast }={\mathcal{S}}^{\ast }\left(1+z-\frac{1}{3}{z}^3\right),$ which was introduced and investigated recently by Wani and Swaminathan [7]. The image of $\mathbb{E}$ under the function $\varphi \left(z\right)=1+z-\frac{1}{3}{z}^3$ is bounded by a nephroid-shaped region.

5. For $\varphi \left(z\right)=e^z,$ the class ${\mathcal{S}}_e^{\ast }={\mathcal{S}}^{\ast }\left(e^z\right)$ has been defined and studied by Mendiratta [8].

$6.$ Taking $\varphi \left(z\right)=z+\sqrt{1+z^2},$ we then get the family ${\mathcal{S}}_{cres}^{\ast }={\mathcal{S}}^{\ast }\left(z+\sqrt{1+z^2}\right),$ which maps $\mathbb{E}$ to a crescent-shaped region and was given by Raina et al. [9].

$7.$ The function $\varphi \left(z\right)=1+{sinh}^{-1}z$ gives the following class introduced by Kumar and Arora [10]:

$${\mathcal{S}}_{\rho }^{\ast }={\mathcal{S}}^{\ast }\left(1+{sinh}^{-1}z\right).$$

The natural extensions of differential inequalities on the real line into the complex plane are known as differential subordinations. Derivatives are an essential tool for understanding the properties of real-valued functions. Differential implications can be found in the complex plane when a function is described using differential subordinations. For example, Noshiro and Warschawski provided the univalency criteria for the analytical function theorem, which showed such differential implications. The range of the combination of the function’s derivatives is frequently used to determine the properties of a function.

Let h be an analytic function defined on $\mathbb{E}$, with $h\left(0\right)=1.$ Recently, Ali et al. [11] have investigated some differential subordination results. More specifically, they studied the following differential subordinations for some particular ranges of $\alpha .$

$$1+\frac{\alpha z{h}^{\prime }\left(z\right)}{h^n\left(z\right)}\prec \sqrt{1+z},n=0,1,2$$

which can ensure that

$$h\left(z\right)\prec \sqrt{1+z}.$$

Similar type results have been investigated by various authors. For example, the articles contributed by Kumar et al. [12,13], Paprocki et al. [14], Raza et al. [15] and Shi et al. [16].

In this paper, we consider the following two subfamilies of analytic functions.

$${\mathcal{S}}_{car}^{\ast }=\left\{u\in \mathcal{A}:\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\prec 1+z+\frac{z^2}{2}\right\}z\in \mathbb{E},$$

(3)

and

$${\mathcal{S}}_{3\mathcal{L}}^{\ast }=\left\{u\in \mathcal{A}:\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\prec 1+\frac{4z}{5}+\frac{z^4}{5}\right\}z\in \mathbb{E},$$

(4)

where the family defined in Equation (3) was introduced by Kumar and Kamaljeet [17], and the family defined in Equation (4) was introduced by Gandhi [18].

The lemma below underlies our considerations in the following sections.

Lemma 1.

[19] For the univalent function $q:\mathbb{E}\to \mathbb{C}$ and the analytic functions λ and v in $q\left(\mathbb{E}\right)\subseteq \mathbb{E}$ with $\lambda \left(z\right)\ne 0$ for $z\in q\left(\mathbb{E}\right),$ define

$$\mathsf{\Theta }\left(z\right)=z{q}^{\prime }\left(z\right)\lambda \left(q\left(z\right)\right)\mathit{and}g\left(z\right)=v\left(q\left(z\right)\right)+\mathsf{\Theta }\left(z\right),z\in \mathbb{E}.$$

 Suppose that

1.

$g\left(z\right)$ is convex, or $\mathsf{\Theta }\left(z\right)$ is starlike.

2.

$\mathrm{Re}\left(\frac{z{g}^{\prime }\left(z\right)}{\mathsf{\Theta }\left(z\right)}\right)>0,$$z\in \mathbb{E}$.

If $h\in \mathcal{S}$ with $h\left(0\right)=q\left(0\right),$$h\left(\mathbb{E}\right)\subset \mathbb{E},$ and

$$v\left(h\left(z\right)+z{h}^{\prime }\left(z\right)\lambda \left(h\left(z\right)\right)\right)\prec v\left(q\left(z\right)+z{q}^{\prime }\left(z\right)\lambda \left(q\left(z\right)\right)\right),$$

then $h\prec q,$ and q is the best dominant.

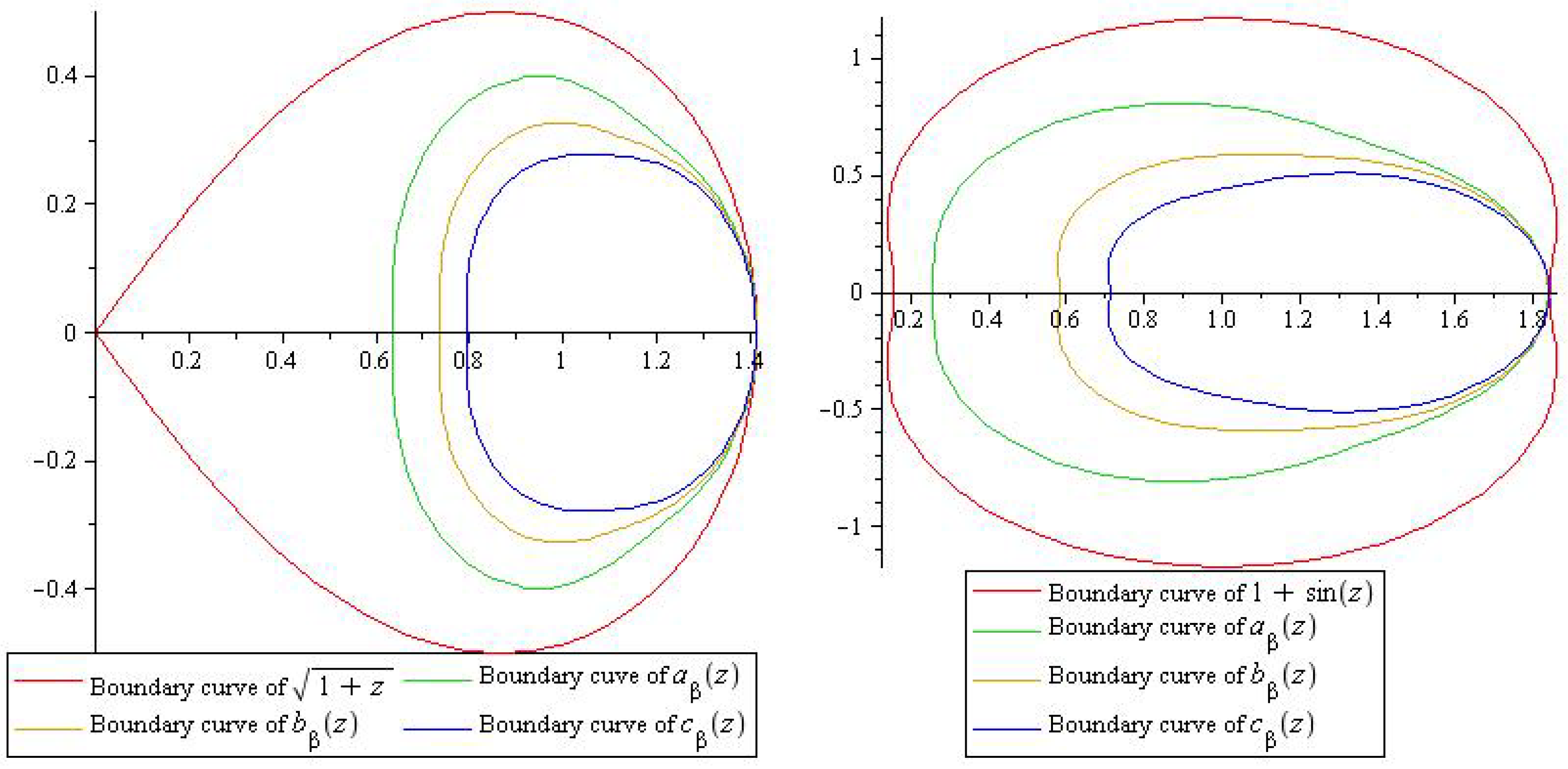
2. Subordination Results for the Class ${\mathcal{S}}_{car}^{\ast }$

Theorem 1.

Let h be an analytic function with $h\left(0\right)=1$ in the unit disc $\mathbb{E}$ and satisfy

$$1+\beta z{h}^{\prime }\left(z\right)\prec 1+z+\frac{z^2}{2}={\varphi }_{car}\left(z\right),z\in \mathbb{E}.$$

Then, we have the following.

1.

$h\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{5}{4\left(\sqrt{2}-1\right)}.$

2.

$h\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{5}{4sin\left(1\right)}.$

3.

$h\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{15}{8}.$

4.

$h\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{3}{4\left(1-e^{-1}\right)}.$

5.

$h\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{3}{4\left(2-\sqrt{2}\right)}.$

6.

$h\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{5}{4{sinh}^{-1}\left(1\right)}.$

Proof. 

Consider the analytic function

$$a_{\beta }\left(z\right)=1+\frac{4z+z^2}{4\beta },$$

which is a solution of the differential subordination equation

$$1+\beta z{h}^{\prime }\left(z\right)\prec 1+z+\frac{z^2}{2}.$$

Let us take $z\in \mathbb{E},$ $q\left(z\right)=a_{\beta }\left(z\right)$, $\nu \left(z\right)=1$, and $\lambda \left(z\right)=\beta$ in Lemma 1. Then, the function $\mathsf{\Theta }:\mathbb{E}\to \mathbb{C}$ is given by $\mathsf{\Theta }\left(z\right)=z{a}_{\beta }^{\prime }\left(z\right)\lambda \left(a_{\beta }\left(z\right)\right)={\varphi }_{car}\left(z\right)-1$, so $h\left(z\right)=1+\mathsf{\Theta }\left(z\right)={\varphi }_{car}\left(z\right)$. Since the function ${\varphi }_{car}\left(z\right)$ maps $\mathbb{E}$ into a starlike region (with respect to 1), the function h is starlike. Further, h satisfies $\mathrm{Re}\left(\frac{z{h}^{\prime }\left(z\right)}{\mathsf{\Theta }\left(z\right)}\right)>0.$ As an application to Lemma 1, we possess the following property:

$$1+\beta z{h}^{\prime }\left(z\right)\prec 1+\beta z{a}_{\beta }^{\prime }\left(z\right)\Rightarrow h\left(z\right)\prec a_{\beta }\left(z\right).$$

Each subordination of Theorem 1, is similar to

$$h\left(z\right)\prec \omega \left(z\right),$$

for each subordinate function in the theorem, which is valid if $a_{\beta }\left(z\right)\prec \omega \left(z\right)$, $z\in \mathbb{E}$. Then,

$$\omega \left(-1\right)\prec a_{\beta }\left(-1\right)\prec a_{\beta }\left(1\right)\prec \omega \left(1\right).$$

(5)

This yields the necessary condition for which $h\left(z\right)\prec \omega \left(z\right),$$z\in \mathbb{E}$. Looking at the geometry of each of these functions $\omega \left(z\right)$, it is noticed that the condition is also sufficient.

1. Let $\omega \left(z\right)=\sqrt{1+z},$ then

$$a_{\beta }\left(-1\right)\ge 0\mathrm{and}{a}_{\beta }\left(1\right)\le \sqrt{2},$$

and these inequalities can be reduced to $\beta \ge \frac{3}{4}={\beta }_1$ and $\beta \ge \frac{5}{4\left(\sqrt{2}-1\right)}={\beta }_2.$ We note that ${\beta }_1-{\beta }_2<0,$ and hence the following subordination holds.

$$a_{\beta }\left(z\right)\prec \sqrt{1+z},\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_2.$$

2. Let $\omega \left(z\right)=1+sin\left(z\right),$ then by (5),

$$\begin{array}{ccc}\hfill a_{\beta }\left(-1\right)& \ge & 1-sin\left(1\right),\mathrm{whenever}\beta \ge \frac{3}{4sin\left(1\right)}={\beta }_1.\hfill \\ \hfill a_{\beta }\left(1\right)& \le & 1+sin\left(1\right),\mathrm{whenever}\beta \ge \frac{5}{4sin\left(1\right)}={\beta }_2.\hfill \end{array}$$

Notice that ${\beta }_1-{\beta }_2<0.$ Thus, the following subordination holds.

$$a_{\beta }\left(z\right)\prec 1+sin\left(z\right),\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_2.$$

3. Let $\omega \left(z\right)=1+z-\frac{z^3}{3},$ then the inequality $a_{\beta }\left(-1\right)\ge \frac{1}{3}$ gives $\beta \ge {\beta }_1$ for ${\beta }_1=\frac{9}{8}$, and $a_{\beta }\left(1\right)\le \frac{5}{3}$ gives $\beta \ge {\beta }_2$ for ${\beta }_2=\frac{15}{8}.$ Moreover, since ${\beta }_1-{\beta }_2<0,$

$$a_{\beta }\left(z\right)\prec 1+z-\frac{z^3}{3},\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_2.$$

4. Let $\omega \left(z\right)=e^z,$ then

$$a_{\beta }\left(-1\right)\ge e^{-1}\mathrm{and}{a}_{\beta }\left(1\right)\le e,$$

and these two inequalities yield $\beta \ge \frac{3}{4\left(1-e^{-1}\right)}={\beta }_1$ and $\beta \ge \frac{5}{4\left(e-1\right)}={\beta }_2.$ Thus,

$$a_{\beta }\left(z\right)\prec \sqrt{1+z},\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_1.$$

5. Let $\omega \left(z\right)=z+\sqrt{1+z^2},$ then by Equation (5) $,$ we have

$$\begin{array}{ccc}\hfill a_{\beta }\left(-1\right)& \ge & -1+\sqrt{2},\mathrm{whenever}\beta \ge \frac{3}{4\left(2-\sqrt{2}\right)}={\beta }_1.\hfill \\ \hfill a_{\beta }\left(1\right)& \le & 1+\sqrt{2},\mathrm{whenever}\beta \ge \frac{5}{4\sqrt{2}}={\beta }_2.\hfill \end{array}$$

Therefore, the subordination $a_{\beta }\left(z\right)\prec z+\sqrt{1+z^2}$ holds if $\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_1$.

6. Let $\omega \left(z\right)=1+{sinh}^{-1}\left(z\right),$ then

$$a_{\beta }\left(-1\right)\ge 1-{sinh}^{-1}\left(1\right)\mathrm{and}{a}_{\beta }\left(1\right)\le 1+{sinh}^{-1}\left(1\right).$$

Thus, two inequalities above yield $\beta \ge \frac{3}{4{sinh}^{-1}\left(1\right)}={\beta }_1$ and $\beta \ge \frac{5}{4{sinh}^{-1}\left(1\right)}={\beta }_2,$ and hence

$$a_{\beta }\left(z\right)\prec 1+{sinh}^{-1}\left(z\right),\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_2.$$

□

Corollary 1.

Let $u\in \mathcal{A}$ that satisfies the following subordination:

$$\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\left(\frac{{\left(z{u}^{\prime }\left(z\right)\right)}^{\prime }}{u^{\prime }\left(z\right)}-\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)\prec \frac{2z+z^2}{2\beta }={\varphi }_{car}\left(z\right),z\in \mathbb{E}.$$

 Then, we have the following results.

1.

$u\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{5}{4\left(\sqrt{2}-1\right)}\approx 3.0178.$

2.

$u\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{5}{4sin\left(1\right)}\approx 1.4855.$

3.

$u\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{15}{8}\approx 1.875.$

4.

$u\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{3}{4\left(1-e^{-1}\right)}\approx 1.1865.$

5.

$u\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{3}{4\left(2-\sqrt{2}\right)}\approx 1.2803.$

6.

$u\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{5}{4{sinh}^{-1}\left(1\right)}\approx 1.4182.$

Theorem 2.

Let h be analytic with $h\left(0\right)=1$ in unit disc $\mathbb{E}$ and assume that

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec 1+z+\frac{z^2}{2}={\varphi }_{car}\left(z\right),z\in \mathbb{E}.$$

 Then, we have the following.

1.

$h\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{5}{4ln\left(\sqrt{2}\right)}.$

2.

$h\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{5}{4ln\left(1+sin\left(1\right)\right)}.$

3.

$h\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{5}{4ln\left(\frac{5}{3}\right)}.$

4.

$h\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{5}{4}.$

5.

$h\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{5}{4ln\left(1+\sqrt{2}\right)}.$

6.

$h\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{5}{4ln\left(1+{sinh}^{-1}\left(1\right)\right)}.$

Proof. 

Consider the analytic function $b_{\beta }:\mathbb{E}\to \mathbb{C}$, defined by

$$b_{\beta }\left(z\right)=exp\left(\frac{4z+z^2}{4\beta }\right),z\in \mathbb{E}.$$

Then, $b_{\beta }$ is a solution of the differential equation

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}=1+z+\frac{z^2}{2}={\varphi }_{car}\left(z\right),z\in \mathbb{E}.$$

If we take $z\in \mathbb{E},$ $q\left(z\right)=b_{\beta }\left(z\right)$, $\nu \left(z\right)=1$, and $\lambda \left(z\right)=\frac{\beta }{z}$ in Lemma 1, then the function $\mathsf{\Theta }:\mathbb{E}\to \mathbb{C}$ is given by $\mathsf{\Theta }\left(z\right)=z{b}_{\beta }^{\prime }\left(z\right)\lambda \left(b_{\beta }\left(z\right)\right)={\varphi }_{car}\left(z\right)-1$, so $h\left(z\right)=1+\mathsf{\Theta }\left(z\right)={\varphi }_{car}\left(z\right).$

Since the function ${\varphi }_{car}\left(z\right)$ maps $\mathbb{E}$ into a starlike region (w.r.to 1), the function h is starlike. Further, h satisfies $\mathrm{Re}\left(\frac{z{h}^{\prime }\left(z\right)}{\mathsf{\Theta }\left(z\right)}\right)>0.$ Applying this to Lemma 1, we possess that

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec 1+\beta \frac{z{b}_{\beta }^{\prime }\left(z\right)}{b_{\beta }\left(z\right)}\Rightarrow h\left(z\right)\prec b_{\beta }\left(z\right).$$

Each subordination of Theorem 1 is similar to

$$h\left(z\right)\prec \omega \left(z\right),$$

for each subordinate function in the theorem, which is valid if $b_{\beta }\left(z\right)\prec \omega \left(z\right),$ $z\in \mathbb{E}$. Here, we use the same technique as in Theorem 1, omitting the rest of the proof. □

Corollary 2.

Let $u\in \mathcal{A}$ that satisfies the following subordination:

$$\left(\frac{{\left(z{u}^{\prime }\left(z\right)\right)}^{\prime }}{u^{\prime }\left(z\right)}-\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)\prec \frac{2z}{2\beta }+\frac{z^2}{2\beta },z\in \mathbb{E}.$$

 Then, we have

1.

$u\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{5}{4ln\left(\sqrt{2}\right)}\approx 3.6067.$

2.

$u\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{5}{4ln\left(1+sin\left(1\right)\right)}\approx 2.0473.$

3.

$u\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{5}{4ln\left(\frac{5}{3}\right)}\approx 2.447.$

4.

$u\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{5}{4}\approx 1.25.$

5.

$u\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{5}{4ln\left(1+\sqrt{2}\right)}\approx 1.4182.$

6.

$u\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{5}{4ln\left(1+{sinh}^{-1}\left(1\right)\right)}\approx 1.9778.$

Theorem 3.

Let h be an analytic function with  $h\left(0\right)=1$ in unit disc $\mathbb{E}$ and satisfy that

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h^2\left(z\right)}\prec 1+z+\frac{z^2}{2}={\varphi }_{car}\left(z\right),z\in \mathbb{E}.$$

 Then, the following results.

1.

$h\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{5\sqrt{2}}{4\left(\sqrt{2}-1\right)}.$

2.

$h\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{5\left(1+sin\left(1\right)\right)}{4sin\left(1\right)}.$

3.

$h\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{25}{8}.$

4.

$h\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{5e}{4\left(e-1\right)}.$

5.

$h\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{5\left(1+\sqrt{2}\right)}{4\sqrt{2}}.$

6.

$h\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{5\left(1+{sinh}^{-1}\left(1\right)\right)}{4{sinh}^{-1}\left(1\right)}.$

Proof. 

Consider the function $c_{\beta }:\mathbb{E}\to \mathbb{C}$, defined by

$$c_{\beta }\left(z\right)={\left(1-\frac{4z+z^2}{4\beta }\right)}^{-1},$$

which is the solution of the differential equation:

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h^2\left(z\right)}=1+z+\frac{z^2}{2}={\varphi }_{car}\left(z\right).$$

In Lemma 1, let $z\in \mathbb{E},$ $q\left(z\right)=c_{\beta }\left(z\right)$, $\nu \left(z\right)=1$, and $\lambda \left(z\right)=\frac{\beta }{z^2}$. Then, the function $\mathsf{\Theta }:\mathbb{E}\to \mathbb{C}$ is given by $\mathsf{\Theta }\left(z\right)=z{c}_{\beta }^{\prime }\left(z\right)\lambda \left(c_{\beta }\left(z\right)\right)={\varphi }_{car}\left(z\right)-1$, so $h\left(z\right)=1+\mathsf{\Theta }\left(z\right)={\varphi }_{car}\left(z\right).$ Since the function ${\varphi }_{car}\left(z\right)$ maps $\mathbb{E}$ into a starlike region (w.r.to 1), the function h is starlike. Further, h satisfies $\mathrm{Re}\left(z{h}^{\prime }\left(z\right)/\mathsf{\Theta }\left(z\right)\right)>0.$ Therefore, from Lemma 1, we possess that

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec 1+\beta \frac{z{c}_{\beta }^{\prime }\left(z\right)}{c_{\beta }\left(z\right)}\Rightarrow h\left(z\right)\prec c_{\beta }\left(z\right).$$

Each subordination of Theorem 2 is similar to

$$h\left(z\right)\prec \omega \left(z\right),$$

for each subordinate function in the theorem, which is valid if $s_{\beta }\left(z\right)\prec \omega \left(z\right),$  $z\in \mathbb{E}$. Here, we use the same technique as we used in Theorem 1, so we omit the rest of the proof. □

Corollary 3.

Let $u\in \mathcal{A}$ that satisfies the following subordination:

$${\left(\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)}^{-1}\left(\frac{{\left(z{u}^{\prime }\left(z\right)\right)}^{\prime }}{u^{\prime }\left(z\right)}-\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)\prec \frac{2z}{2\beta }+\frac{z^2}{2\beta },z\in \mathbb{E}.$$

 Then, we have

1.

$u\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{5\sqrt{2}}{4\left(\sqrt{2}-1\right)}\approx 4.2678.$

2.

$u\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{5\left(1+sin\left(1\right)\right)}{4sin\left(1\right)}\approx 2.7355.$

3.

$u\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{25}{8}\approx 3.125.$

4.

$u\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{5e}{4\left(e-1\right)}.\approx 1.9775.$

5.

$u\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{5\left(1+\sqrt{2}\right)}{4\sqrt{2}}\approx 2.1339.$

6.

$u\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{5\left(1+{sinh}^{-1}\left(1\right)\right)}{4{sinh}^{-1}\left(1\right)}\approx 2.6682.$

At the end of Section 2, as a geometric approach to the problems in differential subordination theory, the following figures in Figure 1 graphically represent the results in the section.

Figure 1. Graphical Representation of Results in Section 2.

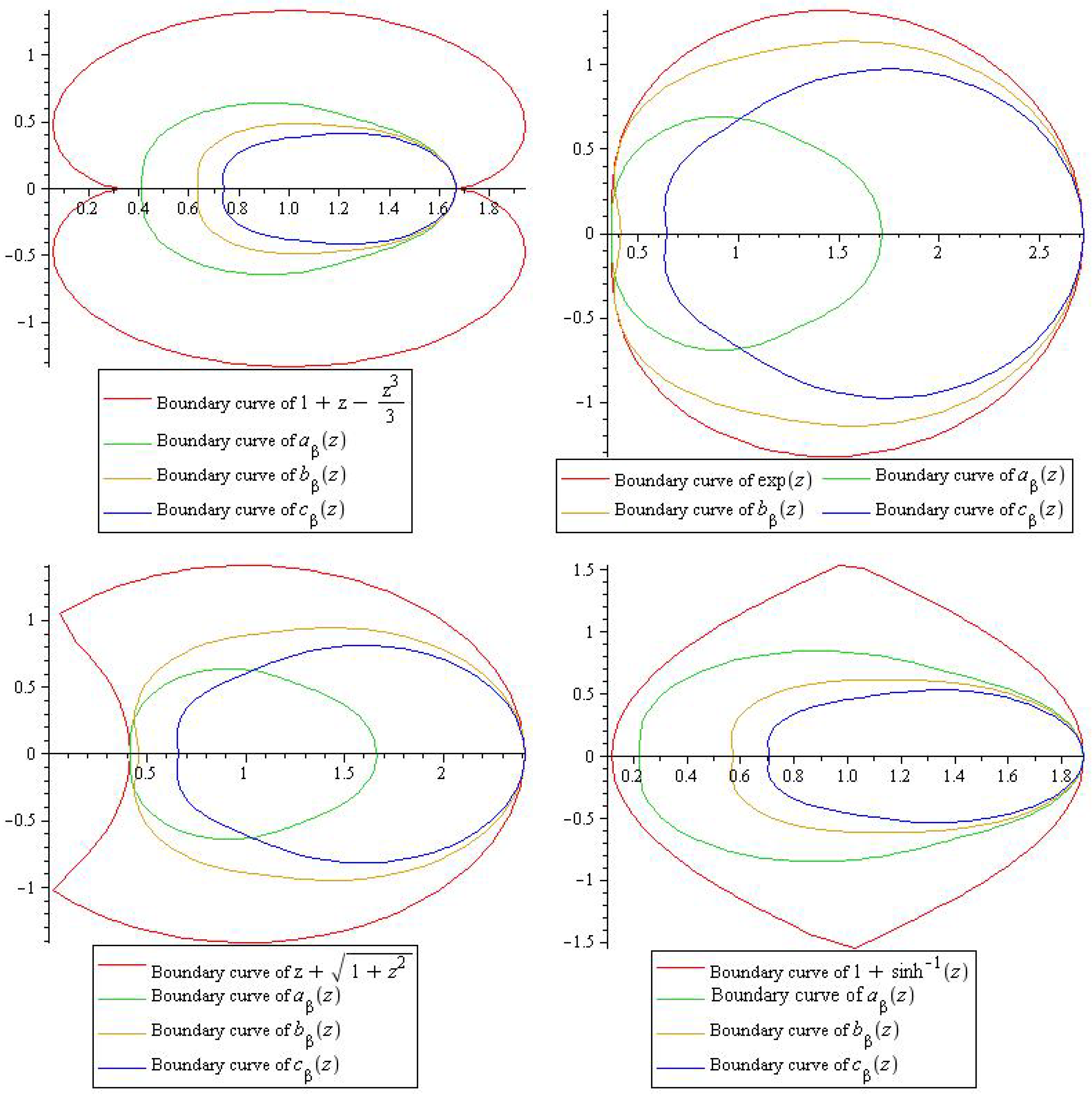
3. Subordination Results for Class ${\mathcal{S}}_{3\mathcal{L}}^{\ast }$

Theorem 4.

Let h be an analytic function with $h\left(0\right)=1$in unit disc$\mathbb{E}$ and satisfy that

$$1+\beta z{h}^{\prime }\left(z\right)\prec 1+\frac{4z}{5}+\frac{z^4}{5},z\in \mathbb{E}.$$

 Then, we have the following.

1.

$h\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{17}{20\left(\sqrt{2}-1\right)}.$

2.

$h\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{17}{20sin\left(1\right)}.$

3.

$h\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{51}{40}.$

4.

$h\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{15}{20\left(1-e^{-1}\right)}.$

5.

$h\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{15}{20\left(2-\sqrt{2}\right)}.$

6.

$h\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{17}{20{sinh}^{-1}\left(1\right)}.$

Proof. 

Consider the differential equation

$$1+\beta z{h}^{\prime }\left(z\right)=1+\frac{4z}{5}+\frac{z^4}{5}.$$

(6)

It is easy to verify that the analytic function $t_{\beta }:\mathbb{E}\to \mathbb{C}$, defined by

$$t_{\beta }\left(z\right)=1+\frac{16z+z^4}{20\beta },$$

is the solution of Equation (6) $.$ In Lemma 1, let $z\in \mathbb{E}$, $q\left(z\right)=t_{\beta }\left(z\right)$, $\nu \left(z\right)=1$, and $\lambda \left(z\right)=\beta$. Then, the function $\mathsf{\Theta }:\mathbb{E}\to \mathbb{C}$ is given by $\mathsf{\Theta }\left(z\right)=z{t}_{\beta }^{\prime }\left(z\right)\lambda \left(t_{\beta }\left(z\right)\right)={\varphi }_{car}\left(z\right)-1$, so $h\left(z\right)=1+\mathsf{\Theta }\left(z\right)={\varphi }_{car}\left(z\right).$ Since the function ${\varphi }_{car}\left(z\right)$ maps $\mathbb{E}$ into a starlike region (w.r.to 1), the function h is starlike. Further, h satisfies $\mathrm{Re}\left(z{h}^{\prime }\left(z\right)/\mathsf{\Theta }\left(z\right)\right)>0.$ It follows from Lemma 1 that

$$1+\beta z{h}^{\prime }\left(z\right)\prec 1+\beta z{t}_{\beta }^{\prime }\left(z\right)\Rightarrow h\left(z\right)\prec t_{\beta }\left(z\right).$$

Each subordination of Theorem 1 is similar to

$$h\left(z\right)\prec \omega \left(z\right),$$

for each subordinate function in the theorem, which is valid if $t_{\beta }\left(z\right)\prec \omega \left(z\right),$$z\in \mathbb{E}$. Then

$$\omega \left(-1\right)\prec t_{\beta }\left(-1\right)\prec t_{\beta }\left(1\right)\prec \omega \left(1\right).$$

(7)

This yields the necessary condition for which $h\left(z\right)\prec \omega \left(z\right),$$z\in \mathbb{E}$. Looking at each of these functions’ $\omega \left(z\right)$ geometry, it can be seen that this condition is also sufficient.

1. Let $\omega \left(z\right)=\sqrt{1+z},$ then

$$t_{\beta }\left(-1\right)\ge 0\mathrm{and}{t}_{\beta }\left(1\right)\le \sqrt{2},$$

and the above inequalities reduce to $\beta \ge \frac{15}{20}={\beta }_1$ and $\beta \ge \frac{17}{20\left(\sqrt{2}-1\right)}={\beta }_1.$ We note that ${\beta }_1-{\beta }_2<0.$ Thus,

$$t_{\beta }\left(z\right)\prec \sqrt{1+z},\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_2.$$

2. Let $\omega \left(z\right)=1+sin\left(z\right),$ then from Equation (5) we have

$$\begin{array}{ccc}\hfill t_{\beta }\left(-1\right)& \ge & 1-sin\left(1\right),\mathrm{whenever}\beta \ge \frac{15}{20sin\left(1\right)}={\beta }_1\hfill \\ \hfill t_{\beta }\left(1\right)& \le & 1+sin\left(1\right),\mathrm{whenever}\beta \ge \frac{17}{20sin\left(1\right)}={\beta }_2.\hfill \end{array}$$

We observe that ${\beta }_1-{\beta }_2<0.$ Therefore the subordination $t_{\beta }\left(z\right)\prec 1+sin\left(z\right)$ holds if $\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_2.$

3. Let $\omega \left(z\right)=1+z-\frac{z^3}{3},$ then the inequality $t_{\beta }\left(-1\right)\ge \frac{1}{3}$ gives $\beta \ge {\beta }_1,$ where ${\beta }_1=\frac{40}{45}$, and $t_{\beta }\left(1\right)\le \frac{5}{3}$ gives $\beta \ge {\beta }_2,$ where ${\beta }_2=\frac{51}{40}.$ Further, we note that ${\beta }_1-{\beta }_2<0.$ Therefore,

$$t_{\beta }\left(z\right)\prec 1+z-\frac{z^3}{3},\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_2.$$

4. Let $\omega \left(z\right)=e^z,$ then

$$t_{\beta }\left(-1\right)\ge e^{-1}\mathrm{and}{t}_{\beta }\left(1\right)\le e,$$

and these two inequalities yield to $\beta \ge \frac{15}{20\left(1-e^{-1}\right)}={\beta }_1$ and $\beta \ge \frac{17}{20\left(e-1\right)}={\beta }_2.$ Thus,

$$t_{\beta }\left(z\right)\prec e^z,\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_1.$$

5. Let $\omega \left(z\right)=z+\sqrt{1+z^2},$ then from Equation (5)

$$\begin{array}{ccc}\hfill t_{\beta }\left(-1\right)& \ge & -1+\sqrt{2},\mathrm{whenever}\beta \ge \frac{15}{20\left(2-\sqrt{2}\right)}={\beta }_1.\hfill \\ \hfill t_{\beta }\left(1\right)& \le & 1+\sqrt{2},\mathrm{whenever}\beta \ge \frac{17}{20\sqrt{2}}={\beta }_2.\hfill \end{array}$$

Therefore, the subordination $t_{\beta }\left(z\right)\prec z+\sqrt{1+z^2}$ holds if $\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_1,$ where ${\beta }_1-{\beta }_2<0.$

6. Let $\omega \left(z\right)=1+{sinh}^{-1}\left(z\right),$ then

$$t_{\beta }\left(-1\right)\ge 1-{sinh}^{-1}\left(1\right)\mathrm{and}{t}_{\beta }\left(1\right)\le 1+{sinh}^{-1}\left(1\right),$$

and these two inequalities yield $\beta \ge -\frac{15}{20{sinh}^{-1}\left(1\right)}={\beta }_1$ and $\beta \ge \frac{17}{20{sinh}^{-1}\left(1\right)}={\beta }_2.$ Thus,

$$t_{\beta }\left(z\right)\prec 1+{sinh}^{-1}\left(z\right),\mathrm{if}\beta \ge max\left\{{\beta }_1,{\beta }_2\right\}={\beta }_2.$$

□

Corollary 4.

Let $u\in \mathcal{A}$ that satisfies the following subordination:

$$\left(\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)\left(\frac{{\left(z{u}^{\prime }\left(z\right)\right)}^{\prime }}{u^{\prime }\left(z\right)}-\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)\prec \frac{4z}{5\beta }+\frac{z^4}{5\beta },z\in \mathbb{E}.$$

 Then,

• $u\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{17}{20\left(\sqrt{2}-1\right)}\approx 2.0521.$
• $u\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{17}{20sin\left(1\right)}\approx 1.0101.$
• $u\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{51}{40}\approx 1.275.$
• $u\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{15}{20\left(1-e^{-1}\right)}\approx 1.1865.$
• $u\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{15}{20\left(2-\sqrt{2}\right)}\approx 1.2803.$
• $u\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{17}{20{sinh}^{-1}\left(1\right)}\approx 0.9644.$

Theorem 5.

Let h be an analytic function with $h\left(0\right)=1$ in open unit disc $\mathbb{E}$ and satisfy that

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec 1+\frac{4z}{5}+\frac{z^4}{5},z\in \mathbb{E}.$$

 Then, we have the following results.

1.

$h\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{17}{20 ln\left(\sqrt{2}\right)}.$

2.

$h\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{17}{20 log\left(1+sin\left(1\right)\right)}.$

3.

$h\in {\mathcal{S}}_{neh}^{\ast },$ for $\beta \ge \frac{17}{20 log\left(\frac{5}{3}\right)}.$

4.

$h\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{17}{20}.$

5.

$h\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{17}{20 log\left(1+\sqrt{2}\right)}.$

6.

$h\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{17}{20 log\left(1+{sinh}^{-1}\left(1\right)\right)}.$

Proof. 

Consider the analytic function $s_{\beta }:\mathbb{E}\to \mathbb{C}$, defined by

$$s_{\beta }\left(z\right)=exp\left(\frac{16z+z^4}{20\beta }\right),z\in \mathbb{E}.$$

Then, $s_{\beta }$ is a solution of the differential equation:

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}=1+\frac{4z}{5}+\frac{z^4}{5},z\in \mathbb{E}.$$

Let $z\in \mathbb{E}$, $q\left(z\right)=s_{\beta }\left(z\right)$, $\nu \left(z\right)=1$, and $\lambda \left(z\right)=\frac{\beta }{z}$. Applying for Lemma 1, the function $\mathsf{\Theta }:\mathbb{E}\to \mathbb{C}$ is given by $\mathsf{\Theta }\left(z\right)=z{s}_{\beta }^{\prime }\left(z\right)\lambda \left(s_{\beta }\left(z\right)\right)={\varphi }_{car}\left(z\right)-1$, and so $h\left(z\right)=1+\mathsf{\Theta }\left(z\right)={\varphi }_{car}\left(z\right).$ Since the function ${\varphi }_{car}\left(z\right)$ maps $\mathbb{E}$ into a starlike region (w.r.to 1), the function h is starlike. Further, h satisfies $\mathrm{Re}\left(z{h}^{\prime }\left(z\right)/\mathsf{\Theta }\left(z\right)\right)>0.$ Applying Lemma 1, we possess that

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec 1+\beta \frac{z{s}_{\beta }^{\prime }\left(z\right)}{s_{\beta }\left(z\right)}\Rightarrow h\left(z\right)\prec {\widehat{s}}_{\beta }\left(z\right).$$

Each subordination of Theorem 1 is similar to

$$h\left(z\right)\prec \omega \left(z\right),$$

for each subordinate function in the theorem, which is valid if $s_{\beta }\left(z\right)\prec \omega \left(z\right),$ $z\in \mathbb{E}$. Here, we use the same technique as in Theorem 1, omitting the rest of the proof. □

Corollary 5.

Let $u\in \mathcal{A}$that satisfies the following subordination.

$$\left(\frac{{\left(z{u}^{\prime }\left(z\right)\right)}^{\prime }}{u^{\prime }\left(z\right)}-\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)\prec \frac{4z}{5\beta }+\frac{z^4}{5\beta },z\in \mathbb{E}.$$

 Then, we have

• $u\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{17}{20ln\left(2\right)}\approx 1.2263.$
• $u\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{17}{20log\left(1+sin\left(1\right)\right)}\approx 1.3922.$
• $u\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{17}{20log\left(\frac{5}{3}\right)}\approx 1.6640.$
• $u\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{17}{20}\approx 0.85.$
• $u\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{17}{20log\left(1+\sqrt{2}\right)}\approx 0.9644.$
• $u\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{17}{20log\left(1+{sinh}^{-1}\left(1\right)\right)}\approx 1.3449.$

Theorem 6.

Let h be an analytic function with $h\left(0\right)=1$ in unit disc $\mathbb{E}$ and satisfy that

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h^2\left(z\right)}\prec 1+\frac{4z}{5}+\frac{z^4}{5},z\in \mathbb{E}.$$

 Then, we have the following.

• $h\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{17\sqrt{2}}{20\left(\sqrt{2}-1\right)}.$
• $h\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{17\left(1+sin\left(1\right)\right)}{20sin\left(1\right)}.$
• $h\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{85}{40}.$
• $h\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{17e}{20\left(e-1\right)}.$
• $h\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{17\left(1+\sqrt{2}\right)}{20\sqrt{2}}.$
• $h\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{17\left(1+{sinh}^{-1}\left(1\right)\right)}{20{sinh}^{-1}\left(1\right)}.$

Proof. 

Consider the function $d_{\beta }:\mathbb{E}\to \mathbb{C}$, defined by

$$d_{\beta }\left(z\right)={\left(1-\frac{16z+z^4}{20\beta }\right)}^{-1},$$

which is the solution of the following differential equation.

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h^2\left(z\right)}=1+\frac{4z}{5}+\frac{z^4}{5}.$$

Let $z\in \mathbb{E},$ take $q\left(z\right)=d_{\beta }\left(z\right)$, $\nu \left(z\right)=1$, and $\lambda \left(z\right)=\frac{\beta }{z^2}$ in Lemma 1. Then, the function $\mathsf{\Theta }:\mathbb{E}\to \mathbb{C}$ is given by $\mathsf{\Theta }\left(z\right)=z{d}_{\beta }^{\prime }\left(z\right)\lambda \left(d_{\beta }\left(z\right)\right)={\varphi }_{car}\left(z\right)-1$, and so $h\left(z\right)=1+\mathsf{\Theta }\left(z\right)={\varphi }_{car}\left(z\right).$ Since the function ${\varphi }_{car}\left(z\right)$ maps $\mathbb{E}$ into a starlike region (with respect to 1), the function h is starlike. Further, h satisfies $\mathrm{Re}\left(z{h}^{\prime }\left(z\right)/\mathsf{\Theta }\left(z\right)\right)>0.$ Applying this to Lemma 1, we find that

$$1+\beta \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}\prec 1+\beta \frac{z{d}_{\beta }^{\prime }\left(z\right)}{d_{\beta }\left(z\right)}\Rightarrow h\left(z\right)\prec {\widehat{d}}_{\beta }\left(z\right).$$

Each subordination of Theorem 2 is similar to

$$h\left(z\right)\prec \omega \left(z\right),$$

for each subordinate function in the theorem, which is valid if $d_{\beta }\left(z\right)\prec \omega \left(z\right),$ $z\in \mathbb{E}$. Here, we use the same technique as in Theorem 1, omitting the rest of the proof. □

Corollary 6.

Let $u\in \mathcal{A}$ that satisfies the following subordination.

$${\left(\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)}^{-1}\left(\frac{{\left(z{u}^{\prime }\left(z\right)\right)}^{\prime }}{u^{\prime }\left(z\right)}-\frac{z{u}^{\prime }\left(z\right)}{u\left(z\right)}\right)\prec \frac{4z}{5\beta }+\frac{z^4}{5\beta },z\in \mathbb{E}.$$

 Then, we have the following results.

1.

$u\in {\mathcal{S}}_{\mathcal{L}}^{\ast },$ for $\beta \ge \frac{17\sqrt{2}}{20\left(\sqrt{2}-1\right)}\approx 2.9021.$

2.

$u\in {\mathcal{S}}_{sin}^{\ast },$ for $\beta \ge \frac{17\left(1+sin\left(1\right)\right)}{20sin\left(1\right)}\approx 1.8601.$

3.

$u\in {\mathcal{S}}_{nep}^{\ast },$ for $\beta \ge \frac{85}{40}\approx 2.125.$

4.

$u\in {\mathcal{S}}_{exp}^{\ast },$ for $\beta \ge \frac{17e}{20\left(e-1\right)}\approx 1.3447.$

5.

$u\in {\mathcal{S}}_{cres}^{\ast },$ for $\beta \ge \frac{17\left(1+\sqrt{2}\right)}{20\sqrt{2}}\approx 1.451.$

6.

$u\in {\mathcal{S}}_{\rho }^{\ast },$ for $\beta \ge \frac{17\left(1+{sinh}^{-1}\left(1\right)\right)}{20{sinh}^{-1}\left(1\right)}\approx 1.8144.$

We finish Section 3 with the following figures in Figure 2, graphically illustrating the results in this section.

Figure 2. Graphical Representation of Results in Section 3.

4. Conclusions

In this article, we have studied the first-order differential subordination for two symmetric image domains, namely the cardioid domain and the domain bounded by three leaf functions. Further, we examined some graphical interpretations of these results. Moreover, this concept can be extended to meromorphic, multivalent, and quantum calculus functions.