A Surface Pencil with Bertrand Curves as Joint Curvature Lines in Euclidean Three-Space

Abstract

The main outcome of this work is the construction of a surface pencil with a similarity to Bertrand curves in Euclidean 3-space ${\mathbb{E}}^3$. Then, by exploiting the Serret–Frenet frame, we deduce the sufficient and necessary conditions for a surface pencil with Bertrand curves as joint curvature lines. Consequently, the expansion to the ruled surface pencil is also designed. As demonstrations of our essential findings, we illustrate some models to emphasize the process.

1. Introduction

The curvature line is one of the most significant curves on a surface, and it plays a main role in differential geometry [1,2,3,4]. It is a helpful tool in surface examination for showing the dissimilarity of the principal direction. The harmonic principal curvature and curvature lines are also significant features on regular surfaces. The curvature line can guide the investigation of surfaces, and it has been applied in geometric design, shape recognition, surface polygonization, and surface accomplishment. For instance, Martin [5] systematically inspected surface patches confined by curvature lines, which are called principal patches. Furthermore, he showed that the presence of such patches depended on the corresponding confirmed situation and the corresponding frame situations along the patch border curves. Alourdas et al. [6] addressed a mode for initializing a net of curvature lines on a B-spline surface. Maekawa et al. [7] proposed a technique to leverage the common advantages of free-shape parametric surfaces for form analysis. Also, they investigated the common advantages of the umbilic and attitude curvature lines that pass through the umbilici on a parametric free-shape surface. Che and Paul [8] expanded a style to resolve and calculate the curvature lines and their geometric features specified on an implicit surface. Moreover, they proposed a new standard for non-umbilical and umbilical points on an implicit surface. Zhang et al. [9] demonstrated a planner for calculating and visualizing the curvature lines defined on an implicit surface. Kalogerakis et al. [10] determined a powerful substructure for initializing curvature lines from point clouds. Their approach is applicable to surfaces of random genus, with or without boundaries, and is statistically robust to noise and outliers while preserving serious surface characteristics. They demonstrated the approach to be efficient over a range of synthetic and real-world input datasets with varying amounts of noise and outliers.

However, crucial work has also focused on the reverse issue: given a 3D curve, how can we locate those surfaces that are to be interfaced with this curve as a distinctive curve, if possible, rather than locating and furnishing curves on analytical curved surfaces? Wang et al. [11] were the first to address the issue of assembling a surface pencil with a designated locative geodesic curve, through which every surface can be a candidate for mode style. They demonstrated the necessary and sufficient conditions for the coefficients to be satisfied by both the iso-parametric and geodesic demands. A variety of studies have investigated the issue of surface pencils with distinctive curves [12,13,14,15,16,17,18,19,20,21,22,23,24]. The similarity among curves is a popular topic in curve theory. The Bertrand curve is one of the traditional private curves. If there is a linear consanguinity among the principal normal vectors of two curves at their matching points, the two curves are considered a Bertrand pair [1,2]. The Bertrand curve can be investigated as the popularization of the helix. Bertrand curves are characteristic examples of offset curves, which are used in computer-aided manufacturing (CAM) and computer-aided design (CAD) (see [25,26,27,28,29]). Nevertheless, to the best of our knowledge, no work has been conducted on establishing surface bundle pairs with Bertrand pairs as principal curves in Euclidean 3-space ${\mathbb{E}}^3$. This work aims to fill this gap.

The major advantage of this work is the establishment of a surface pencil pair from a given Bertrand pair. Hence, the sufficient and necessary conditions for the specified Bertrand pair to be the principal curves are specified in detail. As an implementation, some interesting Bertrand pairs are chosen to create their corresponding surface pencil pairs that have such Bertrand pairs as principal curves. We extended the study to ruled surface pencil pairs.

2. Preliminaries

To provide a foundation for the next section, here, the primary constituents of the theory of curves in the Euclidean 3-space ${\mathbb{E}}^3$ are briefly specified [1,2]. Consider the Serret–Frenet apparatus ${\mathit{\varsigma }}_1\left(u\right),{\mathit{\varsigma }}_2\left(u\right),{\mathit{\varsigma }}_3\left(u\right);$ $\kappa \left(u\right),\tau \left(u\right)\}$ related to the unit speed curve $\mathit{\omega }\left(u\right)$. Then, the Serret–Frenet formulae is expressed as follows:

$$\left(\begin{array}{c}{\mathit{\varsigma }}_1^{\prime }\hfill \\ {\mathit{\varsigma }}_2^{\prime }\hfill \\ {\mathit{\varsigma }}_3^{\prime }\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \kappa \left(u\right)\hfill & 0\hfill \\ -\kappa \left(u\right)\hfill & 0\hfill & \tau \left(u\right)\hfill \\ 0\hfill & -\tau \left(u\right)\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{\varsigma }}_1\hfill \\ {\mathit{\varsigma }}_2\hfill \\ {\mathit{\varsigma }}_3\hfill \end{array}\right),\left({}^{\prime }=\frac{d}{du}\right),$$

(1)

where $\kappa \left(u\right)$ and $\tau \left(u\right)$ are the natural curvature and torsion of $\mathit{\omega }\left(s\right)$, respectively.

Definition 1.

Let $\mathit{\omega }\left(u\right)$ and $\widehat{\mathit{\omega }}\left(u\right)$ be two curves in ${\mathbb{E}}^3$ and ${\mathit{\varsigma }}_2\left(u\right)$ and ${\widehat{\mathit{\varsigma }}}_2\left(u\right)$ are their principal normal vectors, respectively. Then, the pair {$\mathit{\omega }\left(u\right)$, $\widehat{\mathit{\omega }}\left(u\right)$} is named a Bertrand pair if ${\mathit{\varsigma }}_2\left(u\right)$ and ${\widehat{\mathit{\varsigma }}}_2\left(u\right)$ are linearly dependent at the matching points, $\mathit{\omega }\left(u\right)$ is called the Bertrand mate of $\widehat{\mathit{\omega }}\left(u\right)$, and

$$\mathit{\omega }\left(u\right)=\widehat{\mathit{\omega }}\left(u\right)+f{\widehat{\mathit{\varsigma }}}_2\left(u\right),$$

(2)

where f is a constant [1,2].

We denote a surface S as

$$S:\mathbf{r}(u,t)=\left(r_1\left(u,t\right),r_2\left(u,t\right),r_3\left(u,t\right)\right),(u,t)\in \mathbb{D}\subseteq {\mathbb{R}}^2.$$

(3)

If ${\mathbf{r}}_j(u,t)=\frac{\partial \mathbf{r}}{\partial j}$, the surface normal is

$$\mathbf{n}(u,t)={\mathbf{r}}_u\times {\mathbf{r}}_t,\mathrm{with}<\mathbf{n},{\mathbf{r}}_u>=<\mathbf{n},{\mathbf{r}}_t>=0.$$

(4)

The well-known theorem below establishes the conditions for any curve on a surface S to be the principal curve [1,2].

Theorem 1.

(Monge’s Theorem) A curve on a surface is a curvature line if and only if the surface normals along the curve create a developable surface [1,2].

An iso-parametric curve is a curve $\mathit{\omega }\left(u\right)$ on a surface r$(u,t)$ that has a fixed s or t variable. In other words, there exists a value $t_0$ such that $\mathit{\omega }\left(u\right)=\mathit{r}(u,t_0)$ or $\mathit{\omega }\left(t\right)=$r$(s_0,t)$. Let $\mathit{\omega }\left(u\right)$ be a parametric curve, which we call an iso-curvature line (curvature line for short) on the surface $\mathbf{r}(u,t)$ if it is both a curvature line and a parameter curve on $\mathbf{r}(u,t)$.

3. Main Results

This section describes a process for organizing a surface pencil pair with a Bertrand pair as joint curvature lines in ${\mathbb{E}}^3$. With this objective, let $\widehat{\mathit{\omega }}\left(u\right)$ be a unit speed curve, $\mathit{\omega }\left(u\right)$ be its Bertrand mate, and $\{{\widehat{\mathit{\varsigma }}}_1\left(u\right),{\widehat{\mathit{\varsigma }}}_2\left(u\right)$, ${\widehat{\mathit{\varsigma }}}_3\left(u\right)$; $\widehat{\kappa }\left(u\right),\widehat{\tau }\left(u\right)\}$ be the Serret–Frenet apparatus of $\widehat{\mathit{\omega }}\left(u\right)$, as in Equation (1). The surface pencil S with $\mathit{\omega }\left(s\right)$ can be written as [13]

$$S:\mathbf{r}(u,t)=\mathit{\omega }\left(u\right)+\mathfrak{a}(u,t){\mathit{\varsigma }}_1\left(s\right)+\mathfrak{b}(u,t){\mathit{\varsigma }}_2\left(s\right)+\mathfrak{c}(u,t){\mathit{\varsigma }}_3\left(s\right),$$

(5)

and the surface pencil $\widehat{S}$ with $\widehat{\mathit{\omega }}\left(u\right)$ is

$$\widehat{S}:\widehat{\mathbf{r}}(u,t)=\widehat{\mathit{\omega }}\left(u\right)+\mathfrak{a}(u,t){\widehat{\mathit{\varsigma }}}_1\left(s\right)+\mathfrak{b}(u,t){\widehat{\mathit{\varsigma }}}_2\left(s\right)+\mathfrak{c}(u,t){\widehat{\mathit{\varsigma }}}_3\left(s\right).$$

(6)

where $\mathfrak{a}(u,t),$$\mathfrak{b}(u,t)$, $\mathfrak{c}(u,t)$ are all $C^1$ functions, and $T_1\le t_0\le T_2,0\le s\le L$. If the variable t is defined as time, the functions $\mathfrak{a}(u,t),$$\mathfrak{b}(u,t)$, and $\mathfrak{c}(u,t)$ can then be realized as the directed marching distances of a point unit in time t along the orientations ${\widehat{\mathit{\varsigma }}}_1$, ${\widehat{\mathit{\varsigma }}}_2$, and ${\widehat{\mathit{\varsigma }}}_3$, respectively, and the vector $\widehat{\mathit{\omega }}\left(u\right)$ is considered the initial position of this point.

Our aim is to infer the sufficient and necessary conditions for which $\widehat{\mathit{\omega }}\left(s\right)$ is an iso-parametric curvature line on $\widehat{S}$. Firstly, since the directrix $\widehat{\mathit{\omega }}\left(u\right)$ is an iso-parametric curve on $\widehat{S}$, there exists a value $t=t_0$ such that $\widehat{\mathit{\omega }}\left(u\right)=\widehat{\mathbf{r}}(u,t_0)$, that is, we obtain

$$\begin{array}{ccc}\hfill \mathfrak{a}(u,t_0)& =& \mathfrak{b}(u,t_0)=\mathfrak{c}(u,t_0)=0\hfill \\ \hfill \frac{\partial \mathfrak{a}(u,t_0)}{\partial u}& =& \frac{\partial \mathfrak{b}(u,t_0)}{\partial u}=\frac{\partial \mathfrak{c}(u,t_0)}{\partial u}=0.\hfill \end{array}$$

(7)

Then,

$$\widehat{\mathbf{n}}(u,t_0):=\frac{\partial \widehat{\mathbf{r}}(u,t_0)}{\partial u}\times \frac{\partial \widehat{\mathbf{r}}(u,t_0)}{\partial t}=-\frac{\partial \mathfrak{c}(u,t_0)}{\partial t}{\widehat{\mathit{\varsigma }}}_2+\frac{\partial \mathfrak{b}(u,t_0)}{\partial t}{\widehat{\mathit{\varsigma }}}_3.$$

(8)

Secondly, with a definite angle $\phi \left(u\right)$, we have a unit vector

$$\widehat{\mathbf{g}}\left(u\right)=cos\phi {\widehat{\mathit{\varsigma }}}_2\left(u\right)+sin\phi {\widehat{\mathit{\varsigma }}}_3\left(u\right).$$

(9)

Using the Serret-Frenet formulae, we find that

$${\widehat{\mathbf{g}}}^{{}^{\prime }}=({\phi }^{{}^{\prime }}+\widehat{\tau }){\widehat{\mathbf{g}}}^{\perp }-\widehat{\kappa }cos\phi {\widehat{\mathit{\varsigma }}}_1.$$

Moreover, the ruled surface

$$\mathbf{z}(u,t)=\widehat{\mathit{\omega }}\left(u\right)+t\widehat{\mathbf{g}}\left(u\right);t\in \mathbb{R},$$

is a developable one if and only if $det({\widehat{\mathit{\omega }}}^{{}^{\prime }},\widehat{\mathbf{g}},{\widehat{\mathbf{g}}}^{{}^{\prime }})=0$, that is,

$${\phi }^{{}^{\prime }}\left(u\right)+\widehat{\tau }\left(u\right)=0\iff \phi \left(u\right)={\phi }_0-\underset{u_0}{\overset{u}{\int }}\widehat{\tau }\left(u\right)du,$$

where $u_0$ is the initial value of the arc length and ${\phi }_0=\phi \left(u_0\right)$. Hence, via Monge’s Theorem and Equations (8) and (9), $\widehat{\mathit{\omega }}\left(u\right)$ is a curvature line on $\widehat{S}$ if and only if $\widehat{\mathbf{g}}\left(u\right)\parallel \widehat{\mathbf{n}}(u,t_0)$. In other words, there exists a function $\chi \left(u\right)\ne 0$ such that

$$\left.\begin{array}{c}-\frac{\partial c(u,t_0)}{\partial t}=\chi \left(u\right)cos\phi ,\frac{\partial b(u,t_0)}{\partial t}=\chi \left(u\right)sin\phi ,\hfill \\ \phi \left(u\right)={\phi }_0-\underset{u_0}{\overset{u}{\int }}\widehat{\tau }\left(u\right)du.\hfill \end{array}\right\}$$

(10)

From Equations (7) and (10), we obtain the following theorem:

Theorem 2.

$\widehat{\mathit{\omega }}=\widehat{\mathit{\omega }}\left(u\right)$ is a curvature line on $\widehat{S}$ if and only if

$$\left.\begin{array}{c}a(u,t_0)=b(u,t_0)=c(u,t_0)=0,\hfill \\ \frac{\partial c(u,t_0)}{\partial t}=\chi \left(u\right)cos\phi ,\frac{\partial b(u,t_0)}{\partial t}=\chi \left(u\right)sin\phi ,\hfill \\ \phi \left(u\right)={\phi }_0-\underset{u_0}{\overset{u}{\int }}\widehat{\tau }\left(u\right)du,\hfill \end{array}\right\}$$

(11)

where $T_1\le t_0\le T_2,0\le u\le L,$ and $\chi \left(u\right)\ne 0$. The functions $\chi \left(u\right)$ and $\phi \left(u\right)$ are called controlling functions.

We refer to $\widehat{S}$, as defined in Equation (6) and fulfilling (11), a surface pencil with a joint curvature line. Any surface $\widehat{\mathbf{r}}(u,t)$, as defined in (5) and fulfilling (11), is an element of this bundle. For further details, the functions $\mathfrak{a}(u,t)$, $\mathfrak{b}(u,t)$, and $\mathfrak{c}(u,t)$ can be expressed as the product of two factors:

$$\mathfrak{a}(u,t)=\mathfrak{l}\left(u\right)\mathfrak{A}\left(t\right),\mathfrak{b}(u,t)=\mathfrak{m}\left(u\right)\mathfrak{B}\left(t\right),\mathfrak{c}(u,t)=\mathfrak{n}\left(u\right)\mathfrak{C}\left(t\right)$$

(12)

where $\mathfrak{l}\left(s\right)$, $\mathfrak{m}\left(s\right)$, $\mathfrak{A}\left(t\right),$ $\mathfrak{B}\left(t\right)$, and $\mathfrak{C}\left(t\right)$ are $C^1$ functions that do not identically vanish. Then, from Theorem 2, we obtain:

Corollary 1.

$\widehat{\mathit{\omega }}=\widehat{\mathit{\omega }}\left(u\right)$ is a curvature line on $\widehat{S}$ if and only if

$$\left.\begin{array}{c}\mathfrak{A}\left(t_0\right)=\mathfrak{B}\left(t_0\right)=\mathfrak{C}\left(t_0\right)=0,\hfill \\ -\mathfrak{n}\left(u\right)\frac{d\mathfrak{C}\left(t_0\right)}{dt}=\chi \left(u\right)cos\phi ,\mathfrak{m}\left(u\right)\frac{d\mathfrak{B}\left(t_0\right)}{dt}=\chi \left(u\right)sin\phi ,\hfill \\ \phi \left(u\right)={\phi }_0-\underset{u_0}{\overset{u}{\int }}\widehat{\tau }\left(u\right)du,\hfill \end{array}\right\}$$

(13)

where $T_1\le t_0\le T_2,0\le u\le L,$ and $\chi \left(u\right)\ne 0$.

However, we can assume that $\mathfrak{a}(u,t)$, $\mathfrak{b}(u,t)$, and $\mathfrak{c}(u,t)$ are based only on t. In other words, $\mathfrak{l}\left(u\right)=\mathfrak{m}\left(u\right)=\mathfrak{n}\left(u\right)=1$. Then, we inspect condition (13) via the diverse terms of $\phi \left(u\right)$:

(i)

If $\widehat{\tau }\left(u\right)\ne 0$, then $\phi \left(u\right)$ is a non-steady function of variable u, and condition (13) can be expressed as

$$\left.\begin{array}{c}\mathfrak{A}\left(t_0\right)=\mathfrak{B}\left(t_0\right)=\mathfrak{C}\left(t_0\right)=0,\\ -\frac{d\mathfrak{C}\left(t_0\right)}{dt}=\chi \left(u\right)cos\phi ,\frac{d\mathfrak{B}\left(t_0\right)}{dt}=\chi \left(u\right)sin\phi ,\end{array}\right\}$$

(14)

(ii)

If $\widehat{\tau }\left(u\right)=0$, that is, the curve is a planar curve, then $\phi \left(u\right)={\phi }_0$ is fixed and we have:

(a)

In the situation of ${\phi }_0\ne 0$, condition (13) can be expressed as

$$\left.\begin{array}{c}\mathfrak{A}\left(t_0\right)=\mathfrak{B}\left(t_0\right)=\mathfrak{C}\left(t_0\right)=0,\\ -\frac{d\mathfrak{C}\left(t_0\right)}{dt}=\chi \left(u\right)cos{\phi }_0,\frac{d\mathfrak{B}\left(t_0\right)}{dt}=\chi \left(u\right)sin{\phi }_0.\end{array}\right\}$$

(15)

(b)

If ${\phi }_0=0$, condition (13) can be expressed as

$$\left.\begin{array}{c}\mathfrak{A}\left(t_0\right)=\mathfrak{B}\left(t_0\right)=\mathfrak{C}\left(t_0\right)=0=0,\\ -\frac{d\mathfrak{C}\left(t_0\right)}{dt}=\chi \left(u\right),\frac{d\mathfrak{B}\left(t_0\right)}{dt}=0,\end{array}\right\}$$

(16)

and from Equation (13), the normal $\widehat{\mathbf{n}}(s,t_0)$($=\widehat{\mathbf{g}}\left(u\right)$) is coincident with ${\widehat{\mathit{\varsigma }}}_2$. In this case, the curve $\widehat{\mathit{\omega }}=\widehat{\mathit{\omega }}\left(u\right)$ is not only a curvature line but also a geodesic.

Example 1.

Let

$$\widehat{\mathit{\omega }}\left(u\right)=(\frac{1}{\sqrt{2}}cosu,\frac{1}{\sqrt{2}}sinu,\frac{u}{\sqrt{2}}),0\le u\le 2\pi .$$

Then,

$$\left.\begin{array}{c}{\widehat{\mathit{\varsigma }}}_1\left(u\right)=\frac{1}{\sqrt{2}}(-sinu,cosu,1),\\ {\widehat{\mathit{\varsigma }}}_2\left(u\right)=(-cosu,-sins,0),\\ {\widehat{\mathit{\varsigma }}}_3\left(u\right)=\frac{1}{\sqrt{2}}(sinu,-cosu,1),\\ \widehat{\kappa }\left(u\right)=\widehat{\tau }\left(u\right)=\frac{1}{\sqrt{2}}.\end{array}\right\}$$

So, we find that $\phi \left(u\right)=-\frac{u}{\sqrt{2}}+{\phi }_0$. If ${\phi }_0=0$, we have $\phi \left(u\right)=-\frac{u}{\sqrt{2}}$. Let

$$\begin{array}{ccc}\hfill \mathfrak{l}\left(u\right)& =& \mathfrak{m}\left(u\right)=\mathfrak{n}\left(u\right)=1,\hfill \\ \hfill \mathfrak{A}\left(t\right)& =& t,\mathfrak{B}\left(t\right)=-t\chi \left(u\right)sin\frac{u}{\sqrt{2}},\mathfrak{C}\left(t\right)=-t\chi \left(u\right)cos\frac{u}{\sqrt{2}},\chi \left(u\right)\ne 0.\hfill \end{array}$$

Then, from Equation (6), we obtain

$$\begin{array}{ccc}\hfill \widehat{S}& :& \widehat{\mathbf{r}}(u,t)=(\frac{1}{\sqrt{2}}cosu,\frac{1}{\sqrt{2}}sinu,\frac{u}{\sqrt{2}})+t(1,-\chi sin\frac{u}{\sqrt{2}},-\chi cos\frac{u}{\sqrt{2}})\hfill \\ & & \times \left(\begin{array}{ccc}-\frac{1}{\sqrt{2}}sinu& \frac{1}{\sqrt{2}}cosu& \frac{1}{\sqrt{2}}\\ -cosu& -sinu& 0\\ \frac{1}{\sqrt{2}}sinu& -\frac{1}{\sqrt{2}}cosu& \frac{1}{\sqrt{2}}\end{array}\right).\hfill \end{array}$$

Hence, the surface pencil S is obtained as follows: Let $f=\sqrt{2}$ in Equation (2), and we find that

$$\mathit{\omega }\left(u\right)=(-\frac{1}{\sqrt{2}}cosu,-\frac{1}{\sqrt{2}}sinu,\frac{u}{\sqrt{2}}).$$

The Serret–Frenet vectors of $\mathit{\omega }\left(u\right)$ are found as follows:

$${\mathit{\varsigma }}_1\left(u\right)=\frac{1}{\sqrt{2}}(sinu,-cosu,1),{\mathit{\varsigma }}_2\left(u\right)=(cosu,sinu,0),{\mathit{\varsigma }}_3\left(u\right)=\frac{1}{\sqrt{2}}(-sinu,cosu,1).$$

Then,

$$\begin{array}{ccc}\hfill S& :& \mathbf{r}(u,t)=(-\frac{1}{\sqrt{2}}cosu,-\frac{1}{\sqrt{2}}sinu,\frac{u}{\sqrt{2}})+t(1,-\chi sin\frac{u}{\sqrt{2}},-\chi cos\frac{u}{\sqrt{2}})\hfill \\ & & \times \left(\begin{array}{ccc}\frac{1}{\sqrt{2}}sinu& -\frac{1}{\sqrt{2}}cosu& \frac{1}{\sqrt{2}}\\ cosu& sinu& 0\\ -\frac{1}{\sqrt{2}}sinu& \frac{1}{\sqrt{2}}cosu& \frac{1}{\sqrt{2}}\end{array}\right).\hfill \end{array}$$

For $\chi =u$, $-5\le$$t\le 5$, and $0\le$$u\le 2\pi$, the corresponding surfaces are depicted in Figure 1. Figure 2 shows the surface with $\chi =-u$, $-5\le$$t\le 5$, and $0\le$$u\le 2\pi$.

Figure 1. $\widehat{S}$ (red) ∪ S (yellow) surfaces.

Figure 2. $\widehat{S}$ (red) ∪ S (yellow) surfaces.

Example 2.

Let $\widehat{\mathit{\omega }}\left(u\right)$ be expressed as

$$\widehat{\mathit{\omega }}\left(u\right)=(cosu,sinu,0),0\le u\le 2\pi .$$

Then,

$${\widehat{\mathit{\varsigma }}}_1\left(u\right)=(-sinu,cosu,0),{\widehat{\mathit{\varsigma }}}_2\left(u\right)=(-cosu,-sinu,0),{\widehat{\mathit{\varsigma }}}_3\left(u\right)=(0,0,1).$$

The curvatures of this curve are $\widehat{\kappa }=1$, $\widehat{\tau }=0$, and $\phi \left(u\right)=\frac{u}{2}$. By taking

$$\begin{array}{ccc}\hfill l\left(u\right)& =& m\left(u\right)=n\left(u\right)=1,\hfill \\ \hfill A\left(t\right)& =& t,B\left(t\right)=t\chi \left(u\right)sin\frac{u}{2},-C\left(t\right)=t\chi \left(u\right)cos\frac{u}{2},\chi \ne 0.\hfill \end{array}$$

Then,

$$\widehat{S}:\widehat{\mathbf{r}}(u,t)=(cosu,sinu.0)+t(1,-\chi \left(u\right)sin\frac{u}{2},\chi cos\frac{u}{2})\left(\begin{array}{ccc}-sinu& cosu& 0\\ -cosu& -sinu& 0\\ 0& 0& 1\end{array}\right).$$

Let $f=2$ in Equation (2). Then, we obtain

$$\mathit{\omega }\left(u\right)=(-cosu,-sinu,0),$$

and

$${\mathit{\varsigma }}_1\left(u\right)=(sinu,-cosu,0),{\mathit{\varsigma }}_2\left(u\right)=(cosu,sinu,0),{\mathit{\varsigma }}_3\left(u\right)=(0,0,1).$$

Hence, the surface pencil S is

$$S:\mathbf{r}(u,t)=(-cosu,-sinu.0)+t(1,-\chi \left(u\right)sin\frac{u}{2},\chi cos\frac{u}{2})\left(\begin{array}{ccc}sinu& -cosu& 0\\ cosu& sinu& 0\\ 0& 0& 1\end{array}\right).$$

For $\chi =u$, $0\le$$t\le 2$, and $0\le$$u\le 2\pi$, the corresponding surfaces are depicted in Figure 3. Figure 4 shows the surface with $\chi =-u$, $0\le$$t\le 2$, and $0\le$$u\le 2\pi$.

Figure 3. $\widehat{S}$ (red) ∪ S (yellow) surfaces.

Figure 4. $\widehat{S}$ (red) ∪ S (yellow) surfaces.

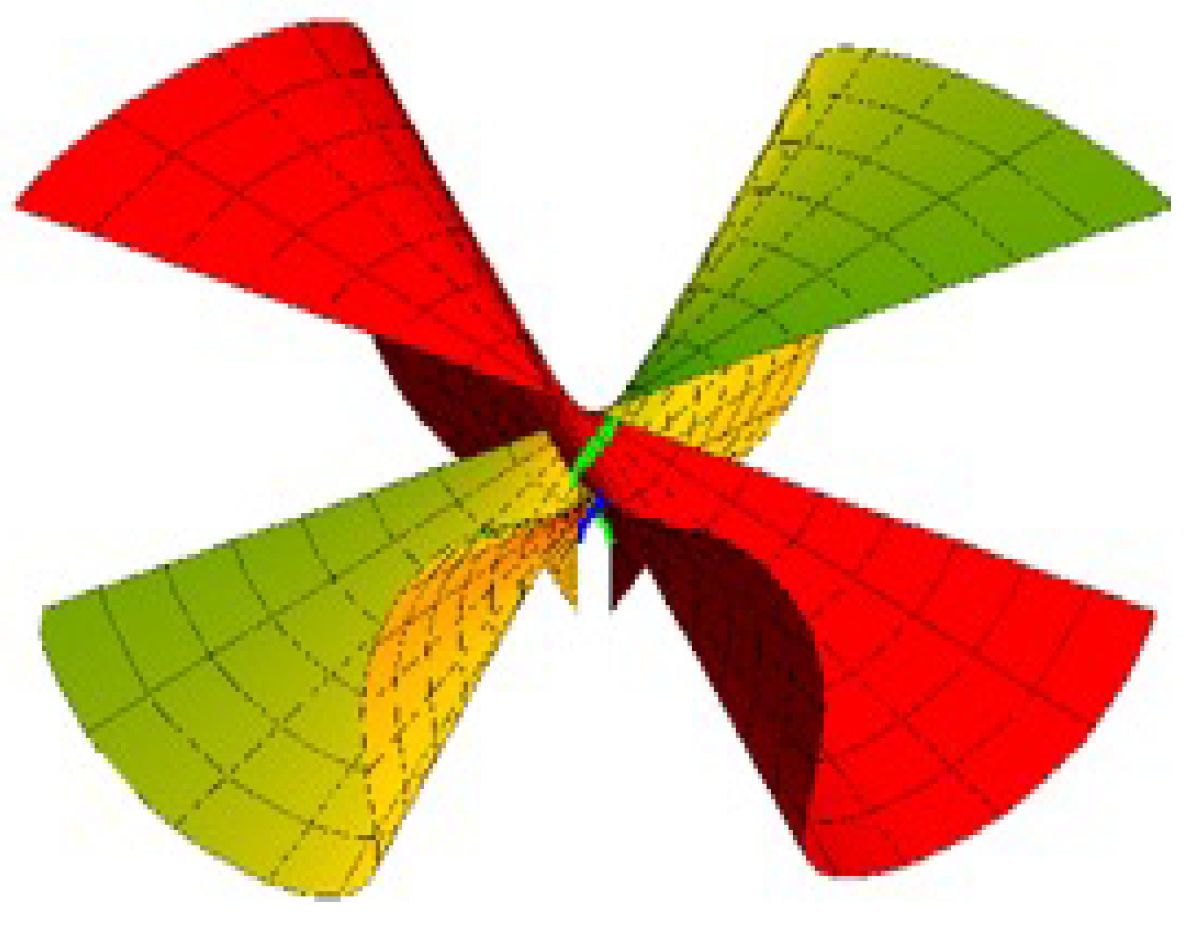
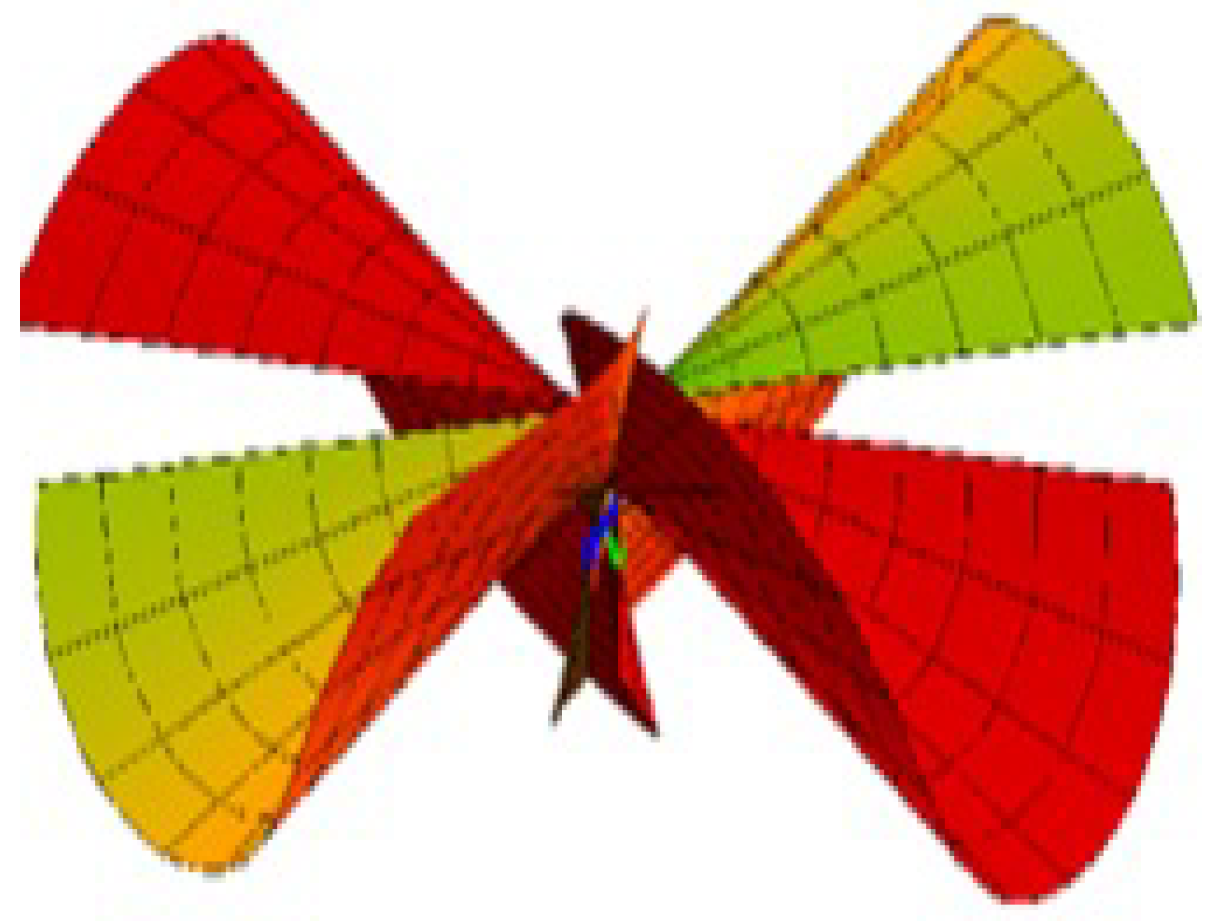
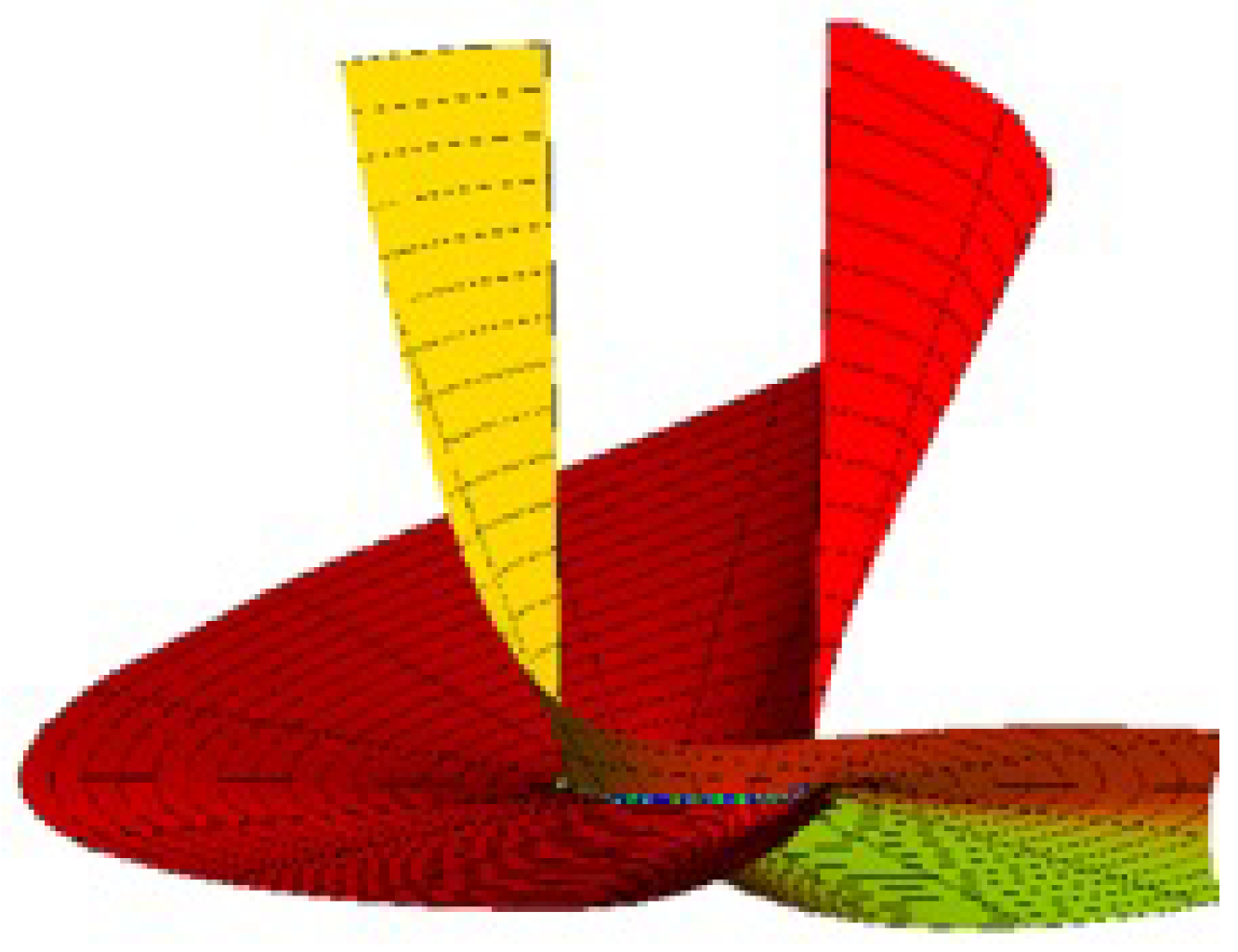
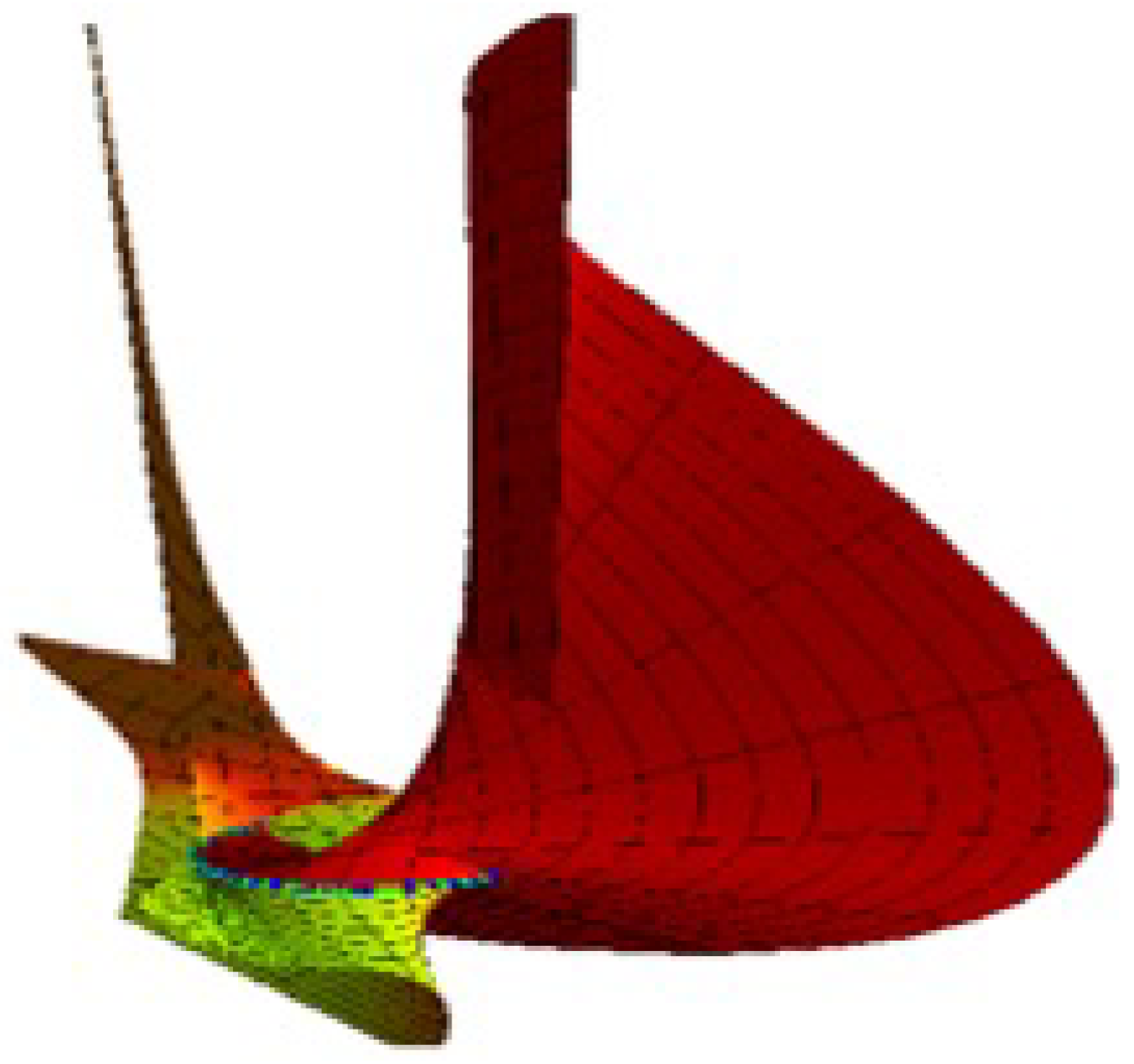
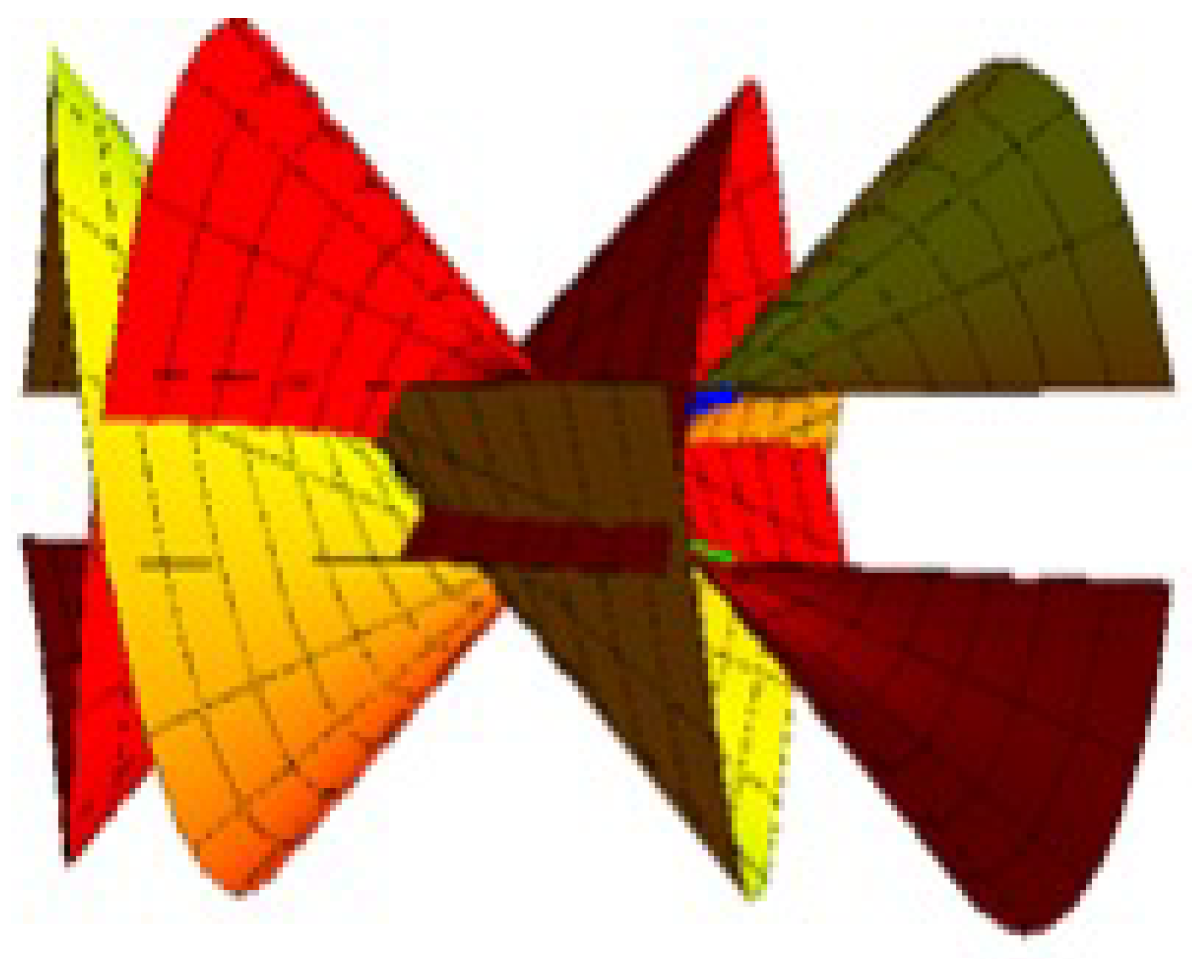
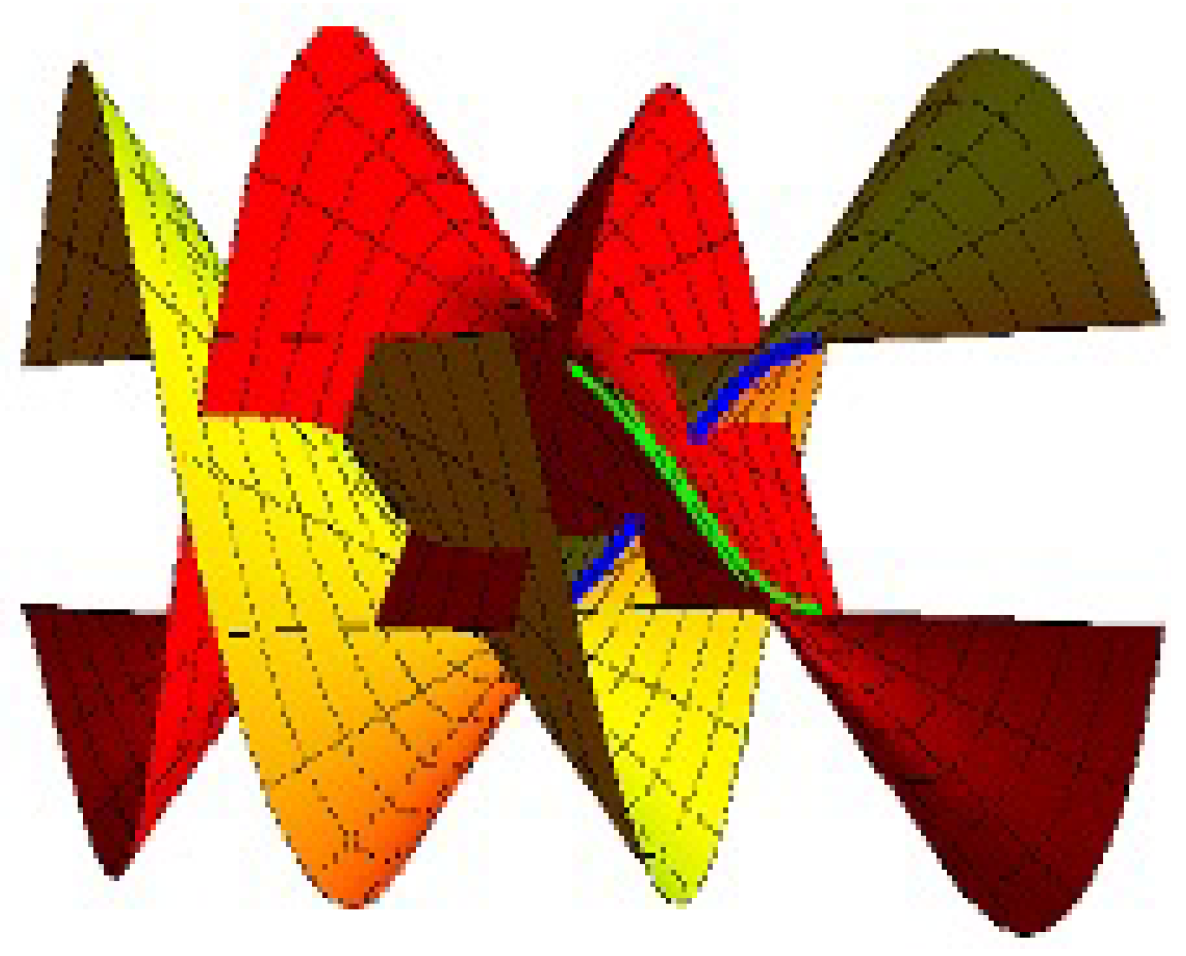
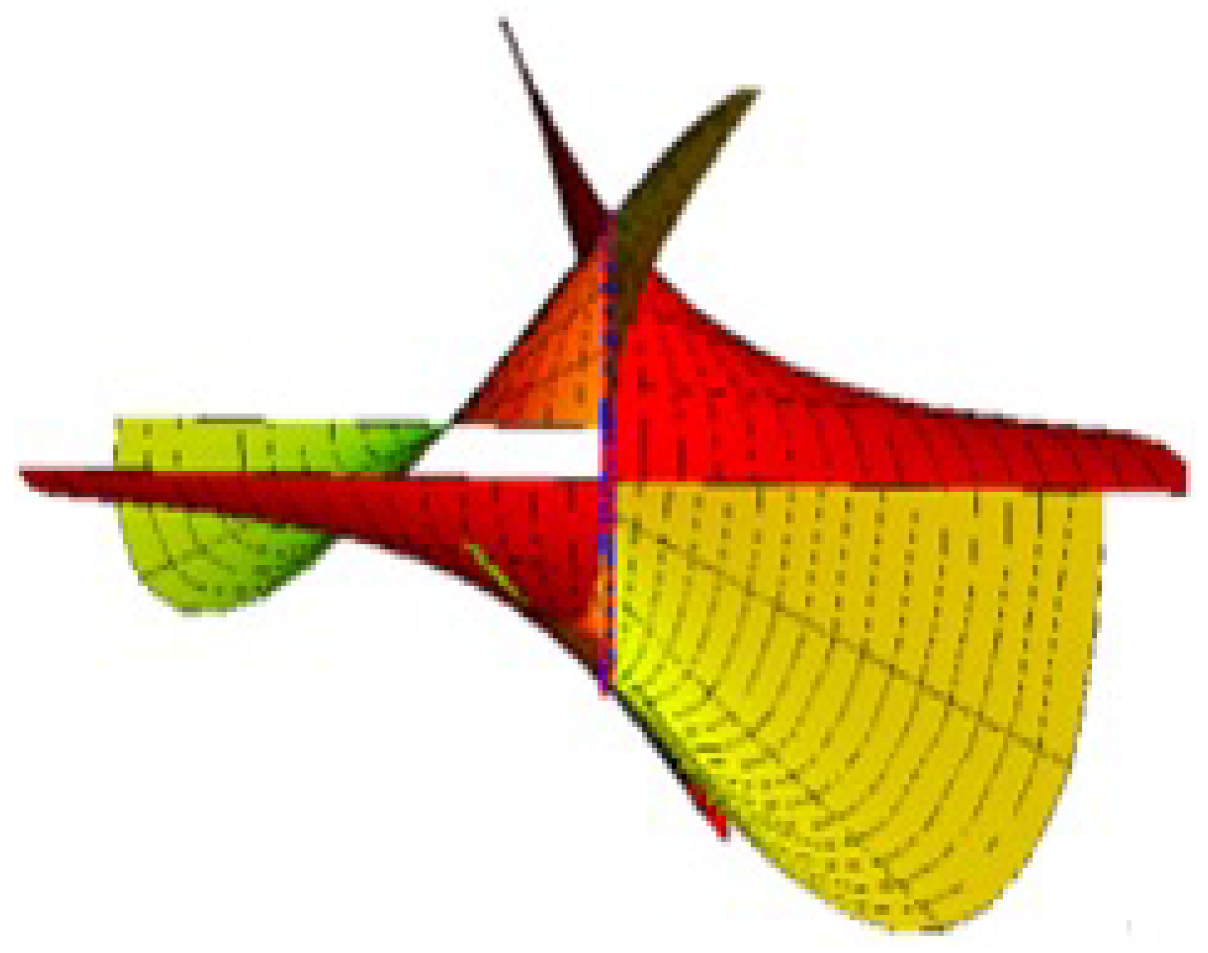
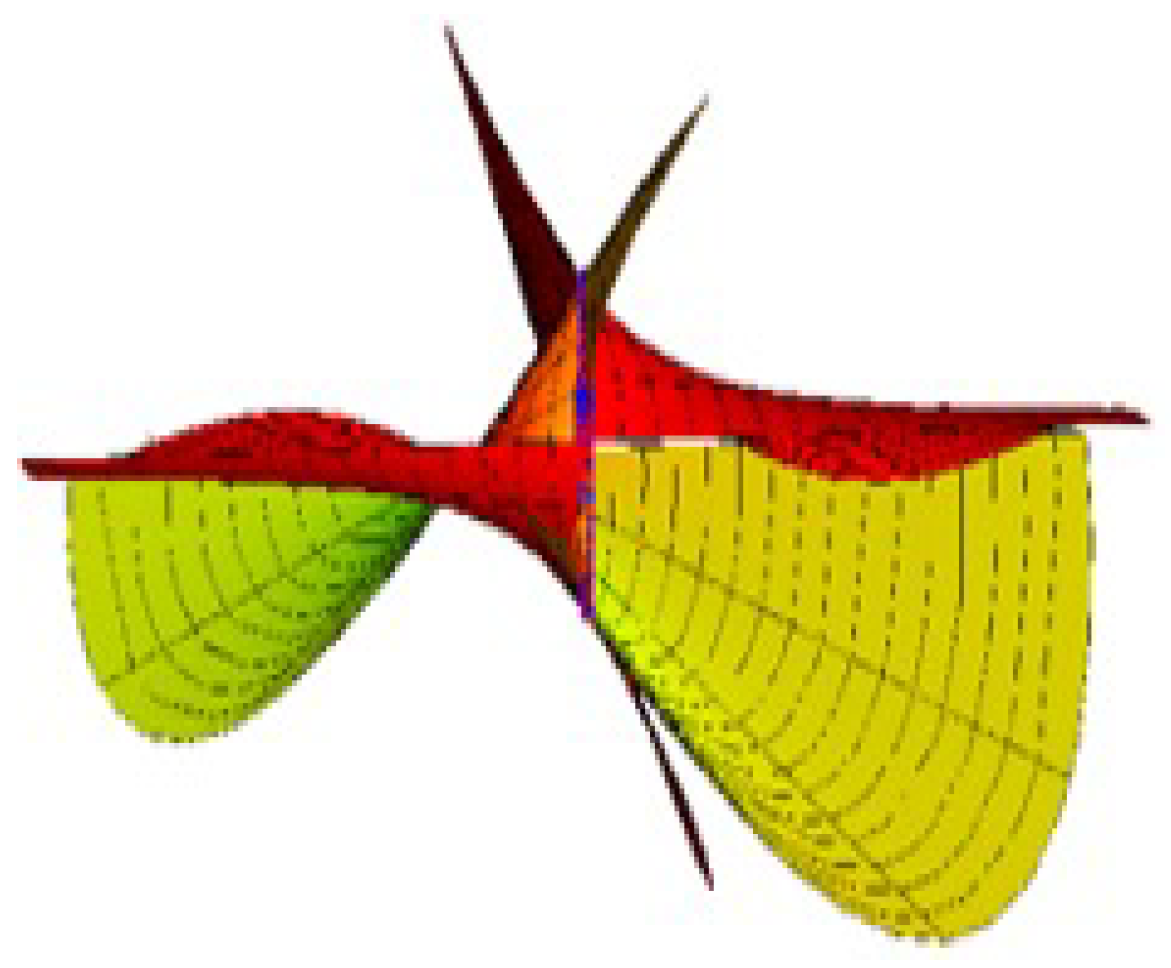
Ruled Surface Pencil Pairs with Bertrand Pairs as Joint Curvature Lines

Let $\widehat{\mathbf{r}}(u,t)$ be a ruled surface with the directrix $\widehat{\mathit{\omega }}\left(u\right)$, and $\widehat{\mathit{\omega }}\left(u\right)$ is also an iso-parametric curve of $\widehat{\mathbf{r}}(u,t)$. Then, there exists a value $t_0$ such that $\widehat{\mathbf{r}}(u,t_0)=\widehat{\mathit{\omega }}\left(u\right)$. From this, it follows that the ruled surface pencil $\widehat{S}$ can be given by

$$\widehat{S}:\widehat{\mathbf{r}}(u,t)-\widehat{\mathbf{r}}(u,t_0)=(t-t_0)\widehat{\mathbf{e}}\left(u\right),0\le s\le L,\mathrm{with},t,t_0\in [T_1,T_2],$$

(17)

where $\widehat{\mathbf{e}}\left(u\right)$ specifies the orientation of the rulings. From Equations (6) and (17), we obtain

$$(t-t_0)\widehat{\mathbf{e}}\left(u\right)=\mathfrak{a}(u,t){\widehat{\mathit{\varsigma }}}_1\left(u\right)+\mathfrak{b}(u,t){\widehat{\mathit{\varsigma }}}_2\left(u\right)+\mathfrak{c}(u,t){\widehat{\mathit{\varsigma }}}_3\left(u\right).$$

(18)

$0\le u\le L,$ with $t,t_0\in [T_1,T_2]$. Equation (20) governs three equations with three unknown functions $\mathfrak{a}(u,t),$ $\mathfrak{b}(u,t)$, and $\mathfrak{b}(u,t)$. By utilizing the scalar product’s rule, we obtain

$$\begin{array}{c}\mathfrak{a}(u,t)=(t-t_0)<\widehat{\mathbf{e}}\left(u\right),{\widehat{\mathit{\varsigma }}}_1\left(u\right)>,\\ \mathfrak{b}(u,t)=(t-t_0)<\widehat{\mathbf{e}}\left(u\right),{\widehat{\mathit{\varsigma }}}_2\left(u\right)>,\\ \mathfrak{b}(u,t)=(t-t_0)<\widehat{\mathbf{e}}\left(u\right),{\widehat{\mathit{\varsigma }}}_3\left(u\right)>.\end{array}$$

(19)

Via Corollary 1, if $\widehat{\mathit{\omega }}\left(u\right)$ is a curvature line of $\widehat{S}$, we obtain

$$\begin{array}{c}a(u,t)=0,\\ \chi \left(u\right)sin\phi =<\widehat{\mathbf{e}}\left(u\right),{\widehat{\mathit{\varsigma }}}_2\left(u\right)>,\\ -\chi \left(u\right)cos\phi =<\widehat{\mathbf{e}}\left(u\right),{\widehat{\mathit{\varsigma }}}_3\left(u\right)>.\end{array}$$

(20)

The above equations are simply the necessary and sufficient conditions for $\widehat{S}$ to be a ruled surface pencil with joint directrix $\beta$$\left(u\right)$. Let us write

$$\widehat{\mathbf{e}}\left(u\right)=\upsilon \left(u\right){\widehat{\mathit{\varsigma }}}_1\left(u\right)+\sigma \left(u\right){\widehat{\mathit{\varsigma }}}_2\left(s\right)+\mu \left(u\right){\widehat{\mathit{\varsigma }}}_3\left(s\right),$$

(21)

where $\upsilon \left(u\right),$ $\sigma \left(u\right)$, and $\mu \left(u\right)$ are all $C^1$ functions. From Equations (19) and (21), we obtain

$$\sigma \left(u\right)=<\widehat{\mathbf{e}}\left(u\right),{\widehat{\mathit{\varsigma }}}_2\left(u\right)>=\chi \left(u\right)sin\phi ,\mu \left(u\right)=<\widehat{\mathbf{e}}\left(u\right),{\widehat{\mathit{\varsigma }}}_3\left(u\right)>=-\chi \left(u\right)cos\phi .$$

Then,

$$\widehat{\mathbf{e}}\left(u\right)=\upsilon \left(u\right){\widehat{\mathit{\varsigma }}}_1\left(u\right)+\chi \left(u\right)sin\phi {\widehat{\mathit{\varsigma }}}_2\left(u\right)-\chi \left(u\right)cos\phi {\widehat{\mathit{\varsigma }}}_3\left(u\right).$$

Hence, the ruled surface pencil $\widehat{S}$ can be designated as

$$\widehat{S}:\widehat{\mathbf{r}}(u,t)=\widehat{\mathit{\omega }}\left(u\right)+t\upsilon \left(u\right){\widehat{\mathit{\varsigma }}}_1\left(u\right)+t\chi \left(u\right)(sin\phi {\widehat{\mathit{\varsigma }}}_2\left(u\right)-cos\phi {\widehat{\mathit{\varsigma }}}_3\left(u\right)),$$

and the ruled surface pencil S is

$$S:\mathbf{r}(u,t)=\mathit{\omega }\left(u\right)+t\upsilon \left(u\right){\mathit{\varsigma }}_1\left(u\right)+t\mathit{\chi }\left(u\right)(sin\phi {\mathit{\varsigma }}_2\left(u\right)-cos\phi {\mathit{\varsigma }}_3\left(u\right)),.$$

where $0\le u\le L,0\le t\le T$, and $\upsilon \left(u\right)$, $\chi \left(u\right)$, and $\phi \left(u\right)$ control the shapes of the surface pencils S and $\widehat{S}$.

Example 3.

Via Example 1, we obtain:

$$\widehat{S}:\widehat{\mathbf{r}}(u,t)=\left(\begin{array}{c}\frac{1}{\sqrt{2}}(cosu-t\upsilon \left(u\right)sinu)+t\chi \left(u\right)(sin\frac{u}{2}cosu+\frac{1}{\sqrt{2}}cos\frac{u}{2}sinu)\\ \frac{1}{\sqrt{2}}(sinu-t\upsilon \left(u\right)cosu)+t\chi \left(u\right)(sin\frac{u}{2}sinu-\frac{1}{\sqrt{2}}cos\frac{u}{2}cosu)\\ \frac{u}{\sqrt{2}}+t(\upsilon \left(u\right)-\chi \left(u\right)cos\frac{u}{2})\end{array}\right),$$

and

$$S:\mathbf{r}(u,t)=\left(\begin{array}{c}\frac{-1}{\sqrt{2}}(cosu-t\upsilon \left(u\right)sinu)+t\chi \left(u\right)(sin\frac{u}{2}cosu+\frac{1}{\sqrt{2}}cos\frac{u}{2}sinu)\\ \frac{-1}{\sqrt{2}}(sinu+t\upsilon \left(u\right)cosu)+t\chi \left(u\right)(sin\frac{u}{2}sinu-\frac{1}{\sqrt{2}}cos\frac{u}{2}cosu)\\ \frac{u}{\sqrt{2}}+t(\upsilon \left(u\right)-\chi \left(u\right)cos\frac{u}{2})\end{array}\right).$$

For $\chi \left(u\right)=\frac{1}{10\sqrt{2}}u$, $\upsilon \left(u\right)=1$, $-5\le$$t\le 5$, and $0\le$$u\le 2\pi$, the corresponding ruled surfaces are depicted in Figure 5. Figure 6 shows the ruled surface with $\chi \left(u\right)=\frac{1}{10\sqrt{2}}u$, $\upsilon \left(u\right)=1$, $-3\le$$t\le 3$, and $0\le$$s\le 2\pi$.

Figure 5. $\widehat{S}$ (red) ∪ S (yellow) ruled surfaces.

Figure 6. $\widehat{S}$ (red) ∪ S (yellow) ruled surfaces.

Example 4.

From Example 2, we obtain:

$$\widehat{S}:\widehat{\mathbf{r}}(u,t)=\left(\begin{array}{c}(1-t\chi \left(u\right)sin\frac{u}{2})cosu-t\upsilon \left(u\right)sinu\\ (1+t\chi \left(u\right)sin\frac{u}{2})sinu+t\upsilon \left(u\right)cosu\\ -t\chi \left(u\right)cos\frac{u}{2}\end{array}\right),$$

and

$$S:\mathbf{r}(u,t)=\left(\begin{array}{c}(-1+t\chi \left(u\right)sin\frac{u}{2})cosu+t\upsilon \left(u\right)sinu\\ -(1+t\chi \left(u\right)sin\frac{u}{2})sinu+t\upsilon \left(u\right)sinu\\ -t\chi \left(u\right)cos\frac{u}{2}\end{array}\right),$$

For $\chi \left(u\right)=cosu$, $\upsilon \left(u\right)=0$, $0\le$$t\le 5$, and $0\le$$u\le 2\pi$, the corresponding ruled surfaces are depicted in Figure 7. Figure 8 shows the ruled surface with $\chi \left(u\right)=cosu$, $\upsilon \left(u\right)=0$, $0\le$$t\le 3$, and $0\le$$u\le 2\pi$.

Figure 7. $\widehat{S}$ (red) ∪ S (yellow) ruled surfaces.

Figure 8. $\widehat{S}$ (red) ∪ S (yellow) ruled surfaces.

4. Conclusions

In this paper, we considered the issue of constructing a surface pencil pair with a Bertrand pair as common curvature lines in Euclidean 3-space ${\mathbb{E}}^3$. The extension to ruled surfaces was also summarized. Meanwhile, significant curves were chosen to construct the surface pencil pair and ruled surface pencil pair with the Bertrand pair as common curvature lines. Hopefully, these scores will be useful in the field of differential geometry and to physicists and others exploring general relativity theory. Our future research will investigate how the principal findings presented in this study can be applied to generate fresh outcomes in conjunction with soliton theory, submanifold theory, and other pertinent fields that have been discussed in [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49].