Abstract
The smallest set of vertices needed to differentiate or categorize every other vertex in a graph is referred to as the graph’s metric dimension. Finding the class of graphs for a particular given metric dimension is an NP-hard problem. This concept has applications in many different domains, including graph theory, network architecture, and facility location problems. A graph G with order n is known as a Toeplitz graph over the subset S of consecutive collections of integers from one to n, and two vertices will be adjacent to each other if their absolute difference is a member of S. A graph is called a zero-divisor graph over the zero divisors of a commutative ring , in which two vertices will be adjacent to each other if their product will leave the remainder zero under modulo n. Since the local fractional metric dimension problem is NP-hard, it is computationally difficult to identify an optimal solution or to precisely determine the minimal size of a local resolving set; in the worst case, the process takes exponential time. Different upper bound sequences of local fractional metric dimension are suggested in this article, along with a comparison analysis for certain families of Toeplitz and zero-divisor graphs. Furthermore, we note that the analyzed local fractional metric dimension upper bounds fall into three metric families: constant, limited, and unbounded.
Keywords:
symmetrical algebraic structure graphs; local fractional metric dimension; Toeplitz graphs; zero-divisor graphs; asymptotic behavior MSC:
05C35; 05C72; 90C35
1. Introduction
Graphs are mathematical structures made up of vertices (nodes) and edges (connections) that are used to illustrate various relationships and links between objects or entities. The need to understand the structural qualities of graphs in terms of the labeling of their vertices and the connections between their nodes led to the development of the idea of metric dimension. Metric dimension has practical implications in network design, graph theory, and optimization [1,2,3].
By determining the minimum number of landmarks or reference points required to uniquely identify locations in a network, we can efficiently design routing protocols, establish communication schemes, and ensure a reliable information flow. Metric dimension also finds applications in facility location problems, where the goal is to identify the optimal locations for facilities to serve a given set of clients or demands. When one takes into account the metric dimension of a graph, we are able to strategically place our facilities so that we can serve all of our customers while keeping the overall cost and the amount of distance traveled to a minimum. The study of metric dimensions, in general, gives us the ability to measure and evaluate the spatial and structural interactions in graphs, which in turn leads to practical applications in network design, facility localization, sensor networks, graph theory, and the analysis of algorithmic complexity.
Melter and Harary were the ones who originally suggested the idea of metric dimension [4]. Within a network, vertices are denoted by nodes, and the connections that exist between the nodes are denoted by edges. This structure makes it possible for agents to travel from one vertex to another. To facilitate agent localization, certain points are designated as landmarks. The metric basis refers to the smallest set of landmarks, while the metric dimension represents the cardinality of this set [5]. Building upon this foundation, Arumugam and Mathew have made significant advancements in the study of the fractional metric dimension (FMD) [6]. Because of their efforts, our basic knowledge of FMD and its characteristics has significantly advanced. In addition, the use of FMD has been investigated in a variety of network topologies, such as lexicographic, hierarchical, Cartesian, corona, and corona-comb networks. These networks are explored utilizing FMD collected from product operations, which reveals helpful insights into the structural properties of the networks themselves [7].
The Fractional Metric Dimension (FMD) in modified Jahangir networks and permutational systems was researched by Wang and Feng [8,9], as well as by Liu et al. [10]. They investigated the FMD’s characteristics as well as various estimate methods while applying them to these network architectures. In addition, Raza et al. contributed further to the knowledge of FMD across multiple graph classes, while Aisyah et al. calculated the boundaries of FMD in metal-organic graphs [11,12]. They recommended FMD to be used for the corona product of systems and proposed a more localized version of the metric dimension that they called the Local Fractional Metric Dimension (LFMD). Their research primarily focused on investigating the LFMD and its applications in a variety of graph compositions and formats. The researchers Liu et al. made significant contributions to the field of LFMD [13]. More recent work was conducted by Ali, Falcón, and other researchers, who studied the LFMD of a collection of circular symmetric planar graphs. This research was carried out in order to investigate further the local fractional metric dimension [14]. The graphs arise as a result of the merging of the edge of an order n cycle with the edges of n additional chorded cycles of the same order n. For more on the subject, see [15] and references therein.
The research carried out by Aisyah et al. contains one of the first known references to LFMD within the context of the corona product of systems [12]. Within the corona product of graphs, the localized fractional metric dimension is taken into account by the LFMD. As a result, it is possible to obtain insights on the localized structure and labeling of vertices in this graph composition [16]. The Corona technique, performed in 2016 by Rodríguez-Velázquez et al., introduces the idea of using local metric dimensions in graphs [17]. In the same year, Marsidi et al. established the local metric dimensions for line graphs, as well as other different graphs [18].
If all the networks that make up a family, represented by F, have the same metric dimension within a collection of linked networks, then it is said that the family has a constant metric [19]. Because a generalized Peterson anti-prism in a network C is a circulant network , each one of them also forms a family with a constant metric dimension. In the course of the inquiry, we also look at the size of wheels and Jahangir networks using metric systems and, with the help of Integer Programming, we acquire a response that is more specific to our idea.
FMD has a significant number of innovative features. For instance, FMD was also employed by Fehr et al. to produce a better solution to a linear programming relaxation [20]. Afterward, Arumugam and Mathew’s contributions helped to shed light on the subject [6]. Moreover, several graph theorists reported a number of findings on the metric dimension and graph labeling on many families of graphs [14,21,22]. Other researchers have studied FMD with respect to various other elements of graph theory [23,24,25,26,27].
Algebraic graph theory is a branch of mathematics that examines and evaluates graph characteristics and structures using algebraic methods. In the field of algebraic graph theory, various problems are still open. For example, the problem of the number of components of a graph, which depends on the modular relation, is still dealt with as a conjuncture. There are several algebraic graphs based on the algebraic structure that have now been studied, and we refer the reader to [28,29,30] and references therein. Here, we discuss a zero-divisor graph that depends on the set of zero divisors of a ring R. A graph is known as a zero-divisor graph whose vertex set is the zero divisors of modular ring , and two vertices will be adjacent to each other if their product will be zero under [31]. The zero-divisor graph for is shown in Figure 1.
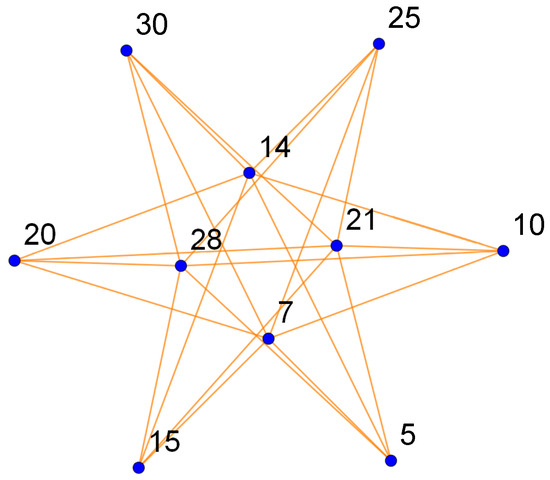
Figure 1.
The zero-divisor graph for .
A graph is called a Toeplitz graph if its vertex set is and two vertices are adjacent to each other if their absolute difference belongs to S, where (). The Toeplitz graph for is shown in Figure 2.
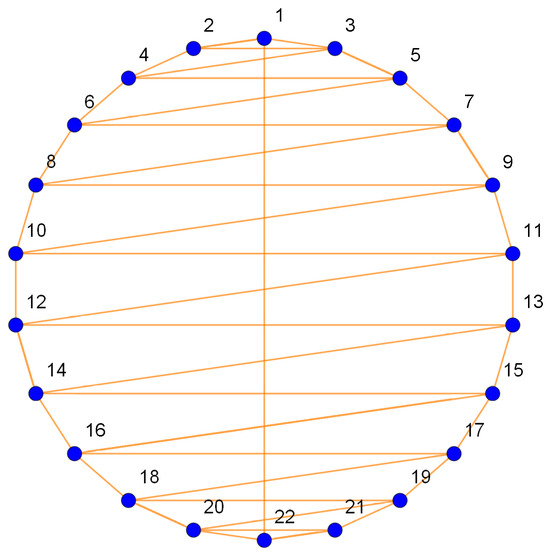
Figure 2.
The Toeplitz graph .
A resolving function [6] of the graph G is any map such that
for every pair of distinct vertices . The fractional metric dimension of the graph G is
The concepts of local resolving neighborhood and local resolving function arise similarly, in the case of dealing with pairs of adjacent vertices only. Then, the local fractional metric dimension of the graph G is defined as
Further, from now on, we denote . In particular, since , for all , one has . The next result follows from all the previous definitions. Lemma 1 and Theorem 1 have a vital importance throughout the manuscript. In particular, it will be used in the proofs of Theorems 2 to 8.
Lemma 1
([12,32]). If is any finite simple graph with order greater than , then
and the local fractional metric dimension is one if, and only if, the graph is a bipartite graph.
Theorem 1
([33]). Let be a simple graph with order n and be the local resolving neighborhood set. Then,
where .
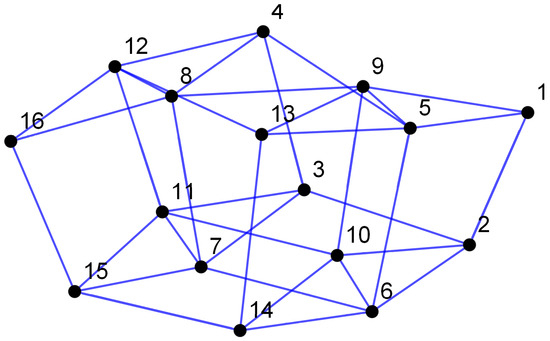
Figure 3.
The Toeplitz graph .
The resolving sets , crossposting to each pair of adjacent vertices, are given as follows:
The cardinalates of the above resolving set are
Since the minimum and maximum cardinalities of the resolving sets are 8 and 14, respectively, it follows by relation (2) and Theorem 1 that
The article is arranged as follows. Section 2 recalls some applications of metric dimension in diverse fields such as navigation, networking, pattern recognition and image processing, combinatorial optimization, image programming, chemistry, and drug discovery. In Section 3, stream values of the LFMD of certain families of Toeplitz graphs are studied. Then, in Section 4, the LFMD for zero-divisor graphs over a zero divisor of is computed while in Section 5, we compute it for zero-divisor graphs over . In Section 6, we give some remarks on finding LFMD for algebraic structure graphs. In Section 7, a few concluding remarks, directions for future work, and some open problems needing further research are discussed.
2. Survey of Applications of Metric Dimension
Metric dimension, a distance-based characteristic, is used to pinpoint the positions of things in space, such as machinery, robots, chemical compounds, etc. The objective is to minimize the number of locations or nodes that are used by these items, as well as to optimize time consumption and the shortest distances between destinations. Applications for metric dimension may be found in the following fields:
- Navigation, to determine the metric dimension in robotics and navigation systems, to set up robots or machines most effectively for effective movement and path planning [34].
- Networking, where metric dimension is used to estimate the bare minimum of nodes required to uniquely identify the network [35].
- Pattern Recognition and Image Processing, where metric dimension helps with tasks such as feature selection and pattern recognition by allowing data points to be represented in a lower-dimensional space while still retaining their key properties [15].
- Combinatorial Optimization, to determine the most effective approach to cover or represent a collection of points in space, where optimization challenges require the usage of metric dimension [36].
- Integer Programming, where the goal is to discover integer solutions that optimize a particular criterion [37].
- Chemistry and Drug Discovery, where metric dimension is used in molecular networks and chemical compound analysis to characterize and describe chemical compounds in a distinctive way, assisting in the identification of novel medications or comprehending chemical interactions [38].
Overall, metric dimension is a parameter that may be used to solve optimization and representation issues in a variety of fields, allowing for effective resource allocation and decision-making while taking distance into account. It is intriguing to observe how this idea is used in disciplines as different as chemistry and computer science.
3. Stream Values of LFMD for Certain Families of Toeplitz Graphs
In this section, we find upper bounds sequences of LFMD for certain families of Toeplitz graphs.
Theorem 2.
Let be a Toeplitz graph. The local fractional metric dimension of is
where and are sets of positive odd integers and positive even integers, respectively.
Proof.
If ℘ is an odd number, then the Toeplitz graph’s vertex set is divided into two separate sets in the following manner:
These two sets form a bipartite graph. So, according to Lemma 1, we have
If ℘ is even, then the resolving sets are
These resolving sets have the following cardinalities:
Since the minimum and maximum cardinalities of the resolving sets are and , respectively, thus, by relation (2) and Theorem 1, we have
The proof is complete. □
Theorem 3.
Let be a Toeplitz graph. Then, the local fractional metric dimension is given by
Proof.
The cardinalities of the above resolving set are
Since the minimum and maximum cardinalities of the resolving sets are and , respectively, by relation (2) and Theorem 1, we have:
Case 3. When the Toeplitz graph has order , then the following resolving sets are
The cardinalities of the above resolving sets are
The minimum and maximum cardinalities of the resolving sets are and , respectively. Therefore, by relation (2) and Theorem 1, one has that
Case 4. When the Toeplitz graph has order , then we have the following resolving sets:
for ℘.
Since the minimum and maximum cardinalities of the resolving sets are and ℘, respectively, it follows by relation (2) and Theorem 1 that
Case 5. When the Toeplitz graph has order , then the resolving sets are
The cardinalities of the above resolving set are
Noting that the minimum and maximum cardinalities of the resolving sets are and , respectively, we conclude by relation (2) and Theorem 1 that
The proof is complete. □
There are five cases to be studied.
Case 1. When the Toeplitz graph has order , then
- If then the resolving sets are
- If then the resolving sets are
- If then the resolving sets are
- If then cardinalities of resolving sets are
- If then cardinalities of resolving sets are
- If , then cardinalities of resolving sets are
Case 2. When the Toeplitz graph has order , then
- If the resolving sets are
- If the resolving sets are
- If , the resolving sets are
The cardinalities of the above resolving set are
- If then
- If then
- If then
- If , then
- If , then
- If then
- If then
- If then
- If then
- If , then
- If then
- If , then we have
The cardinalities of the above resolving set are
- If then
- If then
- If then
- If , then
- If , then
- If then
- If , then
- If , then
- If , then
Theorem 4.
Let , , be a Toeplitz graph. The bounds of the local fractional metric dimension of is
Proof.
The Toeplitz graph has order . Then, we have the following resolving sets:
- , then
- , , , then
- , , , then
- If , , ,
- then
- , then
- , then
- then
- then
- then
- then
- then
- , then
The cardinalities of the above resolving set are
- If , then
- then
- , , then
- , , ,
- , ,
- , , then
- , , then
- then
- then
- , , , then
- , , then
- , , , then
- , , then
- , , , then
- , , then
- , , , then
Since the minimum and maximum cardinalities of the resolving sets are 8 and , respectively, thus, by relation (2) and Theorem 1, we have
which completes the proof. □
Theorem 5.
Let be a Toeplitz graph. The bounds of the local fractional metric dimension of is
Proof.
Let be a Toeplitz graph. One has the following resolving sets:
The cardinalates of the above resolving sets are
In general, is the minimal cardinality and is the maximal cardinality for all prime numbers. So, by relation (2) and Theorem 1, we have
The proof is complete. □
Theorem 6.
Let be a Toeplitz graph where p is a prime number. The local fractional metric dimension of is equal to one, that is,
Proof.
The resolving sets for each adjacent pair of vertices are
So, is the minimal and maximal cardinality for all prime numbers and, by (2) and Theorem 1,
which completes the proof. □
4. LFMD for Zero-Divisor Graphs over the Set of Zero Divisors of
In this section, we compute the LFMD for zero-divisor graphs over the set . These graphs are defined as follows: the vertex set is the set of zero divisors of and two vertices are adjacent to each other if their product is a zero divisor. They are denoted by .
Theorem 7.
Let be a zero-divisor graph. An upper bound of the local fractional metric dimension of is
where p is a prime number.
Proof.
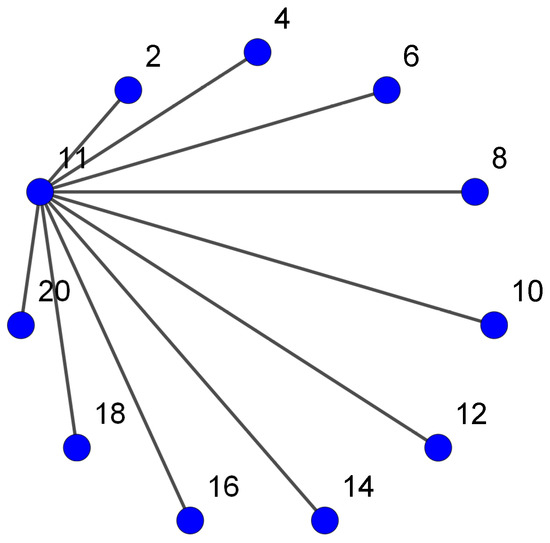
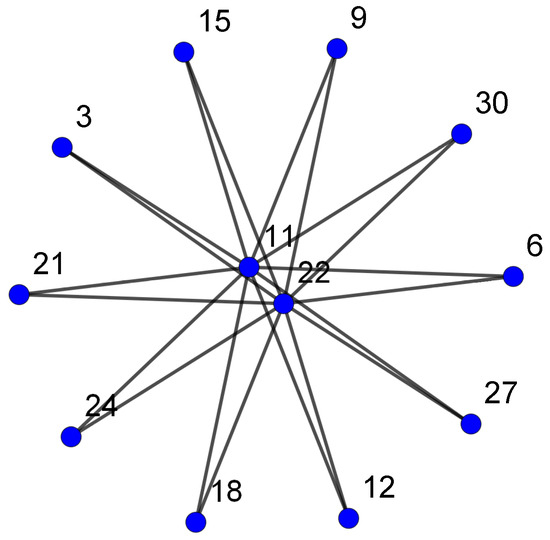
Let be a zero-divisor graph. For the graph is bipartite with partition sets
For illustration, let us take . Then, the zero-divisor graph is shown in Figure 4.

Figure 4.
The zero-divisor graph .
By Lemma 1, .
Similarly, for , the graph is also bipartite with partition sets
For observation, we can take : the zero-divisor graph is shown in Figure 5.

Figure 5.
The zero-divisor graph .
By Lemma 1, .
Let and consider the graph . The resolving sets for each pair of adjacent vertices are
The cardinality of the set (3) is 2 and since the total number of zero divisors of is , we conclude by Lemma 1 and Theorem 1 that
The proof is complete. □
5. LFMD of Zero-Divisor Graphs over
Now, we compute the LFMD for zero-divisor graphs over the set . These graphs are defined as follows: the vertex set is and two vertices are adjacent to each other if their product is a zero divisor. They are denoted by . The zero-divisor graph is shown in Figure 6.
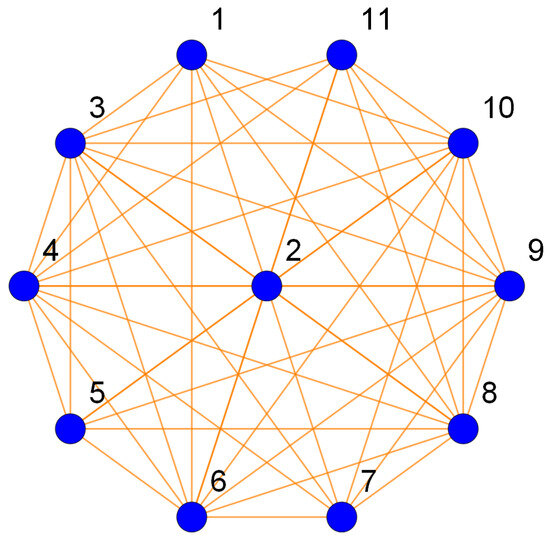
Figure 6.
The zero-divisor graph .
The resolving sets corresponding to each pair of adjacent vertices are
The cardinalates of the above resolving set are
Since the minimum and maximum cardinalities of the resolving sets are 2 and 5, respectively, we know, by relation (2) and Theorem 1, that
Theorem 8.
Let be a zero-divisors graph over . The bounds of the local fractional metric dimension of is given by
where p is a prime number.
Proof.
Let be a zero-divisors graph over . We look to the resolving sets corresponding to each adjacent vertices.
- Let or be an even number, but not both. Without any loss of generality, say is even. Then,
- If and are both even numbers, then
The cardinalities of the above resolving sets are
- If or is an even number but not both, then
- If and are both even numbers, then
Since the minimum and maximum cardinalities of the resolving sets are 2 and , respectively, we conclude by relation (2) and Theorem 1 that
The proof is similar for . Let be a zero-divisors graph over . The resolving sets corresponding to each adjacent vertices are
- If or is a multiple of p, but not both (without any loss of generality, say ), then
- If and are both even numbers, then
The cardinalities of the above resolving sets are
- in the first case,
- while in the second
Since the minimum and maximum cardinalities of the resolving sets are 2 and , respectively, it follows by relation (2) and Theorem 1 that
The proof is complete. □
6. Discussion of Investigated Sequences for the Local Fractional Metric Dimension
We have examined the asymptotic behavior of families of Toeplitz and zero-divisor graphs for the local fractional metric dimension. Note that all obtained sequences are constrained. This is illustrated in Table 1.

Table 1.
Asymptotic behavior of examined sequences over specific families of Toeplitz and zero-divisor graphs for the local fractional metric dimension.
The numerical comparison between the computed bounds of , , and , , , , , , , and , is shown in Table 2, Table 3, Table 4 and Table 5, respectively.

Table 2.
Numerical comparison between upper bound values of , , , , , , , and , .

Table 3.
Numerical comparison between lower bound values of , , , , , , , and , .

Table 4.
Numerical comparison between upper bounds values of , , and .

Table 5.
Numerical comparison between lower bounds values of , , and .
7. Conclusions
The problem of determining the metric dimension of a given graph for a given integer is NP-hard. For big graphs, this means that the computation needed to find the metric dimension rises exponentially as the graph’s size does, making it a difficult task. Metric dimension has proven invaluable in addressing problems across various disciplines, such as computer science, minimum distance calculations, and chemical graph theory. It has played a significant role in improving the representation of networks and graphs in real-world applications. Here, we investigated and discussed the asymptotic behavior of sequences for the local fractional metric dimension in families of Toeplitz and zero-divisor graphs. This sort of study is required in order to understand how the attributes of a particular graph or its properties behave as the graph’s size increases. Without having to manually compute the parameters, asymptotic behavior enables researchers to make predictions about how the parameters will behave in bigger networks. It is also worth observing that constant, bounded, and unbounded metric families all include the obtained upper boundaries for the local fractional metric dimension. This implies that the metric dimension and associated ideas may be categorized and comprehended within certain families or categories of graphs, which can be useful for creating effective algorithms and resolving real-world issues in a variety of fields. We trust that our work has several potential applications. For instance, cryptography depends on coding and decoding, whereas the most attractive coding depends on linear programming problems. If the domain of the coding is the set of consecutive integers or some particular class of integers, then its programming is very suitable for cryptography. In our proposed work, the class of Toeplitz graphs is the zero-divisor graphs that depend on a set of consecutive integers and zero divisors of the commutative ring. We claim that our results can be used for coding and decoding in cryptography.
For future developments, we mention here some interesting open problems:
- Toeplitz graph generalization is still up for debate. For such possible generalizations, it would be great to determine some upper bounds of the local fractional metric dimension for for each subset S of .
- For any positive integer n, upper bounds for the LFMD of zero-divisor graphs are yet unknown.
- For any positive integer n, to obtain upper bounds for the LFMD of zero-divisor graphs over the set is still open.
Author Contributions
Conceptualization, A.S.A. and S.A.; methodology, A.S.A.; software, M.A.; validation, A.S.A., S.A. and D.F.M.T.; formal analysis, S.A.; investigation, S.A. and D.F.M.T.; resources, M.A.; writing—original draft preparation, S.A. and D.F.M.T.; writing—review and editing, S.A., M.A. and D.F.M.T.; visualization, A.S.A.; supervision, S.A. and D.F.M.T.; project administration, A.S.A. and D.F.M.T.; funding acquisition, A.S.A. and D.F.M.T. All authors have read and agreed to the published version of the manuscript.
Funding
A.S.A. was supported by Princess Nourah bint Abdulrahman University under Researchers Supporting Project PNURSP2023R231, Riyadh, Saudi Arabia; D.F.M.T. was supported by the Fundação para a Ciência e a Tecnologia, I.P. (FCT, Funder ID = 50110000187) under CIDMA Grants UIDB/04106/2020 and UIDP/04106/2020, Portugal.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data were used to support this study.
Acknowledgments
A.S.A. is grateful to the support of Princess Nourah bint Abdulrahman University under Project PNURSP2023R231, Riyadh, Saudi Arabia; D.F.M.T. to the support by FCT, projects UIDB/04106/2020 and UIDP/04106/2020, Portugal. The authors would like to express their gratitude to four anonymous reviewers for their meticulous review of the submitted work, as well as for their valuable questions, comments, and suggestions. In light of these insights, the authors have made revisions to the manuscript, resulting in a noticeable enhancement in its quality.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arulperumjothi, M.; Klavžar, S.; Prabhu, S. Redefining fractal cubic networks and determining their metric dimension and fault-tolerant metric dimension. Appl. Math. Comput. 2023, 452, 128037. [Google Scholar] [CrossRef]
- Ghalav, A.; Klavžar, S.; Tavakoli, M. Graphs whose mixed metric dimension is equal to their order. Comput. Appl. Math. 2023, 42, 210. [Google Scholar] [CrossRef]
- DasGupta, B.; Mobasheri, N. On optimal approximability results for computing the strong metric dimension. Discrete Appl. Math. 2017, 221, 18–24. [Google Scholar] [CrossRef]
- Harary, F.; Melter, R.A. On the metric dimension of a graph. Ars. Combin. 1976, 2, 191–195. [Google Scholar]
- Khuller, S.; Raghavachari, B.; Rosenfeld, A. Landmarks in graphs. Discret. Appl. Math. 1996, 70, 217–229. [Google Scholar] [CrossRef]
- Arumugam, S.; Mathew, V. The fractional metric dimension of graphs. Discret. Math. 2012, 312, 1584–1590. [Google Scholar] [CrossRef]
- Arumugam, S.; Mathew, V.; Shen, J. On fractional metric dimension of graphs. Discret. Math. Algorithms Appl. 2013, 5, 1350037. [Google Scholar] [CrossRef]
- Feng, M.; Wang, K. On the metric dimension and fractional metric dimension of the hierarchical product of graphs. Appl. Anal. Discret. Math. 2013, 7, 302–313. [Google Scholar] [CrossRef]
- Feng, M.; Wang, K. On the fractional metric dimension of corona product graphs and lexicographic product graphs. arXiv 2012, arXiv:1206.1906. [Google Scholar]
- Liu, J.B.; Kashif, A.; Rashid, T.; Javaid, M. Fractional metric dimension of generalized Jahangir graph. Mathematics 2019, 7, 100. [Google Scholar] [CrossRef]
- Raza, M.; Alrowaili, D.A.; Javaid, M.; Shabbir, K. Computing bounds of fractional metric dimension of metal organic graphs. J. Chem. 2021, 2021, 5539569. [Google Scholar] [CrossRef]
- Aisyah, S.; Utoyo, M.I.; Susilowati, L. On the local fractional metric dimension of corona product graphs. IOP Conf. Ser. Earth Environ. Sci. 2019, 243, 012043. [Google Scholar] [CrossRef]
- Liu, J.B.; Aslam, M.K.; Javaid, M. Local fractional metric dimensions of rotationally symmetric and planar networks. IEEE Access 2020, 8, 82404–82420. [Google Scholar] [CrossRef]
- Ali, S.; Falcón, R.M.; Mahmood, M.K. Local fractional metric dimension of rotationally symmetric planar graphs arisen from planar chorded cycles. arXiv 2021, arXiv:2105.07808. [Google Scholar]
- Ali, S.; Mahmood, M.K.; Tchier, F.; Tawfiq, F.M.O. Classification of upper bound sequences of local fractional metric dimension of rotationally symmetric hexagonal planar networks. J. Math. 2021, 2021, 6613033. [Google Scholar] [CrossRef]
- Wulancar, E.D.; Kusmayadi, T.A. The local metric dimension of edge corona and corona product of cycle graph and path graph. J. Phys. Conf. Ser. 2019, 1306, 012014. [Google Scholar] [CrossRef]
- Rodríguez-Velázquez, J.A.; Barragán-Ramírez, G.A.; García, G.C. On the local metric dimension of corona product graphs. Bull. Malays. Math. Sci. Soc. 2016, 39, 157–173. [Google Scholar] [CrossRef]
- Marsidi, M.; Dafik, D.; Agustin, I.H.; Alfarisi, R. On the local metric dimension of line graph of special graph. Cauchy J. Mat. Murni Dan Apl. 2016, 4, 125–130. [Google Scholar] [CrossRef][Green Version]
- Tomescu, I.; Javaid, I. On the metric dimension of the Jahangir graph. Bull. MathéMatique SociéTé Des Sci. MathéMatiques Roum. 2007, 50, 371–376. [Google Scholar]
- Fehr, M.; Gosselin, S.; Oellermann, O.R. The metric dimension of Cayley digraphs. Discret. Math. 2006, 306, 31–41. [Google Scholar] [CrossRef]
- Yero, I.G.; Rodríguez-Velázquez, J.A. A note on the partition dimension of Cartesian product graphs. Appl. Math. Comput. 2010, 217, 3571–3574. [Google Scholar] [CrossRef]
- Yero, I.G. On the strong partition dimension of graphs. Electron. J. Comb. 2014, 21, 1–18. [Google Scholar]
- Zafar, H.; Javaid, M.; Bonyah, E. Studies of connected networks via fractional metric dimension. J. Math. 2022, 2022, 1273358. [Google Scholar] [CrossRef]
- Huang, Q.; Labba, M.; Azeem, M.; Jamil, M.K.; Luo, R. Tetrahedral sheets of clay minerals and their edge valency-based entropy measures. Math. Biosci. Eng. 2023, 20, 8068–8084. [Google Scholar] [CrossRef] [PubMed]
- Bukhari, S.; Jamil, M.K.; Azeem, M.; Swaray, S. Patched network and its vertex-edge metric-based dimension. IEEE Access 2023, 11, 4478–4485. [Google Scholar] [CrossRef]
- Azeem, M.; Jamil, M.K.; Shang, Y. Notes on the localization of generalized hexagonal cellular networks. Mathematics 2023, 11, 844. [Google Scholar] [CrossRef]
- Wang, J.; Tian, F.; Liu, Y.; Pang, J.; Miao, L. On Graphs of Order n with Metric Dimension n-4. Graphs Comb. 2023, 39, 29. [Google Scholar] [CrossRef]
- Farsi, C.; Gillaspy, E.; Gonçalves, D. Irreducibility and monicity for representations of k-graph C*-algebras. N. Y. J. Math. 2023, 29, 507–553. [Google Scholar]
- Fu, C.; Geng, S.; Liu, P.; Zhou, Y. On support τ-tilting graphs of gentle algebras. J. Algebra 2023, 628, 189–211. [Google Scholar] [CrossRef]
- Forcey, S.; Ronco, M. Algebraic structures on graph associahedra. J. Lond. Math. Soc. 2022, 106, 1189–1231. [Google Scholar] [CrossRef]
- Livingston, P.S. Structure in Zero-Divisor Graphs of Commutative Rings. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 1997. [Google Scholar]
- Okamoto, F.; Phinezy, B.; Zhang, P. The local metric dimension of a graph. Math. Bohem. 2010, 135, 239–255. [Google Scholar] [CrossRef]
- Javaid, M.; Zafar, H.; Zhu, Q.; Alanazi, A.M. Improved lower bound of LFMD with applications of prism-related networks. Math. Probl. Eng. 2021, 2021, 9950310. [Google Scholar] [CrossRef]
- Sharma, S.K.; Raza, H.; Bhat, V.K. Fault-tolerant resolvability of some graphs of convex polytopes. Discrete Math. Appl. 2023, 33, 177–187. [Google Scholar]
- Goshi, N.; Zafar, S.; Rashid, T. Fractional metric dimension of generalized prism graph. Proyecciones 2022, 41, 1199–1212. [Google Scholar] [CrossRef]
- Sharma, S.K.; Bhat, V.K. On metric dimension of plane graphs with m2 number of 10 sided faces. J. Comb. Optim. 2022, 44, 1433–1458. [Google Scholar] [CrossRef]
- Zafar, H.; Javaid, M. Metric based fractional dimension of Toeplitz networks. Punjab Univ. J. Math. (Lahore) 2023, 55, 1–12. [Google Scholar] [CrossRef]
- Javaid, M.; Aslam, M.K.; Liu, J.-B. On the upper bounds of fractional metric dimension of symmetric networks. J. Math. 2021, 2021, 8417127. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).