Dynamic Response of an Elastic Tube-like Nanostructure Embedded in a Vibrating Medium and under the Action of Moving Nano-Objects
Abstract
1. Introduction
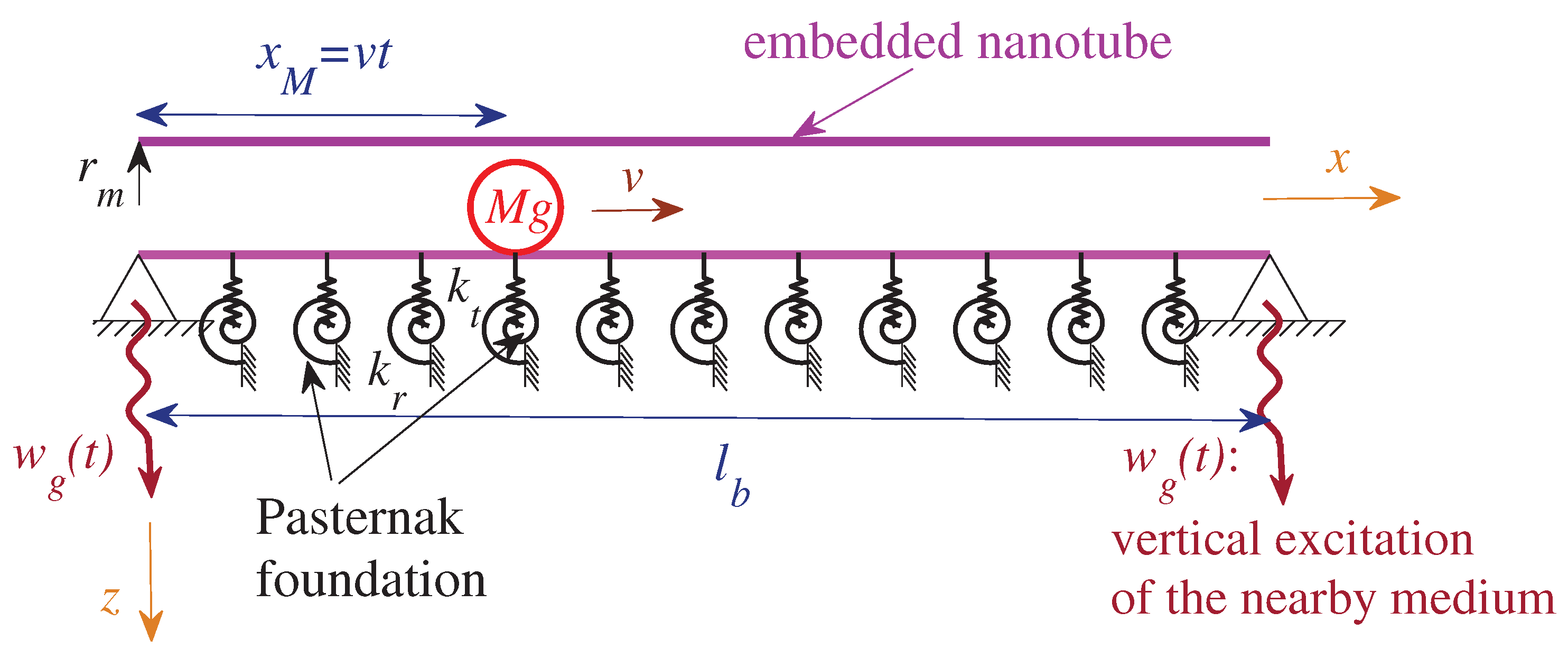
2. Description and Assumptions Used in the Proposed Models
3. Investigating Vibrations under Excitations of Elastic Medium and MNO Based on the NRABT
3.1. Nonlocally Developed Governing Equations
3.2. An Analytically Developed Solution Based on the MNFA ()
3.3. A Numerically Developed Solution Based on the MNMA ()
4. Investigating Vibrations under Excitations of Elastic Medium and MNO Based on the NREBT
4.1. Nonlocally Developed Governing Equations
4.2. An Analytically Developed Solution Based on the MNFA ()
4.3. A Numerically Developed Solution Based on the MNMA ()
4.4. Results and Discussion
4.5. Validation Studies of the Suggested Models
4.5.1. A Comparison between the MNFA’s Results and Those of the MNMA
4.5.2. A Comparison between the Results Predicted by the Model and Those of Another Work in the Case of = 0
4.5.3. A Comparison between the Results Predicted by the Model and Those of Another Work in the Absence of the MNO
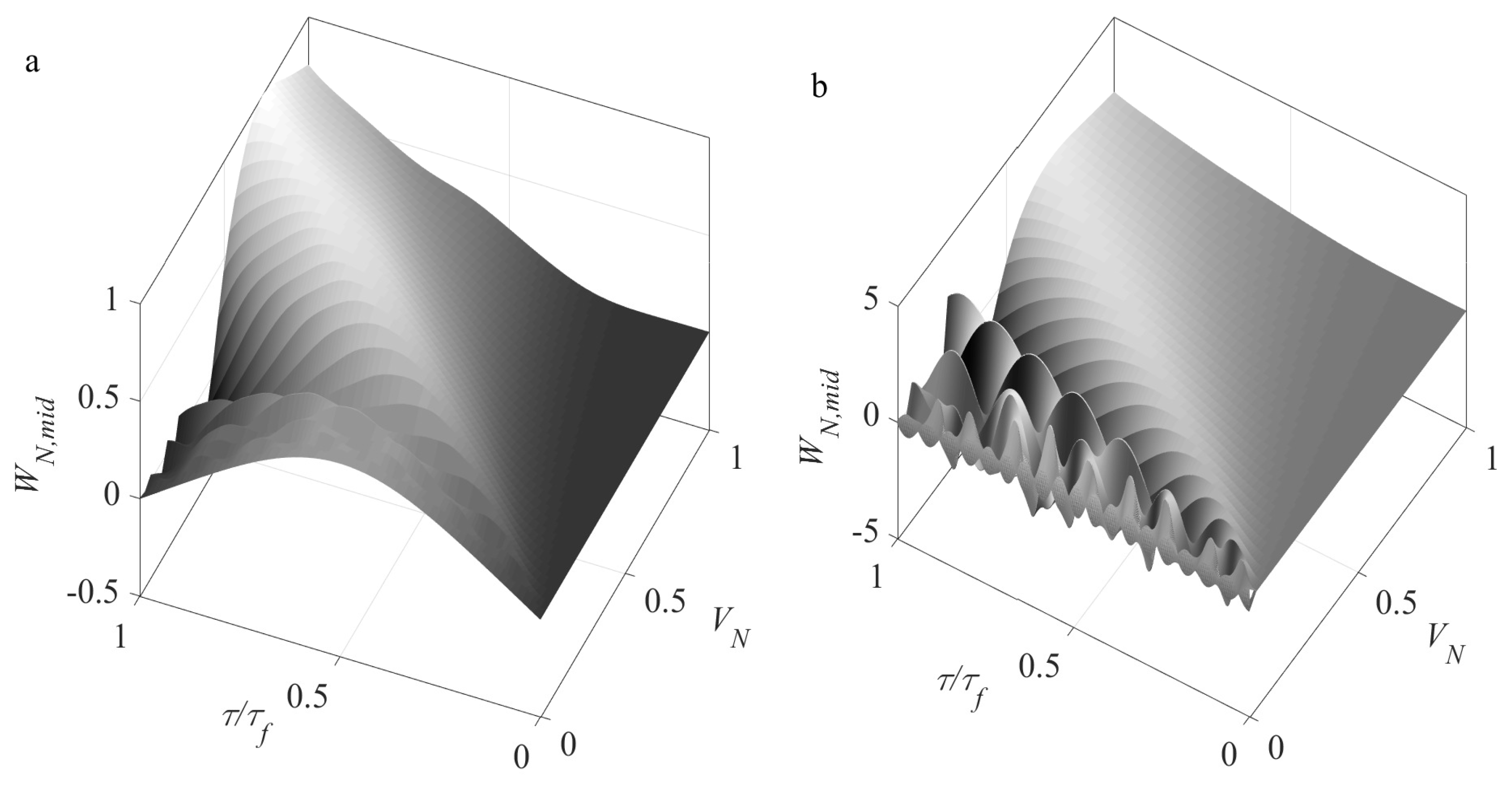
4.6. Time History Analysis of the Mid-Span Deflection
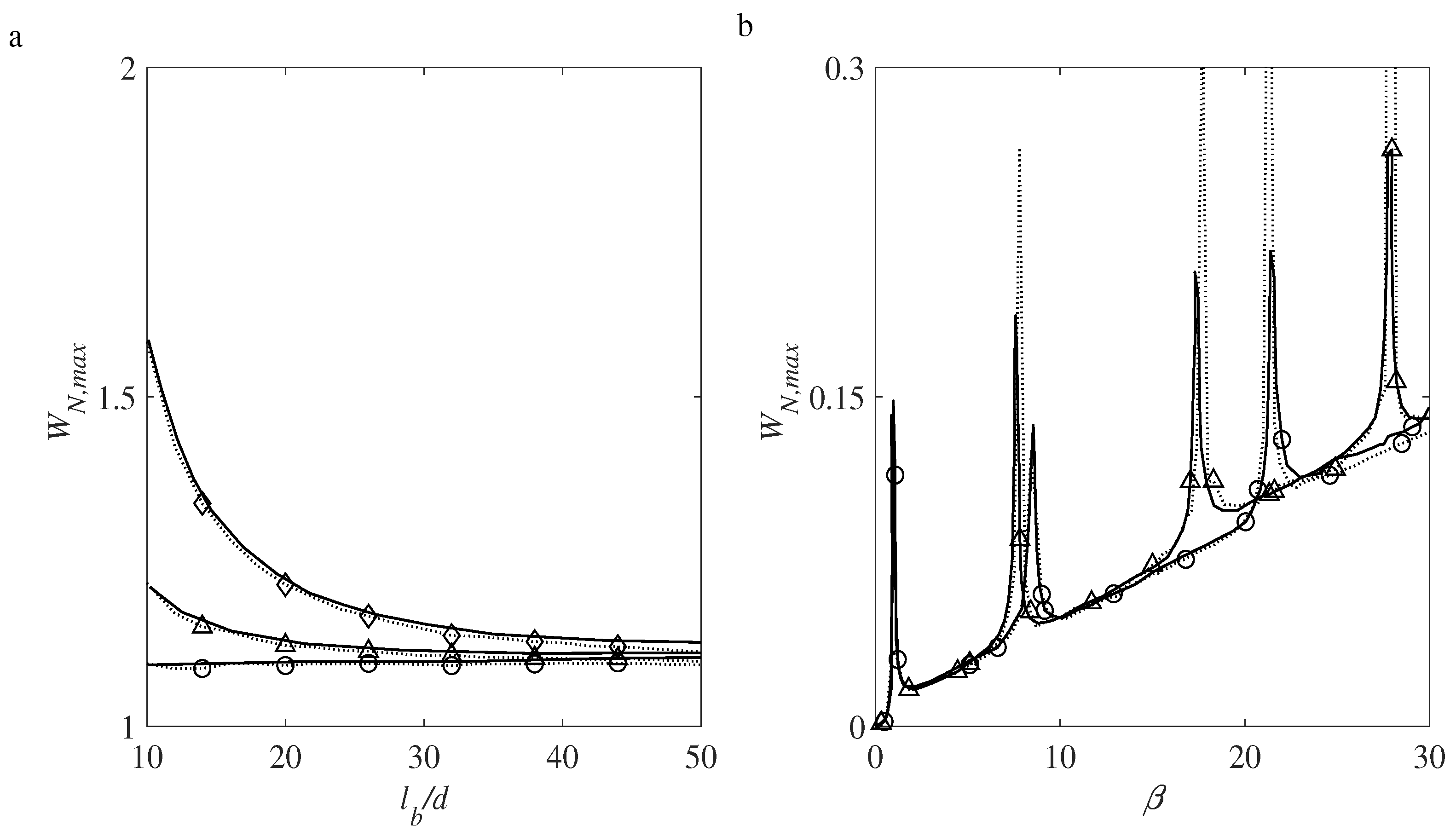
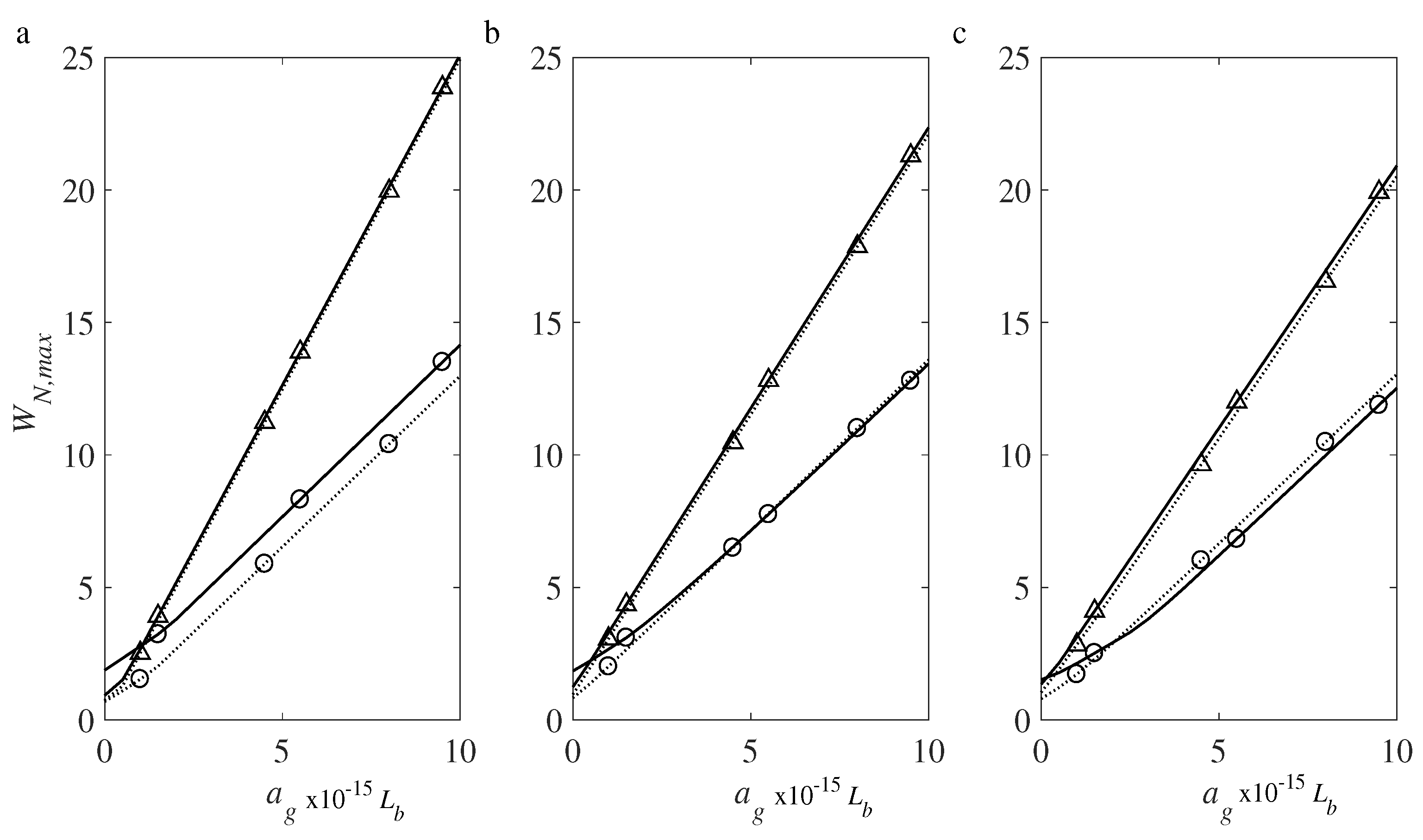
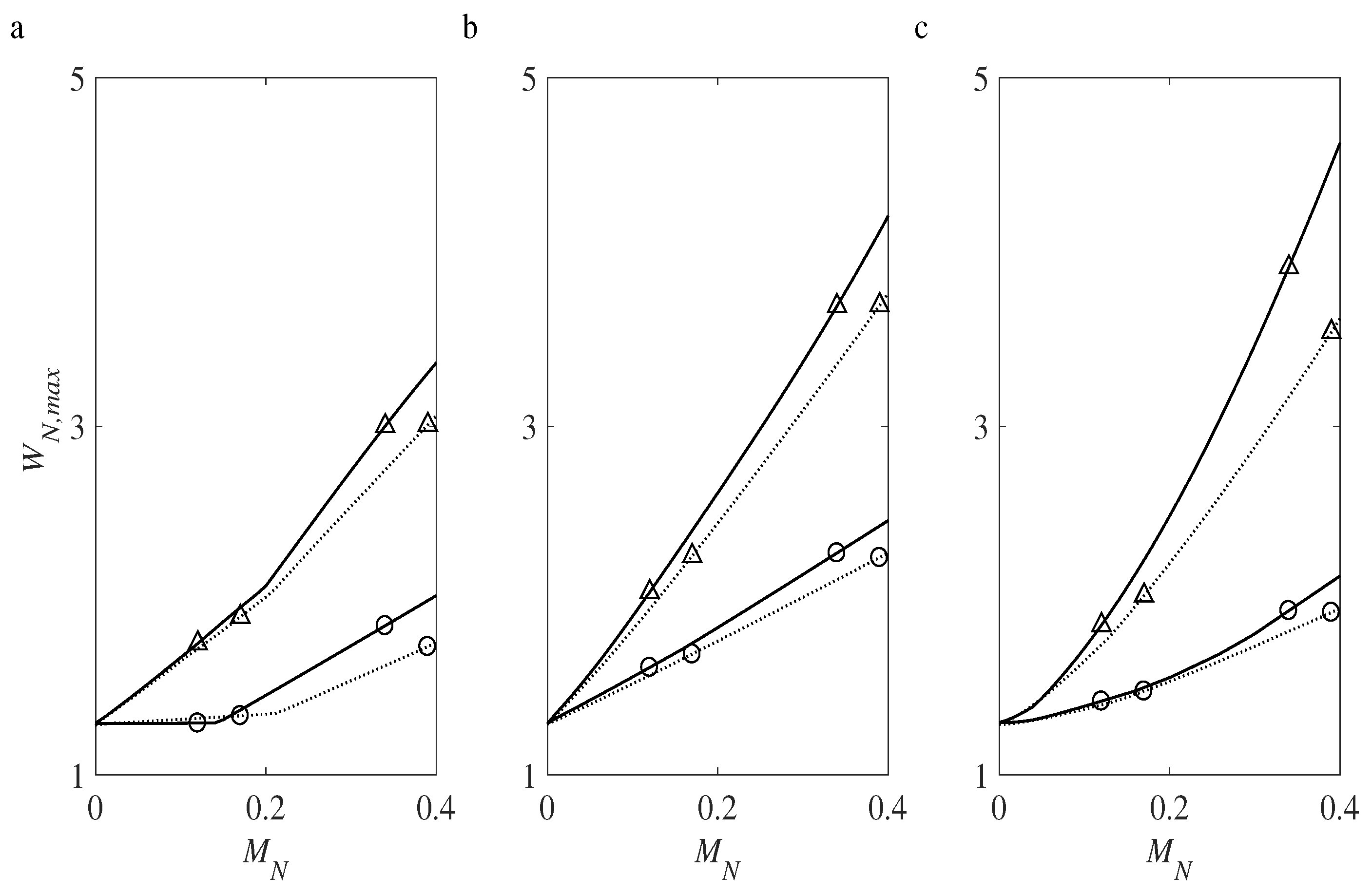
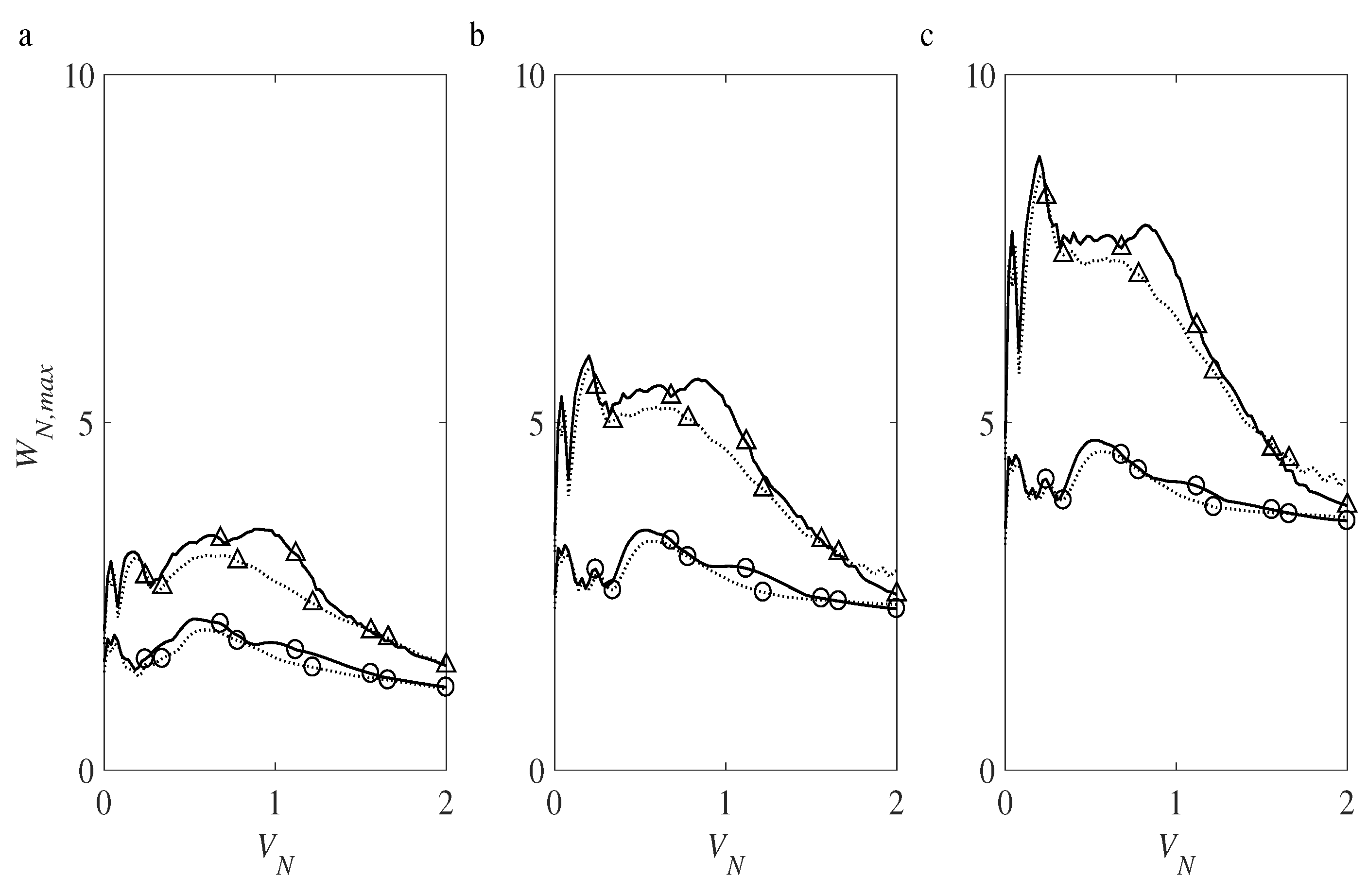
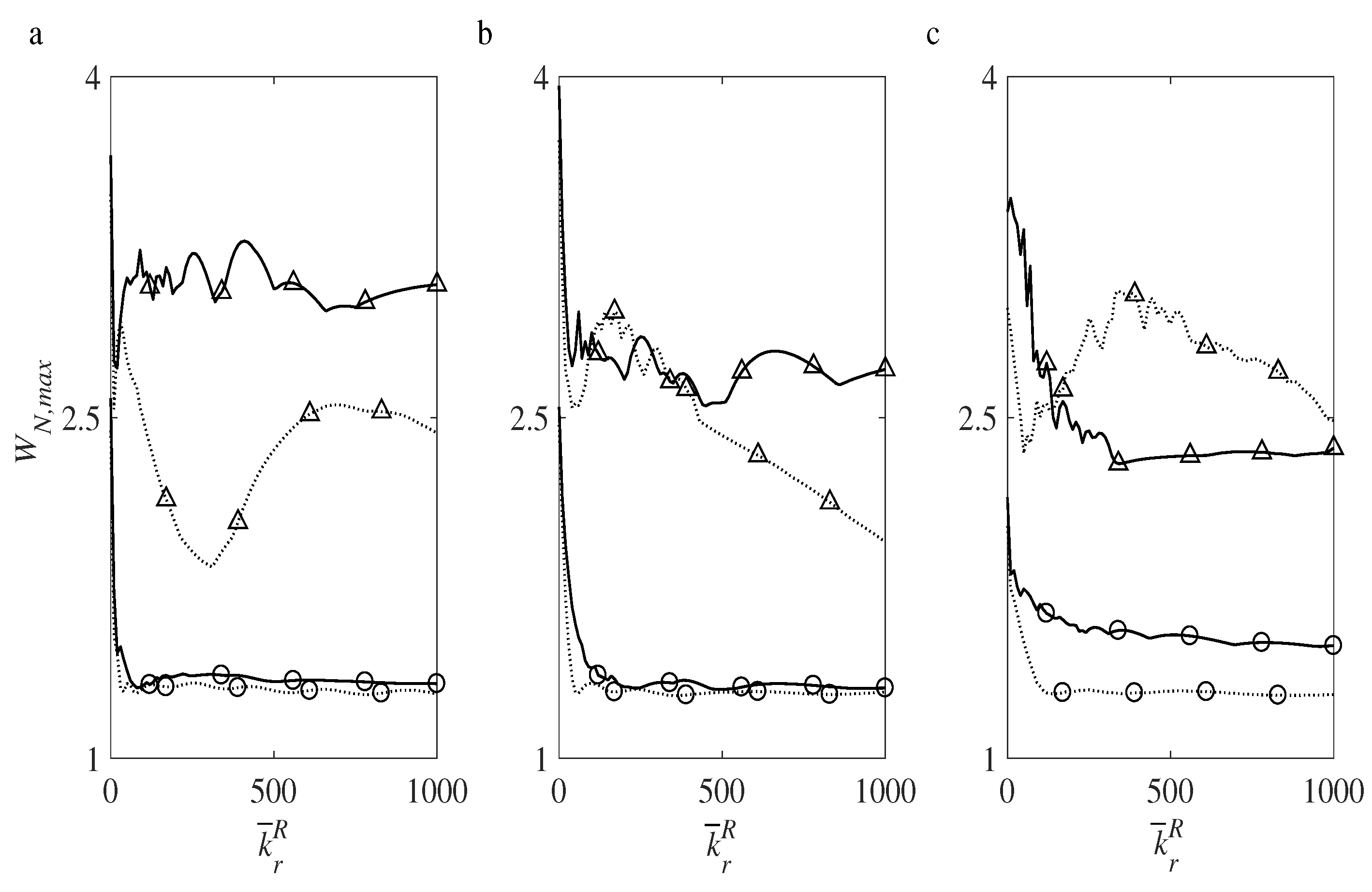
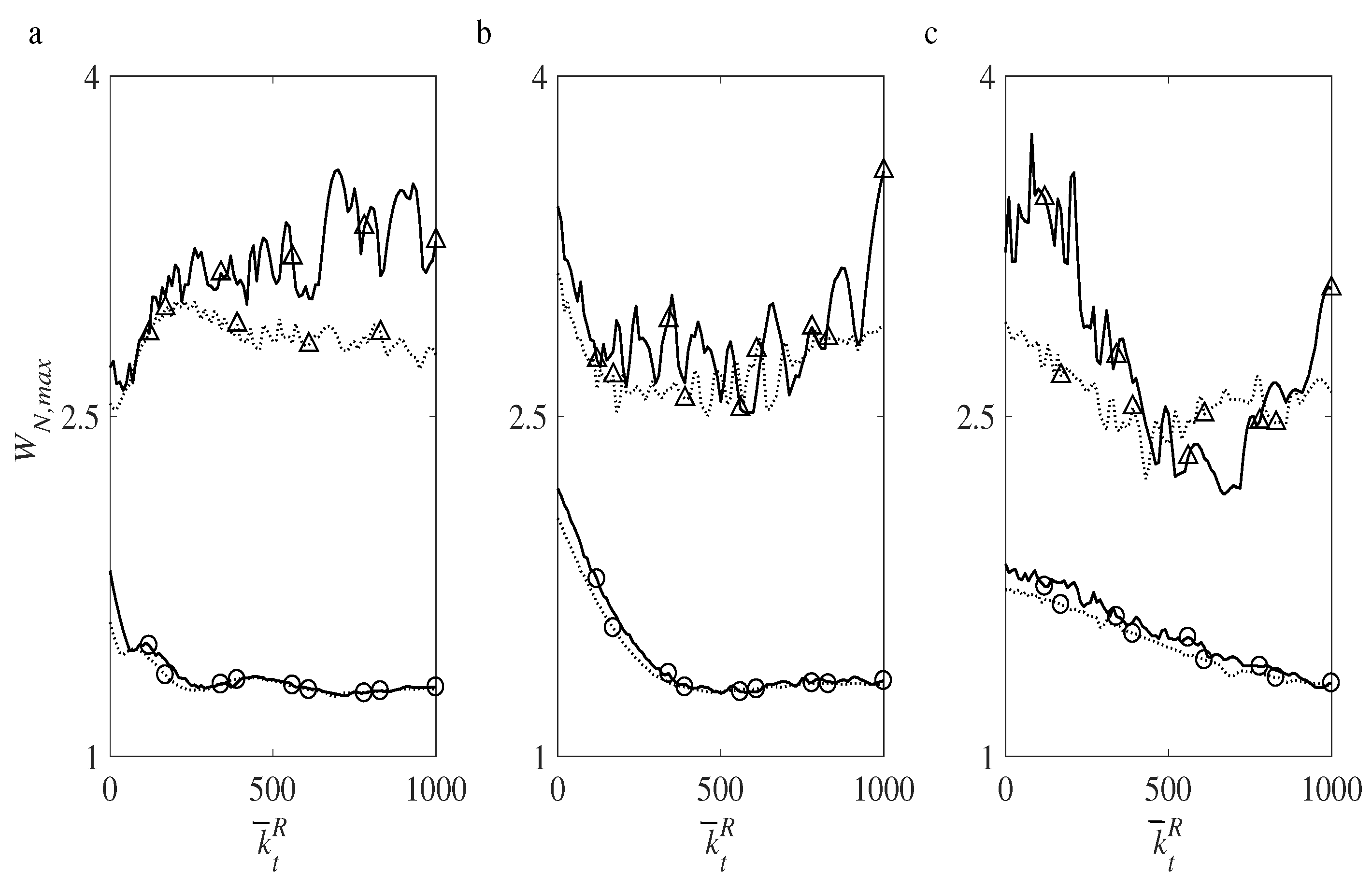
4.7. Influence of the Medium Excitation Parameters on the Maximum Deflection
4.8. Influence of the MNO’s Parameters on the Maximum Deflection
4.9. Influence of the Substrate Parameters on the Maximum Deflection
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube–polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Xie, S.; Li, W.; Pan, Z.; Chang, B.; Sun, L. Mechanical and physical properties on carbon nanotube. J. Phys. Chem. Solids 2000, 61, 1153–1158. [Google Scholar] [CrossRef]
- Oh, E.S. Elastic properties of boron-nitride nanotubes through the continuum lattice approach. Mater. Lett. 2010, 64, 859–862. [Google Scholar] [CrossRef]
- Santosh, M.; Maiti, P.K.; Sood, A.K. Elastic properties of boron nitride nanotubes and their comparison with carbon nanotubes. J. Nanosci. Nanotechnol. 2009, 9, 5425–5430. [Google Scholar] [CrossRef]
- Whitby, M.; Quirke, N. Fluid flow in carbon nanotubes and nanopipes. Nat. Nanotechnol. 2007, 2, 87–94. [Google Scholar] [CrossRef]
- Majumder, M.; Chopra, N.; Andrews, R.; Hinds, B.J. Enhanced flow in carbon nanotubes. Nature 2005, 438, 44. [Google Scholar] [CrossRef]
- Thomas, J.A.; McGaughey, A.J. Reassessing fast water transport through carbon nanotubes. Nano Lett. 2008, 8, 2788–2793. [Google Scholar] [CrossRef]
- Won, C.Y.; Aluru, N.R. Water permeation through a subnanometer boron nitride nanotube. J. Am. Chem. Soc. 2007, 129, 2748–2749. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Yang, R.Y. Fast transport of water molecules across carbon nanotubes induced by static electric fields. Chem. Phys. Lett. 2016, 644, 201–204. [Google Scholar] [CrossRef]
- Ezzati Nazhad Dolatabadi, J.; Omidi, Y.; Losic, D. Carbon nanotubes as an advanced drug and gene delivery nanosystem. Curr. Nanosci. 2011, 7, 297–314. [Google Scholar] [CrossRef]
- Pastorin, G.; Wu, W.; Wieckowski, S.; Briand, J.P.; Kostarelos, K.; Prato, M.; Bianco, A. Double functionalisation of carbon nanotubes for multimodal drug delivery. Chem. Commun. 2006, 11, 1182–1184. [Google Scholar] [CrossRef]
- Sun, X.; Su, X.; Wu, J.; Hinds, B.J. Electrophoretic transport of biomolecules through carbon nanotube membranes. Langmuir 2011, 27, 3150–3156. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chen, Q.; Liang, L.; Zhang, Z.; Wang, Q. Release of an encapsulated peptide from carbon nanotubes driven by electric fields: A molecular dynamics study. ACS Omega 2021, 6, 27485–27490. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Pang, P.; He, J.; Lindsay, S. Optical and electrical detection of single-molecule translocation through carbon nanotubes. ACS Nano 2013, 7, 689–694. [Google Scholar] [CrossRef]
- Jue, M.L.; Buchsbaum, S.F.; Chen, C.; Park, S.J.; Meshot, E.R.; Wu, K.J.J.; Fornasiero, F. Ultra-Permeable Single-Walled Carbon Nanotube Membranes with Exceptional Performance at Scale. Adv. Sci. 2020, 7, 2001670. [Google Scholar] [CrossRef] [PubMed]
- Joseph, S.; Aluru, N.R. Why are carbon nanotubes fast transporters of water? Nano Lett. 2008, 8, 452–458. [Google Scholar] [CrossRef]
- Pantarotto, D.; Briand, J.P.; Prato, M.; Bianco, A. Translocation of bioactive peptides across cell membranes by carbon nanotubes. Chem. Commun. 2004, 1, 16–17. [Google Scholar] [CrossRef] [PubMed]
- Bianco, A.; Kostarelos, K.; Prato, M. Applications of carbon nanotubes in drug delivery. Curr. Opin. Chem. Biol. 2005, 9, 674–679. [Google Scholar] [CrossRef]
- Liu, X.; Marangon, I.; Melinte, G.; Wilhelm, C.; Ménard-Moyon, C.; Pichon, B.P.; Ersen, O.; Aubertin, K.; Baaziz, W.; Pham-Huu, C.; et al. Design of covalently functionalized carbon nanotubes filled with metal oxide nanoparticles for imaging, therapy, and magnetic manipulation. ACS Nano 2014, 8, 11290–11304. [Google Scholar] [CrossRef]
- Gao, H.; Kong, Y.; Cui, D.; Ozkan, C.S. Spontaneous insertion of DNA oligonucleotides into carbon nanotubes. Nano Lett. 2003, 3, 471–473. [Google Scholar] [CrossRef]
- Chen, M.; Zang, J.; Xiao, D.; Zhang, C.; Liu, F. Nanopumping molecules via a carbon nanotube. Nano Res. 2009, 2, 938–944. [Google Scholar] [CrossRef]
- Arsawang, U.; Saengsawang, O.; Rungrotmongkol, T.; Sornmee, P.; Wittayanarakul, K.; Remsungnen, T.; Hannongbua, S. How do carbon nanotubes serve as carriers for gemcitabine transport in a drug delivery system? J. Mol. Graph. Model. 2011, 29, 591–596. [Google Scholar] [CrossRef]
- Xue, Q.; Jing, N.; Chu, L.; Ling, C.; Zhang, H. Release of encapsulated molecules from carbon nanotubes using a displacing method: A MD simulation study. RSC Adv. 2012, 2, 6913–6920. [Google Scholar] [CrossRef]
- Longhurst, M.J.; Quirke, N. Temperature-driven pumping of fluid through single-walled carbon nanotubes. Nano Lett. 2007, 7, 3324–3328. [Google Scholar] [CrossRef] [PubMed]
- Insepov, Z.; Wolf, D.; Hassanein, A. Nanopumping using carbon nanotubes. Nano Lett. 2006, 6, 1893–1895. [Google Scholar] [CrossRef] [PubMed]
- Xue, Q.; Xia, D.; Lv, C.; Jing, N.; Ling, C. Molecule delivery by the domino effect of carbon nanotubes. J. Phys. Chem. C. 2011, 115, 20471–20480. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C. Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 1972, 10, 425–435. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal elasticity and waves. In Continuum Mechanics Aspects of Geodynamics and Rock Fracture Mechanics, Proceedings of the NATO Advanced Study Institute, Reykjavik, Iceland, 11–20 August 1974; Springer: New York, NY, USA, 1974; pp. 81–105. [Google Scholar]
- Eringen, A.C. Vistas of nonlocal continuum physics. Int. J. Eng. Sci. 1992, 30, 1551–1565. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories. Appl. Mech. Rev. 2002, 56, B20–B22. [Google Scholar]
- Mindlin, R.D.; Eshel, N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Toupin, R.A. Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal. 1964, 17, 85–112. [Google Scholar] [CrossRef]
- Toupin, R. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, I.A. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. Effect of surface stress on wave propagation in solids. J. Appl. Phys. 1976, 47, 4414–4421. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M.; Zhang, Y.Y. Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J Appl. Phys. 2007, 101, 024305. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, H.; Sahmani, S. Calibration of the analytical nonlocal shell model for vibrations of double-walled carbon nanotubes with arbitrary boundary conditions using molecular dynamics. Int. J. Mech. Sci. 2011, 53, 786–792. [Google Scholar] [CrossRef]
- Huang, L.Y.; Han, Q.; Liang, Y.J. Calibration of nonlocal scale effect parameter for bending single-layered graphene sheet under molecular dynamics. Nano 2012, 7, 1250033. [Google Scholar] [CrossRef]
- Challamel, N.; Lerbet, J.; Wang, C.M.; Zhang, Z. Analytical length scale calibration of nonlocal continuum from a microstructured buckling model. Z. Angew. Math. Mech. 2014, 94, 402–413. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Challamel, N.; Reddy, J.N.; Wang, C.M. Eringen’s stress gradient model for bending of nonlocal beams. J. Eng. Mech. 2016, 142, 04016095. [Google Scholar] [CrossRef]
- Shaat, M.; Faroughi, S.; Abasiniyan, L. Paradoxes of differential nonlocal cantilever beams: Reasons and a novel solution. arXiv 2017, arXiv:1802.01494. [Google Scholar]
- Ke, L.L.; Xiang, Y.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Comp. Mater. Sci. 2009, 47, 409–417. [Google Scholar] [CrossRef]
- Yang, J.; Ke, L.L.; Kitipornchai, S. Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. Physica E 2010, 42, 1727–1735. [Google Scholar] [CrossRef]
- Kiani, K. Magnetically affected single-walled carbon nanotubes as nanosensors. Mech. Res. Commun. 2014, 60, 33–39. [Google Scholar] [CrossRef]
- Kiani, K. Free vibration of in-plane-aligned membranes of single-walled carbon nanotubes in the presence of in-plane-unidirectional magnetic fields. J. Vib. Control 2016, 22, 3736–3766. [Google Scholar] [CrossRef]
- Kiani, K. Longitudinally varying magnetic field influenced transverse vibration of embedded double-walled carbon nanotubes. Int. J. Mech. Sci. 2014, 87, 179–199. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, H.; Sahmani, S. Free vibration analysis of single-and double-walled carbon nanotubes based on nonlocal elastic shell models. J. Vib. Control 2014, 20, 670–678. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Yao, L.; Zhu, Z. Nonlocal theoretical approaches and atomistic simulations for longitudinal free vibration of nanorods/nanotubes and verification of different nonlocal models. Appl. Math. Model. 2015, 39, 4570–4585. [Google Scholar] [CrossRef]
- Kiani, K. Characterization of free vibration of elastically supported double-walled carbon nanotubes subjected to a longitudinally varying magnetic field. Acta Mech. 2013, 224, 3139–3151. [Google Scholar] [CrossRef]
- Rakrak, K.; Zidour, M.; Heireche, H.; Bousahla, A.A.; Chemi, A. Free vibration analysis of chiral double-walled carbon nanotube using nonlocal elasticity theory. Adv. Nano Res. 2016, 4, 031. [Google Scholar] [CrossRef]
- Rahmanian, M.; Torkaman-Asadi, M.A.; Firouz-Abadi, R.D.; Kouchakzadeh, M.A. Free vibrations analysis of carbon nanotubes resting on Winkler foundations based on nonlocal models. Physica B 2016, 484, 83–94. [Google Scholar] [CrossRef]
- Nikkhoo, A.; Zolfaghari, S.; Kiani, K. A simplified-nonlocal model for transverse vibration of nanotubes acted upon by a moving nanoparticle. J. Braz. Soc. Mech. Sci. 2017, 39, 4929–4941. [Google Scholar] [CrossRef]
- Dihaj, A.; Zidour, M.; Meradjah, M.; Rakrak, K.; Heireche, H.; Chemi, A. Free vibration analysis of chiral double-walled carbon nanotube embedded in an elastic medium using nonlocal elasticity theory and Euler Bernoulli beam model. Struct. Eng. Mech. 2018, 65, 335–342. [Google Scholar]
- Su, Y.C.; Cho, T.Y. Free vibration of a single-walled carbon nanotube based on the nonlocal Timoshenko beam model. J. Mech. 2021, 37, 616–635. [Google Scholar] [CrossRef]
- Kiani, K. Nonlocal and shear effects on column buckling of single-layered membranes from stocky single-walled carbon nanotubes. Compos. Part B-Eng. 2015, 79, 535–552. [Google Scholar] [CrossRef]
- Setoodeh, A.R.; Khosrownejad, M.; Malekzadeh, P. Exact nonlocal solution for postbuckling of single-walled carbon nanotubes. Physica E 2011, 43, 1730–1737. [Google Scholar] [CrossRef]
- Shen, H.S.; Zhang, C.L. Torsional buckling and postbuckling of double-walled carbon nanotubes by nonlocal shear deformable shell model. Compos. Struct. 2010, 92, 1073–1084. [Google Scholar] [CrossRef]
- Ansari, R.; Faghih Shojaei, M.; Mohammadi, V.; Gholami, R.; Rouhi, H. Buckling and postbuckling of single-walled carbon nanotubes based on a nonlocal Timoshenko beam model. Z. Angew. Math. Mech. 2015, 95, 939–951. [Google Scholar] [CrossRef]
- Jamali, M.; Shojaee, T.; Mohammadi, B. Analytical buckling and post-buckling characteristics of Mindlin micro composite plate with central opening by use of nonlocal elasticity theory. J. Comput. Appl. Mech. 2020, 51, 231–238. [Google Scholar]
- Malikan, M.; Uglov, N.S.; Eremeyev, V.A. On instabilities and post-buckling of piezomagnetic and flexomagnetic nanostructures. Int. J. Eng. Sci. 2020, 157, 103395. [Google Scholar] [CrossRef]
- Kiani, K. Elastic waves in uniformly infinite-periodic jungles of single-walled carbon nanotubes under action of longitudinal magnetic fields. J. Braz. Soc. Mech. Sci. 2019, 41, 418. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dehghan, M.; Seyfi, A. Eringen’s nonlocal elasticity theory for wave propagation analysis of magneto-electro-elastic nanotubes. Adv. Nano Res. 2019, 7, 1. [Google Scholar]
- Farajpour, M.R.; Shahidi, A.R.; Farajpour, A. Elastic waves in fluid-conveying carbon nanotubes under magneto-hygro-mechanical loads via a two-phase local/nonlocal mixture model. Mater. Res. Exp. 2019, 6, 0850a8. [Google Scholar] [CrossRef]
- Selvamani, R.; Tornabene, F.; Baleanu, D. Two phase local/nonlocal thermo elastic waves in a graphene oxide composite nanobeam subjected to electrical potential. Z. Angew. Math. Mech. 2023, 103, e202100390. [Google Scholar] [CrossRef]
- Su, Y.C.; Cho, T.Y. Wave propagation in an embedded single-walled carbon nanotube. Mech. Adv. Mater. Struct. 2023, 30, 2850–2862. [Google Scholar] [CrossRef]
- Farhadipour, F.; Mamandi, A. Nonlocal wave propagation analysis of a rotating nanobeam on a Pasternak foundation. J. Vib. Control 2023. [Google Scholar] [CrossRef]
- Kiani, K. Magneto-thermo-elastic fields caused by an unsteady longitudinal magnetic field in a conducting nanowire accounting for eddy-current loss. Mater. Chem. Phys. 2012, 136, 589–598. [Google Scholar] [CrossRef]
- Kiani, K. Nonlocal continuous models for forced vibration analysis of two- and three-dimensional ensembles of single-walled carbon nanotubes. Physica E 2014, 60, 229–245. [Google Scholar] [CrossRef]
- Trabelssi, M.; El-Borgi, S.; Fernandes, R.; Ke, L.L. Nonlocal free and forced vibration of a graded Timoshenko nanobeam resting on a nonlinear elastic foundation. Compos. Part B-Eng. 2019, 157, 331–349. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.F.; Zhu, W.D.; Li, Y.H.; Wan, X.S. Coupled thermoelastic nonlocal forced vibration of an axially moving micro/nano-beam. Int. J. Mech. Sci. 2021, 206, 106600. [Google Scholar] [CrossRef]
- Chen, B.; Lin, B.; Yang, Y.; Zhao, X.; Li, Y. Analytical solutions of nonlocal forced vibration of a functionally graded double-nanobeam system interconnected by a viscoelastic layer. Z. Naturforsch. A 2022, 77, 851–873. [Google Scholar] [CrossRef]
- Kaghazian, A.; Hajnayeb, A.; Foruzande, H. Free vibration analysis of a piezoelectric nanobeam using nonlocal elasticity theory. Struct. Eng. Mech. 2017, 61, 617–624. [Google Scholar] [CrossRef]
- Atanasov, M.S.; Stojanović, V. Nonlocal forced vibrations of rotating cantilever nano-beams. Euro. J. Mech.-A Solids 2020, 79, 103850. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Rahmani, O.; Bayat, S. Thermal effect on forced vibration analysis of FG nanobeam subjected to moving load by Laplace transform method. Mech. Based Des. Struct. 2023, 51, 3803–3822. [Google Scholar] [CrossRef]
- Ma, X.; Kiani, K. Spatially nonlocal instability modeling of torsionaly loaded nanobeams. Eng. Anal. Bound. Elem. 2023, 154, 29–46. [Google Scholar] [CrossRef]
- Ma, X.; Sahmani, S.; Safaei, B. Quasi-3D large deflection nonlinear analysis of isogeometric FGM microplates with variable thickness via nonlocal stress–strain gradient elasticity. Eng. Comput. 2022, 38, 3691–3704. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Rabczuk, T. Dynamics of two-dimensional functionally graded tapered Timoshenko nanobeam in thermal environment using nonlocal strain gradient theory. Compos. Part B-Eng. 2020, 182, 107622. [Google Scholar] [CrossRef]
- Kiani, K.; Mehri, B. Assessment of nanotube structures under a moving nanoparticle using nonlocal beam theories. J. Sound Vib. 2010, 329, 2241–2264. [Google Scholar] [CrossRef]
- Arani, A.G.; Roudbari, M.A. Nonlocal piezoelastic surface effect on the vibration of visco-Pasternak coupled boron nitride nanotube system under a moving nanoparticle. Thin Solid Film. 2013, 542, 232–241. [Google Scholar] [CrossRef]
- Kiani, K.; Wang, Q. On the interaction of a single-walled carbon nanotube with a moving nanoparticle using nonlocal Rayleigh, Timoshenko, and higher-order beam theories. Euro. J. Mech. A-Solids 2012, 31, 179–202. [Google Scholar] [CrossRef]
- Pourseifi, M.; Rahmani, O.; Hoseini, S.A. Active vibration control of nanotube structures under a moving nanoparticle based on the nonlocal continuum theories. Meccanica 2015, 50, 1351–1369. [Google Scholar] [CrossRef]
- Kiani, K.; Roshan, M. Nonlocal dynamic response of double-nanotube-systems for delivery of lagged-inertial-nanoparticles. Int. J. Mech. Sci. 2019, 152, 576–595. [Google Scholar] [CrossRef]
- Yu, G.; Kiani, K.; Roshan, M. Dynamic analysis of multiple-nanobeam-systems acted upon by multiple moving nanoparticles accounting for nonlocality, lag, and lateral inertia. Appl. Math. Model. 2022, 108, 326–354. [Google Scholar] [CrossRef]
- Hashemian, M.; Falsafioon, M.; Pirmoradian, M.; Toghraie, D. Nonlocal dynamic stability analysis of a Timoshenko nanobeam subjected to a sequence of moving nanoparticles considering surface effects. Mech. Mater. 2020, 148, 103452. [Google Scholar] [CrossRef]
- Roudbari, M.A.; Jorshari, T.D.; Arani, A.G.; Lü, C.; Rabczuk, T. Transient responses of two mutually interacting single-walled boron nitride nanotubes induced by a moving nanoparticle. Eur. J. Mech. A-Solids 2020, 82, 103978. [Google Scholar] [CrossRef]
- Jorshari, T.D.; Roudbari, M.A.; Scerrato, D.; Kouzani, A. Vibration suppression of a boron nitride nanotube under a moving nanoparticle using a classical optimal control procedure. Contin. Mech. Therm. 2019, 31, 1825–1842. [Google Scholar] [CrossRef]
- Rezapour, B.; Fariborzi Araghi, M.A.; Vázquez-Leal, H. Application of homotopy perturbation method for dynamic analysis of nanotubes delivering nanoparticles. J. Vib. Control 2021, 27, 802–814. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Khosravi, F.; Ghadiri, M. Effect of external moving torque on dynamic stability of carbon nanotube. J. Nano Res. 2020, 61, 118–135. [Google Scholar] [CrossRef]
- Rezapour, B.; Fariborzi Araghi, M.A. Nanoparticle delivery through single walled carbon nanotube subjected to various boundary conditions. Microsys. Technol. 2019, 25, 1345–1356. [Google Scholar] [CrossRef]
- Farajpour, M.R.; Shahidi, A.R.; Tabataba’i-Nasab, F.; Farajpour, A. Vibration of initially stressed carbon nanotubes under magneto-thermal environment for nanoparticle delivery via higher-order nonlocal strain gradient theory. Eur. Phys. J. Plus. 2018, 133, 1–5. [Google Scholar] [CrossRef]
- Salamat, D.; Sedighi, H.M. The effect of small scale on the vibrational behavior of single-walled carbon nanotubes with a moving nanoparticle. J. Appl. Comp. Mech. 2017, 3, 208–217. [Google Scholar]
- Pirmoradian, M.; Torkan, E.; Toghraie, D. Study on size-dependent vibration and stability of DWCNTs subjected to moving nanoparticles and embedded on two-parameter foundations. Mech. Mater. 2020, 142, 103279. [Google Scholar] [CrossRef]
- Kiani, K. Nonlocal continuum-based modeling of a nanoplate subjected to a moving nanoparticle. Part I: Theoretical formulations. Physica E 2011, 44, 229–248. [Google Scholar] [CrossRef]
- Pouresmaeeli, S.; Fazelzadeh, S.A.; Ghavanloo, E. Exact solution for nonlocal vibration of double-orthotropic nanoplates embedded in elastic medium. Compos. Part B-Eng. 2012, 43, 3384–3390. [Google Scholar] [CrossRef]
- Arani, A.G.; Kolahchi, R.; Gharbi Afshar, H. Dynamic analysis of embedded PVDF nanoplate subjected to a moving nanoparticle on an arbitrary elliptical path. J. Braz. Soc. Mech. Sci. 2015, 37, 973–986. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Hosseini-Hashemi, S. Dynamic response of biaxially loaded double-layer viscoelastic orthotropic nanoplate system under a moving nanoparticle. Int. J. Eng. Sci. 2017, 115, 51–72. [Google Scholar] [CrossRef]
- Pirmoradian, M.; Torkan, E.; Abdali, N.; Hashemian, M.; Toghraie, D. Thermo-mechanical stability of single-layered graphene sheets embedded in an elastic medium under action of a moving nanoparticle. Mech. Mater. 2020, 141, 103248. [Google Scholar] [CrossRef]
- Ejabati, S.M.; Fallah, N. Aerodynamic analysis of temperature-dependent FG-WCNTRC nanoplates under a moving nanoparticle using meshfree finite volume method. Eng. Anal. Bound. Elem. 2022, 134, 510–531. [Google Scholar] [CrossRef]
- Kiani, K. Nonlocal excitation and potential instability of embedded slender and stocky single-walled carbon nanotubes under harmonically vibrated matrix. Physica B 2017, 519, 26–38. [Google Scholar] [CrossRef]
- Nikkhoo, A.; Hassanabadi, M.E.; Azam, S.E.; Amiri, J.V. Vibration of a thin rectangular plate subjected to series of moving inertial loads. Mech. Res. Commun. 2014, 55, 105–113. [Google Scholar] [CrossRef]
- Nikkhoo, A.; Farazandeh, A.; Ebrahimzadeh Hassanabadi, M.; Mariani, S. Simplified modeling of beam vibrations induced by a moving mass by regression analysis. Acta Mech. 2015, 226, 2147–2157. [Google Scholar] [CrossRef]
- Ahmadi, M.; Nikkhoo, A. Utilization of characteristic polynomials in vibration analysis of non-uniform beams under a moving mass excitation. Appl. Math. Model. 2014, 38, 2130–2140. [Google Scholar] [CrossRef]
- Kiani, K.; Nikkhoo, A.; Mehri, B. Assessing dynamic response of multispan viscoelastic thin beams under a moving mass via generalized moving least square method. Acta Mech. Sin. 2010, 26, 721–733. [Google Scholar] [CrossRef]
- Şimşek, M. Vibration analysis of a single-walled carbon nanotube under action of a moving harmonic load based on nonlocal elasticity theory. Physica E 2010, 43, 182–191. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Y.; Zhang, Y.; Yang, J.; Kitipornchai, S. Vibrational characteristics of functionally graded graphene origami-enabled auxetic metamaterial beams based on machine learning assisted models. Aerosp. Sci. Technol. 2022, 130, 107906. [Google Scholar] [CrossRef]
- Gutub, A. Boosting image watermarking authenticity spreading secrecy from counting-based secretsharing. CAAI Trans. Intell. Technol. 2022, 8, 1–13. [Google Scholar]
- Hu, X.; Kuang, Q.; Cai, Q.; Xue, Y.; Zhou, W.; Li, Y. A Coherent pattern mining algorithm based on all contiguous column bicluster. J. Artif. Intell. Technol. 2022, 2, 80–92. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal. Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Zhang, Z.; De Luca, G.; Archambault, B.; Chavez, J.; Rice, B. Traffic dataset and dynamic routing algorithm in traffic simulation. J. Artif. Intell. Technol. 2022, 2, 111–122. [Google Scholar] [CrossRef]
- Li, Z.; Li, S. Recursive recurrent neural network: A novel model for manipulator control with different levels of physical constraints. CAAI Trans. Intell. Technol. 2023, 8, 622–634. [Google Scholar] [CrossRef]
- Jackson-Mills, G.; Barber, A.R.; Blight, A.; Pickering, A.; Boyle, J.H.; Kaddouh, B.; Richardson, R.C. Non-Assembly Walking Mechanism Utilizing a Hexapod Gait. J. Artif. Intell. Technol. 2022, 2, 158–163. [Google Scholar]


| MNFA | MNMA | |||||||
| 1 | 2 | 3 | 1 | 2 | 3 | |||
| 20 | NRABT | 1.846 | 3.671 | 5.497 | 1.896 | 3.685 | 5.517 | |
| (%2.86) | (%0.38) | (%0.36) | ||||||
| NREBT | 1.857 | 3.692 | 5.527 | 1.902 | 3.762 | 5.632 | ||
| (%2.42) | (%1.2) | (%1.9) | ||||||
| 50 | NRABT | 2.285 | 4.213 | 6.145 | 2.353 | 4.238 | 6.170 | |
| (%2.98) | (%0.59) | (%0.60) | ||||||
| NREBT | 2.297 | 4.219 | 6.150 | 2.345 | 4.296 | 6.266 | ||
| (%2.09) | (%1.83) | (%1.87) | ||||||
| 100 | NRABT | 5.169 | 6.998 | 8.859 | 5.212 | 7.024 | 8.953 | |
| (%0.83) | (%0.8) | (%1.06) | ||||||
| NREBT | 5.190 | 7.020 | 8.880 | 5.249 | 7.104 | 9.002 | ||
| (%1.14) | (%1.2) | (%1.37) | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Roshan, M.; Kiani, K.; Nikkhoo, A. Dynamic Response of an Elastic Tube-like Nanostructure Embedded in a Vibrating Medium and under the Action of Moving Nano-Objects. Symmetry 2023, 15, 1827. https://doi.org/10.3390/sym15101827
Ma X, Roshan M, Kiani K, Nikkhoo A. Dynamic Response of an Elastic Tube-like Nanostructure Embedded in a Vibrating Medium and under the Action of Moving Nano-Objects. Symmetry. 2023; 15(10):1827. https://doi.org/10.3390/sym15101827
Chicago/Turabian StyleMa, Xiaoxia, Mojtaba Roshan, Keivan Kiani, and Ali Nikkhoo. 2023. "Dynamic Response of an Elastic Tube-like Nanostructure Embedded in a Vibrating Medium and under the Action of Moving Nano-Objects" Symmetry 15, no. 10: 1827. https://doi.org/10.3390/sym15101827
APA StyleMa, X., Roshan, M., Kiani, K., & Nikkhoo, A. (2023). Dynamic Response of an Elastic Tube-like Nanostructure Embedded in a Vibrating Medium and under the Action of Moving Nano-Objects. Symmetry, 15(10), 1827. https://doi.org/10.3390/sym15101827







